Professor Diminoi
Atividade de 31/08/2020 até 04/09/2020
Fonte de pesquisa geral:
https://professordiminoi.comunidades.net/
Fonte de pesquisa específica:
https://professordiminoi.com.br/atividade-quarentena
7º Ano Ensino Fundamental - 3º bimestre de 2020 - Caderno do Aluno Volume 3/parte 1
Habilidade:
(EF07MA10) Ler, comparar e ordenar números racionais em diferentes contextos e associá-los a pontos da reta numérica.
(EF07MA16) Reconhecer se duas expressões algébricas obtidas para descrever a regularidade de uma mesma sequência numérica são ou não equivalentes.
Objeto de conhecimento:
- Números racionais na representação fracionária e na decimal: usos, ordenação e associação com pontos da reta numérica e operações.
- Equivalência de expressões algébricas: identificação da regularidade de uma sequência numérica.
Orientações: Observa o cronograma de entrega do Caderno do Aluno Volume 3 pela escola e não deixe de ir/ou pedir para o seu responsável retirar na secretaria da escola.
Estando de posse do seu Caderno do Aluno Volume 3 resolva no próprio Parte 1/2020 resolva as questões:
Página 68 as questões 1.1 e 1.2 e da página 69 a questão 1.1.
Após resolver estas questões, tire uma foto das páginas do seu caderno do Aluno com estas questões resolvidas e envie pelo Classroom até o dia 04/09/2020.
Se preferir, use seu caderno normal para fazer os cálculos, mas não precisa copiar o enunciado, apenas indique a página e questão de cada resolução e envie a foto pelo Classroom.
Observação: Essa atividade somente terá validade se for enviada pelo Classroom
Em caso de dívidas/esclarecimento fale com o professor Davi no particular pela paz.
Assista ao vídeo:
https://www.youtube.com/watch?v=8_bfWnbregU
O que são números racionais?
São elementos de um conjunto numérico formado por todos os números que podem ser escritos na forma de fração.

SITUAÇÃO DE APRENDIZAGEM 2 - ATIVIDADE 1 – OS NÚMEROS RACIONAIS NO COTIDIANO – Página 68
1.1 Resolução:
4/5 :1/20
4/1 . 1 .20
80/5
16
Resposta:16 barrinhas. A quantidade de barrinhas não será suficiente.
Observação: o fato de que ele só conseguiria colocar 4/5 do perímetro, já estava dado que a quantidade não é suficiente.
1.2 Resolução:
Como se trata de um estacionamento privativo com mais de 100 vagas, temos:
Deficientes: 2%
100 1200
2 D
100D – 1200 . 2
100D = 2400
D = 2400/100
D = 24
Motociclistas: 10%
100 1200
10 M
100M = 1200 . 10
100M = 12000
M = 12000/100
M = 120
Ciclistas: 7%
100 1200
7 C
100C = 1200 . 7
100C = 8400
C = 8400/100
C = 84
Resposta:
Serão destinadas, 24 vagas para deficientes; 120 vagas para motociclistas e 84 vagas para ciclistas.
SITUAÇÃO DE APRENDIZAGEM 3 - ATIVIDADE 1 – SEQUÊNCIAS NUMÉRICAS E EXPRESSÕES ALGÉBRICAS – Página 69
1.1 Carlos tinha R$ 300,00 quando, em janeiro de 2020, resolveu economizar dinheiro e fez uma tabela com o valor da economia total a cada mês.
|
Janeiro de 2020 |
Fevereiro de 2020 |
Março de 2020 |
Abril de 2020 |
Maio de 2020 |
Junho de 2020 |
Julho de 2020 |
Agosto de 2020 |
|
R$ 300,00 |
R$ 400,00 |
R$ 500,00 |
R$ 600,00 |
R$ 700,00 |
R$ 800,00 |
R$ 900,00 |
R$ 1 000,00 |
Qual quantia Carlos está economizando por mês?
Resolução:
Observando, existe uma regularidade a cada mês partindo do valor inicial, já para o mês seguinte existe um acréscimo de R$ 100,00.
a) Seguindo o mesmo padrão da sequência, qual será o total economizado até julho de 2 021?
Resolução:
Até julho, o total economizado será de R$ 2 100,00.
Nesse item, socialize as estratégias que os estudantes utilizaram para encontrar esse valor.
b) Escreva uma expressão algébrica que determine qual será o total economizado após n meses de economia, partindo de novembro de 2 020.
Resolução:
na = 300 + 100 (n−1)
na − valor do mês correspondente
n indica o mês: mês 1,mês 2,mês 3….ou seja a "posição"
300 − indica o primeiro termo, ou seja n = 1
100 − indica o valor economizado por mês
Atividade de 17/08/2020 até 21/08/2020
7º Ano Ensino Fundamental - 3º bimestre de 2020 - Caderno do Aluno Volume 3/parte 1
Habilidade: (EF07MA10) Ler, comparar e ordenar números racionais em diferentes contextos e associá-los a pontos da reta numérica.
Objeto de conhecimento:
- Números racionais na representação fracionária e na decimal: usos, ordenação e associação com pontos da reta numérica e operações.
Observação: Devido a maiorias das resoluções desta atividade ser figuras, não fou possível inserir as figuras aqui
Fonte de pesquisa:
https://professordiminoi.comunidades.net/
Fonte de pesquisa específica
https://professordiminoi.com.br/atividade-quarentena
Assistas aos vídeos-aulas:
Múltiplos de uma fração - Aula 1
https://www.youtube.com/watch?v=BqRbVKKVdbg&t=13s
Múltiplos de uma fração - Aula 21
https://www.youtube.com/watch?v=B0to8oWECLM&t=65s
Você ainda não recebeu o caderno do Aluno volume 3 portanto faça essa atividade no seu “caderno normal”
OREINTAÇÃO!
Após assistir aos vídeos 1 e 2, em seu “caderno normal” resolva as questões: 3.5(b e c), 3.6, e 3.7(a, b, c, e d).
Assista aos vídeos porque as questões 3.5(b e c), 3.6, e 3.7(a, b, c, e d) estão resolvidas nos dois vídeos.
Aí você vai assistindo e vídeo e posando o vídeo para ir copiar a resolução no seu “caderno normal”
Não precisa copiar o enunciado da questão, basta indicar cada questão e sua respectiva resolução.
Após feito isso, tire uma foto do “caderno normal” em envie pelo Classroom.
Observação 1: Essa atividade somente terá validade se for enviada pelo Classroom.
Em caso de dúvidas, fale com o professor Davi no particular pelo zap.
3.5 Represente, geometricamente, os produtos entre os números racionais a seguir, explicando os procedimentos para encontrá-los.
b) 3/4 . 1/3
Resolução:
c) 2/3 . 1/5
Resolução:
3.6 Sem utilizar a representação geométrica, como você faria a multiplicação: 35 𝑥 78? Explique como deve ser o procedimento para multiplicar frações.
Resolução:
(3/5) . (7/8) = 21/40
Na multiplicação de frações, multiplica-se o numerador da primeira fração pelo numerador da segunda fração. Em relação aos denominadores, segue o mesmo procedimento.
3.7 “Quanto é 2/3 de 9?”. Isso significa que esta operação é a divisão de 9 em 3 partes iguais, e tomamos 2 delas, ou seja:
- Divide-se 9 em 3 partes iguais: 9 : 3 = 3
-Toma-se duas dessas partes: 2 . 3 = 6, logo 2/3 de 9 = 6
Seguindo essa interpretação, resolva as multiplicações a seguir:
a) 5/6 de 18
Resolução:
Divide-se 18 em 6 partes iguais: 18 ÷ 6 = 3
Toma-se cinco dessas partes: 5 . 3 = 6
ou
5/6 . 18 = 90/6 = 15
b) 1/4 de 64
Resolução:
Divide-se 60 em 4 partes iguais: 60 ∶ 4 = 15
Toma-se uma dessas partes: 1 . 15 =15
ou
1/4 . 64 = 64/4 = 15
c) 1/5 de 10
Resolução:
Divide-se 10 em 5 partes iguais: 10 : 5 = 2
Toma-se uma dessas partes: 1 . 2 = 2
ou
1/5 . 10 = 10/5 = 2
d) 2/3 de 90
Resolução:
Divide-se 90 em 3 partes iguais: 90 : 3 = 30
Toma-se duas dessas partes: 2 . 30 = 60
ou
2/3 . 90 = 180/3 = 60
4.1 Carlos pretendia caminhar 2/3 de uma pista de corrida, porém acabou caminhando apenas 1/4 do trecho pretendido. Como podemos descobrir que fração da pista ele percorreu?
Resolução:
Para descobrir a fração relativa à pista toda, vamos dividi-la em partes iguais.
Você poderá encontrar uma maneira diferente para realizar esse cálculo. Você poderá optar pela multiplicação entre os numeradores e entre os denominadores.
4.2 Represente na reta numérica a multiplicação 1/4 de 3/5.
Resolução:
Atividade de 10/08/2020 até 14/08/2020
7º Ano Ensino Fundamental - 3º bimestre de 2020 - Caderno do Aluno Volume 3/parte 1
Habilidade: (EF07MA10) Ler, comparar e ordenar números racionais em diferentes contextos e associá-los a pontos da reta numérica.
(EF07MA11) Compreender e utilizar a multiplicação e a divisão de números racionais, a relação entre elas e suas propriedades operatórias.
Objeto de conhecimento:
- Números racionais na representação fracionária e na decimal: usos, ordenação e associação com pontos da reta numérica e operações.
- Números racionais na representação fracionária e na decimal: usos, ordenação e associação com pontos da reta numérica e operações.
Fonte de pesquisa:
https://professordiminoi.comunidades.net/
Fonte de pesquisa específica
https://professordiminoi.com.br/atividade-quarentena
Assistas aos vídeos-aulas:
Os números e suas diferentes representação - Aula 1
https://www.youtube.com/watch?v=w7wzbA-pedU
Os números e suas diferentes representação - Aula 2
https://www.youtube.com/watch?v=B0to8oWECLM&t=16s
ORIENTAÇÕES: Resolva as questões solicitados a seguir no próprio Caderno do Aluno Volume 3/parte 1.
Após efetuar essa orientação, tire uma foto em envie pelo zap para o professor Davi
Em caso de dúvidas, chame o professor Davi no particular
Observação: Sua entrega de atividade somente terá validade se você enviar também pelo Classroom.
SITUAÇÃO DE APRENDIZAGEM 1– Página 63.
ATIVIDADE 1 – OS NÚMEROS E SUAS DIFERENTES REPRESENTAÇÕES


É comum também, quando falamos de valores monetários, usar as abreviações "mi", "bi" e "tri".
Exemplos:
- O Hospital das Clínicas arrecadou R$ 1,2 mi para compra de máscaras.
- A emenda individual para o orçamento será de R$ 10 mi.
- O time do Barcelona custa mais de R$ 2 bi por ano.
1.1 Os números estão por toda parte e, conforme o contexto, apresentam-se em diferentes representações. Um site publicou a seguinte notícia: “Robôs realizam R$ 1,2 mi em vendas online durante as 24 horas de oferta”. Reescreva esta notícia substituindo a representação do valor R$ 1,2 mi pela sua representação equivalente até a ordem das unidades simples.
Resposta:
“Robôs realizam R$ 1.200.000,00 (um milhão e duzentos mil) em vendas online durante as 24 horas de oferta”.
1.2 Na pasta de receitas de sua mãe, Mariana encontrou duas anotações da receita de Bolo de Chocolate com Morango e ficou sem saber qual utilizar.
Receita A
Bolo de Chocolate com Morango
5 ovos
1/2 xícara de açúcar
1 xícara de farinha de trigo
3 colheres de chocolate em pó
3/4 kg de chocolate ao leite picado
1 lata de creme de leite
2/5 kg de morango lavado
1/2 xícara de leite
1 colher de fermento
Receita B
Bolo de Chocolate com Morango
5 ovos
0,5 xícara de açúcar
1 xícara de farinha de trigo
3 colheres de chocolate em pó
0,75 kg de chocolate ao leite picado
1 lata de creme de leite
0,4 kg de morango lavado
0,5 xícara de leite
1 colher de fermento
Explique para Carla se há diferença entre as duas receitas. Os números apresentados nas duas receitas têm alguma relação?
Resposta:
Não existe diferença entre as duas receitas. Os números apresentados nas duas receitas representam a mesma quantidade, ou seja, 1/2 = 0,5, 3/4 = 0,75 e 2/5 = 0,4. É importante os diferentes tipos de registro de representação dos números racionais e como fazer a conversão entre diferentes representações de um mesmo número racional. Uma possibilidade é o uso da calculadora.
ATIVIDADE 2: EQUIVALÊNCIA – Página 63.
2.1 Junte-se a um colega e analisem os dois blocos de números. Considerando os conhecimentos que já possuem, o que os números do Bloco A têm em comum? E os do Bloco B?
Bloca A: 1/2, 2/4, 3/6, 4/8, 5/10, 6/12, 10/20, 50/100
Resolução:
No Bloco A todas as frações são equivalentes a 1/2
Bloca B: 1/3, 2/6, 3/9, 4/12, 5/15, 6/18, 10/30, 50/150
Resolução:
No Bloco B todas as frações são equivalentes a 1/3
2.2 Usando uma calculadora, converta esses números racionais representados na forma de fração dos Blocos A e B para sua representação decimal. O que eles têm em comum?
Resposta:
A representação decimal no Bloco A corresponde a 0,5. A representação decimal no Bloco B corresponde a 0,333... Os estudantes podem observar que esses números são escritos com vírgula, separando a parte inteira da parte decimal.
2.3 Cláudia decidiu fazer um painel para estudar as frações equivalentes. Iniciou a construção de um painel com tiras, indicando as frações: 1/2 , 1/5 , 1/8 e coloriu cada uma delas. Com seu conhecimento sobre as frações, continue a divisão do painel para as demais frações. (o quadro já está completo, números em vermelho)
|
1 inteiro |
|||||||||||||||||||||||||||||||||
|
1/2 |
1/2 |
1/2 |
|||||||||||||||||||||||||||||||
|
1/3 |
1/3 |
1/3 |
1/3 |
||||||||||||||||||||||||||||||
|
1/4 |
1/4 |
1/4 |
1/4 |
1/4 |
|||||||||||||||||||||||||||||
|
1/5 |
1/5 |
1/5 |
1/5 |
1/5 |
1/5 |
||||||||||||||||||||||||||||
|
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
11/6 |
|||||||||||||||||||||||||||
|
1/7 |
1/7 |
1/7 |
1/7 |
1/7 |
1/7 |
1/7 |
1/7 |
1/7 |
|||||||||||||||||||||||||
|
1/8 |
1/8 |
1/8 |
1/8 |
1/8 |
1/8 |
1/8 |
1/8 |
1/8 |
|||||||||||||||||||||||||
|
1/9 |
1/9 |
1/9 |
1/9 |
1/9 |
1/9 |
1/9 |
1/9 |
1/9 |
1/9 |
||||||||||||||||||||||||
|
1/10 |
1/10 |
1/10 |
1/10 |
1/10 |
1/10 |
1/10 |
1/10 |
1/10 |
1/10 |
1/10 |
|||||||||||||||||||||||
2.4 A partir do painel que você construiu, escolha uma fração entre 1/4 e 3/4. Como você fez para encontrar esse número?
Resposta:
A fração entre 1/4 e 3/4 escolhida é 1/2, pois 1/4 = 0,25 e 3/4 = 0,75, logo 1/2 = 0,5. A explicação de como o estudante encontrou é pessoal, mas compartilhe algumas estratégias diferentes.
2.5 Explore o painel e escolha frações que representam a mesma parte do inteiro. Justifique sua escolha.
Resposta:
A resposta é pessoal, então socialize as possíveis soluções, escolhendo alguns estudantes para apresentarem como realizaram a atividade.
2.6 As frações 2/3 e 8 /x são equivalentes. Determine o valor de x para que essa afirmação seja verdadeira.
Resposta:
(2 . 4) / (3 . 4) = 8/x
x = 12
2.7 Para cada fração dada, encontre três frações equivalentes. Encontrem uma maneira eficiente para escrever essas frações:
a) 4/5
Resposta:
a) 4/5 = 8/10 = 16/20 = 32/40
b) 2/3
Resposta:
2/3 = 4/6 = 8/12 = 16/24
c) 120/180
Resposta:
120/180 = 240/360 = 480/720 = 960/1440
d) 78/16
Resposta:
78/16 = 156/32 = 312/64 = 624/128
2.8 Localize as frações a seguir na reta numérica: 2/5, 1/4, 3/6, 3/4, 5/10. Explique como fez para localizá-las.
Resposta:
Efetuando as divisões de cada uma das frações.
Ponto D: 2/5 = 0,25.
Ponto C: 1/4 = 0,4.
Ponto D: 3/6,
Ponto E: 3/4 = 0,5.
Ponto F: 5/10 = 075.
Atividade de 20/07/2020 até 24/07/2020
https://professordiminoi.comunidades.net/
Instagram: @prof_diminoi
Pesquise: https://professordiminoi.com.br/7-caderno-do-anulo-volume-1
Vídeos-aulas:
Sequência – Aula 1
https://www.youtube.com/watch?v=c_F5k9tDQoM
Sequência – Aula 2
https://www.youtube.com/watch?v=_4LNumsnRfg
Pesquisa específica:
https://professordiminoi.com.br/atividade-quarentena
7º Ano - Ensino Fundamental - 2º bimestre/2020.
Observação 1: Assista aos vídeos de pose com o Caderno do Aluno Volume 2 Patre1/2020. Após assistir os vídeos resolva as questões no próprio caderno do aluno.
Após resolver as questões solicitadas nesta atividade, tire uma foto das páginas correspondentes as questões e envie uma foto para o professor Davi.
Observação 2: Essa atividade deve ser entregue até o dia 24/07/2020.
Álgebra
Habilidade - (EF08MA10): Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.
Objeto de conhecimento: Sequências recursivas e não recursivas
Objetivo: Classificar sequências como recursivas ou não recursivas. Determinar a “regra de formação” para uma sequência e descobrir os próximos termos de uma sequência.
SITUAÇÃO DE APRENDIZAGEM 4 – Página 73.
ATIVIDADE 2 – CLASSIFICANDO SEQUÊNCIAS E ESTABELECENDO PADRÕES – Página 75.
A ordem dos elementos de uma sequência pode caracterizar um padrão, por isso, ao mudar a ordem de qualquer elemento, teremos uma nova sequência. Passaremos a designar os elementos da sequência por “termos de uma sequência” e padrão por “regras de formação”.
Sequência não recursiva.
As sequências não recursivas são aquelas que não dependem de termos anteriores para determinarmos o próximo termo, pode-se determinar o valor de um elemento da sequência apenas pela sua posição.
Sequência recursiva.
Uma sequência é dita recursiva ou recorrente quando um determinado termo pode ser calculado em função de termos antecessores.
Alguns tipos de sequencia
Ao representarmos uma sequência numérica, devemos colocar seus elementos entre parênteses. Veja alguns exemplos de sequências numéricas:
(2, 4, 6, 8, 10, 12, ... ) é uma sequência de números pares positivos.
(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11...) é uma sequência de números naturais.
(10, 20, 30, 40, 50...) é uma sequência de números múltiplos de 10.
(10, 15, 20, 30) é uma sequência de números múltiplos de 5, maiores que cinco e menores que 35.
2.1. Veja as sequências de figuras. Quais os três próximos termos? Explique a “regra de formação” que você utilizou.
a) ![]()
![]()
![]()
![]() _____ _____ _____
_____ _____ _____
Resolução:
(boneco , coração, boneco) – padrão boneco, coração.
b) ![]()

![]() _____ _____ _____
_____ _____ _____
Resolução:
(sol, lua, raio) - padrão raio, sol, lua.
2.2. Na sequência (1, 2, 3, 4, 5, 6, ...), indique quais serão os dois próximos termos e explique por quê.
Resolução:
(1, 2, 3, 4, 5, 6, 7, 8, ...): sequência dos números naturais. Padrão: soma-se uma unidade ao termo anterior para encontrar o próximo termo.
2.3. Escreva a sequência dos números naturais menores que 8 e classifique-a como finita ou infinita.
Resolução:
(0, 1, 2, 3, 4, 5, 6, 7): finita, pois possui uma quantidade determinada de termos.
2.4. Observe a sequência numérica infinita: (2,5,8,11,14, ...). Qual é sua regra de formação?
Resolução:
Note que podemos estabelecer uma regra de formação para definir seus termos: “a partir do primeiro termo obtemos os próximos somando 3 unidades”.
(2, 2+3, 5+3, 8+3, 11+3, ...)
2.5. Descubra qual é a regra de formação e encontre até o oitavo termo de cada sequência.
a) (20, 15, 10, 5, ...)
Resolução:
(20, 15, 10, 5, 0, -5, -10, -15)
Regra: Para encontrar o próximo termo, subtrai-se 5 unidades do anterior.
b) (6, 2, - 2, - 6, - 10, - 14, ...)
Resolução:
(6, 2, -2, -6, -10, -14, -18, -22)
Regra: Para encontrar o próximo termo, subtrai-se 4 unidades do anterior.
c) (1, 4 ,9,16, 25 ...)
Resolução:
(1, 4, 9, 16, 25, 36, 64, 81)
Regra: sequência dos quadrados dos oito primeiros números naturais.
Observação: A questão 2.6 já está com respostas decido ao nível de complexidade.
2.6. Complete a sequência finita com 5 termos, descobrindo a regra de formação, e registre-a:
a) Adicione 4 ao termo anterior. (___, 5, ___, ___, ___)
Resolução:
(1, 5, 9, 13, 17)
b) Multiplique o termo anterior por 3 e subtraia 2. (___, ___, 10, ___, ___)
Resolução:
(1, 5, 9, 13, 17)
c) Divida o termo anterior por 2. (2, ___, ___, ___, ___)
Resolução:
(2, 1, 1/2, 1/4, 1/8)
d) Eleve o termo anterior ao quadrado e divida por 2. (2, ___, ___, ___, ___)
Resolução:
(2, 2, 2, 2, 2)
2.7. Nas sequências abaixo, classifique-as como recursivas ou não recursivas, justificando a sua resposta.
a) (11, 21, 31, 41, ...)
Resolução:
Recursiva, pois ao termo anterior soma-se 10 unidades para se obter o próximo.
b) (8, 8, 13, 12, 13, 10, 9, ...)
Resolução:
Não recursiva, pois não conseguimos estabelecer um padrão, uma regra para formação da sequência.
c) (2, 3, 5, 7, 11, 13, 17, ...)
Resolução:
Não recursiva, pois não conseguimos estabelecer um padrão, uma regra para a formação da sequência.
d) (-6, -3, 0, 3, 6, ...)
Resolução:
Recursiva, pois ao termo anterior soma-se 3 unidades para se obter o próximo.
Atividade de 13/07/2020 até 17/07/2020
Professor Diminoi
https://professordiminoi.comunidades.net/
Instagram: @prof_diminoi
Pesquise: https://professordiminoi.com.br/7-caderno-do-anulo-volume-1
Entre no canal do professor Diminoi, escolha o tema e assista aos vídeos acessando:
https://www.youtube.com/channel/UCHqQ9sNGyaR4Caxi0rfTH3g
Assista aos vídeos-aulas:
Plano cartesiano – Aula 1
https://www.youtube.com/watch?v=mzH9XbCQPhU
Plano cartesiano – Aula 2
https://www.youtube.com/watch?v=lNDeF84tJHg
Observação:
Querido(a) aluno(a), você deve resolver direto no Caderno do Aluno Volume 2/2020 – Parte 1. As questões:
1.1. da Página 68.
2.4. da Página 70.
Após resolver estas duas questões, você tire uma foto e envie até o dia 17/07/2020.
7º Ano – Ensino Fundamental – 2º bimestre /2020
Habilidade: (EF07MA19) Localizar no plano cartesiano pontos (coordenadas) que representam os vértices de um polígono e realizar transformações desses polígonos, decorrentes da multiplicação das coordenadas de seus vértices por um número inteiro.
Objeto de conhecimento: Transformações geométricas de polígonos no plano cartesiano: multiplicação das coordenadas por um número inteiro e obtenção de simétricos em relação aos eixos e à origem.
PLANO CARTESIANO
Conteúdo - SITUAÇÃO DE APRENDIZAGEM 3
ATIVIDADE 1 – QUAL É A LOCALIZAÇÃO? - Conteúdo da página 68, 69 e 70.
Plano cartesiano
O plano cartesiano recebeu esse nome por ter sido idealizado por René Descartes e é usado fundamentalmente para sistematizar técnicas de localização no plano.
O plano cartesiano é formado por duas dessas retas:
Uma responsável pela coordenada horizontal e outra responsável pela coordenada vertical. É comum usar as letras x para a primeira e y para a segunda e os termos “coordenada x” e “coordenada y”.

Plano cartesiano com destaque para a abcissa e a ordenada
Pares ordenados e localizações no plano
Um par ordenado é formado por dois números reais que representam uma coordenada. A ordem escolhida é a seguinte: Primeiro vêm as coordenadas x e, depois, as coordenadas y, que são colocadas entre parênteses para representar uma localização qualquer.
Exemplo:
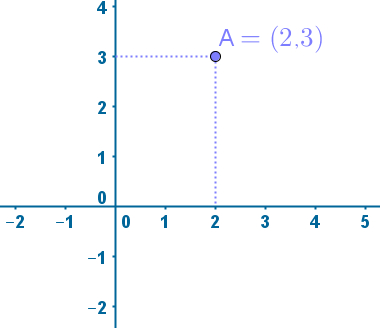
Observação: Os exercícios 01, 02, 03 e 04 a seguir não estão no seu Caderno do Aluno. São exercícios que eu formulei para aprendermos para resolver nas vídeo-aulas e aprendermos como trabalhar com Plano cartesiano.
01) No plano cartesiano a seguir, marque a localização dos pontos A, B, C e D.
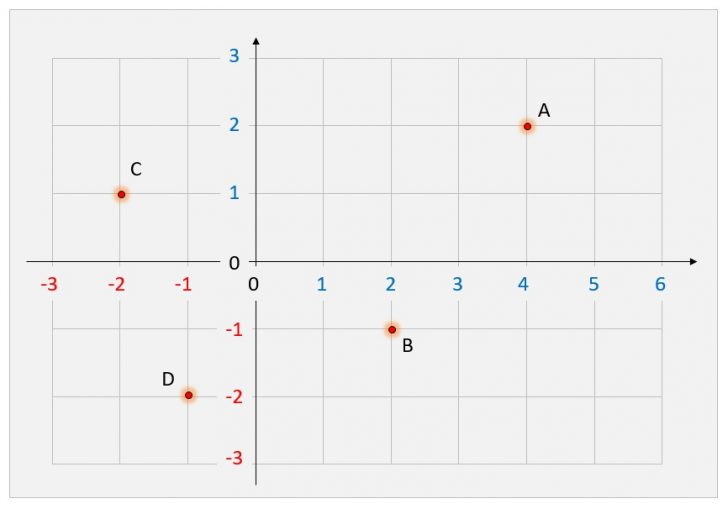
Resolução:
A (4, 2)
B (2, -1)
C (-2, 1)
D (-1, -2)
02) Observe o plano cartesiano abaixo e indique as coordenadas dos pontos A e B.

Resolução:
A (0, 4)
B (4, 4)
C (4, 0)
D (2, 2)
E (0, 2)
04) Observe o plano cartesiano a seguir e indique as coordenadas da piscina, vestiário feminino, quadra de tênis, vestiário masculino e o ginásio
Resolução:
Piscina (3, 5)
Vestiário feminino (1, 4)
Quadra de tênis (5, 3)
Vestiário masculino (2, 3)
Ginásio (2, 1)
SITUAÇÃO DE APRENDIZAGEM 3
ATIVIDADE 1 – QUAL É A LOCALIZAÇÃO?
Página 68.
1.1. Um game apresenta, na sua tela inicial, um instante de um jogo de futebol feminino e as posições de algumas jogadoras. Para facilitar as suas localizações, foi imaginado um Plano Cartesiano com dois eixos, o das abscissas e o das ordenadas, graduados com números inteiros.
Observe com atenção a figura abaixo e escreva as coordenadas referentes a cada posição das jogadoras, conforme o exemplo: As coordenadas da posição da jogadora Ana são representadas pelo par ordenado (-4, -3), lembrando que o primeiro número do par ordenado se refere ao valor de onde a jogadora se encontra em relação ao eixo das abscissas, e o segundo número refere-se ao valor em relação ao eixo das ordenadas. O conjunto dos dois valores resulta na posição exata onde ela se encontra.

Figura no Caderno do Aluno Volume 2 Patre1/2020
a) Dê a localização de cada jogadora por meio de suas coordenadas.
Resolução:
Ivana (-9, 1)
Ana (-4, -3)
Karla (-2, 3)
Luísa (3, -5)
Marta (4, 2); Joana (8, -3).
b) Para ajudar suas companheiras, as jogadoras Ana e Karla devem avançar 3 unidades para a direita e em linha reta, enquanto Joana precisa voltar 2 unidades para a esquerda e em linha reta. Quais serão suas novas coordenadas?
Resolução:
Ana (-1, -3)
Karla (1, 3)
Joana (6, -3).
SITUAÇÃO DE APRENDIZAGEM 3
ATIVIDADE 1 – QUAL É A LOCALIZAÇÃO?
Página 70
2.4.. No Plano Cartesiano abaixo está representado o polígono AVE.

Figura no Caderno do Aluno Volume 2 Patre1/2020
a) Multiplique a abscissa dos vértices por (-1), reescreva as novas coordenadas e represente-as no Plano Cartesiano acima. Explique o que ocorreu.
Resolução:
A’ (-1,1); B’( -2,3); C’(-3,2) . Os alunos devem descobrir que, ao multiplicar a abscissa dos vértices de um polígono por um número negativo, provocamos uma transformação chamada de reflexão em relação ao eixo das ordenadas.
b) Multiplique ordenada dos vértices por (-1), reescreva as novas coordenadas e represente-as no Plano Cartesiano acima. Explique o que ocorreu.
Resolução:
A’’ (1,-1); B’’(2,-3); C’’(3,-2)
Descobrimos também que, ao multiplicar a ordenada dos vértices de um polígono por um número negativo, provocamos uma transformação chamada de reflexão em relação ao eixo das abscissas.
Atividade de 13/07/2020 até 17/07/2020
Professor Diminoi
https://professordiminoi.comunidades.net/
Instagram: @prof_diminoi
Pesquise: https://professordiminoi.com.br/7-caderno-do-anulo-volume-1
Entre no canal do professor Diminoi, escolha o tema e assista aos vídeos acessando:
https://www.youtube.com/channel/UCHqQ9sNGyaR4Caxi0rfTH3g
Assista aos vídeos-aulas:
Plano cartesiano – Aula 1
https://www.youtube.com/watch?v=mzH9XbCQPhU
Plano cartesiano – Aula 2
https://www.youtube.com/watch?v=ULZtuE6eXL0
Observação:
Querido(a) aluno(a), você deve resolver direto no Caderno do Aluno Volume 2/2020 – Parte 1. As questões:
1.1. da Página 68.
2.4. da Página 70.
Após resolver estas duas questões, você tire uma foto e envie até o dia 17/07/2020.
7º Ano – Ensino Fundamental – 2º bimestre /2020
Habilidade: (EF07MA19) Localizar no plano cartesiano pontos (coordenadas) que representam os vértices de um polígono e realizar transformações desses polígonos, decorrentes da multiplicação das coordenadas de seus vértices por um número inteiro.
Objeto de conhecimento: Transformações geométricas de polígonos no plano cartesiano: multiplicação das coordenadas por um número inteiro e obtenção de simétricos em relação aos eixos e à origem.
PLANO CARTESIANO
Conteúdo - SITUAÇÃO DE APRENDIZAGEM 3
ATIVIDADE 1 – QUAL É A LOCALIZAÇÃO? - Conteúdo da página 68, 69 e 70.
Plano cartesiano
O plano cartesiano recebeu esse nome por ter sido idealizado por René Descartes e é usado fundamentalmente para sistematizar técnicas de localização no plano.
O plano cartesiano é formado por duas dessas retas:
Uma responsável pela coordenada horizontal e outra responsável pela coordenada vertical. É comum usar as letras x para a primeira e y para a segunda e os termos “coordenada x” e “coordenada y”.

Plano cartesiano com destaque para a abcissa e a ordenada
Pares ordenados e localizações no plano
Um par ordenado é formado por dois números reais que representam uma coordenada. A ordem escolhida é a seguinte: Primeiro vêm as coordenadas x e, depois, as coordenadas y, que são colocadas entre parênteses para representar uma localização qualquer.
Exemplo:

Observação: Os exercícios 01, 02, 03 e 04 a seguir não estão no seu Caderno do Aluno. São exercícios que eu formulei para aprendermos para resolver nas vídeo-aulas e aprendermos como trabalhar com Plano cartesiano.
01) No plano cartesiano a seguir, marque a localização dos pontos A, B, C e D.

Resolução:
A (4, 2)
B (2, -1)
C (-2, 1)
D (-1, -2)
02) Observe o plano cartesiano abaixo e indique as coordenadas dos pontos A e B.

Resolução:
A (0, 4)
B (4, 4)
C (4, 0)
D (2, 2)
E (0, 2)
04) Observe o plano cartesiano a seguir e indique as coordenadas da piscina, vestiário feminino, quadra de tênis, vestiário masculino e o ginásio
Resolução:
Piscina (3, 5)
Vestiário feminino (1, 4)
Quadra de tênis (5, 3)
Vestiário masculino (2, 3)
Ginásio (2, 1)
SITUAÇÃO DE APRENDIZAGEM 3
ATIVIDADE 1 – QUAL É A LOCALIZAÇÃO?
Página 68.
1.1. Um game apresenta, na sua tela inicial, um instante de um jogo de futebol feminino e as posições de algumas jogadoras. Para facilitar as suas localizações, foi imaginado um Plano Cartesiano com dois eixos, o das abscissas e o das ordenadas, graduados com números inteiros.
Observe com atenção a figura abaixo e escreva as coordenadas referentes a cada posição das jogadoras, conforme o exemplo: As coordenadas da posição da jogadora Ana são representadas pelo par ordenado (-4, -3), lembrando que o primeiro número do par ordenado se refere ao valor de onde a jogadora se encontra em relação ao eixo das abscissas, e o segundo número refere-se ao valor em relação ao eixo das ordenadas. O conjunto dos dois valores resulta na posição exata onde ela se encontra.

Figura no Caderno do Aluno Volume 2 Patre1/2020
a) Dê a localização de cada jogadora por meio de suas coordenadas.
Resolução:
Ivana (-9, 1)
Ana (-4, -3)
Karla (-2, 3)
Luísa (3, -5)
Marta (4, 2); Joana (8, -3).
b) Para ajudar suas companheiras, as jogadoras Ana e Karla devem avançar 3 unidades para a direita e em linha reta, enquanto Joana precisa voltar 2 unidades para a esquerda e em linha reta. Quais serão suas novas coordenadas?
Resolução:
Ana (-1, -3)
Karla (1, 3)
Joana (6, -3).
SITUAÇÃO DE APRENDIZAGEM 3
ATIVIDADE 1 – QUAL É A LOCALIZAÇÃO?
Página 70
2.4.. No Plano Cartesiano abaixo está representado o polígono AVE.
 Figura no Caderno do Aluno Volume 2 Patre1/2020
Figura no Caderno do Aluno Volume 2 Patre1/2020
a) Multiplique a abscissa dos vértices por (-1), reescreva as novas coordenadas e represente-as no Plano Cartesiano acima. Explique o que ocorreu.
Resolução:
A’ (-1,1); B’( -2,3); C’(-3,2) . Os alunos devem descobrir que, ao multiplicar a abscissa dos vértices de um polígono por um número negativo, provocamos uma transformação chamada de reflexão em relação ao eixo das ordenadas.
b) Multiplique ordenada dos vértices por (-1), reescreva as novas coordenadas e represente-as no Plano Cartesiano acima. Explique o que ocorreu.
Resolução:
A’’ (1,-1); B’’(2,-3); C’’(3,-2)
Descobrimos também que, ao multiplicar a ordenada dos vértices de um polígono por um número negativo, provocamos uma transformação chamada de reflexão em relação ao eixo das abscissas.
Atividade de 29/06/2020 até 03/07/2020
Professor Diminoi
https://professordiminoi.comunidades.net/
Instagram: @prof_diminoi
Zap: (11) 98576-2494
Entre no canal do professor Diminoi, escolha o tema e assista aos vídeos acessando:
https://www.youtube.com/channel/UCHqQ9sNGyaR4Caxi0rfTH3g
Números positivos e negativos Aula 1
https://www.youtube.com/watch?v=iccsJzRSQ70
Números positivos e negativos Aula 2
https://www.youtube.com/watch?v=kgKYcy93EbQ
Assista ao vídeo: Números positivos e negativos Aula 3ª
https://www.youtube.com/watch?v=Y3coQNcC4mc
Observação 1: resolva as questões no seu caderno do Aluno (preferencialmente a lápis), tire uma foto e envie a foto para o professor Davi pelo zap: (11) 98576-2494
Observação 2: essa atividade deve ser entregue até o dia 03/07/2020.

7º Ano Caderno do Aluno Volume 2/2020 – Parte 1
SITUAÇÃO DE APRENDIZAGEM 2
ATIVIDADE 4 – RESOLVENDO PROBLEMAS – Página 65, 66, 67
4.1. A professora Eliane promoveu uma gincana de matemática para sua turma. A regra da gincana diz que, ao acertar a resposta, o participante ganha 10 pontos, e perde 15 pontos em caso de erro. A turma da professora Eliane acertou 48 das 60 questões. Qual foi a pontuação final da turma da professora Eliane? Explique sua resposta.
Resolução:
Ao acertar 48 questões, significa que a turma errou 12 questões. Então, 48 . 10 = 480 e 12 . 1 5 = 180, logo 480 – 180 = 300. Portanto, a pontuação final da turma da professora Eliana foi 300 pontos.
4.2 Eduardo ganhou um jogo em seu aniversário, onde acertando os foguetes, eles se transformam em números positivos ou negativos, que devem ser adicionados à pontuação de cada jogador. Durante a partida, Eduardo marcava 11 pontos ganhos e transformou um foguete no número -4. Em seguida, uma nova transformação fez aparecer o número 7, como mostra a figura acima. Quantos pontos ele tem agora? Explique sua resposta:
Resolução:
11 pontos ganhos indicamos por (+11).
Logo, 11 - 4 + 7 = 14.
Agora Eduardo tem 14 pontos.
4.3 Ao final de cada mês, Ana Luiza analisa o saldo de sua conta corrente elaborando uma tabela como a representada abaixo.
|
Saldo bancário mensal – Ana Luiza |
|
|
Janeiro |
-156,00 |
|
Fevereiro |
248,00 |
|
Março |
-223,00 |
|
Abril |
-127,00 |
|
Maio |
58,00 |
|
Junho |
117,00 |
|
Julho |
-34,00 |
|
Agosto |
98,00 |
|
Setembro |
145,00 |
|
Outubro |
202,00 |
|
Novembro |
12,00 |
|
Dezembro |
-267,00 |
|
Dezembro |
-267,00 |
Qual foi a situação financeira de Ana ao final do ano?
Resolução:
Consultando a tabela de saldo da conta corrente de Ana:
(-156) + 248 + (- 223) + (- 127) + 58 + 117+ (-34) + 98 + 145+ 202 + 12 + (- 267) = 73.
Assim, ao final do ano, ela terá um saldo R$ 73,00.
4.4. A temperatura dos planetas depende da atmosfera, do calor e outras condições. Observe a tabela abaixo, que indica a temperatura média de alguns planetas do sistema solar, e responda:
|
Planetas |
Temperatura média |
|
Marte |
-53ºC |
|
Terra |
15ºC |
|
Netuno |
-225ºC |
|
Mercúrio |
420ºC |
|
Júpiter |
-150ºC |
a) Coloque as temperaturas dos planetas em ordem decrescente.
Resolução:
420° C, 15°C, -53°C, -150°C, -225°C
b) Qual é a variação de temperatura entre o planeta Terra e o planeta Marte?
Resolução:
-53°C +15°C = - 38°C
4.6. Na aula de Educação Financeira, Giovana está aprendendo a organizar seus gastos. Ela elaborou uma planilha eletrônica com os gastos do mês de maio.
|
Despesas mensais – Maio |
|
|
Lanche |
R$ 12,00 |
|
Lazer |
R$ 10,00 |
|
Revistas |
R$ 8,00 |
|
Diversos |
R$ 9,00 |
|
Saldo |
|
Sabendo que ela ganhou R$ 50,00 de mesada, calcule o saldo de Giovana. Além dos gastos indicados na planilha, ela esqueceu de incluir R$ 15,00 referente ao gasto com o presente de aniversário de sua mãe. O valor da mesada será suficiente para todos os gastos? Como você resolveria essa situação?
Resolução:
50 - (12 +10 + 8 + 9+15) = 50 – 54 = - 4, logo o saldo de Giovana é – R$ 4,00. Conclusão: A mesada de R$ 50,00 será insuficiente.
4.7 Relacione a coluna A com a coluna B, realizando as operações indicadas, completando a tabela.
|
A |
B |
A + B |
A . B |
A - B |
A;B |
|
8 |
- 2 |
8 + (-2) = 6 |
8 + (-2) = 6 |
8 + (-2) = 6 |
8 + (-2) = 6 |
|
6 |
5 |
5 + 5 = 10 |
5 + 5 = 10 |
5 + 5 = 10 |
5 + 5 = 10 |
|
5 |
- 1 |
6 + (-1) = 5 |
6 + (-1) = 5 |
6 + (-1) = 5 |
6 + (-1) = 5 |
|
- 4 |
2 |
(-4) + 2 = -2 |
(-4) + 2 = -2 |
(-4) + 2 = -2 |
(-4) + 2 = -2 |
|
-10 |
5 |
(-10) + (-5) = -15 |
(-10) + (-5) = -15 |
(-10) + (-5) = -15 |
(-10) + (-5) = -15 |
Atividade de 22/05/2020 até 26/06/2020
Professor Diminoi
https://professordiminoi.comunidades.net/
Instagram: @prof_diminoi
Zap: (11) 98576-2494
Entre no canal do professor Diminoi, escolha o tema e assista aos vídeos acessando:
https://www.youtube.com/channel/UCHqQ9sNGyaR4Caxi0rfTH3g
Números positivos e negativos Aula 1
https://www.youtube.com/watch?v=iccsJzRSQ70
Números positivos e negativos Aula 2
https://www.youtube.com/watch?v=kgKYcy93EbQ
Observação 1: resolva as questões no seu caderno do Aluno (preferencialmente a lápis), tire uma foto e envie a foto para o professor Davi pelo zap: (11) 98576-2494
Observação 2: essa atividade deve ser entregue até o dia 26/06/2020 as18h.

7º Ano Caderno do Aluno Volume 2/2020 – Parte 1 – página 63, 64 e 65.
SITUAÇÃO DE APRENDIZAGEM 4
ATIVIDADE 3 – DESCOBRINDO O QUE VEM ANTES DO ZERO
Habilidade - (EF07MA04): Resolver e elaborar situações- problema que envolvam operações com números inteiro
Tema: Números positivos e negativos
Atividade:
Os números inteiros podem aparecer em tabelas de jogos, escalas termométricas, extratos bancários, medições de altitude e profundidade (abaixo e acima do nível do mar), entre outros exemplos. Mas também podem ser conceituados a partir da simetria em relação aos números inteiros positivos na reta numérica.
3.1. Observe os números inteiros representados na reta numérica. Qual é a correspondência que está indicada? Explique e anote as duas próximas correspondências.
.jpg)
Resolução:
A correspondência indicada trata dos números simétricos ou opostos, sendo as duas próximas correspondências: - 5 e +5; - 6 e + 6.
3.2 Complete a tabela indicando o número oposto ou simétrico em cada caso.
|
+8 |
-8 |
|
-10 |
10 |
|
-36 |
36 |
|
48 |
-48 |
|
-27 |
27 |
|
-58 |
58 |
|
+124 |
-124 |
|
200 |
-200 |
3.3 Escreva os números em ordem crescente: 6, -94, 150, 532, -645, 334, 0, -257, -78, 2 057, -3 670, -127 e 88.
Resolução:
- 3 670, -645, -257, - 127, -94, -78, 0, 6, 88, 150, 334, 532 e 2 057.
3.4 Podemos comparar dois números dizendo se um é maior ou menor do que o outro.
Observe o subconjunto dos números inteiros abaixo:
{-9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9}.
3.5. Diego conferiu o estoque de celulares de sua loja no final do dia 20 e verificou que havia 40 aparelhos. Nos dias posteriores, ele fez a seguintes transações:
Comprou 20 aparelhos;
Vendeu 40 celulares;
Vendeu 10 celulares;
Comprou 15 celulares;
Vendeu 11 celulares.
Após todas essas transações, qual é o número de celulares no estoque da loja do Diego? Explique.
Resolução:
40 + 20 – 40 – 10 + 15 – 11 = 14, logo Diego tem em estoque 14 celulares.
3.6. No final do outono em São Paulo, a temperatura era de 20°C. Com a entrada de uma frente fria, a temperatura baixou para 9°C. De quanto foi a variação de temperatura? Como você calculou essa variação?
Resolução:
20º C – 9º C = 11º C, logo a variação foi de 11º C.
3.7. Luciano fez uma dívida de R$ 50,00 e outra de R$ 96,00, ambas para serem pagas no próximo mês. Quanto ele está devendo? Como você indicaria esse valor?
Resolução:
(-50) + (-96) = -146. Luciano está devendo R$ 146,00.
3.8. O gerente do banco informou a Eduardo que sua conta estava com saldo negativo de R$ 130,00. Ele fez um depósito e seu saldo agora é de R$ 64,00. Qual foi o valor depositado?
Resolução:
Para cobrir o saldo negativo, deveria depositar R$ 130,00. Como após o depósito seu saldo era de R4 64,00; assim, Eduardo depositou: 130 + 64 = 194, logo, o valor depositado foi de R$194,00.
3.9. Na cidade de São Joaquim, a temperatura era de 4°C ao anoitecer. Durante a madrugada, a temperatura teve uma queda de 6°C. Qual foi o registro da temperatura na madrugada?
Resolução:
4°C – 6°C = - 2°C, logo, a temperatura na madrugada registrada foi - 2°C.
Instagram: @prof_diminoi
Zap: (11) 98576-2494
Assista ao vídeo: (acompanhe no youtube durante a semana)
Observação 1: resolva as questões no seu caderno do Aluno (preferencialmente a lápis), tire uma foto e envie a foto para o professor Davi pelo zap: (11) 98576-2494
Observação 2: essa atividade deve ser entregue até o dia 23/06/2020 as18h.
Aula e Atividade referente a 16/06/2020 ATÉ 23/06/2020
Instagram: @prof_diminoi
Zap: (11) 98576-2494
Assista ao vídeo: (acompanhe no youtube durante a semana)
Observação 1: resolva as questões no seu caderno do Aluno (preferencialmente a lápis), tire uma foto e envie a foto para o professor Davi pelo zap: (11) 98576-2494
Observação 2: essa atividade deve ser entregue até o dia 23/06/2020 as18h.
7º Ano Caderno do Aluno Volume 2/2020 – Parte 1 – página 62 e 63
SITUAÇÃO DE APRENDIZAGEM 2
Habilidade - (EF07MA04): Resolver e elaborar situações- problema que envolvam operações com números inteiro
Tema: Números inteiro
ATIVIDADE 2 – NÚMEROS POSITIVOS E NEGATIVOS
2.1 A tabela abaixo apresenta alguns resultados dos times no final de um Campeonato, onde é possível verificar o número de gols marcados, sofridos e o saldo final.
|
Clubes |
Gols marcados |
Gols sofridos |
Slado de gols |
|
São Paulo |
46 |
34 |
12 |
|
Bota fogo |
38 |
46 |
-8 |
|
Paraná |
18 |
57 |
-39 |
|
Atletico |
54 |
37 |
17 |
|
Palmeiras |
64 |
26 |
38 |
|
Chapecoenses |
34 |
50 |
-16 |
|
Corinhitas |
34 |
35 |
-1 |
a) Analisando a tabela, classifique os times em ordem crescente em relação ao saldo de gols.
Resolução:
Paraná (-39), Chapecoense (-16), Botafogo (-8), Corinthians (-1), São Paulo (12), Atlético (17) e Palmeiras (38).
b) Considere o saldo de gols dos times Botafogo, Paraná, Chapecoense e Corinthians. Explique por que o saldo de gols de cada time foi registrado dessa maneira.
Resolução:
O time do Botafogo marcou 38 gols, mas sofreu 45, logo 38 - 46 = -8. Já o Paraná marcou 18, mas sofreu 57 gols, logo 18 - 57 = -39. O Chapecoense marcou 34 gols, mas sofreu 50, logo 34 - 50 = -16. Por fim, o Corinthians marcou 34 gols, mas sofreu 35, logo 34 – 35 = -1.
2.2 Muitas cidades pelo mundo apresentam as quatro estações do ano bem definidas. Observe a tabela abaixo que apresenta as temperaturas médias de algumas cidades do mundo no verão e no inverno.
|
País |
Cidade |
Verão |
Inverno |
|
Canadá |
Toronto |
25ºC |
-10ºC |
|
Japão |
Tóquio |
30ºC |
9ºC |
|
Estados Unidas da América |
New York |
24,5ºC |
-0,6ºC |
|
Brasil |
Campo do Jordão |
16,8ºC |
9,6ºC |
|
Rússia |
Moscou |
18,4ºC |
-9,2ºC |
a) Quais cidades apresentam a maior e a menor temperatura média no verão? Quais são as temperaturas?
Resolução:
Maior temperatura no Verão: Tóquio 30º C. Menor temperatura no Verão: Campos do Jordão 16,8º C.
b) Observe na reta abaixo a representação das temperaturas médias do Canadá. Qual foi a variação de temperatura do inverno para o verão? Explique.
Resolução:
A variação foi de 35ºC, ou seja, 25 - (-10) = 35
2.3 Sabendo que a variação de duas temperaturas é determinada pela diferença entre a temperatura final e a temperatura inicial, calcule a variação de temperatura da cidade de Campos do Jordão, onde a temperatura no verão de 2015 foi de 16,8°C, e no inverno foi de 9,6°C. Explique como você realizou a operação aritmética.
Resolução:
O cálculo foi feito subtraindo a temperatura inicial da temperatura final, isto é:
16,8°C – 9,6°C = 7,2°C
Aula e Atividade referente a 08/06/2020 ATÉ 16/06/2020
Zap: (11) 98576-2494
Pesquisa geral: https://professordiminoi.comunidades.net/
Pesquisa específica: https://professordiminoi.com.br/7-caderno-do-anulo-volume-1
Aula/Plantão de dúvidas: Toda terças-feiras às 16h30 pelo Instagram: @prof_diminoi
FRAÇÃO
É a representação de uma parte de algo inteiro, como ocorre com as maçãs mostradas na figura anterior. Assim, podemos dizer que a fração representa uma quantidade, isto é, uma forma numérica. O conjunto numérico no qual as frações estão contidas é chamado de conjunto dos números racionais, que é representado geralmente da seguinte maneira:
A fração é uma forma de representar algo dividido em partes iguais. Suponha que tenhamos uma barra de chocolate com 8 pedaços.

Observe que a barra é dividida em 8 partes iguais. Imagine agora que foi retirada apenas uma parte dessa barra.

Podemos utilizar a fração para representar essa parte que foi retirada. Essa parte corresponde a um pedaço de oito. Para escrever essa informação matematicamente, basta sobrepor dois números, os quais vamos chamar de numerador e denominador.
![]()
Lemos a fração acima da seguinte maneira: um oitavo ou um sobre oito. Podemos dizer que cada parte da barra corresponde a um oitavo. Observe também que retirar 4 partes da barra é o mesmo que retirar a metade da barra, ou seja, é equivalente.
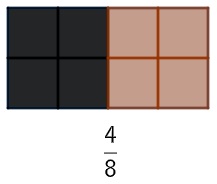
Frações equivalentes
As frações equivalentes são usadas para representar a mesma quantidade. Por exemplo, imagine agora um retângulo partido ao meio. Cada parte desse retângulo será representada pela fração um meio ou um sobre dois, ou seja, vamos dividir a barra pela metade.
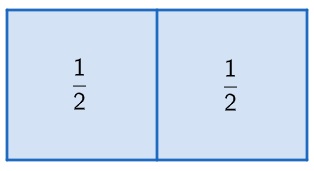
No problema anterior, ao retirar da barra de chocolate 4 partes do total de 8 partes, foi o mesmo que retirar a metade da barra.
1 ÷ 8 = 0,125
Para escrever a fração em sua forma percentual, devemos multiplicar o denominador por um número de forma que a resposta da multiplicação seja igual a 100. Como vimos, se multiplicarmos o denominador por 100, teremos que multiplicar o numerador também.
Veja que 8 · 12,5 = 100, logo vamos multiplicar o numerador e o denominador da fração 1/8 por 12,5.
REXERCÍCIOS RESOLVIDOS
01) Com 16 litros de leite, quantas garrafas de 2/3 de litros poderão ser cheias?
Resolução:
Devemos realizar a seguinte divisão 16 : 2/3.
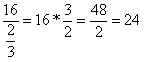
Resposta: com 16 litros de leite podemos encher 24 garrafas com capacidade de 2/3 de litro.
02) Para ladrilhar 3/4 de uma área, 9375 ladrilhos foram usados. Para ladrilhar 7/8 da mesma área, quantos ladrilhos serão necessários?
Resolução:
Temos que 3/4 de uma determinada área de medida x corresponde a 9375 ladrilhos. Portanto temos que:
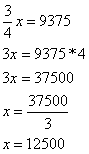
A área possui 12.500 m². Com base nesse valor vamos calcular seus 7/8:
Resposta: de acordo com a área medindo 12.500 m² temos que 7/8 equivale a 10.937,5 m².
03) Dividir R$ 510,00 por três pessoas, de modo que as partes da primeira e da segunda sejam, respectivamente, 1/3 e 4/5 da parte a ser recebida pela terceira.
Resolução:
Parte recebida pela terceira pessoa: x.
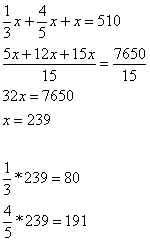
Resposta: a primeira pessoa receberá R$ 80,00, a segunda R$ 191,00 e a terceira R$ 239,00.
04) Márcia tem 2/9 do dinheiro necessário para comprar um apartamento, e seu marido, 3/11 dessa quantia. Se a essa importância o casal adicionar R$ 35.000,00 poderão comprar a casa própria. Qual é o preço do imóvel?
Resolução:
2 x + 3 x + 35.000 = x
9 11
22 x + 27 x + 3.465.000 = 99 x
99 99
22 x + 27 x – 99 x = – 3.465.000
– 50 x = – 3.465.000
x = 69.300
Resposta: o valor do imóvel é correspondente a R$ 69.300,00.
ATIVIDADE: Exercícios do Caderno do Aluno Volume 2.
SITUAÇÃO DE APRENDIZAGEM 1
ATIVIDADE 1 – COMPARAÇÃO DE FRAÇÕES – Página 59
1.1 Ana Cristina está preenchendo um formulário e marcou cada letra em um dos quadradinhos do retângulo quadriculado abaixo. Escrevendo seu nome completo, 2/5 dos quadradinhos da figura toda serão preenchidos. O desafio para você é:
|
A |
N |
A |
|
C |
R |
I |
S |
T |
I |
N |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) Quantas letras deve ter o sobrenome de Ana Cristina para atender os 2/5 dos quadradinhos da figura?
b) Qual é o possível sobrenome de Ana Cristina, atendendo aos critérios do preenchimento?
c) Construa outro formulário com a mesma quantidade de quadradinhos, escreva seu nome completo e indique a fração que ele representa na figura. Compare a fração referente ao seu nome com a fração referente ao nome de Ana, indicando qual é o maior.
1.2. Felipe recebeu duas propostas para vender sorvete em um evento que aconteceria no dia do aniversário de sua cidade. Leia com atenção as duas propostas descritas abaixo e responda o que se pede:
1ª proposta Ganhar o equivalente ao preço de 2 sorvetes para cada 12 sorvetes vendidos.
2ª proposta Ganhar o equivalente ao preço de 3 sorvetes para cada 15 sorvetes vendidos.
Escreva as propostas em forma de fração (razão) e compare-as. Qual proposta é mais vantajosa financeiramente? Por quê?
ATIVIDADE 2 – PROBLEMAS DE RAZÃO ENTRE PARTES DE UMA GRANDEZA - Página 60
2.1. Um segmento de reta de 28 cm foi dividido em dois segmentos na razão 3/4. Quantos centímetros tem cada segmento obtido após a divisão?
2.2. Em uma classe há 35 alunos e sabe-se que a razão entre o número de meninas e o número de meninos é 2/3. Qual é o número de meninos dessa classe?
2.3. Ao confeccionar um colar, Adriana pensou na razão 4/5 entre o número de bolinhas brancas e bolinhas laranjas. Quantas bolinhas brancas e laranjas Adriana vai utilizar para fazer um colar com 180 bolinhas?
2.4. O lucro de 15 mil reais foi dividido entre dois sócios. Porém, o primeiro sócio recebeu o dobro do segundo sócio, uma vez que gastou o dobro para montar o negócio. Calcule que parte do lucro coube a cada um dos sócios.
Instagram: @prof_diminoi
Zap: (11) 98576-2494 - Prof. Diminoi
OBSERVAÇÃO: Nos dias 18, 19, 20 e 22 de maio de 2020 teremos Aula de Matemática as 14h pelo instagram: @prof_diminoi
Revisão Geral para a Avaliação de Aprendizagem em Processo (AAP)
1º Bimestre de 2020 - 7º ano - Prof. Davi
ATENÇÃO: Os conteúdo desta Aula é uma revisão Geral cujo Objetivo e lhe dar suporta para que você se aproprie das habilidades contidas na AAP 1º Bimestre/2020.
INCÓGNITA
São números desconhecidos representados por letras e, na maioria dos casos, essa letra é x. Esses números desconhecidos são chamados de incógnitas.
Exemplo 1:
Encontre o valor de x da equação: 2x + 4 = 8
Resolução: todo valor acompanhado de x de um lado e todo valor que não está acompanhado de x do outro lado.
Quem troca de lado muda o sinal. Se for positivo (+) vira negativo (-) e se for negativa (-) vira positivo (+)
Exemplo 2:
2x + 4 + 8
2x = 8 – 4
2x = 4
x =4 -2
x = 2 (Portanto x vale 2)
Observação: quando temos uma situação-problema dizemos que o valor desconhecido é o x.
Exemplo 3:
No aniversário de Regina ela ganhou vários presentes de seus pais. Foram 5 vestidos, 3 blusas, 4 tênis e vários pares de meias. Sabendo-se que a Regina ganhou 18 presentes, quantos pares de meias ela ganhou?
Resolução:
O total de presentes é 18 com a quantidade de meias e desconhecido vamos chamar o total de meios de x.
x + 5 + 3 + 4 = 18
x = 18 -5 – 3 - 4
x = 18 - 12
x = 6
Repostas: ela ganhou 6 pares de meias.
Sistema de Equação:
Método da adição para sistemas com duas equações e duas incógnitas
Exercícios
01) Encontre os valores de x e y
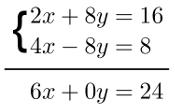
As somas realizadas nesse exemplo foram: 2x + 4x, 8y + (– 8y) = 0 e 16 + 8 = 24.
6x = 24
x = 24
6
x = 4
Para descobrir a incógnita y, basta substituir o valor numérico de x em uma das duas equações do sistema:
2x + 8y = 16
2·4 + 8y = 16
8 + 8y = 16
8y = 16 – 8
8y = 8
y = 8
8
y = 1
x = 4
y = 1
02) Encontre os valores de X e Y
![]()
Resolução:
Adicionamos membro a membro as equações:
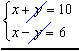
2x = 16
x = 8
Substituímos o valor encontrado de x, em qualquer das equações, determinando y:
x + y = 10
8 + y = 10
y = 10 - 8
y = 2
X = 8
Y = 2
SOMA DOS ÂNGULOS INTERNOS DE UM TRIÂNGULO
A soma dos ângulos internos é igual a 180°
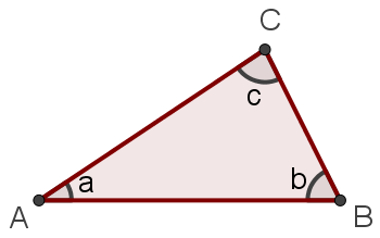
a + b + c = 180º
Exemplo 4:
Qual é a medida do ângulo α na figura a seguir?
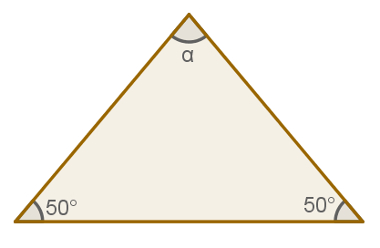
Resolução:
Sabendo que os ângulos internos de um triângulo totalizam 180°, podemos escrever:
α + 50 + 50 = 180
α = 180 – 50 – 50
α = 80°
Exemplo 5:
Calcule o valor de x no triângulo a seguir.
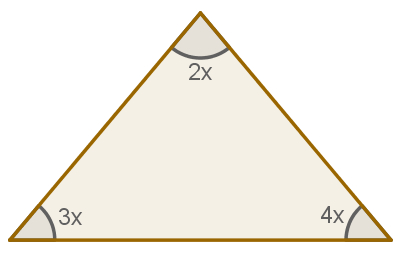
Resolução:
Como já sabemos, a soma dos ângulos internos de um triângulo é 180°. Portanto, podemos escrever:
2x + 3x + 4x = 180
9x = 180
x = 180
9
x = 20
VARIÁVEL E INCOGNITA
Assista ao vídeo para saber e diferença entre Variável e Incógnita.
🎼VARIÁVEL OU INCÓGNITA - Matemática - 7º Ano do Ensino Fundamental
https://www.youtube.com/watch?v=9kHQ9z3fWr8
Incógnita
É um valor desconhecido fixo e que podemos encontra esse valor através de uma equação é encontrar o valor de x que torna essa igualdade verdadeira.
Observa as figuras abaixo e responda o que representa α?
Observação: o valor do ângulo α é fixo porque a soma doa ângulos de um triângulo é 180º
Variável
É um valor desconhecido que da variável, podemos determinar diversos valores para a letra que representa a variável e assim, o valor da expressão numérica estará também variando.
.jpg)
Observação: o valor do ângulo α uma variável porque alterando o arco o ângulo também altera-se.
POTENCIAÇÃO
A potenciação é uma simplificação da forma de expor uma multiplicação de fatores iguais.
Exemplos:
a) 32 = 3 . 3 = 9
c) 33 = 3 . 3 = 27
c) 24 = 2 . 2 . 2 . 2 . 2 = 32
d) 52 = 5 . 5 = 25
Observação: Qual número elevado a zero vale 1
Exemples:
20 =1
80 = 1
50 = 1
Leitura de número em potencial:
24 = “dois elevado a quatro” ou “dois elevado à quarta potência”
25 = “dois elevado a cinco” ou “dois elevado à quinta potência”
26 = “dois elevado a seis” ou “dois elevado à sexta potência”
27 = “dois elevado a sete” ou “dois elevado à sétima potência”
28 = “dois elevado a oito” ou “dois elevado à oitava potência”
29 = “dois elevado a nove” ou “dois elevado à nona potência”
2n = “dois elevado a n” ou “dois elevado à enésima potência”
DECOMPOSIÇÃO EM FATORES PRIMOS
A decomposição em fatores primos é uma ferramenta muito importante no desenvolvimento matemático, pois, com ela, é possível simplificar expressões numéricas ou algébricas e calcular MDC ou MMC de números inteiros.
Exemplo 1:
a) Decomposição de 360 em potências.
Resolução:
360 = 23 . 32 . 51
Exemplo 2:
Decomponha em 234 em fatores primos o valor
Resolução:
234 = 2 . 3 . 3 . 13
2 . 32 . 13
Exemplo 3:
Decomponha em 180 em fatores primos o valor
Resolução:
180 = 2 . 2 . 3 . 3 . 5
22 . 32 . 5
Exemplo 4:
Decomponha em 1620 em fatores primos o valor
Resolução:
Fatore em 1620 em números primos o valor
1620 = 2 . 2 . 3 . 3 . 3 . 3 . 5
22 . 34 . 5
Divisores Comuns entre dois ou mais números
Os divisores comuns entre dou ou mais valores são os números aparecem nas divisão dos nas divisões de ambos.
Exemplo 7:
Em uma escola, há 240 alunos no 7º ano, 288 no 8º ano e 120 no 9º ano. Haverá uma semana cultural, em que todos os alunos serão distribuídos em equipes, sem que se misturem alunos de anos diferentes.
Quais são os divisores comuns nesse caso?
Resolução:
Vamos encontrar os divisores de 240, 288 e 120:
D (240) = {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, 240}
D (288) = {1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288}
D(120) = {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}
Observação: os divisores comuns são os números aparecem nas divisão dos três valores dados que nesse caso os valores são: 240, 288 e 120.
Exemplo 8:
Quais são os divisores comuns entra 12 e 24 esse caso?
Primeiro passo é fatorar as valores
Observação: o Máximo Divisor Comum de 12 e 40
(D)12 = {1,2,3,4,6,12}
(D)40 = {1, 2, 4, 5, 8, 10, 20, 40}
O MDC entre (12, 40), é 4.
Exemplo:
Quais o divisores comuns entre 12 e 40.
Agora e identificar quais valores estão tanto em (D)12 bem como em (D)40.
(D)12 = {1, 2, 3, 4, 6, 12}
(D)40 = {1, 2, 4, 5, 8, 10, 20, 40}
Os divisores comuns são os números que aparecem tanto em (D)12 como em (D)40 e nesse caso são os números: 1, 2 e 4.
Observação: sempre que for preciso encontrar os divisores comuns entre dois valores, basta seguir estas instrução. Caso os valores sejam grandes o procedimento é o mesmo.
Mínimo Múltiplo Comum – MMC – (fatoração)
Dois ou mais números naturais não nulos, denomina-se Mínimo Múltiplo Comum desses números o menor de seus números diferente de zero.
Exemplo:
Qual o MMC de 12, 15 e 20?
Resolução:
12, 15, 20 | 2
6, 15, 10 | 2 MMC (12, 15, 20) = 2 . 2 . 3 . 5 = 60
3, 15, 5 | 3
1, 5, 5 | 5
1, 5, 5 |
Observação: quando se calcula MMC multiplica-se todos os fatores.
Ou seja, nesse caso são 2 . 2 . 3 . 5 = 60.
Conclusão: o MDC de 12, 15 e 20 é 60.
EXERCÍCIOS RESOLVIDOS DE MMC
01) Qual é o menor múltiplo comum MMC positivo de 6 e de 8?
Resolução:
Um modo mais prático de se obter o MMC é através da fatoração simultânea.
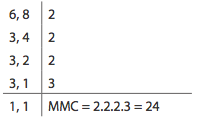
Conclusão: o MMC entre 6 e 8 é 24
MÁXIMO DIVISOR COMUM - MDC
Dois ou mais números naturais, não simultâneos nulos, denomina-se Mínimo Divisor Comum desses números o maior de seus divisores comuns..
Exemplo: Qual o MDC de 40 e 60?
Resolução:
40, 60 | 2 é fator comum
20, 30 | 2 é fator comum
10, 15 | 2 não é fator comum
5, 15 | 3 não é fator comum
5, 5 | 5 é fator comum
1 1 | 1
0 0
Ou seja, nesse caso são 2 . 2 . 5 = 20.
Conclusão: o MDC de 40 e 60 é 20.
EXERCÍCIOS RESOLVIDOS DE MDC
02) Qual o MDC entre os números 36 e 120?
Resolução:

Não se repete os números
Conclusão: 2 . 2 . 3 = 12
EXERCÍCIOS RESOLVIDOS DE MMC MDC
O que é M.M.C.
Dois ou mais números sempre têm múltiplos comuns a eles.
Exemplo:
Quais s múltiplos comuns de 4 e 6:
Múltiplos de 6: 0, 6, 12, 18, 24, 30,...
Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,...
Múltiplos comuns de 4 e 6: 0, 12, 24,...
Dentre estes múltiplos, diferentes de zero, 12 é o menor deles.
Processo da decomposição simultânea
Neste processo, decompomos todos os números ao mesmo tempo, em um dispositivo como mostra a figura ao lado. O produto dos fatores primos que obtemos nessa decomposição é o m.m.c. desses números.
Exemplo 1:
Encontre o m.m.c. entre 15, 24, 60.
Resolução:
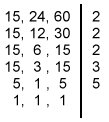
Resposta: o m.m.c.(15, 24, 60) = 2 . 2 . 2 . 3 . 5 = 120
Propriedade do M.M.C.
Exemplo 2:
Entre os números 3, 6 e 30, o número 30 é múltiplo dos outros dois. Neste caso, 30 é o m.m.c.(3, 6, 30).
Resolução:

m.m.c.(3, 6, 30) = 2 . 3 . 5 = 30
Observação: se dois ou mais números, se um deles é múltiplo de todos os outros, então ele é o m.m.c. dos números dados.
Exemplo 2:
Qual o MMN entre os números 4 e 15?
Resolução:

m.m.c.(4,15) = 2 . 2 . 3 . 5 = 60
Dados dois números primos entre si, o m.m.c. deles é o produto desses números.
Cálculo do M.D.C.
Um modo de calcular o m.d.c. de dois ou mais números é utilizar a decomposição desses números em fatores primos.
Exemplo:
Qual o MDC entre 36 e 90?
Resolução:
36 = 2 . 2 . 3 . 3
90 = 2 . 3 . 3 . 5
Os fatores primos comuns m.d.c.(36,90) = 2 . 3 . 3
Portanto m.d.c.(36,90) = 18.
Escrevendo a fatoração do número na forma de potência temos:
36 = 22 . 32
90 = 2 . 32 . 5
Portanto m.d.c.(36, 90) = 2 . 32 = 18.
O m.d.c. de dois ou mais números, quando fatorados, é o produto dos fatores comuns a eles, cada um elevado ao menor expoente.
Cálculo do M.D.C. pelo processo das divisões sucessivas
Nesse processo efetuamos várias divisões até chegar a uma divisão exata. O divisor desta divisão é o m.d.c. Acompanhe o cálculo do m.d.c.(48,30).
Regra prática:
1º) dividimos o número maior pelo número menor;
48 / 30 = 1 (com resto 18)
2º) dividimos o divisor 30, que é divisor da divisão anterior, por 18, que é o resto da divisão anterior, e assim sucessivamente;
30 / 18 = 1 (com resto 12)
18 / 12 = 1 (com resto 6)
12 / 6 = 2 (com resto zero - divisão exata)
3º) O divisor da divisão exata é 6. Então m.d.c.(48, 30) = 6.
Números primos entre si
Observação: Se dois ou mais números são primos entre si quando o máximo divisor comum desses números é 1.
Exemplos:
Os números 35 e 24 são números primos entre si, pois mdc (35, 24) = 1
Os números 35 e 21 não são números primos entre si, pois mdc (35, 21) = 7
Propriedade do M.D.C.
Dentre os números 6, 18 e 30, o número 6 é divisor dos outros dois. Neste caso, 6 é o m.d.c.(6,18,30). Observe:
6 = 2 . 3
18 = 2 . 32
30 = 2 . 3 . 5
Portanto m.d.c.(6,18,30) = 6
Observação: Se dois ou mais números, se um deles é divisor de todos os outros, então ele é o m.d.c. dos números dados.
Mínimo múltiplo comum (M.M.C.)
Dois ou mais números sempre têm múltiplos comuns a eles. Vamos achar os múltiplos comuns de 4 e 6:
Múltiplos de 6: 0, 6, 12, 18, 24, 30,...
Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,...
Múltiplos comuns de 4 e 6: 0, 12, 24,...
Dentre estes múltiplos, diferentes de zero, 12 é o menor deles. Chamamos o 12 de mínimo múltiplo comum de 4 e 6.
Observação: O menor múltiplo comum de dois ou mais números, diferente de zero, é chamado de mínimo múltiplo comum desses números. Usamos a abreviação m.m.c.
Cálculo do M.M.C.
Podemos calcular o m.m.c. de dois ou mais números utilizando a fatoração. Acompanhe o cálculo do m.m.c. de 12 e 30:
1º) decompomos os números em fatores primos
2º) o m.m.c. é o produto dos fatores primos comuns e não-comuns:
12 = 2 . 2 . 3
30 = 2 . 3 . 5
m.m.c (12,30) = 2 . 2 . 3 . 5
Escrevendo a fatoração dos números na forma de potência, temos:
12 = 22 . 3
30 = 2 . 3 . 5
m.m.c (12,30) = 22 . 3 . 5
Observação: o m.m.c. de dois ou mais números, quando fatorados, é o produto dos fatores comuns e não-comuns a eles, cada um elevado ao maior expoente.
Processo da decomposição simultânea
Neste processo, decompomos todos os números ao mesmo tempo, em um dispositivo como mostra a figura ao lado. O produto dos fatores primos que obtemos nessa decomposição é o m.m.c. desses números. A seguir vemos o cálculo do m.m.c.(15,24,60).

Resposta: o m.m.c.(15,24,60) = 2 . 2 . 2 . 3 . 5 = 120
Propriedade do M.M.C.
Entre os números 3, 6 e 30, o número 30 é múltiplo dos outros dois. Neste caso, 30 é o m.m.c. (3, 6, 30). Observe:

Reposta: o m.m.c.(3, 6, 30) = 2 . 3 . 5 = 30
Observação: Dados dois ou mais números, se um deles é múltiplo de todos os outros, então ele é o m.m.c. dos números
Exemplo:
Considere os números 4 e 15, que são primos entre si. O m.m.c.(4, 15) é igual a 60, que é o produto de 4 por 15.
Resolução:

m.m.c.(4,15) = 2 . 2 . 3 . 5 = 60
Observação: Dados dois números primos entre si, o m.m.c. deles é o produto desses números.
PORCENTAGEE (%)
Cálculo de porcentagem com regra de três
Algumas situações envolvendo porcentagem podem ser resolvidas por meio de uma regra de três simples. Entendemos por porcentagem uma razão centesimal (fração com denominador igual a 100) que é denominada de taxa percentual e é representada pelo símbolo % (por cento).
Exemplos 1:
Determine o valor de 95% de R$ 105,00
Resolução:
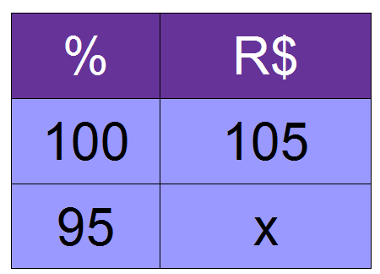
100x = 95 .105
100x = 9975
x = 9975
100
x = 99,75 reais
Resposta: portanto, 95% de R$ 105,00 é igual a R$ 99,75.
Exemplos 2:
Em uma sala de 40 alunos, foi realizada uma pesquisa, a qual apontou que 30 alunos gostam de praticar esportes. Qual é a porcentagem de alunos que gostam de esportes?
Resolução:
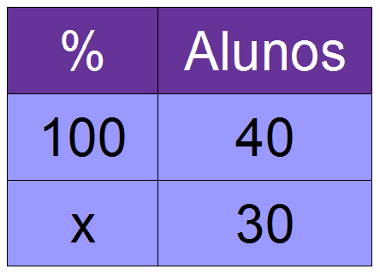
40x = 100 . 30
40x = 3000
x = 3000
40
x = 75%
Resposta: temos que 75% dos alunos dessa classe gostam de esportes.
Exemplos 3:
Pedro acertou 21 questões de uma prova, que correspondem a 70% do total de questões. Quantas questões tinha a prova?
Resolução:
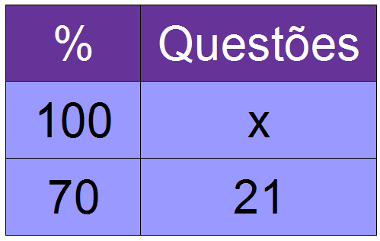
70x = 21.100
70x = 2100
x = 2100
70
x = 30
Resposta: a prova tinha 30 questões.
Exemplos 4:
Em uma promoção, o preço de um objeto foi reduzido de R$ 76,00 para R$ 57,00. Calcule o valor do desconto em porcentagem. Devemos primeiramente determinar o valor real do desconto: 76 – 57 = 19. Ao compararmos o valor do desconto com o valor sem o desconto, obtemos o valor percentual.
Resolução:
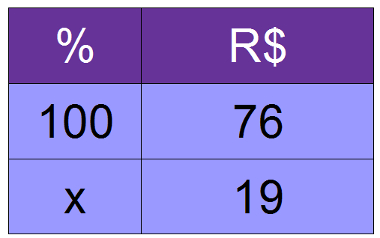
76x = 100 . 19
76x = 1900
x = 1900
76
x = 25%
Resposta: o desconto dado foi de 25%.
Exemplos 5:
Uma conta de restaurante, incluindo os 10% de serviço, ficou em R$ 143,00. Qual o valor da conta sem a taxa de serviço?
Resolução:
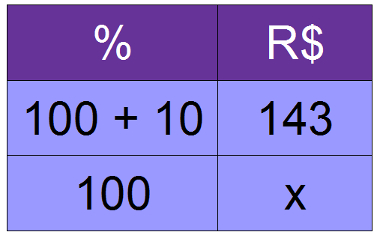
110x = 143 . 100
110x = 14300
x = 14300
110
x = 130
Resposta: a conta sem o valor do serviço é de R$ 130,00.
Exemplos 6:
Um produto que custava R$ 80,00 foi reajustado em 25%. Determine o novo valor do produto.
Resolução:
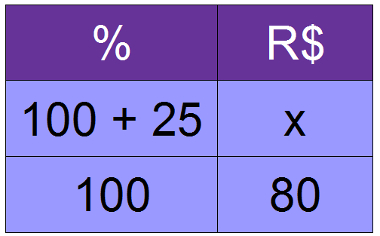
100x = 125 . 80
100x = 10000
x = 100
Resposta: o preço do produto após o reajuste é de R$ 100,00.
Exemplos 7:
O preço de um computador é de R$ 2.200,00. Qual será o preço do computador caso ele sofra um reajuste de 18%?
Resolução:
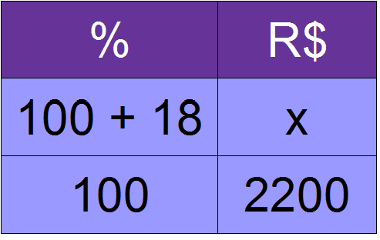
100x = 2200 . 118
100x = 259600
x = 259600
100
x = 2 596
Resposta: caso aconteça o reajuste de 18%, o computador passará a custar R$ 2 596,00.
Exemplos 8:
Considerando que a população de um país é de cerca de 180 milhões de habitantes e que 38 milhões são considerados fumantes, qual a porcentagem de fumantes no país referido?
Resolução:

180x = 3800
x = 3800
180
x = 21,1
Resposta: a porcentagem de fumantes no país referido é de aproximadamente 21,1%.
VOLUME, MASSA, COMPRIMENTO E ÁREA
Medidas de Comprimento
Comprimento é, talvez, a medida mais utilizada no cotidiano. Por isso, acredito que todos devem ter facilidades para entender essa grandeza e sua unidade de medida.
A unidade de medida padrão: metro (m)
Medidas de Capacidade
Medidas de capacidade também é muito importante no nosso cotidiano. A unidade padrão para essa grandeza é o litro (l).
Medidas de Massa
A grandeza massa não é muito usual no dia a dia, mas muito comum quando nos deparamos com problemas de física. Unidade padrão: quilograma (kg)
Medidas de superfície ou Área
Medidas de superfície ou área também está presente no nosso dia a dia. A unidade de medida padrão é: metro quadrado (m²)
Medidas Agrárias
Os fazendeiros devem conhecer essas unidades de medida muito bem e, aqui, você também vai entender. A unidade de medida padrão é: are (a)
Medidas de Volume
Quem nunca quis saber quanto cabe em uma caixa d’água, por exemplo. Para essa grandeza utilizamos a unidade de medida padrão: metro cúbico (m³)
Medidas de Tempo
A unidade de medida de tempo é uma das mais importantes utilizadas na física e também no nosso dia a dia. No sistema internacional de medidas (SI), a medida de tempo é o segundo (s).
NOMENCLATURA DOS ÂNGULOS EM FUNÇÃO DE SUA ABERTURA
O objeto capaz de medir o valor de um ângulo é chamado de transferidor, podendo ele ser de “meia volta” (180º) ou volta inteira (360º).
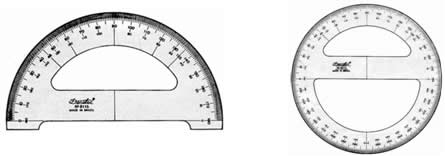
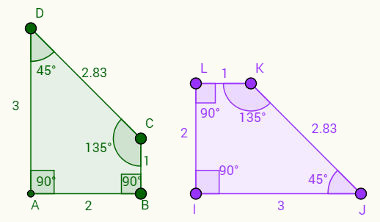
Classificação de ângulos: Os ângulos são classificados de acordo com suas medidas:
EXPRESSÕES NUMÉRICAS
s matemáticas estudadas no Ensino Fundamental são: adição, subtração, multiplicação, divisão, potenciação e radiciação. A ordem em que elas devem ser resolvidas em uma expressão numérica é a seguinte:
Potenciação e radiciação
Em uma expressão numérica, sempre resolva primeiro as potências e raízes antes de qualquer outra operação matemática. A única exceção é para o caso em que aparecem colchetes, chaves ou parênteses. Vale ressaltar que, entre potências e raízes, não há prioridade.
Multiplicação e divisão
Em segundo lugar, quando não houver mais potências ou raízes, devem ser feitas as multiplicações e divisões. Entre essas duas, também não há prioridade. Realize aquela que aparecer primeiro ou que facilitará os cálculos.
Adição e subtração
Por último, realize as somas e diferenças. Também não há prioridade entre elas. Resolva-as na ordem em que aparecerem.
Observação: ordem entre colchetes, chaves e parênteses
Em algumas expressões numéricas, uma parte da expressão pode ter prioridade em relação às outras. Essa parte deve ser separada com parênteses, chaves e/ou colchetes. A prioridade em que as operações devem ser feitas é a seguinte:
Parênteses
Em primeiro lugar, devem ser feitas todas as operações que estiverem dentro dos parênteses. Se houver muitas operações, a ordem que deve ser seguida é a das operações, dada anteriormente
Colchetes
Em segundo lugar, as operações que estiverem dentro de colchetes deverão ser feitas também de acordo com a ordem das operações dada anteriormente.
Observação: lembre-se apenas de que os parênteses aparecem sozinhos ou dentro de colchetes. Nesse caso, quando sobrar apenas um número dentro dos parênteses, estes podem ser eliminados.
Exemplo 1:
30 – 10 + 7
Resolução:
Basta fazer a soma e subtração
30 – 10 + 7
20 + 7
27
Exemplo 2:
87 + 7 . 85 - 120
Resolução:
Basta fazer a soma e subtração e multiplicação
87 + 7 . 85 - 120
87 + 595 - 120
682 – 120
562
Exemplo 2:
11,5 + 05 - 09
Resolução:
Basta fazer a soma e subtração
12 -9
13
Exemplos de situações-problema
Exemplo 1:
O dobro de um número subtraído de 20 é igual a 100. Qual é o número?
Resolução:
Um número: x
O dobro do número: 2x
Como estamos subtraindo 2x de 20 a equação será:
20 – 2x = 100
Resolvendo a equação
20 – 2x = 100
– 2x – 20 + 20 = 100 – 20 (adicionamos 20 aos dois lados da equação)
– 2x = 80 (– 1)
2x = – 80
x = – 80
2
x = – 40
Resposta: número é igual a – 40.
Exemplo 2:
O triplo de um número adicionado ao seu dobro resulta em 600. Qual é o número?
Resolução:
Um número: x
O triplo deste número: 3x
O dobro deste número: 2x
O triplo de um número adicionado ao seu dobro resulta em 600: 3x + 2x = 600
Resolvendo a equação:
3x + 2x = 600
5x = 600
x = 600/5
x = 120
Resposta: o número é igual a 120.
Exemplo 3:
Que número eu sou? O dobro de meu antecessor, menos 3, é igual a 25.
Resolução:
Um número: x
Antecessor: x – 1
O dobro de meu antecessor menos 3: 2(x – 1) – 3 = 25
Resolvendo a equação
2(x – 1) – 3 = 25 (aplicar o método da distribuição)
2x – 2 – 3 = 25
2x – 5 = 25
2x = 25 + 5
2x = 30
x = 30/2
x = 15
Resposta: o número é igual a 15.
Exemplo 4:
Carlos tinha certa quantia em dinheiro, foi ao shopping e gastou 1/3 da quantia na compra de uma revista, gastou 1/4 da quantia na compra de um CD e ainda ficou com R$ 25,00. Qual era a quantia que Carlos possuía?
Resolução:
Quantia: x
Um terço da quantia: 1/3x
Um quarto da quantia: 1/4x
Equação do problema: (1/3)x + (1/4)x + 25 = x
MMC (3,4) = 12
(4/12)x + (3/12)x + 300 = (12/12)x (simplificando os denominadores)
4x + 3x + 300 = 12x
12x – 4x – 3x = 300
12x – 7x = 300
5x = 300
x = 300/5
x = 60
Resposta: Carlos possuía a quantia de R$ 60,00.
Exemplo 5:
Os 44 alunos da 7ª série A de uma escola representam 40% de todos os alunos da 7ª série dessa mesma instituição. Quantos são os alunos da 7ª série dessa escola?
Alunos: x
Resolução:
40% = 40/100 = 2/5 dos alunos
2/5 de x
(2/5)x = 44
2x = 44 . 5
2x = 220
x = 220/2
x = 110
Resposta: A escola possui 110 alunos cursando a 7ª série.
ATIVIDADE - 7º ANO
[Entrega até dia 11/05/2020 - Professor Davi]
RESOLVA AS QUESTÕES A SEGUIR
01) 2x = 16
02) x - 17 = -9
03) 2x + 15 = 49
04) O dobro de um número menos 10, é igual à 50. Podemos escrever esse enunciado da seguinte forma:
2x -10 = 50. Que número é esse?
05) (PM-SP) Ao somar todos os gastos da semana, Maria somou, por engano, duas vezes o valor da conta do supermercado, o que resultou num gasto total de R$ 832,00. Porém, se ela não tivesse somado nenhuma vez a conta do supermercado, o valor encontrado seria R$ 586,00. O valor correto dos gastos de Maria durante essa semana foi.
Resolução:
Sendo x o gasto com o supermercado, podemos montar a seguinte equação do primeiro grau: 586 + 2x = 832.
Resolva a equação para encontrar o valor da conta.
MATEMÁTICA 7º ANO - Atividade de 27/04/2020 a 29/04/2020
ÁLGEBRA
Habilidade: (EF07MA13) Compreender a ideia de variável, representada por letra ou símbolo, para expressar relação entre duas grandezas, diferenciando-a da ideia de incógnita.
Objeto de conhecimento: Linguagem algébrica: variável e incógnita.
Incógnita
São números desconhecidos representados por letras e, na maioria dos casos, essa letra é x.
Observação: um número ao lado de uma letra ambos estão multiplicando-se.
Exemplo 1:
Encontre o valor de x da equação: 2x + 4 = 8
Resolução: todo valor acompanhado de x de um lado e todo valor que não está acompanhado de x do outro lado. Para concluir, o valor que está acompanhado o x passa dividindo número que está sozinho.
Quem troca de lado muda o sinal. Se for positivo (+) vira negativo (-) e se for negativa (-) vira positivo (+)
Vejamos:
2x + 4 = 8
2x = 8 – 4
2x = 4
x =4/2
x = 2 (Portanto x vale 2)
Observação: quando temos uma situação-problema dizemos que o valor desconhecido é o x.
Exemplo 2:
No aniversário de Regina ela ganhou vários presentes de seus pais. Foram 5 vestidos, 3 blusas, 4 tênis e vários pares de meias. Sabendo-se que a Regina ganhou 18 presentes, quantos pares de meias ela ganhou?
Resolução:
O total de presentes é 18 com a quantidade de meias e desconhecido vamos chamar o total de meios de x.
x + 5 + 3 + 4 = 18
x = 18 -5 – 3 - 4
x = 18 - 12
x = 6
Repostas: ela ganhou 6 pares de meias.
MATEMÁTICA 7º ANO - Atividade de 23/03/2020 a 27/03/2020
[RESOLVIDA E COMENTADA]

01) Leia atentamente a seguir a exposição feita por uma professora de matemática e as afirmativas feitas por alguns de seus alunos.


Marque a opção que apresenta o nome do aluno (a) que formulou uma afirmativa correta de acordo com a exposição feita pela professora.
(A) Ana Cláudia
(B) Felipe
(C) João Gabriel
(D) Daniele
Resolução:
D (240) = {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120 e 240}
D (270) = {1,2,3,5,6,9,10,15,18,27,30,45,54,90,135 e 270}
O maior divisor comum entre 240 e 270 é 30
Alternativa: B
02) Roberto foi ao médico, que receitou a ele os seguintes medicamentos:


Sabendo que Roberto tomou ontem, às 19 horas, esses dois medicamentos, depois de quanto tempo (intervalo mínimo possível) ele vai tomar os dois remédios juntos?
Resolução:
MMC(8 , 6)
8 , 6 | 2
4 , 3 | 2
2 , 3 | 2
1 , 3 | 3
1 , 1
2 . 2 . 2 . 3 = 24.
Resposta: depois de 24 horas.
Lei o texto a seguir e responda a questão 03.
Um fabricante de sabão em pó, pensando em aumentar sua produção, planejou oferecer um prêmio, em dinheiro, a quem encontrasse um cartão premiado na caixa desse produto. Preocupado em não perder de vista as embalagens premiadas, programou sua máquina para que incluísse o cartão premiado apenas nas caixas que, pela ordem de fabricação, coincidissem com os múltiplos de 250. Respeitando a ordem de fabricação, também para as vendas, oportunizaria atender a todos os seus comerciantes e evitaria que os prêmios saíssem para uma mesma região.
03) Um comerciante comprou as primeiras 1000 caixas fabricadas, quantas caixas premiadas adquiriu?

Resolução:
Comprando as primeiras 1000 caixas fabricadas ele terá na sua loja quatro prêmios (250, 500, 750 e 1000). Os estudantes deverão observar que nesse intervalo há quatro múltiplos de 250 ou efetuando 1000 ÷ 250 = 4, isto é, em mil há 4 vezes o 250 exatamente, pois 250 é divisor de 1000.
Resposta: 4 caixas
04) (repetida com a 05)
05) Em uma escola, há 240 alunos no 7º ano, 288 no 8º ano e 120 no 9º ano. Haverá uma semana cultural, em que todos os alunos serão distribuídos em equipes, sem que se misturem alunos de anos diferentes. Qual será o máximo de alunos que pode haver em cada equipe nessas condições? Observação: para resolver basta encontrar (os) divisor(es) comuns de 240, 288 e 120.

Resolução:
Encontrar os divisores de 240, 288 e 120:
D (240) = {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, 240}
D (288) = {1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288}
D(120) = {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}
Note que o número 24 é o maior número comum a todos os divisores, portanto o número máximo de alunos que poderá haver em cada equipe é 24.
Ao socializar, formalize o conceito de Máximo Divisor Comum e as formas de indicar esse número.
Resposta: 24 alunos
06) Numa fábrica de retalhos sobraram algumas tiras de 90 cm de comprimento e outras de 75 cm de comprimento. O patrão deu a ordem para que o funcionário cortasse o pano em partes iguais e de maior comprimento possível. Como ele poderá resolver essa situação? Observação: nesse caso basta encontra o MDC(90, 75)

Resolução:
Calculando o MDC(90, 75) = 15 cm.
MDC (75, 90)
75, 90 | 2
75, 45 | 3 mínimo múltiplo comum
25, 15 | 3
25, 5 | 5 mínimo múltiplo comum
5 , 1 | 5
1 |
3 . 5 = 15
Os retalhos deverão ser cortados em pedaços de 15 cm cada um.
Resposta: 15 centímetros.
07) Voltando do intervalo reservado para recreação, os alunos do 6º ano devem subir um lance de escada de 30 degraus para que alcancem o andar onde está situada a sala de aula correspondente a essa turma. Dois alunos, Rubinho e Daniel, começam a subir a escada do primeiro degrau. Rubinho resolve então subir essa escada de 3 em 3 degraus e Daniel de 2 em 2 degraus.

Marque a afirmativa CORRETA relativa à situação apresentada.
(A) Rubinho e Daniel pisarão em cinco degraus em comum, mas não chegarão no 30º degrau juntos.
(B) Rubinho e Daniel pisarão no 30º degrau, logo irão gastar o mesmo tempo para subir a escada.
(C) Rubinho pisará no 23º degrau, mas Daniel não pisará nesse degrau porque 23 não é divisível por 2.
(D) Somente Daniel pisará no 18º degrau, porque 18 é um número par sendo, portanto, divisível por 2.
Resolução:
M (2) = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 13, 14, 15, 16, ...}
M (3) = {0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, ...}
Ao fazer as sequências dos múltiplos de 2 e 3 veremos que Rubinho ao subir 11 degraus já chegou no 30 enquanto Daniel ainda não. Portanto a resposta coerente com as sequências é:
Alternativa: A
Leia o texto a seguir e responda as questões 08, 09 e 10.
Um painel luminoso de uma loja foi construído sobre uma placa semelhante ao quadro, de modo que cada um dos quadrinhos foi marcado com um número para identificar a lâmpada no painel. Assim, o painel foi programado para que as luzes que ocupavam as posições dos números múltiplos de 2 ficassem acesas permanentemente, ao mesmo tempo em que as luzes na posição dos múltiplos de 3 piscassem. Ao ligar o painel, as luzes acenderam, porém não como o esperado.

Com base no texto e a figura responda as questões 08, 09 e 10.
08) Qual foi a razão de o painel não ter funcionado como o esperado?

Resolução:
Ao programar o painel não se levou em consideração o fato de que alguns números são ao mesmo tempo múltiplos de 2 e 3, como por exemplo, o número 6. Neste caso, a lâmpada não poderá atenderá as duas ordens simultaneamente: ficar acesa e piscar simultaneamente. Dizemos, neste caso, que o painel não funcionará como o esperado, pois temos números que são múltiplos comuns de 2 e 3 ao mesmo tempo, como 6, 12, 18, 24, 30. 36, 42 e 48.
09) Por que o painel não tem uma lâmpada identificada com o número 1? Justifique.

Resolução:
Pois o número 1 não é múltiplo de nenhum número, e ao mesmo tempo é divisor de todos os números, nesse caso, se fosse considerado o número 1, essa lâmpada ficaria acesa o tempo todo ou apagada, pois não atenderia a nenhum comando.
10) Como poderia ser uma programação do painel para que funcionasse conforme o planejado?

Resolução:
Ficar acesa permanente as luzes nas posições dos divisores de 45 (3, 5, 9,15 e 45) e piscar as posições dos divisores de 32 (2, 4, 8,16 e 32), não tendo múltiplos comuns. Outras possibilidades podem aparecer, atenção para que não haja múltiplos comuns.
11) Fábio viu que seu pai comprou uma caixa com 24 maçãs e foi ajudar na preparação da comida para o aniversário da sua irmã mais nova. Seu pai lhe pediu que separasse e descascasse 7/12 das maçãs para ele fazer o suco e 3/8 delas para sua mãe colocar nas saladas. Fábio fez tudo o que foi pedido e comentou que tinha sobrado uma maçã. "É isso mesmo", disse sua mãe. "Essa é para enfeitar o bolo."

a) Quantas maçãs foram utilizadas para fazer o suco?

Resolução:
7/12 = 0,583
0,583 . 24 = 13,992
Resposta: 4 maçãs.
b) Quantas maçãs foram utilizadas para o preparo da salada?

Resolução:
3/8 = 0,375
0,375 . 24 = 9
Resposta: 9 maçãs.
12) Helena pretende revestir o chão de sua cozinha, com ladrilhos lisos e decorados. Seu arquiteto orientou que dos 144 ladrilhos, apenas 1/4 deles fossem decorados. Quantos ladrilhos serão os decorados?

Resolução:
Para encontrar fazemos
1/4 = 0,027
0,027 . 144 = 36
Resposta: serão necessários 36 ladrilhos decorados.
13) O que são frações equivalentes? Cite três exemplo

Resposta: São frações escritas de modo diferentes porém tem o mesmo valor
Exemplos:
a) 1/2
b) 9/18
c) 16/32
MATEMÁTICA 7º ANO - Atividade de 30/03/2020 a 03/04/2020
[RESOLVIDA E COMENTADA]
Lê interpretar e fazer conversarão de Escala de Mapas e Plantas
Ler e interpretar escalas em mapas é nosso assunto dessa atividade. Explore o mapa, converse com os estudantes como imaginam que os mapas são elaborados

Escala gráfica:
1 cm no mapa equivale a 250km no tamanho real.
Escala numérica:
1:250 000 000 expressa a razão entre a distância obtida no mapa (1cm) a distância real (25 000 000 cm). Assim, o 1 é o numerador e 25 000 000 o denominador.
Na representação fracionária podemos representar: 1/25 000 00
Observação:
1m = 100cm
1km = 100 000cm
1km = 1000m
Exemplo 1:
Um ponto está localizado a 5cm e a escala é 1:200 000. Qual a distância real dente ponto em km?
Resolução:
Podemos usar regra de três simples
m 1
----- = --------
M n
d = medida no desenho
D = medida real
1/n = escala
5cm 1
------ = --------------
D 200 000
D . 1 = 5 . 200 000 cm
D = 100 0000 cm
Observação: 1km = 10 0000 cm
Transformar cm em km divide-se por 10 000
Portanto, 100 000/10000 = 10
Resposta: nesse caso, a distância real é 10km
Exemplo 1:
No gráfico a seguir e responda qual é a razão da escala numérica adotada nesse gráfico?

Mapa do Estado de São paulo
Observação: dimensão fora de padrão, não use régua nem outro instrumento de medição, aplique apenas o conceito.
Resolução:
A escala é 1:600 000
Exemplo 2:
Em um mapa cuja escala é 1:2 500 000, duas cidades estão separadas, em linha reta, por 5 centímetros. A distância real (no terreno em km) entre essas duas cidades é:
(A) 50 km
(B) 75 km
(C) 125 km
(D) 500 km
(E) 1250 km
Resolução:
Podemos usar regra de três simples
m 1 (numerador)
----- = --------
D n (denominado)
m = medida no desenho
D = medida real
1/n = escala
5cm 1
------ = --------------
M 2 500 000
D . 1 = 5 . 2 500 000
D = 1 250 0000 cm
Observação: 1km = 10 0000 cm
Transformar cm em km divide-se por 10 000
Portanto, 1 250 000/10000 = 125 km
Resposta: a distância real é
Alternativa: C
03) (Caderno o Aluno Volume 1) A professora Maria Angélica tinha 230 amigos em uma rede social, e percebeu que 2/5 deles saíram por receio de terem os seus dados divulgados. Calcule quantos amigos da professora Maria Angélica saíram da sua rede social.
Resolução:
Calcular 2/5 . 230 = 460/5 = 92 amigos saíram e a resposta final é aberta para discussão sobre os perigos da rede social, para essa discussão organize uma roda de conversa.
04) (Caderno o Aluno Volume 1) Na compra de uma mochila, três lojas ofereciam os descontos a seguir. Em que loja será mais vantajoso financeiramente comprar a mochila? Justifique sua resposta.

Resolução:
Antes de calcular, procurar ouvir as hipóteses baseadas apenas na leitura dos números. Educar financeiramente um adolescente consumir conscientemente, provocar discussões sobre a influência que o grupo de amigos e mídia têm sobre as suas decisões na hora da compra. A loja mais vantajosa é a loja C, com valor final de R$ 76,50. Nas lojas A e B os valores finais são R$ 82,80 e R$ 77,90. Apresentar pelo menos duas maneiras possíveis de cálculo: 5% como 5/100 ou 0,05 e depois efetuar a subtração. A outra estratégia de cálculo do valor final, utilizando, por exemplo, 100% - 5% = 95% também poderá ser estimulada, se possível. Idem para as outras lojas.
05) (Caderno o Aluno Volume 1) A professora Cleoneide e a professora Regina juntas tinham 36 bolinhas de gude. Ao final de uma partida, decidiram separar e contar a quantidade de bolinhas de gude que tinha restado para cada um. A professora Cleoneide tinha 1/3 e professora Regina tinha 2/3. Quantas bolinhas ficaram com cada uma delas?
Resolução:
Calcular as bolinhas de Fábio: 1/3 de 36 1/3 . 36 = 36/3 = 12 bolinhas de gude.
Calcular as bolinhas de Carlos: 2/3 de 36 2/3 . 36 = 72/3 = 24 bolinhas de gude.
06) (Caderno o Aluno Volume 1 - Modificado) A Coordenadora Geral Bete comprou uma camiseta por R$ 50,00 e teve um desconto de 30% porque era a última do estoque.

Quanto ela pagou por essa camiseta?
Resolução:
30% de 50 equivale 3 x 10% de 50 = 3 x 5 = 15 ou 30/100 de 50 = 15, ou ainda 0,3 x 50 = 15. Apresentar e discutir as diferentes formas de cálculo. Se necessário, apresentar outros exemplos para descobrirem o preço final do produto e avaliar a compra.
08) (Caderno o Aluno Volume 1) O Professora Luciana foi comprar um notebook e leu na etiqueta o preço de R$ 1.812,00. Perguntou se aquele preço podia ser pago em 5 prestações, o vendedor lhe informou que para fazer à prestação acrescentaria 7,5% sobre aquele valor.

Ajude a Professora Luciana e calcule o valor final do notebook em 5 prestações. Será que vale à pena comprar à prestação?
Resolução:
Hoje, normalmente, as lojas não expõe os preços, à vista, dos produtos, chamar a atenção dos estudantes para a expressão “tantas vezes sem juros”, isto é, prestações que não cobram juros, não é real. Existe um juro mensal embutido nesse preço e é preciso negociar muito para obter alguma vantagem no preço à vista. Se a loja oferece o mesmo preço à vista até em 5 prestações, com certeza o juro mensal é altíssimo. Esta atividade está considerando apenas o acréscimo final ao preço do produto, sabe-se que o juro é calculado como juro composto mensal e depois distribuído equitativamente ao longo das prestações. É importante avaliar sempre as condições de compra, para não fazer dívidas desnecessárias. (7,5%) . 1812 = 135,90.
Valor final: 1812 + 135,90 = 1947,90.
O valor final do notebook será de R$ 11947,90.
Leia o texto a seguir e responda a questão 09.
A Coordenadora Geral Carina, consultou o farmacêutico sobre o número de gotas de um remédio recomendo para crianças. Antes de responder ele leu as seguintes instruções na bula:

A Coordenadora Geral Carina, informou que a criança tinha 2 anos e pesava aproximadamente 11 kg. Ele respondeu, então, que ela deveria dar 17 gotas. O peso das pessoas é muito variável, por isso, uma criança de 2 anos pode ter pesos diferentes, variando de 10 a 13 kg aproximadamente, por exemplo.
(Caderno o Aluno Volume 1 – Modificado)
09) Com base no texto imagine o peso das crianças abaixo qual o número de gotas que elas poderão tomar uma criança de 1 ano com 8 kg, uma criança de 2 anos com 12 kg e uma criança de 3 anos com 14 kg? Respectivamente.
a) 1 ano com 8 kg
Resolução:
2p
2 . 8 = 16 gotas
b) 2 anos com 12 kg
Resolução:
2p -5
2 . 12 -5 = 19 gotas
c) 3 anos com 14 kg
Resolução:
2p - 8
2 . 14 -8 = 20 gotas
10) (Caderno o Aluno Volume 1 - Modificada) Na Pizzaria Nona Rosa é cobrada uma taxa para entrega à domicílio. A taxa é calculada com um valor fixo de R$ 2,00 mais R$ 1,50 por quilometro de deslocamento. Os três personagens abaixo por fazerem parte do grupo de risco em relação ao Coronavírus (mais de 60 anos) fizeram por telefone um pedido na Pizzaria Nona Rosa.
A Coordenadora de Área Bete mora 8km da Pizzaria.

A Coordenadora de Área Regina mora a 11km da Pizzaria

O Diretor Douglas mora a 15km da Pizzaria.

Agora, considerando a taxa de entrega da Pizzaria Nona Rosa, calcule o valor que cada um deles pagou em deslocamento. Respetivamente.
Resolução:
A Coordenadora de Área Regina mora a 11km da Pizzaria
R$ 2,00 mais R$ 1,50
2 + 1,5 . 8 =
2 + 12 = 14
R$ 14,00
Resolução:
A Coordenadora de Área Regina mora a 11km da Pizzaria
R$ 2,00 mais R$ 1,50
2 + 1,5 . 11 =
2 + 16,6 = 18,5
R$ 18,50
Resolução:
O Diretor Douglas mora a 15km da Pizzaria.
R$ 2,00 mais R$ 1,50
2 + 1,5 . 15 =
2 + 22,15 = 24,50
R$ 24,50
Continua...








