EM - VETORES
Professor Diminoi
VETORES
Reta orientada - eixo
Uma reta r é orientada quando é fixado nela um sentido de percurso, considerado positivo, sendo indicado por uma seta.
 Segmento orientado
Segmento orientado
Um segmento orientado é determinado por um par ordenado de pontos, o primeiro chamado origem do segmento, o segundo chamado extremidade.
 Segmento nulo
Segmento nulo
Um segmento nulo é aquele cuja extremidade coincide com a origem.
Segmentos opostos
Se AB é um segmento orientado, o segmento orientado BA é oposto de AB.
Medida de um segmento
Fixada uma unidade de comprimento, cada segmento orientado pode-se associar um número real, não negativo, que é a medida do segmento em relação aquela unidade. A medida do segmento orientado é o seu comprimento ou seu módulo. O comprimento do segmento AB é indicado por .
Assim, o comprimento do segmento AB representado na figura abaixo é de 5 unidades de comprimento:
AB = 5 u.c.
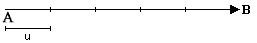 Observações
Observações
Os segmentos nulos têm comprimento igual a zero.
AB = BA.
Direção e sentido dos segmentos
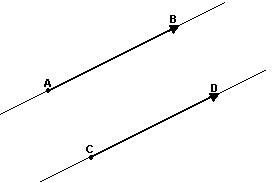
Dois segmentos orientados não nulos AB e CD têm a mesma direção se as retas suportes desses segmentos são paralelas:
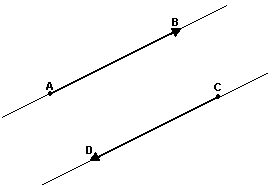 Ou coincidentes:
Ou coincidentes:
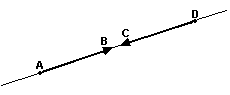
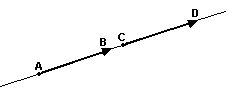 Observações:
Observações:
Só se pode comparar os sentidos de dois segmentos orientados se eles têm mesma direção.
Dois segmentos orientados opostos têm sentidos contrários.
Segmentos equipolentes
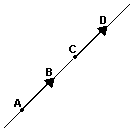
Dois segmentos orientados AB e CD são equipolentes quando têm a mesma direção, o mesmo sentido e o mesmo comprimento.
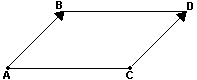
Se os segmentos orientados AB e CD não pertencem à mesma reta, como na segunda figura abaixo, para que AB seja equipolente a CD é necessário que AB//CD e AC//BD, isto é, ABCD deve ser um paralelogramo.
 Observações:
Observações:
Dois segmentos nulos são sempre equipolentes.
A equipolência dos segmentos AB e CD é representada por AB ~ CD.
Propriedades da equipolência
I. AB ~ AB(reflexiva)
II. Se AB ~ CD, CD ~ AB (simétrica)
III. Se AB ~ CD e CD ~ EF, AB ~ EF (transitiva)
IV. Dado o segmento orientado AB e um ponto C, existe um único ponto Dtal que AB ~ CD.
O que é um vetor?
Um vetor determinado por um segmento orientado AB é o conjunto de todos os segmentos orientados equipolentes a AB.
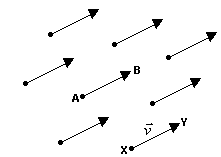 Se indicarmos com v este conjunto, simbolicamente poderemos escrever:
Se indicarmos com v este conjunto, simbolicamente poderemos escrever:
 = {XY/XY ~ AB}
= {XY/XY ~ AB}
Onde XY é um segmento qualquer do conjunto.
O vetor determinado por AB é indicado por
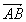 ou B - A ou
ou B - A ou 
Um mesmo vetor AB é determinado por uma infinidade de segmentos orientados, chamados representantes desse vetor, e todos equipolentes entre si. Assim, um segmento determina um conjunto que é o vetor, e qualquer um destes representantes determina o mesmo vetor.
Usando um pouco mais nossa capacidade de abstração, se considerarmos todos os infinitos segmentos orientados de origem comum, estaremos caracterizando, através de representantes, a totalidade dos vetores do espaço.
Ora, cada um destes segmentos é um representante de um só vetor. Consequentemente, todos os vetores se acham representados naquele conjunto que imaginamos.
As características de um vetor v são as mesmas de qualquer um de seus representantes, isto é: o módulo, a direção e o sentido do vetor são o módulo, direção e o sentido de qualquer um de seus representantes.
O módulo de
 Se indica por | |
Se indica por | | 
Alguns tipos de vetores
Vetores iguais
Dois vetores AB e CD são iguais se, e somente se, AB ~ CD.
Vetor Nulo
Os segmentos nulos, por serem equipolentes entre si, determinam um único vetor, chamado vetor nulo ou vetor zero, e que é indicado por 0.
Vetores Opostos
Dado um vetor v = AB, o vetor AB é o oposto de AB e se indica por AB ou por -v.
Vetor Unitário
Um vetor
E unitário se
| | = 1

Versor
Versor de um vetor não nulo v é o vetor unitário de mesma direção e mesmo sentido de v.
Exemplo
Tomemos um vetor v de módulo 3.
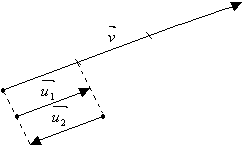 Os vetores u1 e u2 da figura são vetores unitários, pois ambos têm módulo 1. No entanto, apenas u1 tem a mesma direção e o mesmo sentido de v. Portanto, este é o versor de v.
Os vetores u1 e u2 da figura são vetores unitários, pois ambos têm módulo 1. No entanto, apenas u1 tem a mesma direção e o mesmo sentido de v. Portanto, este é o versor de v.
Vetores colineares
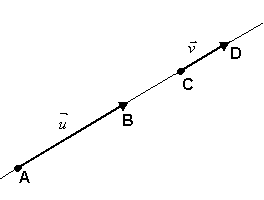
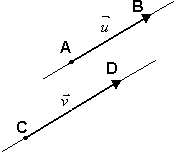
Dois vetores u e v são colineares se tiverem a mesma direção. Em outras palavras: u e v são colineares se tiverem representantes AB e CD pertencentes a uma mesma reta ou a retas paralelas.
 Vetores coplanares
Vetores coplanares
Se os vetores não nulos u, v e w (não importa o número de vetores) possuem representantes AB, CD e EF pertencentes a um mesmo plano p, diz-se que eles são coplanares.
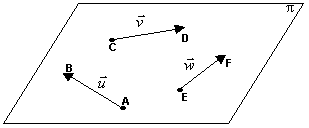 Dois vetores u e v quaisquer são são sempre coplanares, pois podemos sempre tomar um ponto no espaço e, com origem nele, imaginar os dois representantes de u e v pertencendo a um plano p que passa por este ponto.
Dois vetores u e v quaisquer são são sempre coplanares, pois podemos sempre tomar um ponto no espaço e, com origem nele, imaginar os dois representantes de u e v pertencendo a um plano p que passa por este ponto.
Três vetores poderão ou não ser coplanares.
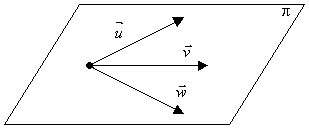 u, v e w são coplanares
u, v e w são coplanares
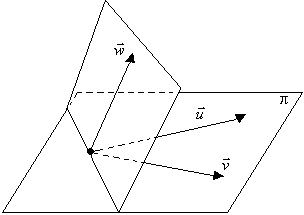 u, v e w não são coplanares
u, v e w não são coplanares
Operações com vetores
Soma de vetores
Se v = (a, b) e w = (c, d), definimos a soma de v e w por:
v + w = (a + c, b + d)
Propriedades da soma de vetores
I) Comutativa:
Para todos os vetores u e v de R2:
v + w = w + v
II) Associativa:
Para todos os vetores u, v e w de R2:
u + (v + w) = (u + v) + w
III) Elemento neutro:
Existe um vetor O = (0,0) em R2 tal que para todo vetor u de R2, se tem:
O + u = u
IV) Elemento oposto:
Para cada vetor v de R2, existe um vetor -v em R2 tal que:
v + (-v) = O
Diferença de vetores
Se v = (a, b) e w = (c, d), definimos a diferença entre v e w por:
v - w = (a - c, b - d)
Produto de um escalar por um vetor
Se v = (a,b) é um vetor e c é um número real, definimos a multiplicação de c por v, como:
c.v = (ca,cb)
Propriedades do produto de escalar por vetor
Quaisquer que sejam k e c escalares, v e w vetores:
a) 1 v = v
b) (k c) v = k (c v) = c (k v)
c) k v = c v implica k = c, se v for não nulo
d) k (v + w) = k v + k w
e) (k + c)v = k v + c v
Módulo de um vetor
O módulo ou comprimento do vetor v = (a, b) é um número real não negativo, definido por:
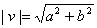 Vetor unitário
Vetor unitário
Vetor unitário é o que tem o módulo igual a 1.
Existem dois vetores unitários que formam a base canônica para o espaço R2, que são dados por:
i = (1,0) j = (0,1)
Para construir um vetor unitário u que tenha a mesma direção e sentido que um outro vetor v, basta dividir o vetor v pelo seu módulo, isto é:
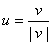 Observação:
Observação:
Para construir um vetor u paralelo a um vetor v, basta tomar u = cv onde c é um escalar não nulo. Nesse caso, u e v serão paralelos.
Se c = 0 então u será o vetor nulo.
Se 0 < c < 1 então u terá comprimento menor do que v.
Se c > 1 então u terá comprimento maior do que v.
Se c < 0 então u terá sentido oposto ao de v.
Produto escalar
Dados os vetores u = (a, b) e v = (c, d), definimos o produto escalar entre os vetores u e v, como o número real obtido por:
u.v = a.c + b.d
Exemplos
O produto escalar entre u = (3, 4) e v = (-2, 5) é:
u.v = 3.(-2) + 4.(5) = -6+20 = 14
O produto escalar entre u = (1, 7) e v = (2, -3) é:
u.v = 1.(2) + 7.(-3) = 2-21 = -19
Propriedades do produto escalar
Quaisquer que sejam os vetores, u, v e w e k escalar:
a) w = w.v
b) v = |v| |v| = |v|2
c) u.(v + w) = v + u.w
d) (kv).w = (kw) = k(v.w)
e) |kv| = |k| |v|
f) |u.v| <= |u| |v| (desigualdade de Schwarz)
g) |u + v| <= |u| + |v| (desigualdade triangular)
Observação: significa menor ou igual
Ângulo entre dois vetores
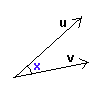
O produto escalar entre os vetores u e v pode ser escrito na forma:
u.v = |u| |v| cos(x)
Onde x é o ângulo formado entre u e v.
 Através desta última definição de produto escalar, podemos obter o ângulo x entre dois vetores genéricos u e v, como.
Através desta última definição de produto escalar, podemos obter o ângulo x entre dois vetores genéricos u e v, como.
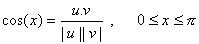 Desde que nenhum deles seja nulo.
Desde que nenhum deles seja nulo.
Vetores ortogonais
Dois vetores u e v são ortogonais se:
U . v = 0
Continua ...












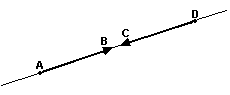



 Se indicarmos com v este conjunto, simbolicamente poderemos escrever:
Se indicarmos com v este conjunto, simbolicamente poderemos escrever: Os vetores u1 e u2 da figura são vetores unitários, pois ambos têm módulo 1. No entanto, apenas u1 tem a mesma direção e o mesmo sentido de v. Portanto, este é o versor de v.
Os vetores u1 e u2 da figura são vetores unitários, pois ambos têm módulo 1. No entanto, apenas u1 tem a mesma direção e o mesmo sentido de v. Portanto, este é o versor de v.


 u, v e w são coplanares
u, v e w são coplanares
 Através desta última definição de produto escalar, podemos obter o ângulo x entre dois vetores genéricos u e v, como.
Através desta última definição de produto escalar, podemos obter o ângulo x entre dois vetores genéricos u e v, como.