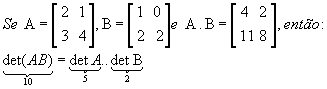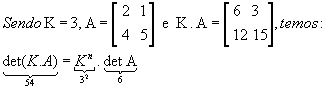EM - DETERMINANTE
Professor Diminoi
DETERMINANTES
Introdução
Como já vimos, matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou seja, é do tipo n x n). A toda matriz quadrada está associado um número ao qual damos o nome de determinante.
Dentre as várias aplicações dos determinantes na Matemática, temos:
- Resolução de alguns tipos de sistemas de equações lineares;
- Cálculo da área de um triângulo situado no plano cartesiano, quando são conhecidas as coordenadas dos seus vértices;
Determinates de 1ª ordem
Dada uma matriz quadrada de 1ª ordem M = [a11], o seu determinante é o número real a11:
det M =Ia11I = a11
Observação: representamos o determinante de uma matriz entre duas barras verticais, que não têm o significado de módulo.
Exemplo
M= [5] det M = 5 ou |5| = 5
M = [-3] det M = -3 ou |-3| = -3
Determinante de 2ª ordem
Dada a matriz
 De ordem 2, por definição o determinante associado a M, de 2ª ordem, é dado por:
De ordem 2, por definição o determinante associado a M, de 2ª ordem, é dado por:
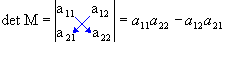 Portanto, o determinante de uma matriz de ordem 2 é dado pela diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária.
Portanto, o determinante de uma matriz de ordem 2 é dado pela diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária.
Observe o exemplo a seguir.
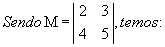
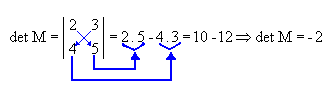 Menor complementar
Menor complementar
Chamamos de menor complementar relativo a um elemento aij de uma matriz M, quadrada e de ordem n > 1, o determinante MCij , de ordem n - 1, associado à matriz obtida de M quando suprimimos a linha e a coluna que passam por aij .
Observe como determiná-lo pelos exemplos a seguir:
a) Dada a matriz
 De ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11), retiramos a linha 1 e a Coluna 1:
De ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11), retiramos a linha 1 e a Coluna 1:
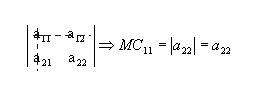 Da mesma forma, o menor complementar relativo ao elemento a12 é:
Da mesma forma, o menor complementar relativo ao elemento a12 é:
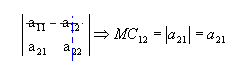 b) Sendo
b) Sendo
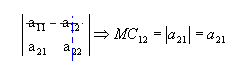 De ordem 3, temos:
De ordem 3, temos:
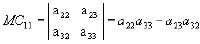
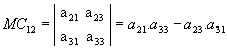 Cofator
Cofator
Chamamos de cofator ou complemento algébrico relativo a um elemento aij de uma matriz quadrada de ordem n o número Aij tal que Aij = (-1)i+j . MCij .
Exemplo
a) Dada
 Os cofatores relativos aos elementos a11 e a12 da matriz M são:
Os cofatores relativos aos elementos a11 e a12 da matriz M são:
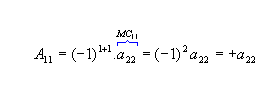
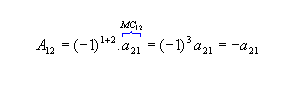 b) Sendo
b) Sendo
 Vamos calcular os cofatores A22, A23 e A31:
Vamos calcular os cofatores A22, A23 e A31:
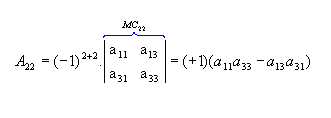
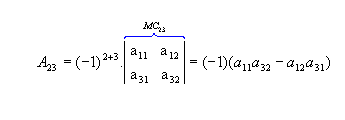
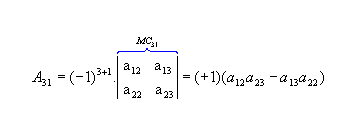 Teorema de Laplace
Teorema de Laplace
O determinante de uma matriz quadrada
M = [aij]mxn
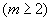
Pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer (linha ou coluna) da matriz M pelos respectivos cofatores.
Assim, fixando
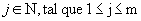 Temos:
Temos:
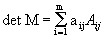 Em que
Em que
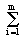 E o somatório de todos os termos de índice i, variando de 1 até m,
E o somatório de todos os termos de índice i, variando de 1 até m,
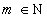 Exemplo
Exemplo
Calcule o determinante da matriz A, aplicando o Teorema de Laplace:
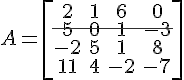 Destacando a segunda linha da matriz, temos
Destacando a segunda linha da matriz, temos
D = 5 . A21 + 0 . A22 + 1 . A23 + (-3) . A24.
Calculando os cofatores:
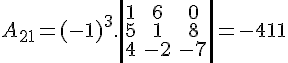
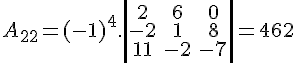
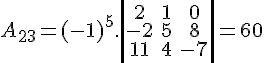
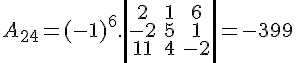
Para finalizar, calculamos o determinante:
D = 5 . A21 + 0 . A22 + 1 . A23 + 3 . A24
D = 5 . (–411) + 0 . (462) + 1 . (60) + (–3) . (–399)
D = –2055 + 0 + 60 + 1197
D = – 798
Regra de Sarrus
O cálculo do determinante de 3ª ordem pode ser feito por meio de um dispositivo prático, denominado regra de Sarrus.
Acompanhe como aplicamos essa regra para
1º passo: Repetimos as duas primeiras colunas ao lado da terceira:
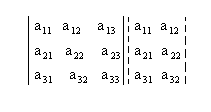 2º passo: Encontramos a soma do produto dos elementos da diagonal principal com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal (a soma deve ser precedida do sinal positivo):
2º passo: Encontramos a soma do produto dos elementos da diagonal principal com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal (a soma deve ser precedida do sinal positivo):
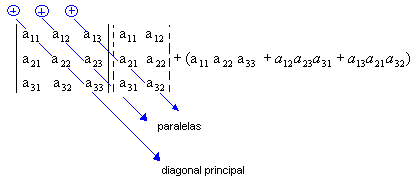 3º passo: Encontramos a soma do produto dos elementos da diagonal secundária com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal (a soma deve ser precedida do sinal negativo):
3º passo: Encontramos a soma do produto dos elementos da diagonal secundária com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal (a soma deve ser precedida do sinal negativo):
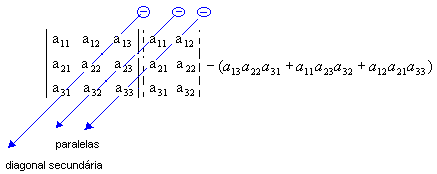 Assim:
Assim:
 Observação: Se desenvolvermos esse determinante de 3ª ordem aplicando o Teorema de Laplace, encontraremos o mesmo número real.
Observação: Se desenvolvermos esse determinante de 3ª ordem aplicando o Teorema de Laplace, encontraremos o mesmo número real.
Determinante de ordem n > 3
Vimos que a regra de Sarrus é válida para o cálculo do determinante de uma matriz de ordem 3.
Quando a matriz é de ordem superior a 3, devemos empregar o Teorema de Laplace para chegar a determinantes de ordem 3 e depois aplicar a regra de Sarrus.
Propriedades dos determinantes
Os determinantes associados a matrizes quadradas de ordem n apresentam as seguintes propriedades:
P1) Quando todos os elementos de uma fila (linha ou coluna) são nulos, o determinante dessa matriz é nulo.
Exemplo
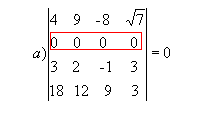
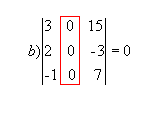
P2) Se duas filas de uma matriz são iguais, então seu determinante é nulo.
Exemplo
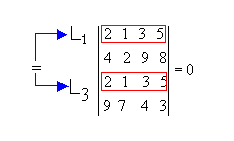 P3) Se duas filas paralelas de uma matriz são proporcionais, então seu determinante é nulo.
P3) Se duas filas paralelas de uma matriz são proporcionais, então seu determinante é nulo.
Exemplo
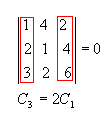 7P4) Se os elementos de uma fila de uma matriz são combinações lineares dos elementos correspondentes de filas paralelas, então seu determinante é nulo.
7P4) Se os elementos de uma fila de uma matriz são combinações lineares dos elementos correspondentes de filas paralelas, então seu determinante é nulo.
Exemplos
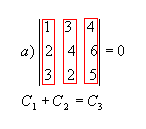
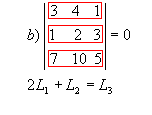
P5) Teorema de Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.
Exemplo
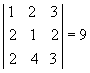
Substituindo a 1ª coluna pela soma dessa mesma coluna com o dobro da 2ª, temos:
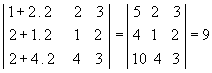
Propriedades dos determinantes (continuação)
P6) O determinante de uma matriz e o de sua transposta são iguais.
Exemplo
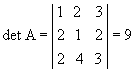
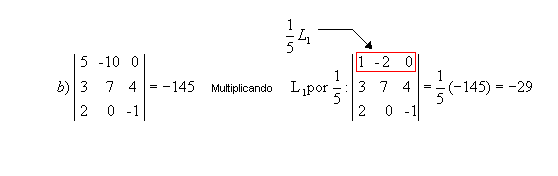
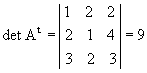 P7) Multiplicando por um número real todos os elementos de uma fila em uma matriz, o determinante dessa matriz fica multiplicado por esse número.
P7) Multiplicando por um número real todos os elementos de uma fila em uma matriz, o determinante dessa matriz fica multiplicado por esse número.
Exemplos
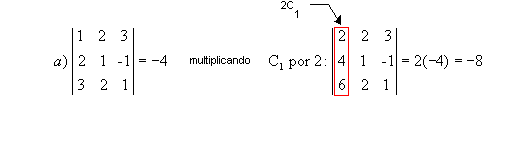
P8) Quando trocamos as posições de duas filas paralelas, o determinante de uma matriz muda de sinal.
Exemplo
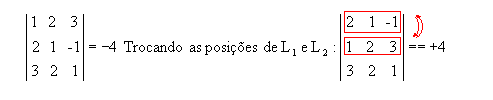 P9) Quando, em uma matriz, os elementos acima ou abaixo da diagonal principal são todos nulos, o determinante é igual ao produto dos elementos dessa diagonal.
P9) Quando, em uma matriz, os elementos acima ou abaixo da diagonal principal são todos nulos, o determinante é igual ao produto dos elementos dessa diagonal.
Exemplos
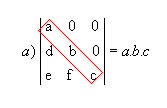
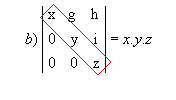
Propriedades dos determinantes (continuação)
P10) Quando, em uma matriz, os elementos acima ou abaixo da diagonal secundária são todos nulos, o determinante é igual ao produto dos elementos dessa diagonal multiplicado por
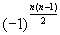 Exemplos
Exemplos
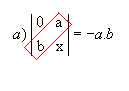
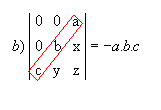
P11) Para A e B matrizes quadradas de mesma ordem n como:

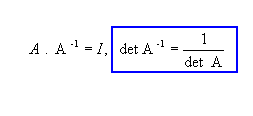 Exemplo
Exemplo
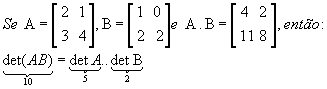 P12)
P12)
 Exemplo
Exemplo
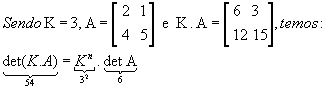
Continua ...









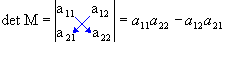
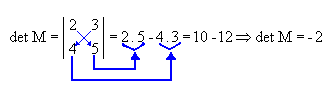
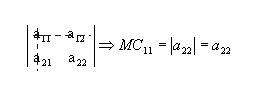
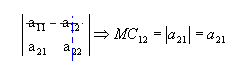
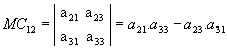
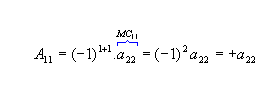
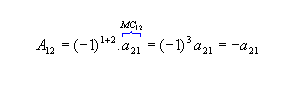

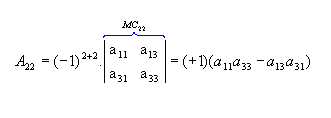
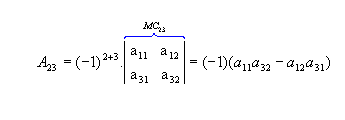
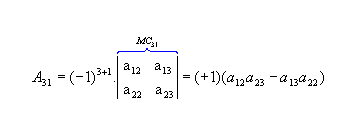
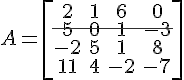
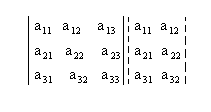

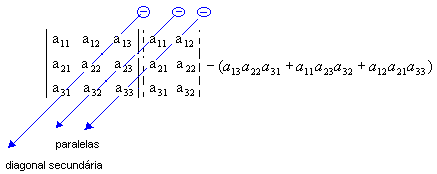 Assim:
Assim:
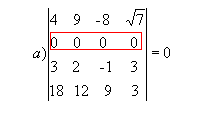
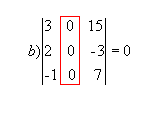

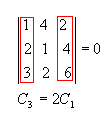
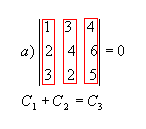
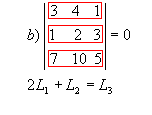
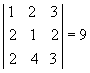
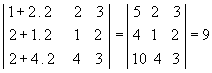
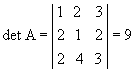
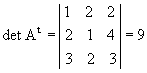
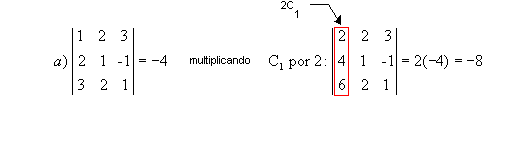

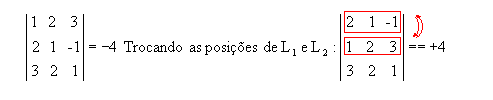
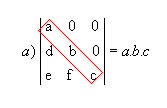
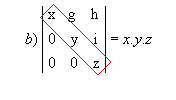
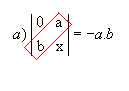
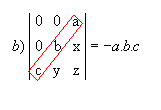
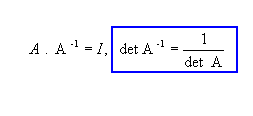 Exemplo
Exemplo