EM - PROBABILIDADE
Professor Diminoi
PROBABILIDADE
Introdução
A história da teoria das probabilidades teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade. A teoria da probabilidade permite que se calcule a chance de ocorrência de um número em um experimento aleatório.
Experimento aleatório
É aquele experimento que, quando repetido em iguais condições, pode fornecer resultados diferentes, ou seja, são resultados explicados ao acaso. Quando se fala de tempo e possibilidades de ganho na loteria, a abordagem envolve cálculo de experimento aleatório.
Espaço amostral
É o conjunto de todos os resultados possíveis de um experimento aleatório. A letra que representa o espaço amostral é S.
Exemplo
Lançando uma moeda e um dado, simultaneamente, sendo S o espaço amostral, constituído pelos 12 elementos:
S = {K1, K2, K3, K4, K5, K6, R1, R2, R3, R4, R5, R6}
Escreva explicitamente os seguintes eventos:
A = {caras e um número par aparece}
B = {um número primo aparece}
C = {coroas e um número ímpar aparecem}
Idem, o evento em que:
a) A ou B ocorrem;
b) B e C ocorrem;
Somente B ocorre.
Quais dos eventos A, B e C são mutuamente exclusivos?
Resolução
Para obter A, escolhemos os elementos de S constituídos de um K e um número par:
A = {K2, K4, K6};
Para obter B, escolhemos os pontos de S constituídos de números primos:
B = {K2,K3,K5,R2,R3,R5};
Para obter C, escolhemos os pontos de S constituídos de um R e um número ímpar:
C = {R1,R3,R5}.
(a) A ou B = AUB = {K2,K4,K6,K3,K5,R2,R3,R5}
(b) B e C = B C = {R3,R5}
(c) Escolhemos os elementos de B que não estão em A ou C:
B (esta contundo em) Ac (esta contido em) Cc = {K3,K5,R2}
A e C são mutuamente exclusivos, porque
A (esta contido em) C = ∅
Conceito de probabilidade
Se em um fenômeno aleatório as possibilidades são igualmente prováveis, então a probabilidade de ocorrer um evento A é:
Por, exemplo, no lançamento de um dado, um número par pode ocorrer de 3 maneiras diferentes dentre 6 igualmente prováveis, portanto, P = 3/6= 1/2 = 50%.
Dizemos que um espaço amostral S (finito) é equiprovável quando seus eventos elementares têm probabilidades iguais de ocorrência. Num espaço amostral equiprovável S (finito), a probabilidade de ocorrência de um evento A é sempre:
Propriedades importantes:
Se A e A’ são eventos complementares, então:
P(A) + P(A') = 1
A probabilidade de um evento é sempre um número entre 0 (probabilidade de evento impossível) e 1 (probabilidade do evento certo).
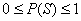Probabilidade condicional
Antes da realização de um experimento, é necessário que já se tenha alguma informação sobre o evento que se deseja observar. Nesse caso, o espaço amostral se modifica e o evento tem a sua probabilidade de ocorrência alterada.
Fórmula de Probabilidade Condicional
P(E1 e E2 e E3 e ...e En-1 e En) é igual a P(E1).P(E2/E1).P(E3/E1 e E2)...P(En/E1 e E2 e ...En-1).
Onde :
- P(E2/E1) é a probabilidade de ocorrer E2, condicionada pelo fato de já ter ocorrido E1;
- P(E3/E1 e E2) é a probabilidade ocorrer E3, condicionada pelo fato de já terem ocorrido E1 e E2;
- P(Pn/E1 e E2 e ...En-1) é a probabilidade de ocorrer En, condicionada ao fato de já ter ocorrido E1 e E2...En-1.
Exemplo
Uma urna tem 30 bolas, sendo 10 vermelhas e 20 azuis. Se ocorrer um sorteio de 2 bolas, uma de cada vez e sem reposição, qual será a probabilidade de a primeira ser vermelha e a segunda ser azul?
Resolução
Seja o espaço amostral S = 30 bolas, vamos considerar os seguintes eventos:
A: vermelha na primeira retirada e P(A) = 10/30
B: azul na segunda retirada e P(B) = 20/29
Assim:
P(A e B) = P(A).(B/A) = 10/30.20/29 = 20/87
Eventos independentes
Dizemos que E1 e E2 e ...En-1, En são eventos independentes quando a probabilidade de ocorrer um deles não depende do fato de os outros terem ou não terem ocorrido.
Fórmula da probabilidade dos eventos independentes:
P(E1 e E2 e E3 e ... e En-1 e En) = P(E1).P(E2).p(E3)...P(En)
Exemplo
Uma urna tem 30 bolas, sendo 10 vermelhas e 20 azuis. Se sortearmos 2 bolas, 1 de cada vez e repondo a sorteada na urna, qual será a probabilidade de a primeira ser vermelha e a segunda ser azul?
Resolução
Como os eventos são independentes, a probabilidade de sair vermelha na primeira retirada e azul na segunda retirada é igual ao produto das probabilidades de cada condição, ou seja:
P(A e B) = P(A).P(B)
Ora, a probabilidade de sair vermelha na primeira retirada é 10/30 e a de sair azul na segunda retirada 20/30.
Daí, usando a regra do produto, temos: 10/30.20/30 = 2/9.
Observe que na segunda retirada forma consideradas todas as bolas, pois houve reposição.
Assim, P(B/A) = P(B), porque o fato de sair bola vermelha na primeira retirada não influenciou a segunda retirada, já que ela foi reposta na urna.
Probabilidade de ocorrer a união de eventos
Fórmula da probabilidade de ocorrer a união de eventos
P(E1 ou E2) = P(E1) + P(E2) - P(E1 e E2)
De fato, se existirem elementos comuns a E1 e E2, estes eventos estarão computados no cálculo de P(E1) e P(E2).
Para que sejam considerados uma vez só, subtraímos P(E1 e E2).
Fórmula de probabilidade de ocorrer a união de eventos mutuamente exclusivos
P(E1 ou E2 ou E3 ou ... ou En) = P(E1) + P(E2) + ... + P(En)
Exemplo
Se dois dados, azul e branco, forem lançados, qual a probabilidade de sair 5 no azul ou 3 no branco?
Resolucao
Considerando os eventos:
A: Tirar 5 no dado azul e P(A) = 1/6
B: Tirar 3 no dado branco e P(B) = 1/6
Sendo S o espaço amostral de todos os possíveis resultados, temos:
n(S) = 6.6 = 36 possibilidades. Daí, temos: P(A ou B) = 1/6 + 1/6 – 1/36 = 11/36
Exemplo
Se retirarmos aleatoriamente uma carta de baralho com 52 cartas, qual a probabilidade de ser um 8 ou um Rei?
Resolucao
Sendo S o espaço amostral de todos os resultados possíveis, temos: n(S) = 52 cartas. Considere os eventos:
A: sair 8 e P(A) = 4/52
B: sair um rei e P(B) = 4/52
Assim, P(A ou B) = 4/52 + 4/52 – 0 = 8/52 = 2/13.
Note que P(A e B) = 0, pois uma carta não pode ser 8 e rei ao mesmo tempo. Quando isso ocorre dizemos que os eventos A e B são mutuamente exclusivos.
Continua ...
