Professor Diminoi

CINEMÁTICA

Cinemática - É a parte da Mecânica que estuda os movimentos sem que haja preocupação com suas causas e efeitos. Alguns conceitos de Cinemática são muito importantes para a correta compreensão de fenômenos físicos e pleno entendimento da forma de se construir o raciocínio necessário para a resolução de problemas.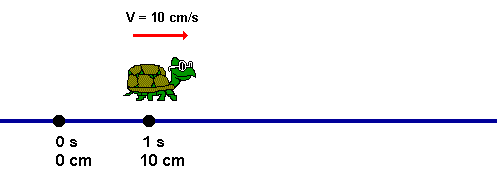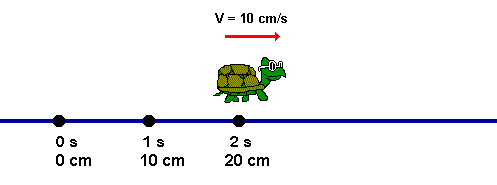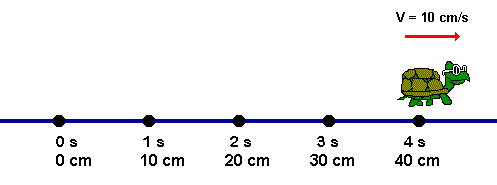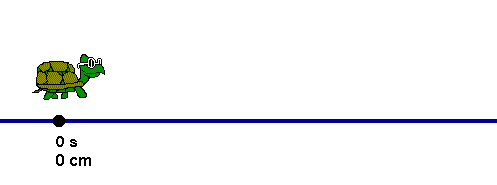
Observação: cinemática estuda o movimento dos corpos sem se preocupar com a causa deste movimento.
O movimento esta presente em toda a natureza: nos movimentos de translação e de rotação dos astros, nas massa de ar, nas marés, na migração de aves, entre inúmeros outros exemplos. A maioria das atividades humanas também está relacionada as movimento. Movimentos como o do leão fugindo dos búfalos bem como os movimentos dos búfalos afugentando o leão representado na figura abaixo. Neste link estudarmos CINEMÁTICA que é a parte da física que descreve os movimentos sem se preocupar com suas causas e consequências.
Neste link estudarmos CINEMÁTICA que é a parte da física que descreve os movimentos sem se preocupar com suas causas e consequências.


Trajetória/Trajeto – É o caminho descrito pelo móvel (nem sempre o trajeto para se ir de um ponto A um ponto B e igual a distância em linha reta entre A a B).
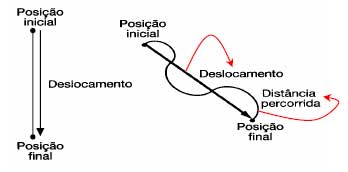
Observação: A Trajetória é uma linha imaginária que representa as sucessivas posições de o corpo ocupa ao longo do tempo.
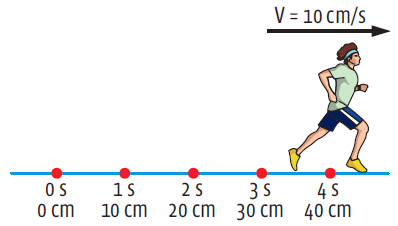
No Sistema Internacional a velocidade e em metros por segundo (m/s) e o tempo em segundo (s).
Observação: para transformar m/s em km/h basta multiplicar o valor por 3,6 e para transformar k/h em m/s basta dividir o valor por 3,6.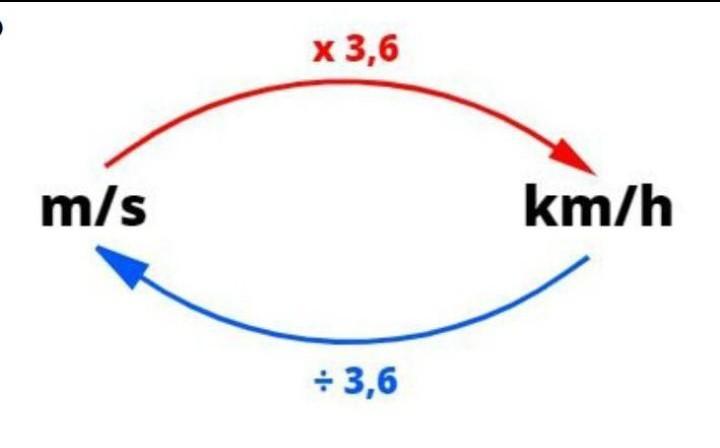 Ponto material - É um corpo cujas dimensões pode ser desprezada na resolução do problema (quando estudamos a velocidade da luz do Sol até chegar a Terra.
Ponto material - É um corpo cujas dimensões pode ser desprezada na resolução do problema (quando estudamos a velocidade da luz do Sol até chegar a Terra. Posição de um corpo - É onde o corpo se encontra no momento em questão.
Posição de um corpo - É onde o corpo se encontra no momento em questão.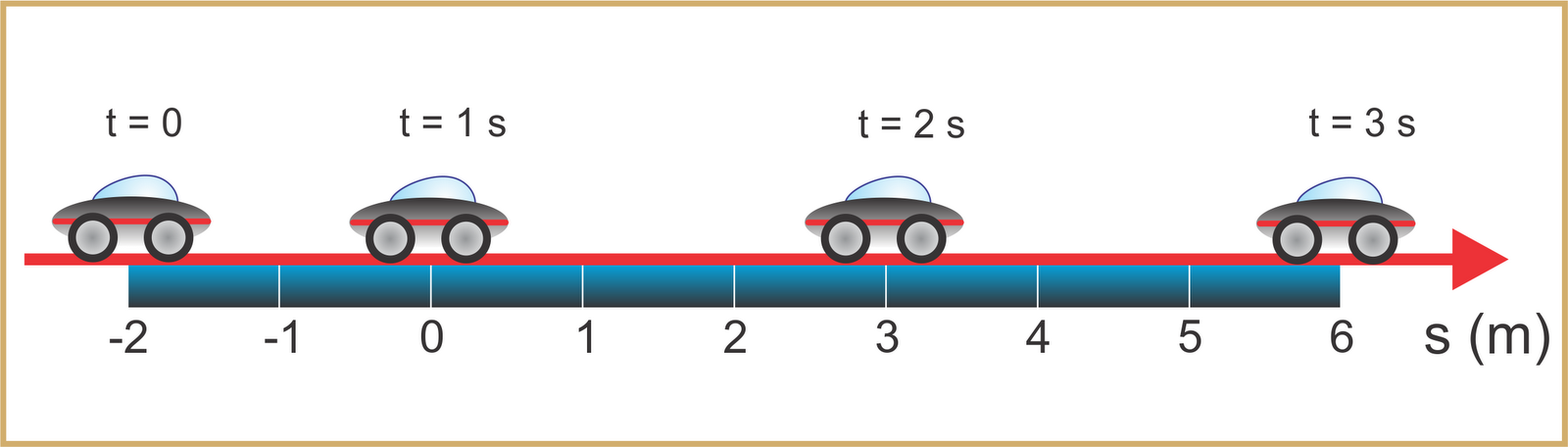 Referencial - É qualquer corpo que adotamos para comparar com outro. Na figura abaixo tomamos como referencial o homem sentado no morrinho ao lado da rodovia.
Referencial - É qualquer corpo que adotamos para comparar com outro. Na figura abaixo tomamos como referencial o homem sentado no morrinho ao lado da rodovia.
Corpo em movimento ou repouso - Para saber se um corpo esta em movimento ou em repouso é necessário adotarmos um referencial (observe o item anterior). Se a posição entre o ônibus e o homem estiver variando no decorrer do tempo, o ônibus esta em movimento em relação ao homem, assim, como o homem está em movimento em relação ao ônibus e aos passageiro.  Também podemos dizer: o ônibus está em movimento em relação ao homem e em repouso em relação aos passageiros.
Também podemos dizer: o ônibus está em movimento em relação ao homem e em repouso em relação aos passageiros.

Observe a ilustração: na ilustração temos o 1 carro, 1 home, 1 passarinho e 2 árvores. Pergunta-se, quem esta em movimento? Quem está em repouso? Justifique sua resposta. Espaço percorrido – É a distância percorrida pelo móvel ou seja, a posição final (S) menos a posição inicia (So).
Espaço percorrido – É a distância percorrida pelo móvel ou seja, a posição final (S) menos a posição inicia (So). MOVIMENTO UNIFORME
MOVIMENTO UNIFORME
Movimento Uniforme (MU) - O Movimento Uniforme é qualquer movimento realizado por um corpo que percorre distâncias iguais em tempos iguais. No MU, o corpo não necessita estar se movimentando em linha reta, em círculos ou em qualquer outra forma, basta que a sua velocidade escalar se mantenha a mesma por todo o tempo.
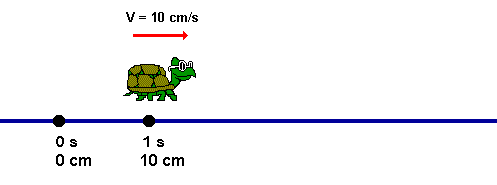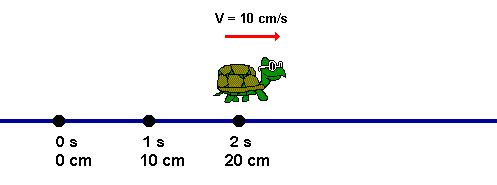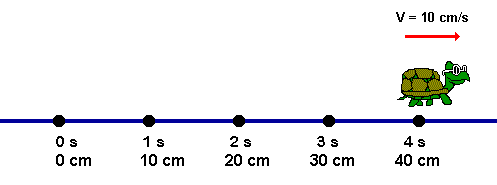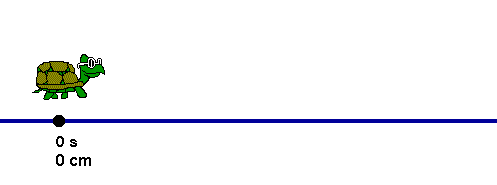
Um corpo está em movimento uniforme quando sua velocidade é constante, isso é não vaia no decorrer do tempo. Isto é, Percorre distâncias iguais em intervalos de temos iguais.
MOVIMENTO RETILÍNEO UNIFORME
Movimento Retilíneo Uniforme (MRU) - É a mesma coisa que o MU, exceto pelo fato de que, obrigatóriamente, o trajeto percorrido pelo corpo deve ser uma linha reta. Gráficos do Movimento Uniforme (MU)
Gráficos do Movimento Uniforme (MU) VELOCIDADE MÉDIA
VELOCIDADE MÉDIA
Velocidade Média - A velocidade média de um móvel pode ser interpretada como o valor da velocidade constante que um segundo móvel deveria manter para fazer o mesmo percurso no mesmo tempo que o móvel em estudo.
Sabemos que o conceito de deslocamento é a medida da distância entre duas posições ocupadas pelo corpo em movimento, sobre uma trajetória. Essa medida costuma ser obtida entre duas referências como, por exemplo, entre marcos quilométricos de uma estrada.
Velocidade Escalar Média - Já o conceito de velocidade escalar nos dá a ideia numérica da rapidez com que o corpo se movimenta e em que orientação ele o faz. Essa velocidade pode estar relacionada a um intervalo de tempo, quando é denominada velocidade escalar média. A velocidade escalar instantânea representa a velocidade de um móvel num determinado instante de seu movimento.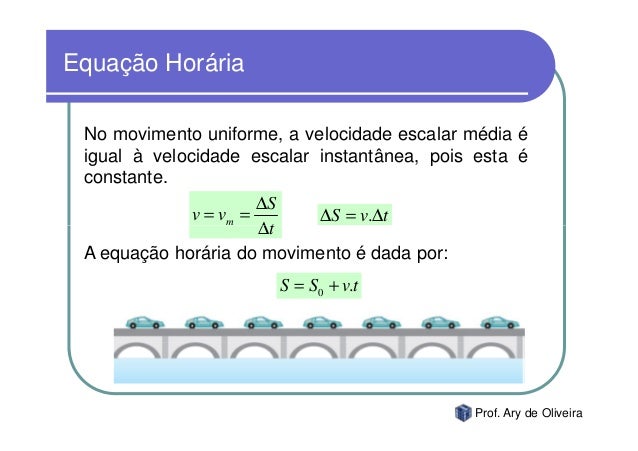 Exemplo: para saber qual a velocidade média desenvolvida pelo carro entre as posição A e B use: Vm=ΔS/t . Portanto ΔS = B - A → ΔS = 100 - 0 → ΔS = 100. Bastas dividir 100m pelo tempo que é 5s e você terá a velocidade média que é: Vm = 20m/s.
Exemplo: para saber qual a velocidade média desenvolvida pelo carro entre as posição A e B use: Vm=ΔS/t . Portanto ΔS = B - A → ΔS = 100 - 0 → ΔS = 100. Bastas dividir 100m pelo tempo que é 5s e você terá a velocidade média que é: Vm = 20m/s. Gráfico da Velocidade em Função do Tempo (velocidade mádia).
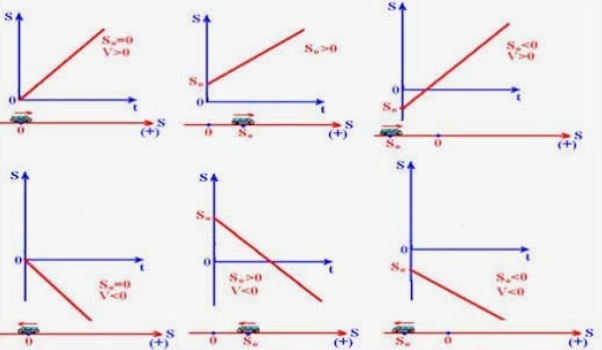
Gráfico da Velocidade em Função do Tempo (velocidade mádia). Movimento Progressivo ou Movimento a Favor da Trajetória - Um móvel está em movimento progressivo quando seu deslocamento tem sentido a favor da trajetória, isto é, se afasta da origem das posição. Nesse caso a velocidade é positiva.
Movimento Progressivo ou Movimento a Favor da Trajetória - Um móvel está em movimento progressivo quando seu deslocamento tem sentido a favor da trajetória, isto é, se afasta da origem das posição. Nesse caso a velocidade é positiva.
Movimento Retrógrado ou Movimento Contrário a Trajetória - Um móvel está em movimento retrógrado quando seu deslocamento tem sentido contrário a trajetória, isto é, se aproxima da origem das posição. Nesse caso a velocidade é negativa.
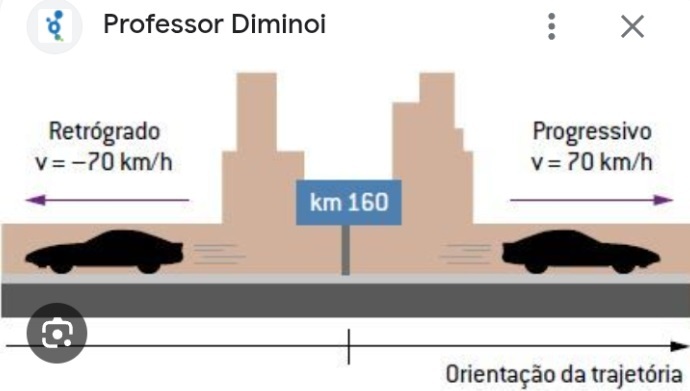

 Gráfico do Movimento Progressivo e Movimento Retrógrado
Gráfico do Movimento Progressivo e Movimento Retrógrado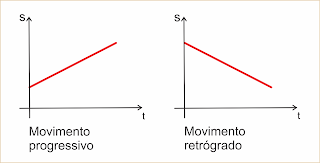 Gráficos do Movimento Uniforme (MU)
Gráficos do Movimento Uniforme (MU) Gráficos do Movimento Uniformemente Variado
Gráficos do Movimento Uniformemente Variado
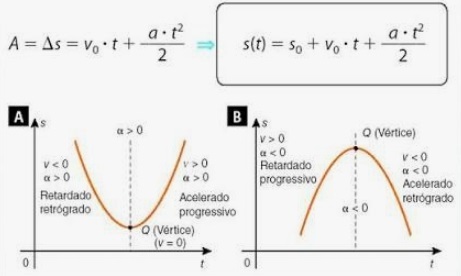
Diferentemente do Movimento Uniforme, o Movimento Uniformemente Variado possui velocidade escalar média variável, e aceleração constante (a = cte) e diferente de zero (a ≠ 0).
Função horária dos espaços s = f(t).
A função horária dos espaços no MUV é uma função do 2º grau dada por:
S = So + Vo .t + a . t2
2
S = espaço final (m)
S0 = espaço inicial (m)
V0 = velocidade inicial (m/s)
t = tempo (s)
a = aceleração (m/s2)
Por ser do 2º grau, a representação gráfica da função é uma parábola.
Gráficos
Gráficos da Aceleração
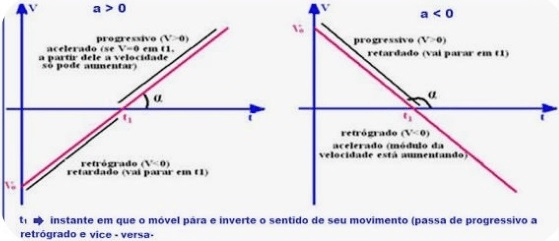
No Movimento Uniformemente Variado, a aceleração é constante e diferente de zero, logo, a função da velocidade é uma função constate, e o gráfico que representa essa função é uma reta paralela ao eixo dos tempos.
Função horária da velocidade v = f(t)
A função horária da velocidade é uma função do 1º grau, representada por:
v = v0 + a.t
Por ser uma função de primeiro grau, a representação gráfica dessa função é uma reta.
QUESTÕES DE CINEMÁTICA - RESOLVIDAS
01) (UELONDRINA-PR) Em 1984, o navegador Amyr Klink atravessou o Oceano Atlântico em um barco a remo, percorrendo a distância de, aproximadamente, 7000 km em 100 dias.
Nessa tarefa, sua velocidade média foi, em km/h, igual a:
(A) 1,4
(B) 2,9
(C) 6,0
(D) 7,0
(E) 70
Resolução:
Temos que 1 dia = 24 h, logo 100 dias = 2400h
Como Vm = ΔS/Δt, podemos dizer que Vm = 7000 km/ 2400h, então: Vm = 2,9 km/h
Alternativa: B
02) (MACKENZIE-SP) Um motorista deseja fazer uma viagem de 230 km em 2,5 horas. Se na primeira hora ele viajar com velocidade média de 80 km/h, a velocidade média no restante do percurso deve ser de:
(A) 120 km/h
(B) 110 km/h
(C) 100 km/h
(D) 90 km/h
(E) 85 km/h
Resolução:
Vm = ΔS/Δt, logo para a primeira hora temos: ΔS = Vm . Δt
ΔS = 80 . 1, então: ΔS = 80 Km. Ainda falta percorrer 150 km em 1,5 h. Logo sua velocidade média deverá ser:
Vm = 150/1,5, que nos dá um resultado de: Vm = 100km/h
Alternativa: C
03) Uma composição ferroviária com 1 locomotiva e 14 vagões desloca-se à velocidade constante de 10 m/s. Tanto a locomotiva quanto cada vagão medem 12 m. Então, quanto tempo ela demorará para atravessar um viaduto com 200 m de comprimento?
Resolução:
O comprimento total do trem é 15 . 12 = 180 m.
Devemos levar em consideração além do comprimento do trem, a extensão da ponte do viaduto.
Nesse caso, esses dois valores devem ser somados:
ΔS = 180 + 200, logo ΔS = 380 m
O tempo necessário para que o trem atravesse a ponte será:
Δt = ΔS/Vm
Então: Δt = 380/10 = 38
O tempo necessário para o trem atravessar o viaduto será igual a 38 segundos.
04) Qual será a distância total percorrida por um automóvel que parte de um hotel, no km 78 de uma rodovia, leva os hóspedes até uma fazenda de gado, no km 127 dela, e depois retorna ao local de saída?
Resolução:
A distância total percorrida na ida é dada pela subtração da posição final pela posição inicial, logo: 127 - 78 = 49 km
Contando a ida e volta, temos: 49 x 2 = 98 km
05) (UNIFICADO-RJ) A nave espacial New Horizons foi lançada pela agência espacial NASA para estudar o planeta anão Plutão em janeiro de 2006. Em julho de 2015, a nave chegou muito próximo a Plutão e conseguiu enviar imagens de sua superfície. A distância estimada entre a Terra e a nave, quando ela estava bem próxima a Plutão, era de 32 unidades astronômicas (1 unidade astronômica = 150 milhões de quilômetros).
Se a velocidade da luz é de 300 mil quilômetros por segundo, a imagem recebida pelos observatórios terrestres levou, da New Horizons até a Terra, aproximadamente
(A) 0,1 microssegundo
(B) 1 hora
(C) 4 horas e meia
(D) 2 dias
(E) zero segundos
Resolução:
Determinando a distância em quilômetros entre a Terra e Plutão, teremos:
32 UA x 150 .106 km = 4,8.109 km
Sabendo que a velocidade da luz é de 3.105 km/s, podemos utilizar a equação da velocidade média e determinar o tempo gasto pela l= Δs ÷ Δt
3.105 = 4,8.109 ÷ Δt
Δt = 4,8.109 ÷ 3.105
Δt = 1,6 . 104 s = 16000 s
Uma hora possui 3600 s, logo, 16000 s divididos por 3600 s resultam em 4,4 h, aproximadamente 4,5 h.
Alternativa: C
06) (UEFS) Pela experiência cotidiana, sabe-se que o movimento representa uma mudança contínua na posição de um corpo em relação a um dado referencial. A posição de uma partícula movendo-se ao longo do eixo z varia no tempo, de acordo com a expressão z(t) = 5t3 – 3t, em que z está em metros e t, em segundos.
Com base nessas informações, analise as afirmativas e marque com V as verdadeiras e com F as falsas.
( ) O movimento da partícula é retilíneo e uniformemente acelerado.
( ) A partícula apresenta um movimento progressivo em toda sua trajetória.
( ) A velocidade média da partícula entre os instantes t = 1,0 s e t = 2,0 s é igual a 32,0m/s.
( ) Em t = 0s e em, aproximadamente, t = 0,77s, a partícula passa pela origem da sua trajetória.
A alternativa que contém a sequência correta, de cima para baixo, é a
(A) F V V F
(B) F V F V
(C) F F V V
(D) V V F F
(E) V F F V
Resolução:
Antes de analisar as afirmações, devemos notar que:
Ao dividir todos os termos da equação pelo tempo, temos:
v = 5t2 – 3
Isso revela que a velocidade pode ter valores positivos ou negativos para diferentes instantes de tempo, o que indica a possibilidade de inversão de sentido da velocidade.
Ao dividirmos os termos da equação da velocidade pelo tempo, temos:
a = 5.t – (3/t)
Isso mostra que a aceleração está em função do tempo. Portanto, as afirmações são:
Falsa. O movimento possui aceleração variável;
Falsa. A velocidade muda de sentindo, sendo assim, o movimento não será progressivo em toda a sua trajetória;
Verdadeira. Aplicando-se os valores 1 s e 2 s na função da posição em função do tempo, os resultados serão, respectivamente, 2 m e 34 m. Assim, a velocidade média será:
V = Δs ÷ Δt
V = (34 – 2) ÷ (2 – 1)
V = 32 m/s
Verdadeira. Aplicando-se t = 0 s, o resultado final será nulo. Já para t = 0,77 s, a posição indicada será de, aproximadamente, 0,03 m.
Alternativa: C
07) Analise as afirmações a respeito das características do movimento uniforme.
I) O movimento dito progressivo é aquele que ocorre a favor do sentido positivo da trajetória.
II) O gráfico da função horária da posição para o movimento retilíneo uniforme sempre é uma reta crescente.
III) Se o movimento for retrógrado, o gráfico da posição em função do tempo será uma reta crescente.
IV) O coeficiente angular da reta do gráfico da posição versus o tempo é igual à velocidade do móvel.
É verdadeiro o que se diz em:
(A) I e II
(B) I, III e IV
(C) I, II e IV
(D) II e IV
(E) II e III
Resolução:
I) Verdadeira: O movimento dito progressivo realmente é aquele que ocorre a favor do sentido positivo da trajetória.
II) Falsa: Se o movimento for retrógrado, a velocidade será negativa e, assim, a reta do gráfico da função horária da posição para o movimento uniforme será decrescente.
III) Falsa. O movimento retrógrado apresenta velocidade negativa, logo, o gráfico é decrescente.
IV) Verdadeira. Em um gráfico de espaço versus tempo, a tangente do ângulo formado pela reta é dada pela razão Δs ÷ Δt, razão essa que determina a velocidade do móvel.
Alternativa: C
08) Um móvel em uma rodovia sai da posição 18 km e anda de acordo com o sentido positivo da trajetória com velocidade constante de 30 km/h. Outro móvel sai da posição 2 km e anda no sentido positivo da trajetória com velocidade constante de 50 km/h.
Determine o ponto onde os dois móveis se encontrarão.
(A) 30 km
(B) 38 km
(C) 40 km
(D) 42 km
(E) 50 km
Resolução:
Escrevendo a função horária da posição para cada um dos móveis, temos:
S1 = 18 + 30.t
S2 = 2 + 50.t
No momento do encontro, as posições dos móveis serão as mesmas, sendo assim, igualando as funções acima, teremos:
S1 = S2
18 + 30.t = 2 + 50.t
20.t = 16
t = 0,8 s
O tempo para o encontro é de 0,8 s. Assim, a posição de encontro para os móveis é:
S1 = 18 + 30.t = 18 + 30.0,8 = 18 + 24 = 42 km
S2 = 2 + 50.t = 2 + 50.0,8 = 2+ 40 = 42 km
Alternativa: D
09) Imagine que um paraquedista saltará de uma aeronave que se movimenta em uma trajetória retilínea, horizontal e para a direita.
Ao saltar e deixar o movimento acontecer naturalmente, qual será a trajetória do paraquedista até chegar ao chão?
(A) A trajetória do paraquedista será retilínea, vertical e para baixo.
(B) A trajetória do paraquedista será uma reta, na diagonal, para baixo e para a esquerda.
(C) A trajetória do paraquedista será uma reta, na diagonal, para baixo e para a direita.
(D) A trajetória do paraquedista será uma curva para baixo e para a esquerda.
(E) A trajetória do paraquedista será uma curva para baixo e para a direita.
Resolução:
O movimento do paraquedista, por inércia, acompanha o da aeronave, portanto, seu movimento será para a direita. A queda do paraquedista é composta por duas velocidades: uma na vertical e para baixo e outra na horizontal para a direita. Sendo assim, o movimento resultante é uma curva para a direita.
Alternativa: E
10) A respeito da ideia de referencial, marque a alternativa correta:
(A) O Sol, por ter uma massa correspondente a 98% de toda a massa do sistema solar, deve ser sempre considerado o referencial para quaisquer fenômenos.
(B) Os fenômenos devem sempre ser analisados a partir de um referencial parado.
(C) Referencial é o corpo em movimento retilíneo uniforme a partir do qual se analisam os movimentos.
(D) Referencial é o corpo a partir do qual os fenômenos são analisados.
(E) O movimento e o repouso são absolutos e não dependem de um referencial.
Resolução:
A definição de referencial mostra que ele é o corpo a partir do qual as análises são feitas. É o lugar do observador, aquele que descreve o fenômeno da forma como vê.
Alternativa: D
11) Um professor de Física, durante uma de suas aulas, perguntou aos alunos: “Por que podemos dizer que estamos todos em movimento mesmo que sentados em nossas carteiras?” Ao dar a resposta correta, um dos alunos disse:
(A) Porque o Sol sempre é o referencial adotado, uma vez que é o corpo mais massivo do sistema solar; então, estamos executando o movimento de translação com a Terra.
(B) Porque se adotarmos um referencial no espaço, como a Lua, a Terra estará em movimento e nós nos movimentamos com o planeta.
(C) Porque a Terra executa um movimento de translação ao redor de seu próprio eixo.D) Porque nada pode permanecer totalmente parado.
(E) n.d.a.
Resolução:
O movimento e o repouso são conceitos relativos, pois dependem de um referencial adotado. Assim, se um corpo fora da Terra é adotado como referencial, a Terra executa, no mínimo, dois movimentos (rotação e translação), e nós nos movimentamos com ela.
Alternativa: B
12) A respeito dos conceitos de movimento, repouso, trajetória e referencial, marque a alternativa correta.
(A) A trajetória é o caminho feito por um corpo independentemente do referencial adotado.
(B) Movimento e repouso são conceitos relativos, pois dependem da trajetória adotada pelo móvel.
(C) O referencial é o corpo a partir do qual as observações dos fenômenos são feitas. O Sol é considerado um referencial privilegiado porque é o corpo mais massivo do sistema solar.
(D) A trajetória é o caminho executado por um móvel em relação a um referencial adotado.
(E) Mesmo que a Terra seja tomada como referencial, nunca poderemos dizer que os prédios e as demais construções estão em repouso.
Alternativa: D
13) (MACK-SP) Em um mesmo plano vertical, perpendicular à rua, temos os segmentos de reta AB e PQ, paralelos entre si. Um ônibus se desloca com velocidade constante de módulo v1, em relação à rua, ao longo de AB, no sentido de A para B, enquanto um passageiro se desloca no interior do ônibus, com velocidade constante de módulo v2, em relação ao veículo, ao longo de PQ no sentido de P para Q. 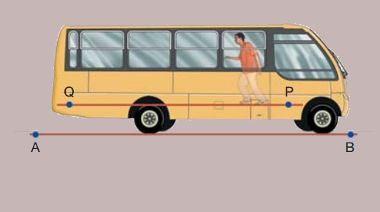 Sendo v1 > v2, o módulo da velocidade do passageiro em relação ao ponto B da rua é:
Sendo v1 > v2, o módulo da velocidade do passageiro em relação ao ponto B da rua é:
(A) v1 + v2
(B) v1 - v2
(C) v2 + v1
(D) v1
(E) v2
Resolução:
Em relação ao ponto adotado como referencial, existem duas velocidades: v1, que é a velocidade do ônibus para a direita, e v2, que é a velocidade do passageiro para a esquerda. Como a velocidade do ônibus é maior, podemos dizer que a velocidade resultante (vR) do passageiro é:
vR = v1 – v2
Alternativa: B
14) Um móvel com velocidade constante percorre uma trajetória retilínea à qual se fixou um eixo de coordenadas. Sabe-se que no instante t0 = 0, a posição do móvel é x0 = 500m e, no instante t = 20s, a posição é x = 200m.
Determine:
a. A velocidade do móvel.
b. A função da posição.
c. A posição nos instantes t = 1s e t = 15s.
d. O instante em que ele passa pela origem.
Resolução:
(a) A velocidade do móvel
v = Δs/Δt
v = (200-500)/(20-0)
v = -300/20
v = -15m/s (velocidade negativa implica em movimento retrógrado)
(b) função da posição
x = x0 + v.t
x = 500 - 15t
A posição nos instantes t = 1s e t = 15s
(c1) Para t = 1s temos:
x = 500 - 15.1
x = 500 – 15
x = 485m
(c2) Para t = 15s temos:
x = 500 – 15.15
x = 500 – 225
x = 275m
(d) O instante em que ele passa pela origem para x = 0 temos que:
0 = 500 – 15.t
15.t = 500
t = 500/15
t = 33,3 s em valor aproximado
15) Dois carros A e B encontram-se sobre uma mesma pista retilínea com velocidades constantes no qual a função horária das posições de ambos para um mesmo instante são dadas a seguir: xA = 200 + 20.t e xB = 100 + 40.t.
Com base nessas informações, responda as questões abaixo.
(a) É possível que o móvel B ultrapasse o móvel A? Justifique.
(b) Determine o instante em que o móvel B alcançará o móvel A, caso este alcance aconteça.
Resolução:
(a) Sim, pois a posição do móvel B é anterior a de A, e B possui uma velocidade constante maior que a de A; estando eles em uma mesma trajetória retilínea dentro de um intervalo de tempo Δt, B irá passar A.
(b) xA = xB
200 + 20.t = 100 + 40.t
t - 20.t = 200 - 100
20.t = 100
t = 100/20
t = 5s
16) A função horária do espaço de um carro em movimento retilíneo uniforme é dada pela seguinte expressão: x = 100 + 8.t. Determine em que instante esse móvel passará pela posição 260m.
Resolução:
x = 100 + 8.t
260 = 100 + 8.t
8.t = 160
t = 160/8
t = 20s
18) Um móvel em M.R.U gasta 10h para percorrer 1100 km com velocidade constante. Qual a distância percorrida após 3 horas da partida?
Resolução:
V = S/t
V = 1100/10
V = 110km/h
110 = S/3
S = 330 km.
19) Determine o tempo necessário para que os móveis da figura a seguir se encontrem.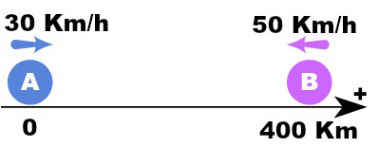 (A) 2h
(A) 2h
(B) 3h
(C) 4h
(D) 5h
(E) 6h
Resolução:
Escrevendo a função horária da posição do movimento uniforme para os corpos A e B, temos:
SA = S0 + v.t → SA = 0 + 30.t → SA = 30.t
SB = S0 – v.t → SB = 400 – 50.t
Sabendo que no momento do encontro SA = SB, temos:
SA = SB
30.t = 400 – 50.t
50.t + 30.t = 400
80.t = 400
t = 400
80
t = 5 h
Alternativa: D
20) A partir do gráfico abaixo, escreva a função horária da posição para o móvel que executa movimento uniforme.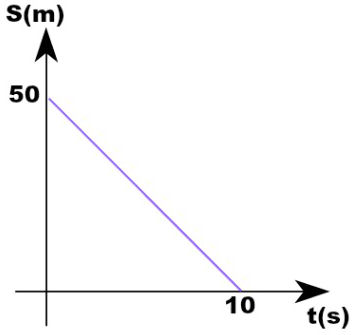 (A) S = 50 + 5.t
(A) S = 50 + 5.t
(B) S = 50 + 15.t
(C) S = 50 – 5.t
(D) S = 50 + 10.t
(E) S =
Resolução:
Analisando o gráfico, temos:
Posição inicial: S0 = 50 m;
Tempo até atingir a posição 0: t = 10 s;
Tipo de movimento: Reta decrescente indica movimento retrógrado, logo, a velocidade é negativa.
A partir da definição de velocidade média, podemos determinar a velocidade do móvel:
v = Δs
Δt
v = (0 – 50)
10
v = - 5m/s
De posse da velocidade, podemos determinar a função horária da posição para esse móvel.
S = S0 + v.t
S = 50 – 5.t
Alternativa: C
21) Um móvel com velocidade constante igual a 20 m/s parte da posição 5 m de uma reta numerada e anda de acordo com o sentido positivo da reta. Determine a posição do móvel após 15 s de movimento.
(A) 105 m
(B) 205 m
(C) 305 m
(D) 405 m
(E) 505 m
Resolução:
A partir dos dados fornecidos, temos:
v = 20 m/s
S0 = 5m
t = 15s
A partir da função horária da posição para o movimento uniforme, temos:
S = S0 + v.t
S = 5 + 20.15
S = 5 + 300
S = 305 m
Alternativa: C
22) Um homem sai da posição 15 m de uma pista de caminhada e anda até a posição 875 m mantendo uma velocidade constante de 2 m/s. Sabendo disso, determine o tempo gasto para completar a caminhada.
(A) 430 s
(B) 320 s
(C) 450 s
(D) 630 s
(E) 530 s
Resolução:
Do enunciado da questão, temos:
S0 = 15 m
S = 875 m
v = 2 m/s
A partir da função horária da posição para o movimento uniforme, podemos escrever que:
S = S0 + v.t
875 = 15 + 2.t
875 – 15 = 2.t
2.t = 860
t = 430 s
Alternativa: A
23) (AFA) Considere dois veículos deslocando-se em sentidos opostos em uma mesma rodovia. Um veículo tem velocidade escalar de 72 km/h e o outro de 108 km/h, em módulo. Um passageiro, viajando no veículo mais lento, resolve cronometrar o tempo decorrido até que os veículos se cruzem e encontra o intervalo de 30 segundos.
A distância, em km, de separação dos veículos, no início da cronometragem, era de:
(A) 0,5 km
(B) 1,5 km
(C) 2 km
(D) 2,5 km
Resolução:
Adotando que o veículo mais lento executa seu movimento de acordo com o sentido positivo da trajetória e sendo x a distância que separa os dois veículos no início da cronometragem, temos:
Veículo mais lento:
Velocidade: v = 72 km/h ÷ 3,6 = 20 m/s (Multiplicamos por 3,6 passar km/h para m/s)
Função horária da posição: S = S0 + v.t → S = 0 + 20.t → S = 20.t
Veículo mais rápido:
Velocidade: v = 108 Km/h ÷ 3,6 = 30 m/s
Função horária da posição: S' = S'0 + v.t → S' = x – 30.t
No momento do encontro dos móveis, as posições S e S' são iguais:
S = S'
20.t = x – 30.t
20.t + 30.t = x
x = 50.t
Sabendo que o encontro dos móveis ocorre em 30 s, temos:
x = 50.30
x = 1500 m = 1,5 km
Alternativa: B
MOVIMENTO UNIFORMEMENTE VARIADO (MUV)
Movimento Uniformemente Variado – É um movimento que possui uma aceleração constante, sua velocidade varia uniformemente de acordo com o tempo e o espaço percorrido aumenta proporcionalmente ao quadrado do tempo. Característica de movimento uniformemente variado (MUV)
Característica de movimento uniformemente variado (MUV)
- a velocidade varia com o passar do tempo.
- a aceleração é constante.
Aceleração – É a grandeza que faz varia a velocidade de um móvel. Ela é uma grandeza vetorial que possui: módulo, direção e sentido.

Aceleração Média – É a variação da velocidade dividida pela variação do tempo.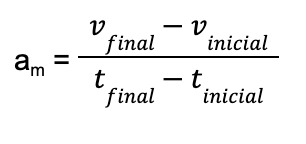 am = aceleração média (m/s2)
am = aceleração média (m/s2)
V = velocidade final (m/s)
V0 = velocidade inicial (m/s)
Δt = variação do tempo (s)
ΔV= V0 – V (variação da velocidade)
Δt = t – t0 (variação do tempo)
Observação: Quando a sua velocidade é crescente dizemos que o movimento é uniformemente acelerado, e se diminui sua velocidade dizemos que ele está em movimento uniformemente retardado.
MOVIMENTO RETILÍNEO UNIFORMEMENTE VARIADO (MRUV)
É um movimento em linha reta, que possui uma aceleração constante, sua velocidade varia uniformemente de acordo com o tempo e o espaço percorrido aumenta proporcionalmente ao quadrado do tempo.
Característica de movimento retilíneo uniformemente variado (MRUV)
A trajetória é uma reta
A velocidade varia com o passar do tempo.
A aceleração é constante.
Equação Horária da Velocidade (MUV)
V = V0 + at
V = velocidade final (m/s)
V0 = velocidade inicial (m/s)
a = aceleração (m/s2)
t = tempo (s)
Equação horária das posições ou Função horária das posições
![]()
Sf = posição final (m)
S0 = posição inicial (m)
ΔS = Sf - S0 – deslocamento (m)
vf = velocidade final (m/s)
v0 = velocidade inicial (m/s)
a = aceleração média (m/s²)
t = intervalo de tempo (s)
Equação de Torricelli
Equação de Torricelli - Ela descreve a velocidade de um corpo em função da sua trajetória. Perceba que precisamos saber a orientação da trajetória para saber se a velocidade será positiva ou negativa.
Observação: geralmente usamos essa equação quando o tempo não é dado
v2 = v02 + 2aΔS
v2 = velocidade final (m)
v0 = velocidade inicial (m/s)
a = aceleração (m/s2)
ΔS = distância percorrida (m)
Gráfico do Movimento Uniformemente Variado


QUESTÕES RESOLVIDAS - (M.U.V.)
01) (PUC) Testes realizados com o carro Gol mostraram que ele vai de 0 a 100 km/h em 10s. Calcule a aceleração aproximada do veículo nesse intervalo de tempo. (adote 100 km/h = 28 m/s)
(A) 2,0 m/s²
(B) 2,8 m/s²
(C) 4,1 m/s²
(D) 5,3 m/s²
(E) 8,1 m/s²
Resolução
v0 = 0
v = 100 km/h = 28 m/s
t = 10 s
v = v0 + a.t
28 = 0 + a . 10
10a = 28
a = 28/10
a = 2,8 m/s²
Alternativa: B
02) (Vuesp) Um automóvel que vinha a 25 m/s freou e parou em 25 s. O valor da aceleração escalar média do automóvel durante a freada foi de:
(A) zero
(B) -1,0 m/s²
(C) 1,0 m/s²
(D) -3,6 m/s²
(E) 4,0 m/s²
Resolução
v0 = 25 m/s
v = 0
t = 25 s
v = v0 + a.t
0 = 25 + a . 25
25 + a . 25 = 0
25a = -25
a = -25/25
a = -1 m/s²
Alternativa: B
03) (Fuvest) Um avião a jato, partindo do repouso. é submetido a uma aceleração constante de 4 m/s². Qual o intervalo de tempo de aplicação desta aceleração para que o jato atinja a velocidade de decolagem de 160 m/s ?
(A) 80s
(B) 20s
(C) 20s
(D) 40s
(E) 40s
Resolução
v0 = 0
v = 160 m/s
a = 4 m/s²
v = v0 + a.t
160 = 0 + 4.t
t = 160/4
t = 40 s
Alternativa: D
EXERCÍCIOS RESOLVIDOS – (MUV)
04) (FUVEST) Um veículo parte do repouso em movimento retilíneo e acelera com aceleração escalar constante e igual a 2,0 m/s2.
Pode-se dizer que sua velocidade escalar e a distância percorrida após 3,0 segundos, valem, respectivamente:
(A) 6,0 m/s e 9,0m;
(B) 6,0m/s e 18m;
(C) 3,0 m/s e 12m;
(D) 12 m/s e 35m;
(E) 2,0 m/s e 12 m.
Resolução:
a = 2,0 m/s2
t = 3 s
v0 = 0 (pois o veículo parte do repouso)
Utilizamos a equação v = v0 + at:
v = 0 + 2 . 3
v = 6 m/s
Também utilizamos a função horária do espaço para o movimento uniformemente variado:
S = S0 + v0t + 1 at2
2
Como S0 e v0 são iguais a zero, reescrevemos a fórmula da seguinte forma:
S = 1 at2
2
S = 1 at2
2
S = 1 . 2 .32
2
S = 9 m
Alternativa: A
05) (UFPA) Um ponto material parte do repouso em movimento uniformemente variado e, após percorrer 12 m, está animado de uma velocidade escalar de 6,0 m/s.
A aceleração escalar do ponto material, em m/s, vale:
(A) 1,5
(B) 1,0
(C) 2,5
(D) 2,0
(E) n.d.a.
Resolução:
Dados:
Δs = 12 m
v = 6 m/s
v0 = 0
Para calcular a aceleração com esses dados, devemos utilizar a equação de Torricelli:
v2 = v02 + 2.a.Δs
62 = 02 + 2.a.12
36 = 24a
a = 36
24
a = 1,5 m/s2
Alternativa: A
06) Uma pedra é lançada do décimo andar de um prédio com velocidade inicial de 5m/s. Sendo a altura nesse ponto igual a 30 m e a aceleração da gravidade igual a 10 m/s2, a velocidade da pedra ao atingir o chão é:
(A) 5 m/s
(B) 25 m/s
(C) 50 m/s
(D) 30 m/s
(E) 10 m/s
Resolução:
Dados:
v0 = 5 m/s
h = 30 m
g = 10 m/s2
Utilizamos a equação de Torricelli para calcular a velocidade da pedra no final da queda livre:
v2 = v02 + 2.a.h
v2 = 52 + 2.10.30
v2 = 25 + 600
v2 = 625
v = √625
v = 25 m/s
Alternativa: B
07) Um móvel parte do repouso e percorre uma distância de 200 m em 20s. A aceleração desse móvel, em m/s2, é:
(A) 0,5
(B) 0,75
(C) 1
(D) 1,5
(E) 2
Resolução:
S = 200 m
t = 20 s
v0 = 0
Utilizamos a função horária da posição:
S = S0 + v0t + 1 at2
2
200 = 0 + 0.20 + 1.a.202
2
200 = 1a . 400
2
200 = 200 a
a = 200/200
a = 1 m/s2
Alternativa: C
01) (UEL-PR) Um trem de 200 m de comprimento, com velocidade escalar constante de 60 km/h, gasta 36 s para atravessar completamente uma ponte.
A extensão da ponte, em metros, é de:
(A) 200
(B) 400
(C) 500
(D) 600
(E) 800
Resolução:
Dados:
L = 200 m
V = 60 km/h = 16,7 m/s
T = 36 s
S = v.t
S = x + 200
x + 200 = 16,7 . 36
x = 600 – 200
x = 400 m
Alternativa: B
02) (FEI-SP) No movimento retilíneo uniformemente variado, com velocidade inicial nula, a distância percorrida é:
(A) diretamente proporcional ao tempo de percurso
(B) inversamente proporcional ao tempo de percurso
(C) diretamente proporcional ao quadrado do tempo de percurso
(D) inversamente proporcional ao quadrado do tempo de percurso
(E) diretamente proporcional à velocidade
Resolução:
A equação que relaciona a velocidade inicial, a distância percorrida e o tempo é:
S = S0 + v0t + 1 at2
2
Quando v0 é igual a zero e se considerarmos que S0 também é zero no início movimento, podemos reescrever a equação acima da seguinte forma:
S = 1 at2
2
Assim, podemos concluir que a distância percorrida é proporcional ao quadrado do tempo.
Alternativa: C
03) Um automóvel parte do repouso e atinge a velocidade de 100 km/h em 8s. Qual é a aceleração desse automóvel?
Resolução:
Dados:
V = 100 km/h = 27,7 m/s
t = 8 s
Utilizamos a equação:
a = v
t
E substituímos os dados:
a = 27,7
8
a = 3,46 m/s2
04) Uma partícula em movimento retilíneo movimenta-se de acordo com a equação v = 10 + 3t, com o espaço em metros e o tempo em segundos. Determine para essa partícula:
a) A velocidade inicial
b) A aceleração
c) A velocidade quando t=5s e t= 10s
Resolução:
a) Para encontrar o valor da velocidade inicial, devemos comparar a equação acima com a função horária da velocidade:
V = vo + at
V = 10 + 3t
A partir dessa comparação, vemos que o termo que substituiu a velocidade inicial (v0) da fórmula é o número 10. Portanto, podemos concluir que v0 = 10 m/s
b) Comparando novamente as equações, vemos que o que substitui a aceleração (a) na equação é o número 3.
Portanto, a = 3 m/s2
c) Quando t = 5s
v = 10 + 3.5
v = 10 + 15
v = 25 m/s
Quando t = 10 s
v = 10 + 3.10
v = 10 + 30
v = 40 m/s
03) A velocidade de uma patícula aumenta uniformemente de 36km/h para 108km/h em 5 segundos em linha reta.
Calcule:
a) a sua aceleração
b) a distância percorrida em 40 segundos
c) a sua velocidade em t = 25 segundos
d) o instante onde a sua velocidade é 50m/s
Resolução:
a) a sua aceleração
vo = 36 km/h = 10 m/s
v = 108 km/h = 30 m/s
t = 5 s
a = Δv/Δt
a = (30m/s - 10m/s)/5s
a = 20 / 5
a = 4 m/s2
b) a distância percorrida em 40 segundos (Área da região limitada pelo gráfico de v = 10 + 4.t no intervalo de 0 a 40 s e o eixo dos tempos)
c) a sua velocidade em t = 25 segundos
v = 10 + 4.t
v = 10 + 4.25
v = 10 + 100
v = 110 m/s
d) o instante onde a sua velocidade é 50m/s
v = 10 4.t
50 = 10 +4t
50 - 10 = 4t
40 = 4t
t = 40/4
t = 10 s
08) No instante t = 0s um uma moto encontra parada em um sinal luminoso quando passa por ela um carro com velocidade constante de 72km/h. Neste mesmo instante a moto parte em linha reta com aceleração constante de 4m/s².
Determine:
a) o instante que a moto acompanha o carro
b) a distância que cada um percorre até o encontro
Resolução:
v = 72 km/h = 20 m/s
a = 4 m/s2
SM = So + (1/2). 4t2 Sc = So + 20t
a) o instante que a moto acompanha o carro
1/2.4t2 = 20t
2t2 - 20t = 0
t(2t - 20) = 0
t = 0 ou 2t - 20 = 0
2t = 20
t = 20/2
t = 10 s
b) a distância que cada um percorre até o encontro
ΔS = v . t
ΔS = 20 m/s . 10s
ΔS = 200 m
09) Um ônibus entra em um viaduto de 180m de comprimento com velocidade 108km/h e sai do mesmo com velocidade de 36km/h em 10 segundos. Qual o tamanho do referido ônibus?
Resolução:
vo = 36 km/h = 10 m/s v = 108 km/h = 30 m/s
Δt =10 s
Sejam Vm = ΔS/Δt e Vm = (vo + v)/2
ΔS/Δt = (Vo + V)/2
(180 + x)/10 = (10 + 30)/2
(180 + x)/10 = 20
180 + x = 200
x = 200 - 180
x = 20 m
16) A função horária de uma partícula é v = 50 + at e em 15 segundos ele alcança 200 m/s. Determine a distância percorrida entre 10 e 30 segundos e a velocidade média neste intervalo.
Resolução:
(5000m e 250 m/s)
200 = 50 + a.15
200 - 50 = 15.a
150 = 15a
a = 150/15
a = 10 m/s2
Esta é a função horária: v = 50 + 10t (é só fazer o gráfico v x t e calcular a área da região limitada pelo gráfico e o eixo dos tempos, do referido intervalo de tempo, para achar a distância Δs percorrida. Usa v = Δs/Δt com Δt =20s para calcular a velocidade média)
GRANDEZA VETORIAL
Introdução - Os vetores apareceram no final do século 19, quando o americano Josiah Willard Gibbs e o inglês Oliver Heaviside desenvolveram independentemente a análise de vetores para expressar as novas leis do eletromagnetismo, que foram descobertas pelo físico escocês James Clerk Maxwell. Desde aquela época, os vetores se tornaram essenciais na física, mecânica, engenharia e em outras ciências para descrever forças matematicamente. Cinemática Vetorial - Os conceitos da cinemática escalar vistos até aqui podem ser aplicados à cinemática vetorial, que também estuda o movimento dos corpos, mas definindo as grandezas vetoriais.
Cinemática Vetorial - Os conceitos da cinemática escalar vistos até aqui podem ser aplicados à cinemática vetorial, que também estuda o movimento dos corpos, mas definindo as grandezas vetoriais.
CNIMEÁTICA VETORIAL
módulo, direção e sentido.
Grandezas
É tudo aquilo que pode ser medido ou contado, como comprimento, massa, tempo, velocidade, volume e temperatura, sendo fundamentais para descrever e quantificar a realidade física e matemática, e podem ser escalares (apenas módulo, ex: massa, tempo) ou vetoriais (módulo, direção e sentido, ex: força, velocidade).
Vetor: é um segmento de reta orientado que representa as três características de uma grandeza vetorial.
Grandezas escalares - São aquelas que podem ser completamente determinadas apenas pelo valor numérico e pela unidade de medida.
Grandezas vetoriais - São aquelas que, além do valor numérico e da unidade de medida, necessitam também de direção e sentido para serem totalmente determinadas.
Módulo: o valor numérico associado ao vetor, geralmente acompanhado de uma unidade de medida. No caso da figura anterior, o módulo do vetor é 8 metros.
Direção: a posição do vetor no espaço, ou seja, horizontal, vertical ou diagonal. O vetor do exemplo representa um deslocamento na horizontal.
Sentido: a orientação do vetor, que determina seu sinal. Geralmente, considera-se o sentido para a direita e para cima como positivo e para a esquerda e para baixo como negativo, porém isso pode variar de problema para problema. Para o vetor deslocamento apresentado, o sinal é positivo, já que seu sentido é para a direita.
Assim, toda grandeza vetorial tem três características:
- Módulo
- - Direção
- - Sentido
Resultante – É o resultado da soma, subtração ou multiplicação de vetores
Adição de vetores
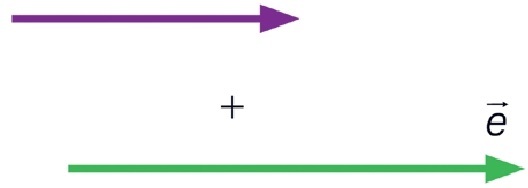
Mesma direção e mesmo sentido: resulta em outro vetor (vetor resultante r) cujo módulo é igual à soma dos módulos dos vetores.
A direção e o sentido - Soma de dois vetores de mesma direção e mesmo sentido.
Adição de vetores de mesma direção e sentidos opostos a resulta em outro vetor (vetor resultante r) cujo módulo é igual à diferença entre os módulos dos vetores.
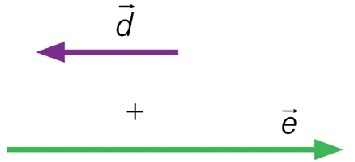
Adição de vetores pelo método da linha poligonal
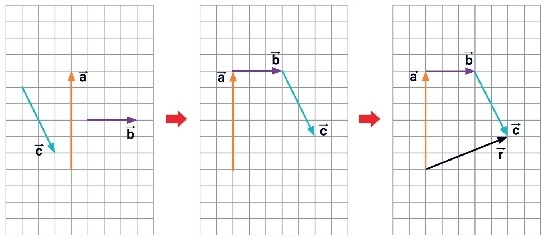
Representação da determinação do vetor resultante (r) pelo método da linha poligonal.
Adição de vetores pelo método do paralelogramo
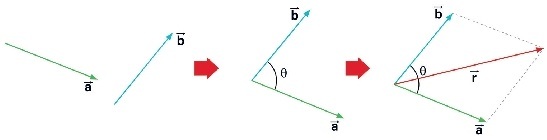
Representação da determinação do vetor resultante (r) pelo método do paralelogramo.
Determinação do módulo do vetor resultante:
r2 = a2 + b2 + 2 . a . b . cos θ
Determinação do módulo do vetor resultante para θ = 90°:
r2 = a2 + b2
Subtração de vetores:
r = a – b ↔ r = a + (-b)
em que (-b) tem o mesmo módulo e a mesma direção de b, mas sentido oposto.
Decomposição vetorial nas componentes x e y:
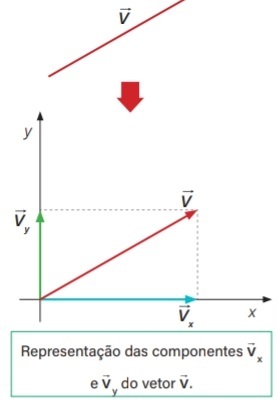
Determinação dos módulos das componentes x e y:
|v x| = |v| . cos θ e |v y| = |v| . sen θ
Multiplicação de um vetor por um número escalar: ao multiplicar um vetor v por um número escalar k, obtém-se outro vetor z = k · v, que apresenta: a mesma direção do vetor v;
- - o mesmo sentido de v se k > 0 e sentido oposto ao de v se k < 0;
- - o módulo dado por | z| = |k| · |v|.
Decomposição de vetores
Os vetores possuem como característica a possibilidade de serem decompostos em dois outros vetores, horizontal (componente x) e vertical (componente y).
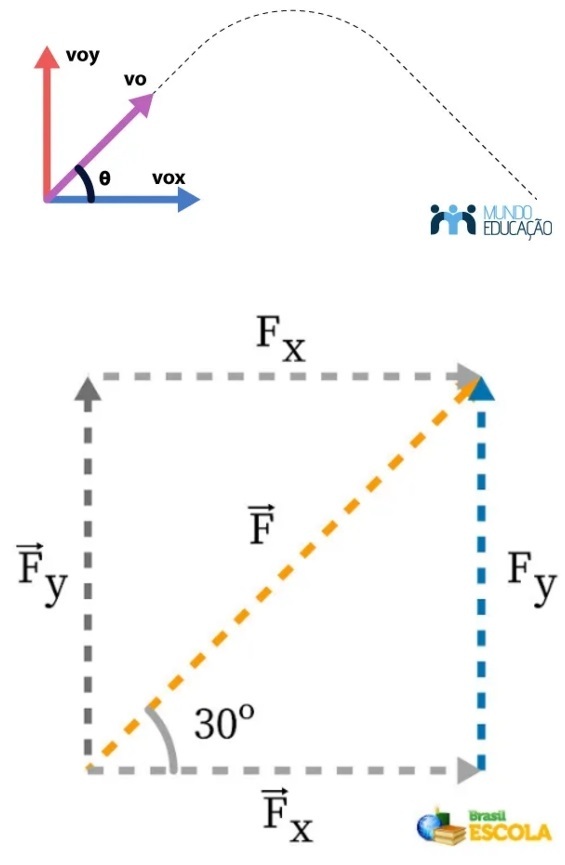
Componente Horizontal (x)
Vox = Vo . cos θ
Componente Vertical (y)
Voy= Vo . sen θ
Componente X + Y
Vo2 = VoX2 + VoY2
QUESTÕES RESOLVIDAS
01) (Livro do Aluno SEDUC/2026) Classifique as grandezas físicas a seguir em escalares ou vetoriais.
1- Velocidade
2 - Temperatura
3 - Densidade
4 - Velocidade
5 - Temperatura
6 - Densidade
7 - Aceleração
8 - Comprimento
9 - Deslocamento
10 -Tempo
Resolução:
As grandezas escalares (descritas apenas por valor numérico e unidade) são:
- volume
- área
- temperatura
- densidade
- comprimento
- tempo
As grandezas vetoriais (necessitam de módulo, direção e sentido) são:
- força
- velocidade
- aceleração
- deslocamento
02) (Livro do Aluno SEDUC/2026) Durante uma brincadeira, três amigos amarram cordas a uma caixa e puxam-na, aplicando forças de mesma direção. A ilustração mostra a representação das forças exercidas pelos três amigos.
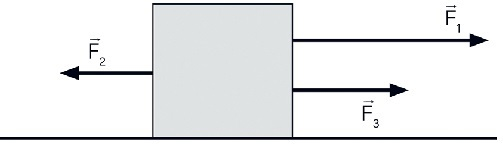
a) Desenhe uma caixa e represente nela a força resultante FR, obtida pela soma vetorial das três forças (o módulo pode ser aproximado).
Resolução:
A imagem a seguir representa a força resultante, com módulo aproximado:
b) Considere: |F1| = 9 unidades, |F2| = 4 unidades e |F3| = 5 unidades. Determine o módulo da resultante |FR|.
Resolução:
Sendo |F1| = 9 unidades, |F2| = 4 unidades e |F3| = 5 unidades, |F| será:
|FR| = |F1| – |F2| + |F3| |FR| = 9 – 4 + 5 |FR| = 10 unidades de medida
03) (Livro do Aluno SEDUC/2026) (UNIFOR 2003 – Adaptada) Três vetores, de intensidades iguais a 5 unidades de medida, orientam-se de acordo com o esquema a seguir.
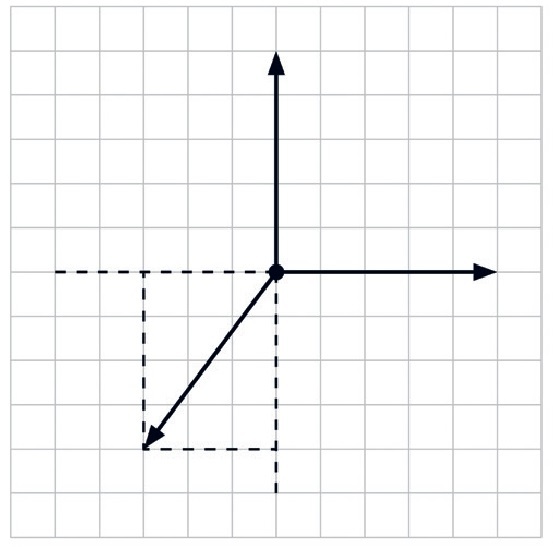
O módulo do vetor resultante dos três é:
(A) 2,0
(B) √5
(C) √7
(D) 3,0
(E) √15
Resolução:
Como precisamos somar três vetores, podemos usar o método gráfico da linha poligonal.
Nesse método, colocamos cada vetor a partir da extremidade do anterior, e o vetor resultante é dado pelo segmento que liga a origem do primeiro vetor à extremidade do último. Dessa forma, podemos determinar, graficamente, o vetor resultante da seguinte maneira:
Podemos notar que o módulo (r) do vetor resultante é igual à medida da diagonal de um retângulo de base igual a 2 unidades de medida e altura igual a 1 unidade de medida. Utilizando o Teorema de Pitágoras, obtemos:
r2 = 12 + 22
r2 = 1 + 4
r2 = 5
r = 5 unidades de medida
Alternativa: B
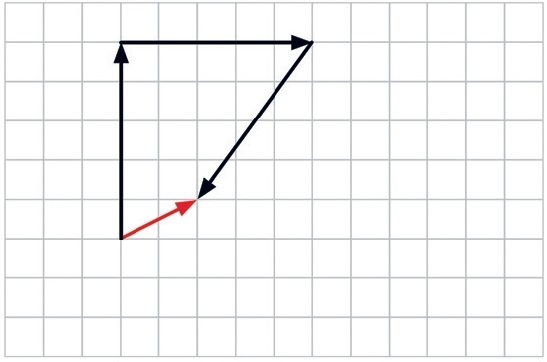
04) (Livro do Aluno SEDUC/2026) Sobre uma bola atuam duas forças, representadas na imagem pelos vetores F1 e F2
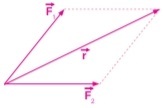
a) Determine graficamente o vetor resultante (r) da soma F1 + F2.
Resolução:
Utilizando o método do paralelogramo, o vetor resultante será:
b) Considerando os módulos F1 = 5 unidades de medida e F2 = 7 unidades de medida, e que o ângulo entre eles é θ = 60°, determine o valor do módulo r.
Resolução:
Sabendo que F1 = 5 unidades de medida e F2 = 7 unidades de medida, e que o ângulo entre eles é θ = 60°, o módulo r será:
r2 = F12 + F22 + 2 · F1 · F2 · cos 60°
r2 = F12 + F22 + 2 · F1 · F2 · cos 60°
r2 = 25 + 49 + 2 · 5 · 7 · 0,5
r2 = 25 + 49 + 35
r2 = 109
r2 = √109
O módulo do vetor resultante é, portanto, r = √109.
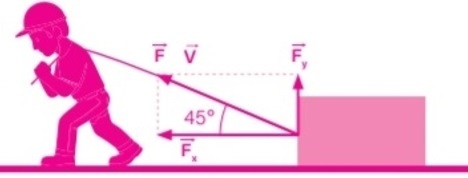
05) (Livro do Aluno SEDUC/2026) Uma pessoa puxa uma caixa por meio de uma corda que forma um ângulo de 45° com o solo. A força aplicada é F = 60,0 unidades de medida ao longo da corda. (Considere 2 = 1,41)
a) Represente graficamente a situação descrita, indicando também as componentes x e y da força F.
Resolução:
A situação descrita pode ser representada graficamente da seguinte forma:
b) Quais são os valores dos módulos das componentes Fx e Fy da força F?
Resolução:
Utilizando o método da decomposição vetorial, sabendo que o módulo do vetor F é F = 60 unidades de medida e θ = 45°, os módulos dos componentes de F serão:
Fy = F · sen 45°
Fy = 60 . 2√
2
Fy = 30 . 1,41
Fy = 42,3 unidades de medida.
Fx = F · cos 45°
Fx = 60 . 2√
2
Fx = 30 · 1,41
Fx = 42,3 unidades de medida.
06) (Enem) A força de atrito é uma força que depende do contato entre corpos. Pode ser definida como uma força de oposição à tendência de deslocamento dos corpos e é gerada devido a irregularidades entre duas superfícies em contato. Na figura, as setas representam forças que atuam no corpo e o ponto ampliado representa as irregularidades que existem entre as duas superfícies.
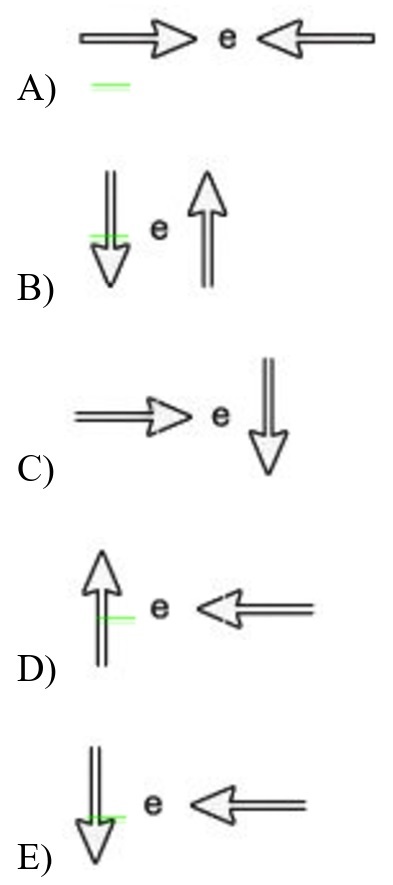
Na figura, os vetores que representam as forças que provocam o deslocamento e o atrito são, respectivamente:
Resolução:
Como o movimento é feito na direção horizontal, o par ação e reação possui sentido oposto.
Alternativa A
07) (Mackenzie – SP) Um corpo é atirado verticalmente para cima a partir do solo com velocidade inicial de módulo 50 m/s. O módulo de sua velocidade vetorial média entre o instante de lançamento e o instante em que retorna ao solo é:
(A) 50 m/s
(B) 25 m/s
(C) 5,0 m/s
(D) 2,5 m/s
(E) zero
Resolução:
Como a definição de velocidade vetorial é a razão entre deslocamento e intervalo de tempo, a velocidade vetorial média do móvel é zero, já que seu deslocamento é nulo.
Alternativa: E
08) (PUC-SP) Se a velocidade vetorial de um ponto material é constante e não nula, sua trajetória:
(A) é uma parábola.
(B) pode ser retilínea, mas não necessariamente.
(C) deve ser retilínea.
(D) é uma circunferência.
(E) pode ser uma curva qualquer.
Resolução:
Para a velocidade vetorial ser constante, é necessário que seu módulo, direção e sentido sejam constantes. Logo, somente é possível que a trajetória seja retilínea.
Alternativa: C
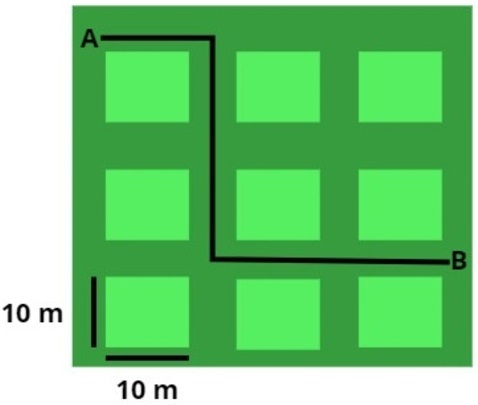
09) Um carteiro desloca-se entre os pontos A e B de certo bairro. Sabendo que cada quarteirão é aproximadamente quadrado e apresenta 10 m de lado, assinale a alternativa que apresenta corretamente o módulo do deslocamento vetorial do carteiro.
(A) 10√3 m
(B) 10 m
(C) 50 m
(D) 1300 m
(E) 10√13 m
Resolução:
Para calcular o deslocamento vetorial, consideramos a distância entre os pontos final e inicial. Observe a figura a seguir:
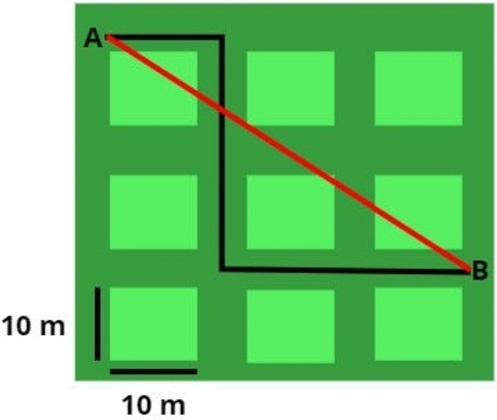
É possível ver por meio da figura que o deslocamento entre os pontos A e B apresenta 30,0 m na horizontal e 20,0 m na vertical. Podemos descrevê-lo, portanto, como um vetor:
ΔS = (30 e 20)
Para calcular o módulo desse deslocamento, utilizamos o Teorema de Pitágoras temos:
h2 = a2 + b2
h2 = 900 + 400
h2 = √1300
h = 10√13
Logo, o deslocamento vetorial do carteiro é de aproximadamente 36 m.
Alternativa: E
10) (Mackenzie) Um avião, após deslocar-se 120 km para nordeste (NE), desloca-se 160 km para sudeste (SE). Sendo um quarto de hora o tempo total dessa viagem, o módulo da velocidade vetorial média do avião, nesse tempo, foi de:
(A) 320 km/h
(B) 480 km/h
(C) 540 km/h
(D) 640 km/h
(E) 800 km/h
Resolução:
As direções norte e nordeste são perpendiculares entre si, portanto, calcularemos o deslocamento vetorial desse avião utilizando o teorema de Pitágoras. Observe a figura seguinte que ilustra a situação descrita e o cálculo a ser realizado inicialmente:
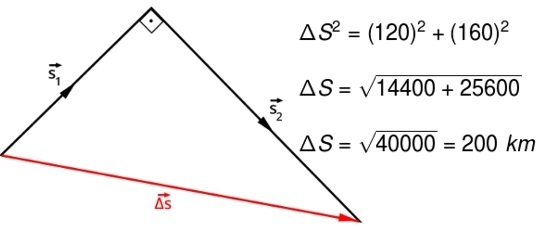
Depois de calcularmos o módulo do deslocamento vetorial, basta calcularmos a velocidade vetorial média, dividindo-a pelo intervalo de tempo, que é de 1/4 de hora (0,25 h):
V = 200
0,25
V = 800 km/h
Com base nisso, descobrimos que a velocidade do avião é de 800 km/h.
Alternativa: E
11) (Ufal) A localização de um lago, em relação a uma caverna pré-histórica, exigia que se caminhasse 200 m numa certa direção e, a seguir, 480 m numa direção perpendicular à primeira. A distância em linha reta, da caverna ao lago, era, em metros,
(A) 680
(B) 600
(C) 540
(D) 520
(E) 500
Resolução:
O exercício fala de dois deslocamentos perpendiculares. Para descobrirmos a distância entre os pontos final e inicial, devemos utilizar o teorema de Pitágoras.
, observe:
h2 = a2 + b2
h2 = 200 + 480
h2 = 40000 + 230400
h = √40000 + 230400
h = 520 m
Alternativa: B
12) (Uemg 2015) O tempo é um rio que corre. O tempo não é um relógio. Ele é muito mais do que isso. O tempo passa, quer se tenha um relógio ou não. Uma pessoa quer atravessar um rio num local onde a distância entre as margens é de 50 m. Para isso, ela orienta o seu barco perpendicularmente às margens. Considere que a velocidade do barco em relação às águas seja de 2,0 m/s e que a correnteza tenha uma velocidade de 4,0 m/s. Sobre a travessia desse barco, assinale a afirmação CORRETA:
(A) Se a correnteza não existisse, o barco levaria 25 s para atravessar o rio. Com a correnteza, o barco levaria mais do que 25 s na travessia.
(B) Como a velocidade do barco é perpendicular às margens, a correnteza não afeta o tempo de travessia.
(C) O tempo de travessia, em nenhuma situação, seria afetado pela correnteza.
(D) Com a correnteza, o tempo de travessia do barco seria menor que 25 s, pois ela aumenta vetorialmente a velocidade do barco.
Resolução:
Independentemente da velocidade da correnteza, o tempo de travessia do barco será o mesmo, uma vez que a sua travessia dá-se de modo perpendicular às margens.
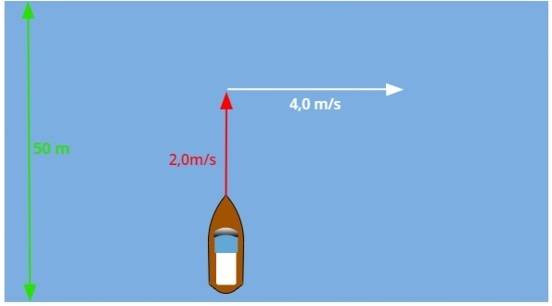
Entenda: a composição das duas velocidades do barco faz com que ele se mova na direção resultante delas, desse modo, a direção perpendicular ao rio, que tem 50 m de comprimento, é sempre percorrida pela velocidade do barco, que é de 2,0 m/s, e, por isso, o tempo de travessia não é afetado.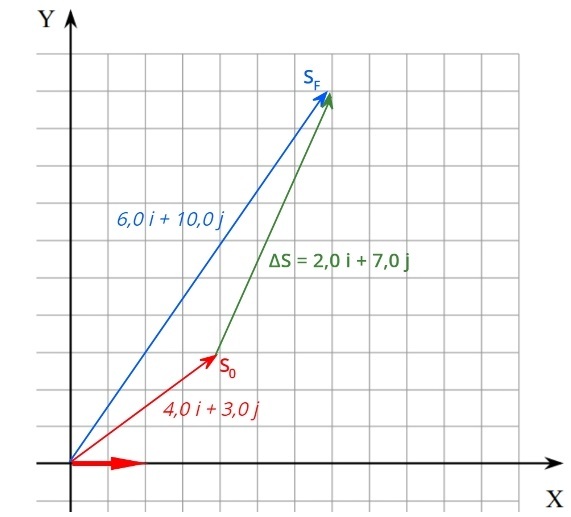
Alternativa: C
13) (Fatec) Um automóvel percorre 6,0 km para o norte e, em seguida, 8,0 km para o leste. A intensidade do vetor posição, em relação ao ponto de partida, é:
(A) 10 km
(B) 14 km
(C) 2,0 km
(D) 12 km
(E) 8,0 km
Resolução:
Nesse caso temos uma composição de movimentos, então calcularemos a intensidade do vetor posição por meio do teorema de Pitágoras:
h2 = a2 + b2
h2 = 62 + 82
h2 = 36 + 64
h2 = 1002
h = √100
h = 10
Alternativa: A
14) (PUC) Se a velocidade vetorial de um ponto material é constante e não nula, sua trajetória:
(A) é uma parábola.
(B) pode ser retilínea, mas não necessariamente.
(C) deve ser retilínea.
(D) é uma circunferência.
(E) pode ser uma curva qualquer.
Resolução:
Considerando a velocidade vetorial constante e não nula, a sua trajetória será retilínea, já que a velocidade vetorial terá a mesma direção, o mesmo sentido e o mesmo módulo em todos os pontos.
Alternativa: C
15) (Cefet) Duas pedras são lançadas do mesmo ponto no solo no mesmo sentido. A primeira tem velocidade inicial de módulo 20 m/s e forma um ângulo de 60° com a horizontal, enquanto para a outra pedra o ângulo é de 30°. O módulo da velocidade inicial da segunda pedra, de modo que ambas tenham o mesmo alcance, é:
DESPREZE A RESISTÊNCIA DO AR.
(A) 10 m/s
(B) 10√3 m/s
(C) 15 m/s
(D) 20 m/s
(E) 20√3 m/s
Resolução:
Para que as duas pedras lançadas tenham o mesmo alcance, sabendo que seus ângulos são complementares, ou seja, sua soma é igual a 90º, é necessário que as velocidades iniciais sejam iguais, então a velocidade inicial da segunda pedra é igual a 20 m/s.
Alternativa: D
16) (Unicamp - Adaptada) Até os experimentos de Galileu Galilei, pensava-se que, quando um projétil era arremessado, o seu movimento devia-se ao impetus, o qual mantinha o projétil em linha reta e com velocidade constante. Quando o impetus acabasse, o projétil cairia verticalmente até atingir o chão. Galileu demonstrou que a noção de impetus era equivocada.
Consideremos que um canhão dispara projéteis com uma velocidade inicial de 100 m/s, fazendo um ângulo de 30º com a horizontal. Dois artilheiros calcularam a trajetória de um projétil: um deles, Simplício, utilizou a noção de impetus; o outro, Salviati, as ideias de Galileu. Os dois artilheiros concordavam apenas em uma coisa: o alcance do projétil.
Qual é o alcance do projétil?
Considere √3 =1,8; sen 30º = 0,5; cos 30º = 0,9.
Despreze a resistência do ar.
(A) 900 m
(B) 1000 m
(C) 1100 m
(D) 1200 m
(E) 1300 m
Resolução:
Primeiramente, calcularemos a componente horizontal da velocidade e a componente vertical da velocidade através das suas fórmulas:
Vox = Vox . cos (θ)
Vox = 100 . cos30°
Vox = 100 . 0,9
Vox = 90 m/s
Voy = Voy . sem (θ)
Voy = 100 . sen30°
Voy = 100 . 0,5
Voy = 50 m/s
Calcularemos o alcance do projétil através da fórmula que o relaciona à componente horizontal da velocidade e à componente vertical da velocidade:
A = 2 . Vox . Voy
g
A = 2 . 90 . ⋅50
10
A = 900 m
Alternativa: A
17) (UFPE - Adaptada) Um projétil é lançado obliquamente no ar, com velocidade inicial vo = 20 m/s , a partir do solo. No ponto mais alto de sua trajetória, verifica-se que ele tem velocidade igual à metade de sua velocidade inicial. Qual a altura máxima, em metros, atingida pelo projétil? (Despreze a resistência do ar e considere g = 10 m/s2 ).
(A) 11 m
(B) 12 m
(C) 13 m
(D) 14 m
(E) 15 m
Resolução:
No ponto mais alto da trajetória, a velocidade é igual à metade da velocidade inicial, então:
Vx = Vox = Vo
2
Vx = Vox = Vo
20
Vx = Vox = 10 m/s
Depois, calcularemos a velocidade vertical inicial voy através da fórmula:
Vo2 = Vox2 + Voy2
202 = 102 + Voy2
400 = 100 + Voy2
400 – 100 = Voy2
300 = Voy2
√300 = Voy2
Por fim, calcularemos a altura máxima através da sua fórmula:
Hmáx = Voy2
2g
hmáx = (3√00)2
2 . 10
hmáx = 300
20
hmáx = 15 m
Alternativa: E
18) (PUC) Observando a parábola do dardo arremessado por um atleta, um matemático resolveu obter uma expressão que lhe permitisse calcular a altura y, em metros, do dardo em relação ao solo, decorridos t segundos do instante de seu lançamento (t = 0). Se o dardo chegou à altura máxima de 20 m e atingiu o solo 4 segundos após o seu lançamento, então, desprezada a altura do atleta, considerando g = 10 m/s2, a expressão que o matemático encontrou foi
(A) y = -5t2 + 20t
(B) y = -5t2 + 10t
(C) y = -5t2 + t
(D) y = -10t2 + 50
(E) y = -10t2 + 10t
Resolução:
Primeiramente, calcularemos a velocidade vertical inicial através da fórmula da altura máxima:
Hmáx = Voy2
2g
20 = Voy2
2 . 10
20 = Voy2
20
Voy2 = 20 . 20
Voy2 = 400
Voy = √400
Voy = 20
Por fim, substituiremos na função horária da posição no movimento vertical:
Y −Yo = Voy . t −g .⋅t2
2
Y −0 = Voy . t −10 . t2
2
Y = 20 . t −10 . t2
2
Y = 20 . t . −5. t2
Alternativa: A
19) Em uma partida de beisebol, um estudante lança a bola para cima formando um ângulo de 70º com a horizontal. Sabendo que a sua velocidade inicial de lançamento foi de 20 m/s, encontre a componente horizontal da velocidade inicial e a componente vertical da velocidade inicial.
Considere. Sem 70º = 09 e cos 70º = 0,3
(A) vox = 1 m/s e voy = 3 m/s
(B) vox = 5 m/s e voy = 15 m/s
(C) vox = 6 m/s e voy = 18 m/s
(D) vox = 15 m/s e voy = 5 m/s
(E) vox =1 8 m/s e voy = 6 m/s
Resolução:
Primeiramente, calcularemos a componente horizontal da velocidade inicial, através da sua fórmula:
Vox = Vo . cos θ
Vox = 20 . cos70°
Vox = 20 . 0,3
Vox = 6 m/s
Por fim, calcularemos a componente vertical da velocidade inicial, através da sua fórmula:
Voy = Vo . sem θ
Voy = 20 . sen 70°
Voy = 20 . 0,9
Voy = 18 m/s
Alternativa: C
20) Qual a distância vertical percorrida, após 2 segundos, por uma boneca que é chutada com um ângulo de 30º à velocidade inicial de 25 m/s?
Considere g = 10 m/s2.
(A) 5 m
(B) 10 m
(C) 15 m
(D) 20 m
(E) 25 m
Resolução:
Calcularemos a distância vertical percorrida pelo corpo através da fórmula da função horária da posição no lançamento oblíquo:
Δy = Voy ⋅ t −g . t2
2
Δy = sem θ . t - g . t2
2
Δy = Vo . sen θ ⋅ t −g . t2
2
Δy = 25 . 0,5. 2 . −10 . 4
2
Δy = 25 − 20
Δy = 5 m
Alternativa: A
21) Um móvel é lançado obliquamente com um ângulo de 45º e velocidade inicial de 10 m/s. Com essas informações, calcule a altura máxima atingida por esse móvel.
Considere: sem 45º = cos 45º = 0,7 e g = 10ms2
(A) 0,94 m
(B) 1,81 m
(C) 1,72 m
(D) 2,13 m
(E) 2,45 m
Resolução:
Hmáx = Voy2
2g
Hmáx = (Voy . semθ) 2
2g
Hmáx = (10 . sem 45) 2
2 . 10
Hmáx = (10 . 0,7) 2
20
Hmáx = (7) 2
20
Hmáx = 49
20
Hmáx = 2, 45 m
Alternativa: A
22) Determine a velocidade vertical final de uma bola após 0,5 segundo, sabendo que ela possui componente vertical da velocidade inicial igual a 15 m/s.
Considere g = 10 m/s2.
(A) -5 m/s
(B) 0 m/s
(C) 5 m/s
(D) 10 m/s
(E) 15 m/s
Resolução:
Calcularemos a velocidade vertical final da bola através da fórmula da função horária da velocidade no lançamento oblíquo:
Vy = Voy −g . t
Vy =15−10 . 0,5
Vy = 15 −5
Vy = 10 m/s
Alternativa: D
23) Sabendo que um corpo é lançado obliquamente com ângulo de 60º e velocidade inicial de 2 m/s, qual foi a distância horizontal percorrida por esse corpo após 10 segundos?
(A) 5 m
(B) 10 m
(C) 15 m
(D) 20 m
(E) 25 m
Resolução:
Calcularemos a distância horizontal percorrida pelo corpo através da fórmula do movimento na horizontal:
Δx = Vox ⋅ t
Δx = vo . cosθ . t
Δx = 2 . cos60° . 10
Δx = 2 . 0,5 .10
Δx = 10 m
Alternativa: B
24) Calcule o tempo de subida de uma bola que é lançada obliquamente com um ângulo de 30º e velocidade inicial de 5 m/s. Considere g=10 m/s2
(A) 0,05 s
(B) 0,10 s
(C) 0,15 s
(D) 0,20 s
(E) 0,25 s
Resolução:
Calcularemos o tempo de subida da bola através da sua fórmula:
ts = Voy
g
ts = Vo . senθ
g
ts = 5 . 30
10
ts = 5 . 0,5
10
ts = 0,25 s
Alternativa: E
25) Determine a aceleração da gravidade de um planeta em que o pulo de uma pessoa tem alcance horizontal de 100 m quando a sua velocidade inicial é de 5 m/s.
(A) 0,125 m/s2
(B) 0,250 m/s2
(C) 0,500 m/s2
(D) 1,000 m/s2
(E) 2,000 m/s2
Resolução:
Calcularemos a aceleração da gravidade do planeta, através da fórmula do alcance horizontal:
A = Vo2 . sem (2⋅θ)
g
100 = 52 . sem (2 . 15)
g
100 = 25 . sem (30)
g
100 = 25 . 0,5
g
g = 25 . 0,5
100
g= 0,125 m/s2
Alternativa: A
26) Quais das alternativas apresentam as unidades de medidas correspondentes às grandezas físicas estudadas no lançamento oblíquo?
I. A altura é medida em metros.
II. O tempo é medido em metros.
III. A velocidade de queda é medida em metros por segundo ao quadrado.
IV. A aceleração da gravidade é medida em metros por segundo ao quadrado.
Está(ão) correta(s):
(A) I, II.
(B) III, IV.
(C) I, IV.
(D) II, III.
(E) I, II e III.
Resolução:
I. A altura é medida em metros. (correta)
II. O tempo é medido em metros. (incorreta)
O tempo é medido em segundos.
III. A velocidade de queda é medida em metros por segundo ao quadrado. (incorreta)
A velocidade de queda é medida em metros por segundo.
iV. A aceleração da gravidade é medida em metros por segundo ao quadrado. (correta)
Alternativa: C
27) Assinale a alternativa que contém apenas grandezas vetoriais.
(A) Aceleração, velocidade, força, impulso, empuxo e trabalho.
(B) Trabalho, aceleração, campo magnético, força centrípeta e temperatura.
(C) Momento linear, campo magnético, campo elétrico e força.
(D) Quantidade de movimento, campo magnético, energia e tempo
(E) Energia, massa, peso, empuxo, campo elétrico e velocidade.
Resolução:
As grandezas vetoriais são aquelas que possuem módulo, direção e sentido. As grandezas que possuem apenas valor numérico (módulo) são chamadas de escalares.
A) Errada. Trabalho é uma quantidade de energia, por isso, é uma grandeza escalar.
B) Errada. Trabalho e temperatura são escalares.
C) Correta.
D) Errada. Energia e tempo são escalares.
E) Errada. Energia e massa são escalares.
Alternativa: C
28) Cotidianamente as grandezas massa e peso são confundidas como se fossem exatamente iguais.
Assinale a alternativa que indica corretamente a diferença entre massa e peso.
(A) A massa é a quantidade de matéria de um corpo, por isso, é uma grandeza vetorial. O peso é a força com a qual o corpo é atraído pela Terra, por isso, é uma grandeza escalar.
(B) O peso de um corpo é a força com a qual ele é atraído pela Terra, sendo, por essa razão, uma grandeza vetorial. A massa é a quantidade de matéria que compõe o corpo e é uma grandeza escalar.
(C) Massa e peso são grandezas vetoriais. A diferença é que a definição de peso leva em consideração a aceleração da gravidade.
(D) O peso é fruto do produto da massa pela gravidade, e a massa é fruto do produto do peso pela gravidade.
(E) Todas as alternativas estão incorretas.
Resolução:
A força peso é o produto da massa pela aceleração da gravidade e é uma grandeza vetorial. A massa de um corpo é a quantidade de matéria que o compõe e é uma grandeza de tratamento escalar.
Alternativa: B
29) Ao perguntar a diferença entre grandezas escalares e vetoriais, um professor de Física obteve as seguintes respostas:
João: As grandezas escalares possuem apenas valores numéricos. Já as vetoriais possuem, além de valor numérico, direção e sentido. Força e aceleração são exemplos de grandezas vetoriais. Massa e empuxo são exemplos de grandezas escalares.
Pedro: As vetoriais têm duas características: módulo e direção. As escalares possuem apenas valor numérico. Força e velocidade são vetoriais. Massa e tempo são escalares.
A partir das respostas dos alunos, marque a alternativa correta:
(A) Pedro e João estão corretos.
(B) Somente João está correto.
(C) Somente Pedro está correto.
(D) João errou as definições e acertou os exemplos, e Pedro errou os exemplos e acertou as definições.
(E) João acertou as definições e errou ao dar os exemplos. Pedro acertou os exemplos e errou ao dar as definições.
Resolução
As definições dadas por João estão corretas. O erro cometido por ele foi classificar o empuxo como uma grandeza escalar. Os exemplos dados por Pedro estão corretos, mas ele cometeu erro ao dizer que as grandezas vetoriais possuem apenas módulo e direção, uma vez que o correto é módulo, direção e sentido.
Alternativa: E
30) A imagem a seguir mostra o deslocamento de uma partícula.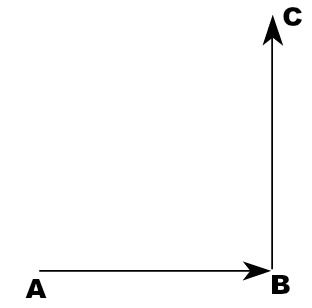 Marque a alternativa correta sabendo que o caminho AB possui 3 mm, BC possui 4 mm e que as retas AB e BC são perpendiculares.
Marque a alternativa correta sabendo que o caminho AB possui 3 mm, BC possui 4 mm e que as retas AB e BC são perpendiculares.
(A) O deslocamento vetorial da partícula é 7 mm.
(B) A distância total percorrida pela partícula é 7 mm, e o deslocamento é 5 mm.
(C) Tanto a distância total percorrida quanto o deslocamento da partícula são iguais a 7 mm.
(D) A determinação do deslocamento vetorial é dada pela soma das distâncias AB e BC.
(E) Mesmo que o ângulo entre as retas AB e BC fosse diferente, o deslocamento vetorial seria igual a 5 mm.
Resolução:
A distância total percorrida é a soma de cada uma das etapas feitas pela partícula, ou seja:
AB + BC = 3 mm + 4 mm = 7 mm
O deslocamento é a reta que une o ponto de partida ao ponto de chagada. Assim, a figura formada é um triângulo retângulo, e a hipotenusa desse triângulo corresponde ao deslocamento AC da partícula.
Aplicando o teorema de Pitágoras, temos:
AC2 = AB2 + BC2
AC2 = 32 + 42
AC2 = 9 + 16
AC2 = 25 = AC = √25 = AC = 5
AC = 5 mm
Alternativa: B
MOVIMENTO CIRCULAR
UNIFORME: ENTRE ROTAÇÕES
E TRANSMISSÕES
Movimento circular uniforme
Chamamos de movimento circular o deslocamento de um ponto material cuja trajetória seja uma circunferência ou um arco de circunferência.
Quando um ponto material descreve um movimento circular com velocidade constante, dizemos que ele realiza um
movimento circular uniforme (MCU).
Um movimento circular é aquele em que o objeto ou ponto material se desloca em uma trajetória circular. Neste tipo de movimento, existe uma força centrípeta que muda a direção do vetor velocidade e é aplicada para o centro do círculo. A força centrípeta também é responsável pela aceleração centrípeta, a qual é orientada para o centro da circunferência-trajetória.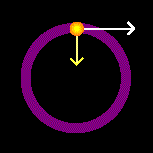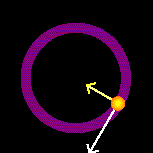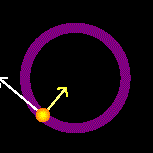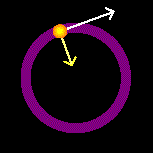 Movimento Circular Uniforme (MCU) - No movimento uniforme, o móvel percorre distâncias iguais em intervalos de tempo iguais. No caso particular do movimento circular uniforme, como a trajetória é circular, decorre que o intervalo de tempo de cada volta completa é sempre o mesmo, isto é, de tempos em tempos iguais o móvel passa pela mesma posição. Portanto o MCU é um movimento periódico. Seu período T é o intervalo de tempo de uma volta completa. O número de voltas na unidade de tempo é sua frequência f.
Movimento Circular Uniforme (MCU) - No movimento uniforme, o móvel percorre distâncias iguais em intervalos de tempo iguais. No caso particular do movimento circular uniforme, como a trajetória é circular, decorre que o intervalo de tempo de cada volta completa é sempre o mesmo, isto é, de tempos em tempos iguais o móvel passa pela mesma posição. Portanto o MCU é um movimento periódico. Seu período T é o intervalo de tempo de uma volta completa. O número de voltas na unidade de tempo é sua frequência f.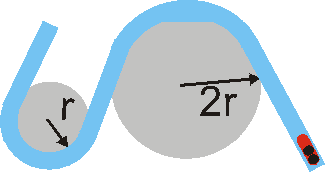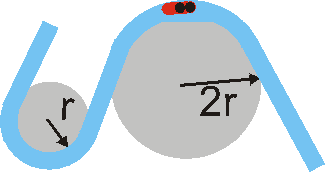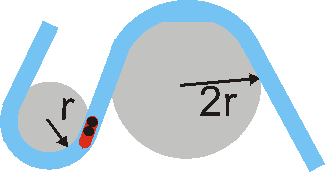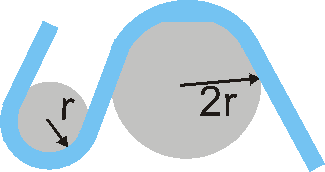
Observando o dia a dia:

Movimentos circulares estão presentes em várias situações — como no movimento dos ponteiros de um relógio.
- Qual é a trajetória descrita pelos ponteiros e quanto tempo cada ponteiro leva para completar uma volta?
- O que ventiladores, rodas-gigantes e ponteiros de relógio têm em comum?
Período e frequência
Chamamos de período (T) o tempo que um ponto material leva para completar uma volta em uma trajetória circular. Se esse ponto material realiza n voltas em um intervalo de tempo Δt, temos:
T = Δt
n
No Sistema Internacional de Unidades (SI), o período é medido em segundos (s).
Período e frequência
Chamamos de frequência (f) o número de voltas realizadas por unidade de tempo:
f = n
Δt
No SI, a frequência é medida em hertz (Hz).
1 Hz = 1s
Grandezas angulares
A velocidade angular (ω) mostra com que rapidez esse ângulo está sendo percorrido:
ω = ∆𝛉
∆t
Enquanto a velocidade linear mede “quantos metros por segundo” o ponto anda, a velocidade angular mede “quantas voltas por segundo” ele dá.
Relações entre grandezas
A velocidade angular é calculada por:
ω = ∆θ
∆t
Para uma volta completa:
∆θ = 2π rad e ∆t = T
Portanto:
ω = 𝟐𝛑
T
Relações entre grandezas
Se o movimento é periódico, a cada volta são percorridos 2π rad, e como f = 𝟏/T temos também:
ω = 2π . f
A unidade de medida da velocidade angular no SI é o radiano por segundo (rad/s).
Grandezas angulares
Todo movimento circular possui também uma velocidade escalar, chamada velocidade tangencial (v). Seu módulo é dado por: v = ∆S
∆t
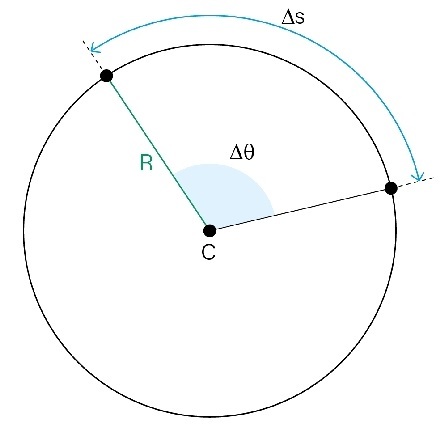
Onde ΔS é o comprimento do arco percorrido. Como ΔS = Δθ . R, temos:
v = ω . R
Relações entre grandezas
A velocidade tangencial é calculada por:
v = ∆S
∆t
Para uma volta completa:
∆S = 2 . π . R e Δt = T
Logo, podemos reescrever a equação da seguinte forma:
v = ∆S
∆t
Portanto:
v = 𝟐𝛑 · 𝐑 = 𝟐𝛑 . R . f
T
Grandezas angulares
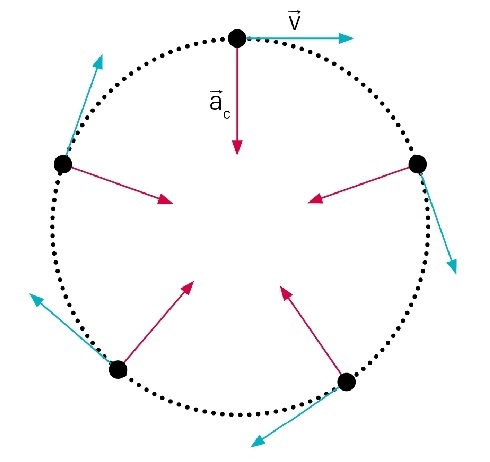
No MCU, a velocidade é sempre tangente à trajetória. Embora o módulo seja constante, a direção muda em cada ponto. As setas na figura mostram direção e sentido da velocidade em diferentes posições do movimento.
Aceleração centrípeta
Qualquer variação na velocidade, mesmo que só na direção, indica aceleração. A variação da direção da velocidade tangencial gera a aceleração centrípeta (ac). A variação do módulo gera a aceleração tangencial (at), que no MCU é nula.
Aceleração centrípeta
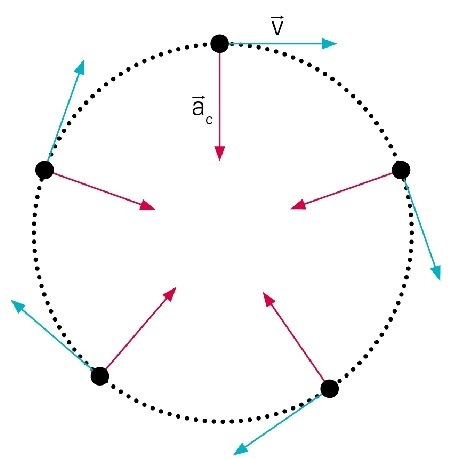
O módulo da aceleração centrípeta é dado por:
ac = v2
R
ac = ω2 . R
Sua direção é sempre perpendicular à velocidade e aponta para o centro da trajetória.
Transmissão de movimento
A transmissão de movimento circular pode ocorrer entre engrenagens, polias e outros elementos, seja por contato direto ou pelo uso de correias, correntes ou eixos.
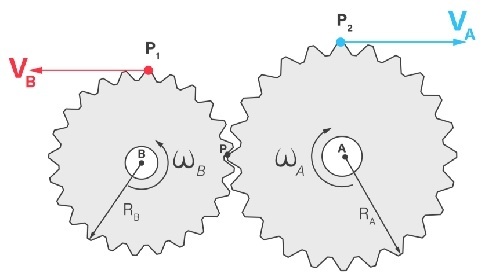
Transmissão por contato direto engrenagens: velocidades tangenciais iguais, mas sentidos opostos.
Transmissão por correia ou corrente: velocidades tangenciais iguais e no mesmo sentido.
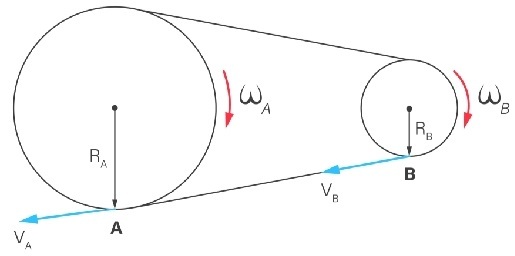
Nos sistemas de transmissão por contato ou por correia, todos os pontos da polia ou da engrenagem possuem o mesmo módulo de velocidade tangencial, ou seja, vA = vB.
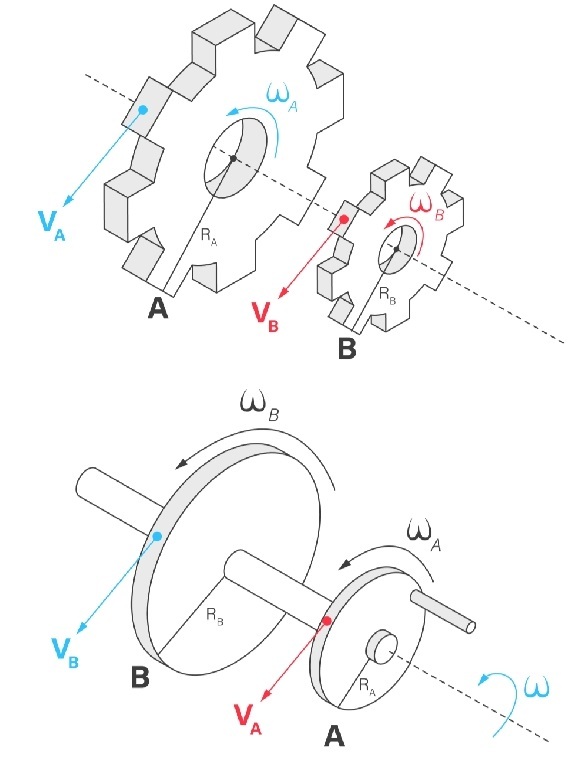
Observação:
Engrenagens ou polias, quando conectadas pelo mesmo eixo, possuem velocidades angulares iguais.
Porém, suas velocidades tangenciais são diferentes.
Transmissão de movimento
Em uma engrenagem o número (n) de dentes é diretamente proporcional ao seu raio (R). Por esse motivo, também é válida a relação:

fA . nA = fB . nB
f = frequência (Hz)
Transmissão de movimento
Quando polias ou engrenagens estão no mesmo eixo:
As velocidades angulares são iguais (ωA= ωB)
As velocidades tangenciais são diferentes, pois dependem do raio.

Sendo
ω= 2π . f
ωA = ωB
2π· fA = 2π· fB
fA = fB
Como a velocidade angular também pode ser calculada por
ω = v
R
Temos:
ωA = ωB
𝐯𝐀 = 𝐯𝐁
RA RB

QUESTÕES RESOLVIDAS
01) (Livro do Aluno SEDUC/2026) (UECE 2022) Em um torno mecânico de bancada, duas polias são conectadas por meio de uma correia. Uma das polias tem 10 cm de raio e realiza 80 voltas por segundo. O número de voltas que a segunda polia dará por minuto, caso tenha 20 cm de raio, é
(A) 1200.
(B) 2400.
(C) 7200.
(D) 3600.
Resolução:
Como as polias são conectadas por uma correia, chamando uma polia de A e a outra de B, podemos afirmar que:
vA= vB
Mas como v = ω· R e ω= 2π· f, então:
vA = vB
ωA. RA= ωB·.RB
fA· RA= fB· RB
De acordo com o enunciado, uma das polias (A) possui raio RA = 10 cm e fA = 80 voltas por segundo, ou seja, fA = 80 Hz. Se considerarmos que a outra polia possua raio RB = 20 cm, então sua frequência será: 80 · 10 = fB · 20 fB = 800 20 = 40 Hz Porém, o enunciado pede a frequência da segunda polia em voltas por minuto, ou seja, em rpm. Para converter um valor de frequência que está em Hertz para rpm, basta multiplicá-lo por 60.
Logo: fB = 40 · 60
fB = 2400 rpm.
Alternativa: B
02) (Livro do Aluno SEDUC/2026) (PUCGO MEDICINA 2023 – Adaptada) Até o início de novembro, a cidade de São Paulo aguardava, ainda para o segundo semestre de 2022, a inauguração da maior roda-gigante da América Latina. A “Roda São Paulo” terá 91 metros de altura e 42 cabines de observação. Está sendo construída no Parque Cândido Portinari, na Zona Oeste da capital. Cada volta completa terá duração de 25 minutos.
A partir das informações apresentadas e supondo-se que a Roda São Paulo desenvolva uma velocidade angular constante, marque a única alternativa que apresenta, aproximadamente, o módulo da velocidade linear e da aceleração radial desenvolvida por uma cabine durante a realização de uma volta completa:
Dado: considere π = 3.
(A) 1,2 m/s e 2,2 . 10–2m/s2.
(B) 3,5 m/s e 1,6 . 10–2m/s2.
(C) 0,18 m/s e 7,1 . 10–4m/s2.
(D) 0,56 m/s e 3,2 . 10–4m/s2.
Resolução:
Sendo R = 45,5 m e a velocidade tangencial v = 0,182, a aceleração centrípeta de uma cabine da roda-gigante será: ac = v2 R
ac = 0,1822 45,5
ac = 0,033124 45,5
ac = 0,000728
ac = 7,28 · 10–4 m/s2
Alternativa: C
03) (Livro do Aluno SEDUC/2026) (UERJ 2024 – Adaptada) Sirius, a nova fonte de radiação síncrotron brasileira, funciona como um grande microscópio que − ao revelar a estrutura atômica, molecular e eletrônica dos mais diversos materiais − permite pesquisas com aplicações em praticamente todas as áreas do conhecimento. Para produzir a radiação síncrotron, feixes de elétrons são acelerados em várias etapas até alcançarem o anel principal do acelerador Sirius, um tubo fechado onde se produz vácuo. Nesse espaço confinado, os elétrons se movimentam em trajetória circular com rapidez próxima à da luz.
Adaptado de lnls.cnpem.br.
Calcule, em segundos, o período do movimento circular dos elétrons, e determine, em m/s, a rapidez alcançada por esses elétrons no acelerador Sirius e a velocidade angular, em rad/s.
Resolução:
O enunciado diz que os feixes de elétrons completam 80 000 voltas por segundo. Como voltas por segundo correspondem à definição de frequência f = n/Δt, podemos afirmar que f = 80 000 Hz. Logo, o período do movimento circular dos elétrons é:
T = 1/f
T = 1/80 000
T = 0,000125 = 1,25 · 10–5 s
Sabendo que a frequência do movimento circular dos elétrons é f = 80 000 Hz e que o raio do anel principal do Sirius vale R = 500 m, a velocidade tangencial dos feixes (rapidez) será:
v = 2π · R · f
v = 2 · 3 · 500 · 80 000
v = 240 000 000 = 2,4 · 108 m/s
A velocidade angular será:
v = ω · R
ω = v/R
ω = 2,4 . 108
500
ω = 0,0048 · 108
ω = 4,8 · 105 rad/s
04) (Livro do Aluno SEDUC/2026) (PUCGO MEDICINA 2023 – Adaptada) Até o início de novembro, a cidade de São Paulo aguardava, ainda para o segundo semestre de 2022, a inauguração da maior roda-gigante da América Latina. A “Roda São Paulo” terá 91 metros de altura e 42 cabines de observação. Está sendo construída no Parque Cândido Portinari, na Zona Oeste da capital. Cada volta completa terá duração de 25 minutos.
A partir das informações apresentadas e supondo-se que a Roda São Paulo desenvolva uma velocidade angular constante, marque a única alternativa que apresenta, aproximadamente, o módulo da velocidade linear e da aceleração radial desenvolvida por uma cabine durante a realização de uma volta completa:
Dado: considere π = 3.
(A) 1,2 m/s e 2,2 · 10–2 m/s2
(B) 3,5 m/s e 1,6 · 10–2 m/s2
(C) 0,18 m/s e 7,1 · 10–4 m/s2
(D) 0,56 m/s e 3,2 · 10–4 m/s2
Resolução:
O enunciado afirma que cada volta completa da roda-gigante terá duração de 25 minutos. O tempo para que um objeto em MCU complete uma volta corresponde ao período. Logo, T = 25 minutos = 1 500 s. A altura de 91 m corresponde ao diâmetro da roda, logo, seu raio será R = 45,5 m. Portanto, a velocidade tangencial (linear) dessa roda gigante será:
v = 2π . R
T
v = 2 . 3 . 45,5
1500
v = 0,182 m/s
Sendo R = 45,5 m e a velocidade tangencial v = 0,182, a aceleração centrípeta de uma cabine da roda-gigante será:
ac = v2
R
ac = 0, 1822
45,52
ac = 0 033124
45,5
ac = 0,000728
ac = 7,28 . 10–4 m/s2
Alternativa: C
05) (Livro do Aluno SEDUC/2026) (UECE 2022) Em um torno mecânico de bancada, duas polias são conectadas por meio de uma correia. Uma das polias tem 10 cm de raio e realiza 80 voltas por segundo. O número de voltas que a segunda polia dará por minuto, caso tenha 20 cm de raio, é:
(A) 1200
(B) 2400
(C) 7200
(D) 3600
Resolução:
Como as polias são conectadas por uma correia, chamando uma polia de A e a outra de B, podemos afirmar que:
vA = vB
Mas como v = ω · R e ω = 2π · f, então:
vA = vB
ωA · RA = ωB · RB
fA · RA = fB · RB
De acordo com o enunciado, uma das polias (A) tem raio RA = 10 cm e fA = 80 voltas por segundo, ou seja, fA = 80 Hz.
Se considerarmos que a outra polia possua raio RB = 20 cm, então sua frequência será:
80 · 10 = fB · 20
fB = 800 20 = 40 Hz
Porém, o enunciado pede a frequência da segunda polia em voltas por minuto, ou seja, em rpm.
Para converter um valor de frequência que está em Hertz para rpm, basta multiplicá-lo por 60.
Logo:
fB = 40 · 60
fB = 2400 rpm.
Alternativa: B
06) (Livro do Aluno SEDUC/2026) (UFPA 2016) Durante os festejos do Círio de Nazaré, em Belém, uma das atrações é o parque de brinquedos situado ao lado da Basílica, no qual um dos brinquedos mais cobiçados é a Roda Gigante, que gira com velocidade angular ω, constante.

Considerando-se que a velocidade escalar de um ponto qualquer da periferia da Roda é V = 1 m/s e que o raio é de 15 m, pode-se afirmar que a frequência de rotação f, em Hertz, e a velocidade angular ω, em rad/s, são respectivamente:
(A) 1/30μ e 2/25
(B) 1/15μ e 2/15
(C) 1/30μ e 1/15
(D) 1/15μ e 1/15
(E) 1/30μ e 1/30μ
Resolução:
De acordo com o enunciado, a velocidade linear (tangencial) de um ponto qualquer da periferia da roda é v = 1 m/s, e o raio é R = 15 m. Sabendo que a velocidade tangencial pode ser calculada por
V = 2π · R · f, a frequência de rotação da roda gigante é:
V = 2π · R · f
1 = 2π · 15 · f
1 = 30π · f
f = 1/30π
A velocidade angular de um MCU se relaciona com a velocidade tangencial pela equação:
V = ω · R
Como V = 1 m/s e R = 15 m, a velocidade angular da roda gigante é:
V = ω · R
1 = ω · 15
ω = 1/15 rad/s
Alternativa: C
07) (Livro do Aluno SEDUC/2026) (UNICAMP 2020 – Adaptada) As agências espaciais NASA (norte-americana) e ESA (europeia) desenvolvem um projeto para desviar a trajetória de um asteroide através da colisão com uma sonda especialmente enviada para esse fim. A previsão é que a sonda DART (do inglês “Teste de Redirecionamento de Asteroides Duplos”) será lançada com a finalidade de se chocar, em 2022, com Didymoon, um pequeno asteroide que orbita um asteroide maior chamado Didymos.
O asteroide satélite Didymoon descreve uma órbita circular em torno do asteroide principal Didymos. O raio da órbita é r = 1,6 km e o período é T = 12 h. A aceleração centrípeta do satélite vale: (Adote π = 3)
(A) 8,0 . 10–1 km/h2
(B) 4,0 . 10–1 km/h2
(C) 3,125 . 10–1 km/h2
(D) 6,667 . 10–2 km/h2
Resolução;
Como o período do movimento do satélite é T = 12 h, ω será:
ω = 2π
T
ω = 2π = μ rad/h
12 6
Como r = 1,6 km e ac = ω2 · R:
ac = ω2 · R
ac = (μ/6)2 . 1,6
ac = (3/6)2 . 1,6
ac = (1/2)2 . 1,6
ac = (1/4)2 . 1,6
ac = 0,4
ac = 4. 10-1 km/h2
Alternativa: B
08) (Livro do Aluno SEDUC/2026) (ESPCEX 2019) Duas polias, A e B, ligadas por uma correia inextensível têm raios RA = 60 cm e RB = 20 cm, conforme o desenho a seguir.
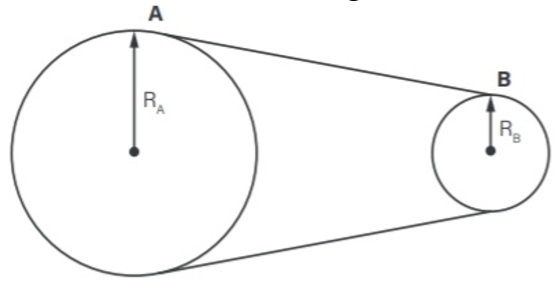
Admitindo que não haja escorregamento da correia e sabendo que a frequência da polia A é fA = 30 rpm, então a frequência da polia B é:
(A) 10 rpm.
(B) 20 rpm.
(C) 80 rpm.
(D) 90 rpm.
(E) 120 rpm.
Resolução:
Como as duas polias estão ligadas por uma correia, as velocidades tangenciais delas são iguais:
vA = vB
Como v = ω · R e ω = 2π · f, temos:
2π · fA · RA = 2π · fB · RB
30 · 60 = fB · 20
fB = 1800
20
fB = 90 rpm
Alternativa: D
09) (MACK-SP) Devido ao movimento de rotação da Terra, uma pessoa sentada sobre a linha do Equador tem velocidade escalar, em relação ao centro da Terra, igual a:
Adote: Raio equatorial da Terra = 6 300 km e π = 22
7
(A) 2250 Km/h
(B) 1650 Km/h
(C) 1300 Km/h
(D) 980 Km/h
(E) 460 Km/h
Resolução:
Sabemos que a velocidade angular pode ser dada por w = 2 π e que a velocidade linear é fruto do produto da velocidade angular T pelo raio da trajetória. Sendo assim, temos:
v = w . R
v = 2 π . R
T
Sabendo que o período de rotação da Terra é de 24h, temos:
v = 2 . 22 . 6300
7 24
v = 2 . 22 . 6300 . 1
7 24
v = 277200
168
v = 1650 km/h
Alternativa: B
10) (UFCE) Um automóvel se desloca em uma estrada horizontal com velocidade constante de modo tal que os seus pneus rolam sem qualquer deslizamento na pista. Cada pneu tem diâmetro D = 0,50 m, e um medidor colocado em um deles registra uma frequência de 840 rpm.
A velocidade do automóvel é de:
(A) 3 π m/s
(B) 4 π m/s
(C) 5 π m/s
(D) 6 π m/s
(E) 7 π m/s
Resolução:
- Para encontrar o valor da frequência em Hz, basta dividi-la por 60. Logo, f = 14 Hz
- O raio do pneu é dado pela metade de seu diâmetro, portanto: R = 0,25 m
- Da relação entre velocidade linear e velocidade angular, temos:
v = w . R
v = 2. π . f . R
v = 2 . π . 14 . 0,25
v = 7 π m/s
Alternativa: E
11) (UFPR) Um ponto em movimento circular uniforme descreve 15 voltas por segundo em uma circunferência de 8,0 cm de raio.
A sua velocidade angular, o seu período e a sua velocidade linear são, respectivamente:
(A) 20 rad/s; (1/15) s; 280 π cm/s
(B) 30 rad/s; (1/10) s; 160 π cm/s
(C) 30 π rad/s; (1/15) s; 240 π cm/s
(D) 60 π rad/s; 15 s; 240 π cm/s
(E) 40 π rad/s; 15 s; 200 π cm/s
Resolução:
A frequência do ponto em movimento é 15 Hz, e o raio da trajetória circular, 8 cm. Sendo assim, temos:
- A velocidade angular: w = 2. π . f = 2 . π . 15 = 30 π Rad/s
- Período (T): é dado pelo inverso da frequência → T = 1 = 1 s
f 15
- A velocidade linear: v = w . R → v = 30 π . 8 → v = 240 π m/s
Alternativa: C
12) O tacômetro é um equipamento que fica no painel do carro para indicar ao motorista em tempo real qual é a frequência de rotação do motor.
Supondo que um tacômetro esteja indicando 3000 rpm, determine a velocidade angular de rotação do motor em rad/s.
(A) 80 π
(B) 90 π
(C) 100 π
(D)150 π
(E)200 π
Resolução:
O valor da frequência em rpm, ao ser dividido por 60, é transformado em Hz. Sendo assim, a frequência de rotação do motor é de 50 Hz.
A velocidade angular é dada por
w = 2. π.f
w = 2. π. 50
w = 100 π rad/s
Alternativa: C
13) Uma serra circular possui 30 cm de diâmetro e opera com frequência máxima de 1200 rpm. Determine a velocidade linear de um ponto na extremidade da serra.
Adote: π = 3
(A) 12 m/s
(B) 14 m/s
(C) 16 m/s
(D) 18 m/s
(E) 20 m/s
Resolução:
O raio da serra é metade de seu diâmetro, sendo, portanto, de 15 cm ou 0,15m. O valor da frequência em rpm pode ser dividido por 60 e ser transformado para Hz. Então, temos f = 20 Hz
Da relação entre velocidade linear e velocidade angular, temos:
v = w . R
v = 2. π . f . R
v = 2 . 3 . 20 . 0,15
v = 18 m/s
Alternativa: D
14) Um eucalipto encontra-se plantado perpendicularmente a uma superfície plana. A árvore é cortada junto ao chão e leva 4s para deixar a posição vertical e ficar no chão na posição horizontal. Determine o valor aproximado da velocidade angular média de queda desse eucalipto.
Adote: π = 3,14
(A) 0,30 rad/s
(B) 0,40 rad/s
(C) 0,50 rad/s
(D) 0,56 rad/s
(E) 0,70 rad/s
Resolução:
Ao cair, o eucalipto descreve um arco de 90° ou π rad/s. A velocidade angular pode ser definida 2
como a razão entre o ângulo percorrido pelo intervalo de tempo. Sendo assim, temos:
w = Δθ
Δt
w = π
2
4
w = π. 1
2 4
w = π
8
w = 3,14 ≈ 0,40 rad/s
8
Alternativa: B
EXERCÍCIOS – PERÍODO / FREQUÊNCIA (MCU)
15) (PUC) A respeito do período e da frequência no movimento circular uniforme (MCU), indique o que for correto.
(A) O período é diretamente proporcional à frequência de giro de um corpo em MCU.
(B) Sabendo que o período de giro do ponteiro dos minutos é de 1 min, podemos dizer que a sua frequência será, aproximadamente, de 0,017 Hz.
(C) Se a frequência do ponteiro dos segundos é de 1 min, podemos calcular a sua frequência aproximada como de 0,017 Hz.
(D) A frequência é diretamente proporcional ao período.
(E) Um corpo de giro com frequência de 20 Hz possui período igual a 0,02 s.
Resolução:
A frequência do ponteiro dos segundos é exatamente 60 s (1 min). Podemos determiná-la sabendo que ela é o inverso do período, portanto:
f = 1 = 0,0166 ≈ 0,017 Hz
60
Alternativa: C
03) (Vunesp) Marque a alternativa que indica o período de revolução de um satélite geoestacionário.
(A) 48h
(B) 12h
(C) 72h
(D) 24h
(E) 10h
Resolução:
Os satélites chamados de geoestacionários são aqueles que giram sobre um ponto da Linha do Equador e que possuem período igual à rotação da Terra, logo, o período de revolução desses equipamentos é de 24 h. Alternativa: D
04) (Fuvest) O período de translação da lua ao redor da Terra corresponde a 28 dias, sendo assim, determine a porcentagem diária aproximada da translação da lua.
(A) 3,6 %
(B) 6,5 %
(C) 7,5 %
(D) 4,0 %
(E) 3,0 %
Resolução:
Se determinarmos a frequência de translação da lua, teremos:
f = 1 = 0,035 rotação por dia
28 dias
Podemos concluir, portanto, que, a cada dia, a lua percorre 3,5% de um 1 giro completo. Alternativa: A
05) (Metodista) Um corredor mantém em uma pista circular uma velocidade constante de 2 m/s e completa uma volta em 80 s.
Determine a frequência de giro do corredor e o tamanho da pista circular.
(A) 0,00150 Hz e 180 m
(B) 0,0125 Hz e 170 m
(C) 0,0125 Hz e 160 m
(D) 0,0325 Hz e 180 m
(E) 0,0525 Hz e 160 m
Resolução:
O tempo de 80s corresponde exatamente ao período de rotação do corredor. Sabendo que a frequência é o inverso do período, temos:
f = 1 =0,0125 Hz
80
A partir da equação da velocidade média, podemos encontrar o tamanho da pista:
v = Δs
Δt
2 = Δs
80
Δs = 2 . 80 = 160m
Alternativa: C
EXERCÍCIOS - MOVIMENTO CIRCULAR UNIFORMEMENTE VARIADO (MCUV)
01) (UNESP) Um “motorzinho” de dentista gira com frequência de 2000 Hz até a broca de raio 2,0mm encostar no dente do paciente, quando, após 1,5s, passa a ter frequência de 500Hz. Determine o módulo da aceleração escalar média neste intervalo de tempo.
Resolução:
ω = ωo + y.t
2.Л.f = 2.Л.fo + y.t
2.Л.500 = 2.Л.2000 + y.1,5
1000. Л = 4000.Л + 1,5y
1,5y = -3000.Л
y = -3000.Л/1,5
y = -2000.Л rad/s²
Como a = y.r
Temos que: a = -2000.Л.2.10-3 = 4.Лm/s²
03) (Fuvest) A velocidade angular de um móvel em trajetória circular é diminuída de 30.π rad/s para 20. π rad/s em um intervalo de tempo igual à 2s. Sabendo que o raio do círculo mede 0,5m e o movimento é uniformemente variado; determine a aceleração escalar deste móvel.
Resolução:
ω = ωo + y.t
20. π = 30. π + y.2
2.y = -10. π
y = -5. π rad/s
a = y.r
a = -5.0,5
a = 2,5m/s²
DISTÂNCIA DO SOL A TERRA
Depois dos artigos superinteressante sobre o sol que fala da temperatura do sol de uma pergunta superinteressante chegamos a outra.
Sabemos que a distância entre a Lua e a Terra é de uns 300 mil quilômetros o que leva a luz entre a lua e a Terra percorrer esta distância em 1 segundo pois a velocidade da Luz é perto de 300 mil km/s.
Poucos sabem mas o tempo que a Luz leva para percorrer a distância entre o SOL e a Terra é de 8 minutos e uns 20 segundos ou seja 500 segundos.
Então, qual é a distância entre o sol e a terra?
A distância varia em relação a translação da Terra (movimento elíptico que a terra faz em torno do Sol, não confundir com o movimento de rotação que é o movimento que a terra faz em torno de si mesma).
Para chegar a esse numero só calcular aproximadamente 300 mil km x 500 segundos que é a velocidade da luz x o tempo que ela leva para percorrer o caminho entre o sol e a Terra.
Ou seja o sol esta quase 500 vezes mais longe do que a lua esta da Terra. o que da um resultado médio de 150 milhões de quilômetros.
Resultado médio pois em seu periélio (distância mais próxima do Sol) a Terra se encontra perto dos 147 milhões de quilômetros do Sol e em seu Afélio (maior distância do Sol) por volta de 152 milhões de quilômetros.
Como queremos saber é a distancia média que é de 149,6 milhões de quilômetros. (essa distância varia devido ao movimento elíptico da Terra em volta do Sol).
A primeira tentativa de calculo da distância entre a terra e o Sol aconteceu 200 anos AC onde Aristarque estimou a distância entre 1.7 milhões de km e 2.7 milhões de km, muito bom em relação a capacidade técnica presente naquela época.
Foi Nicolau Copérnico que demonstrou que a Terra gira em torno do Sol criando a teoria do Heliocentrismo no século XVI, e Kepler descobriu que a terra tinha uma trajetória elíptica em torno do Sol calculando a distância dos planetas do Sol.
Mas somente no século XX que chegamos a números próximos da real distância entre a Terra e o Sol
Casos Especiais
Caso 1: - É possível estudar dois ou mais corpos descrevendo simultaneamente a mesma trajetória porem com velocidades e sentidos diferentes.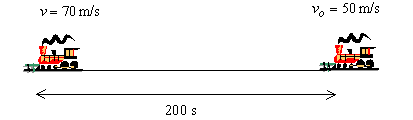
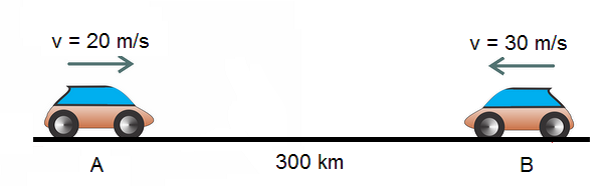 Caso 2: No cotidiano ha situações em que é possível estudar o movimento de um ponto material como onde ele descreve a mesma trajetória porém com trecho com velocidades diferentes.
Caso 2: No cotidiano ha situações em que é possível estudar o movimento de um ponto material como onde ele descreve a mesma trajetória porém com trecho com velocidades diferentes.
EXERCÍCIOS - QUESTÕES RESOLVIDAS
01) (PUC) Um macaco que pula de galho em galho em um zoológico, demora 6 segundos para atravessar sua jaula, que mede 12 metros. Qual a velocidade média dele?
Resolução:
S = 12m
t = 6s
v = ?
02) (Fuvest) Um carro viaja de uma cidade A a uma cidade B, distantes 200km. Seu percurso demora 4 horas, pois decorrida uma hora de viagem, o pneu dianteiro esquerdo furou e precisou ser trocado, levando 1 hora e 20 minutos do tempo total gasto. Qual foi a velocidade média que o carro desenvolveu durante a viagem?
Resolução:
S = 200km
t = 4h
v = ?
Mesmo o carro tendo ficado parado algum tempo durante a viagem, para o cálculo da velocidade média não levamos isso em consideração.
03) (Fuvest) No exercício anterior, qual foi a velocidade nos intervalos antes e depois de o pneu furar? Sabendo que o incidente ocorreu quando faltavam 115 km para chegar à cidade B.
Resolução:
Antes da parada:
S = 200-115 = 85km
t = 1hora
v = ?
Depois da parada:
S = 115km
t = 4h-1h-1h20min= 1h40min=1,66h (utilizando-se regra de três simples)
v = ?
04) (Unesp) Um bola de basebol é lançada com velocidade igual a 108m/s, e leva 0,6 segundo para chegar ao rebatedor. Supondo que a bola se desloque com velocidade constante. Qual a distância entre o arremessador e o rebatedor?
Resolução:
, se isolarmos S:
05) (Vunesp) Durante uma corrida de 100 metros rasos, um competidor se desloca com velocidade média de 5m/s. Quanto tempo ele demora para completar o percurso?
Resolução:, se isolarmos t:
06) (PUC) Um carro desloca-se em uma trajetória retilínea descrita pela função S = 20 + 5t (no SI). Determine:
(a) a posição inicial;
(b) a velocidade;
(c) a posição no instante 4s;
(d) o espaço percorrido após 8s;
(e) o instante em que o carro passa pela posição 80m;
(f) o instante em que o carro passa pela posição 20m.
Resolução:
(a) Posição inicial = 20m
(b) Velocidade = 5m/s
(c) S = 20+5t
S = 20+5.4
S = 40m
(d) S = 20+5.8
S = 60m
(e) 80= 20+5t
80 - 20 = 5t
60 = 5t
12s = t
(f) 20 = 20+5t
20- 20 = 5t
t = 0
07) (PUC) Em um trecho de declive de 10km, a velocidade máxima permitida é de 70km/h. Suponha que um carro inicie este trecho com velocidade igual a máxima permitida, ao mesmo tempo em que uma bicicleta o faz com velocidade igual a 30km/h. Qual a distância entre o carro e a bicicleta quando o carro completar o trajeto?
Resposta:
Carro:
S = 10km
v = 70km/h
t = ?
S = 70t
10 = 70t
0,14h = t
t = 8,57min (usando regra de três simples)
Bicicleta:
O tempo usado para o cálculo da distância alcançada pela bicicleta, é o tempo em que o carro chegou ao final do trajeto: t = 0,14h
Resposta:
v = 30km/h
t = 0,14h
S = ?
S = 0+30.(0,14)
S = 4,28Km
08) (UEL-PR) O gráfico a seguir mostra as posições em função do tempo de dois ônibus. Um parte de uma cidade A em direção a uma cidade B, e o outro da cidade B para a cidade A. As distâncias são medidas a partir da cidade A. A que distância os ônibus vão se encontrar?Para que seja possível fazer este cálculo, precisamos saber a velocidade de algum dos dois ônibus, e depois, calcular a distância percorrida até o momento em que acontece o encontro dos dois, onde as trajetórias se cruzam.
Calculando a velocidade ônibus que sai da cidade A em direção a cidade B (linha azul)
Resolução:
Sabendo a velocidade, é possível calcular a posição do encontro, quando t=3h.
09) (Vunesp) Um carro, se desloca a uma velocidade de 20m/s em um primeiro momento, logo após passa a se deslocar com velocidade igual a 40m/s, assim como mostra o gráfico abaixo. Qual foi o distância percorrida pelo carro?Tendo o gráfico da v x t, o deslocamento é igual à área sob a reta da velocidade.
Resolução:
S = Área A + Área B
S =20 5 + 40 (15-5)
S =100 + 400
S = 500m
10) (Fei) Dois trens partem simultaneamente de um mesmo local e percorrem a mesma trajetória retilínea com velocidades, respectivamente, iguais a 300km/h e 250km/h. Há comunicação entre os dois trens se a distância entre eles não ultrapassar 10km. Depois de quanto tempo após a saída os trens perderão a comunicação via rádio?
Para este cálculo estabelece-se a velocidade relativa entre os trens, assim pode-se calcular o movimento como se o trem mais rápido estivesse se movendo com velocidade igual a 50km/h (300km/h-250km/h) e o outro parado.
Resolução:
v = 50km/h
S = 10km
t = ?
EXERCÍCIOS ESPECIAIS DE VELOCIDADE MÉDIA - (MRU)
02) (Enem) Uma empresa de transportes precisa efetuar a entrega de uma encomenda o mais breve possível. Para tanto, a equipe de logística analisa o trajeto desde a empresa até o local da entrega. Ela verifica que o trajeto apresenta dois trechos de distâncias diferentes e velocidades máximas permitidas diferentes. No primeiro trecho, a velocidade máxima permitida é de 80 km/h e a distância a ser percorrida é de 80 km. No segundo trecho, cujo comprimento vale 60 km, a velocidade máxima permitida é 120 km/h.
Supondo que as condições de trânsito sejam favoráveis para que o veículo da empresa ande continuamente na velocidade máxima permitida, qual será o tempo necessário, em horas, para a realização da entrega?
(A) 0,7
(B) 1,4
(C) 1,5
(D) 2,0
(E) 3,0
Resolução:
Observação: pelo enunciado entende-se que as distâncias em cada trecho não são iguais, e as velocidades também são diferentes ele quiser saber o tempo total. Neste caso é um exercícios simples, para isso basta encontrar o tempo gasto em cada trecho (t1 e T2) e somar os dois tempos.
Vm1 = 80
t1 = x
ΔS1 = 80
Vm1 = ΔS/t1
80 = 80/t1
08t1 = 80
t1 = 80/80
T1 = 1h
Vm2 = 120
t2 = x
ΔS1 = 60
Vm2 = ΔS/t1
120 = 60/t1
120t1 = 60
t1 = 60/120
T1 = 0,5h
T total = T1 + T2
T total = 1,0 + 0,5
T total = 1,5h
Alternativa: C
CORPOS EXTENSOS – (MRU)
03) Uma composição ferroviária com 1 locomotiva e 14 vagões desloca-se à velocidade constante de 10m/s. Tanto a locomotiva quanto cada vagão medem 12m. Então, quanto tempo ela demorará para atravessar um viaduto com 200m de comprimento?
Resolução:
Neste caos os dois o trem e o viaduto são corpos extensos, portanto tenho que considerar o tamanho do trem e o tamanho do viaduto.
- Tamanho do trem é 15 . 12 = 180 m.
- Tamanho do trem é 200 m.
ΔS = 180 + 200
ΔS = 380 m.
O tempo necessário para que o trem atravesse a ponte será:
Δt = ΔS/Vm
Δt = 380/10 = 38.
Resposta: o tempo de travessar será de 38s.
04) Uma composição ferroviária com 1 locomotiva e 14 vagões desloca-se à velocidade constante de 10m/s. Tanto a locomotiva quanto cada vagão medem 12m. Então, quanto tempo ela demorará para atravessar um sinaleiro
Resolução:
Neste caos apenas o trem e considerado corpo extenso, portanto devo considerar apenas o tamanho do trem.
- Tamanho do trem é 15 . 12 = 180 m.
O tempo necessário para que o trem atravesse o sinalerio será:
Δt = ΔS/Vm
Δt = 200/10 = 38
Δt = 20s
ENCONTRO DE DOIS MÓVEIS/ MESMO SENTIDO – (MRU)
05) Um móvel em uma rodovia sai da posição 18km e anda de acordo com o sentido positivo da trajetória com velocidade constante de 30km/h. Outro móvel sai da posição 2km e anda no sentido positivo da trajetória com velocidade constante de 50km/h. Determine o ponto onde os dois móveis se encontrarão.
(A) 30 km
(B) 38 km
(C) 40 km
(D) 42 km
(E) 50 km
Resolução:
Função horária da posição para cada um dos móveis:
S1 = 18 + 30.t
S2 = 2 + 50.t
No momento do encontro, as posições dos móveis serão as mesmas, sendo assim, igualando as funções acima, teremos:
S1 = S2
18 + 30.t = 2 + 50.t
20.t = 16
t = 0,8h
O tempo para o encontro é de 0,8h. Assim, a posição de encontro para os móveis é:
S1 = 18 + 30.t
S1 = 18 + 30.0,8
S1 = 42 km
S2 = 2 + 50.t
S2 = 2 + 50.0,8
S2 = 42 km
Alternativa: D
06) Dois carros, A e B, de dimensões desprezíveis, movem-se em movimento uniforme e no mesmo sentido com velocidades iguais a 20m/s e 15m/s, respectivamente. No instante t = 0, os carros encontram-se nas posições:
S0A = 30m
S0B = 180m
Responda:
a) depois de quanto tempo A alcança B.
S = So + v.t
SA = 30 + 20.t
SB = 180 + 15.t
Iguale as funções
SA = SB
30 + 20.t = 180 + 15.t
5.t = 150
t = 30s
b) em que posição ocorre o encontro.
Substituir o valor do instante de encontro em uma das funções horárias. Usando a função horária do espaço de A, tem-se:
SA = 30 + 20.t
SA = 30 + 20. 30
SA = 630 m
Resposta: o encontro acontece após 30s e na posição 630m.
07) Duas cidades, A e B, distam entre si 400km. Da cidade A parte um móvel P dirigindo-se à cidade B; no mesmo instante, parte do B outro móvel Q dirigindo-se a A. Os móveis P e Q executam movimentos uniformes e suas velocidades escalares são de 30km/h e 50km/h, respectivamente. A distância da cidade A ao ponto de encontro dos móveis P e Q, em km, vale:
(A) 120
(B) 150
(C) 200
(D) 240
(E) 250
Resolução
S = So + v.t
SP = 0 + 30.t
SQ = 400 - 50.t (movimento é retrógrado -V)
Agora se igualam as funções:
SP = SQ
30.t = 400 - 50.t
80.t = 400
t = 5
Substituindo o valor do instante de encontro em uma das funções horárias encontraremos a posição de encontro..
SP = 30.t
SP = 30 . 5
SP = 150
Alternativa: B
VELOCIDADE RELATIVA ENTRE DOIS MÓVEIS – (MRU)
08) Três móveis A, B e C, encontram-se numa trajetória retilínea descrevendo movimentos uniformes sendo que: VA = 5m/s, VB = 8m/s e VC = 4m/s. Sendo que A e B se movimentam-se no sentido favorável a trajetória e C movimenta-se no sentido contrário a trajetória.
Determine:
a) a velocidade de A em relação a B;
VAB = VA - VB
VAB = 5 – 8
VAB = - 3 m/s
b) a velocidade de B em relação a C;
VBC = VB – VC
VBC = 8 – (-4)
VBC = 12 m/s
c) a velocidade de C em relação a A.
VCA = VC - VA
VCA = -4 - 5
VCA = - 9 m/s
ENCONTRO DE DOIS MÓVEIS COM VELOCIDADE RELATIVA – (MRU)
09) Dois carros, A e B, movem-se no mesmo sentido, em uma estrada reta, com velocidades constantes VA = 100km/h e VB = 80km/h. Responda:
Resolução:
a) Qual é, em módulo, a velocidade do carro B em relação a um observador no carro A?
VR = | VB - VA |
|VR| = |80 - 100|
|VR| = 20 km/h =20/3,6 m/s
b) Em um dado instante, o carro B está 600 m à frente do carro A. Quanto tempo, em horas, decorre até que A alcance B?
DSR = 600 m
O tempo para ocorrer o encontro é:
DSR = |VR| . t
600 = 20/3,6 . t
t = 108s
Resposta: O módulo da velocidade do carro B em relação ao carro A é 20 km/h e o tempo para que o carro A alcance o carro B é 108s
EXERCÍCIO ESPECIAL - (MRUV)
10) (Enem 2017) Um motorista que atende a uma chamada de celular é levado a desatenção, aumentando a possibilidade de acidente ocorrerem em razão ao aumento do seu tempo de reação. Considere dois motoristas, o primeiro atento e o segundo utilizando o celular enquanto dirige. Eles aceleram seus carros inicialmente a 1,00 m/s2. Em resposta a uma emergência, freiam com uma desaceleração igual a 5,00 ms2. O motorista atento aciona o freio à velocidade de 14,0m/s, enquanto o desatento, em situação análoga, leva 1,00 segundo a mais para iniciar a frenagem.
Que distância o motorista desatento percorre a mais do que o motorista atento, até a parada total dos carros?
(A) 2,90 m
(B) 14,0 m
(C) 14,5 m
(D) 15,0 m
(E) 17,4 m
Resolução:
Motorista atento:
O motorista desatendo levou 1 segundo para pisar no freio o que temos: V1=14m/s e V2 = 15m/s. Nesse intervalos a distância percorrida é dada pela fórmula.
ΔS1/ Δt = (V1 + V2)/2
ΔS1/ 1 = (14 + 15)/2
ΔS1 = 14,5m
Observação: não temos o tempo de frenagem e quanto o tempo não é dado podemos aplicar a equação de Torricelli para cada um dos motoristas.
Motorista atento:
V2 = Vo2 + 2a. ΔS
02 = 142 + 2 . -5ΔS
0 = 196 - 10ΔS
-196 = -10ΔS
-56/-10 = ΔS
ΔS2 = 19,6m
Motorista desatento:
V2 = Vo2 + 2a. ΔS
02 = 152 + 2 . -5 ΔS
0 = 225 - 10ΔS
-225 = -10ΔS
-225/-10 = ΔS
ΔS3 = 22,5m
Temos:
ΔS1 = 14,5m
ΔS2 = 19,6m
ΔS2 = 37m
Espaço percorrido em cada situação
ΔS1 = 14,5m
ΔS2 = 19,6m
ΔS3 = 22,5m
Motorista desatento:
ΔS1 antes de iniciar a frenagem
ΔS3 durante a frenagem.
Motorista atento:
ΔS2 durante a fenagem ele percorreu.
Pergunta: Que distância o motorista desatento percorre a mais do que o motorista atento, até a parada total dos carros?
Fazendo a (distância percorrida do motorista desatento) menos a (distância percorrida pelo motorista atento) temos:
(ΔS1 + ΔS3) - ΔS2
(14,5 + 22,5) - 19,6
17,4
Alternativa: E
MARCO ZERO DE SÃO PAULO Inaugurado em 18 de setembro de 1934, o Marco Zero foi uma ideia elaborada vários anos antes, precisamente em 1921, quando o local ainda era conhecido popularmente como “Largo da Catedral” que ainda encontrava-se em obras. O projeto e local de construção do monumento surgiu das mãos do Dr. Américo Netto, à época diretor da Associação Paulista de Boas Estradas (órgão extinto no final dos anos 20).
Inaugurado em 18 de setembro de 1934, o Marco Zero foi uma ideia elaborada vários anos antes, precisamente em 1921, quando o local ainda era conhecido popularmente como “Largo da Catedral” que ainda encontrava-se em obras. O projeto e local de construção do monumento surgiu das mãos do Dr. Américo Netto, à época diretor da Associação Paulista de Boas Estradas (órgão extinto no final dos anos 20).
Entretanto o Marco Zero caiu no esquecimento e só voltou a ser discutido no final de 1933, quando o braço paulista do Touring Clube do Brasil procurou a prefeitura para sugerir a instalação do marco, que foi prontamente aceito. Totem hexagonal feito em autêntico mármore paulista e com base em granito, o marco tem uma altura que permite a qualquer adulto consultar facilmente a placa de bronze fixada em seu tampo. As laterais do marco possuem direções para 6 importantes pontos do Brasil, cada uma delas com uma ilustração que caracteriza a região mostrada.
Totem hexagonal feito em autêntico mármore paulista e com base em granito, o marco tem uma altura que permite a qualquer adulto consultar facilmente a placa de bronze fixada em seu tampo. As laterais do marco possuem direções para 6 importantes pontos do Brasil, cada uma delas com uma ilustração que caracteriza a região mostrada. Na foto, Minas Gerais, Goiás e Mato Grosso
Na foto, Minas Gerais, Goiás e Mato Grosso
A cidade de Santos (direção sudeste) é representada por um navio a vapor, o Estado do Paraná (direção sul) por uma Araucária, Rio de Janeiro (direção nordeste) com uma bananeira e o Pão de Açúcar, Minas Gerais (direção norte) com equipamento de mineração, Goiás (noroeste) a bateia usada no garimpo e Mato Grosso (direção sudoeste) com as indumentárias dos bandeirantes.
Em seu tampo, a placa de bronze tem um mapa parcial da Cidade de São Paulo, com o símbolo e a oferta do Touring Club do Brasil, e as principais vias paulistanas daquela época identificadas, como as avenidas Celso Garcia, Paulista e São João, além de locais de interesse público, como o Museu do Ipiranga e a Faculdade de Medicina. Um detalhe curioso a se observar é a ilha, já desaparecida, que havia no rio Tietê. Hoje ali existe o Shopping Center Norte. Outro ponto importante a salientar sobre o Marco Zero de São Paulo é que ele não só serve como um importante ponto turístico da cidade. Ele primeiramente serve ao propósito de que o próprio nome já indica, representando o centro geográfico do município, de onde todas as medições de distâncias das placas toponímicas paulistanas se iniciam.
Outro ponto importante a salientar sobre o Marco Zero de São Paulo é que ele não só serve como um importante ponto turístico da cidade. Ele primeiramente serve ao propósito de que o próprio nome já indica, representando o centro geográfico do município, de onde todas as medições de distâncias das placas toponímicas paulistanas se iniciam.
É por este motivo que as numerações dos logradouros da cidade são mais baixos no ponto mais próximo ao centro e mais distantes a medida que se afastam dele. Se alguém disser para você ir no número 100 da avenida São João, por exemplo, você já sabe que o 100 fica no ponto mais próximo ao centro, e não no outro lado na região da Barra Funda. Em 2007 o Marco Zero foi definitivamente tombado pelo órgão municipal responsável pelo patrimônio histórico da cidade, ano também que a obra recebeu uma restauração.
Em 2007 o Marco Zero foi definitivamente tombado pelo órgão municipal responsável pelo patrimônio histórico da cidade, ano também que a obra recebeu uma restauração.
DO MARCO ZERO AO SACI PERERÊ
Quando observamos os belos desenhos que representam as regiões brasileiras nas laterais do marco, não há qualquer menção ao artista. Porém, a obra é fruto do trabalho de um grande ilustrador francês: Jean Gabriel Villin. Nascido em Amiens, França, em 1906, Jean Gabriel Villin mudou-se para o Brasil ainda jovem, em 1925, para ir trabalhar na cidade de Porto Ferreira (SP) como desenhista em um fábrica de louças. Ele ficaria naquela cidade até 1927, quando veio para a capital atendendo um convite para trabalhar como desenhista no serviço público.
Nascido em Amiens, França, em 1906, Jean Gabriel Villin mudou-se para o Brasil ainda jovem, em 1925, para ir trabalhar na cidade de Porto Ferreira (SP) como desenhista em um fábrica de louças. Ele ficaria naquela cidade até 1927, quando veio para a capital atendendo um convite para trabalhar como desenhista no serviço público.
Foi nesta época, quando já estava bem estabelecido em São Paulo, que acabou conhecendo a figura de Monteiro Lobato, que entre 1929 e 1930 o convidou para ilustrar seus livros. Seu primeiro trabalho com o grande escritor brasileiro foi na ilustração do livro Reinações de Narizinho. Villin também é conhecido por ter sido o primeiro a desenhar e imortalizar o personagem Saci.
O nome de Jean Gabriel Villin também é muito conhecido e respeitado na área de desenhos publicitários, onde também destacou-se com muito sucesso. Mesmo sendo de origem francesa, Villin colocava em seus trabalhos muito do folclore e coisas típicas do brasil, dando um cunho totalmente nacional para a nossa propaganda, razão que foi chamado em sua época de “o mais brasileiro dos publicitários brasileiros”. Faleceu em 1979.
Fonte: http://www.saopauloantiga.com.br/marco-zero/
Acessado em: 04/03/2018 às 15:44
LANÇAMENTO HORIZONTAL e LANÇAMENTO OBLÍQUO
LANÇAMENTO HORIZONTAL
O lançamento horizontal é o movimento em que não temos velocidade inicial na direção vertical, apenas velocidade na direção horizontal.
O lançamento horizontal é um movimento no qual lança-se um corpo na horizontal, e, simultaneamente, ele continua movendo-se para frente e sendo atraído para o centro da Terra pela aceleração da gravidade.
Resumo sobre o lançamento horizontal
- O lançamento horizontal é o movimento em que não se tem velocidade inicial na direção vertical, apenas velocidade na direção horizontal.
-No lançamento horizontal, podemos calcular a posição final na horizontal e vertical do corpo, a velocidade final na horizontal e vertical do corpo, a velocidade inicial do corpo, e o tempo de queda do corpo.
-No lançamento horizontal, temos um movimento uniformemente variado (MUV) ocorrendo na direção vertical, já que a aceleração é não nula e igual à aceleração da gravidade.
-No lançamento horizontal, também temos um movimento uniforme (MU) ocorrendo na direção horizontal, já que a aceleração na horizontal é nula.
- Enquanto o lançamento horizontal é aquele em que não temos velocidade inicial na direção vertical, apenas velocidade na direção horizontal, o lançamento oblíquo é aquele em que temos velocidade inicial na direção vertical e velocidade na direção horizontal.
Lançamento horizontal: movimento de um objeto lançado na direção horizontal a partir de certa altura. Desprezando a resistência do ar, sua trajetória lateral é parabólica.
Para analisá-lo, decompomos em dois movimentos simultâneos: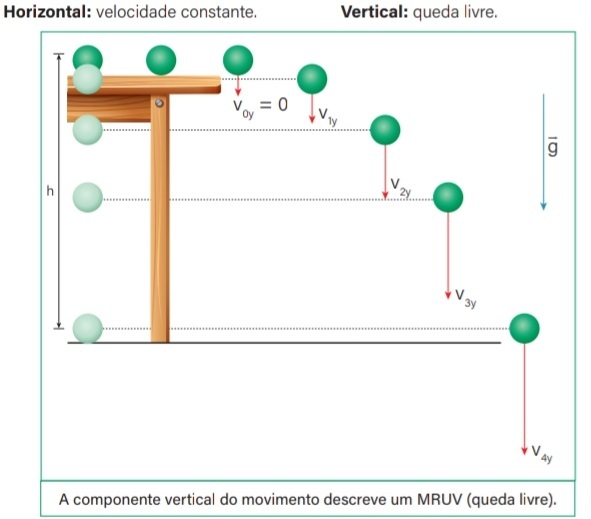
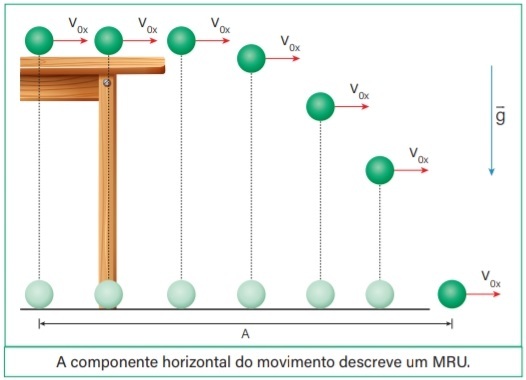
Tempo de queda e alcance horizontal: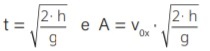
LANÇAMENTO OBLÍQUO ou LANÇAMENTO BALÍSITCO
LANÇAMENTO OBLÍQUO
O lançamento oblíquo é um movimento caracterizado pelo lançamento de um corpo com certo ângulo, diferente de 0º, 90º, 180º e 270º, em relação à horizontal.
O lançamento oblíquo é todo movimento parabólico com velocidade horizontal constante (desconsiderando a resistência do ar) durante o movimento e velocidade vertical nula na altura máxima, que ocorre quando os corpos são lançados com um ângulo de lançamento entre 0º e 90º ou entre 90º e 180º.
Resumo sobre lançamento oblíquo
- O lançamento oblíquo é o movimento de uma partícula lançada com uma velocidade inicial e com um ângulo de lançamento que varia entre 0º e 90º ou entre 90º e 180º.
- Na direção vertical no lançamento oblíquo, temos um movimento uniformemente variado (MUV).
- Na direção horizontal no lançamento oblíquo, temos um movimento uniforme (MU).
- No lançamento oblíquo é possível calcularmos a velocidade inicial do corpo, o tempo de subida e descida, o seu alcance horizontal e muitas outras grandezas.
- No movimento oblíquo transformamos todas as fórmulas do lançamento oblíquo em função do ângulo de lançamento do corpo.
Lançamento oblíquo: movimento em que um objeto é lançado de modo que sua velocidade inicial v0 forme um ângulo θ (0° < θ < 90°) com a direção horizontal.
Desprezando-se a resistência do ar, e visto de forma lateral, a trajetória descrita por um objeto lançado bliquamente é uma parábola.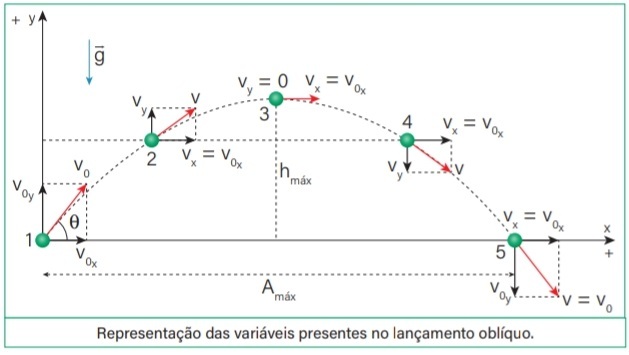
Componentes da velocidade inicial:![]()
Altura máxima: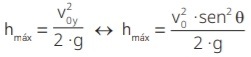
Tempo de subida: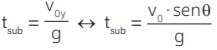
Tempo de subida (se tsub = tdesc):![]()
Alcance horizontal: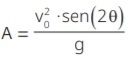
QUESTÕES RESOLVIDAS
01)
Continua...







