EF II - QUADRILATEROS
Professor Diminoi
QUADRILATEROS
Definição
Quadrilátero é um polígono de quatro lados.
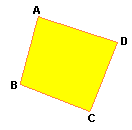
Quadrilátero ABCD
Em um quadrilátero, dois lados ou dois ângulos não consecutivos são chamados opostos.
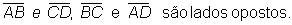
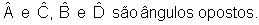
Elementos
Na figura abaixo, temos:
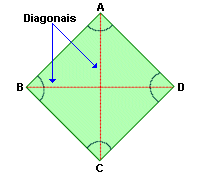 Quadrilátero ABCD
Quadrilátero ABCD
Vértices: A, B, C, e D.
Lados:

Diagonais
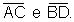
Ângulos internos ou ângulos do
quadrilátero ABCD:
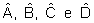
Observações
- Todo quadrilátero tem duas diagonais.
- O perímetro de um quadrilátero ABCD é a soma das medidas de seus lados, ou seja:
AB + BC + CD + DA.
Côncavos e Convexos
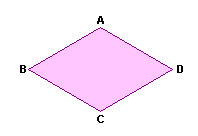
Os quadriláteros podem ser convexos ou côncavos. Um quadrilátero é convexo quando a reta que une dois vértices consecutivos não encontra o lado formado pelos dois outros vértices.
Quadrilátero convexo
 Quadrilátero côncavo
Quadrilátero côncavo
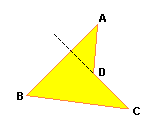 Soma das medidas dos ângulos internos de um quadrilátero convexo
Soma das medidas dos ângulos internos de um quadrilátero convexo
A soma do ângulos internos de um quadrilátero convexo é 360º.
Podemos provar tal afirmação decompondo o quadrilátero ABCD nos triângulos ABD e BCD.
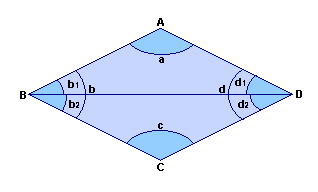 Do triângulo ABD, temos :
Do triângulo ABD, temos :
a + b1 + d1 = 180º. (1)
Do triângulo BCD, temos
c + b2 + d2 = 180º. (2)
Adicionando (1) com (2), obtemos:
a + b1 + d1 + c + b2 + d2 = 180º + 180º
a + b1 + d1 + c + b2 + d2 = 360º
a + b + c + d = 360º
Observações:
1. Termos uma fórmula geral para determinação da soma dos ângulos internos de qualquer polígono convexo:
Si = (n - 2) . 180º, onde n é o número de lados do polígono.
2. A soma dos ângulos externos de um polígono convexo qualquer é 360º.
Se = 360º
Paralelogramo
Paralelogramo é o quadrilátero que tem os lados opostos paralelos.
Exemplo
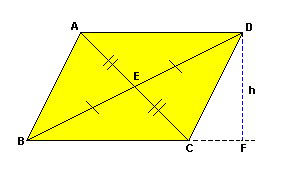
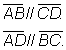
h é a altura do paralelogramo.
O ponto de intersecção das diagonais (E) é chamado centro de simetria.
Destacaremos a seguir alguns paralelogramos.
Retângulo
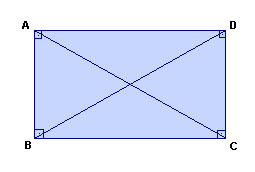
Retângulo é o paralelogramo em que os quatro ângulos são congruentes (retos).
Exemplo
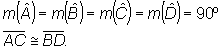
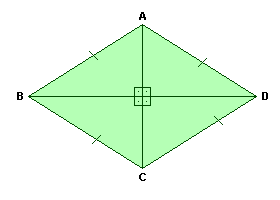
Losango
Losango é o paralelogramo em que os quatro lados são congruentes.
Exemplo

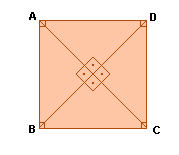
Quadrado
Quadrado é o paralelogramo em que os quatro lados e os quatro ângulos são congruentes.
Exemplo
 É o único quadrilátero regular. É, simultaneamente retângulo e losango.
É o único quadrilátero regular. É, simultaneamente retângulo e losango.
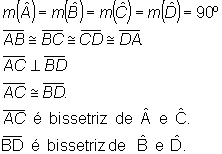
Trapézio
É o quadrilátero que apresenta somente dois lados paralelos, chamados bases.
Exemplo
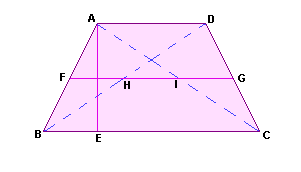
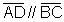

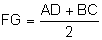

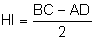 Denominamos trapezoide o quadrilátero que não apresenta lados paralelos.
Denominamos trapezoide o quadrilátero que não apresenta lados paralelos.
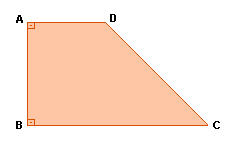
Trapézio retângulo
É aquele que apresenta dois ângulos retos.
Exemplo
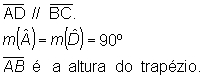
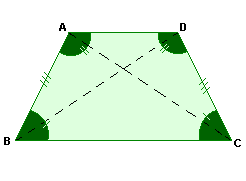
Trapézio isósceles
É aquele em que os lados não paralelos são congruentes.
Exemplo

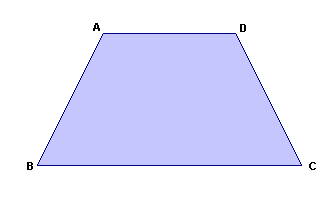
Trapézio escaleno
É aquele em que os lados não paralelos não são congruentes.
Exemplo:

Propriedades dos paralelogramos
1ª propriedade
Os lados opostos de um paralelogramo são congruentes.
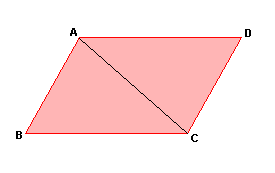 H: ABCD é paralelogramo.
H: ABCD é paralelogramo.
T: 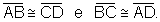
Demonstração:
Afirmativa
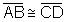
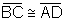
Justificativa
Segmentos de paralelas entre paralelas.
Segmentos de paralelas entre paralelas.
2ª propriedade
Cada diagonal do paralelogramo o divide em dois triângulos congruentes.
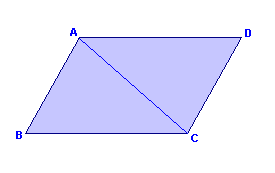 H: ABCD é paralelogramo.
H: ABCD é paralelogramo.
T: 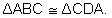
Demonstração:
Afirmativa
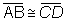
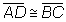
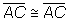
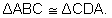
Justificativa
Hipótese.
Hipótese.
Lado comum.
Caso L.L.L.
3ª propriedade
Os ângulos opostos de um paralelogramo são congruentes.
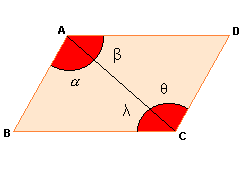 H: ABCD é paralelogramo
H: ABCD é paralelogramo
T: 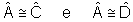
Demonstração
Afirmativa
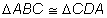
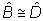
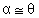
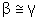
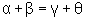
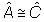
Justificativa
ACé diagonal (2ª propriedade)
Ângulos correspondentes em triângulos congruentes.
Ângulos correspondentes em triângulos congruentes.
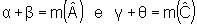
4ª propriedade
As diagonais de um paralelogramo interceptam-se mutuamente ao meio.
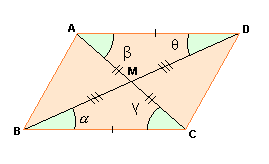 H: ABCD é paralelogramo.
H: ABCD é paralelogramo.
Demonstração
Afirmativa
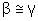
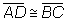
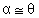
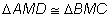
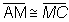
Justificativa
Ângulos alternos internos.
Lados opostos (1ª propriedade).
Ângulos alternos internos.
Caso A.L.A.
Lados correspondentes em triângulos congruentes.
Resumindo
Num paralelogramo:
- os lados opostos são congruentes;
- cada diagonal o divide em dois triângulos congruentes;
- os ângulos opostos são congruentes;
- as diagonais interceptam-se em seu ponto médio.
Propriedade caracteristica do retangulo
As diagonais de um retângulo são congruentes.
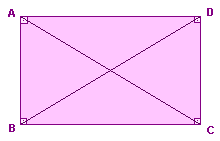 T: ABCD é retângulo.
T: ABCD é retângulo.
H: 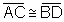
Continua ...














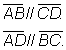

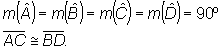



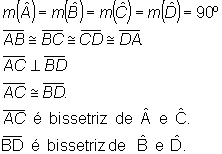




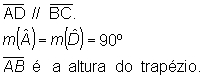



 H: ABCD é paralelogramo.
H: ABCD é paralelogramo. H: ABCD é paralelogramo.
H: ABCD é paralelogramo. H: ABCD é paralelogramo
H: ABCD é paralelogramo
 T: ABCD é retângulo.
T: ABCD é retângulo.