Professor Diminoi ESTATICA DOS ÓLIDOS
ESTATICA DOS ÓLIDOS
É o capítulo da Mecânica que estuda corpos que não se movem, estáticos.
A ausência de movimento é um caso especial de aceleração nula, ou seja, pelas Leis de Newton, uma situação em que todas as forças que atuam sobre um corpo se equilibram.
E a parte da física que estuda sistemas sob a ação de forças que se equilibram. De acordo com a segunda lei de Newton, a aceleração destes sistemas é nula.
De acordo com a primeira lei de Newton, todas as partes de um sistema em equilíbrio também estão em equilíbrio.
ESTÁTICA DOS SÓLIDOS
Estática é a parte da mecânica que estuda os corpos em equilíbrio.
A condição necessária para um corpo estar em equilíbrio é que a resultante de todas as forças que agem sobre ele seja nula.
EQUILÍBRIO = RESULTANTE NULA
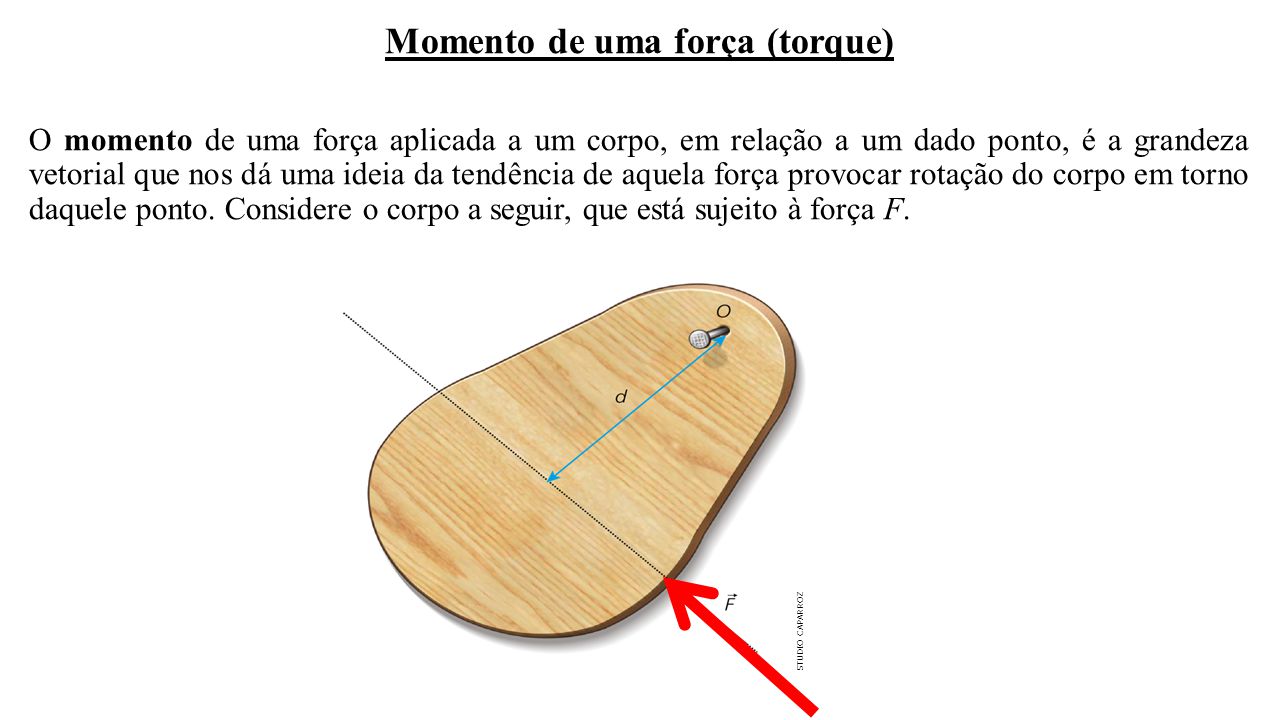
Momento (M)
Momento é a ação de uma força para fazer um corpo girar em torno de um eixo. Considere, por exemplo, um parafuso e uma chave.
O momento de uma força é dado por:
M = F . d
O momento pode ser denominado de momento horário quando a força tende a girar o corpo no sentido horário ou momento anti-horário quando a força tende a girar o corpo no sentido anti-horário. Condições de equilíbrio
Condições de equilíbrio
Na prática, a resultante nula impede o movimento de translação do corpo (inicialmente em repouso), entretanto pode não impedir o movimento de rotação de um corpo extenso.
Na barra da figura anterior a resultante é nula porém pode existir movimento de rotação. Para não haver rotação é necessário que o momento horário seja igual ao momento anti-horário.
Condições gerais de equilíbrio
Um corpo rígido qualquer somente estará em equilíbrio de for nulo o somatório de todas as forças e o somatório de todos os momentos (torques) que sobre ele atuam.

Um corpo rígido estará em equilibro, nas seguintes condições:
- Repouso
- Movimento retilíneo uniforme
- Movimento de rotação uniforme
O repouso é um caso de equilibro estático. O movimento retilíneo uniforme e o movimento de rotação uniforme, por sua vez, são casos de equilibro dinâmico.
Quando um corpo está em repouso (equilibro estático), o mesmo poderá ser de três tipos: estável, instável ou indiferente.
O equilíbrio é estável quando o corpo retorna à posição de equilíbrio inicial, caso seja ligeiramente afastado dela.
O equilíbrio é instável quando o corpo, ao ser afastado levemente da posição de equilibro, tende a se afastar mais ainda dela.
Finalmente, tem-se o equilibro indiferente quando o corpo se mantiver em equilibro, qualquer que seja o afastamento que experimente em relação à posição inicial.
MOMENTO DE UMA FORÇA
Até agora estudamos a dinâmica dos movimentos de translação. A dinâmica dos movimentos de rotação só é estudada em cursos de nível avançado pois exige conhecimentos de matemática que não fazem parte do curso de nível médio.
No entanto há um caso particular cujo estudo é simples: a estática de rotação, isto é, a condição para que um corpo extenso não sofra rotação.
Para isso precisamos introduzir o conceito de momento de uma força.
Consideremos uma força atuando em um corpo, como ilustra a Fig. 1.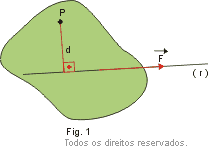 F é o módulo da força e d é a distância do ponto P à reta suporte de (que é a reta r na figura). A escolha do sinal depende da tendência de rotação produzida por . Em geral adota-se o sinal positivoquando a tendência da força é produzir rotação no sentido anti-horário (Fig. 2) e negativo quando a tendência é produzir rotação no sentido horário (Fig. 3).
F é o módulo da força e d é a distância do ponto P à reta suporte de (que é a reta r na figura). A escolha do sinal depende da tendência de rotação produzida por . Em geral adota-se o sinal positivoquando a tendência da força é produzir rotação no sentido anti-horário (Fig. 2) e negativo quando a tendência é produzir rotação no sentido horário (Fig. 3).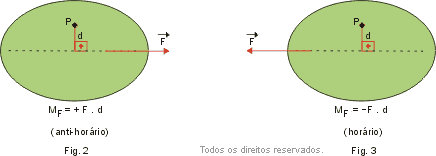
No Sistema Internacional, a unidade de momento é o N.m que, dimensionalmente, é idêntica à unidade de trabalho. No entanto, trabalho e momento são grandezas distintas.
Exemplo 1
Uma força de intensidade F = 20 N é aplicada a um corpo, como mostra a figura, de modo que a distância entre um ponto P e a reta suporte da força é d = 3,0m.
A tendência de é produzir uma rotação do corpo no sentido anti-horário, em torno de P e, assim, o momento será positivo:
MF = + F . d = (20 N) (3,0m) = + 60 N . m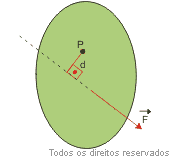 Observações:
Observações:
O ponto P é denominado polo.
O momento é também chamado de torque.
Propriedade:
O momento de uma força depende, obviamente, do polo escolhido. No entanto, temos a seguinte propriedade:
Consideramos n forças. .
Se MF1 + MF2 + ... MFn = 0
em relação a um polo P, então a soma será também nula em relação a qualquer outro polo.
Suponhamos que um corpo esteja sob a ação de n forças .
Estática de um Ponto Material.
Para um corpo estar em movimento retilíneo com velocidade constante ou em repouso, o somatório das forças que agem nele deve ser nulo.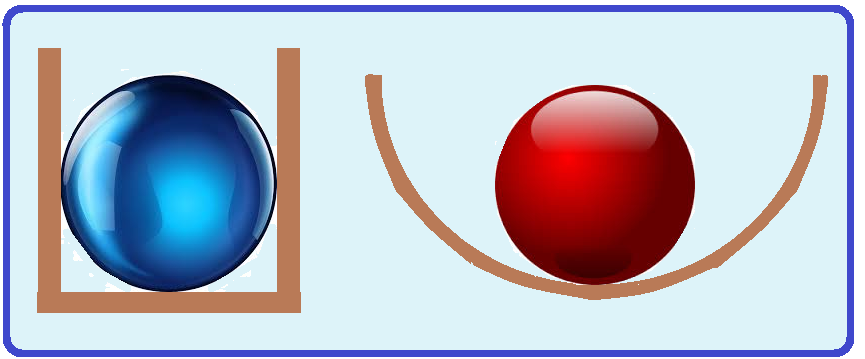
A primeira Lei de Newton diz: que um corpo está em repouso ou em movimento retilíneo e uniforme se a resultante das forças que atuam sobre ele é nula. Nesse caso dizemos que o corpo está em equilíbrio estático quando o corpo está em repouso.
Força de atrito
É uma força que se opõe ao movimento dos corpos. Ela pode ser estática, se o corpo estiver em repouso, ou dinâmica, para corpos em movimento. ... “A força de atrito é uma força que se opõe ao movimento dos corpos.”

Equilíbrio do Ponto Material
Define-se como ponto material todo corpo cujas dimensões, para o estudo em questão, não são importantes, não interferem no resultado final.Por exemplo, o estudo da trajetória de um atleta de saltos ornamentais na piscina a partir de uma plataforma de 10 m. Se o estudo está focalizado na trajetória do atleta da plataforma até a piscina, e não nos seus movimentos em torno de si mesmo, pode-se adotar o centro de massa do atleta, ignorar seu tamanho e desenvolver o estudo. (Caso outros estudos, dos movimentos do atleta em torno do seu centro de massa, sejam necessários, eles poderão ser realizados posteriormente.)
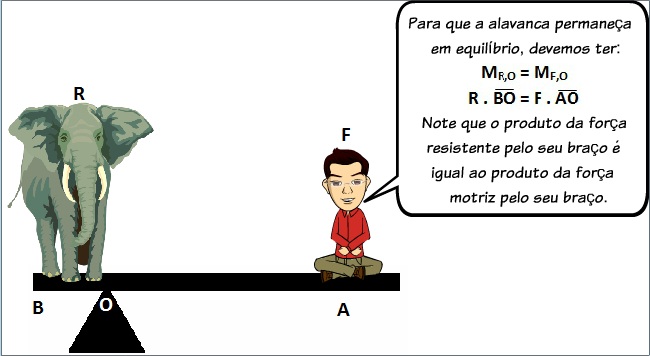
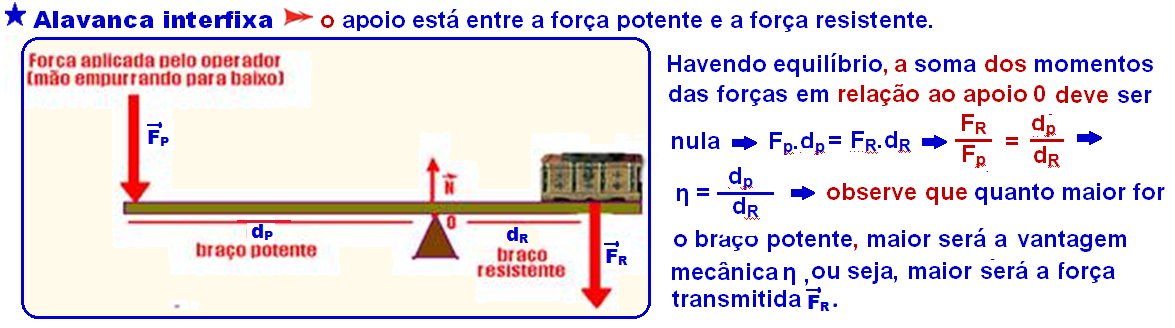
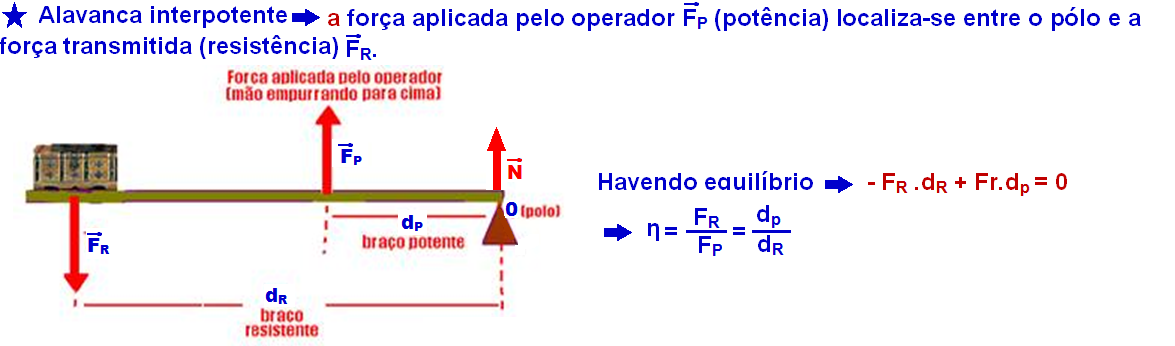


RESOLVIDOS - TORQUE
01) (Mackenzie-SP)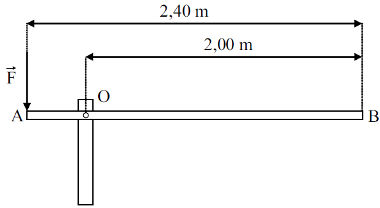 Uma cancela manual é constituída de uma barra homogênea AB de comprimento L = 2,40 m e massa M = 10,0 kg e está articulada no ponto O, onde o atrito é desprezível. A força F tem direção vertical e sentido descendente, como mostra a figura acima. Considerando a aceleração da gravidade g = 10,0 m/s2, a intensidade da força mínima que se deve aplicar em A para iniciar o movimento de subida da cancela é:
Uma cancela manual é constituída de uma barra homogênea AB de comprimento L = 2,40 m e massa M = 10,0 kg e está articulada no ponto O, onde o atrito é desprezível. A força F tem direção vertical e sentido descendente, como mostra a figura acima. Considerando a aceleração da gravidade g = 10,0 m/s2, a intensidade da força mínima que se deve aplicar em A para iniciar o movimento de subida da cancela é:
(A) 150 N
(B) 175 N
(C) 200 N
(D) 125 N
(E) 100 N
Resolução:
Pelo fato de a barra ser homogênea, podemos afirmar que o seu peso está concentrado em seu centro. Sendo assim, teremos: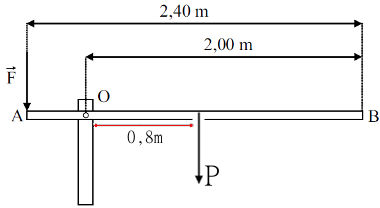 Para que o equilíbrio seja mantido, o torque gerado pela força F, no sentido anti-horário, deve ser exatamente igual ao torque gerado pela força peso, no sentido horário.
Para que o equilíbrio seja mantido, o torque gerado pela força F, no sentido anti-horário, deve ser exatamente igual ao torque gerado pela força peso, no sentido horário.
τF = τPESO
F . 0,4 = P. 0,8
F . 0,4 = m.g.0,8
F . 0,4 = 10 . 10 . 0,8
F = 80 ÷ 0,4
F = 200 N
A força de 200 N mantém a cancela em equilíbrio, portanto, qualquer força maior que 200 N fará o sistema rotacionar.
Alternativa: C
02) (Udesc) Ao se fechar uma porta, aplica-se uma força na maçaneta para ela rotacionar em torno de um eixo fixo onde estão as dobradiças. Com relação ao movimento dessa porta, analise as proposições.
I. Quanto maior a distância perpendicular entre a maçaneta e as dobradiças, menos efetivo é o torque da força.
II. A unidade do torque da força no SI é o N.m, podendo também ser medida em Joule (J).
III. O torque da força depende da distância perpendicular entre a maçaneta e as dobradiças.
IV. Qualquer que seja a direção da força, o seu torque será não nulo, consequentemente, a porta rotacionará sempre.
Assinale a alternativa correta.
(A) Somente a afirmativa II é verdadeira.
(B) Somente as afirmativas I e II são verdadeiras.
(C) Somente a afirmativa IV é verdadeira.
(D) Somente a afirmativa III é verdadeira.
(E) Somente as afirmativas II e III são verdadeiras.
Resolução:
I: Errada: Quanto maior a distância entre a maçaneta e as dobradiças, maior e mais efetivo será o torque da força;
II: Errada: A unidade joule (J) destina-se à medição de quantidades de energia, portanto, jamais poderá ser utilizada para a determinação do torque;
III: Correta: A força que gera o torque deve ser aplicada perpendicularmente ao eixo de rotação (dobradiças);
IV: Errada: Se a força for paralela ao eixo de rotação (dobradiças), não haverá torque.
Alternativa: D
03) Dois garotos estão sobre uma gangorra que se encontra em uma praça. Um dos garotos tem massa de 50 kg e está a 1,5 m do centro do brinquedo. Sabendo que a massa do segundo garoto é de 62,5 kg, determine a distância entre ele e o centro da gangorra para que o brinquedo permaneça equilibrado na posição vertical.
(A) 1,2
(B) 2,0
(C) 1,5
(D) 0,8
(E) 1,0
Resolução:
Para que exista o equilíbrio, o torque gerado pelo peso de cada um dos garotos deve ser o mesmo. Sendo assim, podemos escrever:
Τgaroto 1 = τgaroto 2
P1.x = P2. 1,5
62,5 . 10 . x = 50 . 10 . 1,5
625.x = 750
x = 1,2 m.
O garoto mais pesado está a 1,2 m do centro da gangorra.
Alternativa: A
04) Leia as afirmações a seguir:
I – O torque é uma grandeza escalar que possui unidade de medida, definida pelo Sistema Internacional de Unidades, N.m;
II – A força que gera o torque deverá ser aplicada perpendicularmente em relação ao eixo de rotação;
III – Mesmo que a resultante do torque gerado por forças distintas não seja nula, haverá equilíbrio;
IV – A posição ideal para a instalação de maçanetas é no extremo oposto em relação às dobradiças. Nessa posição, a força necessária para girar a porta será a menor possível.
Está correto o que se afirma em:
(A) I
(B) I e II
(C) III e IV
(D) II e IV
(E) II, III e IV
Resolução:
I: Errada – O torque é uma grandeza vetorial;
II: Correta;
III: Errada – Uma das condições de equilíbrio é que a soma dos torques gerados no sistema seja nula;
IV: Correta – Quanto maior a distância em relação ao eixo de rotação, menor será a força necessária para a rotação de um sistema.
Alternativa: D
RESOLVIDOS – EQUÍLIBRIO ESTÁTICO DE UM CORPO EXTENSO
05) (PUC-MG) Uma haste, com massa uniformemente distribuída ao longo do seu comprimento, encontra-se em equilíbrio, na horizontal, apoiada no ponto P, tendo duas massas M e M’ nas suas extremidades, conforme a figura abaixo. Nessas condições, é CORRETO afirmar: (A) M’ < M
(A) M’ < M
(B) M’ = M
(C) M < M’ < 2M
(D) M’ > 2M
Resolução: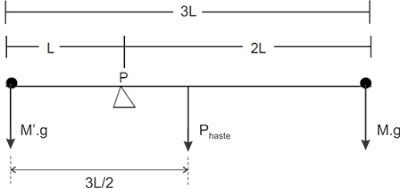 Tomando o ponto P como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Tomando o ponto P como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Phaste . (L/2) + Mg . 2L = M’g . L
M’ = 2M + Phaste/2g
Portanto, M’ > 2M
Alternativa: B
06) (UFSM-RGS) A figura representa uma barra homogênea em equilíbrio horizontal, de massa m e comprimento L, estando uma das extremidades articulada a uma parede. Na extremidade oposta, está suspenso um corpo de massa M, estando essa barra sustentada em sua metade por uma mola de constante elástica K. Nessa situação, a mola está distendida de: (A) (M/K).g
(A) (M/K).g
(B) (2M/K).g
(C) [(M+m)/K].g
(D) [(2M+m)/K].g
Resolução:
Tomando a articulação como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Mg . L + mg . (L/2) = Kx . (L/2)
x = (2M+m) . g/K
Alternativa: B
07) (Mackenzie-SP) A figura mostra um móbile constituído por duas barras de massas desprezíveis que sustentam os corpos A, B e C por fios ideais. Sendo a massa do corpo A 45 g, a massa do corpo C, que mantém o conjunto em equilíbrio na posição indicada, deve ser igual a: (A) 10 g.
(A) 10 g.
(B) 20 g.
(C) 30 g.
(D) 40 g.
(E) 50 g.
Resolução:  mB.g.30 = mA.g.10
mB.g.30 = mA.g.10
mB = mA/3 = 15 gramas.
T = mA.g + mB.g
60.g T.20 = mC.g.30
T.20 = mC.g.30
60.g.20 = mC.g.30
mC = 40 gramas
Alternativa: B
08) (PUC-MG) Na figura desta questão, um jovem de peso igual a 600 N corre por uma prancha homogênea, apoiada em A e articulada no apoio B. A prancha tem o peso de 900 N e mede 9,0 m. Ela não está presa em A e pode girar em torno de B. A máxima distância que o jovem pode percorrer, medida a partir de B, sem que a prancha gire, é: (A) 1,75 m.
(A) 1,75 m.
(B) 2,00 m.
(C) 2,25 m.
(D) 2,50 m.
Resolução:
A máxima distância que o jovem pode percorrer, medida a partir de B, sem que a prancha gire, corresponde ao instante em que a força normal em A torna-se nula.  Nestas condições, tomando o ponto B como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Nestas condições, tomando o ponto B como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Pprancha x 1,5 = Pjovem x d
900 x 1,5 = 600 x d
d = 2,25 m
Alternativa: C
09) (PUC-MG) Uma placa de publicidade, para ser colocada em local visível, foi afixada com uma barra homogênea e rígida e um fino cabo de aço à parede de um edifício, conforme ilustração. Considerando-se a gravidade como 10 m/s2, o peso da placa como 200 N, o comprimento da barra como 8 m, sua massa como 10 kg, a distância AC como 6 m e as demais massas desprezíveis, pode-se afirmar que a força de tração sobre o cabo de aço tem intensidade:
Considerando-se a gravidade como 10 m/s2, o peso da placa como 200 N, o comprimento da barra como 8 m, sua massa como 10 kg, a distância AC como 6 m e as demais massas desprezíveis, pode-se afirmar que a força de tração sobre o cabo de aço tem intensidade:
(A) 417 N
(B) 870 N
(C) 300 N
(D) 1200 N
Resolução:  Tomando o ponto A como referência:
Tomando o ponto A como referência:
MPplaca + MPbarra = MT . senB
200 . 8 + 100.4 = T . (6/10).8
1600 + 400 = T . 4,8
T = 2000/4,8
T = 416,66 N
T ≅ 417 N
Alternativa: A
RESOLVIDAS – CORPOS RÍGIDOS
10) Na figura abaixo temos uma barra homogênea AB de peso 80 N, que está em equilíbrio sob ação das forças e , apoiadas no suporte S, no ponto O.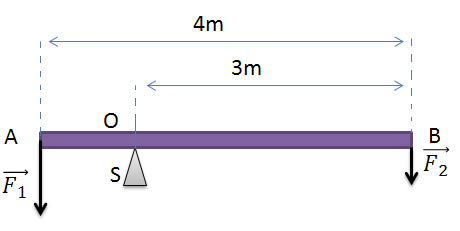 Sendo = 200 N, qual será a intensidade da força normal exercida pelo suporte S sobre a barra?
Sendo = 200 N, qual será a intensidade da força normal exercida pelo suporte S sobre a barra?
(A) 40 N e 320 N
(B) 60 N e 320 N
(C) 40 N e 200 N
(D) 50 N e 200 N
(E) 200 N e 40 N
Resolução:
Todas as forças que atuam na barra foram colocadas na figura. Como a barra é homogênea, todo o seu peso está em seu centro (centro de gravidade).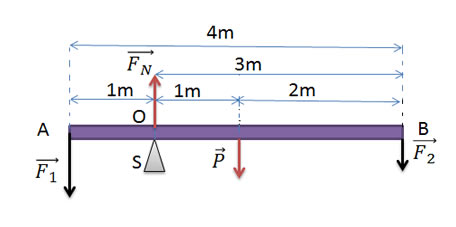 Agora vamos aplicar as duas condições de equilíbrio.
Agora vamos aplicar as duas condições de equilíbrio.
1º: A soma de todos os momentos deve ser nula.
Como não sabemos o valor da força , vamos escolher a origem O como nosso centro de rotação, assim o momento de uma força da força se torna nulo.
Como M = +F.d (se o momento de uma força tende a produzir rotação no sentido anti-horário em volta do polo de origem da rotação) e M = -F.d (se o momento de uma força tende a produzir rotação no sentido horário em volta do polo de origem da rotação),
temos:
MF1 = + F1 .(1)
MP = - P . (1)
MF2 = - F2 . (3)
Para uma situação de equilíbrio, a soma do momento de todas as forças deve ser igual a zero, lembrando que MFN = 0, pois está no polo de rotação:
MF1 + MP + MF2 + MFN = 0
F1 .(1) - P . (1) - F2 . (3) + 0 = 0
200 . (1) – 80 . (1) - F2 . (3) = 0
200 – 80 – 3F2 = 0
3F2 = 120
F2 = 120/3
F2 = 40 N
Para que a barra esteja em equilíbrio, é necessária outra condição, a resultante das forças também tem que ser nula. Logo:
- F1 - P - F2 + FN = 0
FN = F1 + P + F2
FN = 200 + 80 + 40
FN = 320 N
Alternativa: A
11) Na figura abaixo, os dois blocos, A e B, estão em equilíbrio.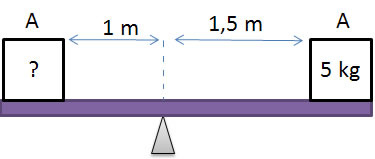 Calcule a massa do bloco A, sabendo que a massa do bloco B é 5 kg. Considere =10m/s².
Calcule a massa do bloco A, sabendo que a massa do bloco B é 5 kg. Considere =10m/s².
Resolução:
Como os dois blocos estão em equilíbrio, a resultante do momento de todas as forças deve ser nula: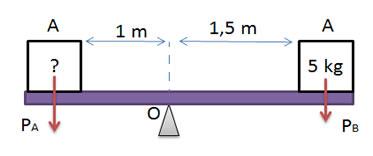 Se a massa de B é 5 kg, seu peso será:
Se a massa de B é 5 kg, seu peso será:
PB=mB .g
PB=5 .10
PB=50N
Como o torque resultante tem que ser nulo, escolhendo como polo de rotação a origem da figura acima O, temos: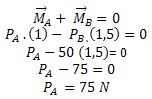 Lembrando que estamos interessados em calcular a massa e não o peso do bloco A, então:
Lembrando que estamos interessados em calcular a massa e não o peso do bloco A, então:
PA=mA .g
75 = mA .10
mA=75/10
mA=7,5 kg
Resposta: a massa do bloco A é 7,5 kg.
EXERCÍCIOS RESOLVIDOS
01) Três partículas localizam-se em posições: a (2,4), b (3,-1), c (1,0), d (-5,-2), e (0,0). Sendo a massa destas partículas, respectivamente, 5kg, 16kg, 0,1kg, 0,9kg e 10kg. Qual é o centro de massa deste sistema?
Resolução:
Utilizando o princípio da média aritmética ponderada, podemos calcular o centro de massa em cada eixo do plano cartesiano:
Logo CM (1,67 , 0,04)
02) Para abrir uma porta de madeira de um metro de largura é necessário aplicar uma força perpendicular de intensidade 50N na sua extremidade contrária à dobradiça. Ao tentar abrir esta porta empurrando-a pelo seu meio, qual deve ser a intensidade da força perpendicular aplicada?
Resolução:
03) Uma barra homogênea de 5kg e 2m apoiada sob um ponto em uma parede é segurada por um cabo ideal, em um ponto A, distante 1,5m da ponta da barra e há um bloco de massa 1kg preso a outra extremidade da barra. Qual a força aplicada ao cabo para que o sistema esteja em equilíbrio?Resolução:
Conhecendo as duas condições de equilíbrio de um ponto rígido:
1ª condição:
Mas as forças não estão aplicadas sobre a mesma linha de aplicação, então a força válida é a calculada pela segunda condição de equilíbrio:
2ª condição:
EXERCÍCIO RESOLVIDO
01) Dado um corpo arbitrário com massa 12kg concentrada em um ponto P ligado a outro de massa 10kg concentrada em um ponto Q ligado por um fio ideal que atravessa uma polia ideal, assim como na figura abaixo. Qual deve ser o coeficiente de atrito para que este sistema esteja em equilíbrio?Resolução:
Analisando individualmente cada um dos pontos onde há alguma força aplicada: e
No sentido vertical para P:
Montando um sistema de equações com as forças aplicadas em cada corpo temos:
Mas para que o corpo esteja em equilíbrio a=0. Então somando o sistema acima temos:
02) Dois cabos seguram um bloco de massa 20kg, um deles, com intensidade 20N, forma um ângulo de 45° com a horizontal. O outro, forma um ângulo de 120° partindo da horizontal. Qual a força aplicada a este cabo para que o bloco fique em equilíbrio verticalmente?Resolução:
Verticalmente:
EXERCÍCIOS RESOLVIDOS – SEDU-SP/2025)
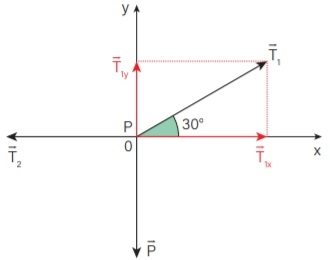
01) (Livro do aluno – SEDU´SP/2025) Na figura a seguir, um corpo de peso 100 N encontra-se em equilíbrio, pendurado por duas cordas, 1 e 2.
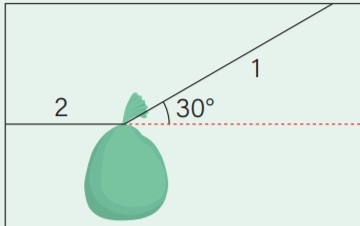
Calcule o valor da tensão nessas duas cordas.
Dados: cos 30° = 0,8 e sen 30° = 0,5
Resolução:
Como o corpo está em equilíbrio:

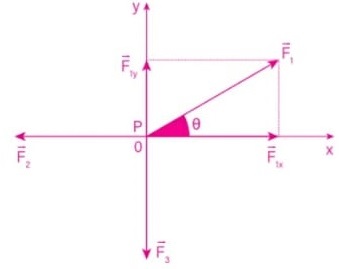
02) (Livro do aluno – SEDU´SP/2025) Um ponto material P, submetido à ação de três forças coplanares, F1, F2 e F3, como ilustrado na figura a seguir, permanece em equilíbrio estático. Sabendo que F1 = 10,0 N,sen θ = 0,60 e cos θ = 0,80, determine a intensidade das forças F2 e F3.
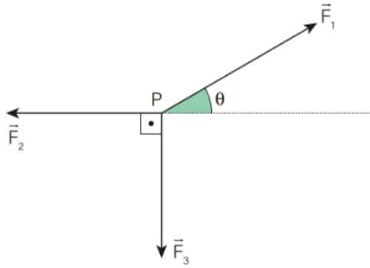
Resolução:

03) (Livro do aluno – SEDU´SP/2025) Durante a preparação para uma festa junina, usando alguns fios, o professor de arte de uma escola pendurou um enfeite, que permaneceu em repouso, de acordo com o seguinte esquema:
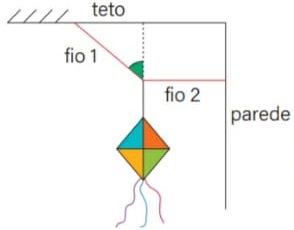
Considerando que o valor do ângulo entre o fio 1 e a linha vertical tracejada vale 45° e a força de tração no fio 2 tem intensidade igual a 50 N, responda aos seguintes questionamentos:
a) Qual a intensidade da força de tração no fio 1?
b) Qual é o valor da massa do enfeite em kg? (g = 10 m/s2)
Resolução:

04) (Livro do aluno – SEDU´SP/2025 - ENEM 2019) Slackline é um esporte no qual o atleta deve se equilibrar e executar manobras estando sobre uma fita esticada. Para a prática do esporte, as duas extremidades da fita são fixadas de forma que ela fique a alguns centímetros do solo. Quando uma atleta de massa igual a 80 kg está exatamente no meio da fita, essa se desloca verticalmente, formando um ângulo de 10° com a horizontal, como esquematizado na figura.
Sabe-se que a aceleração da gravidade é igual a 10 m s‑2, cos(10°) = 0,98 e sen(10°) = 0,17.
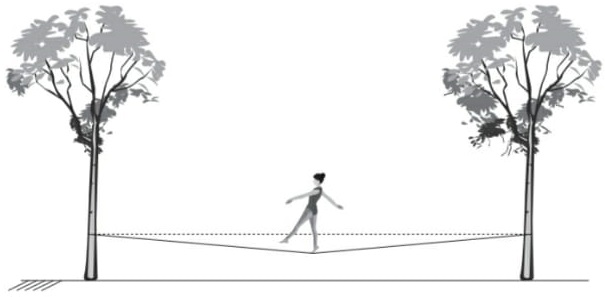
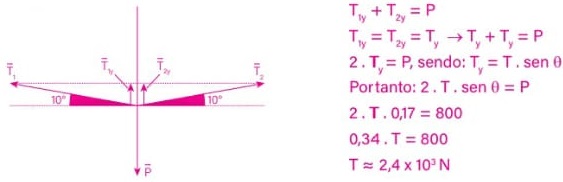
Qual é a força que a fita exerce em cada uma das árvores por causa da presença da atleta?
Resolução:
A atleta, nessa situação, considerada um ponto material, encontra-se em equilíbrio. Sendo assim, a resultante das forças que atuam sobre ela é nula. Ao decompormos a força de tração no eixo vertical, teremos:
Alternativa: D
05) (Livro do aluno – SEDU´SP/2025 - UNESP 2010) Um professor de física pendurou uma pequena esfera, pelo seu centro de gravidade, no teto da sala de aula, conforme a figura:
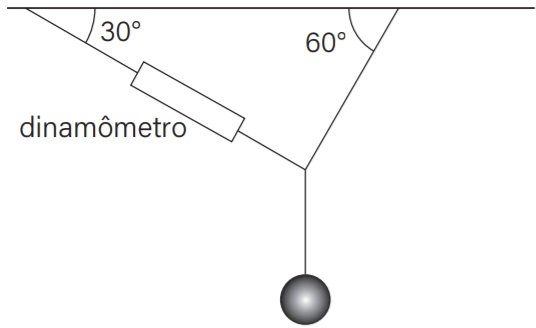
Em um dos fios que sustentava a esfera, ele acoplou um dinamômetro e verificou que, com o sistema em equilíbrio, ele marcava 10 N. Qual o valor do peso, em Newtons, da esfera pendurada?
(A) 5√3
(B) 10
(C) 10√3
(D) 20
(E) 20√3
Resolução:
Como o sistema está em equilíbrio, a força resultante é nula e o polígono formado pelos vetores representantes de todas é fechado:

Alternativa: D
06) (Livro do aluno – SEDU´SP/2025) Dois garotos estão brincando em uma gangorra de 20 m de comprimento. Um dos garotos, com massa de 45 kg, está sentado exatamente na extremidade direita da gangorra, enquanto o outro, de massa 60 kg, encontra-se sentado em um ponto
à esquerda da gangorra. O eixo de rotação da gangorra está exatamente em seu meio. Qual deverá ser a distância entre o garoto da esquerda e o eixo de rotação da gangorra para que ela se mantenha em equilíbrio? Adote g = 10 m/s2. Considere a gangorra uma prancha homogênea.
Resolução:
Para que a barra fique em equilíbrio, a soma dos momentos escalares das forças precisa ser nula. Assim, temos:
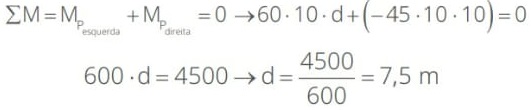
07) (Livro do aluno – SEDU´SP/2025 - ENCEJA – 2017) A imagem representa uma balança utilizada para a medida da massa de uma fruta. A massa colocada no prato direito da balança é de 100 g e o sistema encontra-se em equilíbrio.
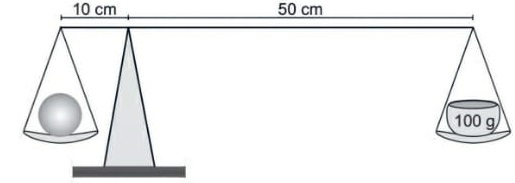
A massa dessa fruta, em gramas, é:
(A) 100
(B) 120
(C) 500
(D) 600
Resolução:
Como o sistema está em equilíbrio, podemos usar o equilíbrio dos momentos em relação ao apoio da balança. Assim temos:

Alternativa: C
08) (Livro do aluno – SEDU´SP/2025 - UNICAMP) A figura a seguir mostra ao braço de um toca-disco de vinil. Nela são indicadas, nos seus respectivos pontos de atuação, as seguintes forças: peso do braço (PB), peso do contrapeso (PC) e força normal aplicada pelo suporte do braço (N). Para que o braço fique em equilíbrio, é necessário que a soma dos torques seja igual azero. No caso do braço da figura, o módulo do torque de cada força em relação ao ponto O (suporte do braço) é igual ao produto do módulo da força pela distância do ponto de aplicação da força até O. adote torque positivo para as forças que tendem a acelerar o braço no sentido horário e torque negativo para o sentido anti-horário.
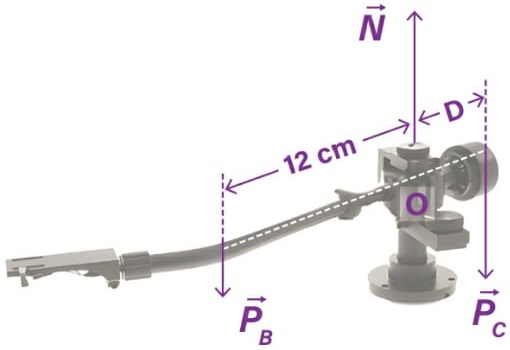
Sendo PC |= 1,5 N, PB |= 0,3 N e |N| = 1,8 N , qual deve ser a distância D do contrapeso ao ponto O para que o braço fique em equilíbrio?
Resolução:
Como o sistema está em equilíbrio, podemos usar o equilíbrio dos momentos em relação ao apoio da balança. Assim temos:
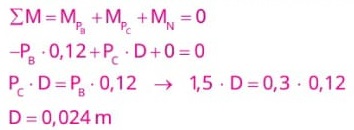
Portanto: D = 2,4 cm
Alternativa: C
09) (Livro do aluno – SEDU´SP/2025 - ENEM 2015) Em um experimento, um professor levou para a sala de aula um saco de arroz, um pedaço de madeira triangular e uma barra de ferro cilíndrica e homogênea. Ele propôs que fizessem a medição da massa da barra utilizando esses objetos. Para isso, os alunos fizeram marcações na barra, dividindo-a em oito partes iguais, e, em seguida, apoiaram-na sobre a base triangular, com o saco de arroz pendurado em uma de suas extremidades, até atingir a situação de equilíbrio.
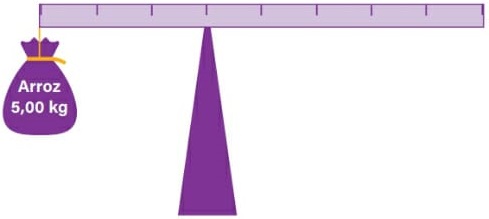
Nessa situação, qual foi a massa da barra obtida pelos alunos?
(A) 3 kg
(B) 3,75 kg
(C) 5 kg
(D) 6 kg
(E) 15 kg
Resolução:
Vamos começar desenhando as forças aplicadas na barra de ferro. Em seguida, escolheremos o ponto de referência, também chamado polo. Nesse caso, o ponto adotado é o local no qual a barra está apoiada na base triangular. Além disso, chamaremos de x a distância entre duas marcações consecutivas na barra, conforme ilustrado na figura.

Para que a barra fique em equilíbrio, a soma dos momentos escalares das forças deve ser nula:
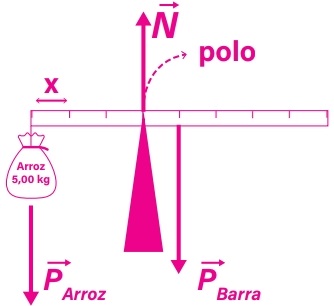
Alternativa: E
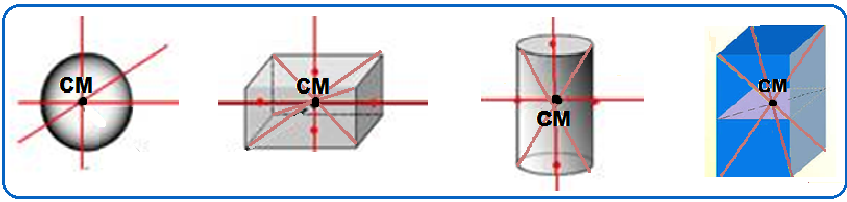
10) (Livro do aluno – SEDU´SP/2025 - ENEM 2024) Nos automóveis, é importante garantir que o centro de massa (CM) de cada conjunto roda/pneu coincida com o seu centro geométrico. Esse processo é realizado em uma máquina de balanceamento, na qual o conjunto roda e pneu é colocado para girar a uma velocidade de valor constante. Com base nas oscilações medidas, a máquina indica a posição do centro de massa do conjunto, e pequenas peças de chumbo são fixadas em lugares específicos da roda até que as vibrações diminuam. Durante o treinamento de sua equipe, a fim de corrigir a posição do centro de massa indicada pela máquina, um mecânico apresenta o esquema a seguir, com cinco possíveis pontos da roda para posicionar uma peça de chumbo.
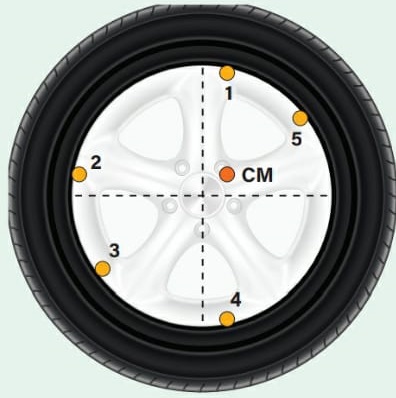
Em qual ponto deve ser fixada a peça de chumbo para corrigir a posição do centro de massa desse conjunto roda/pneu?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Resolução:
Na imagem, observa-se que o centro de massa (CM) do conjunto roda/pneu está posicionado acima e à direita do centro. Para que o CM retorne ao centro da figura, será preciso equilibrar o sistema com um contrapeso colocado abaixo e à esquerda do centro, o que nos remete a fixar a peça de chumbo na posição 3.
Alternativa: C
11) (Livro do aluno – SEDU´SP/2025) Duas esferas, de massas M1 = 10 kg e M2 = 5 kg, estão presas por uma haste de massa desprezível. Considere que L = 12 cm é a distância do centro de massa da esfera 1 em relação ao centro de massa da esfera 2.
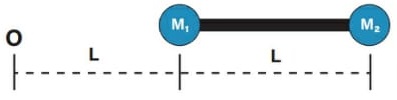
Qual a distância, em centímetros, do centro de massa do sistema em relação ao ponto O?
Resolução:

12) (Livro do aluno – SEDU´SP/2025) Três corpos de massa m1 = 3 kg, m2 = 4 kg e m3 = 5 kg encontram-se dispostos em um plano de acordo com a figura a seguir:
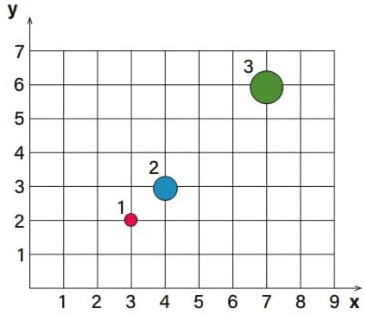
Determine o ponto, com as coordenadas x e y, no qual se encontra o centro de gravidade do sistema composto dos três corpos.
Resolução:

13) (Livro do aluno – SEDU´SP/2025) - UNICENTRO 2020) Considere três partículas de massas m1 = 2,0 kg, m2 = 3,0 kg em3 = 5,0 kg, separadas pelas distâncias indicadas, conforme mostra a figura.
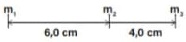
Após análise da figura e com base nos conhecimentos de mecânica, é correto afirmar que o centro de massa do sistema se encontra a uma distância da massa m1em cm, igual a:
(A) 5,7
(B) 6,8
(C) 7,3
(D) 8,1
(E) 9,5
Resolução:
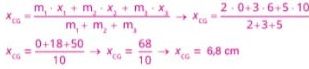
Alternativa: B
14) (Livro do aluno – SEDU´SP/2025) Na imagem adiante, é representada uma barra metálica composta de duas partes: uma feita de metal A e outra, de metal B. Considerando que a massa do metal A é de 4 kg e a massa do metal B é de 12 kg e admitindo que a distribuição de massa é uniforme em cada uma das partes, determine a posição do centro de gravidade da barra.
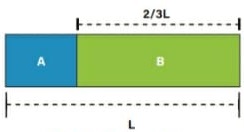
Resolução:
Cálculo do centro de gravidade:
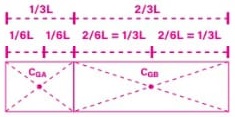
CGA – Centro de gravidade da barra A
(coincide com o centro de massa). CGB – Centro de gravidade da barra B (coincide com o centro de massa).
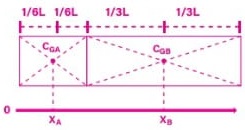
Observando a imagem, podemos determinar XA e XB:
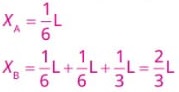
Calculando o centro de gravidade da barra:
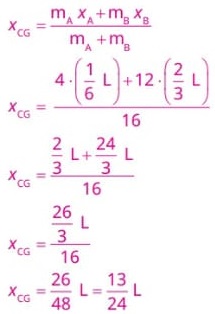
15) (Livro do aluno – SEDU´SP/2025) Observe a figura e responda à questão.

Na figura, é possível observar esculturas construídas a partir da sobreposição de pedras.
Com base em seus conhecimentos sobre equilíbrio e estática, é correto afirmar que cada uma das esculturas está em equilíbrio estático:
(A) instável, pois o momento de força atuante na pedra superior varia com o tempo.
(B) estável, pois a resultante das forças que atuam sobre a última pedra é positiva.
(C) instável, pois a resultante das forças que atuam sobre o conjunto das pedras é nula.
(D) estável, pois a resultante das forças que atuam sobre a primeira pedra é positiva.
(E) instável, pois a resultante das forças que atuam sobre o conjunto das pedras é
Resolução:
a) Neste caso, a rotação na pedra superior de qualquer uma das esculturas, caso ocorra, é proveniente do momento de força, ou seja, é o indicativo de que a resultante das forças que atuam sobre a pedra não é nula.
b) A disposição das pedras no formato de esculturas, conforme apresentado na figura, não permite que haja equilíbrio estático estável, portanto o equilíbrio é estático instável e a resultante das forças deve ser nula.
c) As esculturas apresentam equilíbrio estático instável. Só é possível manter as pedras posicionadas no formato de esculturas quando a resultante das forças que atuam sobre o conjunto das pedras for, obrigatoriamente, nula.
d) A disposição das pedras no formato de esculturas, conforme apresentado na figura, não permite que haja equilíbrio estático estável, portanto o equilíbrio é estático instável e a resultante das forças deve ser nula.
e) As esculturas apresentam equilíbrio estático instável. Só é possível manter as pedras posicionadas no formato de pequenas torres quando a resultante das forças que atuam sobre o conjunto das pedras for, obrigatoriamente, nula.
Se houvesse resultante diferente de zero, o conjunto ou alguma pedra se moveria.
Alternativa: C
16) (Livro do aluno – SEDU´SP/2025) Com base na imagem, responda à pergunta.

Qual a explicação física para a moça conseguir levar a cesta apoiada na cabeça sem que ela caia?
Resolução:
A moça precisa deixar o centro de gravidade da cesta sob a sua cabeça de tal forma que uma linha de ação do peso da cesta intercepte a região de apoio da própria cabeça.
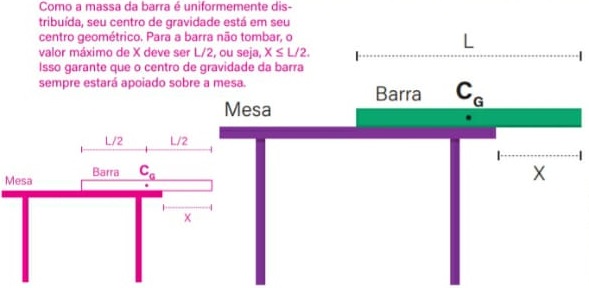
17) (Livro do aluno – SEDU´SP/2025) Na figura adiante, temos uma barra de comprimento L apoiada sobre uma mesa, com um trecho de comprimento X para fora da mesa. Sabendo disso, qual deve ser o comprimento máximo de X para que a barra não tombe? Considere a massa da barra uniformemente distribuída e CG o seu centro de gravidade.
Resolução:
18) (Livro do aluno – SEDU´SP/2025 - UNICHRISTUS 2015) João-Bobo, também conhecido como João-Teimoso, é aquele brinquedo inflável, de base arredondada, que não importa o quanto batemos, socamos, golpeamos, ele nunca permanece caído, retornando sempre à posição vertical.
Os conceitos acerca do equilíbrio de um corpo extenso estão presentes na justificativa da teimosia do João-Bobo.
Assim, o tipo de equilíbrio assumido pelo João-Teimoso e a razão desse equilíbrio estão mais bem representados, respectivamente, em:
(A) instável devido ao baixo centro de gravidade.
(B) indiferente devido ao baixo centro de gravidade.
(C) estável devido ao alto centro de gravidade.
(D) instável devido ao alto centro de gravidade.
(E) estável devido ao baixo centro de gravidade.
Resolução:
No caso do João-Teimoso, o centro de gravidade é baixo, localizado próximo à base do brinquedo. A base do João-Teimoso é preenchida com um material mais pesado, como areia ou água, enquanto a parte superior é mais leve e geralmente preenchida com ar.
Alternativa: E
19) (Livro do aluno – SEDU´SP/2025 - ENEM 2018) As pessoas que utilizam objetos cujo princípio de funcionamento é o mesmo que o das alavancas aplicam uma força, chamada força potente, em um dado ponto da barra, para superar ou equilibrar uma segunda força, chamada resistente, em outro ponto da barra. Por causa das diferentes distâncias entre os pontos de aplicação das forças, potente e resistente, seus efeitos também são diferentes. A figura mostra alguns exemplos desses objetos.
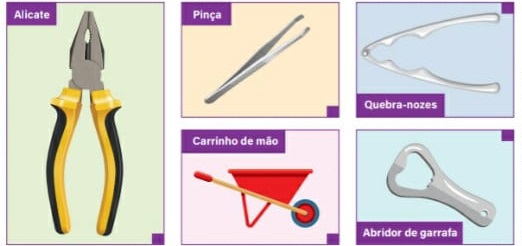
Em qual dos objetos a força potente é maior que a força resistente?
(A) Pinça.
(B) Alicate.
(C) Quebra-nozes.
(D) Carrinho de mão.
(E) Abridor de garrafa.
Resolução:
O objeto em que a força potente é maior que a força resistente é a pinça. Isso acontece porque, nela, a força aplicada (potente) está mais próxima do ponto de apoio (ponto fixo) do que a força resistente.
Alternativa: A
20) (Livro do aluno – SEDU´SP/2025 - ACAFE 2016) Basicamente, uma alavanca é uma barra que pode girar em torno de um ponto de apoio, chamado polo. Mesmo no nosso corpo existem muitas alavancas, já que existem muitas partes articuláveis.
Na figura a seguir, vemos o exemplo de três tipos de alavanca diferentes: no pé (1), no braço/antebraço (2) e na cabeça (3).
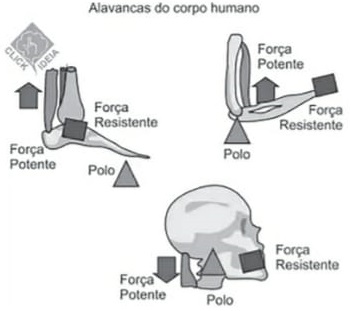
A alternativa correta que mostra na sequência (1), (2) e (3) a classificação conforme a posição do ponto de apoio em relação às forças aplicadas é:
(A) interfixa; interpotente e inter-resistente.
(B) inter-resistente; interfixa e interpotente.
(C) interpotente; interfixa e inter-resistente.
(D) inter-resistente; interpotente e interfixa.
Resolução:
Como sabemos, as alavancas inter-resistentes são aquelas em que a força resistente é aplicada entre o ponto de apoio e o ponto de aplicação da força potente, o que pode ser observado na primeira imagem. Na segunda imagem, em que se vê o braço, percebe-se que a força potente é aplicada entre os pontos de apoio e a força resistente,
Alternativa: D
21) (Livro do aluno – SEDU´SP/2025 - UFRGS 2020) A figura abaixo representa esquematicamente o braço e o antebraço de uma pessoa que está sustentando um peso P. O antebraço forma um ângulo de 90° com o braço. FB é a força exercida pelo bíceps sobre o antebraço e FC é a força na articulação do cotovelo.
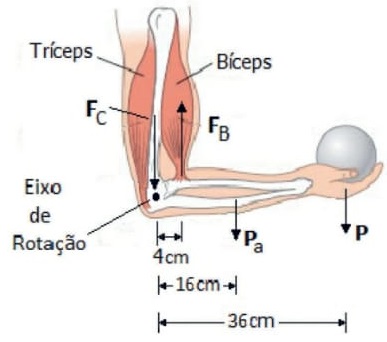
Sendo o módulo do peso P = 50 N e o módulo do peso do antebraço Pa = 20 N, qual é o módulo da força FB ?
(A) 70 N
(B) 370 N
(C) 450 N
(D) 460 N
(E) 530 N
Resolução:
Aplicando-se a segunda lei de Newton para o movimento rotacional, tem-se que a soma de todos os torques produzidos pelas forças que atuam no sistema braço-antebraço é nula.
Tomando-se o sentido horário como positivo, pode-se escrever:
P . 36 + PA . 16 - FB . 4 = 0
Como P = 50 N e Pa = 20 N, então:
50 . 36 + 20 . 16 -FB . 4 = 0
FB = 530 N
Alternativa: E
Continua...





