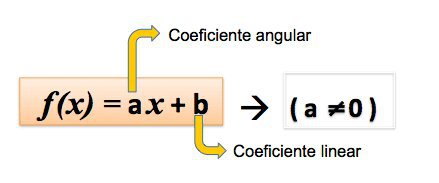
FUNÇÃO/COEFICIENTE LINEAR/ANGULA E EQUAÇÃO DA RETA
Professor Diminoi
Exemplo de gráfico da função constante: f(x) = 2
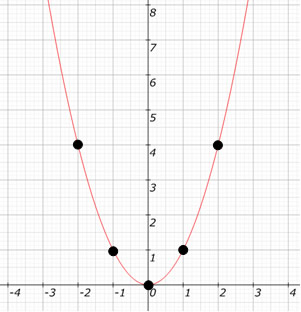
Exemplo de gráfico da função par: f(x) = x2
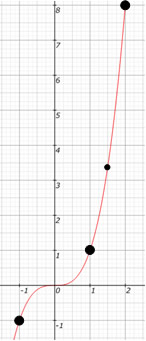
Exemplo de gráfico da função ímpar: f(x) = 3x
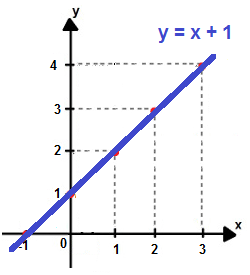
Exemplo de gráfico da função polinomial do primeiro grau: f(x) = 4x + 1
Exemplo de gráfico da função linear: f(x) = -x/3
Exemplo de gráfico da função crescente: f(x) = 5x
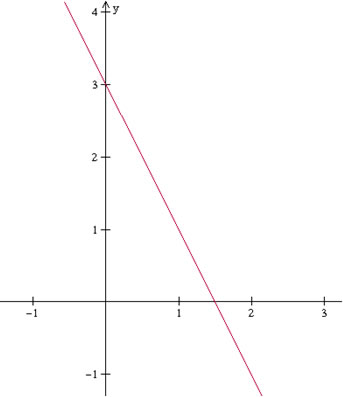
Exemplo de gráfico da função decrescente: f(x) = - 5x
Exemplo de gráfico da função polinomial do segundo grau: f(x) = x2 – 6x + 5
Exemplo de gráfico da função modular: f(x) =
Exemplo de gráfico da função exponencial crescente: f(x) = (2)x, para a = 2
Exemplo de gráfico da função logarítmica: f(x) = log10 (5x - 6)
Exemplo de gráfico da função trigonométrica seno: f(x) = sen (x + 2)
Exemplo de gráfico da função raiz: f(x) = (x)1/2
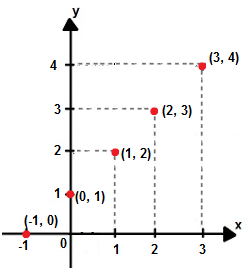
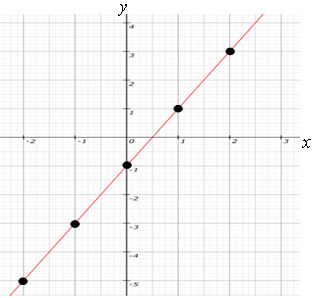
Observe a tabela de valores para essa função:
Função crescente: à medida que os valores de x aumentam, os valores correspondentes em y também aumentam.
E o y do vértice é o resultado da fórmula:
a) o instante em que a bola retornará ao solo.
y = 2.(–2) – 1
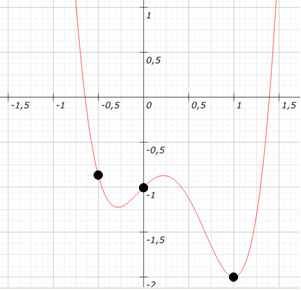
y = 4 * (0,5)4 – 5 * (0,5)3 – 0,52 + 0,5 – 1 = 0,25 – 0,625 – 0,25 + 0,5 – 1 = – 1,155
Professor Diminoi
Exemplo de gráfico da função constante: f(x) = 2
Exemplo de gráfico da função par: f(x) = x2
Exemplo de gráfico da função ímpar: f(x) = 3x
Exemplo de gráfico da função polinomial do primeiro grau: f(x) = 4x + 1
Exemplo de gráfico da função linear: f(x) = -x/3
Exemplo de gráfico da função crescente: f(x) = 5x
Exemplo de gráfico da função decrescente: f(x) = - 5x
Exemplo de gráfico da função polinomial do segundo grau: f(x) = x2 – 6x + 5
Exemplo de gráfico da função modular: f(x) =
Exemplo de gráfico da função exponencial crescente: f(x) = (2)x, para a = 2
Exemplo de gráfico da função logarítmica: f(x) = log10 (5x - 6)
Exemplo de gráfico da função trigonométrica seno: f(x) = sen (x + 2)
Exemplo de gráfico da função raiz: f(x) = (x)1/2
Observe a tabela de valores para essa função:
Função crescente: à medida que os valores de x aumentam, os valores correspondentes em y também aumentam.
O x do vértice é dado pela fórmula:
E o y do vértice é o resultado da fórmula:
a) o instante em que a bola retornará ao solo.
y = 2.(–2) – 1
y = 4 * (0,5)4 – 5 * (0,5)3 – 0,52 + 0,5 – 1 = 0,25 – 0,625 – 0,25 + 0,5 – 1 = – 1,155
- INICIO
- ENEM
- UNIVERSIDADES
- VESTIBULAR
- VESTIBULANDO
- MATEMÁTICA EF & EM
- ATIVIDADES ESCOLARES - 2021/2022/2023/2024
- PEI
- SE/SP
- VESTIBULINHOS
- ELETRICIDADE
- ONDULATÓRIA
- ÓPTICA
- MAGNETISMO
- ACUSTICA
- ASTRONOMIA
- FORMULAS E EQUAÇÕES - [A]
- FORMULAS E EQUACOE - [B]
- ENERGIA E SUAS TRANSFORMAÇÕES
- FÍSICA - [ Vídeo ]
- HORA DE ESTUDAR [ FÍSICA]
- FIES / SISU / ProUni / PRONATEC
- PROVAS E GABARITOS
- ESTUDE PARA O VESTIBULAR
- FÍSICA DE PARTÍCULA - [PESQUISA]
- NOTAÇÃO CIENTÍFICA
- FISICA - ENEM
- FISICA MODERNA
- CINEMATICA
- CINEMÁTICA-MU/MUV-M. PROGRESSIVO E RETROGAD
- TERMOLOGIA
- DINÂMICA II
- ESTÁTICA DOS SÓLIDOS
- MECÂNICA
- HIDROSTÁTICA
- CANAL DO EDUCADOR
- VESTIBULANDO
- MATEMÁTICA - ENSINO MÉDIO
- PORCENTAGEM
- GRÁFICOS I
- GEOMETRIA PLANA III
- GEOMETRIA ESPACIAL II
- EQUAÇÃO DO 1º E DO 2º GRAU
- PLANO CARTSIANO I
- PA & PG
- FUNÇÃO/COEFICIENTE LINEAR/ANGULA E EQUAÇÃO DA RETA
- PONTO/RETA/ALINHAMENTO
- MATRIZES
- REGRA DE TRES GRANDEZA DIRA/INVRS
- FRAÇÃO
- MMC e MDC
- EXPRESSÕES NUMÉRICAS I
- RADICIAÇÃO POTENCIAÇÃO
- ATRIBUIÇÕES DO QUANDO DO MAGISTÉRIO
- ORGANIZAÇÃO CURRICULAR
- QUESTÕES DE MATEMATCA - 9º ANO
- EQUANCÃO DO 2º GRAU - 9º ANO
- MATEMÁTICE 9 ANO BLOG - PEI TEREZA DELATA
- MATEMÁTICA - E. FUNDAMENTAL
- GEOMETRIA GERAL - EF
- CONJUNTOS NUMÉRICOS
- POLÍGONO
- CIRCULOS, CIRCINFERENCIAS E ARCOS
- VISTAS ORTOGONIAS DE FIGURAS ESPECIAIS
- PROBABILIDADE, PERMUTAÇÃO, ARRANJOS E FATORIAL
- ESTATÍSTICA
- AAP/VESTIBULINHOS
- QUARENTENA - 7 ANO
- PARTE DIVERSIFICADA DO CURRICULO
- MATEMÁTICA & ENEM II
- ORIENTAÇÃO DE ESTDUDOS
- MATEMÁTICA FINACEIRA I
- QUARENTENA - PARTE DIVERSIFICADA
- PLANIFICACAO DE SOLIDOS GEOMATRICOS
- AULA REMOTAS - 2021
- FISICA - 3ª SERIE
- FISICA - 2ª SERIE
- TEOREMA DE PITÁGORAS
- FRAÇÃO GERATIZ
- ADR/AAP/SEQUENCIA DIDÁTICA
- Números decimais
- POLINÔMIOS
- POLINÔMIO-EF
- POLINÔMIOS E PRODUTAS NOTÁVEIS
- MATRIZES ENERGÉTICA
- PROBLEMAS MATEMÁRICOS
- PROVAS TERMOMECÂNICA
- PROVA SENAI
- PROVAS ETEC
- PROVAS ENEM
- QUESTÕES SARESP
- PROVAS AAP/ADE
- TEOREMA DE TALES & PROPORCIONALIDADE
- GRANDEZA/RAZÃO/PROPORÇÃO
- PEI Tereza Delta - Atividades 2021
- PROBABILIDADE - ESTATISTICA
- MATEMÁTICA E SUAS HABILIDADES
- FATORACAO
- FRAÇÃO E NÚMEROS MISTOS
- ANÁLISE COMBINATÓRIA/A
- CMSP & AVALIAÇÕES EXTERNAS
- PROVAS ENEM COMENTADA
- DOCUMENTOS - PEI
- OBMEP
- POLINÔMIO & FATORAÇÃO ALGÉBRICA
- NIVELAMENTO / RECUPERAÇÃO / REFORÇO
- QUSTÕES - ETEC
- QUESTÕES DO SARESP
- QUESTÕES - TERMOMECANICA
- QEUSTÕES PROVA BRASIL
- QUESTÕES SENAI
- QUESTÕES JUROS SIMPLES
- QUESTÕES - JUROS COMPOSTOS
- ESTATISTICA GERAL
- UNIDADE DE MEDIDA
- DIVISAO/MULTIPLICACAO/SOMA/SUBTRACAO
- MMC & MDC
- EXPRESSAO NUMERICA
- NUMEROS DECIMAIS
- NOTACAO CIENTIFICA 1
- RAIZ QUADRADA & RAIZ CUBICA
- DIZIMA PERIODICA
- PRODUTOS NOTAVIES
- CIRCUNFERENCIA
- GRANDEZA DIRETAMENTE & INVERSAMENTE PROPORCIONAL
- TERMOMECANICA/2022 - MATEMÁTICA
- FRACAO 2022
- EXPRESSAO DO 1º GRAU
- EQUACAO DO 2º GRAU
- LOGARITMO
- NUMEROS MISTOS E/OU FRACOES IMPROPRIAS
- FRACAO GERATRIZ
- PROPRIEDADES DA POTENCIACAO
- OPERACOES COM RADICAIS
- MODULO DE UM NUMERO
- EF II - FRACAO
- EF II - ALGARISMOS ROMANO
- EF II - ANGULOS
- EF II - EQUACAO DO 2º GRAU
- EF II - EQUACAOES DO 1º GRAU COM UMA VARIAVEL
- EF II - EQUACAOES DO 1º GRAU COM DUAS VARIAVEL
- EF II - GEOMETRIA PALNA
- EF - GRANDEZAS PROPORCIONAIS
- EF - INEQUACAOES DO 1º GRAU
- EF II - DIVISIBILIDADE
- EF - DIZIMA PERIODICA
- EF II - MEDIAS
- EF II - MEDIDAS DE CAPACIDADE
- EF II - MEDIDAS DE COMPRIMENTO
- EF II - MEDIDAS DE TEMPO
- EF II - MEDIDAS DE VOLUME
- EF II - MEDIDAS DE SUPERFICIES
- EF II - MEDIDAS DE MASSA
- EF II - POTENCIACAO
- EF II - POCENTAGEM
- EF II - NUMEROS DECIMAIS
- EF II - OPERACOES COM NUMEROS RACIONAIS DECIMAIS
- EF II - PROPORCAO
- EF II - SEMALHANCA DE POLIGONO
- EF II - REGRA DE TRES
- EF II - RAZAO
- EF II - RAZOES TRIGONOMETRICAS
- EF II - QUADRILATEROS
- EF II - RADICIACAO
- MATEMATICA - E. FUNDAMENTA II
- EM - ANALISE COMBINATORIA
- EM - BINOMIO DE NEWTON
- EM - DETERMINANTE
- EM - EQUACOES TRIGONOMETRICA
- EM - FUNCAO DO 1º OU FUNCAO AFIM
- EM - FUNCAO QUADRATICA
- EM - FUNCAO
- EM - GEOMETRIA ANALITICA CIRCUNFERENCIA
- MATEMATICA - ENSINO MEDIO
- EM - GEOMETRIA ANALITICA CONICAS
- EM - GEOMETRIA ANALITICA RETAS
- EM - GEOMETRIA ESPACIAL
- EM - POLINOMIO
- EM - INEQUACOES TRIGONOMETRICAS
- EM - LOGARITMO
- EM - MATEMATICA FINANCEIRA
- EM - MATRIZES
- EM - NUMEROS COMPLEXOS
- EM - PROBABILIDADE
- EM - PROGRESSAO
- EM - SISTEMA LINEARES
- EM - TEORIA DOS CONJUNTOS
- EM - VETORES
- EM - CONJUNTOS NUMÉRICOS
- ENEM 2022 - PARTE I
- ENEM 2022 - PARTE II
- ENEM 2022 - PARTE III
- ENEM 2022 - PARTE IV
- REGRA DE TRÊS COMPOSTA
- FUVEST 2023 - PARTE I
- FUVEST 2023 - PARTE II
- SEQUÊNCIA NUMÉRICA - PA & PG
- SEQUÊNCIA NUMÉRICA - PA & PG - I
- PROBABILIDADE
- LEITURA E INTERPRETAÇÃO DE TEXTO I
- INTERPRETAÇÃO DE TEXTO II
- LEITURA E INTERPRETAÇÃO DE TEXTO III
- INTERPRETAÇÃO DE TEXTO - PRPOV BRASIL - 9º ANO
- PROVINHA DE PORTUGUES
- PROVA PAULISTA 1ºBim/2023-HISTORIA 6
- PROVA PAULISTA -1ºBim/2023-GEOGRAFIA 6
- PROVA PAULISTA 1ºBim/2023-CIEÊNCIAS 9
- PROVA PAULISTA -1ºBim/2023-HISTÓRIA 9
- PROVA PAULISTA -1ºBim/2023-GEOGRAFIA 9
- PROVA PAULISTA 1ºBim/2023-PORTUGUES 9
- PROVA PAULISTA-1ºBim/2023-M-G-H-9
- PROVA PAULISTA 1ºBim/2023-HISTÓRIA 7
- PROVA PAULISTA 1ºBim/2023-CIENCIAS 7
- PROVA PAULISTA 1ºBim/2023-GEOGRAFIA 7
- PROVA PAULISTA 1ºBim/2023-PORTUGUES 7
- PROVA PAULISTA- 1ºBim/2023-M-G-H-7
- PROVA PAULISTA-1ºBim/2023-M-G-H-C-8
- PROVA PAULISTA 1ºBim/2023-CIENCIAS 8
- PROVA PAULISTA 1ºBim/2023-HISTORIA 8
- PROVA PAULISTA 1ºBim/2023-GEOGRAFIA 8
- PROVA PAULISTA 1ºBim/2023-PORTUGUES 8
- PROVA PAULISTA-1ºBim/2023-M-G-H-C-6
- PROVA PAULISTA -1ºBim/2023-PORTUGUES 6
- PROVA PAULISTA -1ºBim/2023-CIENCIAS 6
- PP-M-1ª-1ºBIM-2023
- PP-M-2ºBim-1ª-2023
- PP-M-3ª-1ºBIM-2023
- PP-M-1ª-2ºBIM-2023
- PP-M-2ª-2ºBIM-2023
- PP-M-2ºBim-3ª-2023
- FUNÇÃO E.FUNDAMENATL - II
- FUNCAO LOGARITMICA E TRIGONOMETRICA
- PROPRIEDADES DA POTENCIAÇÃO - EF
- MONÔMIOS & EXPRESSÕES ALGÉBRICAS
- P.P-MAT/GEO/HIS-3ºB-9ºANO-2023
- PP-LPT/ING/CIE-3ºB-9ºANO/2023
- P.P-MAT/GEO/HIS-3ºB-6ºA/2023
- P.P-LPT/ING/CIE-3ºB-6ºA-2023
- P.P-MAT/GEO/HIS-3ºB-7ºA/2023
- P.P-LPT/ING/CIE-3ºB-7º A-2023
- P.P-MAT/GEO/HIS-3ºB-8ºANO/2023
- P.P-LPT/ING/CIE-3ºB-8ºA-2023
- MONOMIOS
- TERMOMECANICA VESTIBULINHO 2024
- ENEM 2023-1ºDIA
- ENEM 2023-2ºDIA
- FUVEST 2024
- ETEC - 1º Semestre/2024
- 1ªEM-Matemática, Ciências Humanas e Redação
- 1ªEM-Linguagens e Códigos Ciências da Natureza
- 2ªEM-Matemática, Ciências Humanas e Redação
- 2ªEM-Linguagens e Códigos Ciências da Natureza
- 3ºEM-Matemática, Ciências Humanas e Redação
- 3ªEM-Linguagens e Códigos Ciências da Natureza
- SIMULADO SARESP 9ºANO - PORTUGUÊS
- SIMULADO SARESP 9º - CIÊNCIAS DA NATUREZA
- SIMULADO SARESP 9º - CIÊNCIAS DA HUMANAS
- SIMULADO SARESP 9ºANO - MATEMÁTICA
- SARESP-GEO&HIST-EF&EM
- SARESP-MATEMÁTIC/EM
- MOVIMENTO UNIFORME - (MU)
- MOVIMENTO UNIFORMEMENTE VARIADO (MUV)
- MOVIMENTO PROGRESSIVO OU TRETRÓGRADO
- IMPULO/QUANTIDADE DE MOVIMENT0/COLISÃO
- DINAMICA I
- FISICA - ENEM/VESTIBULAR
- RAZAO E PROPOCAO
- ALBERT EINSTEIN
- PROPRIEDADES DA POTENCIACAO
- 1ª PROVA PAULISTA - 6º ANO/2024
- 5º-LINGUAGENS E CIÊNCIAS HUMANAS
- 1ª PROVA PAULISTA 2024
- PROPROEDADE DISTRIBUITIVA
- 2ª PROVA PAULISTA 2024
- JUROS SIMPLES & JUROS COMPOSTOS
- Área Reservada
- LIVRO DE FÍSICA
|
31 |









.jpg)
.jpg)
.jpg)
.jpg)
 Função Subjuntora ou ou sobrejetiva
Função Subjuntora ou ou sobrejetiva Função bijuntora ou bijetiva
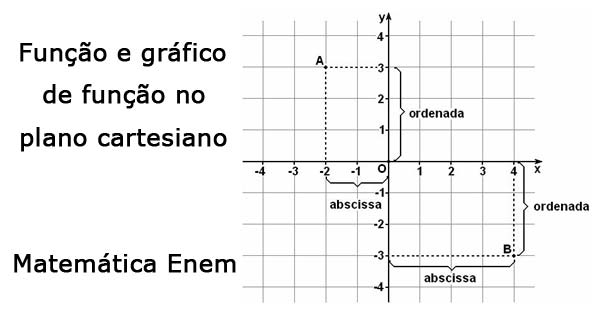
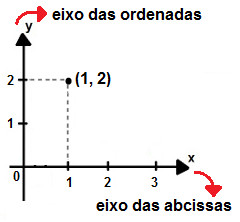
Função bijuntora ou bijetiva As funções podem ser representadas graficamente. Para que isso seja feito, utilizamos duas coordenadas, que são x e y. O plano desenhado é bidimensional. A coordenada x é chamada de abscissa e a y, de ordenada. Juntas em funções, elas formam leis de formação. Veja a imagem do gráfico do eixo x e y:
As funções podem ser representadas graficamente. Para que isso seja feito, utilizamos duas coordenadas, que são x e y. O plano desenhado é bidimensional. A coordenada x é chamada de abscissa e a y, de ordenada. Juntas em funções, elas formam leis de formação. Veja a imagem do gráfico do eixo x e y:

%3D3x.jpg)
%3D4x%2B1.jpg)
%3D-x3.jpg)
%3D5x.jpg)
%3D-5x.jpg)
%3D%20x%5E2%20-6x%2B5%3D0.jpg)
%3D2x%20%2B%206-f(x)%3D-(2x%2B6).jpg)
%3D2%5Ex.jpg)
%3D(1-2x)%5E2.jpg)
%20%3D%20log%20(5x%20-%206).jpg)
%3Dsen(x%2B2).jpg)
%3Dcos(x%2B2).jpg)
%3Dtan(x%2B2).jpg)
%3D%20x%5E1-2.jpg)
.jpg)
.jpg)

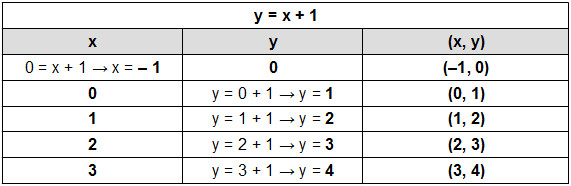
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
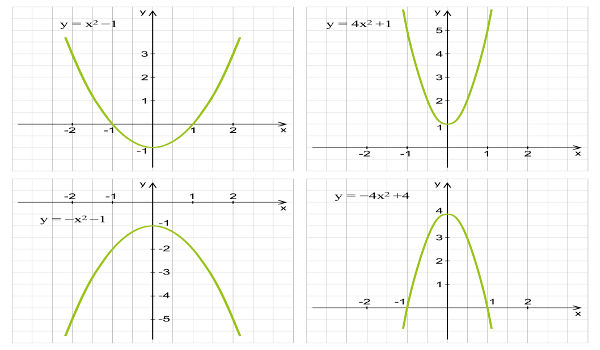 O gráfico da função de 2º grau é formado pela parábola, que pode ter concavidade para baixo ou para cima.
O gráfico da função de 2º grau é formado pela parábola, que pode ter concavidade para baixo ou para cima.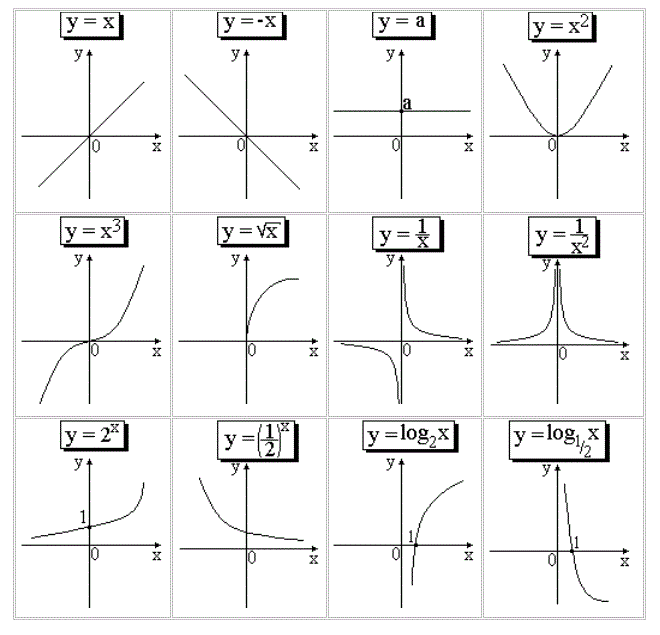
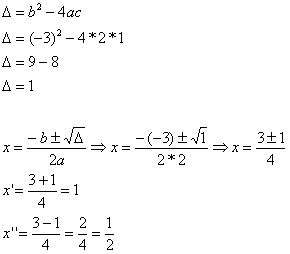
.jpg)
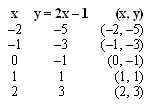
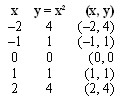
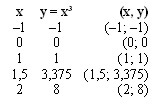
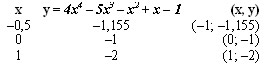



.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)