FRAÇÃO
Professor Diminoi

FRAÇÃO
Fração é a forma de dividir alguma coisa através da razão de dois números inteiros. Dessa forma, nada mais é do que uma divisão onde o dividendo é numerador e o divisor é o denominador.
 Quando dividimos uma pizza, por exemplo, estamos fracionando a pizza. Cada fatia representa uma parte da pizza, ou seja, uma fração. Geralmente ela é dividida em 8 pedaços, então cada pedaço de uma pizza representa 1 / 8 (um oitavo) de uma pizza.
Quando dividimos uma pizza, por exemplo, estamos fracionando a pizza. Cada fatia representa uma parte da pizza, ou seja, uma fração. Geralmente ela é dividida em 8 pedaços, então cada pedaço de uma pizza representa 1 / 8 (um oitavo) de uma pizza.
Exemplo - 1

Exemplo - 2
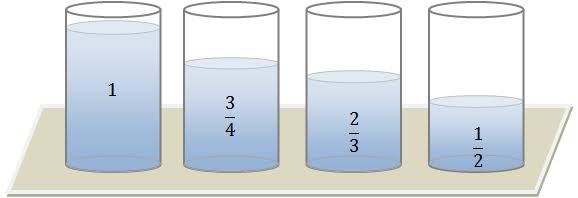
Tipos de frações
As frações, na matemática, recebem classificações, para orientar o estudante. Os nomes servem somente para dizer de que tipo de solução se trata aquele problema matemático.
As frações podem ser representadas de quatro formas distintas que podem ser:
Fração Própria - A fração é própria quando o numerador é menor que o denominador.

Fração Imprópria - A fração é imprópria quando o numerador é maior que o denominador.

Mista - A fração é mista quando ela for constituída por um número inteiro e também por uma fração própria.
 ,
, 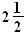 ,
, 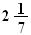 ,
, 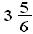
Fração aparente - É um tipo de fração imprópria onde o numerador é divisível pelo denominador, portanto, equivale a quantidades inteiras.

Frações equivalentes - São frações que representam a mesma parte do todo. são equivalentes. Para encontrar frações equivalentes, devemos multiplicar o numerador e o denominador por um mesmo número natural, diferente de zero.
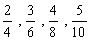
Multiplicação de fração
Basta multiplicar o numerador de uma fração pelo numerador (número de cima) da outra fração, e multiplicar o denominador ( número de baixo) de uma pelo denominador da outra.
Exemplos:
.jpg)
Divisão de fração
Copia a primeira e multiplica pelo inverso da segunda
Exemplos:
.jpg)
Adição e subtração com denominadores iguais
Basta subtrair e/ou somar os numeradores e conservar apenas “um” denominador.
Exemplos:
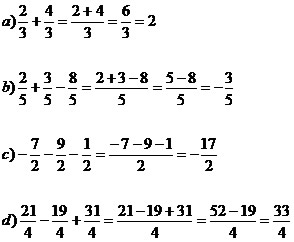
Adição e/ou Subtração com denominadores diferentes
Passo 1: Calcular o mínimo múltiplo comum entre os denominadores. ...
Passo 2: Reescrever as frações com o novo denominador, deixando o espaço do numerador para os números que serão encontrados no passo seguinte. ...
Passo 3: Encontre os numeradores das novas frações.
Exemplos:
(1).jpg)
REVISANDO:
Efetuar adição e subtração de frações com denominadores diferentes
Método do MMC
Exemplo – 1:
Determine o MMC (8,4) utilizando a decomposição em fatores primos.

Logo, o MMC (8,4) = 2 · 2 ·2 = 8, como mostrou o primeiro método.
Exemplo – 2:
Calcule o mínimo múltiplo comum entre 5 e 21.
Como os números não possuem divisor em comum, ou seja, são primos entre si, o menor múltiplo entre eles é o produto entre eles, assim, MMC (21,5) = 21 · 5 = 105.
De fato, isso é verdade, como podemos ver na decomposição em fatores primos.

MMC (21 ,5) = 3 ·5 ·7 = 105
Exemplo - 3:
Como as frações possuem denominadores diferentes, não é possível somá-las ou subtraí-las diretamente. O MMC entre seus denominadores 4, 12 e 50 será:
4, 12, 50| 2
2, 6, 25| 2
1, 3, 25| 3
1, 1, 25| 5
1, 1, 5| 5
, 1, 1| 300
O número 300 será o denominador das frações equivalentes, por isso, podemos escrever:
2 + 10 – 2 = + –
4 12 50 300 300 300
Encontrar o numerador
Para encontrar o primeiro numerador, utilize a primeira fração da soma original. Divida o MMC encontrado pelo denominador da primeira fração e multiplique o resultado pelo seu numerador. O número obtido será o numerador da primeira fração equivalente.
(300:4)·2 = 75·2 = 150. Então, basta colocar o numerador da primeira fração em seu lugar. Observe:
2 + 10 – 2 = 150 + –
4 12 50 300 300 300
Encontrar o restante dos numeradores
Repita o procedimento anterior para cada fração presente na operação. Ao final, terá encontrado todas as frações equivalentes.
Agora realizando o mesmo procedimento para as duas últimas frações, encontraremos os resultados (300:12)·10 = 25·10 = 250 e (300:50)·2 = 6·2 = 12.
2 + 10 – 2 = 150 + 250 – 12
4 12 50 300 300 300
Após encontrar todas as frações equivalentes, elas terão denominadores iguais e sua adição ou subtração poderá ser feita exatamente como no primeiro caso – de frações que possuem denominadores iguais. No exemplo utilizado, o resultado da primeira soma de frações é equivalente ao resultado da segunda, portanto:
2 + 10 – 2 = 150 + 250 – 12 = 150 + 250 – 12 = 400 – 12 = 388
4 12 50 300 300 300 300 300 300
Dessa maneira, podemos escrever o seguinte:
2 + 10 – 2 = 388
4 12 50 300
Soma de frações com denominadores diferentes
Se os denominadores forem números diferentes, existem duas formas de realizar a soma: descobrindo o Mínimo Múltiplo Comum (MMC) dos denominadores ou multiplicando os mesmos.
Método do MMC
Exemplo:
1/4+ 3/8 + 5/10 =
O primeiro passo é determinar o MMC de 4, 8 e 10.

Cálculo do Mínimo Múltiplo Comum (MMC)
Sabe-se que o denominador em comum é 40. Por isso, devemos fazer as seguintes substituições para a soma das frações acima: dividir o termo resultante do MMC (40) pelos denominadores das frações (4,8 e 10). Com o resultado da divisão, multiplica-se os valores pelos numeradores (1,3,5).

Sistema do MMC
Após as operações obtivemos uma fração em que os termos de cima são quocientes da divisão seguida da multiplicação, sendo o denominador o próprio resultado do MMC. Ou seja, a soma será estabelecida por:

Soma de denominadores diferentes
Simplificando a fração:

Simplificação
Então, o resultado da soma das frações acima é 9/8.
EXERCÍCIOS RESOLVIDOS E COMENTADOS:
01) (TJ - CE) Qual a fração que dá origem à dízima 2,54646… em representação decimal?
(A) 2.521 / 990
(B) 2.546 / 999
(C) 2.546 / 990
(D) 2.546 / 900
(E) 2.521 / 999
Resolução:
Veja que o 46 está se repetindo infinitamente a partir da segunda casa decimal.
2,5 + 0,04646…
25/10 + 46/990
(2475 + 46)990
2521/990
Alternativa: A
02) (TJ - RS) Se cada círculo desenhado abaixo está dividido em partes iguais entre si, assinale a alternativa que apresenta o círculo que tem 12,5% de sua área hachurada.
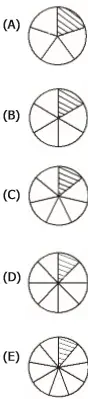
Resolução:
A fração que corresponde a 12,5% é:
12,5/100 = 125/1000 = 1/8
Como os círculos estão divididos em partes iguais, o desenho corresponde a uma parte de oito.
Alternativa: D
03) Resolva as operações
Resolução:
.jpg)
04) Resolva as operações
Resolução:
.jpg) Sempre que resolver uma equação desse modelo, fique atento aos sinais existentes e ao jogo de sinal em algumas multiplicações. Ao trocar um elemento de membro, não se esqueça de inverter o sinal. Veja mais exemplos resolvidos detalhadamente:
Sempre que resolver uma equação desse modelo, fique atento aos sinais existentes e ao jogo de sinal em algumas multiplicações. Ao trocar um elemento de membro, não se esqueça de inverter o sinal. Veja mais exemplos resolvidos detalhadamente:
05) Resolva as operações
Resolução:
.jpg)
06) Resolva as operações
Resolução:
.jpg)
07) (ENEM) O polímero de PET (Politereftalato de Etileno) é um dos plásticos mais reciclados em todo o mundo devido à sua extensa gama de aplicações, entre elas, fibras têxteis, tapetes, embalagens, filmes e cordas. Os gráficos mostram o destino do PET reciclado no Brasil, sendo que, no ano de 2010, o total de PET reciclado foi de 282 kton (quilotoneladas).
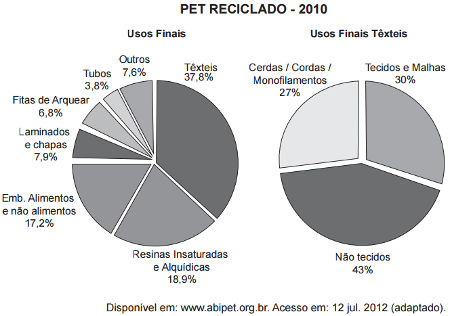 De acordo com os gráficos, a quantidade de embalagens PET recicladas destinadas à produção de tecidos e malhas, em kton, é mais aproximada de
De acordo com os gráficos, a quantidade de embalagens PET recicladas destinadas à produção de tecidos e malhas, em kton, é mais aproximada de
(A) 16,0
(B) 22,9
(C) 32,0
(D) 84,6
(E) 106,6
Resolução:
Observe que a porcentagem destinada a tecidos e malhas é 30% dos usos finais têxteis, que, por sua vez, é uma porcentagem de 37,8% de todos os usos finais. Sendo assim, precisaremos calcular 30% de 37,8% de 282 kton. Esse cálculo pode ser expresso por multiplicações da seguinte maneira:
30%·37,8%·282
Para resolver essa questão, lembre-se de que uma porcentagem é uma fração de denominador 100. Logo, podemos transformar a multiplicação acima na multiplicação de frações a seguir:
30 · 37,8·282
100 100
Conforme as regras de multiplicação de frações dadas no início do texto, basta multiplicar numeradores por numeradores e denominadores por denominadores. A única observação é a de que o denominador de 282 é 1.
30 · 37,8·282 = 319788
100 100 10000
Dividindo numerador por denominador, pois toda fração representa uma divisão, teremos:
319788 = 31,9788
10000
Esse valor é aproximadamente 32 kton.
Alternativa: C
08) (ENEM) – A expressão “Fórmula de Young” é utilizada para calcular a dose infantil de um medicamento, dada a dose do adulto:
Dose de criança = Idade da criança (em anos) · dose de adulto
Idade da criança (em anos) + 12
Uma enfermeira deve administrar um medicamento X a uma criança inconsciente, cuja dosagem de adulto é de 60 mg. A enfermeira não consegue descobrir onde está registrada a idade da criança no prontuário, mas identifica que, algumas horas antes, foi administrada a ela uma dose de 14 mg do medicamento Y, cuja dosagem de adulto é 42 mg. Sabe-se que a dose da medicação Y administrada à criança estava correta.
Então, a enfermeira deverá ministrar uma dosagem do medicamento X, em miligramas, igual a
(A) 15
(B) 20
(C) 30
(D) 36
(E) 40
Resolução:
Esse exercício envolverá uma multiplicação de frações, mas, antes, é preciso resolver equações. Para resolvê-lo, mudaremos a fórmula para facilitar a organização dos cálculos, portanto, C = dose da criança, i = Idade da criança e A = Dose do adulto.
C = i · A
i + 12
Substituindo os valores conhecidos para o medicamento Y, teremos:
14 = i · 42
i + 12
Resolvendo a equação, teremos:
(i + 12)14 = i . 42
14i + 168 = 42i
42i – 14i = 168
28i = 168
i = 168
28
i = 6
Sabendo que a idade da criança é 6 anos, temos que:
C = 6 · 60
6 + 12
C = 6 · 60
18
Observe que é necessário multiplicar uma fração por um número inteiro. Como todo número inteiro é uma fração de denominador 1, teremos:
C = 6 · 60 = 360
18 1 18
Dividindo numerador por denominador, encontraremos 20 mg como dosagem do medicamento X.
Alternativa: B
09) Determine qual das opções abaixo não é equivalente a:
11
12
(A) 22
24
(B) 121
132
(C) 164
180
(D) 220
240
(E) 440
480
Resolução:
Existem várias maneiras de descobrir se uma fração é equivalente à outra. A primeira é tentar simplificá-las. Se forem equivalentes, terão a mesma fração irredutível ao final da simplificação. A segunda maneira é dividir o numerador pelo denominador para conferir o resultado. Frações equivalentes têm resultados exatamente iguais. Observe:
a) Equivalente!
Note que é possível simplificar essa fração por 2, obtendo o seguinte resultado:
22 = 11
24 12
b) Equivalente!
Simplificando a fração por 11, teremos:
121 = 11
132 12
c) Não equivalente!
Simplificando a fração por 4, teremos:
164 = 41
180 35
Essa fração irredutível com certeza é diferente da fração proposta no exercício.
d) Equivalente!
Simplificando a fração por 20, encontraremos 11/22.
e) Equivalente!
Simplificando a fração por 40, encontraremos 11/22.
Alternativa: C
10) Determine qual das imagens abaixo não representa uma fração equivalente a:
2
8
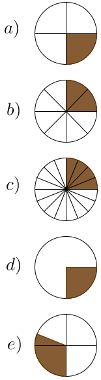
Resolução:
Observe que a fração 2/8 pode ser simplificada e que sua irredutível é 1/4. Sendo assim, basta procurar entre os desenhos qual é aquele que não representa 1/4.
Na letra a), temos exatamente um quarto. Na letra b), temos exatamente dois oitavos. Na letra c), temos três doze avos, que podem ser simplificados para um quarto. A letra d), apesar de não mostrar a divisão, aproxima-se muito de um quarto. A letra e) mostra como a figura foi dividida em quatro partes e como o espaço colorido cobriu uma por inteiro e avançou sobre outra. Logo, a alternativa e) é a fração não equivalente a dois oitavos.
Alternativa: E
11) Determinado condomínio trocou seu reservatório de água, com capacidade para 15000 litros, por outro dois terços maior. Qual é a capacidade do novo reservatório?
(A) 10000 l.
(B) 15000 l.
(C) 20000 l.
(D) 25000 l.
(E) 0,0000 l.
Resolução:
Essa questão pode ser resolvida por meio de equivalência de frações. Para tanto, basta encontrar uma fração equivalente a dois terços e que o denominador seja 15000. Nesse caso, o numerador é exatamente o valor que deve ser acrescido ao novo reservatório para obtermos sua capacidade total. Observe:
2 . 5000 = 10000
3 . 5000 15000
Multiplicamos numerador e denominador por 5000, pois, assim, a fração iguala seu denominador a 15000 como pretendido. Dessa maneira, o acréscimo foi de 10000 litros e a capacidade do novo reservatório é:
10000 + 15000 = 25000 litros
Alternativa: D
12) Para redução de custos e aumento de lucratividade, determinada lanchonete diminuiu em sete vinte avos a quantidade de bacon presente em todos os sanduíches. Sabendo que eram gastos 100 g de bacon por sanduíche, qual é a nova quantidade gasta?
(A) 35 g
(B) 65 g
(C) 45 g
(D) 25 g
(E) 55 g
Resolução:
Para encontrar a quantidade de bacon retirada do sanduíche, basta encontrar uma fração equivalente a sete vinte avos que possua 100 no denominador. Para tanto, multiplicaremos a fração por 5. Observe:
7.5 = 35
20 . 5 100
Assim, a quantidade de bacon retirada do sanduíche foi de 35 g. Dessa maneira, teremos:
100 – 35 = 65 g de bacon
Alternativa: B
13) (ENEM) A música e a matemática se encontram na representação dos tempos das notas musicais, conforme a figura seguinte.
 Um compasso é uma unidade musical composta por determinada quantidade de notas musicais em que a soma das durações coincide com a fração indicada como fórmula do compasso. Por exemplo, se a fórmula de compasso for 1/2, poderia ter um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, poderia ter um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, sendo possível a combinação de diferentes figuras. Um trecho musical de oito compassos, cuja fórmula é 3/4 , poderia ser preenchido com:
Um compasso é uma unidade musical composta por determinada quantidade de notas musicais em que a soma das durações coincide com a fração indicada como fórmula do compasso. Por exemplo, se a fórmula de compasso for 1/2, poderia ter um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, poderia ter um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, sendo possível a combinação de diferentes figuras. Um trecho musical de oito compassos, cuja fórmula é 3/4 , poderia ser preenchido com:
(A) 24 fusas.
(B) 3 semínimas.
(C) 8 semínimas.
(D) 24 colcheias e 12 semínimas.
(E) 16 semínimas e 8 semicolcheias.
Resolução:
Para solucionar essa questão, devemos inicialmente calcular quanto vale 8 compassos de 3/4
8 de 3 = 8 x 3 = 24 = 6
4 4 4
Temos então que a alternativa correta para essa questão será aquela que apresentar 6 como resultado da fórmula do compasso.
Por meio do método de tentativas, verificaremos a alternativa correta.
a) 24 fusas
1 fusa = 1 , então 24 fusas de 1 é ?
32 32
24 de 1 = 24 x 1 = 24 : 8 = 3 = 0,75
32 32 32 : 8 4
A alternativa a não é a correta.
b) 3 semínimas
1 semínima = 1 , então 3 semínimas de 1 são?
4 4
3 de 1 = 3 x 1 = 3 = 0,75
4 4 4
A alternativa b não é a correta.
c) 8 semínimas
1 semínima = 1 , então 8 semínimas de 1 são ?
4 4
8 de 1 = 8 x 1 = 8 = 2
4 4 4
A alternativa c não é a correta.
d) 24 colcheias e 12 semínimas.
Na alternativa d, devemos efetuar a soma entre: 24 colcheias + 12 semínimas
1 colcheia = 1 , então 24 colcheias de 1 são ?
8 8
24 de 1 = 24 x 1 = 24 = 3
8 8 8
1 semínima = 1 , então 12 semínimas de 1 são ?
4 4
12 de 1 = 12 x 1 = 12 = 3
4 4 4
24 colcheias + 12 semínimas = 3 + 3 = 6
Obtivemos 6 como resultado da fórmula do compasso.
Alternativa: D
14) Carlos fez uma viagem de 1.210 km, sendo 7/11 de aeroplano; 2/5 do resto, de trem, 3/8 do novo resto, de automóvel e os demais quilômetros, a cavalo. Calcule quantos quilômetros Carlos percorreu a cavalo.
Resolução:
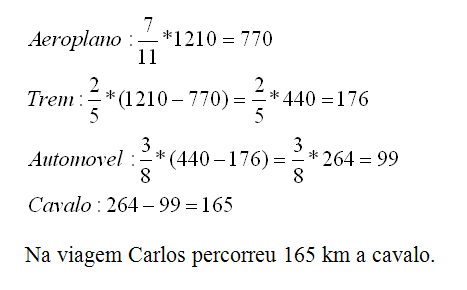
15) Se 7/8 de um terreno valem R$ 21.000,00, qual é o valor de 5/48 do mesmo terreno?
Resolução:
.gif)
16) Juliana tinha R$ 245,00 e gastou 1/7 de 1/5 dessa importância. Quanto sobrou?
Resolução:
.gif) Conclusão: Juliana tinha R$ 245,00 e gastou R$ 7,00, portanto ficou com R$ 238,00.
Conclusão: Juliana tinha R$ 245,00 e gastou R$ 7,00, portanto ficou com R$ 238,00.
17) (Vunesp) Duas empreiteiras farão conjuntamente a pavimentação de uma estrada, cada uma trabalhando a partir de uma das extremidades. Se uma delas pavimentar 2/5 da estrada e a outra os 81 quilômetros restantes, determine a extensão total dessa estrada.
Resolução:
Uma das empresas irá pavimentar 2/5 e a outra os 81 quilômetros restantes que representam, na forma de fração, 3/5. Dessa forma, temos que cada 1/5 de pavimentação corresponde a 27 quilômetros. Portanto, as cinco partes de pavimentação correspondem a 5 * 27 = 135 quilômetros.
Podemos resolver o problema utilizando a equação:
.gif)
.gif)
18) (Uece) Uma peça de tecido, após a lavagem, perdeu 1/10 de seu comprimento e este ficou medindo 36 metros. Determine o comprimento, em metros, da peça antes da lavagem.
Resolução:
Podemos resolver diretamente pela equação:
.gif)
.gif)
19) (Olimpíada Brasileira de Matemática) Toda a produção mensal de latas de refrigerante de uma certa fábrica foi vendida à três lojas. Para a loja A foi vendida a metade da produção; para a loja B foram vendidos 2/5 da produção e para a loja C foram vendidas 2500 unidades. Qual foi a produção mensal dessa fábrica?
Resolução:

20) Quando as frações possuem denominadores diferentes, é necessário encontrar outras frações equivalentes a essas que possuam denominadores iguais.
10 + 12 – 3
4 5 6
Resolução:
Passo 1: Calcular o mínimo múltiplo comum entre os denominadores. O valor encontrado será o denominador comum que possibilitará substituir as frações dadas por outras com denominadores iguais. No exemplo, temos:
4,5,6| 2
2,5,3| 2
1,5,3| 3
1,5,1| 5
1,1,1| 60
Passo 2: Reescrever as frações com o novo denominador, deixando o espaço do numerador para os números que serão encontrados no passo seguinte.
10 + 12 – 3 = + –
4 5 6 60 60 60
Passo 3: Encontre os numeradores das novas frações. Para isso, o seguinte cálculo deverá ser feito: Para encontrar o numerador da primeira fração, divida o MMC pelo denominador da primeira fração e multiplique o resultado pelo seu numerador. O resultado obtido por esse cálculo será o numerador da primeira fração que possui denominador igual ao MMC. Repita o procedimento para todas as frações presentes na soma ou subtração.
10 + 12 – 3 = 150 + 144 – 30
4 5 6 60 60 60
21) Lúcio comprou uma pizza pequena. Em um primeiro momento, comeu metade da pizza e, posteriormente, conseguiu comer mais um pedaço equivalente à sexta parte dessa mesma pizza. Que fração representa a quantidade total de pizza que Lúcio comeu?
Resolução:
Basta observar que a metade é representada pela fração um meio 1 / 2 e que a sexta parte é representada por um sexto 1 / 6.
Somando essas frações, teremos a quantidade ingerida por Lúcio.
1 + 1
2 6
Primeiro passo, teremos: MMC (2, 6) = 6. De fato,
2, 6| 2
1, 3| 3
1, 1| 6
Segundo passo, teremos:
1 + 1 = +
2 6 6 6
Terceiro passo, teremos: (6 / 2) · 1 = 3 e (6 / 6)·1 = 1
1 + 1 = 3 + 1
2 6 6 6
Quarto passo, teremos:
1 + 1 = 3 + 1 = 4
2 6 6 6 6
Conclusão: Lúcio comeu quatro sextos, número que, simplificado, é equivalente a dois terços 2 / 3 da quantidade total de pizza disponível.
22) A rua onde Cláudia mora está sendo asfaltada. Os 5/9 da rua já foram asfaltados. Que fração da rua ainda resta asfaltar?
(A) 1/9
(B) 2/9
(C) 3/9
(D) 4/9
Resolução:
Quando as frações possuem denominadores iguais, conserve-se o dinominadores e subtra-se os numeradores.
Sabemos que 9/9 = 1 (um inteiro). Portanto, 9/9 – 5/9 = 4/9
Alternativa: D
23) Em uma sala de aula com 10 alunos, 3/5 tiraram nota acima de 7 numa prova de matemática. 1/5 foram reprovados, pois tiraram notas abaixo de 5. Calcule a quantidade de alunos que tiraram notas 5, 6 ou 7. Respectivamente.
(A) 1
(B) 2
(C) 3
(D) 4
Resolução:
3/5 de 10 alunos é 3/5 . 10 = 30/5 = 6. Temos que 6 alunos tiraram nota acima de 7.
1/5 de 10 alunos é 1/5 . 10 = 10/5 = 2. Temos que 2 alunos foram reprovados com notas abaixo de 5.
Usando o raciocínio lógico temos:
6 + 2 = 8
Então, sendo assim, temos que 2 alunos tiraram notas 5, 6 ou 7, pois 6 (nota 7) + 2 (nota 5) = 8 e 10 (total de alunos) – 8 = 2.
Alternativa: B
24) 20 colegas de trabalho resolveram fazer uma aposta e premiar aqueles que mais acertassem os resultados dos jogos de um campeonato de futebol.
Sabendo que cada pessoa contribuiu com 30 reais e que os prêmios seriam distribuídos da seguinte forma:
1º primeiro colocado: 1/2 do valor arrecadado;
2º primeiro colocado: 1/3 do valor arrecadado;
3º primeiro colocado: recebe a quantia restante.
Quanto, respectivamente, cada participante premiado recebeu?
(A) R$ 350; R$ 150; R$ 100
(B) R$ 400; R$ 150; R$ 50
(C) R$ 250; R$ 200; R$ 150
(D) R$ 300; R$ 200; R$ 100
Resolução:
Resposta correta: b) R$ 300; R$ 200; R$ 100.
Primeiramente, devemos calcular o valor arrecadado.
20 x R$ 30 = R$ 600
Como cada uma das 20 pessoas contribuíram com R$ 30, então a quantia utilizada para premiação foi de R$ 600.
Para saber quanto cada ganhador recebeu devemos realizar a divisão do valor total pela fração correspondente.
1º colocado: 600/1/2 = 600/2 = 300
2º colocado: 600/1/23 = 600/3 = 200
3º colocado:
Para o último premiado, devemos somar quanto os outros ganhadores receberam e subtrair do valor arrecadado.
300 + 200 = 500
600 - 500 = 100
Portanto, temos a seguinte premiação:
1º colocado: R$ 300,00;
2º colocado: R$ 200,00;
3º colocado: R$ 100,00.
Alternativa: D
04) (ETEC/SP) Tradicionalmente, os paulistas costumam comer pizza nos finais de semana. A família de João, composta por ele, sua esposa e seus filhos, comprou uma pizza tamanho gigante cortada em 20 pedaços iguais. Sabe-se que João comeu 3/12 e sua esposa comeu 2/5 e sobraram N pedaços para seus filhos. O valor de N é?
(A) 4
(B) 6
(C) 7
(D) 10
Resolução:
Sabemos que as frações representam a parte de um todo, que nesse caso são os 20 pedaços de uma pizza gigante.
Para resolver esse problema, temos que obter a quantidade de pedaços correspondente a cada fração:
João: comeu 3/12
Esposa de João: comeu 2/5
N: o que sobrou (?)
Vamos então descobrir quantos pedaços que cada um deles comeu:
João: 3/12 temso 20 = 3/12 . 20 = 60/12 = 5 pedaços
Esposa: 2/5 temso 20 = 2/5 . 20 = 8 pedaços. Somarmos os dois valores (5 + 8 = 13) temos a quantidade de fatias que foram comidas por eles.
Portanto, sobraram 7 pedaços que foram divididos entre os filhos.
Alternativa: C
Continua...











.jpg)
.jpg)
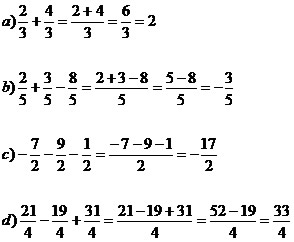
(1).jpg)







.jpg)
.jpg)
.jpg)
.jpg)
 De acordo com os gráficos, a quantidade de embalagens PET recicladas destinadas à produção de tecidos e malhas, em kton, é mais aproximada de
De acordo com os gráficos, a quantidade de embalagens PET recicladas destinadas à produção de tecidos e malhas, em kton, é mais aproximada de
 Um compasso é uma unidade musical composta por determinada quantidade de notas musicais em que a soma das durações coincide com a fração indicada como fórmula do compasso. Por exemplo, se a fórmula de compasso for 1/2, poderia ter um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, poderia ter um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, sendo possível a combinação de diferentes figuras. Um trecho musical de oito compassos, cuja fórmula é 3/4 , poderia ser preenchido com:
Um compasso é uma unidade musical composta por determinada quantidade de notas musicais em que a soma das durações coincide com a fração indicada como fórmula do compasso. Por exemplo, se a fórmula de compasso for 1/2, poderia ter um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, poderia ter um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, sendo possível a combinação de diferentes figuras. Um trecho musical de oito compassos, cuja fórmula é 3/4 , poderia ser preenchido com: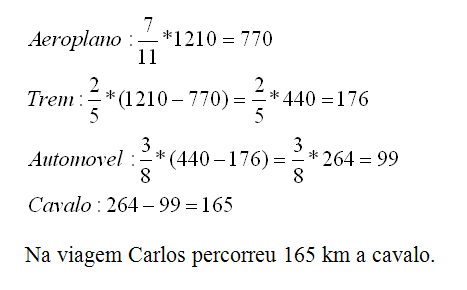
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)

