PROBABILIDADE

Professor Diminoi
O estudo da probabilidade é de grande importância para a tomada de decisões em nossa sociedade. Conhecemos como probabilidade a área da matemática que estuda a chance de um determinado evento acontecer.
A probabilidade conta com conceitos importantes, como experimento aleatório, evento, espaço amostral, e eventos equiprováveis.
O valor da probabilidade é sempre um número entre 0 e 1 ou uma porcentagem entre 0% e 100%, e é calculado com base na razão entre os casos favoráveis e os casos possíveis.

O que é probabilidade?
Perceber o comportamento de eventos aleatórios é de grande importância para a nossa sociedade, e a área de estudo conhecida como probabilidade faz a análise desses eventos para entender quais são as chances reais de eles ocorrerem.

Há várias aplicações do estudo da probabilidade no cotidiano, um deles ocorre na pandemia de Covid-19, assim como pode ocorrer em outras possíveis futuras pandemias, nela ferramentas da estatística e da probabilidade são utilizadas para prever-se o comportamento da transmissão da doença nas próximas semanas.

É também com base na probabilidade que se faz as estimativas para que os governadores e prefeitos tomem providências em relação ao afrouxamento ou endurecimento de medidas de isolamento social.
Para compreender o cálculo da probabilidade, antes, precisamos dominar alguns conceitos, como espaço amostral, evento e experimento aleatório.

Experimento aleatório
É o experimento que, ao ser realizado várias vezes nas mesmas condições, ainda sim, gera um resultado imprevisível. Estamos cercados de experimentos aleatórios no nosso cotidiano, por exemplo, ao realizarmos o lançamento de um dado comum, ainda que seja possível calcular a chance de cada um dos resultados ocorrer, é impossível termos, com precisão, o resultado do lançamento.
Ao lançarmos o dado uma vez e obtermos, por exemplo, 1 como resultado, ao realizarmos um novo lançamento, respeitando as mesmas condições, o resultado continua sendo imprevisível, ele pode ou não ser 1 novamente.

Há vários outros exemplos de experimentos aleatórios nas outras áreas de conhecimento, como na biologia, mais especificamente no estudo da genética.

Espaço amostral
É o conjunto de todos os resultados possíveis de um evento aleatório. Conhecido também como conjunto universo, o espaço amostral pode ser representado pelo símbolo grego Ω (lê-se: ômega).
Em um experimento aleatório, conhecer o espaço amostral é essencial para que a gente consiga calcular a probabilidade desse evento acontecer. Por exemplo, em um lançamento de um dado normal, o espaço amostral será Ω: {1,2,3,4,5,6}, outra possibilidade é escolher uma vogal do alfabeto ao acaso, logo, nesse experimento aleatório, o espaço amostral será Ω:{a, e, i, o, u}.

Ponto amostral
É um elemento que pertence ao espaço amostral, ou seja, um entre os vários resultados possíveis do experimento aleatório. Por exemplo, ao lançar-se uma moeda para o alto, o resultado coroa é um ponto amostral assim como o resultado cara, a depender de qual dos lados aparece após a queda do objeto. Dessa forma, um ponto amostral de um experimento aleatório nada mais é do que um dos seus resultados possíveis.

Evento
É qualquer subconjunto do espaço amostral. O evento pode ser representado utilizando-se notação de conjuntos, ou seja, por letras maiúscula. Geralmente o evento é o conjunto de resultados satisfatórios, ou seja, é um subconjunto do espaço amostral que contém os elementos com os quais se calcula a probabilidade

Exemplo:
Em um experimento aleatório, será sorteado ao acaso um estado brasileiro. Nesse experimento podemos tirar vários possíveis eventos, por exemplo, podemos pensar no resultado ser um estado do Sul, logo, meu evento pode ser representado pelo conjunto
A: {Rio Grande do Sul, Paraná, Santa Catarina}.
Outro possível evento é o conjunto de estados cujos nomes comecem com a letra s, nesse caso o evento será o conjunto
B: {Santa Catarina, Sergipe, São Paulo}.

Evento certo
É o que possui 100% de chance de ocorrer.

Exemplo:
Ao lançarmos um dado e observarmos, após a queda, sua face superior, um evento certo é que encontraremos nela um número menor que 7, logo, meu conjunto E será {1,2,3,4,5,6}, pois, ao lançar-se um dado, não existe outra opção a não ser um desses resultados, o que torna esse evento certo.

Evento impossível
É aquele que possui 0% de chance de ocorrer, ou seja, que não ocorrerá.

Exemplo:
Utilizando-se do mesmo experimento de lançamento de um dado comum, um evento impossível será obter-se um número maior que 6.

Cálculo de probabilidade
Todos os conceitos vistos são essenciais para compreender-se o cálculo da probabilidade. Dado um experimento aleatório, calculamos a chance de um determinado evento ocorrer, essa probabilidade é dada pela razão entre o número de elementos do meu conjunto evento, ou seja, o número de casos favoráveis sobre o número de elementos no meu espaço amostral, ou seja, o número de casos possíveis.

P(A) = probabilidade do evento A
n(A) = número de elementos no conjunto A
n(Ω) = número de elementos no conjunto

Observação:
- A probabilidade pode ser representada como fração, como porcentagem ou como número decimal.
- A probabilidade é sempre um número decimal entre 0 e 1, ou uma porcentagem entre 0% e 100%.
- Se P(A) = 0 então A é um evento impossível.
- Se P(A) = 1 então A é um evento certo.

POSSÍVEIS EVENTOS: A PRESENÇA DO ALEATÓRIO
01) (Currículo em Ação Volume 1/2023-SEESP) Em um sorteio entre 20 participantes, cada um recebeu um número, entre 1 e 20, sem repetição. Sabendo que cada participante teve direito a um único número, escreva:

a) Os elementos que formam o espaço amostral desse sorteio.
Resolução
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}.

b) Os elementos que descrevem o evento: “O resultado de um número par maior que 4 e menor que 20”.
Resolução
Sendo o evento um subconjunto do espaço amostral do sorteio, temos:
E = {6, 8, 10,12, 14, 16, 18}.

c) O número de elementos do evento que resultem em um número primo.
Resolução
Dentro do espaço amostral descrito, temos como números primos
E = {2, 3, 5, 7, 11, 13, 17, 19}.
Então, n(E) = 8

d) A probabilidade de, ao se sortear um número ao acaso, esse número seja múltiplo de 6.
Resolução
Espaço Amostral do sorteio: S= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}.
Números múltiplos de 6 que possam sair no evento: E = {6, 12, 18}, então n(E) = 3.
Probabilidade de ocorrer o evento:

3/3 = 0,15 = 15%

02) (Currículo em Ação Volume 1/2023-SEESP) Ao dividir ao acaso o número 60 por um de seus divisores positivos naturais, qual é a chance de essa divisão ser feita por um número que seja par e múltiplo de 5? Expresse o resultado em forma de porcentagem.
Resolução
Espaço Amostral dos divisores positivos de 60: S = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}, sendo assim temos:
n(S) = 12 elementos.
Divisor de 60 que seja par e múltiplo de 5:
E = {10, 20, 30, 60), então,
n(E) = 4.

4/12 = 1/3 0,333... = 33,33% 

04) (Currículo em Ação Volume 1/2023-SEESP) Uma criança está brincando com bolinhas numeradas de 1 a 15, que estão dentro de uma caixa. Sabendo que durante a brincadeira a criança derrubou uma das bolinhas no chão, determine a probabilidade de ocorrerem os seguintes eventos:

a) O número da bolinha que caiu ser par.
Resolução
O espaço amostral é S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}.
n(S) = 15
Com base no espaço amostral, formamos o evento de ter caído bolinha de número par.
E = {2, 4, 6, 8,10, 12, 14}
n(E) = 7.
7/15 = 0,4666 = 4,6%

b) O número da bolinha que caiu ser primo.
Resolução
Com base no espaço amostral, formamos o evento de ter caído bolinha de número primo.
E = {2, 3, 5, 7, 11, 13}, então n(E) = 6
6/15 = 0,4 = 40%

c) O número da bolinha que caiu ser par e primo.
Resolução
Bolinha de número par E1= {2, 4, 6, 8, 10, 12, 14}, isto é, 7 possibilidades entre 15, n(E1) = 7.
Bolinha de número primo E2 = {2, 3, 5, 7, 11,13}, isto é, 6 possibilidades entre 15, n(E2) = 6.
Bolinha de número par e primo corresponde à intersecção entre os dois eventos, ou seja, E1 ∩ E2 = {2}, isto é, 1 possibilidade entre 15, n(E1 ∩ E2) = 1.

d) Ter caído qualquer uma das bolinhas, independentemente do número marcado.
Resolução
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
n(S) = 15
E = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
n(E) = 15
15/15 = 1 = 100%

07) (Currículo em Ação Volume 1/2023-SEESP) Agora e com você! Junte-se com outros dois colegas de sua sala e formulem uma situação-problema que envolva o princípio multiplicativo da contagem e o cálculo de probabilidades. Quando a situação estiver pronta, proponha a um outro trio de colegas que discutam e resolvam o problema formulado por vocês. Ah, não se esqueçam de também resolverem o problema proposto por outra dupla. Quando tudo estiver pronto, verifiquem as respostas e discutam os raciocínios que foram traçados durante a resolução.
Resolução
Verifique se os estudantes estão elaborando uma situação-problema de contagem que contemple o princípio multiplicativo e cálculo de probabilidade, além de propiciar um momento de interação entre os estudantes, fazendo-os pensar, discutir, argumentar sobre suas propostas e seus raciocínios empregados na elaboração e resolução da atividade.

08) Uma urna contém bolas brancas, vermelhas e verdes. Sabendo-se que nela há 12 bolas brancas, 8 vermelhas e que as 5 restantes são brancas, se uma bola for retirada ao acaso, qual é a probabilidade de que ela seja:

a) Branca
Resolução
Nosso evento A é  → sair uma bola branca. Sabemos que
n(A) = 12, ou seja, há
12 casos favoráveis.
Nosso espaço amostral possui um total de 12 + 8 + 5 = 25, então n(Ω) = 25.
Dessa forma, a probabilidade de o evento A ocorrer pode ser representada por:

b) Não branca
Resolução
Nosso evento B é → sair uma bola não branca. Sabemos que n(B) = 13.
Como o espaço amostral continua o mesmo, então n(Ω) = 25.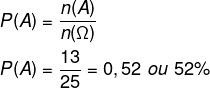

09) (ENEM) Em uma central de atendimento, cem pessoas receberam senhas numeradas de 1 até 100. Uma das senhas é sorteada ao acaso. Qual é a probabilidade de a senha ser um número de 1 a 20.
(A) 1/100
(B) 19/100
(C) 20/100
(D) 21/100
(E) 80/100
Resolução
Seja A o evento, para sair um número de 1 a 20, então n(A) = 20.
Por outro lado, no espaço amostral há 100 bolas, então n(Ω) = 100.
Assim, a probabilidade do evento A ocorrer será:
P(A) = n(A)/n(Ω)
P(A) = 20/100
Alternativa C

10) (Fundatec – 2019) Ao lançar uma moeda não viciada três vezes consecutivas, a probabilidade de sair pelo menos duas caras é de:
(A) 10%
(B) 20%
(C 30%
(D 40%
(E) 50%
Resolução
A cada lançamento da moeda, há duas opções, cara ou coroa. Como a moeda será lançada três vezes, há um total de 2³ resultados possíveis, logo, n(Ω) = 8.
Analisando os resultados possíveis, queremos os que possuem pelo menos duas caras.
c → cara
k → coroa
Ω: {(c, c, c); (c, c, k); (c, k, c); (k, c, c); (k, k, k); (k, k, c); (k, c, k); (c, k, k)}
Seja A o evento, para sair pelo menos duas caras, os casos favoráveis, ou seja, os que possuem pelo menos duas caras, são:
A: {(c, c, c); (c, c, k); (c, k, c); (k, c, c)}, então n(A) = 4.
Assim P(A) = n(A)/ n(Ω)
P(A) = 4/8 = 0,5 ou 50%
Alternativa E
 

Continua ...