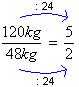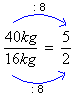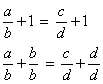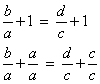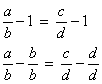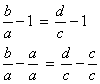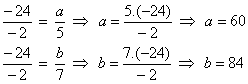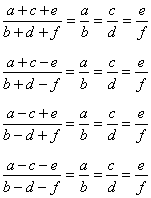EF II - PROPORCAO
Professor Diminoi
PROPORCAO
O que é uma proporção?
Proporção é uma igualdade entre duas razões.
Exemplo
Rogerião e Claudinho passeiam com seus cachorros. Rogerião pesa 120kg, e seu cão, 40kg. Claudinho, por sua vez, pesa 48kg, e seu cão, 16kg.
Observe a razão entre o peso dos dois rapazes:
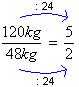Observe, agora, a razão entre o peso dos cachorros:
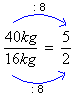Verificamos que as duas razões são iguais. Nesse caso, podemos afirmar que a igualdade
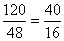Elementos de uma proporção
Dados quatro números racionais a, b, c, d, não-nulos, nessa ordem, dizemos que eles formam uma proporção quando a razão do 1º para o 2º for igual à razão do 3º para o 4º.
Assim:
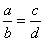
ou
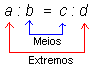
a : b = c : d
(lê-se "a está para b assim como c está para d")
Os números a, b, c e d são os termos da proporção, sendo:
b e c os meios da proporção.
a e d os extremos da proporção.
Exemplo
Dada a proporção
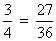temos:
Leitura: 3 está para 4 assim como 27 está para 36.
Meios: 4 e 27
Extremos: 3 e 36
Propriedade fundamental das proporções
Observe as seguintes proporções:
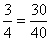Produto dos meios = 4.30 = 120
Produto dos extremos = 3.40 = 120
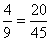Produto dos meios = 9.20 = 180
Produto dos extremos = 4.45 = 180
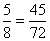
Produto dos meios = 8.45 = 360
Produto dos extremos = 5.72 = 360
De modo geral, temos que:
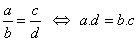Daí podemos enunciar a propriedade fundamental das proporções:
Em toda proporção, o produto dos meios é igual ao produto dos extremos.
Aplicações da propriedade fundamental
Determinação do termo desconhecido de uma proporção
Exemplos
Determine o valor de x na proporção:
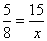Resoliucao
5 . x = 8 . 15
Aplicando a propriedade fundamental5 . x = 120
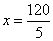x = 24Logo, o valor de x é 24.
Determine o valor de x na proporção:
Resolucao
5 . (x-3) = 4 . (2x+1)
Aplicando a propriedade fundamental
5x - 15 = 8x + 4
5x - 8x = 4 + 15
-3x = 19
3x = -19
x = -19 : 3
Logo, o valor de x é
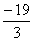
Os números 5, 8, 35 e x formam, nessa ordem, uma proporção. Determine o valor de x.
Resolucao
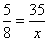Aplicando a propriedade fundamental
5 . x = 8 . 35
5x = 280
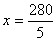
x = 56
Logo, o valor de x é 56.
Resolução de problemas envolvendo proporções
Exemplo
Numa salina, de cada metro cúbico (m3) de água salgada, são retirados 40 dm3 de sal. Para obtermos 2 m3 de sal, quantos metros cúbicos de água salgada são necessários?
Resolucao
A quantidade de sal retirada é proporcional ao volume de água salgada. Indicamos por x a quantidade de água salgada a ser determinada e armamos a proporção:
Lembre-se que 40dm3 = 0,04m3.
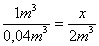Aplicando a propriedade fundamental
1 . 2 = 0,04 . x
0,04x = 2
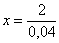x = 50 m3
Logo, são necessários 50 m3 de água salgada.
Quarta proporcional
Dados três números racionais a, b e c, não-nulos, denomina-se quarta proporcional desses números um número x tal que:
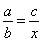Exemplo
Determine a quarta proporcional dos números 8, 12 e 6.
Resolucao
Indicamos por x a quarta proporcional e armamos a proporção:
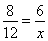
Aplicando a propriedade fundamental
8 . x = 12 . 6
8 . x = 72
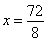
x = 9
Logo, a quarta proporcional é 9.
Proporção contínua
Considere a seguinte proporção:
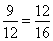Observe que os seus meios são iguais, sendo por isso denominada proporção contínua.
Observacao
Proporção contínua é toda a proporção que apresenta os meios iguais.
De um modo geral, uma proporção contínua pode ser representada por:
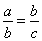Terceira proporcional
Dados dois números naturais a e b, não-nulos, denomina-se terceira proporcional desses números o número x tal que:
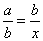Exemplo
Determine a terceira proporcional dos números 20 e 10.
Resolucao
Indicamos por x a terceira proporcional e armamos a proporção:
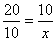Aplicando a propriedade fundamental
20 . x = 10 . 10
20x = 100
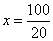x = 5
Logo, a terceira proporcional é 5.
Média geométrica ou média proporcional
Dada uma proporção contínua
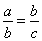O número b é denominado média geométrica ou média proporcional entre a e c.
Exemplo
Determine a média geométrica positiva entre 5 e 20.
Resolucao
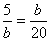5 . 20 = b . b
100 = b2
b2 = 100
b =
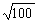b = 10
Logo, a média geométrica positiva é 10.
Propriedades das proporções
1ª propriedade
Em uma proporção, a soma dos dois primeiros termos está para o 2º (ou 1º) termo, assim como a soma dos dois últimos está para o 4º (ou 3º).
Demonstração:
Considere as proporções:
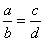e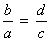 
Adicionando 1 a cada membro da primeira proporção, obtemos:
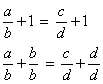
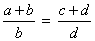
Fazendo o mesmo na segunda proporção, temos:
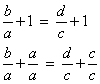
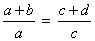
Exemplo
Determine x e y na proporção
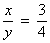Sabendo que x + y = 84.
Resolucao
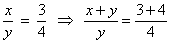Assim:
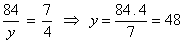x + y = 84
x = 84 – y
x = 84 – 48
x = 36.
Logo, x = 36 e y = 48
2ª propriedade
Em uma proporção, a diferença dos dois primeiros termos está para o 2º (ou 1º) termo, assim como a diferença dos dois últimos está para o 4º (ou 3º).
Demonstração:
Considere as proporções:
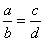e
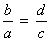Subtraindo 1 a cada membro da primeira proporção, obtemos:
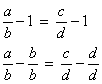
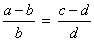Fazendo o mesmo na segunda proporção, temos
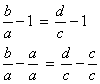
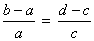(Mult. os 2 membros por -1)
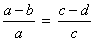Exemplo
Sabendo-se que x – y = 18, determine x e y na proporção
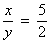Resolucao
Pela 2ª propriedade, temos que:
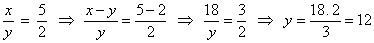x - y = 18
x = 18 + y
x = 18 + 12
x = 30.
Logo, x = 30 e y = 12
3ª propriedade:
Em uma proporção, a soma dos antecedentes está para a soma dos consequentes, assim como cada antecedente está para o seu consequente.
Demonstração:
Considere a proporção:
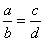Permutando os meios, temos:
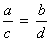Aplicando a 1ª propriedade, obtemos:
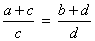Permutando os meios, finalmente obtemos:
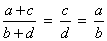4ª propriedade:
Em uma proporção, a diferença dos antecedentes está para a diferença dos consequentes, assim como cada antecedente está para o seu consequente.
Demonstração:
Considere a proporção:
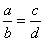Permutando os meios, temos:
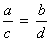Aplicando a 2ª propriedade, obtemos:
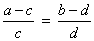Permutando os meios, finalmente obtemos:
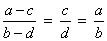Exemplo
Sabendo que a - b = -24, determine a e b na proporção
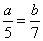Resolucao
Pela 4ª propriedade, temos que
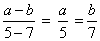
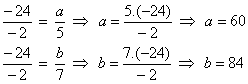5ª propriedade:
Em uma proporção, o produto dos antecedentes está para o produto dos consequentes, assim como o quadrado de cada antecedente está para quadrado do seu consequente.
Demonstração:
Considere a proporção:
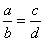Multiplicando os dois membros por
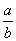Temos:
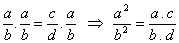Assim:
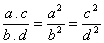Observação: a 5ª propriedade pode ser estendida para qualquer número de razões.
Exemplo
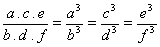Proporção múltipla
Denominamos proporção múltipla uma série de razões iguais.
Assim:
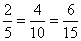E uma proporção múltipla.
Dada a série de razões iguais
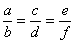De acordo com a 3ª e 4ª propriedade, podemos escrever:
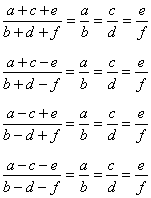
Continua ...
