POLÍGONO

Professor Diminoi

Polígonos

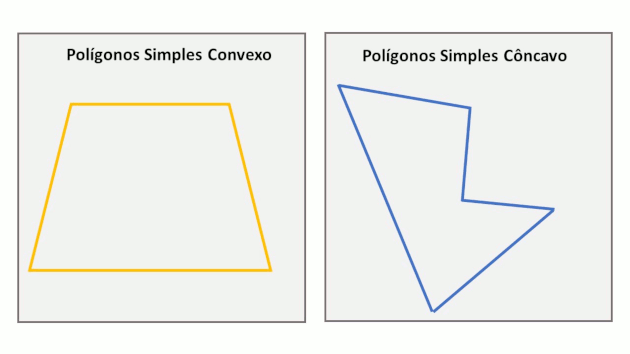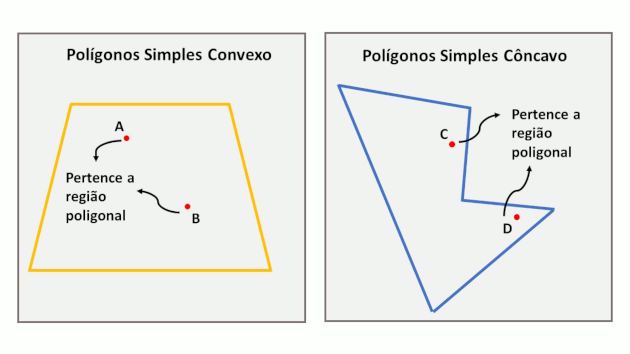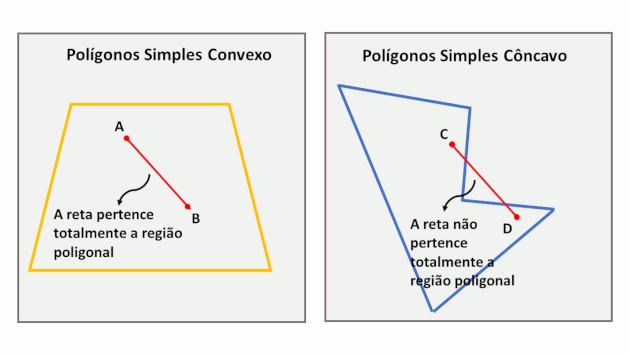
São linhas fechadas formadas apenas por segmentos de reta que não se cruzam e que estão no mesmo plano. Em outras palavras, um polígono é uma figura geométrica limitada por lados. Os polígonos são chamados regulares quando são convexos, possuem todos os lados com a mesma medida e todos os ângulos internos congruentes.

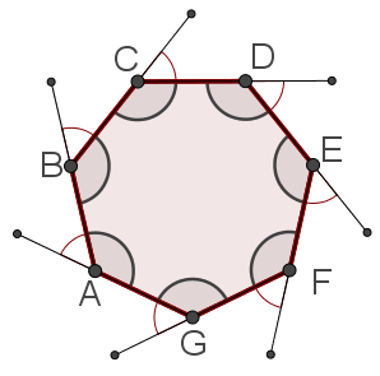
O polígono a seguir é um exemplo de hexágono regular. Observe as medidas de seus lados e ângulos:

Polígonos convexos e regulares

Para serem considerados convexos e regulares, os polígonos devem cumprir alguns pré-requisitos.

Polígono é uma figura geométrica plana formada por diversos elementos. Todavia, apenas um desses elementos é responsável pela definição dessas figuras: o lado.

O lado de um polígono é um segmento de reta qualquer pertencente ao seu contorno. Os triângulos, por exemplo, possuem três lados; os retângulos possuem quatro lados, e os pentágonos possuem cinco lados, exatamente a mesma quantidade de segmentos de reta do contorno desses polígonos.

Os outros elementos presentes nos polígonos são:

Ângulos internos

Ângulos externos

Diagonais

Vértices.

Para ser considerada polígono, uma figura geométrica precisa ser formada por uma linha única, fechada e formada apenas por segmentos de reta. Além disso, esses segmentos de reta não podem cruzar-se.

A figura abaixo apresenta alguns exemplos de polígonos:

Os polígonos A, B e C são formados por 4, 5 e 6 segmentos de reta, respectivamente. Note que esses segmentos, em cada polígono, formam uma linha fechada e não se cruzam de forma alguma. A imagem seguinte apresenta alguns exemplos de figuras geométricas que não são polígonos.

As figuras geométricas A, B e C não são fechadas, portanto, não podem ser consideradas polígonos. Já a figura D possui um cruzamento de segmentos de reta e, por essa razão, também não pode ser considerada polígono.

Polígonos convexos:

Dados dois pontos A e B quaisquer interiores a um polígono, se o segmento de reta determinado por esses dois pontos estiver inteiramente contido no interior do polígono, então esse polígono será convexo.

A figura abaixo apresenta alguns exemplos de polígonos convexos.

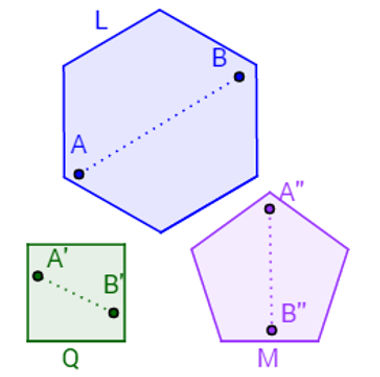
Note que, independentemente da posição dos pontos A e B, A' e B' ou A'' e B'', o segmento determinado por esses pontos sempre estará inteiramente contido no interior de seus respectivos polígonos. Por outro lado, a imagem abaixo representa um polígono não convexo. Isso acontece porque o segmento AB não está totalmente contido no interior do polígono, mesmo que os pontos A e B estejam.

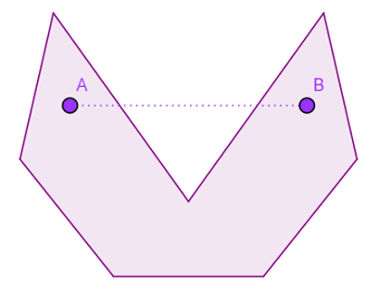
Observação: Os polígonos que têm um vértice voltado para dentro, formando uma espécie de “boca”, não são convexos.

Polígonos Regulares:

Um polígono é considerado regular quando ele é convexo e possui todos os lados e ângulos com a mesma medida.

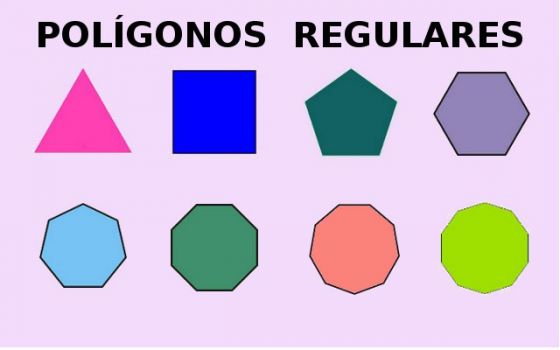
Observação: na imagem abaixo alguns exemplos de polígonos regulares.

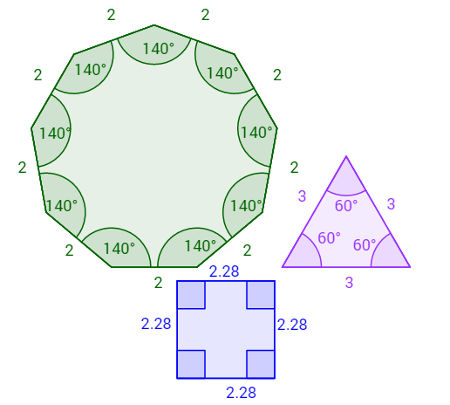
Observação: em cada polígono da imagem acima, todos os lados e ângulos têm a mesma medida. Veja que também que um polígono regular de quatro lados é sempre um quadrado e um polígono regular de três lados é sempre um triângulo equilátero.

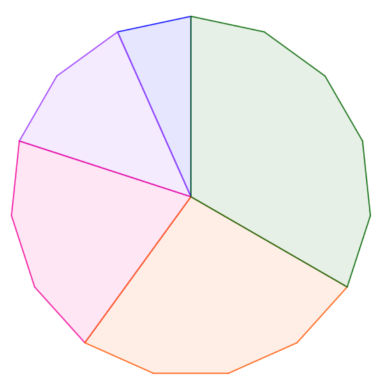
Polígono formado por outros polígonos com número de lados em progressão aritmética

Propriedades dos polígonos regulares

1ª Propriedade

Todo polígono regular possui o mesmo número de vértices, lados, ângulos internos e ângulos externos. Para verificar isso, observe no exemplo a seguir um heptágono regular com sete lados, sete vértices, sete ângulos internos e sete ângulos externos.

2ª Propriedade

A medida de cada ângulo interno de um polígono regular.

a = (n – 2)180
n

Essa fórmula é usada para encontrar a soma das medidas dos ângulos internos de um polígono convexo dividido pelo número de lados que o polígono possui.

Como exemplo, temos que cada ângulo interno de um octógono regular mede 135°, pois:

a = (n – 2)180
n

a = (8 – 2)180
8

a = (6)180
8

a = 1080
8

a = 135°

3ª Propriedade

A medida de cada ângulo externo de um polígono regular é obtida pela seguinte fórmula:

e = 360
n

Nessa fórmula, n é o número de lados do polígono.

Assim, cada ângulo externo de um hexágono regular mede 60°, pois:

e = 360
n

e = 360
6

e = 60°

OBSERVAÇÃO: a somo ao ângulos externos de um polígono qualquer (independente da quantidade de lados) é sempre igual a 360º.

FÓRMULAS

EXERCÍCIOS RESOLVIDOS

01) Qual a soma dos ângulos internos de um icoságono convexo?

Resolução:

Os icoságonos são polígonos que possuem 20 lados. A soma dos ângulos internos é:

S = (n – 2)180

S = (20 – 2)180

S = 18·180

S = 3280°

Qual é a medida de cada ângulo interno de um icoságono regular?

Polígonos regulares possuem ângulos congruentes. Assim, já sabendo que a soma dos ângulos internos do icoságono é 3280°, cada ângulo dele é igual a:

3280 = 162°
20

Resposta: 162º

02) Qual é a soma dos ângulos internos de um heptágono regular?

Resolução:

O heptágono possui 7 lados.
S = (n – 2) * 180º
S = (7 – 2) * 180º
S = 5 * 180º
S = 900º
A soma dos ângulos internos de um heptágono é 900º.

03) Qual a soma dos ângulos internos de um icoságono (20 lados)?

Resolução:

Aplicando a fórmula:
S = (n – 2) * 180º
S = (20 – 2) * 180º
S = 18 * 180º
S = 3240º
A soma dos ângulos internos de um icoságono é 3240º.

Observação: podemos utilizar a fórmula da soma dos ângulos internos para calcular o número de lados de qualquer polígono, desde que a soma dos ângulos internos seja dada.

04) Quantos lados possui um polígono cuja soma dos ângulos internos é igual a 2340º?

Resolução:

S = (n – 2) * 180º
2340º = (n – 2) * 180º
2340º = 180n – 360º
2340 + 360 = 180n
2700 = 180n
180n = 2700
n = 2700/180
n = 15
O polígono possui 15 lados.

Observação: a soma dos ângulos externos de qualquer polígono regular é 360º. Para calcular a medida do ângulo externo de um polígono é preciso dividir 360º pelo número de lados da figura poligonal.

04) Quanto mede o ângulo externo do hexágono?

Resolução:

O hexágono possui seis lados, então:

ai = 360º / 6

ai = 60º

Resposta: cada ângulo externo de um hexágono mede 60º.

05) A respeito das classificações que os polígonos podem sofrer, assinale a alternativa que for correta:

(A) Um polígono é chamado convexo quando, dados os pontos A e B em seu interior, existe um único segmento que liga esses pontos.

(B) Um polígono é chamado não convexo quando, dados os pontos A e B, nem todos os pontos do segmento AB estão no interior do polígono.

(D) Um polígono é chamado regular quando todos os seus lados possuem a mesma medida.

(E) Um polígono convexo não pode ser regular.

Resolução:

a) Incorreta!

No plano, sempre existirá um segmento de reta que ligará dois pontos. Portanto, a afirmativa é inconclusiva. Apenas com essa afirmativa é impossível determinar se um polígono é convexo ou não, pois, para que um polígono seja convexo, é necessário que nenhum dos pontos do segmento AB seja exterior ao polígono, quando os pontos A e B estiverem em seu interior.

b) Correta!

c) Incorreta!

Um polígono é regular quando seus ângulos internos têm a mesma medida e, ao mesmo tempo, seus lados são todos congruentes.

d) Incorreta!

Os ângulos desse polígono precisam ter a mesma medida para que ele seja regular.

e) Incorreta!

Para que um polígono seja regular, ele precisa obrigatoriamente ser convexo.

Alternativa: B

06) Todo polígono é composto por elementos que são outras figuras geométricas e que recebem um nome especial por causa de sua função, definição e propriedades. A respeito desses elementos dos polígonos, assinale a alternativa correta:

(A) Os triângulos não possuem diagonais.

(B) Uma diagonal de um polígono é qualquer segmento de reta que liga dois de seus vértices.

(D) Os quadrados possuem apenas uma diagonal.

(E) Os retângulos e os quadrados possuem um número diferente de diagonais.

Resolução:

a) Correta!

As diagonais são segmentos de reta que ligam dois vértices não consecutivos de um polígono. Não existem vértices que não sejam consecutivos em um triângulo, por isso não existem diagonais nele.

b) Incorreta!

Para ser diagonal, o segmento de reta precisa ligar dois vértices não consecutivos do polígono.

c) Incorreta!

Um ângulo externo é a abertura entre um lado e o prolongamento do lado adjacente a ele. Portanto, não é qualquer ângulo que pode ser considerado um ângulo externo de um polígono.

d) Incorreta!

Os quadrados possuem duas diagonais.e) Incorreta!

Quadrados e retângulos possuem o mesmo número de diagonais.

Alternativa: A

07) Um polígono convexo que possua exatamente 170 diagonais é formado por quantos lados?

(A) 10 lados

(B) 13 lados

(D) 17 lados

(E) 20 lados

Resolução:

Para descobrir o número de lados de um polígono convexo, sabendo-se seu número de diagonais, basta usar a fórmula da soma das diagonais de um polígono convexo. Substituindo nessa fórmula o número de diagonais desse polígono, teremos:

S = n(n – 3)
2

170 = n(n – 3)
2

170·2 = n(n – 3)

340 = n² – 3n

n² – 3n – 340 = 0

Δ = b² – 4·a·c

Δ = (– 3)² – 4·1·(– 340)

Δ = 9 + 1360

Δ = 1369

n = – b ± √Δ
2a

n = – (– 3) ± √1369
2

n = 3 ± 37
2

n’ = 3 + 37 = 40 = 20
2 2

n’’ = 3 – 37 = – 34 = – 17
2 2

Como não pode existir um polígono com – 17 lados, então essa figura tem exatamente 20 lados.

Alternativa: E

08) Qual é a medida de um ângulo interno de um eneágono regular?

(A) 100°

(B) 110°

(D) 140°

(E) 150°

Resolução:

Um eneágono é um polígono que possui nove lados. A medida de cada um dos ângulos internos dessa figura é dada pela seguinte expressão:

A = (n – 2)180
n

A = (9 – 2)180
9

A = (7)180
9

A = 1260
9

A = 140°

Cada ângulo interno de um polígono convexo que possua nove lados mede 140°.

Alternativa: D

09) Os polígonos podem ser classificados como convexos ou não convexos, regulares ou não regulares. A respeito dessa classificação, assinale a alternativa correta:

(A) Um polígono é dito convexo quando possui todos os lados iguais.

(B) Um polígono é dito convexo quando possui todos os ângulos iguais.

(D) Um polígono é convexo quando qualquer segmento de reta, que possui extremidades em seu interior, não possui pontos fora dele.

(E) Um polígono é dito regular quando um segmento de reta, que possui extremidades em seu interior, possui pontos fora dele.

Resolução:

Um polígono é dito convexo quando não existe nenhum segmento de reta com extremidades em seu interior com pontos fora dele. Um polígono é dito regular quando seus lados são congruentes e todos os seus ângulos internos têm a mesma medida. Assim, as alternativas a, b, c e e estão incorretas.

Alternativa: D

10) Considerando os elementos dos polígonos convexos e suas definições básicas, assinale a alternativa correta:

(A) Os lados de um polígono são segmentos de reta que podem cruzar-se em qualquer ponto.

(B) O vértice de um polígono é o ponto de encontro entre seus dois maiores lados.

(C) Os ângulos externos de um polígono são a abertura entre dois lados consecutivos, só que pelo lado externo do polígono.

(D) Os ângulos internos do polígono são a abertura entre dois lados consecutivos do polígono, em seu interior.

(E) As diagonais de um polígono são segmentos de reta que ligam dois de seus vértices.

Resolução:

a) Incorreta!

Os lados de um polígono são segmentos de reta que não se cruzam. Esses elementos encontram-se apenas em suas extremidades.

b) Incorreta!

Os vértices de um polígono são todos os pontos de encontro entre seus lados.

c) Incorreta!

Os ângulos externos de um polígono são a abertura entre um lado e o prolongamento do lado adjacente.

d) Correta!

e) Incorreta!

As diagonais de um polígono são segmentos de reta que ligam dois de seus vértices, com a condição de que esses vértices não sejam consecutivos. O segmento de reta que liga dois vértices consecutivos de um polígono é o lado.

Alternativa D

11) A soma dos ângulos internos de um polígono convexo é igual a 2340°. Quantos lados esse polígono possui?

(A) 13 lados

(B) 15 lados

(D) 19 lados

(E) 21 lados

Resolução:

Para fazer esse cálculo, basta usar a fórmula:

S = (n – 2)180

Em que S é a soma dos ângulos internos do polígono e n é seu número de lados. Substituindo 2340° nessa fórmula, teremos:

2340 = (n – 2)180

2340 = n – 2
180

13 = n – 2

n = 13 + 2

n = 15

O polígono possui 15 lados.

Alternativa B

12) Um polígono convexo possui 25 lados. Qual é o número total de diagonais que esse polígono possui?

(A) 200

(B) 225

() 260

(E) 275

Resolução:

Para encontrar o número de diagonais de um polígono convexo, basta usar a fórmula:

d = n(n – 3)
2

Na qual n é o número de lados do polígono. Substituindo n por 25, teremos:

d = n(n – 3)
2

d = 25(25 – 3)
2

d = 25(22)
2

d = 25·11

d = 275

Alternativa E

13) Calcule a soma dos ângulos internos de um triângulo qualquer e de um retângulo qualquer.

Resolução:

Independentemente do polígono a que o exercício ou situação se refira, a soma dos seus ângulos internos tem valor fixo e é dada pela fórmula S = (n – 2)·180, em que n é o número de lados do polígono. Logo,

Soma dos ângulos internos do triângulo:

S = (3 – 2)·180

S = 1·180

S = 180°

Qualquer que seja o triângulo, a soma de seus ângulos internos sempre será igual a 180°. Isso pode ser usado quando conhecemos as medidas de dois dos ângulos internos de um triângulo e é necessário calcular o valor da última.

Soma dos ângulos internos de um retângulo:

S = (4 – 2)·180

S = 2·180

S = 360°

Não só retângulos, mas qualquer que seja o quadrilátero, a soma de seus ângulos internos será 360°.

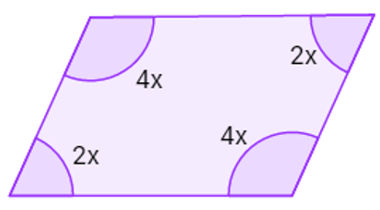
14) Calcule o valor de cada ângulo do quadrilátero seguinte:

Resolução:

A soma dos ângulos internos de um quadrilátero é dada por:

S = (n – 2)·180

Sabendo que o número de lados da figura é 4, basta substituir n por 4:

S = (4 – 2)·180

S = 2·180

S = 360°

Agora some os ângulos internos dessa figura e iguale o resultado a 360°:

2x + 4x + 2x + 4x = 360

12x = 360

x = 360
12

x = 30

Agora basta substituir x em cada ângulo para descobrir os seus valores.

4x = 4·30 = 120° e

2x = 2·30 = 60°

Os ângulos são 120° e 60°.

15) (UNIFESP - 2003) Pentágonos regulares congruentes podem ser conectados lado a lado, formando uma estrela de cinco pontas, conforme destacado na figura a seguir

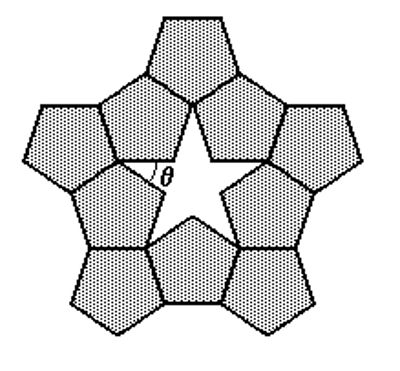
Nessas condições, o ângulo θ mede:

(A) 108°.

(B) 72°.

(D) 36°.

(E) 18°.

Resolução:

Na ponta da estrela onde está destacado o ângulo θ, temos o encontro de três ângulos internos de pentágonos regulares. Para descobrir a medida de cada um desses ângulos, basta calcular a soma dos ângulos internos do pentágono e dividir por 5.

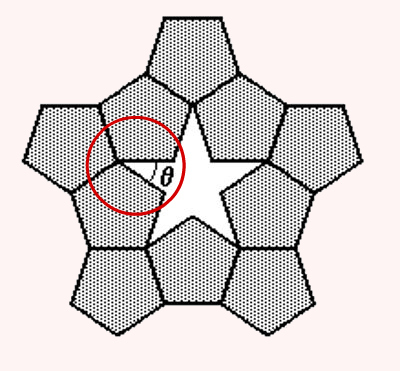
A fórmula para calcular a soma dos ângulos internos de um polígono é:

S = (n – 2)·180

*n é o número de lados do polígono. No caso desse exercício:

S = (5 – 2)·180

S = 3·180

S = 540

Dividindo a soma dos ângulos internos por 5, pois um pentágono possui cinco ângulos internos, encontraremos 108° como medida de cada ângulo interno.

Observe na imagem anterior que a soma de três ângulos internos do pentágono com o ângulo θ tem como resultado 360°.

108 + 108 + 108 + θ = 360

324 + θ = 360

θ = 360 – 324

θ = 36°

Alternativa: D

16) (FAAP-97) A medida mais próxima de cada ângulo externo do heptágono regular da moeda de R$ 0,25 é:

(A) 60°

(B) 45°

(D) 83°

(E) 51°

Resolução:

Heptágonos são figuras geométricas que possuem sete lados, sete vértices e sete ângulos. Como esse heptágono é regular, então todos os seus ângulos e lados possuem a mesma medida.

A soma dos ângulos internos do heptágono é:

S = (n – 2)·180

S = (7 – 2)·180

S = 5·180

S = 900°

Cada ângulo interno do heptágono regular mede a soma dos ângulos internos dividida por 7.

900 = 128,57
7

Agora, resta apenas descobrir o valor de um ângulo externo. Os ângulos externos de um polígono são suplementares aos ângulos internos respectivos. Portanto, a soma entre um ângulo interno e seu ângulo externo tem como resultado 180°. Dessa forma, os ângulos externos da moeda de 25 centavos medem:

128,57 + x = 180

x = 180 – 128,57

x = 51,43°

Alternativa: E

Continua...