FUNÇÃO E.FUNDAMENATL - II

Professor Diminoi

ENSINO FUNDAMENTAL II

Função
Uma função é uma regra que relaciona cada elemento de um conjunto a um único elemento de outro.
Função inversa: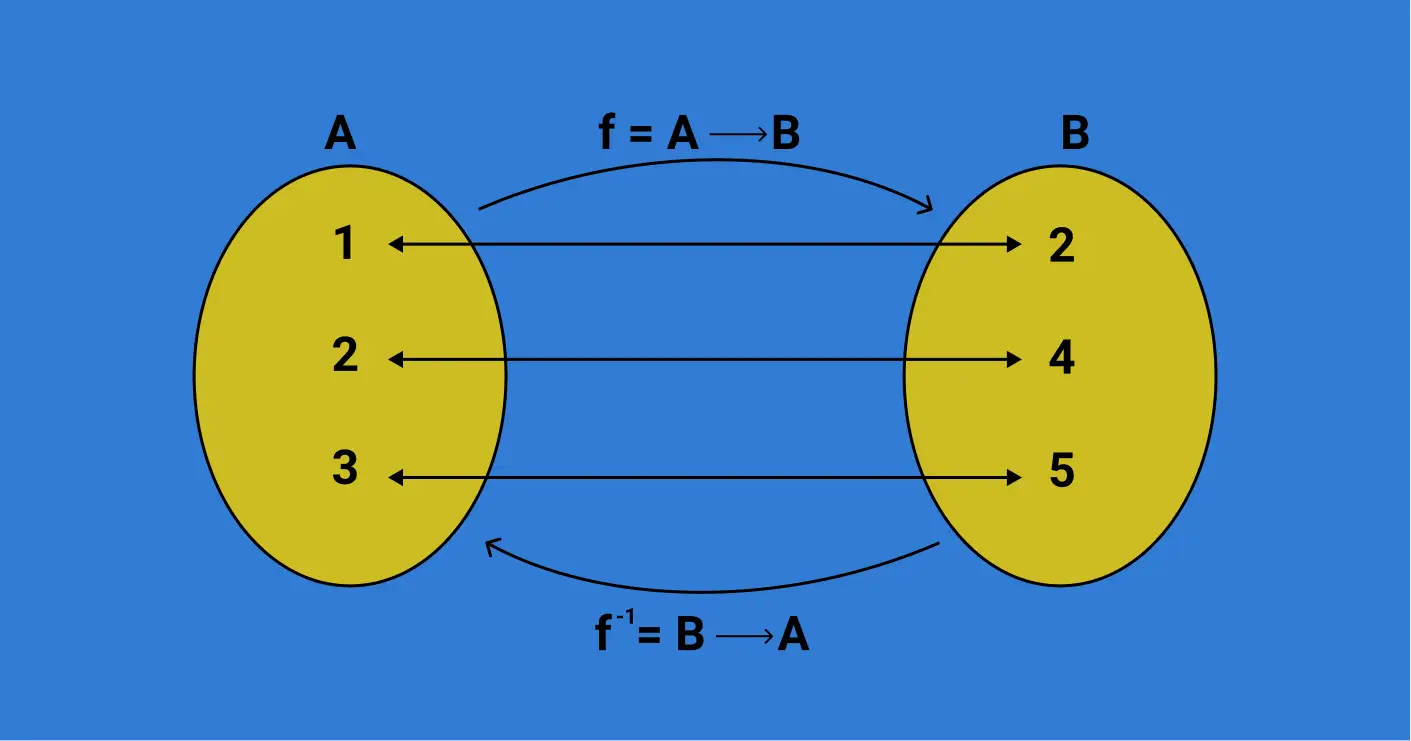
As formulações matemáticas que envolvem equações podem ser estruturadas por meio de funções

A função determina uma relação entre os elementos de dois conjuntos. Podemos defini-la utilizando uma lei de formação, em que, para cada valor de x, temos um valor de f(x). Chamamos x de domínio e f(x) ou y de imagem da função.

Observe o exemplo abaixo:
Seja X um conjunto com elementos de x e Y um conjunto dos elementos de y, temos que:
f: x → y
Domínio (D), Contradomínio e Imagem (Im)
O primeiro conjunto é chamado de domínio, e o segundo, contradomínio da função.

Exemplo 1: 
Exempo 2:

TIPOS DE FUNÇÃO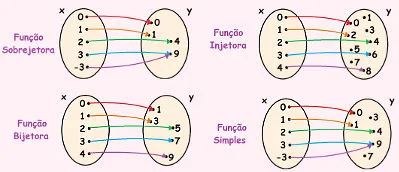

1 - Função INJETOTA ou INJETIVA
Uma função f: A → B é injetora ou injetiva se, e somente se, os elementos distintos em A possuem elementos distintos em B.

Como podemos ver pelo diagrama de flechas que todo elemento de B possui somente uma flecha apontada para ele.
Diminuo, Contradomínio e Imagem de uma Função:
- O conjunto A é o domínio;
- O conjunto B é o contradomínio;
- Os elementos de B, que estão relacionados a elementos em A é chamado imagem da função.

Exemplo: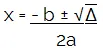
Analisando a figura, podemos definir o seguinte:
O conjunto A é o domínio;
O conjunto B é o contradomínio;

Os elementos de B, que estão relacionados a elementos em A é chamado imagem da função.

- Conjunto dos elementos do domínio da função: D(f) = {-1,5, +2, +8}

- Conjunto dos elementos da imagem da função: Im(f) = {A, C, D}

- Conjunto dos elementos do contradomínio da função: CD(f) = {A, B, C, D}

2 - Função SOBREJETORA ou SOBREJETIVA
Temos que f : A → B é sobrejetora ou sobrejetiva se, e somente se, todo elemento de B é imagem de pelo menos um elemento de A.
Pelo diagrama de flechas vemos que todos os elementos de B é atingido por pelo menos uma flecha de pelo menos um elemento de A.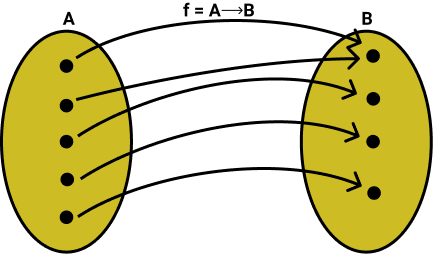
Exemplo:
Analisando a figura, podemos definir o seguinte: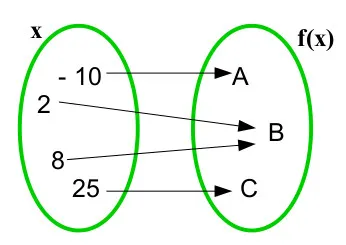
O conjunto A é o domínio;
O conjunto B é o contradomínio;
Os elementos de B, que estão relacionados a elementos em A é chamado imagem da função.

- Conjunto dos elementos do domínio da função: D(f) = {-10, 2, 8, 25}

- Conjunto dos elementos da imagem da função: Im (f) = {A, B, C}

- Conjunto dos elementos do contradomínio da função: CD (f) = {A, B, C}

3 - Função BIJETORA ou BIJETIVA
Uma função f : A → B é bijetora ou bijetiva se, e somente se, ela for injetora e sobrejetora. Isto é, todos os elementos de B é imagem de apenas um elemento de A.
Como vemos no diagrama de flechas que todos os elementos de B é imagem de apenas um elemento de A, assim sendo injetora e sobrejetora e, portanto, é bijetora.

Exemplo: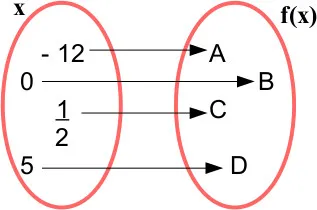

Analisando a figura, podemos definir o seguinte:
O conjunto A é o domínio;
O conjunto B é o contradomínio;

Os elementos de B, que estão relacionados a elementos em A é chamado imagem da função.
- Conjunto dos elementos do domínio da função: D(f) = {-12, 0, 1/2, 5}
- Conjunto dos elementos da imagem da função: Im (f) = {A, B, C, D}
- Conjunto dos elementos do contradomínio da função: CD (f) = {A, B, C, D}

4 - Função COMPOSTA
Sejam os conjuntos A, B e C, e duas funções f : A → B e g : B → C, chamamos de composta uma função h = gof: A → C, definida por R = gof(x) = g(f(x)).
QUESTÕES RESOLIVIDAS
01) Observe a função abaixo
Encontre o Domínio, a imagem e o contradomínio da função
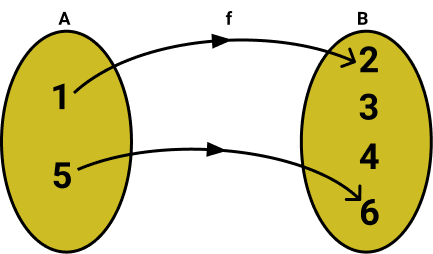 Resolução:
Diminuo e Imagem de uma Função:
- O conjunto A é o domínio;
- Os elementos de B, que estão relacionados a elementos em A é chamado imagem da função.
D = {1,5}
Im = [2, 6}

02) Considere o seguinte gráfico de uma função qualquer:
Pelo gráfico acima, podemos afirmar que a função possui um domínio limitado no intervalo [1, 3], para valores no eixo x (eixo das abcissas). Os valores do intervalo [1, 4], no eixo y (eixo das ordenadas), é a imagem da função. Sendo assim encontre o Domínio e a Imagem da função.
Resolução:
Domínio: D = [1, 3]
Imagem: Im = [1, 4]

04) Observando o esquema das flechas encontre o Domínio D e a Imagem Im.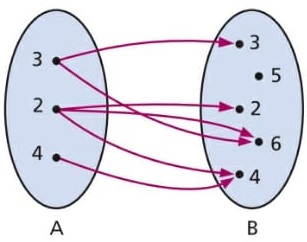
Resolução:
R = {(2, 2), (2, 4) (2, 6), (3, 3), (3, 6), (4, 4)}
D = {2, 3, 4}
Im = {2, 3, 4, 6}

05) Dada a função (fx) = 3x −5, encontre o valor de f(3).
Resolução:
Substituímos o 3 em vez do x na função:
f(3) =3x −5
f(3) =3(3) −5
f(3) = 9 −5
f(3) = 4
Esta resposta pode ser considerada como o par ordenado (3, 4).

06) Observando o esquema das flechas encontre o Domínio D e a Imagem Im.
Resolução:
O domínio D é igual ao conjunto A e o conjunto imagem Im é subconjunto do contradomínio B.
D = A = {1, 5}
Im = {2, 6}

As funções podem ser representadas graficamente.
Para que isso seja feito, utilizamos duas coordenadas, que são x e y.
O plano desenhado é bidimensional. A coordenada x é chamada de abscissa e a y, de ordenada. Juntas em funções, elas formam leis de formação.

Observe o gráfico do eixo x e y:
Do último ano do Fundamental e ao longo do Ensino Médio, geralmente estudamos doze funções, que são:
1 – Função constante;
2 – Função par;
3 – Função ímpar;
4 – Função afim ou polinomial do primeiro grau;
5 – Função Linear;
6 – Função crescente;
7 – Função decrescente;
8 – Função quadrática ou polinomial do segundo grau;
9 – Função modular;
10 – Função exponencial;
11 – Função logarítmica;
12 – Funções trigonométricas;
13 – Função raiz.

5 - Função CONTANTE
Na função constante, todo valor do domínio (x) tem a mesma imagem (y).

Fórmula geral da função constante:
f(x) = c
x = Domínio
f(x) = Imagem
c = constante, que pode ser qualquer número do conjunto doa reais.

Gráfico da função constante: f(x) = 2

6 - Função PAR
A função par é simétrica em relação ao eixo vertical, ou seja, à ordenada y. Entenda simetria como sendo uma figura/gráfico que, ao dividi-la em partes iguais e sobrepô-las, as partes coincidem-se perfeitamente.

Fórmula geral da função par:
f(x) = f(- x)
x = domínio
f(x) = imagem
- x = simétrico do domínio

Gráfico da função par: f(x) = x²
7 - Função ÍMPAR
A função ímpar é simétrica (figura/gráfico que, ao dividi-la em partes iguais e sobrepô-las, as partes coincidem-se perfeitamente) em relação ao eixo horizontal, ou seja, à abscissa x.

Fórmula GERALDA FUNÇÃO ÍMPAR
f(– x) = – f(x)
– x = domínio
f(– x) = imagem
- f(x) = simétrico da imagem

Gráfico da função ímpar: f(x) = 3x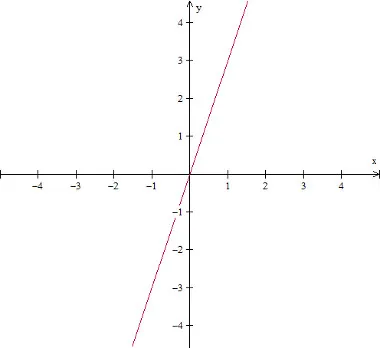

8 - Função AFIM ou POLINOMINAL DO 1º GRAU
Para saber se uma função é polinomial do primeiro grau, devemos observar o maior grau da variável x (termo desconhecido), que sempre deve ser igual a 1. Nessa função, o gráfico é uma reta. Além disso, ela possui: domínio x, imagem f(x) e coeficientes a e b.

Fórmula geral da função afim ou polinomial do primeiro grau
f(x) = ax + b
x = domínio
f(x) = imagem
a = coeficiente
b = coeficiente

Gráfico da função polinomial do primeiro grau: f(x) = 4x + 1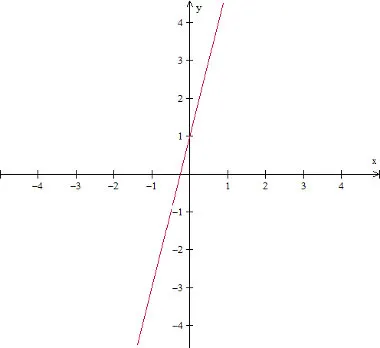

9 - Função LINEAR
A função linear tem sua origem na função do primeiro grau (f(x) = ax + b). Trata-se de um caso particular, pois b sempre será igual a zero.

Fórmula GERAL DA FUNÇÃO LINEAR
f(x) = ax
x = domínio
f(x) = imagem
a = coeficiente

Gráfico da função linear: f(x) = -x/3

10 - Função CRESCENTE
A função polinomial do primeiro grau será crescente quando o coeficiente a for diferente de zero e maior que um (a > 1).

Fórmula geral da função crescente
f(x) = + ax + b
x = domínio
f(x) = imagem
a = coeficiente sempre positivo
b = coeficiente

Gráfico da função crescente: f(x) = 5x

11 - Função DECRESENTE
Na função decrescente, o coeficiente a da função do primeiro grau (f(x) = ax + b) é sempre negativo.

Fórmula geral da função decrescente
f(x) = - ax + b
x = domínio/ incógnita
f(x) = imagem
- a = coeficiente sempre negativo
b = coeficiente

Gráfico da função decrescente: f(x) = - 5x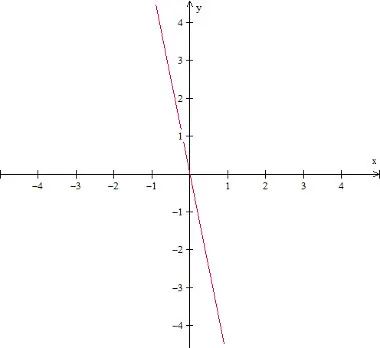

Com os valores de x e y formamos as coordenadas, que são pares ordenados que colocamos no plano cartesiano para formar a reta.

Observe: No eixo vertical colocamos os valores de y e no eixo horizontal colocamos os valores de x.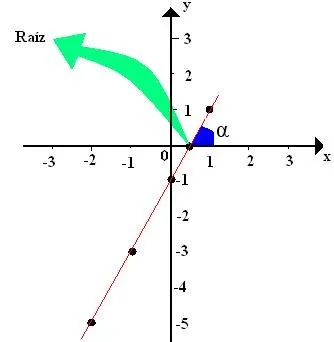

"Quando a < 0
Isso indica que a será negativo. Por exemplo, dada a função f(x) = - x + 1 ou y = - x + 1, onde a = -1 e b = 1.
Para construirmos seu gráfico devemos atribuir valores reais para x, para que possamos achar os valores correspondentes em y.
 x         y
-2        3
-1        2
0        1
 1       0
"Podemos observar que conforme o valor de x aumenta o valor de y diminui, então dizemos que quando a < 0 a função é decrescente.
Com os valores de x e y formamos as coordenadas que são pares ordenados que colocamos no plano cartesiano para formar a reta.

Observe: No eixo vertical colocamos os valores de y e no eixo horizontal colocamos os valores de x."
Características de um gráfico de uma função do 1º grau
• Com a > 0 o gráfico será crescente.
• Com a < 0 o gráfico será decrescente.
• O ângulo α formado com a reta e com o eixo x será agudo (menor que 90°) quando a > 0.
• O ângulo α formado com reta e com o eixo x será obtuso (maior que 90º) quando a < 0.
• Na construção de um gráfico de uma função do 1º grau basta indicar apenas dois valores pra x, pois o gráfico é uma reta e uma reta é formada por, no mínimo, 2 pontos.
• Apenas um ponto corta o eixo x, e esse ponto é a raiz da função.
• Apenas um ponto corta o eixo y, esse ponto é o valor de b."

QUESTÓES COMENTADAS
07) Uma empresa de telefonia oferece dois tipos de planos:
- Plano Plus: 3,5 GB de internet, mais ligações ilimitadas para telefones fixos e celulares.
- Plano Econômico: 3,5 GB de internet, mais 50 min de ligações para telefones fixos e celulares.
O plano Plus custa por mês R$ 65,90, já o plano Econômico custa R$ 10,80, sendo que é cobrado R$ 1,90 por minuto quando o cliente exceder os 50 min incluídos no plano.
Considerando esses dois planos, usando quantos minutos de ligações por mês, o plano Plus passa a ser mais econômico?
(A) 30 min
(B) 50 min
(C) 60 min
(D) 70 min
(E) 80 min
Resolução:
O custo mensal do plano Econômico, quando o cliente excede os minutos incluídos no plano, pode ser indicado pela função f(x), sendo x os minutos excedentes. Assim, a função será:
f(x) = 10,8 + 1,9x
Então, para sabermos a partir de quantos minutos mensais vale adquirir o plano Plus, vamos igualar essa função ao valor deste plano:
10,8 + 1,9x = 65,9
1,9x = 65,9 – 10,8
1,9x = 55,1
x = 55,1 / 1,9
x = 29
Como é dado uma franquia de 50 min, então para quem gasta por mês 79 min (50+29) os dois planos possuem o mesmo valor. Portanto, usando 80 min, o plano Plus passa a ser mais econômico.
Alternativa: E

08) Um atleta ao ser submetido a um determinado treino específico apresenta, ao longo do tempo, ganho de massa muscular. A função P(t) = P₀ + 0,19 t, expressa o peso do atleta em função do tempo ao realizar esse treinamento, sendo P₀ o seu peso inicial e t o tempo em dias.
Considere um atleta que antes do treinamento apresentava 55 kg e que necessita chegar ao peso de 60 kg, em um mês. Fazendo unicamente esse treinamento, será possível alcançar o resultado esperado?
Resolução:
Resposta correta: Sim.
Substituindo o tempo indicado na função, podemos encontrar o peso do atleta ao final de um mês de treinamento e comparar com o peso que se deseja alcançar.
Vamos então substituir na função o peso inicial (P₀) por 55 e o tempo por 30, pois seu valor deve ser dado em dias:
P(30) = 55 + 0,19.30
P(30) = 55 + 0,19.30
P(30) = 55 + 5,7
P(30) = 60,7
Assim, o atleta terá ao final de 30 dias, 60,7 kg. Portanto, usando o treinamento será possível sim atingir a meta.

09) (UFSM) Sabe-se que o preço a ser pago por uma corrida de táxi inclui uma parcela fixa, que é denominada bandeirada, e uma parcela variável, que é função da distância percorrida. Se o preço da bandeirada é de R$ 4,60 e o quilômetro rodado é R$ 0,96, a distância percorrida pelo passageiro que pagou R$ 19 para ir de sua casa ao shopping é de:
(A) 5 km
(B) 10 km
(C) 15 km
(D) 20 km
(E) 25 km
Resolução:
Seja d a distância percorrida em quilômetros, sabemos que:
19 = 0,96d + 4,6
Isolando a incógnita, temos que:
19 – 4,6 = 0,96d
14,4 = 0,96d
d = 14,4 : 0,96
d = 15
Alternativa: C

10) Um fazendeiro resolveu investir em uma colheitadeira para facilitar o serviço na plantação. Sabendo que o valor pago foi de R$ 300.000 no ano da compra, é bastante comum que máquinas desse porte percam o seu valor V ao decorrer dos anos t. Supondo que a taxa de depreciação de uma máquina desse porte é de R$ 22.000 por ano, devido ao seu constante uso, podemos afirmar que o valor da colheitadeira, ao final de 7 anos, será de:
(A) R$ 154.000
(B) R$ 246.000
(C) R$ 146.000
(D) R$ 174.000
(E) R$ 210.000
Resolução:
A função que descreve o valor em função do tempo possui a lei de formação:
V(t) = -22.000t + 300.000
Como o tempo foi de 7 anos, então faremos t = 7.
V(7) = -22.000 · 7 + 300.000
V(7) = -154.000 + 300.000
V(7) = 146.000
Alternativa: C

11) Podemos afirmar que o zero da função f(x) = -2x + 5 é igual a:(A) 2
(B) 2,5
(C) -2,5
(D) -3
(E) 3
Resolução:
Para encontrar o zero da função, vamos igualar a função a zero e resolver a equação, então, temos que:
-2x + 5 = 0
-2x = -5
x = (-5) : (-2)
x = 2,5
Alternativa: B

12) (Encceja 2018) Uma prestadora de serviços cobra pela visita à residência do cliente e pelo tempo necessário para realizar o serviço na residência.
O valor da visita é R$ 40 e o valor da hora para realização do serviço é R$ 20.
Uma expressão que indica o valor a ser pago (P) em função das horas (h) necessárias à execução do serviço é:
(A) P = 40h
(B) P = 60h
(C) P = 20 + 40h
(D) P = 40 + 20h

Resolução:
A função é descrita por P = ah + b, em que b é a taxa fixa, que, no caso, é o valor da visita, que é R$ 40. Já o coeficiente a é a taxa que depende do número de horas, no caso, R$ 20. Substituindo, temos que:
P = 20h + 40
P = 40 + 20h
Alternativa: D

13) Uma determinada espécie de pimenta, ao atingir 20 centímetros de altura, começa a crescer de forma linear. A cada dia que se passa, essa planta aumenta 2,5 centímetros. Assim, é possível descrever essa situação como uma função do 1º grau, em que a altura h(d) está em função dos dias, cuja lei de formação é:
(A) h(d) = 2,5d
(B) h(d) = 2,5d + 20
(C) h(d) = 20d + 2,5
(D) h(d) = 20d
(E) h(d) = 2,5d – 20
Resolução:
Seja h(d) = ad + b uma função afim, sabemos que b é a taxa fixa, no caso, 20 cm, e que, além disso, a cada dia, ela aumenta 2,5 cm, ou seja, 2,5 d. Dessa forma, a lei de formação que melhor descreve essa situação é:
h(d) = 2,5d + 20
Alternativa: B

14) (Enem 2016) Uma cisterna de 6 000 L foi esvaziada em um período de 3 h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada com a primeira.
O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.
Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?
(A) 1 000
(B) 1 250
(C) 1 500
(D) 2 000
(E) 2 500
Resolução:
No primeiro momento até a primeira hora, o volume vai de 6000 litros para 5000 litros, ou seja, ocorre uma diferença de 1000 litros, logo, a vazão da primeira bomba é de 1000 L/h. Agora, após ligar a segunda bomba, note que ela foi inteiramente esvaziada, ou seja, nas outras 2 horas, foi possível retirar 5000 L. Realizando a divisão 5000 : 2 = 2500, a soma das vazões das bombas foi de 2500 L/h.
Sabemos que a primeira bomba tem vazão de 1000 L/h, então, para descobrir a vazão da segunda, temos que: 2500 – 1000 = 1500 L.
Alternativa: C

15) Classifique cada uma das funções seguintes em crescente ou decrescente:
 a) y = 4x + 6
 b) f(x) = – x + 10
 c) y = (x + 2)²– (x – 1)²
Resolução:
Em uma função do tipo y = ax + b, o coeficiente a de x indica se a função é crescente ou decrescente.

a) y = 4x + 6
Nessa função, a = 4 > 0, portanto, y é uma função crescente.

b) f(x) = – x + 10
Como a = – 1 < 0, f(x) é uma função decrescente.

c) y = (x + 2)²– (x – 1)²
Nesse caso precisamos desenvolver os parênteses através dos produtos notáveis.
x² + 4x + 4 – (x – 1)²
x² + 4x + 4 – (x² – 2x + 1)
x² + 4x + 4 – x² + 2x – 1
6x + 3
y = 6x + 3. Como a = 6 > 0, y é uma função crescente.
 
O que é uma função do 2º grau?
Uma função polinomial é conhecida como função do 2º grau, ou também como função quadrática, quando em sua lei de formação ela possui um polinômio de grau dois, ou seja, f(x) = ax² + bx + c, em que a, b e c são números reais, e a ≠ 0.
Além da lei de formação, essa função possui domínio e contradomínio no conjunto dos números reais, ou seja, f: R→ R.
O gráfico da função do 2º grau é sempre uma parábola.
Exemplos:
a) f(x) = 2x² + 3x + 1
a = 2
b = 3
c=1

b) g(x) = -x² + 4
a = -1
b = 0
c = 4

c) h(x) = x² – x
a = 1
b = -1
c = 0

Valor numérico de uma função
Para encontrar o valor numérico de qualquer função, conhecendo a sua lei de formação, basta realizarmos a substituição do valor de x para encontrar a imagem f(x).

Exemplos:
Dada a função f(x) = x² + 2x – 3, calcule:

a)f(0)
f(0) = 0² + 2 . 0 – 3 = 0 + 0 – 3 = –3

b)f(1)
f(1) = 1² + 2·1 + 3  = 1+2 – 3 = 0

c)f(2)
f(2) = 2² + 2 . 2 + 3 = 4 + 4 –3 = 5

d)f(-2)
f(-2) = (-2)² + 2 . (-2) – 3
f(-2) = 4  - 4 – 3 = –3

 
Raízes da função de 2º grau
Para encontrar as raízes da função quadrática, conhecidas também como zero da função, é necessário o domínio das equação do 2º grau. Para resolver uma equação do segundo grau, há vários métodos, como a fórmula de Bhaskara e a soma e produto.
A raízes de uma função quadrática são os valores de x que fazem com que f(x) = 0. Sendo assim, para encontrar as raízes de uma equação do 2º grau, faremos ax² + bx + c = 0.

Exemplo:
f(x) = x² +2x – 3
a = 1
b = 2
c = –3
Δ = b² – 4ac
Δ = 2² – 4 ·1·(-3)
Δ = 4 +12
Δ = 16
 
Então, os zeros da função são {1, -3}.

O valor do delta nos permite saber quantos zeros a função quadrática vai ter. Podemos separar em três casos:
Δ > 0 → a função possui duas raízes reais distintas;
Δ = 0 → a função possui uma única raiz real;
Δ < 0 → a função não possui raiz real.

Gráfico de uma função do 2º grau
O gráfico de uma função do 2º grau é representado sempre por uma parábola.
Existem duas possibilidades, dependendo do valor do coeficiente “a”: a concavidade da parábola pode ser para cima ou para baixo.

Observação: Se a > 0, a concavidade é para cima:
O ponto V representa o que conhecemos como vértice da parábola, que, nesse caso, é o ponto de mínimo, ou seja, o menor valor que f(x) pode assumir.

Observação: Se a < 0, a concavidade é para baixo: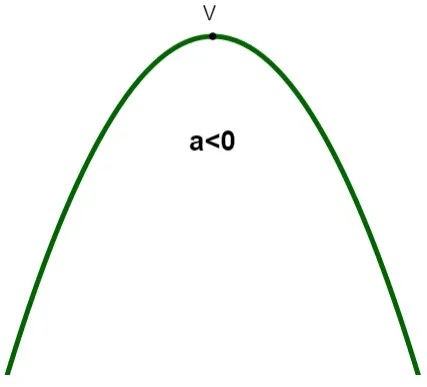
Quando isso ocorre, perceba que, nesse caso, o vértice é o ponto de máximo da função, ou seja, maior valor que f(x) pode assumir.
Para fazer o esboço do gráfico, precisamos encontrar:
- os zeros da função;
- o ponto em que a função intercepta o eixo y;
- o ponto de máximo ou de mínimo da parábola, que conhecemos como vértice da parábola. 

Vértice da parábola
Como vimos anteriormente, o vértice da parábola é o ponto de mínimo ou de máximo do gráfico. Para encontrar o valor de x e y no vértice, utilizamos uma fórmula específica. Vale ressaltar que o vértice é um ponto V, logo ele possui coordenadas, representadas por x_v e y_v.
Para calcular o valor de V (x_v, y_v), utilizamos as fórmulas:

Exemplo:
Encontre o vértice da parábola f(x) = –x² +4x – 3.
a = -1.
b = 4.
c = -3
Calculando o Δ e aplicando a fórmula de Bhaskara, temos que:
Δ = b² – 4ac
Δ = 4² – 4(-1) . (-3)
Δ = 16 – 12
Δ = 4

Representação gráfica de uma função do 2º grau
Para realizar o esboço do gráfico de uma função, é necessário encontrar três elementos: os zeros ou raízes da função, o vértice e o ponto em que a função toca o eixo y, conforme o exemplo a seguir.

 

Exemplo:
f(x) = x² – 6x + 8
1º passo: As raízes da função são os pontos em que a parábola toca o eixo x, logo queremos encontrar os pontos (x’, 0) e (x”,0).
Para isso faremos f(x) = 0, então temos que:
x² – 6x + 8 = 0
a = 1
b = -6
c = 8
Δ = b² -4ac
Δ = (-6)² -4 .1 .8
Δ = 36 – 32
Δ = 4

Já temos dois pontos para o gráfico, o ponto A(4,0) e o ponto B (2,0).

2º passo: encontrar o vértice da parábola.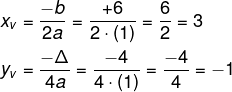

Então o vértice da parábola é o ponto V(3, -1).

3º passo: encontrar o ponto de intersecção da parábola com o eixo y.
Para isso, basta calcular f(0):
f(x) =x² – 6x + 8
f(0) = 0² -6·0 + 8
f(0) = 8
Por fim, o ponto C (0,8) pertence ao gráfico.

4º passo: Agora que temos os pontos, vamos marcá-los no plano cartesiano e fazer o esboço do gráfico da parábola.
A(4,0)
B(2,0)
V(3,-1)
C(0,8)



12 - Função QUADRÁTICA ou POLINOMINAL do 2º GRAU
Identificamos que uma função é do segundo grau quando o maior expoente que acompanha a variável x (termo desconhecido) é 2. O gráfico da função polinomial do segundo grau sempre será uma parábola. A sua concavidade muda de acordo com o valor do coeficiente a. Sendo assim, se a é positivo, a concavidade é para cima e, se for negativo, é para baixo.

Fórmula geral da função quadrática ou polinomial do segundo grau
f(x) = ax² + bx + c
x = domínio
f(x) = imagem
a = coeficiente que determina a concavidade da parábola.
b = coeficiente.
c = coeficiente.

Gráfico da função polinomial do segundo grau: f(x) = x² – 6x + 5

13 - Função MODULAR
A  função modular apresenta o módulo, que é considerado o valor absoluto de um número e é caracterizado por (| |). Como o módulo sempre é positivo, esse valor pode ser obtido tanto negativo quanto positivo.

Exemplo:
|x| = + x ou |x| = - x

Fórmula geral da função modular
f(x) = x, se x≥ 0
ou
f(x) = – x, se x < 0
x = domínio
f(x) = imagem
- x = simétrico do domínio

Gráfico da função modular: f(x) =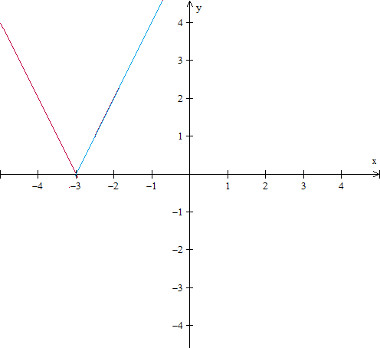

14 - Função EXPONENCIAL
Uma função será considerada exponencial quando a variável x estiver no expoente em relação à base de um termo numérico ou algébrico. Caso esse termo seja maior que 1, o gráfico da função exponencial é crescente.

Mas se o termo for um número entre 0 e 1, o gráfico da função exponencial é decrescente.

Fórmula geral da função exponencial
f(x) = a^x
a > 1 ou 0 < a < 1
x = domínio
f(x) = imagem
a = Termo numérico ou algébrico

Gráfico da função exponencial crescente: f(x) = (2)^x, para a = 2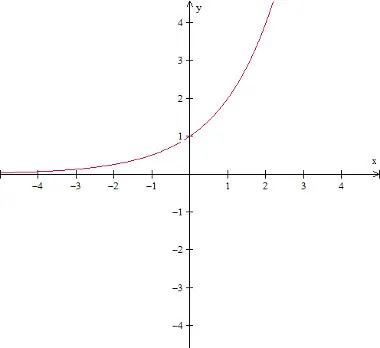

Gráfico da função exponencial decrescente: f(x) = (1/2)^x para a = 1/2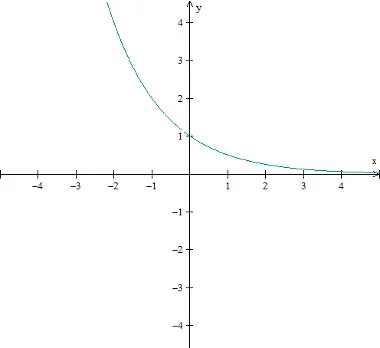

QUESTÕES RESOLVIDAS
26) Encontre o valor de f(x) = x² + 3x – 10 para que f(x) = 0
Resolução:
Os coeficientes dessa função são: a = 1, b = 3 e c = – 10. Para resolver essa equação, vamos utilizar a fórmula de Bhaskara:

Δ = b² – 4.a.c
Δ = 3² – 4.1.(– 10)
Δ = 9 + 40
Δ = 49
x = – b ± √Δ
        2.a
x = – 3 ± √49
           2.1
x = – 3 ± 7
      2
x₁ = – 3 + 7
        2
x₁ = 4
       2
x₁ = 2
x₂ = – 3 – 7
         2
x₂ = – 10
        2
x₂ = – 5
Os dois valores de x para que f(x) = 0 são x₁ = 2 e x₂ = – 5.

27) Calcule o valor de 5x² + 15x = 0 para que f(x) = 0
Resolução:
Vamos resolver essa função do 2° grau isolando a variável x:
5x² + 15x = 0
5x.(x + 3) = 0
x₁ = 0
x₂ + 3 = 0
x₂ = – 3
Portanto, os valores de x para os quais f(x) = 0 são 0 e – 3.

28) (UfSCar–SP) Uma bola, ao ser chutada num tiro de meta por um goleiro, numa partida de futebol, teve sua trajetória descrita pela equação h(t) = – 2t² + 8t (t ≥ 0) , onde t é o tempo medido em segundo e h(t) é a altura em metros da bola no instante t. Determine, após o chute:
a) o instante em que a bola retornará ao solo.
b) a altura atingida pela bola.
Resolução:
a) Houve dois momentos em que a bola tocou o chão: o primeiro foi antes de ela ser chutada e o segundo foi quando ela terminou sua trajetória e retornou para o chão. Em ambos os momentos a altura h(t) era igual a zero, sendo assim:
h(t) = – 2t² + 8t
0 = – 2t² + 8t
2t² – 8t = 0
2t.(t – 4) = 0
t' = 0
t'' – 4 = 0
t'' = 4
Portanto, o segundo momento em que a bola tocou no chão foi no instante de quatro segundos.

b) A altura máxima atingida pela bola é dada pelo vértice da parábola. As coordenadas do seu vértice podem ser encontradas através de:
x_v = – b
          2a
y_v = – Δ
        4a
No caso apresentado, é interessante encontrar apenas y_v:
y_v = – Δ
        4a
y_v = – (b² – 4.a.c)
       4a
y_v = – (8² – 4.(–2).0)
           4.(– 2)
y_v = – (64 – 0)
          – 8
y_v = 8
Portanto, a altura máxima atingida pela bola foi de 8 metros.

29) Determine x pertence aos reais tal que (x² – 100x)².(x² – 101x + 100)² = 0.
Resolução:
Devemos encontrar as raízes de cada equação dentro dos parênteses. Para isso, vamos resolver a primeira equação colocando x em evidência:
x² – 100x = 0
x(x – 100) = 0
x₁ = 0
x₂ – 100 = 0
x₂ = 100
A segunda equação pode ser resolvida pela fórmula de Bhaskara:

x² – 101x + 100 = 0
Δ = b² – 4.a.c
Δ = (– 101)² – 4.1.100
Δ = 10201 – 400
Δ = 9801
x = – b ± √Δ
      2.a
x = – (– 101) ± √9801
         2.1
x = 101 ± 99
      2
x₃ = 101 + 99
      2
x₃ = 200
        2
x₃ = 100
x₄ = 101 – 99
       2
x₄ = 2
       2
x₄ = 1
Os valores de x que satisfazem a equação são 0, 1 e 100.

30) Calcule o valor de k de modo que a função f(x) = 4x² – 4x – k não tenha raízes, isto é, o gráfico da parábola não possui ponto em comum com o eixo x.
Resolução:
∆ < 0
b² – 4ac < 0
(–4)² – 4 .  4 . (–k) < 0
16 + 16k < 0
16k < – 16
k < –1
O valor de k para que a função não tenha raízes reais deve ser menor que – 1.

31) Determine os valores de m, para que a função f(x) = (m – 2)x² – 2x + 6 admita raízes reais.
Resolução:
Para essa situação temos que ∆ ≥ 0.

∆ ≥ 0
b² – 4ac ≥ 0
(–2)² – 4 . (m – 2)  . 6 ≥ 0
4 – 4 . (6m – 12) ≥ 0
4 – 24m + 48 ≥ 0
– 24m ≥ – 48 – 4
– 24m ≥ – 52
24m ≤ 52
m ≤ 52/24
m ≤ 13/6
O valor de m que satisfaça a condição exigida é m ≤ 13/6.

32) (Vunesp-SP) O gráfico da função quadrática definida por y = x² – mx + (m – 1), em que m Є R, tem um único ponto em comum com o eixo das abscissas.
Determine y associado ao valor de x = 2.
Resolução:
Um ponto em comum significa dizer uma única raiz, então ∆ = 0.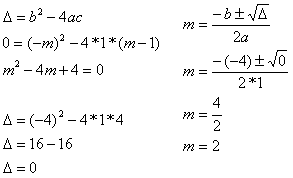

y = x² – mx + (m – 1)
Substituir m = 2, no intuito de obter a lei da função
y = x² – 2x + (2 – 1)
y = x² – 2x +1
Substituindo x = 2, para determinarmos o valor de y
y = 2² – 2 . 2 + 1
y = 4 – 4 + 1
y = 1
Temos que a equação possui a lei de formação y = x² – 2x +1. E quando x = 2, o valor de y se torna igual a 1.

33) (UCSal-BA) Determine os pontos de intersecção da parábola da função f(x) = 2x² – 3x + 1, com o eixo das abscissas.
Resolução:
No instante em que a parábola cruza o eixo das abscissas o valo de y ou f(x) é igual a zero. Portanto:
f(x) = 0
2x² – 3x + 1 = 0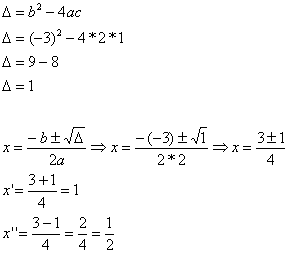

Os pontos de interseção são:
x = 1 e y = 0
x = 1/2 e y = 0

34) Considerando a equação y = x² - 5x + 4, calcule suas raízes, ache o vértice e descreva qual será a concavidade da parábola.
Resolução:
Cálculo das raízes:
Δ = b² – 4ac
Δ = (-5)² – 4 . 1 . 4)
Δ = 25 – 16
Δ = 9.
x = (-b ± √Δ) / 2.a
x = (5 ±√9) / 2.1
x₁ = 1
x₂ = 4
Cálculo do vértice:
Xv = – b/2.a
Xv = -(-5)/2.1
Xv = 5/2
Yv = – Δ/4.a
Yv = – 9/4.1
Yv = -9/4

35) Determine as raízes ou zeros da função quadrática f(x) = x² – 4x – 5.
Resolução:
f(x) = 0
x² – 4x – 5 = 0, temos uma equação do segundo grau.
Coeficientes: a = 1, b = -4 e c = -5
Δ = b² – 4ac = -4² – 4 . 1 . (-5) = 16 + 20 = 36
Raízes:
x’ = (- b + √Δ)/2a = (-(-4) + √36)/(2 . 1) = (4 + 6) / 2 = 10/2 = 5
x” = (- b – √Δ)/2a = (-(-4) – √36)/(2 . 1) = (4 – 6) / 2 = – 2/2 = – 1
Portanto, as raízes da função são -1 e 5.

36) Seja a função quadrática f(x) = 3x² – 5x + 4, calcule f(-1), f(-2), f(10) e f(2).
Resolução:
Atribuindo os valores em f(x) = 3x² – 5x + 4, temos:
f(-1) = 3(-1)² – 5(-1) + 4 = 3 + 5 + 4 = 12
f(-2) = 3(-2)² – 5(-2) + 4 = 12 + 10 + 4 = 26
f(2) = 3 . 2² – 5 . 2 + 4 = 12 – 10 + 4 = 6
f(10) = 3(10)² – 5(10) + 4 = 300 – 50 + 4 = 254

37) Desenhe o gráfico para a função y = x² + x – 2.
Resolução:
Analisando a função percebemos que o gráfico tem concavidade para cima, pois x² é positivo.
Para desenhar o gráfico, vamos atribuir valores a x e determinar a respectiva imagem f(x), formando pares ordenados (x, f(x)).
x = -2; f(x) = 0
x = -1; f(x) = -2
x = 0; f(x) = -2
x = 1; f(x) = 0
x = 2; f(x) = 4
Portanto, temos o seguinte gráfico: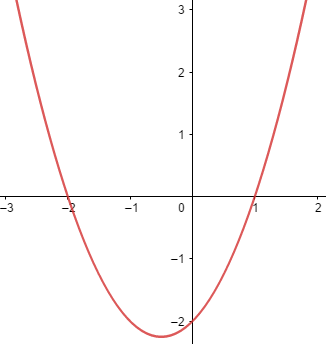


38) Determine o vértice da função quadrática y = 8x² – 3x – 5.
Resolução:
Calculamos o vértice da parábola da seguinte forma: .
Então, y = 8x² – 3x – 5 possui coeficientes:
a = 8, b = -3 e c = -5
x do vértice é:
xv = – (-3)/(2 . 8) = 3/16
y do vértice é:
Δ = b² – 4 . a . c = (-3)² – 4 . 8 . (-5) = 9 + 160 = 169
xv = – 169/(4 . 8) = – 169/32
Portanto, o vértice para a função é: V = (3/16, -169/32)

39) O esboço do gráfico para a função y = -x² + 2x é:
Resolução:
Primeiro devemos atribuir valores a x e calcularmos as imagens f(x), formar os pares ordenados (x, f(x)) e representar no plano cartesiano.
x = -1; f(x) = -3
x = 0; f(x) = 0
x = 1; f(x) = 1
x = 2; f(x) = 0
x = 3; f(x) = -3
Portanto, o gráfico tem a seguinte forma:
 

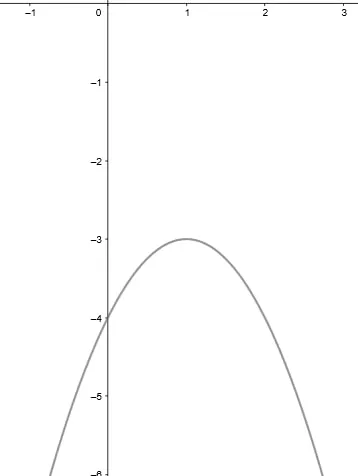
40) (Enem 2013 – PPL) Uma pequena fábrica vende seus bonés em pacotes com quantidades de unidades variáveis. O lucro obtido é dado pela expressão L(x) = -x²+ 12x - 20, onde x representa a quantidade de bonés contidos no pacote. A empresa pretende fazer um único tipo de empacotamento, obtendo um lucro máximo.
Para obter o lucro máximo nas vendas, os pacotes devem conter uma quantidade de bonés igual a:
(A) 4
(B) 6
(C) 9
(D) 10
(E) 14
Resolução
Sabendo que a função lucro L(x) é uma função do 2º grau, a = -1, ou seja, o seu gráfico é uma parábola com concavidade para baixo, queremos encontrar o ponto de máximo da função, ou seja, o vértice. Como x representa a quantidade de bonés, então a quantidade de bonés que maximiza o lucro é o x_v.

b = 12
a = -1
Alternativa: B

41) (Enem 2009) Um posto de combustível vende 10.000 litros de álcool por dia a R$ 1,50 cada litro. Seu proprietário percebeu que, para cada centavo de desconto que concedia por litro, eram vendidos 100 litros a mais por dia. Por exemplo, no dia em que o preço do álcool foi R$ 1,48, foram vendidos 10.200 litros.
Considerando x o valor, em centavos, do desconto dado no preço de cada litro, e V o valor, em R$, arrecadado por dia com a venda do álcool, então a expressão que relaciona V e x é
(A) V = 10.000 + 50x – x².
(B) V = 10.000 + 50x + x².
(C) V = 15.000 – 50x – x².
(D) V = 15.000 + 50x – x².
(E) V = 15.000 – 50x + x².
Resolução
Analisando a situação, com o combustível a R$ 1,50, são vendidos 10.000 litros, logo é faturado um total de:
10.000·1,50 = 15.000 → R$ 15.000,00.
É possível perceber que o valor arrecadado (V) é igual ao produto da quantidade Q pelo preço P.
V = Q . P
Quando se abaixa 1 centavo, a quantidade vendida aumenta em 100 litros, ou seja:
Q = 10.000 + 100x
Por outro lado, o preço terá o desconto de 1 centavo, o que podemos representar por:
P = 1,50 – 0,01x
Sendo assim, o valor é calculado por:
V = Q·P
V = (10.000 + 100x) ·(1,50 – 0,01x)
Aplicando a propriedade distributiva, temos que:
V = 15.000 – 100x + 150x – x²
V = 15.000 +50x – x²
Alternativa: D

42)  Dada a função f(x) = -x² + 2x – 4. Determine:
a) A intersecção com o eixo OY.
b) A intersecção com o eixo OX.
c) Esboce o gráfico da função.
Resolução:
a) Para determinar a intersecção com eixo OY , basta tomar o valor de x =

b) -(0)2 +2(0) – 4
0 + 0 – 4
-4
Assim, temos o par ordenado (0, -4).

c) Para encontrar a intersecção com o eixo OX, basta tomar o valor de y = 0. Assim:
-x² +2x – 4 = 0
Utilizando o método de Bhaskara, temos que:
Δ = b² - 4ac
 Δ = (2)² - 4(-1)(-4)
 Δ = 4 - 16
Δ = -12
Como o valor do discriminante é menor que zero, a função não intercepta o eixo X.

d) Para fazer o esboço do gráfico, devemos olhar os pontos de intersecção e analisar a concavidade da parábola. Como a < 0, a parábola será côncava para baixo. Assim:
 

43) (Enem 2018 – PPL) Uma indústria automobilística está testando um novo modelo de carro. Cinquenta litros de combustível são colocados no tanque desse carro, que é dirigido em uma pista de testes até que todo o combustível tenha sido consumido. O segmento de reta no gráfico mostra o resultado desse teste, no qual a quantidade de combustível no tanque é indicada no eixo y (vertical), e a distância percorrida pelo automóvel é indicada no eixo x (horizontal).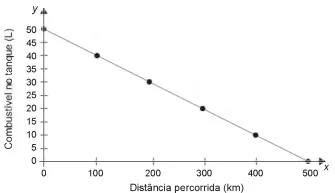
A expressão algébrica que relaciona a quantidade de combustível no tanque e a distância percorrida pelo automóvel é:

Resolução:
Sabemos que essa situação é uma função do 1º grau, já que o gráfico é uma reta. Além disso, o ponto em que a reta toca o eixo y é o ponto (0,50).
Então, seja f(x) = ax + b:
f(0) = 50
50 = a · 0 + b
b = 50
Sendo b = 50, para encontrar o valor de a, basta encontrar outro ponto no gráfico. Usaremos o ponto (0,500):

Alternativa: B

44) (Encceja 2018) Uma prestadora de serviços cobra pela visita à residência do cliente e pelo tempo necessário para realizar o serviço na residência. O valor da visita é R$ 40 e o valor da hora para realização do serviço é R$ 20.
Uma expressão que indica o valor a ser pago (P) em função das horas (h) necessárias à execução do serviço é:
(A) P = 40h
(B) P = 60h
(C) P = 20 + 40h
(D) P = 40 + 20h
Resolução:
A função é descrita por P = ah + b, em que b é a taxa fixa, que, no caso, é o valor da visita, que é R$ 40. Já o coeficiente a é a taxa que depende do número de horas, no caso, R$ 20. Substituindo, temos que:
P = 20h + 40
P = 40 + 20h
Alternativa: D

45) (Enem 2016) Uma cisterna de 6 000 L foi esvaziada em um período de 3 h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.
Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?
(A) 1 000
(B) 1 250
(C) 1 500
(D) 2 000
(E) 2 500
Resolução:
No primeiro momento até a primeira hora, o volume vai de 6000 litros para 5000 litros, ou seja, ocorre uma diferença de 1000 litros, logo, a vazão da primeira bomba é de 1000 L/h. Agora, após ligar a segunda bomba, note que ela foi inteiramente esvaziada, ou seja, nas outras 2 horas, foi possível retirar 5000 L. Realizando a divisão 5000 : 2 = 2500, a soma das vazões das bombas foi de 2500 L/h.
Sabemos que a primeira bomba tem vazão de 1000 L/h, então, para descobrir a vazão da segunda, temos que: 2500 – 1000 = 1500 L.
Alternativa: C

46) (UFSM) Sabe-se que o preço a ser pago por uma corrida de táxi inclui uma parcela fixa, que é denominada bandeirada, e uma parcela variável, que é função da distância percorrida. Se o preço da bandeirada é de R$ 4,60 e o quilômetro rodado é R$ 0,96, a distância percorrida pelo passageiro que pagou R$ 19 para ir de sua casa ao shopping é de:
(A) 5 km
(B) 10 km
(C) 15 km
(D) 20 km
(E) 25 km
Resolução:
Seja d a distância percorrida em quilômetros, sabemos que:
19 = 0,96d + 4,6
Isolando a incógnita, temos que:
19 – 4,6 = 0,96d
14,4 = 0,96d
d = 14,4 : 0,96
d = 15
Alternativa: C

47) Uma determinada espécie de pimenta, ao atingir 20 centímetros de altura, começa a crescer de forma linear. A cada dia que se passa, essa planta aumenta 2,5 centímetros. Assim, é possível descrever essa situação como uma função do 1º grau, em que a altura h(d) está em função dos dias, cuja lei de formação é:
(A) h(d) = 2,5d
(B) h(d) = 2,5d + 20
(C) h(d) = 20d + 2,5
(D) h(d) = 20d
(E) h(d) = 2,5d – 20
Resolução:
Seja h(d) = ad + b uma função afim, sabemos que b é a taxa fixa, no caso, 20 cm, e que, além disso, a cada dia, ela aumenta 2,5 cm, ou seja, 2,5 d. Dessa forma, a lei de formação que melhor descreve essa situação é:
h(d) = 2,5d + 20
Alternativa: B

48) Um fazendeiro resolveu investir em uma colheitadeira para facilitar o serviço na plantação. Sabendo que o valor pago foi de R$ 300.000 no ano da compra, é bastante comum que máquinas desse porte percam o seu valor V ao decorrer dos anos t. Supondo que a taxa de depreciação de uma máquina desse porte é de R$ 22.000 por ano, devido ao seu constante uso, podemos afirmar que o valor da colheitadeira, ao final de 7 anos, será de:
(A) R$ 154.000
(B) R$ 246.000
(C) R$ 146.000
(D) R$ 174.000
(E) R$ 210.000
Resolução:
A função que descreve o valor em função do tempo possui a lei de formação:
V(t) = -22.000t + 300.000
Como o tempo foi de 7 anos, então faremos t = 7.
V(7) = -22.000 · 7 + 300.000
V(7) = -154.000 + 300.000
V(7) = 146.000
Alternativa: C

49) O uso de aplicativos para realizar viagens é cada vez mais comum no cotidiano. Supõe-se que, para calcular o valor da viagem em um aplicativo, há um valor fixo mais um total de R$ 1,40 por quilômetros rodado. Sabendo que um cliente pagou R$ 15,60 ao final da viagem, a quantidade de quilômetros rodados foi de 8 km, então o valor fixo da viagem foi de:
(A) R$ 2
(B) R$ 2,50
(C) R$ 3,60
(D) R$ 4,40
(E) R$ 5
Resolução:
Sabemos que o valor pago é calculado por:
V(q) = 1,40q + T
Sendo T a taxa fixa e q os quilômetros rodados, substituindo os valores conhecidos, temos:
15,60 = 1,40 · 8 + T
15,60 = 11,20 + T
15,60 – 11,20 = T
T = 4,40
Alternativa: D

50) Dada a função afim f(x) = ax + b, sabendo-se que f(3) = 6 e f (-2) = -3, o valor do coeficiente angular dessa função é:
(A) 9/5
(B) 5/9
(C) 3
(D) 3/5
(E) 5/3
Resolução:
Sabemos que f(x) = ax + b.
Substituindo os valores conhecidos, temos que:
f(3) = 6
f(3) = 3a + b → 3a + b = 6
f(-2) = -3
f(-2) = -2a + b → -2a + b = -3
Dessa foma, vamos resolver o sistema de equação:
3a + b = 6
-2a + b = -3
Realizando a subtração do primeiro pelo segundo sistema, temos que:
5a = 9
a = 9/5
Alternativa: A

51) Podemos afirmar que o zero da função f(x) = -2x + 5 é igual a:
(A) 2
(B) 2,5
(C) -2,5
(D) -3
(E) 3
Resolução:
Para encontrar o zero da função, vamos igualar a função a zero e resolver a equação, então, temos que:
-2x + 5 = 0
-2x = -5
x = (-5) : (-2)
x = 2,5
Alternativa: B

52) Seja f(x) e g(x), funções cujas leis de formação são, respectivamente, f(x) = 2x -5 e g(x) = -x + 2, podemos afirmar que o valor de f(g(2)) – g(-3) é igual a:
(A) 0
(B) 5
(C) -5
(D) -10
(E) -12
Resolução:
Sabendo que:
f(x) = 2x -5 e que g(x) = -x + 2, vamos calcular o valor da expressão: f(g(2)) – g(-3). Para isso calcularemos os valores separados.
Primeiro g(2):
g(2) = -2 + 2 = 0
Então, f(g(2)) = f(0):
f(g(2)) = f(0) = 2 · 0 – 5 = -5
Por fim, vamos calcular o valor de g(-3):
g(-3) = - (-3) + 2 = 3 + 2 = 5
Sendo assim, temos que:
f(g(2)) – g(-3) = -5 – 5 = -10
Alternativa: D

53) Julgue as afirmativas a seguir sobre a função f(x) = 2x – 3. Podemos afirmar que:
I – O coeficiente angular é 2.
II – O coeficiente linear é 3.
III – A imagem da função para x = 1 é -1.
De acordo com o julgamento das afirmativas, é correto afirmar que:
(A) Somente I é verdadeira.
(B) Somente I e II são verdadeiras.
(C) Somente III é verdadeira.
(D) Somente I e III são verdadeiras.
(E) Todas são verdadeiras.
Resolução:
I → Verdadeira, pois o coeficiente angular é o termo que acompanha a incógnita x, que, no caso, é igual a 2.
II → Falsa, pois o coeficiente linear é o termo independente, que, nesse caso, é -3.
III → Verdadeira, pois f(1) = 2 · 1 – 3 = 2 – 3 = -1.
Então, podemos concluir que I e III são verdadeiras e que II é falsa.
Alternativa: D

54) Sobre o comportamento da função f(x) = 4x – 3, marque a alternativa correta:
(A) f(x) é crescente, pois seu coeficiente angular é positivo e igual a 4.
(B) f(x) é decrescente, pois seu coeficiente angular é positivo e igual a 4.
(C) f(x) é decrescente, pois seu coeficiente angular é positivo e igual a -3.
(D) f(x) é crescente, pois seu coeficiente angular é negativo e igual a -3.
(E) f(x) é decrescente, pois o seu coeficiente linear é negativo e igual a -3.
Resolução:
Para saber se a função é crescente ou decrescente, basta olhar o coeficiente angular. Se ele for positivo, a função é crescente, se for negativo, ela será decrescente. Nesse caso a = 4, então, a função é crescente, pois seu coeficiente angular é positivo e igual a 4.
Alternativa: A


Continua....