Professor Diminoi ONDULATÓRIA
ONDULATÓRIA
É a parte da Física que estuda as ondas, como por exemplo, a onda numa corda, onda do mar, ondas eletromagnéticas, como a luz, ondas sonoras, como o som, etc.Característica Fundamental das Ondas - As ondas transportam energia mas não transportam matéria. Onda - É uma pertubação que se propaga em um determinado meio.
Onda - É uma pertubação que se propaga em um determinado meio. Pulso de onda - Qualquer perturbação (vibração, abalo) que se propaga em um determinado meio.
Pulso de onda - Qualquer perturbação (vibração, abalo) que se propaga em um determinado meio. Fonte - Qualquer elemento que origine os pulsos provocando a perturbação. A fonte fornece energia ao sistema (meio) no qual as ondas vão se propagar.Meio - Local onde a onda está se propagando.
Fonte - Qualquer elemento que origine os pulsos provocando a perturbação. A fonte fornece energia ao sistema (meio) no qual as ondas vão se propagar.Meio - Local onde a onda está se propagando. Formação de onda na superfície de um líquido
Formação de onda na superfície de um líquido
 V = velocidade (m/s)ƒ = frequênçia (Hz)λ = comprimento (m)T = período (tempo) (s)
V = velocidade (m/s)ƒ = frequênçia (Hz)λ = comprimento (m)T = período (tempo) (s)
QUESTÕES RESOLVIDAS – ONDULATÓRIA
01) (IFRS) O som é a propagação de uma onda mecânica longitudinal que se propaga apenas em meios materiais. O som possui qualidades diversas que o ouvido humano normal é capaz de distinguir. Associe corretamente as qualidades fisiológicas do som apresentadas a seguir com as situações apresentadas logo abaixo.Qualidades fisiológicas(1) Intensidade(2) Timbre(3) FrequênciaSituações( ) Abaixar o volume do rádio ou da televisão.( ) Distinguir uma voz aguda de mulher de uma voz grave de homem.( ) Distinguir sons de mesma altura e intensidade produzidos por vozes de pessoas diferentes.( ) Distinguir a nota Dó emitida por um violino e por uma flauta.( ) Distinguir as notas musicais emitidas por um violão.A sequência correta de preenchimento dos parênteses, de cima para baixo, é
(A) 1 – 2 – 3 – 3 – 2
(B) 1 – 3 – 2 – 2 – 3
(C) 2 – 3 – 2 – 2 – 1
(D) 3 – 2 – 1 – 1 – 2
(E) 3 – 2 – 2 – 1 – 1
Resolução:(1) – O volume está relacionado à intensidade, energia propagada por unidade de área dentro de um intervalo de tempo.(3) – Ondas graves possuem baixa frequência, já as ondas agudas possuem alta frequência.(2) – O timbre é a característica que nos faz diferenciar sons de mesma intensidade e altura produzidos por fontes distintas.(2) – O timbre é a característica que nos faz diferenciar sons de mesma intensidade e altura produzidos por fontes distintas.(3) – Cada nota musical possui uma frequência característica.Alternativa: B
02) (Uece) Sobre as ondas sonoras, é correto afirmar que não se propagam:
(A) na atmosfera.
(B) na água.
(C) no vácuo.
(D) nos meios metálicos.
Resolução:
O som é uma onda do tipo mecânica, e isso significa que as ondas sonoras precisam de um meio de propagação, um lugar por onde se movem. No vácuo, não existem moléculas capazes de sofrerem vibrações e produzirem sons.
Alternativa: C
03) Marque a alternativa correta a respeito da velocidade de propagação das ondas sonoras.
(A) O som pode propagar-se apenas em meios gasosos.(B) Em meios líquidos, a velocidade do som é maior do que em meios sólidos.
(C) A velocidade de propagação do som no aço é maior do que na água.
(D) A velocidade de propagação do som na água é maior do que no aço.
(E) O som, assim como as ondas eletromagnéticas, pode ser propagado no vácuo.
Resolução:
O som é uma onda mecânica, por isso, precisa de uma meio de propagação. Quanto maior for a proximidade das moléculas que compõem o meio de propagação das ondas sonoras, maior será a sua velocidade. Dessa forma, a velocidade do som nos sólidos é maior que nos líquidos e nos gases.
Alternativa: C
04) Marque a alternativa que responde corretamente o fato de a frequência das ondas não ser alterada na ocorrência da refração.
(A) A única mudança que ocorre na refração é da velocidade das ondas.
(B) Caso a frequência fosse alterada, a onda sofreria colapso e seria completamente anulada.
(C) A frequência de todas as ondas é a mesma, por isso, essa grandeza não pode ser alterada na refração.(D) A frequência depende somente da fonte que produz as oscilações. Essa grandeza só será alterada caso a própria fonte aumente ou diminua sua frequência.
(E) Todas as alternativas estão incorretas.
Resolução:
A frequência é definida como a quantidade de ondas produzidas dentro de um intervalo de tempo. Essa característica das ondas depende apenas da fonte geradora delas, sendo assim, mesmo na ocorrência de uma refração, a frequência das ondas será mantida.Alternativa: D
05) UFMG) Uma pessoa toca no piano uma tecla correspondente à nota mi e, em seguida, a que corresponde a sol.Pode-se afirmar que serão ouvidos dois sons diferentes porque as ondas sonoras correspondentes a essas notas têm:
(A) amplitudes diferentes
(B) frequências diferentes
(C) intensidades diferentes
(D) timbres diferentes
(E) velocidade de propagação diferentes
Resolução:
Cada nota musical possui uma frequência característica, logo, os sons serão diferentes porque as notas possuem frequências distintas.
Alternativa: B
06) (UFPE) Diante de uma grande parede vertical, um garoto bate palmas e recebe o eco um segundo depois. Se a velocidade do som no ar é 340 m/s, o garoto pode concluir que a parede está situada a uma distância aproximada de:
(A) 17 m
(B) 34 m
(C) 68 m
(D) 170 m
(E) 340 m
Resolução:Aqui podemos utilizar a equação que define velocidade:v = Δs ÷ ΔtPara que haja eco, o som deve sair da fonte, chocar-se com um obstáculo e voltar. Sendo assim, o espaço percorrido deve ser multiplicado por 2:v = 2Δs ÷ Δt340 = 2Δs ÷ 1340 = 2Δs340 ÷ 2 = ΔsΔs = 170 m
Alternativa: D
07) A respeito da classificação das ondas, marque a alternativa incorreta:
(A) As ondas classificadas como longitudinais possuem vibração paralela à propagação. Um exemplo desse tipo de onda é o som.
(B) O som é uma onda mecânica, longitudinal e tridimensional.
(C) Todas as ondas eletromagnéticas são transversais.
(D) A frequência representa o número de ondas geradas dentro de um intervalo de tempo específico. A unidade Hz (Hertz) significa ondas geradas (por segundo.
(E) Quanto à sua natureza, as ondas podem ser classificadas em mecânicas, eletromagnéticas, transversais e longitudinais.
Resolução:Os termos longitudinais e transversais referem-se à classificação das ondas quanto à direção de propagação.
Alternativa: E
08) Uma determinada fonte gera 3600 ondas por minuto com comprimento de onda igual a 10 m. Determine a velocidade de propagação dessas ondas.
(A) 500 m/s
(B) 360 m/s
(C) 600 m/s
(D) 60 m/s
(E) 100 m/s
Resolução:
A frequência deve estar em rotações por segundo (Hz). Sabendo que 1 min = 60 s, temos:F = 3600 ÷ 60 = 60 HzSendo assim, temos:v = λ.fv = 10. 60 = 600 m/s
Alternativa: C
09) (Mackenzie SP/2006) As antenas das emissoras de rádio emitem ondas eletromagnéticas que se propagam na atmosfera com a velocidade da luz (3,0.105 km/s) e com frequências que variam de uma estação para a outra.A rádio CBN emite uma onda de frequência 90,5 MHz e comprimento de onda aproximadamente igual a:
(A) 2,8 m
(B) 3,3 m
(C) 4,2 m
(D) 4,9 m
(E) 5,2 m
Resolução:f = 90,5 MHz = 90,5 . 106 HzVelocidade da luz (c) = 3,0 . 105 km/s = 3,0 . 108 m/sPodemos utilizar a equação: v = λ . f, mas nesse caso trocaremos “v” por “c” por se tratar da velocidade da luz.Logo:c = λ . f3,0 . 108 = λ . 90,5 . 106λ = 3,0 . 108 90,5.106λ = 0,033 . 108-6 = 0,033 . 10²λ = 3,3 m
Alternativa: B
10) (Unifor/CE/Conh. Gerais) Na figura está representada a configuração de uma onda mecânica que se propaga com velocidade de 20 m/s.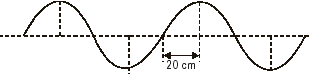 A frequência da onda, em hertz, vale:
A frequência da onda, em hertz, vale:
(A) 5,0
(B) 10
(C) 20
(D) 25
(E) 50
Resolução:
Pela figura podemos perceber que λ/4 = 20 cmLogo λ = 80 cm = 0,8 mComo v = λ . f e sabendo que v = 20 m/s, temos: 20 = 0,8 . ff = 200,8f = 25 Hz
Alternativa: D
11) É correto afirmar sobre as ondas mecânicas:
(A) transportam massa e energia
(B) transportam massa e quantidade de movimento
(C) transportam matéria
(D) Transportam energia e quantidade de movimento
(E) Nda
Resolução;
As ondas mecânicas são perturbações de um meio material elástico que se propagam por esse meio, transportando energia e quantidade de movimento.Portanto, na propagação das ondas há transporte de energia e quantidade de movimento.
Alternativa: D
12) Suponha uma corda de 10 m de comprimento e massa igual a 500 g. Uma força de intensidade 300 N a traciona, determine a velocidade de propagação de um pulso nessa corda.
Resolução:
O comprimento da corda (L) = 10 mm = 500 g = 0,5 kgμ = m/Lμ = 0,5/10μ = 0,05 kg/mv = √F/μv = √300/0,05v = √6000 v = 77 m/s
TIPOS DE ONDAS Ondas MecânicasSão ondas que dependem de um meio material para se propagar, ou seja, sua propagação envolve o transporte de energia cinética e potencial e depende da elasticidade do meio. Por isto não é capaz de propagar-se no vácuo. Alguns exemplos são os que acontecem em molas e cordas, sons e em superfícies de líquidos. Onda na corda
Onda na corda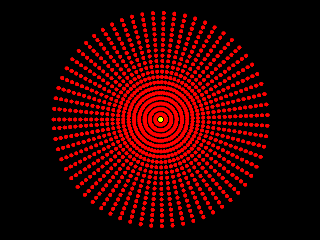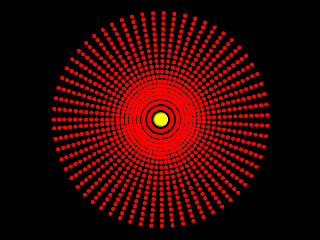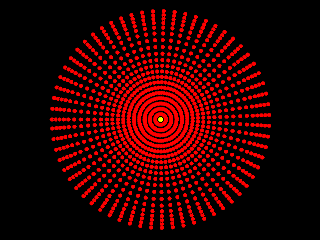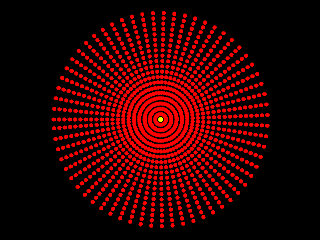 Onda sonoraOndas EletromagnéticasSão ondas geradas por cargas elétricas oscilantes e sua propagação não depende de um meio material para se propagar, podendo propagar-se no vácuo e em determinados meios materiais.Alguns exemplos são as ondas de rádio, de radar, os raios x e as microondas e a luz.
Onda sonoraOndas EletromagnéticasSão ondas geradas por cargas elétricas oscilantes e sua propagação não depende de um meio material para se propagar, podendo propagar-se no vácuo e em determinados meios materiais.Alguns exemplos são as ondas de rádio, de radar, os raios x e as microondas e a luz. Observação: Todas as ondas eletromagnéticas tem em comum a sua velocidade de propagação no vácuo, próxima a 300000km/s, que é equivalente a 1080000000km/h.CLASSIFICAÇÃO DAS ONDASClassificação em relação à direção de propagaçãoOndas UnidimensionaisSó se propagam em uma direção (uma dimensão), como uma onda em uma corda.
Observação: Todas as ondas eletromagnéticas tem em comum a sua velocidade de propagação no vácuo, próxima a 300000km/s, que é equivalente a 1080000000km/h.CLASSIFICAÇÃO DAS ONDASClassificação em relação à direção de propagaçãoOndas UnidimensionaisSó se propagam em uma direção (uma dimensão), como uma onda em uma corda.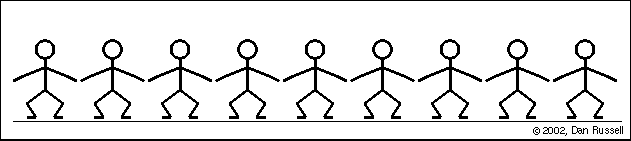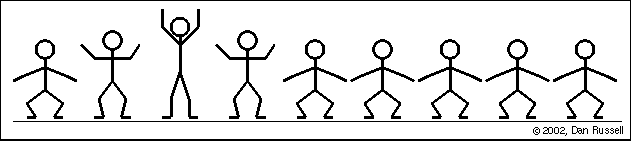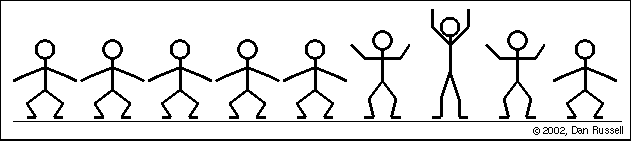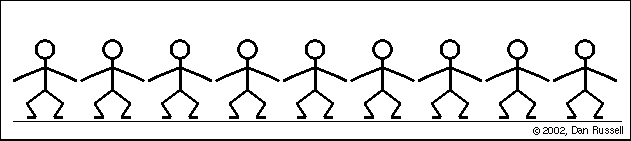
 Ondas BidimensionaisPodem se propagar em duas direções (x e y do plano cartesiano), como a onda provocada pela queda de um objeto na superfície da água.
Ondas BidimensionaisPodem se propagar em duas direções (x e y do plano cartesiano), como a onda provocada pela queda de um objeto na superfície da água. Ondas TridimensionaisEstas se propagam em todas as direções possíveis, como ondas sonoras, a luz, etc.
Ondas TridimensionaisEstas se propagam em todas as direções possíveis, como ondas sonoras, a luz, etc. RESUMO:
RESUMO: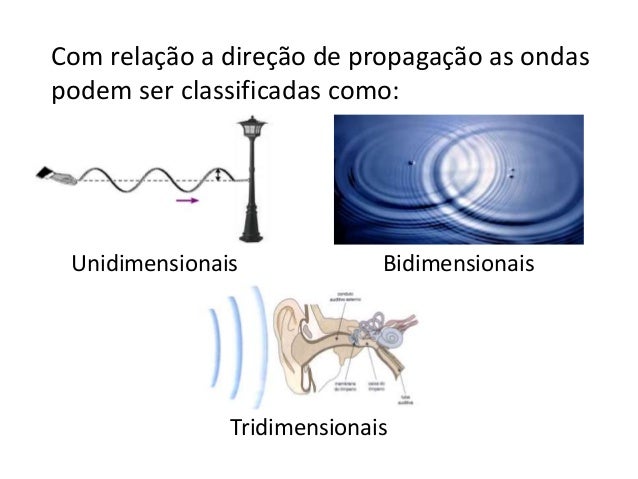 Classificação quanto a direção de propagaçãoOndas LongitudinaisNas ondas longitudinais, a vibração da fonte é paralela ao deslocamento da onda.
Classificação quanto a direção de propagaçãoOndas LongitudinaisNas ondas longitudinais, a vibração da fonte é paralela ao deslocamento da onda. Ondas TransversaisSão ondas em que a direção da propagação e a direção da vibração são perpendiculares.
Ondas TransversaisSão ondas em que a direção da propagação e a direção da vibração são perpendiculares. CARACTERÍSTICA FUNDAMENTAL DE UMA ONDASe onda nas transporta matéria como os surfista pegam ondas?Uma onda no mar ou uma corda balançando possuem esta aparência. Este tipo de onda pode ser caracterizada da seguinte forma:
CARACTERÍSTICA FUNDAMENTAL DE UMA ONDASe onda nas transporta matéria como os surfista pegam ondas?Uma onda no mar ou uma corda balançando possuem esta aparência. Este tipo de onda pode ser caracterizada da seguinte forma: "A onda está propagando-se da esquerda para a direita, na horizontal, mas qualquer ponto da corda move-se para cima e para baixo, na vertical. Como a direção de propagação da onda é perpendicular, ou seja, forma um ângulo de 90º com a direção de oscilação de qualquer ponto sobre a corda, dizemos que ela é transversal".Observar a praia, além de trazer uma excelente sensação de bem estar, ajuda a perceber que uma onda possui certa velocidade, e que ela inicia seu movimento no oceano vindo quebrar na praia. Obviamente, observando este fenômeno, podemos concluir que esta onda pode mover-se de um lugar para o outro. Se você estiver dentro da água, e uma onda passar por você antes dela "estourar", que movimento seu corpo irá realizar? O corpo movimentar-se-á na direção de vibração da onda do mar, isto é, seu corpo irá subir e depois descer.Observação: Não esqueça, as onda NÃO transporta matéria, apenas energia. Sendo assim, o surfista é movido pela arrebentação da onda (ou seja, a onda está se destruindo) e não pela onda em si.
"A onda está propagando-se da esquerda para a direita, na horizontal, mas qualquer ponto da corda move-se para cima e para baixo, na vertical. Como a direção de propagação da onda é perpendicular, ou seja, forma um ângulo de 90º com a direção de oscilação de qualquer ponto sobre a corda, dizemos que ela é transversal".Observar a praia, além de trazer uma excelente sensação de bem estar, ajuda a perceber que uma onda possui certa velocidade, e que ela inicia seu movimento no oceano vindo quebrar na praia. Obviamente, observando este fenômeno, podemos concluir que esta onda pode mover-se de um lugar para o outro. Se você estiver dentro da água, e uma onda passar por você antes dela "estourar", que movimento seu corpo irá realizar? O corpo movimentar-se-á na direção de vibração da onda do mar, isto é, seu corpo irá subir e depois descer.Observação: Não esqueça, as onda NÃO transporta matéria, apenas energia. Sendo assim, o surfista é movido pela arrebentação da onda (ou seja, a onda está se destruindo) e não pela onda em si. COMPONENTES DE UMA ONDAComponentes de uma onda.
COMPONENTES DE UMA ONDAComponentes de uma onda.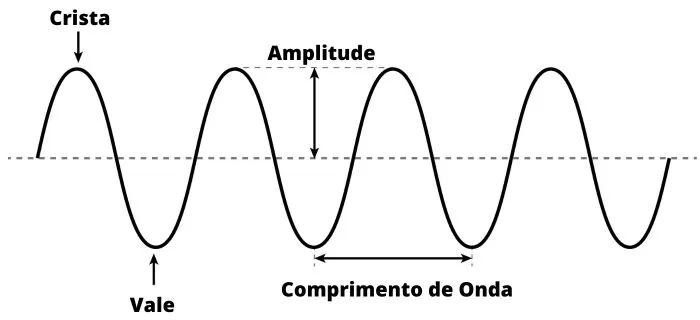 Eixo ou Linha de Equilíbrio: é a linha que "passa" na metade da onda.Comprimento: é o tamanho de uma onda, que pode ser medida em três pontos diferentes: de crista a crista, do início ao final de um período ou de vale a vale. Crista é a parte alta da onda, vale, a parte baixa. É representada no SI pela letra grega lambda (λ)Amplitude: é a distância entre o eixo da onda até a crista ou distância entre o eixo da onda até a vale. Quanto maior for a amplitude, maior será a quantidade de energia transportada.FREQUÊNCIA É o número de oscilações da onda, por um certo período de tempo. A unidade de frequência do Sistema Internacional (SI), é o hertz (Hz) , que equivale a 1 segundo, e é representada pela letra f. Então, quando dizemos que uma onda vibra a 60Hz, significa que ela oscila 60 vezes por segundo.Observação: a frequência de uma onda só muda quando houver alterações na fonte.Exemplo: No caso de frequência cardíaca é quantos pulsos (batidas) o coração dar em um segundo.
Eixo ou Linha de Equilíbrio: é a linha que "passa" na metade da onda.Comprimento: é o tamanho de uma onda, que pode ser medida em três pontos diferentes: de crista a crista, do início ao final de um período ou de vale a vale. Crista é a parte alta da onda, vale, a parte baixa. É representada no SI pela letra grega lambda (λ)Amplitude: é a distância entre o eixo da onda até a crista ou distância entre o eixo da onda até a vale. Quanto maior for a amplitude, maior será a quantidade de energia transportada.FREQUÊNCIA É o número de oscilações da onda, por um certo período de tempo. A unidade de frequência do Sistema Internacional (SI), é o hertz (Hz) , que equivale a 1 segundo, e é representada pela letra f. Então, quando dizemos que uma onda vibra a 60Hz, significa que ela oscila 60 vezes por segundo.Observação: a frequência de uma onda só muda quando houver alterações na fonte.Exemplo: No caso de frequência cardíaca é quantos pulsos (batidas) o coração dar em um segundo.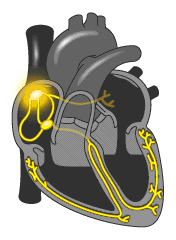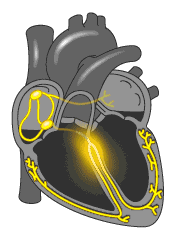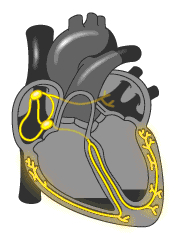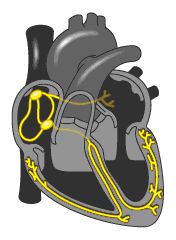
 PERÍODO É o intervalo de tempo necessário para para que um fenômeno se repita, ou seja, complete um ciclo. No caso do relógio o período para que o ponteiro maior sai e chegue ao nume 12 é de 1 hora.
PERÍODO É o intervalo de tempo necessário para para que um fenômeno se repita, ou seja, complete um ciclo. No caso do relógio o período para que o ponteiro maior sai e chegue ao nume 12 é de 1 hora. Período - É o tempo necessário para a fonte produzir uma onda completa. No SI, é representado pela letra T, e é medido em segundos.
Período - É o tempo necessário para a fonte produzir uma onda completa. No SI, é representado pela letra T, e é medido em segundos.PARTICULARIDADES DE UMA ONDAVelocidade de uma ondaTodas as ondas possuem uma velocidade, que sempre é determinada pela distância percorrida, sobre o tempo gasto. Nas ondas, essa equação fica:

 Característica fundamenta das onda - Transportam energia mas não transportam matéria (massa)
Característica fundamenta das onda - Transportam energia mas não transportam matéria (massa) Interferência de ondas - Consiste na superposição de duas ondas no espaço. Esse fenômeno pode ser classificado de duas formas: interferência construtiva ou destrutiva.Você percebeu que quando o celular toca perto das caixinhas de som de um computador ocorre um barulho estranho? Você também já ouviu dizer que deve-se deixar o celular desligado ao viajar de avião? Pois é, tanto num caso como no outro o que ocorre são interferências de ondas.
Interferência de ondas - Consiste na superposição de duas ondas no espaço. Esse fenômeno pode ser classificado de duas formas: interferência construtiva ou destrutiva.Você percebeu que quando o celular toca perto das caixinhas de som de um computador ocorre um barulho estranho? Você também já ouviu dizer que deve-se deixar o celular desligado ao viajar de avião? Pois é, tanto num caso como no outro o que ocorre são interferências de ondas.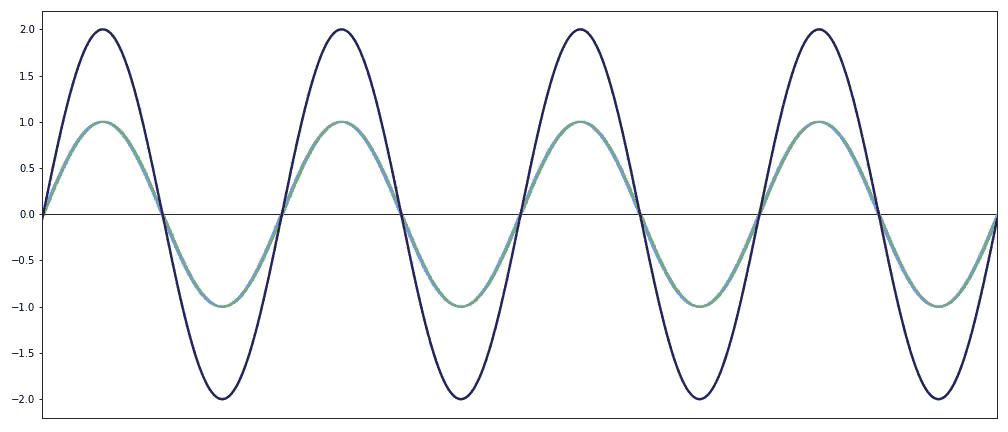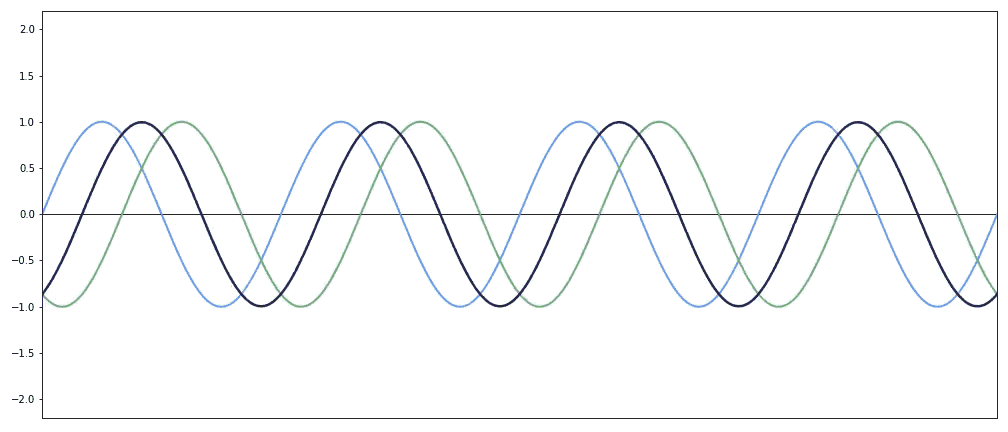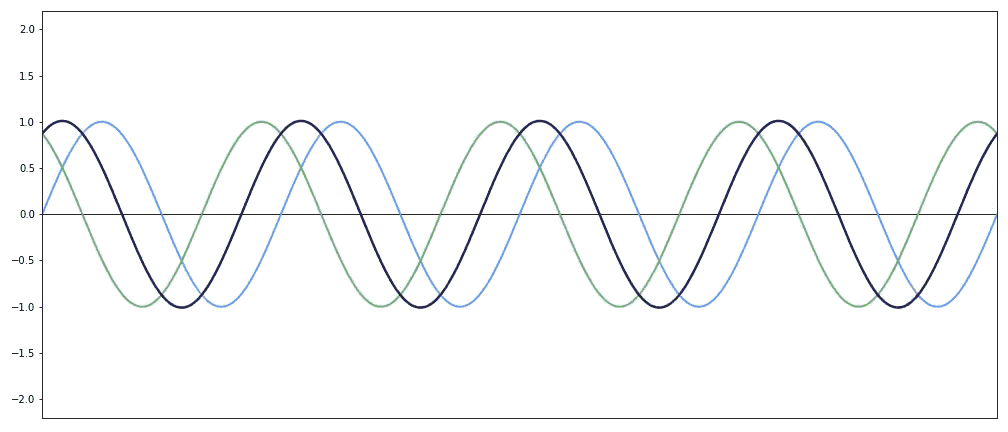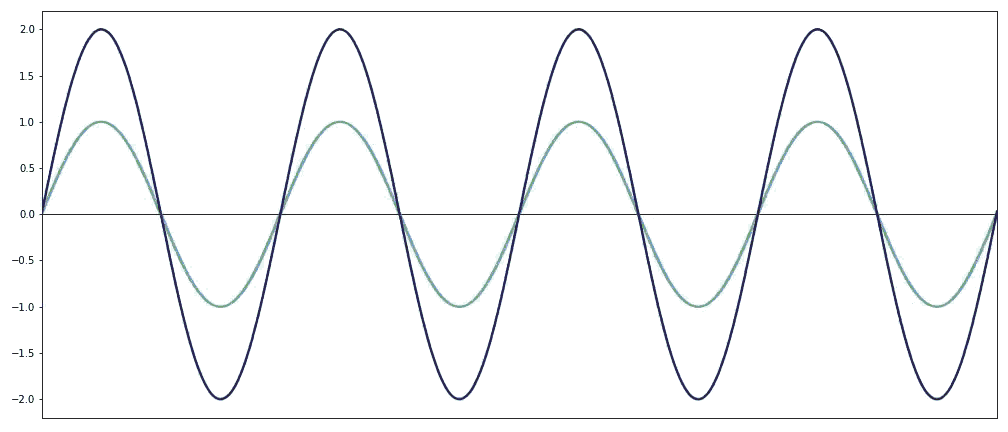


INTERFERÊNCIAS ENTRE ONDAS
Ondas Construtivas
Ondas construtivas são ondas que se sobrepõem e se combinam para formar uma onda maior. Esse fenômeno é chamado de interferência construtiva.
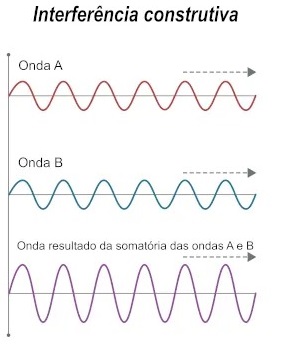
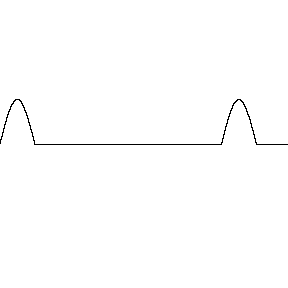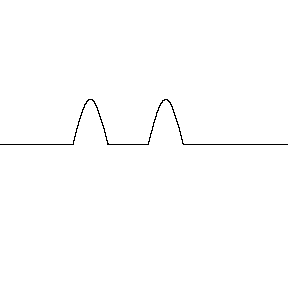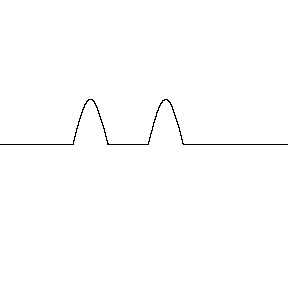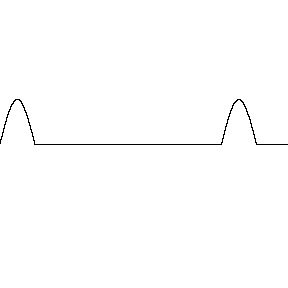
Como ocorre a interferência construtiva?
- As ondas se sobrepõem e suas cristas se alinham
- As ondas estão "em fase" ou sincronizadas
- As ondas reforçam uma à outra, aumentando a amplitude e a intensidade
Onde é possível observar a interferência construtiva? Na óptica, Em manchas de óleo, Em bolhas de sabão.
Ondas Destrutivas
Ondas destrutivas são ondas que se anulam quando se encontram e se combinam, resultando em uma onda com amplitude menor que as ondas originais. Este fenômeno é conhecido como interferência destrutiva.
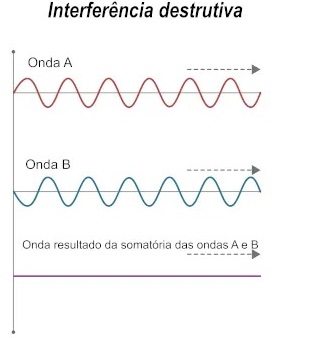
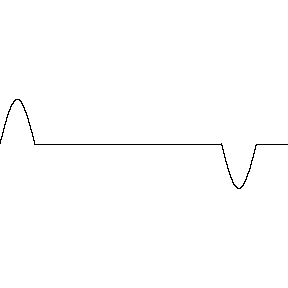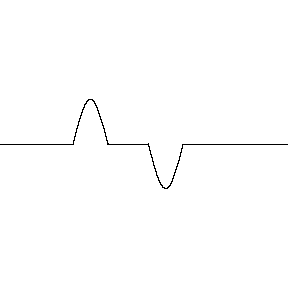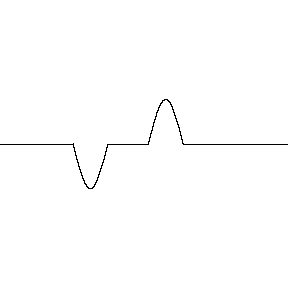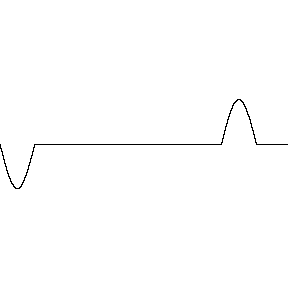
Explicação
- A interferência destrutiva ocorre quando as ondas estão em oposição de fase, ou seja, o pico de uma onda coincide com o vale da outra.
- A amplitude da onda resultante é menor do que pelo menos uma das amplitudes das ondas que se superpõem.
Se duas ondas iguais sofrem interferência destrutiva, ocorrerá a anulação ou aniquilação das ondas.
ONDULATÓRA - QUESTÕES RESOLVIDAS
13) (UFMG) Uma pessoa toca no piano uma tecla correspondente à nota mi e, em seguida, a que corresponde a sol. Pode-se afirmar que serão ouvidos dois sons diferentes porque as ondas sonoras correspondentes a essas notas têm:
(A) amplitudes diferentes
(B) frequências diferentes
(C) intensidades diferentes
(D) timbres diferentes
(E) velocidade de propagação diferentes
Resolução:
Cada nota musical possui uma frequência característica, logo, os sons serão diferentes porque as notas possuem frequências distintas.
Alternativa: B
14) (UFPE) Diante de uma grande parede vertical, um garoto bate palmas e recebe o eco um segundo depois. Se a velocidade do som no ar é 340 m/s, o garoto pode concluir que a parede está situada a uma distância aproximada de:
(A) 17 m
(B) 34 m
(C) 68 m
(D) 170 m
(E) 340 m
Resolução:
Aqui podemos utilizar a equação que define velocidade:v = Δs ÷ ΔtPara que haja eco, o som deve sair da fonte, chocar-se com um obstáculo e voltar. Sendo assim, o espaço percorrido deve ser multiplicado por 2:v = 2Δs ÷ Δt340 = 2Δs ÷ 1340 = 2Δs340 ÷ 2 = ΔsΔs = 170 m
Alternativa: D
15) A respeito da classificação das ondas, marque a alternativa incorreta:
(A) As ondas classificadas como longitudinais possuem vibração paralela à propagação. Um exemplo desse tipo de onda é o som.
(B) O som é uma onda mecânica, longitudinal e tridimensional.
(C) Todas as ondas eletromagnéticas são transversais.
(D) A frequência representa o número de ondas geradas dentro de um intervalo de tempo específico. A unidade Hz (Hertz) significa ondas geradas por segundo.
(E) Quanto à sua natureza, as ondas podem ser classificadas em mecânicas, eletromagnéticas, transversais e longitudinais.
Resolução:
Os termos longitudinais e transversais referem-se à classificação das ondas quanto à direção de propagação.Alternativa: E
16) Uma determinada fonte gera 3600 ondas por minuto com comprimento de onda igual a 10 m. Determine a velocidade de propagação dessas ondas.
(A) 500 m/s
(B) 360 m/s
(C) 600 m/s
(D) 60 m/s
(E) 100 m/s
Resolução:
A frequência deve estar em rotações por segundo (Hz). Sabendo que 1 min = 60 s, temos:F = 3600 ÷ 60 = 60 HzSendo assim, temos:v = λ.fv = 10. 60 = 600 m/s
Alternativa: C
17) (FAMEMA-SP) Com o objetivo de simular as ondas no mar, foram geradas, em uma cuba de ondas de um laboratório, as ondas bidimensionais representadas na figura, que se propagam de uma região mais funda (região 1) para uma região mais rasa (região 2).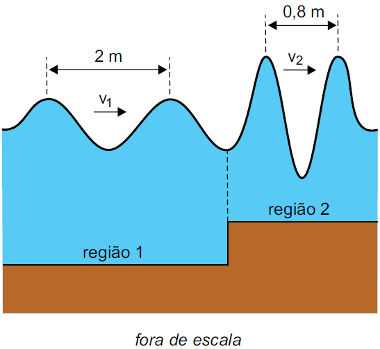 Sabendo que, quando as ondas passam de uma região para a outra, sua frequência de oscilação não se altera e considerando as medidas indicadas na figura, é correto afirmar que a razão entre as velocidades de propagação das ondas nas regiões 1 e 2 é igual a:
Sabendo que, quando as ondas passam de uma região para a outra, sua frequência de oscilação não se altera e considerando as medidas indicadas na figura, é correto afirmar que a razão entre as velocidades de propagação das ondas nas regiões 1 e 2 é igual a:
(A) 1,6.
(B) 0,4.
(C) 2,8.
(D) 2,5.
(E) 1,2.
Resolução: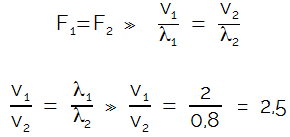 Os valores 2 m e 0,8 m representam os comprimentos das ondas nas regiões 1 e 2, respectivamente.A frequência das ondas deve ser a mesma nas duas regiões, pois, na mudança de lugar de propagação, a frequência de uma onda não é alterada. Sendo assim, temos:F1 = F2Sabendo que a velocidade de uma onda é dada pelo produto do comprimento de onda e a velocidade, podemos entender que a frequência é a razão da velocidade pelo comprimento de onda:
Os valores 2 m e 0,8 m representam os comprimentos das ondas nas regiões 1 e 2, respectivamente.A frequência das ondas deve ser a mesma nas duas regiões, pois, na mudança de lugar de propagação, a frequência de uma onda não é alterada. Sendo assim, temos:F1 = F2Sabendo que a velocidade de uma onda é dada pelo produto do comprimento de onda e a velocidade, podemos entender que a frequência é a razão da velocidade pelo comprimento de onda:
Alternativa: D
18) (IFGO) As ondas são formas de transferência de energia de uma região para outra. Existem ondas mecânicas – que precisam de meios materiais para se propagarem – e ondas eletromagnéticas – que podem se propagar tanto no vácuo como em alguns meios materiais. Sobre ondas, podemos afirmar corretamente que
(A) a energia transferida por uma onda eletromagnética é diretamente proporcional à frequência dessa onda.
(B) o som é uma espécie de onda eletromagnética e, por isso, pode ser transmitido de uma antena à outra, como ocorre nas transmissões de TV e rádio.
(C) a luz visível é uma onda mecânica que somente se propaga de forma transversal.
(D) existem ondas eletromagnéticas que são visíveis aos olhos humanos, como o ultravioleta, o infravermelho e as micro-ondas.
(E) o infrassom é uma onda eletromagnética com frequência abaixo da audível.
Resolução:
A) Correta
B) Errado: O som é uma onda mecânica.
C) Errado: A luz visível é uma onda eletromagnética.
D) Errado: O ultravioleta e infravermelho não são ondas que compõem o espectro visível.
E) Errado: O infrassom é uma onda mecânica com frequência abaixo do audível.
Alternativa: A
19) A respeito das características das ondas, marque a alternativa errada.
(A) Ondas sonoras e ondas sísmicas são exemplos de ondas mecânicas.
(B) A descrição do comportamento das ondas mecânicas é feita pelas leis de Newton.
(C) As ondas eletromagnéticas resultam da combinação de um campo elétrico com um campo magnético.
(D) A descrição das ondas eletromagnéticas é feita por meio das equações de Maxwell.
(E) Quanto à direção de propagação, as ondas geradas em um lago pela queda de uma pedra na água são classificadas como tridimensionais.
Resolução:
As ondas geradas em um lago pela queda de uma pedra na água são classificadas como bidimensionais, pois existem apenas sobre a superfície da água.
Alternativa: E
20) O som mais grave que o ouvido humano é capaz de ouvir possui comprimento de onda igual a 17 m. Sendo assim, determine a mínima frequência capaz de ser percebida pelo ouvido humano.Dados: Velocidade do som no ar = 340 m/s
(A) 10 Hz
(B) 15 Hz
(C) 17 Hz
(D) 20 Hz
(E) 34 Hz
Resolução:
A partir da equação da velocidade de uma onda, podemos escrever que:v = λ . ff = v ÷ λf = 340 ÷ 17f = 20 HzAlternativa: D
21) (Enem/2015) Certos tipos de superfícies na natureza podem refletir luz de forma a gerar um efeito de arco-íris. Essa característica é conhecida como iridescência e ocorre por causa do fenômeno da interferência de película fina. A figura ilustra o esquema de uma fina camada iridescente de óleo sobre uma poça d’água. Parte do feixe de luz branca incidente (1) reflete na interface ar/óleo e sofre inversão de fase (2), o que equivale a uma mudança de meio comprimento de onda. A parte refratada do feixe (3) incide na interface óleo/água e sofre reflexão sem inversão de fase (4). O observador indicado enxergará aquela região do filme com coloração equivalente à do comprimento de onda que sofre interferência completamente construtiva entre os raios (2) e (5), mas essa condição só é possível para uma espessura mínima da película. Considere que o caminho percorrido em (3) e (4) corresponde ao dobro da espessura E da película de óleo. Expressa em termos do comprimento de onda (λ), a espessura mínima é igual a:
Expressa em termos do comprimento de onda (λ), a espessura mínima é igual a:
(A) λ/4
(B) λ/2
(C) 3λ/4
(D) λ
(E) 2λ
Resolução:A diferença de caminho entre as ondas que se superpõem é o dobro da espessura E da lâmina. Sendo a interferência construtiva, temos:2E = i.λ / 2sendo i = 1, 3, 5, ...A espessura mínima corresponde a i = 1:2E = 1 . λ /2E = λ / 4
Resposta: A
22) (ENEM) Uma manifestação comum das torcidas em estádios de futebol é a ola mexicana. Os espectadores de uma linha, sem sair do lugar e sem se deslocarem lateralmente, ficam de pé e se sentam, sincronizados com os da linha adjacente. O efeito coletivo se propaga pelos espectadores do estádio, formando uma onda progressiva, conforme ilustração.Ola mexicana feita por torcedores em estádios de futebol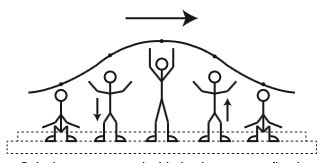 Ola mexicana feita por torcedores em estádios de futebolCalcula-se que a velocidade de propagação dessa “onda humana” é 45 km/h, e que cada período de oscilação contém 16 pessoas, que se levantam e sentam organizadamente e distanciadas entre si por 80 cm.Disponível em: www.ufsm.br.Acesso em: 7 dez. 2012 (adaptado). Nessa olá mexicana, a frequência da onda, em hertz, é um valor mais próximo de
Ola mexicana feita por torcedores em estádios de futebolCalcula-se que a velocidade de propagação dessa “onda humana” é 45 km/h, e que cada período de oscilação contém 16 pessoas, que se levantam e sentam organizadamente e distanciadas entre si por 80 cm.Disponível em: www.ufsm.br.Acesso em: 7 dez. 2012 (adaptado). Nessa olá mexicana, a frequência da onda, em hertz, é um valor mais próximo de
(A) 0,3
(B) 0,5
(C) 1,0
(D) 1,9
(E) 3,7.
Resolução
Inicialmente podemos calcular o comprimento de onda multiplicando a distância entre as pessoas, 0,8 (80 cm = 0,8m), pelo número de “distâncias”, que é 15, visto que há 16 pessoas:λ = 15 . 0,8λ = 12 mEm seguida, calcula-se a frequência através da seguinte expressão:f = v λ Dada a velocidade (v = 45 km/h), devemos passar sua unidade de medida para m/s. Para isso, basta dividi-la por 3,6:v = 45 = 12,5 m/s 3,6Substituindo na equação:f = 12,5 = 1,04 12Alternativa: C
23) (ENEM) A radiação ultravioleta (UV) é dividida, de acordo com três faixas de frequência, em UV-A, UV-B e UV-C, conforme a figura.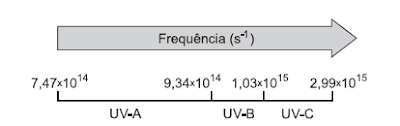 Para selecionar um filtro solar que apresente absorção máxima na faixa UV-B, uma pessoa analisou os espectros de absorção da radiação UV de cinco filtros solares:Observação: velocidade da luz = 3,0 x 108 m/s e 1 nm = 1,0 x 10-9 m.
Para selecionar um filtro solar que apresente absorção máxima na faixa UV-B, uma pessoa analisou os espectros de absorção da radiação UV de cinco filtros solares:Observação: velocidade da luz = 3,0 x 108 m/s e 1 nm = 1,0 x 10-9 m.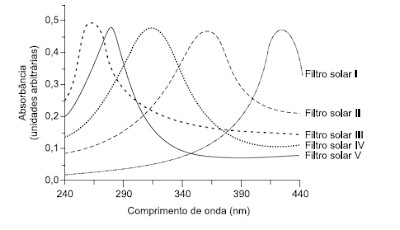 O filtro solar que a pessoa deve selecionar é o
O filtro solar que a pessoa deve selecionar é o
(A) V
(B) IV
(C) III
(D) II
(E) I
Resolução:
Cálculo dos comprimentos de onda das frequências extremas da faixa UV-B.c = λ.fλ= c / fλmin = 3,0.108 / 1,03.1015λmin ≅ 2,9.10-7 m = 290 nmλmáx = 3,0.108 / 9,34.1014λmáx ≅ 3,2.10-7 m = 320 nmEntre 290 nm e 320 nm, o filtro que apresenta absorção máxima é o filtro solar IV.
Resposta: B
24) (Enem) Para obter a posição de um telefone celular, a polícia baseia-se em informações do tempo de resposta do aparelho em relação às torres de celular da região de onde se originou a ligação. Em uma região, um aparelho está na área de cobertura de cinco torres, conforme o esquema. Considerando que as torres e o celular são puntiformes e que estão sob o mesmo plano, qual o número mínimo de torres necessárias para se localizar a posição do telefone celular que originou a ligação?
Considerando que as torres e o celular são puntiformes e que estão sob o mesmo plano, qual o número mínimo de torres necessárias para se localizar a posição do telefone celular que originou a ligação?
(A) Uma.
(B) Duas.
(C) Três.
(D) Quatro.
(E) Cinco.
Resolução:
Observação: o sinas da torre e transmitido através de ondas e nesse caos ondas circulares e portanto seu alcance atinge a um determinado raio.Conhecendo-se pelo menos as distâncias a três torres é possível localizar a posição do celular, por meio de um processo chamado triangulação.Seja d1 a distância do celular à primeira torre. O celular pode estar em qualquer ponto da circunferência de centro na primeira torre A1 e raio d1 (figura a). Seja d2 a distância do celular à segunda torre A2. O celular pode estar num dos dois pontos P1 ou P2 em que as circunferências se interceptam (figura b). Seja d3 a distância do celular à terceira torre A3. A intersecção das três circunferências ocorre num ponto P onde se localiza o celular (figura c).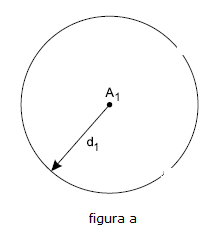
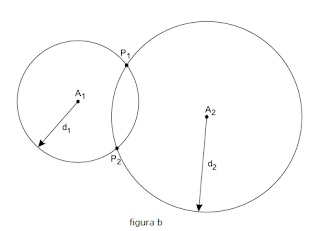
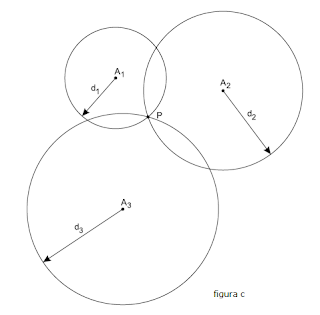 Alternativa: C
Alternativa: C
25) (Mackenzie SP/2006) As antenas das emissoras de rádio emitem ondas eletromagnéticas que se propagam na atmosfera com a velocidade da luz (3,0.105 km/s) e com frequências que variam de uma estação para a outra.A rádio CBN emite uma onda de frequência 90,5 MHz e comprimento de onda aproximadamente igual a:
(A) 2,8 m
(B) 3,3 m
(C) 4,2 m
(D) 4,9 m
(E) 5,2 m
Resolução:
f = 90,5 MHz = 90,5 . 106 HzVelocidade da luz (c)c = 3,0 . 105 km/souc = 3,0 . 108 m/sPodemos utilizar a equação: v = λ . f, mas nesse caso trocaremos “v” por “c” por se tratar da velocidade da luz.Então:c = λ . f3,0 . 108 = λ . 90,5 . 106λ = 3,0 . 108 90,5.106λ = 0,033 . 108-6 → = 0,033 . 10² λ = 3,3 mAlternativa: B
26) (Unifor/CE) Na figura está representada a configuração de uma onda mecânica que se propaga com velocidade de 20 m/s. A frequência da onda, em hertz, vale:
A frequência da onda, em hertz, vale:
(A) 5,0
(B) 10
(C) 20
(D) 25
(E) 50
Resolução:
Pela figura podemos perceber que λ = 20 cm 4Logo λ = 80 cm = 0,8 mv = λ . fSabendo que v = 20 m/s, temos:20 = 0,8 . ff = 20 0,8f = 25 HzAlternativa: D
27) (Velocidade de onda) Ao dobrarmos a freqüência com que vibra uma fonte de ondas produzidas na água, numa experiência com ondas de água em um tanque:
(A) dobra o período
(B) dobra a velocidade de propagação da onda.
(C) o período não se altera
(D) a velocidade de propagação da onda se reduz à metade
(E) o comprimento de onda se reduz à metade
Resolução
A velocidade de propagação da onda na água é constante.Logo, b e d são falsas.O período é o inverso da freqüência, se esta última dobrou, implica a redução do período pela metade. Então, a e c são falsas.A velocidade de onda é dada por:V = λ.fOnde λ é o comprimento de onda e f é a freqüência da onda e V é a velocidade de propagação da onda.Se f’ = 2 fV = λ’.f’V = λ’ . 2 f = λ . fλ' = λ / 2Alternativa: E
28) (Fuvest 2002) Radiações como raios X, luz verde, luz ultravioleta, microondas ou ondas de rádio são caracterizadas por seu comprimento de onda (l) e por sua freqüência (f).Quando essas radiações propagam-se no vácuo, todas apresentam o mesmo valor para:
(A) λ
(B) f
(C) λ.f
(D) λ / f
(E) λ2 / f
Resolução
Todas as radiações citadas no enunciado do exercício são ondas eletromagnéticas. As ondas eletromagnéticas se propagam no vácuo com velocidade igual a velocidade da luz.A equação para velocidade de onda é v = λ.f. Alternativa: C
29) (UFPA) Uma onda tem frequência de 10 Hz e se propaga com velocidade de 400 m/s. então, seu comprimento de onda vale, em metros.
(A) 0,04
(B) 0,4
(C) 4
(D) 40
(E) 400
Resolução
São dados do exercício:V = 400 m/sf = 10 HzComo os dados já estão no sistema internacional de unidades, basta utilizar a equação de velocidade de onda:V = λ.fLogo,λ = V /fλ = 400 / 10λ = 40 mAlternativa: D
30) (Enem) As ondas eletromagnéticas, como a luz visível e as ondas de rádio, viajam em linha reta em um meio homogêneo. Então, as ondas de rádio emitidas na região litorânea do Brasil não alcançariam a região amazônica do Brasil por causa da curvatura da Terra. Entretanto sabemos que é possível transmitir ondas de rádio entre essas duas localidades em virtude da ionosfera.Com a ajuda da ionosfera, a transmissão de ondas planas entre o litoral do Brasil e a região amazônica é possível por meio da:
(A) Reflexão
(B) Refração
(C) Difração
(D) Polarização
(E) Interferência
Resolução
As ondas eletromagnéticas, emitidas no litoral do Brasil, chegam até a Amazônia após sofrer reflexão na ionosfera.
Alternativa: A
32) Na Terra, certo pêndulo simples executa oscilações com período de 1s.a) Qual o período desse pêndulo se posto a oscilar na Lua, onde a aceleração da gravidade é 6 vezes menor?b) Que aconteceria com o período desse pêndulo à medida que fosse removido para uma região livre de ações gravitacionais?Resolução:Um pêndulo simples é um corpo ideal, constituído por uma partícula suspensa por um fio inextensível e de massa desprezível. Quando esta partícula é afastada de sua posição de equilíbrio e solta, o pêndulo oscila em um plano vertical sob á ação da aceleração gravitacional. O movimento do pêndulo é periódico e oscilatório e podemos determinar o período do movimento pela seguinte equação: a) Aplicando a equação definimos o período de um pêndulo na Terra e outro na Lua:
a) Aplicando a equação definimos o período de um pêndulo na Terra e outro na Lua: A razão entre estas duas equações nos fornecerá o período do pêndulo na Lua.
A razão entre estas duas equações nos fornecerá o período do pêndulo na Lua. Como gL = gT / 6, temos:
Como gL = gT / 6, temos: Sabendo que TT = 1s:
Sabendo que TT = 1s: b) remover o pêndulo para uma região livre de ações gravitacionais é o mesmo que dizer que a aceleração gravitacional tende a zero. Pela equação do período do pêndulo simples, este período tenderia a infinito.
b) remover o pêndulo para uma região livre de ações gravitacionais é o mesmo que dizer que a aceleração gravitacional tende a zero. Pela equação do período do pêndulo simples, este período tenderia a infinito.
QUESTÕES RESOLVIDAS
Observação: alguns desses exercícios abordam fenômenos que envolvem as ondas sonoras e as ondas luminosas. Portanto, para resolvê-los, você precisa conhecer as características e fenômenos relacionados ao som e a luz.
33) (ENEM/2015) Certos tipos de superfícies na natureza podem refletir luz de forma a gerar um efeito de arco-íris. Essa característica é conhecida como iridescência e ocorre por causa do fenômeno da interferência de película fina. A figura ilustra o esquema de uma fina camada iridescente de óleo sobre uma poça d’água. Parte do feixe de luz branca incidente (1) reflete na interface ar/óleo e sofre inversão de fase (2), o que equivale a uma mudança de meio comprimento de onda. A parte refratada do feixe (3) incide na interface óleo/água e sofre reflexão sem inversão de fase (4). O observador indicado enxergará aquela região do filme com coloração equivalente à do comprimento de onda que sofre interferência completamente construtiva entre os raios (2) e (5), mas essa condição só é possível para uma espessura mínima da película. Considere que o caminho percorrido em (3) e (4) corresponde ao dobro da espessura E da película de óleo. Expressa em termos do comprimento de onda (λ), a espessura mínima é igual a:
Expressa em termos do comprimento de onda (λ), a espessura mínima é igual a:
(A) λ/4
(B) λ/2
(C) 3λ/4
(D) λ
(E) 2λ
Resolução:
A diferença de caminho entre as ondas que se superpõem é o dobro da espessura E da lâmina. Sendo a interferência construtiva, temos:
2E = i.λ / 2
sendo i = 1, 3, 5, ...
A espessura mínima corresponde a i = 1:
2E = 1 . λ /2
E = λ / 4
Resposta: A
34) (ENEM) Uma manifestação comum das torcidas em estádios de futebol é a ola mexicana. Os espectadores de uma linha, sem sair do lugar e sem se deslocarem lateralmente, ficam de pé e se sentam, sincronizados com os da linha adjacente. O efeito coletivo se propaga pelos espectadores do estádio, formando uma onda progressiva, conforme ilustração.
Ola mexicana feita por torcedores em estádios de futebol Ola mexicana feita por torcedores em estádios de futebol
Ola mexicana feita por torcedores em estádios de futebol
Calcula-se que a velocidade de propagação dessa “onda humana” é 45 km/h, e que cada período de oscilação contém 16 pessoas, que se levantam e sentam organizadamente e distanciadas entre si por 80 cm.
Nessa olá mexicana, a frequência da onda, em hertz, é um valor mais próximo de
(A) 0,3
(B) 0,5
(C) 1,0
(D) 1,9
(E) 3,7.
Resolução
Inicialmente podemos calcular o comprimento de onda multiplicando a distância entre as pessoas, 0,8 (80 cm = 0,8m), pelo número de “distâncias”, que é 15, visto que há 16 pessoas:
λ = 15 . 0,8
λ = 12 m
Em seguida, calcula-se a frequência através da seguinte expressão:
f = v
λ
Dada a velocidade (v = 45 km/h), devemos passar sua unidade de medida para m/s. Para isso, basta dividi-la por 3,6:
v = 45 = 12,5 m/s
3,6
Substituindo na equação:
f = 12,5 = 1,04
12
Alternativa: C
35) (ENM/2005) A radiação ultravioleta (UV) é dividida, de acordo com três faixas de frequência, em UV-A, UV-B e UV-C, conforme a figura. Para selecionar um filtro solar que apresente absorção máxima na faixa UV-B, uma pessoa analisou os espectros de absorção da radiação UV de cinco filtros solares:
Para selecionar um filtro solar que apresente absorção máxima na faixa UV-B, uma pessoa analisou os espectros de absorção da radiação UV de cinco filtros solares:
Observação: velocidade da luz = 3,0 x 108 m/s e 1 nm = 1,0 x 10-9 m. O filtro solar que a pessoa deve selecionar é o
O filtro solar que a pessoa deve selecionar é o
(A) V
(B) IV
(C) III
(D) II
(E) I
Resolução:
Cálculo dos comprimentos de onda das frequências extremas da faixa UV-B.
c = λ.f
λ= c / f
λmin = 3,0.108 / 1,03.1015
λmin ≅ 2,9.10-7 m = 290 nm
λmáx = 3,0.108 / 9,34.1014
λmáx ≅ 3,2.10-7 m = 320 nm
Entre 290 nm e 320 nm, o filtro que apresenta absorção máxima é o filtro solar IV.
Resposta: B
36) (ENEM/2015) Para obter a posição de um telefone celular, a polícia baseia-se em informações do tempo de resposta do aparelho em relação às torres de celular da região de onde se originou a ligação. Em uma região, um aparelho está na área de cobertura de cinco torres, conforme o esquema. Considerando que as torres e o celular são puntiformes e que estão sob o mesmo plano, qual o número mínimo de torres necessárias para se localizar a posição do telefone celular que originou a ligação?
Considerando que as torres e o celular são puntiformes e que estão sob o mesmo plano, qual o número mínimo de torres necessárias para se localizar a posição do telefone celular que originou a ligação?
(A) Uma.
(B) Duas.
(C) Três.
(D) Quatro.
(E) Cinco.
Resolução:
Observação: o sinas da torre e transmitido através de ondas e nesse caos ondas circulares e portanto seu alcance atinge a um determinado raio.
Conhecendo-se pelo menos as distâncias a três torres é possível localizar a posição do celular, por meio de um processo chamado triangulação.
Seja d1 a distância do celular à primeira torre. O celular pode estar em qualquer ponto da circunferência de centro na primeira torre A1 e raio d1 (figura a). Seja d2 a distância do celular à segunda torre A2. O celular pode estar num dos dois pontos P1 ou P2 em que as circunferências se interceptam (figura b). Seja d3 a distância do celular à terceira torre A3. A intersecção das três circunferências ocorre num ponto P onde se localiza o celular (figura c).


Alternativa: C
37) (Mackenzie SP/2006) As antenas das emissoras de rádio emitem ondas eletromagnéticas que se propagam na atmosfera com a velocidade da luz (3,0.105 km/s) e com frequências que variam de uma estação para a outra.
A rádio CBN emite uma onda de frequência 90,5 MHz e comprimento de onda aproximadamente igual a:
(A) 2,8 m
(B) 3,3 m
(C) 4,2 m
(D) 4,9 m
(E) 5,2 m
Resolução:
f = 90,5 MHz = 90,5 . 106 Hz
Velocidade da luz (c) = 3,0 . 105 km/s → c = 3,0 . 108 m/s
Podemos utilizar a equação: v = λ . f, mas nesse caso trocaremos “v” por “c” por se tratar da velocidade da luz.
Então:
c = λ . f
3,0 . 108 = λ . 90,5 . 106
λ = 3,0 . 108
90,5.106
λ = 0,033 . 108-6 → = 0,033 . 10²
λ = 3,3 m
Alternativa: B
38) (Unifor/CE) Na figura está representada a configuração de uma onda mecânica que se propaga com velocidade de 20 m/s. A frequência da onda, em hertz, vale:
A frequência da onda, em hertz, vale:
(A) 5,0
(B) 10
(C) 20
(D) 25
(E) 50
Resolução:
Pela figura podemos perceber que λ = 20 cm
4
Logo λ = 80 cm = 0,8 m
v = λ . f
Sabendo que v = 20 m/s, temos: 20 = 0,8 . f
f = 20
0,8
f = 25 Hz
Alternativa: D
39) (Velocidade de onda) Ao dobrarmos a freqüência com que vibra uma fonte de ondas produzidas na água, numa experiência com ondas de água em um tanque:
(A) dobra o período
(B) dobra a velocidade de propagação da onda.
(C) o período não se altera
(D) a velocidade de propagação da onda se reduz à metade
(E) o comprimento de onda se reduz à metade
Resolução
A velocidade de propagação da onda na água é constante.
Logo, b e d são falsas.
O período é o inverso da freqüência, se esta última dobrou, implica a redução do período pela metade. Então, a e c são falsas.
A velocidade de onda é dada por:
V = λ.f
Onde λ é o comprimento de onda e f é a freqüência da onda e V é a velocidade de propagação da onda.
Se f’ = 2 f
V = λ’.f’
V = λ’ . 2 f = λ . f
λ' = λ / 2
Alternativa: E
40) (Fuvest 2002) Radiações como raios X, luz verde, luz ultravioleta, microondas ou ondas de rádio são caracterizadas por seu comprimento de onda (l) e por sua freqüência (f).
Quando essas radiações propagam-se no vácuo, todas apresentam o mesmo valor para:
(A) λ
(B) f
(C) λ.f
(D) λ / f
(E) λ2 / f
Resolução
Todas as radiações citadas no enunciado do exercício são ondas eletromagnéticas. As ondas eletromagnéticas se propagam no vácuo com velocidade igual a velocidade da luz.
A equação para velocidade de onda é v = λ.f
Alternativa: C
41) (UFPA) Uma onda tem frequência de 10 Hz e se propaga com velocidade de 400 m/s. então, seu comprimento de onda vale, em metros.
(A) 0,04
(B) 0,4
(C) 4
(D) 40
(E) 400
Resolução
São dados do exercício:
V = 400 m/s
f = 10 Hz
Como os dados já estão no sistema internacional de unidades, basta utilizar a equação de velocidade de onda:
V = λ.f
Logo,
λ = V /f
λ = 400 / 10
λ = 40 m
Alternativa: D
42) (ENEM) As ondas eletromagnéticas, como a luz visível e as ondas de rádio, viajam em linha reta em um meio homogêneo. Então, as ondas de rádio emitidas na região litorânea do Brasil não alcançariam a região amazônica do Brasil por causa da curvatura da Terra. Entretanto sabemos que é possível transmitir ondas de rádio entre essas duas localidades em virtude da ionosfera.
Com a ajuda da ionosfera, a transmissão de ondas planas entre o litoral do Brasil e a região amazônica é possível por meio da:
(A) Reflexão
(B) Refração
(C) Difração
(D) Polarização
(E) Interferência
Resolução
As ondas eletromagnéticas, emitidas no litoral do Brasil, chegam até a Amazônia após sofrer reflexão na ionosfera.
Alternativa: A
46) Na Terra, certo pêndulo simples executa oscilações com período de 1s.
a) Qual o período desse pêndulo se posto a oscilar na Lua, onde a aceleração da gravidade é 6 vezes menor?
b) Que aconteceria com o período desse pêndulo à medida que fosse removido para uma região livre de ações gravitacionais?
Resolução:
Um pêndulo simples é um corpo ideal, constituído por uma partícula suspensa por um fio inextensível e de massa desprezível. Quando esta partícula é afastada de sua posição de equilíbrio e solta, o pêndulo oscila em um plano vertical sob á ação da aceleração gravitacional. O movimento do pêndulo é periódico e oscilatório e podemos determinar o período do movimento pela seguinte equação: a) Aplicando a equação definimos o período de um pêndulo na Terra e outro na Lua:
a) Aplicando a equação definimos o período de um pêndulo na Terra e outro na Lua: A razão entre estas duas equações nos fornecerá o período do pêndulo na Lua.
A razão entre estas duas equações nos fornecerá o período do pêndulo na Lua. Como gL = gT / 6, temos:
Como gL = gT / 6, temos: Sabendo que TT = 1s:
Sabendo que TT = 1s: b) remover o pêndulo para uma região livre de ações gravitacionais é o mesmo que dizer que a aceleração gravitacional tende a zero. Pela equação do período do pêndulo simples, este período tenderia a infinito.
b) remover o pêndulo para uma região livre de ações gravitacionais é o mesmo que dizer que a aceleração gravitacional tende a zero. Pela equação do período do pêndulo simples, este período tenderia a infinito.
EXERCÍCIOS DE FIXAÇÃO/RESOLVIDOS
01) (Uece) Sobre as ondas sonoras, é correto afirmar que não se propagam:
(A) na atmosfera.
(B) na água.
(C) no vácuo.
(D) nos meios metálicos.
Resolução:
O som é uma onda do tipo mecânica, e isso significa que as ondas sonoras precisam de um meio de propagação, um lugar por onde se movem. No vácuo, não existem moléculas capazes de sofrerem vibrações e produzirem sons.
Alternativa: C
02) Marque a alternativa correta a respeito da velocidade de propagação das ondas sonoras.
(A) O som pode propagar-se apenas em meios gasosos.
(B) Em meios líquidos, a velocidade do som é maior do que em meios sólidos.
(C) A velocidade de propagação do som no aço é maior do que na água.
(D) A velocidade de propagação do som na água é maior do que no aço.
(E) O som, assim como as ondas eletromagnéticas, pode ser propagado no vácuo.
Resolução:
O som é uma onda mecânica, por isso, precisa de uma meio de propagação. Quanto maior for a proximidade das moléculas que compõem o meio de propagação das ondas sonoras, maior será a sua velocidade. Dessa forma, a velocidade do som nos sólidos é maior que nos líquidos e nos gases.
Alternativa: C
03) (UFPA) Uma onda tem frequência de 10 Hz e se propaga com velocidade de 400 m/s. então, seu comprimento de onda vale, em metros.
(A) 0,04
(B) 0,4
(C) 4
(D) 40
(E) 400
Resolução
São dados do exercício:
V = 400 m/s
f = 10 Hz
Como os dados já estão no sistema internacional de unidades, basta utilizar a equação de velocidade de onda:
V = λ.f
Logo,
λ = V /f
λ = 400 / 10
λ = 40 m
Alternativa: D
04) O som mais grave que o ouvido humano é capaz de ouvir possui comprimento de onda igual a 17m. Sendo assim, determine a mínima frequência capaz de ser percebida pelo ouvido humano.
Dados: Velocidade do som no ar = 340 m/s
(A) 10 Hz
(B) 15 Hz
(C) 17 Hz
(D) 20 Hz
(E) 34 Hz
Resolução:
A partir da equação da velocidade de uma onda, podemos escrever que:
v = λ . f
f = v ÷ λ
f = 340 ÷ 17
f = 20 Hz
Alternativa: D
05) (UFPE) Diante de uma grande parede vertical, um garoto bate palmas e recebe o eco um segundo depois. Se a velocidade do som no ar é 340 m/s, o garoto pode concluir que a parede está situada a uma distância aproximada de:
(A) 17 m
(B) 34 m
(C) 68 m
(D) 170 m
(E) 340 m
Resolução:
Aqui podemos utilizar a equação que define velocidade:
v = Δs ÷ Δt
Para que haja eco, o som deve sair da fonte, chocar-se com um obstáculo e voltar. Sendo assim, o espaço percorrido deve ser multiplicado por 2:
v = 2Δs ÷ Δt
340 = 2Δs ÷ 1
340 = 2Δs
340 ÷ 2 = Δs
Δs = 170 m
Alternativa: D
06) Unifor/CE/Janeiro/Conh. Gerais/2001) Na figura está representada a configuração de uma onda mecânica que se propaga com velocidade de 20 m/s. A frequência da onda, em hertz, vale:
A frequência da onda, em hertz, vale:
(A) 5,0
(B) 10
(C) 20
(D) 25
(E) 50
Resolução:
Pela figura podemos perceber que λ = 20 cm
4
Logo λ = 80 cm = 0,8 m
Como v = λ . f e sabendo que v = 20 m/s, temos: 20 = 0,8 . f
f = 20
0,8
f = 25 Hz
Alternativa: D
07) É correto afirmar sobre as ondas mecânicas:
(A) transportam massa e energia
(B) transportam massa e quantidade de movimento
(C) transportam matéria
(D) Transportam energia e quantidade de movimento
(E) Nda
Resolução:
As ondas mecânicas são perturbações de um meio material elástico que se propagam por esse meio, transportando energia e quantidade de movimento.
Portanto, na propagação das ondas há transporte de energia e quantidade de movimento.
Alternativa: D
08) Uma determinada fonte gera 3600 ondas por minuto com comprimento de onda igual a 10 m. Determine a velocidade de propagação dessas ondas.
(A) 500 m/s
(B) 360 m/s
(C) 600 m/s
(D) 60 m/s
(E) 100 m/s
Resolução:
A frequência deve estar em rotações por segundo (Hz). Sabendo que 1 min = 60 s, temos:
F = 3600 ÷ 60 = 60 Hz
Sendo assim, temos:
v = λ.f
v = 10. 60 = 600 m/s
Alternativa: C
09) O gráfico abaixo representa uma onda que se propaga com velocidade igual a 300m/s.Com base na representação acima determine:
(1) a amplitude da onda.
Resolução:
A Amplitude da onda é dada pela distância da origem até a crista da onda, ou seja:![]()
(2) o comprimento de onda.
Resolução:
O comprimento de onda é dado pela distância entre duas cristas ou entre 3 nodos, ou seja:
Como a figura mostra a medida de três "meios-comprimento de onda", podemos calculá-lo: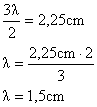
(3) a frequência.
Resolução:
Sabendo a velocidade de propagação e o comprimento de onda, podemos calcular a frequência através da equação:![]()
Substituindo os valores na equação:
(4) o período.
Resolução
Como o período é igual ao inverso da frequência: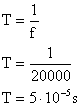
Refração das ondas
10) Uma agulha vibratória produz ondas com velocidade de propagação igual a 160m/s e comprimento de onda de 1mm, chegando em uma diferença de profundidade com um ângulo formado de 45° e sendo refratado. Após a mudança de profundidades o ângulo refratado passa a ser de 30°. Qual é a nova velocidade de progação da onda?
E o comprimento das ondas refratadas?
Ângulos de incidência e refração
A imagem abaixo mostra um raio de luz sofrendo refração, passando de um meio com índice de refração n1 para outro meio com índice n2. Lei de Snell-Descartes
Lei de Snell-Descartes
A lei de Snell-Descartes relaciona os ângulos formados entre os raios de luz e a reta normal com os índices de refração dos meios em análise.![]() Esta lei determina que o produto do seno do ângulo formado entre o raio de luz e a reta normal e o índice de refração do meio deve ser constante. A partir da imagem anterior, podemos escrever esta lei da seguinte forma:
Esta lei determina que o produto do seno do ângulo formado entre o raio de luz e a reta normal e o índice de refração do meio deve ser constante. A partir da imagem anterior, podemos escrever esta lei da seguinte forma:
Caso o raio de luz passe para uma região de maior índice de refração, ocorrerá diminuição no valor da velocidade, e então ele se aproximará da reta normal. Se o raio de luz mudar para uma região de menor índice de refração, ocorrerá aumento no valor da velocidade, e então ele se afastará da reta normal.
Utilizando a Lei de Snell:![]()
00) (UEFS BA) Um raio luminoso incide sobre a superfície de separação entre o ar e o vidro com um ângulo α = 60° e refrata com um ângulo β = 30°, como mostra a figura. Considerando sen30º = cos60º = 0,5; sen60º = cos30º = 0,87; o índice de refração do ar igual a 1 e o índice de refração do vidro igual a n, então o valor de n é igual a
Considerando sen30º = cos60º = 0,5; sen60º = cos30º = 0,87; o índice de refração do ar igual a 1 e o índice de refração do vidro igual a n, então o valor de n é igual a
(A) 1,48
(B) 1,57
(C) 1,63
(D) 1,74
(E) 1,83
Resolução:
A partir da aplicação da lei de Snell-Descartes, podemos definir o índice de refração do vidro.
11) Marque a alternativa que responde corretamente o fato de a frequência das ondas não ser alterada na ocorrência da refração.
(A) A única mudança que ocorre na refração é da velocidade das ondas.
(B) Caso a frequência fosse alterada, a onda sofreria colapso e seria completamente anulada.
(C) A frequência de todas as ondas é a mesma, por isso, essa grandeza não pode ser alterada na refração.
(D) A frequência depende somente da fonte que produz as oscilações. Essa grandeza só será alterada caso a própria fonte aumente ou diminua sua frequência.
(E) Todas as alternativas estão incorretas.
Resolução:
A frequência é definida como a quantidade de ondas produzidas dentro de um intervalo de tempo. Essa característica das ondas depende apenas da fonte geradora delas, sendo assim, mesmo na ocorrência de uma refração, a frequência das ondas será mantida.
Alternativa: D
12) Marque a alternativa que responde corretamente o fato de a frequência das ondas não ser alterada na ocorrência da refração.
(A) A única mudança que ocorre na refração é da velocidade das ondas.
(B) Caso a frequência fosse alterada, a onda sofreria colapso e seria completamente anulada.
(C) A frequência de todas as ondas é a mesma, por isso, essa grandeza não pode ser alterada na refração.
(D) A frequência depende somente da fonte que produz as oscilações. Essa grandeza só será alterada caso a própria fonte aumente ou diminua sua frequência.
(E) Todas as alternativas estão incorretas.
Resolução:
A frequência é definida como a quantidade de ondas produzidas dentro de um intervalo de tempo. Essa característica das ondas depende apenas da fonte geradora delas, sendo assim, mesmo na ocorrência de uma refração, a frequência das ondas será mantida.
Alternativa: D
QUESTÕES RESOLVIDAS -SEDUC-SP/2025
01) (Livro do aluno/2025-SEDUC-SP -UFSM 2006) Quando o badalo bate num sino, e o faz vibrar comprimindo e rarefazendo o ar nas suas proximidades, produz-se uma onda sonora. As ondas sonoras no ar são _______________ e _____________. A velocidade das ondas sonoras em outro meio é _______________.
Selecione a alternativa que preenche corretamente as lacunas.
(A) eletromagnéticas – transversais – igual.
(B) mecânicas – longitudinais – igual.
(C) mecânicas – transversais – diferente.
(D) eletromagnéticas – longitudinais – igual.
(E) mecânicas – longitudinais – diferente
Alternativa: E
02) (Livro do aluno/2025-SEDUC-SP - UFPEL 2006 – Adaptada) Recentemente, o físico Marcos Pontes se tornou o primeiro astronauta brasileiro a ultrapassar a atmosfera terrestre. Diariamente existiam contatos entre Marcos e a base, e alguns deles eram transmitidos por intermédio dos meios de comunicação. Com base no texto e em seus conhecimentos, é correto afirmar que conseguíamos “ouvir” e “falar” com Marcos porque, para essa conversa, estavam envolvidas:
(A) apenas ondas mecânicas – transversais – já que estas se propagam tanto no vácuo quanto no ar.
(B) apenas ondas eletromagnéticas – longitudinais – já que estas se propagam tanto no vácuo quanto no ar.
(C) ondas eletromagnéticas – transversais – que apresentam as mesmas frequências, velocidade e comprimento de onda, ao passar de um meio para outro.
(D) ondas mecânicas – transversais – que apresentam as mesmas frequências, velocidade e comprimento de onda, ao passar de um meio para outro.
(E) tanto ondas eletromagnéticas – transversais – que se propagam no vácuo, quanto ondas mecânicas – longitudinais – que necessitam de um meio material para a sua propagação.
Alternativa: E
03) (Livro do aluno/2025-SEDUC-SP - UFMG 2006) Enquanto brinca, Gabriela produz uma onda transversal em uma corda esticada. Em certo instante, parte dessa corda tem a forma mostrada na figura a seguir. A direção de propagação da onda na corda também está indicada na figura. Assinale a alternativa em que estão representados CORRETAMENTE a direção e o sentido do deslocamento do ponto P da corda, no instante mostrado.
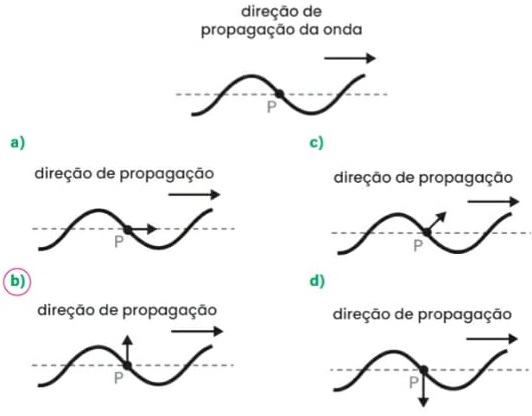
Resolução:
Sabendo que uma onda numa corda é a transversal, a direção de vibração/oscilação da onda, isto é, de deslocamento do ponto P, só pode ser perpendicular à direção de propagação. Restam as alternativas “b”e “d”.
Como a onda se propaga da esquerda para a direita, a crista está se aproximando do ponto P, que, por isso, tem sentido de propagação para cima.
04) (Livro do aluno/2025-SEDUC-SP - ENEM 2013) Uma manifestação comum das torcidas em estádios de futebol é a olá mexicana. Os espectadores de uma linha, sem sair do lugar e sem se deslocar lateralmente, ficam de pé e se sentam, sincronizados com os da linha adjacente. O efeito coletivo se propaga pelos espectadores do estádio, formando uma onda progressiva, conforme ilustração. Calcula-se que a velocidade de propagação dessa “onda humana” é 45 km/h, e que cada período de oscilação contém 16 pessoas, que se levantam e sentam organizadamente e distanciadas entre si por 80 cm.
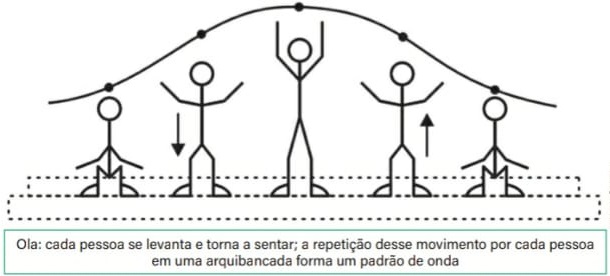
Nessa olá mexicana, a frequência da onda, em hertz, é um valor mais próximo de:
(A) 0,3
(B) 0,5
(C) 1,0
(D) 1,9
(E) 3,7
Resolução:
De acordo com o enunciado, na "ola mexicana", 16 pessoas ficam de pé e se sentam de forma sincronizada, criando um efeito de onda que se propaga pelo estádio. Entre essas 16 pessoas, há 15 espaços, cada um medindo 0,8 m. Assim, o comprimento de onda (λ) é calculado da seguinte maneira.
λ = 15 · 0,8 = 12 m
Convertendo km/h para m/s:
45 km/h ÷ 3,6 = 12,5 m/s
Aplicando a equação fundamental:
Alternativa: C
05) (Livro do aluno/2025-SEDUC-SP - UDESC 2014) Em uma corda, dois pulsos de onda propagam-se em sentidos opostos, conforme mostra a figura.
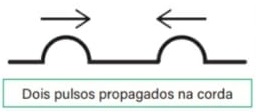
Assinale a alternativa que representa corretamente a propagação dos pulsos de onda, nos seguintes momentos: antes da interferência (I), durante a interferência (II) e após a interferência (III), respectivamente:
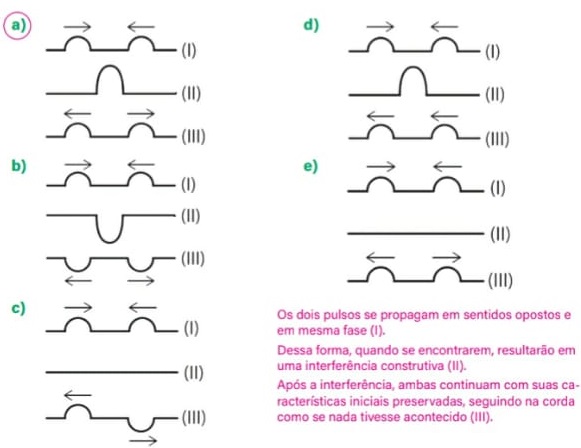
Alternativa: A
06) (Livro do aluno/2025-SEDUC-SP - UFPR 2021) Uma onda é produzida numa corda de modo que a velocidade de propagação vale v = 5 m/s. Sabe-se que a distância entre dois nós sucessivos dessa onda é de 5 mm. Considerando as informações apresentadas, assinale a alternativa que apresenta corretamente o período T da onda na corda.
(A) 1 ms
(B) 2 ms
(C) 5 ms
(D) 10 ms
(E) 20 ms
Resolução:

Alternativa: B
07) (Livro do aluno/2025-SEDUC-SP - UFTM 2011 – Adaptada) Sílvia e Patrícia brincavam com uma corda quando perceberam que, prendendo uma das pontas num pequeno poste e agitando a outra ponta em um mesmo plano, faziam com que a corda oscilasse de forma que alguns de seus pontos permaneciam parados, ou seja, se estabelecia na corda uma onda estacionária.
A figura 1 mostra a configuração da corda quando Sílvia está brincando e a figura 2 mostra a configuração da mesma corda quando Patrícia está brincando. Considerando-se iguais, nas duas situações, as velocidades de propagação das ondas na corda, e chamando de fs e fp as frequências com que Sílvia e Patrícia, respectivamente, estão fazendo a corda oscilar, calcule a razão fS/fP.

08) (Livro do aluno/2025-SEDUC-SP - FCMSCSP 2024) Nas transmissões de corridas automobilísticas, é perceptível que a frequência do som emitido pelo motor de um automóvel, captado por um microfone estático quando o automóvel dele se aproxima, é diferente da frequência quando ele se afasta.
A frequência do som captado quando o automóvel se aproxima e a frequência do som captado quando se afasta, em relação à frequência do som emitido pelo motor, são, respectivamente:
(A) igual e maior.
(B) igual e menor.
(C) maior e menor.
(D) menor e igual.
Resolução:
A causa do efeito Doppler está relacionada ao espaçamento das linhas de onda, que muda devido ao movimento da fonte (F), como ilustrado na figura a seguir
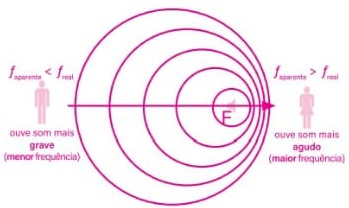
Na aproximação (à direita), as linhas de onda estão mais próximas umas das outras, resultando em uma frequência aparente maior. Por outro lado, no afastamento (à esquerda), as linhas de onda se afastam, levando a uma frequência aparente menor.
Alternativa: C
09) (Livro do aluno/2025-SEDUC-SP - URCA 2018) Um observador em repouso, munido de um detector de frequências sonoras, detecta uma frequência igual a f1 quando uma fonte sonora se aproxima, e uma frequência igual a f2 quando essa mesma fonte sonora se afasta.
O fenômeno relacionado à alteração da frequência detectada por um observador e uma fonte sonora devido ao movimento relativo entre eles é chamado Efeito Doppler. Seja vs a velocidade de propagação do som no ar, podemos afirmar que a velocidade da fonte sonora é igual a:

Resolução:
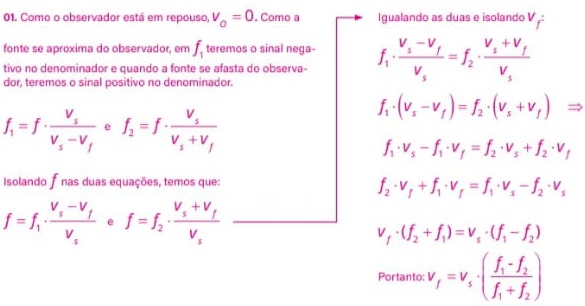
Partindo da equação da frequência observada e sabendo que (i) o observador está em repouso (vO = 0) e (ii) o automóvel (fonte sonora) se aproxima, usaremos o sinal de menos no denominador da equação. Assim, teremos:

Alternativa: B
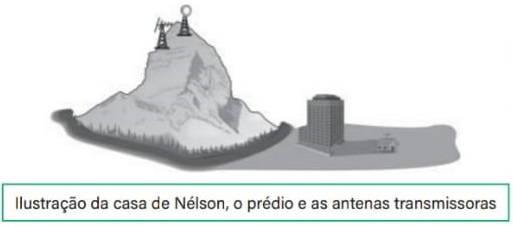
10) (Livro do aluno/2025-SEDUC-SP - UFMG 2005 ― Adaptada) No alto da Serra do Curral, estão instaladas duas antenas transmissoras – uma de rádio AM e outra de rádio FM. Entre essa serra e a casa de Nélson, há um prédio, como mostrado nesta figura abaixo.
Na casa de Nélson, a recepção de rádio FM é ruim, mas a de rádio AM é boa.
Com base nessas informações e sabendo que λAM > λFM, EXPLIQUE por que isso acontece.
Resolução:
Como há um obstáculo entre a casa e as antenas transmissoras (prédio), para chegar à casa de Nélson, a onda de rádio deverá sofrer difração.
Para termos uma acentuação na difração, o comprimento de onda deverá ser maior ou igual ao tamanho do obstáculo a ser “contornado”.
Sabendo que λAM > λFM, podemos concluir que o comprimento de onda das frequências AM é mais próximo da ordem de grandeza do comprimento do prédio, garantindo que as ondas sofram uma difração mais acentuada que as ondas FM e consigam se propagar na direção da antena da casa de Nélson.
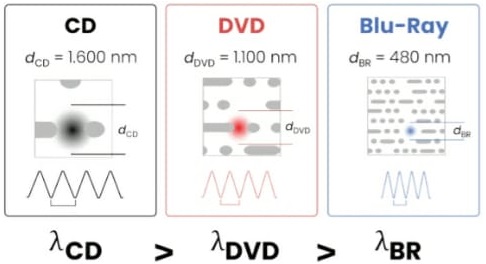
11) (Livro do aluno/2025-SEDUC-SP - UNICAMP 2021) Um dos fatores que determinam a capacidade de armazenamento de dados nos discos laser é o comprimento de onda do laser usado para gravação e leitura (ver figura abaixo). Isto porque o diâmetro d do feixe laser no ponto de leitura no disco é diretamente proporcional ao comprimento de onda, λ. No caso do blu-ray, usa--se um comprimento de onda na faixa azul (daí o nome, em inglês), que é menor que o do CD e o do DVD. As lentes usadas no leitor de blu-ray são tais que vale a relação dBR ≡ 1,2λ BR. A partir das informações da figura, conclui-se que a frequência do laser usado no leitor blu-ray é:
(A) 3,2 ∙ 1014 Hz
(B) 5,2 ∙ 1014 Hz
(C) 6,2 ∙ 1014 Hz
(D) 7,5 ∙ 1014 Hz
Resolução:

Alternativa: D
12) (Livro do aluno/2025-SEDUC-SP - UFPR 2010 – Adaptada) O primeiro forno de micro-ondas foi patenteado no início da década de 1950, nos Estados Unidos, pelo engenheiro eletrônico Percy Spence. Fornos de micro-ondas mais práticos e eficientes foram desenvolvidos nos anos 1970 e, a partir daí, ganharam grande popularidade, sendo amplamente utilizados em residências e no comércio. Em geral, a frequência das ondas eletromagnéticas geradas em um forno de micro-ondas é de 2 450 MHz. Em relação à física de um forno de micro-ondas, considere as seguintes afirmativas:
I Um forno de micro-ondas transmite calor para assar e esquentar alimentos sólidos e líquidos.
II O comprimento de onda dessas ondas é de aproximadamente 12,2 cm.
III As ondas eletromagnéticas geradas ficam confinadas no interior do aparelho, pois sofrem reflexões nas paredes metálicas do forno e na grade metálica que recobre o vidro da porta.
Classifique as afirmações como verdadeira ou falsa e justifique.
Resolução:
I) Falso. Um forno de micro-ondas não emite calor, mas sim micro-ondas que penetram nas moléculas de comida e interagem com as moléculas de água, fazendo-as vibrar, aquecendo o alimento.
II) Verdadeiro. A partir da equação fundamental:
v = λ . f
3 . 108 = λ. 2450 . 106
λ = 3 . 10 8
2,45 . 109
λ = 0,122 m = 12,2 m
III) Verdadeiro. As micro-ondas ficam confinadas dentro do forno devido à blindagem eletrostática, que impede a passagem de ondas eletromagnéticas através de superfícies metálicas. A grade da porta do forno atua como uma barreira para as micro-ondas. Para garantir o aquecimento uniforme dos alimentos, é necessário movê-los, evitando que alguma parte fique na posição de um nó da onda, onde o aquecimento é ineficaz. Como as ondas estacionárias são causadas pela reflexão e interferência, essa afirmação é verdadeira
13) (Livro do aluno/2025-SEDUC-SP - (UFG 2004) As ondas eletromagnéticas foram previstas por Maxwell e comprovadas experimentalmente por Hertz (final do século XlX). Essa descoberta revolucionou o mundo moderno. Sobre as ondas eletromagnéticas, são feitas as afirmações:
I Ondas eletromagnéticas são ondas longitudinais que se propagam no vácuo com velocidade constante c = 3,0 ⋅ 108 m/s.
II Variações no campo magnético produzem campos elétricos variáveis que, por sua vez, produzem campos magnéticos também dependentes do tempo, e assim por diante, permitindo que energia e informações sejam transmitidas a grandes distâncias.
III São exemplos de ondas eletromagnéticas muito frequentes no cotidiano: ondas de rádio, sonoras, micro-ondas e raios X.
Está correto o que se afirmar em:
(A) I, apenas.
(B) II, apenas.
(C) I e II, apenas.
(D) I e III, apenas.
(E) II e III, apenas
Alternativa: B
14) (Livro do aluno/2025-SEDUC-SP) Qual(is) das alternativas apresenta(m) a unidade de medida (de acordo com o Sistema Internacional) correspondente à grandeza física estudada em ondulatória? Classifique as afirmações como Verdadeira (V) ou Falsa (F).
I A velocidade de propagação da onda é medida em metros por segundos ao quadrado.
II A frequência é medida em segundos.
III O período é medido em segundos.
IV O comprimento de onda é medido em metros.
V O número de oscilações é medido em segundos.
Classifique as afirmações como Verdadeira (V) ou Falsa (F)
Resolução:
I. Falso. A velocidade de propagação da onda é medida em metros por segundo (m/s).
II. Falso. A frequência da onda é medida em Hertz (Hz).
III. Verdadeiro.
IV. Verdadeiro.
V. Falso. O número de oscilações é adimensional.
15) (Livro do aluno/2025-SEDUC-SP - ENEM 2021) O eletrocardiograma é um exame cardíaco que mede a intensidade dos sinais elétricos advindos do coração. A imagem apresenta o resultado típico obtido em um paciente saudável e a intensidade do sinal em função do tempo.
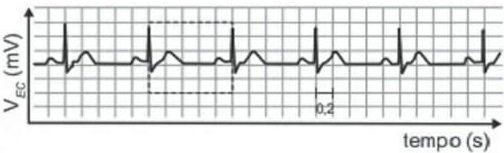
De acordo com o eletrocardiograma apresentado, qual foi o número de batimentos cardíacos por minuto desse paciente durante o exame?
(A) 60
(B) 180
(C) 100
(D) 30
(E) 120
Resolução:
Analisando o gráfico, notamos que cada quadradinho corresponde a um intervalo de tempo de 0,2 s. Como existem 5 quadradinhos em uma oscilação completa, temos o período (T):
T = 5 · 0,2 = 1 s.
Além disso, sabemos que f = T
1 ; portanto f = 1 Hz. Isso significa que o coração avaliado por esse exame realiza 1 batimento por segundo. Como 1 minuto = 60 segundos, e o coração bate 1 vez por segundo, então o número de batimentos por minuto desse paciente foi 60.
Alternativa: A
16) (Livro do aluno/2025-SEDUC-SP - ENEM 2018) O sonorizador é um dispositivo físico implantado sobre a superfície de uma rodovia de modo que provoque uma trepidação e ruído quando da passagem de um veículo sobre ele, alertando para uma situação atípica à frente, como obras, pedágios ou travessia de pedestres. Ao passar sobre os sonorizadores, a suspensão do veículo sofre vibrações que produzem ondas sonoras, resultando em um barulho peculiar.
Considere um veículo que passe com velocidade constante igual a 108 km/h sobre um sonorizador cujas faixas são separadas por uma distância de 8 cm.
A frequência da vibração do automóvel percebida pelo condutor durante a passagem nesse sonorizador é mais próxima de:
(A) 8,6 Hz
(B) 13,5 Hz
(C) 375 Hz
(D) 1350 Hz
(E) 4860 Hz
Resolução:
Automóvel se aproximando do observador parado:
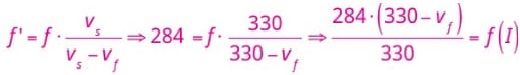
Automóvel se afastando do observador parado:
![]()
Para resolver esta questão, é importante entender que a distância entre duas faixas consecutivas representa o comprimento de onda, λ = 8 cm = 0,08 m. Em seguida, para avançar na resolução, precisamos converter a velocidade de km/h para m/s. Assim, temos: v = 108 km/h = 30 m/s. Por último, para calcular a frequência da vibração do automóvel percebida pelo condutor, utilizaremos a equação fundamental da ondulatória.
Assim, obteremos:
![]()
Alternativa: C
17) (Livro do aluno/2025-SEDUC-SP - ITA 2002) Um pesquisador percebe que a frequência de uma nota emitida pela buzina de um automóvel parece cair de 284 Hz para 266 Hz à medida que o automóvel passa por ele. Sabendo que a velocidade do som no ar é 330 m/s, qual das alternativas melhor representa a velocidade do automóvel?
(A) 10,8 m/s
(B) 21,6 m/s
(C) 5,4 m/s
(D) 16,2 m/s
(E) 8,6 m/s
Resolução:
Como as equações I e II calculam a mesma grandeza, a frequência do som emitido, podemos afirmar:
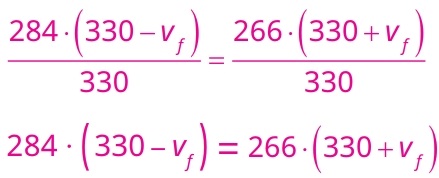
Resolvendo estes cálculos, obtemos:
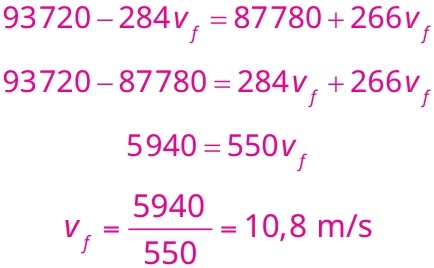
Alternativa: A
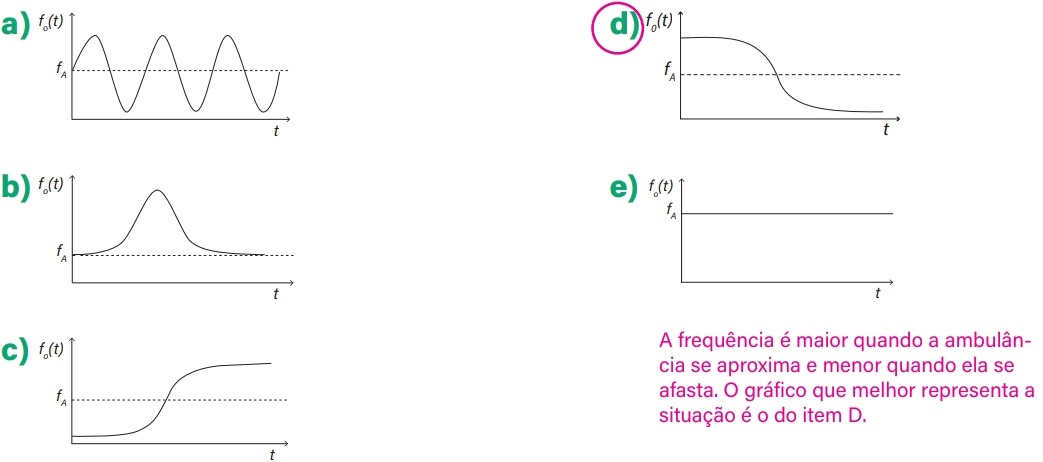
18) (Livro do aluno/2025-SEDUC-SP - ENEM 2016) Uma ambulância A em movimento retilíneo e uniforme aproxima-se de um observador O em repouso. A sirene emite um som de frequência constante f A. O desenho ilustra as frentes de onda do som emitido pela ambulância. O observador possui um detector que consegue registrar, no esboço de um gráfico, a frequência da onda sonora detectada em função do tempo fo (t), antes e depois da passagem da ambulância por ele.
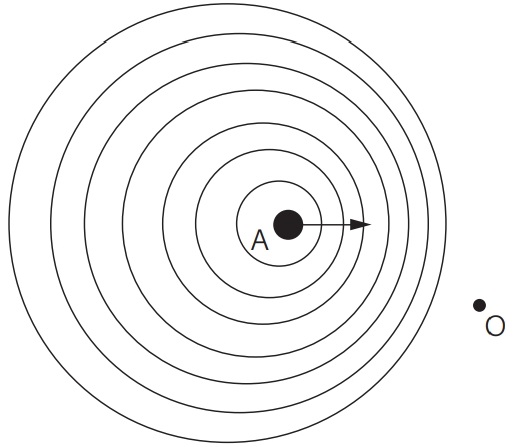
Qual esboço gráfico representa a frequência fo(t) detectada pelo observador?
19) (Livro do aluno/2025-SEDUC-SP - ENEM 2011) Ao se diminuir o tamanho de um orifício atravessado por um feixe de luz, passa menos luz por intervalo de tempo, e, próximo da situação de completo fechamento do orifício, verifica-se que a luz apresenta um comportamento como o ilustrado nas figuras. Sabe-se que o som, dentro de suas particularidades, também pode se comportar dessa forma. Em qual das situações a seguir está representado o fenômeno descrito no texto?
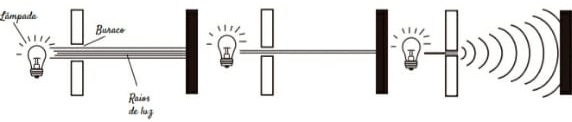
(A) Ao se esconder atrás de um muro, um menino ouve a conversa de seus colegas.
(B) Ao gritar diante de um desfiladeiro, uma pessoa ouve a repetição do seu próprio grito.
(C) Ao encostar o ouvido no chão, um homem percebe o som de uma locomotiva antes de ouvi-lo pelo ar.
(D) Ao ouvir uma ambulância se aproximando, uma pessoa percebe o som mais agudo do que quando aquela se afasta.
(E) Ao emitir uma nota musical muito aguda, uma cantora de ópera faz que uma taça de cristal se despedace.
Resolução:
A onda sonora “contorna” o obstáculo, o muro, por meio do fenômeno da difração, portanto a alternativa correta é a A.
Alternativa: A
20) (Livro do aluno/2025-SEDUC-SP - ENEM 2014) Ao assistir a uma apresentação musical, um músico que estava na plateia percebeu que conseguia ouvir quase perfeitamente o som da banda, perdendo um pouco de nitidez nas notas mais agudas. Ele verificou que havia muitas pessoas bem mais altas à sua frente, bloqueando a visão direta do palco e o acesso aos alto-falantes. Sabe-se que a velocidade do som no ar é 340 m/s e que a região de frequências das notas emitidas é de, aproximadamente, 20 Hz a 4000 Hz.
Qual fenômeno ondulatório foi o principal responsável para que o músico percebesse essa diferenciação do som?
(A) Difração.
(B) Reflexão.
(C) Refração.
(D) Atenuação.
(E) Interferência
Resolução:
A difração é o fenômeno responsável por “contornar” as pessoas que estão na frente e chegar ao músico, portanto a alternativa correta é a A
Alternativa: A
21) (Livro do aluno/2025-SEDUC-SP - ENEM 2017 – Adaptada) O osciloscópio é um instrumento que permite observar uma diferença de potencial (ddp) em um circuito elétrico em função do tempo. A leitura do sinal é feita em uma tela sob a forma de um gráfico de ddp em função do tempo.
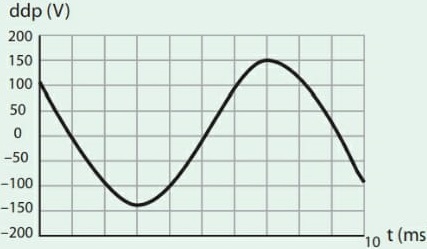
Com base no gráfico apresentado, determine a frequência de oscilação do circuito elétrico estudado.
Resolução:
A metade do período corresponde ao intervalo entre um vale e um pico, representando metade de uma oscilação completa, como podemos observar no gráfico.
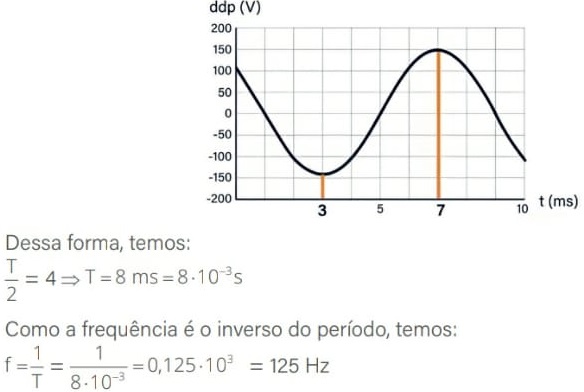
Continua...







