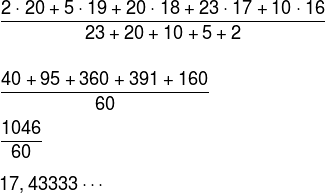ESTATÍSTICA
Professor Diminoi

Estatística
A Estatística é bastante utilizada em diversos ramos da sociedade, no intuito de realizar pesquisas, colher dados e processá-los, analisar informações, apresentar situações através de gráficos de fácil compreensão. Os meios de comunicação, ao utilizarem gráficos, deixam a leitura mais agradável. O IBGE (Instituto Brasileiro de Geografia e Estatística) é considerado um órgão importante e conceituado na área. No intuito de conhecer e aprofundar nos estudos estatísticos precisamos conhecer alguns conceitos e fundamentos primordiais para o desenvolvimento de uma pesquisa.
Conceitos e Fundamentos
População: conjunto de elementos, número de pessoas de uma cidade.
Amostra: parte representativa de uma população.
Variável: depende da abordagem da pesquisa, da pergunta que será feita.
Exemplo:
Qual sua marca de carro favorita? Ford, Volks, Fiat, Peugeot, Nissan são alguns exemplos de resposta.
Frequência absoluta: valor exato, número de vezes que o valor da variável é citado.
Frequência relativa: valor representado através de porcentagem, divisão entre a frequência absoluta de cada variável e o somatório das frequências absolutas.
Medidas de Tendência Central
Média aritmética
Medida de tendência central. Somatório dos valores dos elementos, dividido pelo número de elementos.
Seja os números reais x1, x2, … , xn a média aritmética é definida por:
 M = média aritmética
M = média aritmética
n = o total de valores somados
Média aritmética ponderada
Somatório dos valores dos elementos multiplicado pelos seus respectivos pesos, dividido pela soma dos pesos atribuídos.
Seja x1, x2, x3, … , xn números reais positivos, com p1, p2, p3, …, pn números positivos, a média ponderada é definida por:
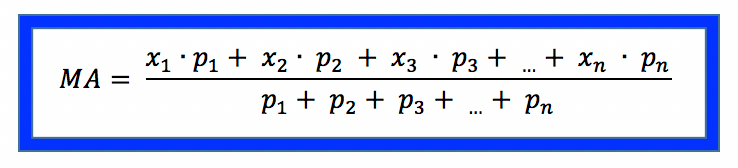 Ou seja, a média ponderada é a soma do produto de cada valor pelo seu respectivo peso e dividido pelas soma dos pesos.
Ou seja, a média ponderada é a soma do produto de cada valor pelo seu respectivo peso e dividido pelas soma dos pesos.
Moda
Valor de maior frequência em uma série de dados, o que mais se repete. Para calcular a moda de um conjunto de dados só é preciso observar os dados que aparecem com maior frequência no conjunto.
Exercícios resolvidos
01) Considere o conjunto de dados a seguir:
A = {2, 23, 4, 2, 5}
Resolução:
A moda para esse conjunto é: Mo = 2. É o número que aparece o maior número de vezes.
02) Considere o conjunto de dados a seguir:
B = {17, 21, 2, 21, 8, 2}
Resolução:
Neste exemplo, a moda é: Mo = 2 ou 21. Então, podemos dizer que o conjunto B é bimodal (possui duas modas).
Mediana
A Mediana (Md) é o valor de centro de um conjunto de dados. Para calcular, primeiro devemos ordenar o conjunto de dados.
Para calcular a mediana:
- Devemos ordenar o conjunto de dados em ordem crescente.
- Se o número de elementos for par, então a mediana é a média dos dois valores centrais ou seja a soma os dois valores centrais e divide o resultado por 2: (a + b)/2.
- Se o número de elementos for ímpar, então a mediana é o valor central.
03) Sejam os conjuntos de dados a seguir:
A = {3, 1, 8}
Resolução:
Ordenar o conjunto: A = {1, 3, 8}
O número de elementos é ímpar, então a mediana é o valor central: Md = 3
B = {6, 4, 7, 2}
Resolução:
Ordenar o conjunto: B = {2, 4, 6, 7}
O número de elementos é par, então a mediana são os dois valores centrais dividido por 2: Md = (4 + 6)/2 = 5
C = {6, 7, 2, 1, 8}
Resolução:
Ordenar o conjunto: C = {1, 2, 6, 7, 8}
O número de elementos é ímpar, então: Md = 6
Medidas de dispersão
Amplitude
Subtração entre o maior valor e o menor valor dos elementos do conjunto.
A amplitude (H) ou intervalo total é calculada pegando os valores extremos do conjunto de dados.
H = x1 – xn
H = é a amplitude;
x1 = é o primeiro valor;
xn = é o último valor.
Variância
Dispersão dos dados variáveis em relação à média.
 V = é a variância
V = é a variância
xi = é um valor qualquer no conjunto de dados não posição i
MA = é a média aritmética
N = é o total dos dados do conjunto
Desvio
Os desvio serve para medir a dispersão entre uma variável em relação a medida de tendência central.
Di = xi – MA
Di = é o desvio
xi = é uma variável qualquer
MA = é a média aritmética dos dados
Desvio Médio
O desvio médio é calculado fazendo a diferença entre uma variável pela média. O desvio médio serve para indicar a distância de cada elemento da amostra e o seu valor médio.
 DM = é o desvio médio
DM = é o desvio médio
xi = é um valor qualquer no conjunto de dados não posição i
MA = é a média aritmética
N = é o total dos dados do conjunto
Desvio Padrão
O desvio padrão serve para calcular a uniformidade do conjunto de dados. Assim, quanto mais próximo de 0 (zero), mais próximo da média estão os dados do conjunto.
 DP = é o desvio padrão
DP = é o desvio padrão
xi = é um valor qualquer no conjunto de dados não posição i
MA = é a média aritmética
N = é a quantidade total dos dados do conjunto
População e Amostra
Na estatística, população é o conjunto total dos dados e amostra é um subconjunto da população.
População
População é o conjunto de elementos que possuem características em comum. É um termo bem mais amplo que no senso comum, podendo haver reunião de pessoas, objetos ou até mesmo ideias.
Exemplo:
Todos as pessoas com ensino superior no Brasil.
Amostras
Amostras, na estatística, são subconjuntos da população e possuem as mesmas características que a população tem. A técnica de retirada de uma amostra da população é chamada de amostragem.
Exemplo
2000 pessoas com ensino superior no Brasil.
Parâmetros
Os parâmetros são as características numéricas da população.
Exemplo:
As média das notas das pessoas com ensino superior no Brasil.
Medidas de Dispersão
As medidas de dispersão servem para indicar o quanto os dados estão dispersos em torno da região central.
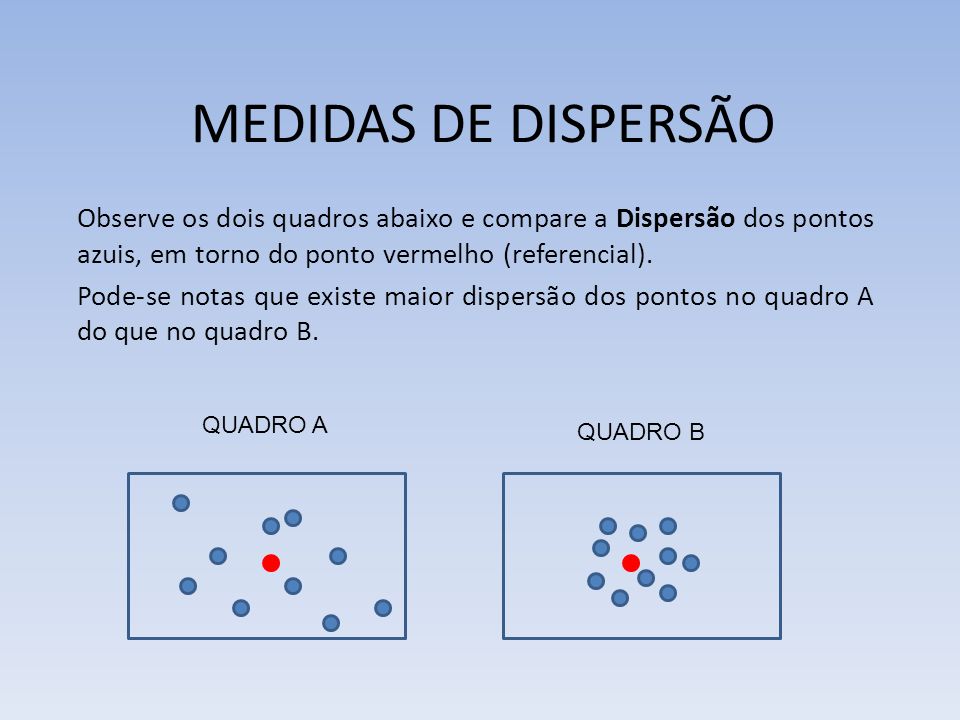
Observe a situação a seguir:
Suponha que dois alunos tenham alcançado a mesma média na escola: 7,0. As notas do primeiro aluno foram: 8,0; 7,0; 7,0 e 6;0. Já as notas do segundo foram 4,0; 5,0; 9,0 e 10,0. Será possível determinar qual dos dois alunos teve o maior progresso a partir apenas de suas médias?
A resposta é não!
É preciso saber todas as notas desses alunos para descobrir que o primeiro regrediu e o segundo teve um excelente desenvolvimento, ainda que ambos tenham alcançado a mesma média. Também é possível determinar essa diferença por meio das medidas usadas para encontrar o grau de variação, nesse caso, das notas dos alunos.
TIPOS DE GRÁFICOS
Em estatística é muito comum a utilização de diagramas para representar dados, diagramas são gráficos construídos em duas dimensões, isto é, no plano. Existem vários modos de representá-los, as principais são: gráfico de pontos, gráfico de linha, gráfico de barra, gráfico de coluna e gráfico de setor.
Gráficos da Barras

Gráfico de Barras Agrupadas

Pictograma

Gráfico de Linhas

Gráfico de Caule e Folhas

Gráfico Circular

Histograma

Polígono de Frequência

Diagrama de Extremos e Quartis
04) (TSE) Para uma população de 10 indivíduos é retirada uma amostra de 3 indivíduos, sem reposição. Assim, o número de amostras possíveis é
(A) 80.
(B) 120.
(C) 240.
(D) 720.
Resolução:
A questão informa o tamanho da população (10 pessoas) e o tamanho da amostra (3 pessoas).
Como precisamos calcular a quantidade de amostras possíveis, basta calcularmos a quantidade de combinações de 10 pessoas, tomadas 3 a 3.
C3,3 = 10! / 7! . 3! = 10 . 9 . 8/3 . 2 . 1 = 120
Alternativa: B
05) (SUDAM AM – IADES) Em 20 dias de aula, um professor de estatística anotou o número de alunos ausentes. Depois, fez a seguinte tabela de frequências:
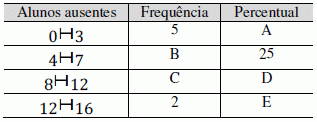 A letra B representa o número
A letra B representa o número
(A) 5.
(B) 6.
(C) 7.
(D) 8.
(E) 9.
Resolução:
Analisando a segunda classe, temos que B representa 25% da quantidade de dias de aula.
Como o professor fez a pesquisa durante 20 dias, temos que B = 5.
Alternativa: A
06) Em um grupo de pessoas, as idades são: 10, 12, 15 e 17 anos. Caso uma pessoa de 16 anos junte-se ao grupo, o que acontece com a média das idades do grupo?
Resolução:
.gif)
07) A distribuição de salários de uma empresa é fornecido pela tabela a seguir:
.gif)
Calcule a média salarial dessa empresa.
Resolução:
.gif)
08) (Unicamp-SP) Para votar, cinco eleitores demoraram, respectivamente, 3min 38s, 3min 18s, 2min 46s, 2min 57s e 3min 26s. Qual foi a média do tempo de votação (em minutos e segundos) desses eleitores?
Resolução:
.jpg)
09) (Unifor-CE) Em certa eleição municipal foram obtidos os seguintes resultados:
.gif) O número de votos obtido pelo candidato vencedor foi:
O número de votos obtido pelo candidato vencedor foi:
(A) 178
(B) 182
(C) 184
(D) 188
(E) 191
Resolução:
Calcular o índice percentual de votos nulos e brancos:
x + 26% + 24% + 22% = 100%
x = 100% – 72%
x = 28%
Calcular o total de votos com base nos votos nulos e brancos:
28% de x = 196
0,28x = 196
x = 196/0,28
x = 700
O total de votos é igual a 700, e o candidato vencedor teve 26% desses votos, então:
26% de 700 → 0,26 * 700 → 182 votos
Alternativa: B
10) (FGV-SP) A tabela abaixo representa a distribuição de frequência dos salários de um grupo de 50 empregados de uma empresa, em certo mês. O salário médio desses empregados, nesse mês, foi de:
.gif) (A) R$ 2 637,00
(A) R$ 2 637,00
(B) R$ 2 520,00
(C) R$ 2 500,00
(D) R$ 2 420,00
(E) R$ 2 400,00
Resolução:
.jpg)
11) (PM - MG) O Comandante da 500ª CIA PM promoveu um torneio operacional, de forma que os militares da CIA PM foram divididos em 04 equipes para realizarem 03 provas distintas, no valor de 10 pontos cada uma, com os seguintes temas: técnica policial-militar, abordagem a veículos e controle de distúrbios. As provas teriam pesos 3, 2 e 1, respectivamente.
TABELA: notas das provas da gincana da 500ª CIA PM, por equipe e tema:
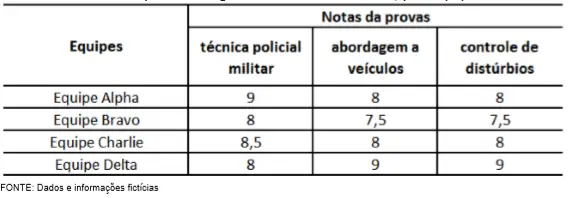
Considerando a média ponderada de cada equipe, marque a alternativa CORRETA.
(A) A Equipe Alpha obteve média ponderada inferior à Equipe Charlie.
(B) A Equipe Bravo obteve média ponderada de 8,25.
(C) A Equipe Delta obteve a mesma média ponderada que a equipe Alpha.
(D) A Equipe Charlie obteve média ponderada superior à Equipe Delta.
Resolução:
Calculando a média ponderada de cada uma das equipes:
Equipe Alpha
(3 . 9 + 2 . 8 + 1 . 8) / 6 = 8,5
Equipe Bravo
(3 . 8 + 2 . 7,5 + 1 . 7,5) / 6 = 7,75
Equipe Charlie
(3 . 8,5 + 2 . 8 + 1 . 8) / 6 = 8,25
Equipe Delta
(3 . 8 + 2 . 9 + 1 . 9) / 6 = 8,5
Alternativa: C
12) (ENEM) Os planos de controle e erradicação de doenças em animais envolvem ações de profilaxia e dependem em grande medida da correta utilização e interpretação de testes diagnósticos. O quadro abaixo mostra um exemplo hipotético de aplicação de um teste diagnóstico
 Considerando que, no teste diagnostico, a sensibilidade é a probabilidade de um animal infectado ser classificado como positivo e a especificidade é a probabilidade de um animal não ser infectado e ter resultado negativo, a interpretação do quadro permite inferir que
Considerando que, no teste diagnostico, a sensibilidade é a probabilidade de um animal infectado ser classificado como positivo e a especificidade é a probabilidade de um animal não ser infectado e ter resultado negativo, a interpretação do quadro permite inferir que
(A) A especificidade aponta um número de 5 falsos positivos.
(B) O teste, a cada 100 indivíduos infectados, classificaria 90 como positivos.
(C) O teste classificaria 96 como positivos em cada 100 indivíduos não infectados.
(D) Ações de profilaxia são medidas adotadas para o tratamento de falsos positivos.
(E) Testes de alta sensibilidade resultam em maior número de falsos negativos comparado a um teste de baixa sensibilidade.
Resolução:
Não existe outra maneira de solucionar esse exercício do que procurar os dados que comprovem ou refutem as alternativas na tabela e no texto ao redor dela. ATENÇÃO: o texto que o exercício traz é tão importante quanto os dados da tabela. Prova disso é a alternativa A, pois a especificidade é definida no texto, e não na tabela, como a probabilidade de um animal não ser infectado e ter um resultado negativo. Observando a tabela, a especificidade é de 912 animais. Portanto, a alternativa está incorreta.
A alternativa correta é a letra B. Para verificar isso, observe que o texto da alternativa menciona apenas o número de indivíduos infectados. Há uma coluna somente para isso na tabela. São 45 indivíduos com teste positivo para cada 50 infectados. Por regra de 3, a cada 100 infectados, 90 terão resultado positivo no teste.
13) (ENEM) O gráfico, obtido a partir de dados do Ministério do Meio Ambiente, mostra o crescimento do número de espécies da fauna brasileira ameaçadas de extinção.
Se mantida, pelos próximos anos, a tendência de crescimento mostrada no gráfico, o número de espécies ameaçadas de extinção em 2011 será igual a:
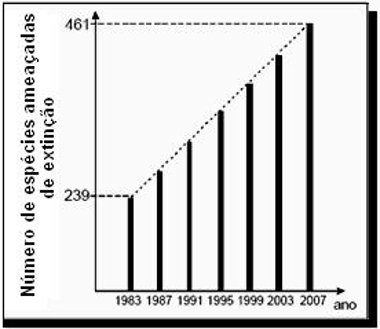 (A) 465
(A) 465
(B) 493
(C) 498
(D) 538
(E) 699
Resolução:
Observe que o título do gráfico não aparece em sua parte superior, mas do lado esquerdo. O importante é que, assim como na tabela, expresse a informação necessária para compreensão dos dados. Esse gráfico é conhecido como gráfico de colunas, pois cada quantidade é expressa por meio de uma barra vertical.
Observe que o crescimento do número de espécies ameaçadas de extinção é linear e está demarcado em períodos de quatro anos no gráfico. A pergunta é exatamente para o fim de mais um período de quatro anos, logo, basta descobrir o aumento do número de animais em cada período de quatro anos e somar esse acréscimo a 461.
Para tanto, usaremos conhecimentos de progressão aritmética, mais especificamente a fórmula para encontrar um termo qualquer. Se 239 for o primeiro e 461 for o último (sétimo), basta encontrar a razão para saber o aumento em um período de quatro anos. Observe:
a7 = a1 + (n – 1)r
461 = 239 + (7 – 1)r
461 – 239 = 6r
222 = 6r
r = 222
6
r = 37
Assim, em 2011, o número de espécies ameaçadas de extinção será:
461 + 37 = 498
Alternativa: C
14) (ENEM) O quadro seguinte mostra o desempenho de um time de futebol no último campeonato. A coluna da esquerda mostra o número de gols marcados e a coluna da direita informa em quantos jogos o time marcou aquele número de gols.
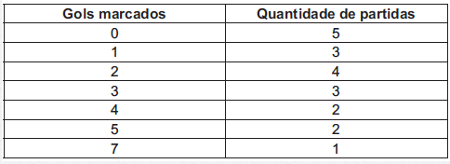 Se X, Y e Z são, respectivamente, a média, a mediana e a moda dessa distribuição, então
Se X, Y e Z são, respectivamente, a média, a mediana e a moda dessa distribuição, então
(A) X = Y < Z.
(B) Z < X = Y.
(C) Y < Z < X.
(D) Z < X < Y.
(E) Z < Y < X.
Resolução:
Observe primeiramente que a moda é zero, pois foi o número de gols marcado no maior número de partidas.
As quantidades de gols devem ser colocadas em ordem crescente para encontrar a mediana:
0, 0, 0, 0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 7
Observe que existem dois valores centrais. Portanto, a mediana será:
2 + 2 = 4 = 2
2 2
Já a média pode ser obtida pela técnica de média ponderada ou de média simples. Para tanto, basta somar os elementos da lista acima e dividir o resultado por 20 ou, como média ponderada, considerar o número de partidas como peso. Ambos os cálculos darão o mesmo resultado.
0 + 0 + 0 + 0 + 0 + 1 + 1 + 1 + 2 + 2 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 + 5 + 7 =
20
45 = 2,25
20
Sabendo que a média é X = 2,25, a mediana é Y = 2 e a moda é Z = 0, teremos:
X > Y > Z ou Z < Y < X
Alternativa: E
15) (Fuvest-SP) A distribuição das idades dos alunos de uma classe é dada pelo seguinte gráfico:
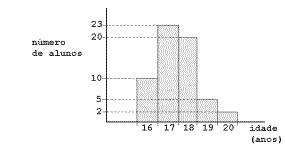 Qual das alternativas representa melhor a média de idade dos alunos?
Qual das alternativas representa melhor a média de idade dos alunos?
(A) 16 anos e 10 meses
(B) 17 anos e 1 mês
(C) 17 anos e 5 meses
(D) 18 anos e 6 meses
(E) 19 anos e 2 meses
Resolução:
Note que o eixo x do gráfico fornece-nos a idade dos alunos e o eixo y fornece-nos a frequência de cada uma das idades, ou seja, a quantidade de vezes que a idade aparece. Assim, devemos utilizar a média ponderada para calcular a média das idades.
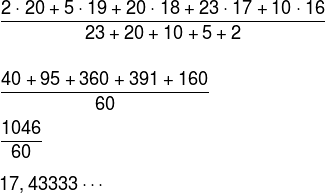 Sabemos que 17,43333… = 17 + 0,4333… . Para transformar 0,43333… em meses devemos multiplicá-lo por 12, logo:
Sabemos que 17,43333… = 17 + 0,4333… . Para transformar 0,43333… em meses devemos multiplicá-lo por 12, logo:
0,4333 · 12 = 5 meses
Portanto, a média de idade desses alunos é de 17 anos e 5 meses.
Alternativa: C
18) As notas de um candidato em suas provas de um con
curso foram: 8,4; 9,1; 7,2; 6,8; 8,7 e 7,2.
A nota média, a nota mediana e a nota modal desse aluno, são respectivamente:
(A) 7,9; 7,8; 7,2
(B) 7,2; 7,8; 7,9
(C) 7,8; 7,8; 7,9
(D) 7,2; 7,8; 7,9
(E) 7,8; 7,9; 7,2
Resolução:
O cálculo da mediana é feito pelo termo médio da amostra em rol (quando a quantidade de termos é ímpar), ou pela média aritmética dos termos centrais em rol (quando a quantidade de termos é par).
Dispondo os termos em rol teremos [6,8 ; 7,2 ; 7,2 ; 8,4 ; 8,7 ; 9,1] , nesse caso temos 6 termos e a mediana é a média dos termos centrais que são o 3º(7,2) e o 4º(8,4), ou seja a mediana é 7,8.
19) Segundo estudos realizados em um centro de pesquisas geológicas, a probabilidade de um terremoto ocorrer no mar de certa cidade é de70%, e a probabilidade de ocorrer em terra é de 30%. Em ambos os casos podem ou não ocorrer danos à cidade. Se o terremoto ocorre no mar há 60% de chances de ocorrer danos à cidade. Se o terremoto ocorre em terra, a probabilidade de ocorrer danos é de 82%. Qual é a probabilidade de um terremoto ocorrer no mar e não haver danos à cidade?
(A) 57,4%
(B) 12,6%
(C) 42%
(D) 28%
Resolução:
A probabilidade de ocorrer no mar é de 70% e de que não ocorram danos é de 40% (note que o exercício não fala nesses 40%, você vai deduzir isso baseado no fato de que se a chance de ocorrer danos é de 60% e os são eventos complementares, então a de não ocorrer danos é de 40%), logo temos, 70% . 40% = 0,7 . 0,4 = 0,28 ou 28%
21) (ENEM) A tabela a seguir mostra a evolução da receita bruta anual nos três últimos anos de cinco microempresas (ME) que se encontram à venda.
 Um investidor deseja comprar duas das empresas listadas na tabela. Para tal, ele calcula a média da receita bruta anual dos últimos três anos (de 2009 até 2011) e escolhe as duas empresas de maior média anual. As empresas que este investidor escolhe comprar são:
Um investidor deseja comprar duas das empresas listadas na tabela. Para tal, ele calcula a média da receita bruta anual dos últimos três anos (de 2009 até 2011) e escolhe as duas empresas de maior média anual. As empresas que este investidor escolhe comprar são:
(A) Balas W e Pizzaria Y.
(B) Chocolates X e Tecelagem Z.
(C) Pizzaria Y e Alfinetes V.
(D) Pizzaria Y e Chocolates X.
(E) Tecelagem Z e Alfinetes V.
Resolução:
Vamos calcular a média de cada empresa, somando receita de 2009, 2010 e 2011 e dividindo por 3.
Média de V = (200 + 220 + 240)/3 = 220
Média de V = (200 + 230 + 200)/3 = 210
Média de V = (250 + 210 + 215)/3 = 225
Média de V = (230 + 230 + 230)/3 = 230
Média de V = (160 + 210 + 245)/3 = 205
As duas maiores médias são X e Y, com 225 e 230 respectivamente.
Alternativa: D
22) (ENEM) Ao final de uma competição de ciências em uma escola, restaram apenas três candidatos. De acordo com as regras, o vencedor será o candidato que obtiver a maior média ponderada entre as notas das provas finais de química e física, considerando, respectivamente, os pesos 4 e 6 para elas. As notas são sempre números inteiros. Por questões médicas, o candidato II ainda não fez a prova final de química. No dia em que sua avaliação for aplicada, as notas dos outros dois candidatos, em ambas as disciplinas, já terão sido divulgadas.
O quadro apresenta as notas obtidas pelos finalistas nas provas finais.
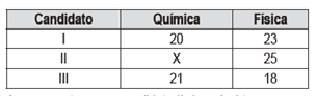 A menor nota que o candidato II deverá obter na prova final de química par vencer a competição é:
A menor nota que o candidato II deverá obter na prova final de química par vencer a competição é:
(A) 18
(B) 19
(C) 22
(D) 25
(E) 26
Resolução:
Como já vimos média ponderada: É a média em que os valores tem pesos diferentes entre si, ou seja, cada valor deverá ser multiplicado pelo seu respectivo peso. A média ponderada é calculada através do somatório das multiplicações entre valores e pesos divididos pelos somatórios dos pesos.
Como pelo enunciado química tem peso 4 e física peso 6.
Média ponderada candidato 1:
MP1 = (20 . 4 + 23 . 6)/10 = 21,8 ~ 22
Média ponderada candidato 3:
MP3 = (21 . 4 + 18 . 6)/10 = 19,2 ~ 19
A média ponderada do candidato 2 deve ser maior que 22 para ele ganhar. Então:
MP2 = (X . 4 + 25 . 6)/10 > 22
MP2 = (X . 4 + 25 . 6)/10 = 22
4X + 150 = 220
4X = 70
X = 70 ÷ 4
X = 17,5
X >17,5 ~18
Como as notas são sempre números inteiros a menor nota que o candidato 2 deve tirar para ser campeão é 18.
Alternativa: A
23) (ENEM) As notas de um professor que participou de um processo seletivo, em que a banca avaliadora era composta por cinco membros, são apresentadas no gráfico. Sabe-se que cada membro da banca atribuiu duas notas ao professor, uma relativa aos conhecimentos específicos da área de atuação e outra, aos conhecimentos pedagógicos, e que a média final do professor foi dada pela média aritmética de todas as notas atribuídas pela banca avaliadora.
 Utilizando um novo critério, essa banca avaliadora resolveu descartar a maior e a menor notas atribuídas ao professor. A nova média, em relação à média anterior, é
Utilizando um novo critério, essa banca avaliadora resolveu descartar a maior e a menor notas atribuídas ao professor. A nova média, em relação à média anterior, é
(A) 0,25 ponto maior.
(B) 1,00 ponto maior.
(C) 1,00 ponto menor.
(D) 1,25 ponto maior.
(E) 2,00 pontos menor.
Resolução:
No novo critério a média final será a média aritmética das notas, descartando a maior e a menor nota.
Total de notas = 5 (n⁰ de avaliadores) x 2 (n⁰ de notas) = 10
Média pelo critério anterior (todas as notas)
Total de notas = 5 (n⁰ de avaliadores) x 2 (n⁰ de notas) = 10
Média aritmética 1 = (18+16+17+13+14+1+19+14+16+12) ÷ 10
Média aritmética 1 = 140 ÷ 10
Média aritmética = 14
Média pelo novo critério (descartando 2 notas)
Total de notas = 10 -2 = 8
Notas que serão descartadas: maior nota: 19 e menor nota: 1
Média aritmética 2 = (18+16+17+13+14+14+16+12) ÷ 8
Média aritmética 1 = 120 ÷ 8
Média aritmética = 15
A nova média será 1,0 ponto maior que a anterior.
Alternativa: B
24) (ENEM) Foi realizado um levantamento nos 200 hotéis de uma cidade, no qual foram anotados os valores, em reais, das diárias para um quarto padrão de casal e a quantidade de hotéis para cada valor da diária. Os valores das diárias foram: A = R$ 200,00; B = R$ 300,00; C = R$ 400,00 e D = R$ 600,00. No gráfico, as áreas representam as quantidades de hotéis pesquisados, em porcentagem, para cada valor da diária.
 O valor mediano da diária, em reais, para o quarto padrão de casal nessa cidade, é
O valor mediano da diária, em reais, para o quarto padrão de casal nessa cidade, é
(A) 300,00.
(B) 345,00.
(C) 350,00.
(D) 400,00.
Resolução:
Mediana é o valor que fica na posição central quando os dados estão em ordem. Se o número total for par, a mediana será a média aritmética dos 2 valores centrais.
Ordenando os dados em ordem crescente de valor temos:
Valor da diária %
A 200 25
B 300 25
C 400 40
D 600 10
Como são 200 hotéis, a mediana será o média aritmética dos dois valores centrais. Nas posições centrais ficaram o 300 e 400.
A média deles é: (300+400) ÷2 =350
Alternativa: C
Continua...









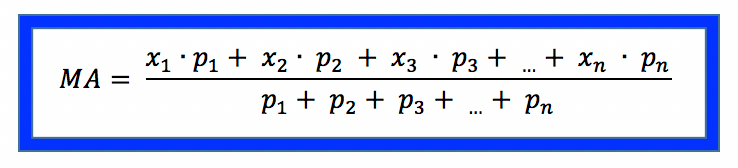














.gif)
.gif)
.gif)
.jpg)
.gif)
.gif)
.jpg)