PP-M-2ºBim-1ª-2023
Professor Diminoi
PROVA PAULISTA - MATEMÁICA - 2º BIM - 1ª SÉRIE EM/2023
01) (Prova Paulista – 1ª Serie EM) Uma doceria produz docinhos embalados para festa e os preços dependem da quantidade de embalagens que for encomendada, mais uma taxa fixa de R$ 12,00 para o frete. Sabendo que a cada embalagem custa R$ 37,00, qual é a expressão que nos fornece o valor P a ser cobrado em função da quantidade X de embalagens vendidas?
(A) P = 12,00X + 37,00
(B) P = 37,00X
(C) P = 49,00X
(D) P = 12,00 + 37,00X
(E) P = 12X
02) (Prova Paulista – 1ª Serie EM) Sendo a função f(x) = 2x + 1, com o domínio {2, 3, 4} e o contradomínio composto pelos naturais entre 1 e 10, qual das opções abaixo representa o conjunto imagem dessa função ?
(A) {4, 6, 8}
(B) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(C) {2, 3, 4}
(D) {1, 2, 3, 4}
(E) {5, 7, 9}
03) (Prova Paulista – 1ª Serie EM) Os conjuntos domínio e imagem da função representada pela reta abaixo, são respectivamente:
(A) D(f) = R e Im(f) = { 2 }
(B) D(f) = R e Im(f) = R
(C) D(f) = { 2 } e Im(f) = R
(D) D(f) = { 0 } e Im(f) = { 2 }
(E) D(f) = { 2 } e Im(f) = { 0 }
04) (Prova Paulista – 1ª Serie EM) Qual a representação algébrica da reta r do gráfico abaixo:
(A) y = x + 1
(B) y = x - 1
(C) y = - x + 1
(D) y = - x - 1
(E)
05) (Prova Paulista – 1ª Serie EM) O ganho G(x) de um vendedor é composto por um valor fixo, mais um valor por produtos vendidos, conforme a função afim representada pelo gráfico abaixo:
Nessas condições, quantos produtos ele terá que vender para ter um ganho de R$ 4.500,00?
(A) 2000
(B) 200
(C) 125
(D) 100
(E) 20
06) (Prova Paulista – 1ª Serie EM) Uma pessoa, ao escolher um plano de saúde, ficou em dúvida entre duas opções.
Observe:
Se essa pessoa pretende fazer 11 consultas no mês, quanto pagará no Plano A e no Plano B, respectivamente?
(A) R$ 440,00 e R$ 650,00
(B) R$ 550,00 e R$ 440,0
(C) R$ 600,00 e R$ 580,00
(D) R$ 620,00 e R$ 550,00
(E) R$ 650,00 e R$ 620,00
07) (Prova Paulista – 1ª Serie EM) O gráfico a seguir está representando a função:
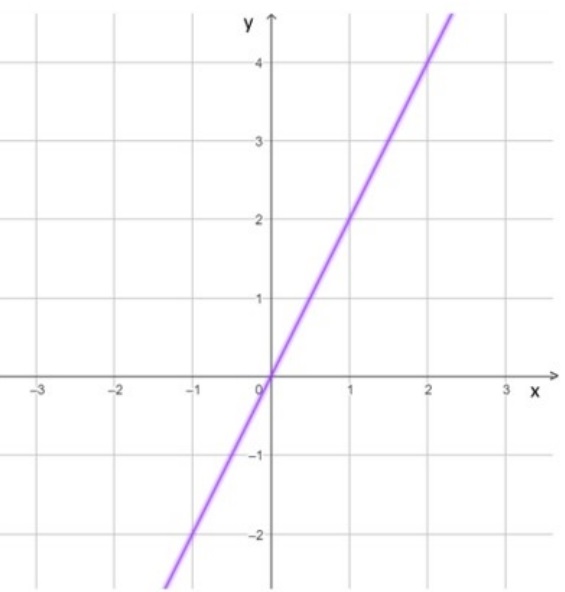(A) f(x) = x
(B) f(x) = - x
(C) f(x) = 2x
(D) f(x) = - 2x
(E) f(x) = 2
08) (Prova Paulista – 1ª Serie EM) Considerando os conjuntos A = {-1, 0, 1} e B = { -1, 1, 3}, em qual das funções a seguir, A e B representam Domínio e Imagem respectivamente?
(A) f(x) = x
(B) g(x) = 2x - 1
(C) h(x) = 2x + 1
(D) i(x) = 2x
(E) j(x) = -2x
09) (Prova Paulista – 1ª Serie EM) Observe a representação gráfica da função f(x) e assinale a alternativa correta.
Em relação a f(x), pode-se afirmar que
(A) os seus coeficientes linear e angular são ambos positivos.
(B) os seus coeficientes linear e angular tem valor zero.
(C) o seu coeficiente linear é negativo e o seu coeficiente angular é positivo.
(D) os seus coeficientes linear e angular são ambos negativos.
(E) o seu coeficiente linear é positivo e o seu coeficiente angular é negativo.
10) (Prova Paulista – 1ª Serie EM) Observe o quadro de preços de um restaurante que vende comida a quilo (self service).
É correto afirmar que o preço do quilograma da comida neste restaurante é de:
(A) R$70,00
(B) R$50,00
(C) R$47,50
(D) R$42,50
(E) R$25,00
11) (Prova Paulista – 1ª Serie EM) O grêmio estudantil de uma escola, junto com a equipe gestora, decidiram realizar uma festa junina para arrecadar fundos para a formatura. Para preparar a festa foram gastos R$ 600,00 e o ingresso por pessoa será R$15,00. Com a festa, espera-se ter lucro de R$1200,00. Para estimar o lucro os estudantes criaram o seguinte gráfico:
Analisando o gráfico, qual alternativa descreve corretamente a representação algébrica e a quantidade de pessoas necessárias para se ter o lucro esperado.
(A) y =15x - 600; 120 pessoas
(B) y = -15x + 600; 80 pessoas
(C) y =15x + 1200; 40 pessoas
(D) y = - 600x + 1200; 40 pessoas
(E) y =15x + 600; 120 pessoas
12) (Prova Paulista – 1ª Serie EM) O gráfico abaixo exibe o lucro líquido (em milhares de reais) de três empresas A, B e C, nos anos de 2013 e 2014.
Com relação ao lucro líquido podemos afirmar que a empresa:
(A) C teve um crescimento maior do que A.
(B) A teve lucro negativo enquanto B teve lucro positivo.
(C) B teve um crescimento igual a C.
(D) A teve um crescimento menor do que B.
(E) Todos tiveram o mesmo crescimento.
13) (Prova Paulista – 1ª Serie EM) O esboço a seguir, ilustra uma função para qualquer valor real x.
É verdade que...
(A) O conjunto imagem da função é o intervalo - 4 < y < 14,06.
(B) No intervalo - 2,56 ≤ x ≤ -0,5 a função é crescente e seu sinal é positivo.
(C) No intervalo -3 ≤ x ≤ -2 a função é crescente e seu sinal é negativo.
(D) No intervalo -0,5 ≤ x ≤ 1,56 a função é decrescente e seu sinal é positivo.
(E) No intervalo -0,5 ≤ x ≤ 1 a função é decrescente e seu sinal é positivo.
14) (Prova Paulista – 1ª Serie EM) Determinando o zero da função abaixo
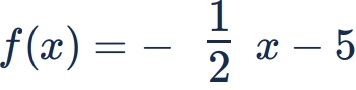Temos como resulta:
(A) - 10
(B) 10
(C) 5/2
(D) – 5/2
(E) 0
15) (Prova Paulista – 1ª Serie EM) Uma microempresa produz e comercializa biscoitos. Para fabricá-los, no mês de maio de 2023, o custo fixo foi de R$2100,00 (aluguel, impostos, luz, água etc). Além deste custo fixo, ainda há um custo variável que depende da quantidade de biscoitos produzidos. Estima-se que o custo de produção de cada biscoito seja R$0,20. O preço de venda unitário de cada biscoito é de R$0,50. Se a microempresa comercializar 7000 biscoitos
(A) ela terá um lucro de R$3500,00.
(B) ela terá um prejuízo de R$3500,00.
(C) ela terá lucro de R$1400,00.
(D) ela terá prejuízo de R$1400,00.
(E) ela não terá lucro e não terá prejuízo.
16) (Prova Paulista – 1ª Serie EM) Dada a função abaixo de
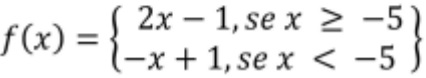Determine f(– 4):
(A) 7
(B) 5
(C) 3
(D) - 7
(E) - 9
17) (Prova Paulista – 1ª Serie EM) Qual das alternativas representa a inequação do gráfico?
(A) y ≤ x
(B) y ≥ x
(C) y ≤ x + 1
(D) y ≥ x + 1
(E) y ≥ x - 1
18) (Prova Paulista – 1ª Serie EM) No triângulo ABC e no retângulo DEGF, estão indicadas as medidas de seus lados.
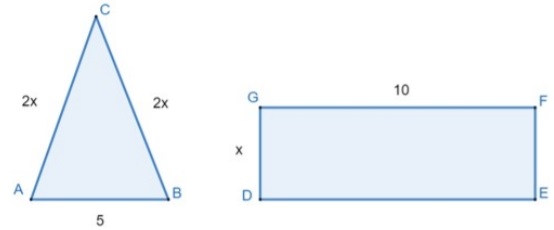Qual é o maior valor absoluto que x pode assumir para que o perímetro do retângulo seja menor que o perímetro do triângulo?
(A) 
(B)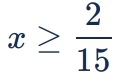 
(C) 
(D) 
(E)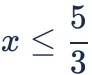 
19) (Prova Paulista – 1ª Serie EM) Se um termo qualquer de uma sequência é dado por
O termo a2 será ?
(A) 2
(B) - 2
(C) – 2/5
(D) + 2/3
(E) 1/2
20) (Prova Paulista – 1ª Serie EM) Observe a sequência de figuras a seguir:
É correto afirmar que:
(A) O quadrado ocupa apenas posições ímpares.
(B) Na 30ª posição temos um triângulo.
(C) Na 30ª posição temos um triângulo.
(D) Na 34ª posição temos um círculo.
(E) O triângulo ocupa apenas posições pares.
GABARITO
01D – 02E – 03A – 04C – 05D – 06E – 07C – 08C – 09E – 10B – 11A – 12B – 13E – 14A – 15E – 16E – 17C – 18A – 19B – 20D.
