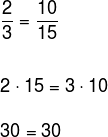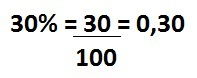GRANDEZA/RAZÃO/PROPORÇÃO

Professor Diminoi

Grandeza
Uma grandeza é tudo aquilo que pode ser medido e possibilita que tenhamos características baseadas em informações numéricas e/ou geométricas.

Proporcionalidade
Proporcionalidade é uma relação de proporção existente entre duas razões, podendo esta ser inversa ou direta.

Proporcionalidade entre Grandezas
Definimos por grandeza tudo aquilo que pode ser contado e medido, como o tempo, a velocidade, comprimento, preço, idade, temperatura entre outros. As grandezas são classificadas em: diretamente proporcionais e inversamente proporcionais.

Grandezas diretamente proporcionais
As grandezas diretamente proporcionais são aquelas em que quando uma aumenta a outra também aumenta.

Exemplo:
Ao abastecer o carro em um posto de combustível, quanto, mas litros de álcool eu colocar maior será o valor que eu vou pagar.

Grandezas inversamente proporcionais
As grandezas inversamente proporcionais são aquelas em que quando uma aumenta a outra diminui.

Exemplo:
Ao sair de casa par vir a escola, se eu vier correndo o tempo que eu levo para chegar a escola será menor que que se eu vier andando.

Observação: para percorrer a mesma distância, quando a velocidade aumenta o tempo diminui e quando a velocidade diminui o tempo aumenta.

Razão
A razão entre dois números é dada pela sua divisão obedecendo a ordem na qual eles foram dados. A razão pode ser representada na forma fracionária, decimal e percentual.

Exemplo
A razão entre os números:

a) 3 e 4

b) 5 e 7

O primeiro número sempre será o numerador, e o segundo número sempre será o denominador.


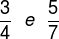
Definição de proporção: Quando igualamos duas razões, estamos formando uma proporção.
Considere duas razões em que b ≠ 0 e y ≠ 0:

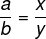
Se multiplicarmos cruzado encontrarmos uma igualdade verdadeira, então teremos uma proporção.

Exemplo:
Verificar se os números 2, 3, 10 e 15 são proporcionais nessa ordem.
Para isso, devemos montar a razão entre esses números e, em seguida, multiplicar cruzado. Se encontrarmos uma igualdade verdadeira, então eles serão proporcionais, caso contrário, eles não serão proporcionais.


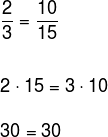
Portanto, os números nessa ordem formam uma proporção.

Ordem de grandeza
Ordem de grandeza de uma medida é uma estimativa de potência de base 10 mais próxima de uma determinada medida.
Geralmente quando estudamos alguns exercícios envolvendo cálculos sobre questões de Física, Química ou Matemática, optamos pelo valor aproximado de uma grandeza e em outros, não há um valor exato.
Imagine que você e mais três amigos resolveram acampar em uma mata por um período de sete dias. Sem ter a certeza de que encontrariam água limpa para beber, vocês resolveram levar água em quantidade suficiente para toda a viagem. Então, qual é a quantidade de água que vocês devem levar?
Em geral, para fazermos cálculos aproximados, precisamos de certa dose de intuição e algum conhecimento referente à situação estudada. No nosso exemplo, podemos partir do fato de que devemos beber cerca de dois litros de água por dia. Como são quatro escoteiros, são necessários pelo menos oito litros de água por dia. Em uma semana, o número de litros de água que cada pessoa necessitará é 56.
Para dar certa margem de segurança, podemos arredondar esse número para 60. Assim, o ideal é que as pessoas levem pelo menos 60 litros de água. Esse é um exemplo básico do caso em que não existe um valor exato, pois o que se pode fazer é um cálculo aproximado.

Quando nossos cálculos são aproximados, costumamos dar o resultado final, ou seja, a resposta expressa em potência de 10 mais próxima do resultado encontrado. A resposta dada dessa maneira costuma ser chamada de ordem de grandeza. Assim, no exemplo citado anteriormente, em que a quantidade de água foi estimada em 60 litros, podemos observar que as potências de 10 mais próximas de 60 são 10¹ e 10²:
10¹ < 60 < 10²
Mas 60 está mais próximo de 10² que de 10¹, assim, a ordem de grandeza de 60 é 10².
Consideremos, por exemplo, o número 850. As potências de 10 mais próximas do número 850 são 10² e 10³:
10² < 850 < 10³

Porém, o número 850 está mais próximo de 10³ do que 10². Assim, a ordem de grandeza de 850 é 10³.
Para obtermos a ordem de grandeza de um número N qualquer, em primeiro lugar, devemos fazer a sua representação na notação científica:
N = x .10^y
1 ≤ x <10 e="" y="" um="" n="" mero="" inteiro="" strong="">
Em seguida, verificamos se x é maior ou menor que 5,5. Portanto:
Se x > 5,5 fazemos x ≈ 10
Se x < 5,5 fazemos x ≈ 1

QUESTÕES RESOLVIDDAS
01) Qual a razão entre 40 e 20?
Lembre-se que numa fração, o numerador é o número acima e o denominador, o de baixo.

Se o denominador for igual a 100, temos uma razão do tipo porcentagem, também chamada de razão centesimal.

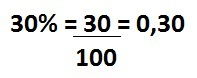
Além disso, nas razões, o coeficiente que está localizado acima é chamado de antecedente
(A), enquanto o de baixo é chamado de consequente
(B).


02) Qual o valor de x na proporção abaixo?

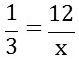
3 . 12 = x
x = 36
Assim, quando temos três valores conhecidos, podemos descobrir o quarto, também chamado de “quarta proporcional”.
Na proporção, os elementos são denominados de termos. A primeira fração é formada pelos primeiros termos (A/B), enquanto a segunda são os segundos termos (C/D).
Nos problemas onde a resolução é feita através de regra de três, utilizamos o cálculo da proporção para encontrar o valor procurado.

Propriedades da Proporção
03) O produto dos meios é igual ao produto dos extremos, por exemplo:

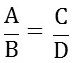
Logo:
A . D = B . C
Essa propriedade é denominada de multiplicação cruzada.

04) É possível trocar os extremos e os meios de lugar, por exemplo:

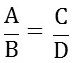
É equivalente

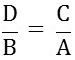
Logo,
A = C. B

05) Calcule a razão entre os números:
a) 120:20
b) 345:15
c) 121:11
d) 2040:40
Resolução:
a) 6

b) 23

c) 11

d) 51

06) Qual das proporções abaixo são iguais à razão entre 4 e 6?
(A) 2 e 3
(B) 2 e 4
(C) 4 e 12
(D) 4 e 8
Resolução:
Alternativa a: 2 e 3
 

Continua....