PROPRIEDADES DA POTENCIAÇÃO - EF

Professor Diminoi

PROPRIEDADES DA POTENCIAÇÃO

Potenciação

Objetivo:
- Rever o conceito de potenciação;
- Solucionar problemas que envolvam o cálculo com números naturais.
 
 

 

 



 

 

 

 

 

 

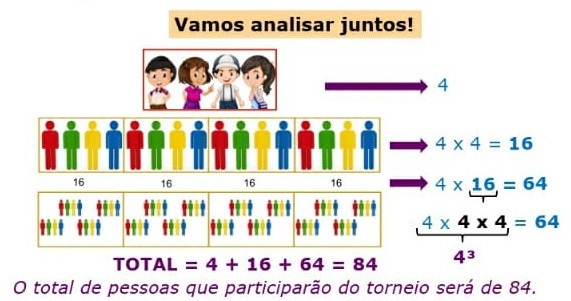
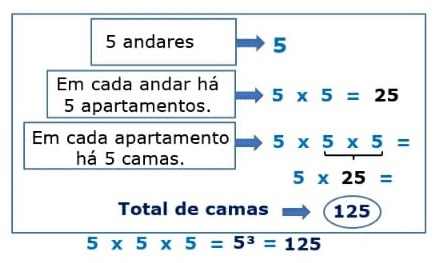
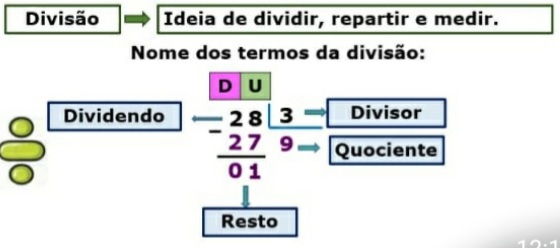
Potência de um número real com expoente inteiro – I
Calcular potência de números racionais.

Exemplo 1: Verdadeiro ou falso 0,3² = 0,9?
Resolução: Essa afirmação é falsa, pois 0,3² = 0,3 x 0,3 = 0,09.

01) Para os números racionais, valem as mesmas regras da potenciação, porém é necessário ter atenção às propriedades para não errar!


Observação:
Se o expoente for par, a potência será sempre um número positivo.
Se o expoente for ímpar, a potência terá sempre o mesmo sinal da base.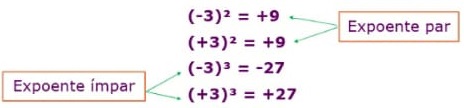


02) Vamos observar essas regras com os números racionais na forma decimal.
( - 0,2)³ = (- 0,2) . (- 0,2) . (- 0,2) = -0,008
( - 0,3)² = (- 0,3) . (- 0,3) = +0,09

Exemplo 4:
Numa expressão numérica, temos a seguinte ordem de resolução:
1º) potência e radiciação
2º) multiplicação e divisão
3º) adição e subtração

Então, vamos começar pelas potências!

Termos da potenciação

5³ =  5 . 5 . 5 . 5 = 125
Base: fator que se repete de acordo com o expoente.
Expoente: determina a quantidade de vezes que o fator irá se repetir.
Potência: resultado da potenciação.

03) Qual é o valor da expressão numérica (- 0,5)³ - (- 0,5)² - (-0,5)?
(A) 0,125
(B) 0,75
(C) -0,125
(D) -0,75
Resolução:
(-0,5)³ =  expoente ímpar, usaremos sinal da base
(-0,5)² → expoente par, resultado será positivo.
(-0,5)³ - (-0,5)² -(-0,5)
(-0,125) – (+0,25) – (-0,5)
Eliminando os parênteses.
(-0,5)³ = - 0,125
(-0,5)² = + 0,25
Agora vamos eliminar os parênteses fazendo a regra de sinais:

Junte os números de sinais iguais e subtrair números de sinais diferentes.
(-0,5)³ - (-0,5)² -(-0,5)
(-0,125) – (+0,25) – (-0,5)
- 0,125 – 0,25 + 0,5
Junte os números de sinais iguais e subtrair números de sinais diferentes.
(-0,5)³ – (-0,5)² – (-0,5)
(-0,125) – (+0,25) – (-0,5)
-0,125 – 0,25 + 0,5
-0,375 + 0,5 = + 0,125
Finalmente, fazer as adições.
Junte os números de sinais iguais e subtrair números de sinais diferentes.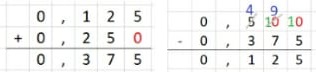

Alternativa: C

04) Resolva a expressão abaixo
Resolução:


Potência de um número real com expoente inteiro I
- Calcular potência de números racionais;
- Compreender algumas propriedades de potenciação;
- Compreender procedimentos de cálculo de potência com expoente positivo e negativo.

05) É correto dizer que um número contido no intervalo ]0, 1[ ao quadrado resulta num número menor do que antes de elevar ao quadrado?
Resolução:
Se o expoente for par, a potência será sempre um número positivo.
Se o expoente for ímpar, a potência terá sempre o mesmo sinal da base.

Termos da potenciação
5³ =  5 . 5 . 5 . 5 = 125

Base: fator que se repete de acordo com o expoente.
Expoente: determina a quantidade de vezes que o fator irá se repetir.

Potência: resultado da potenciação.

06) Quando o expoente for negativo, fazemos:

Observação:

07) Encontre o resultado da potência abaixo na forma decimal:
Resolução: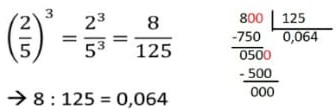

08) Quanto vale a potência abaixo?

(A) 12,5
(B) 0,125
(C) 0,0125
(D) 0,00125
Resolução:
Alternativa: C

09) Quanto vale a potência abaixo:
(A) 0,625
(B) −0,625
(C) 16
(D) −16
Resolução: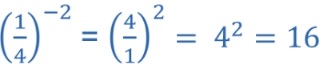

Alternativa: C

10) Quanto vale a potência abaixo?
(A) 0,625
(B) −0,625
(C) 16
(D) −16
Resolução:

Alternativa: C

Propriedades das potências: multiplicação de potências de mesma base
- Conhecer a propriedade do produto de potências de mesma base;
- Resolver problemas usando as propriedades da potência.

11) Quem está certo?
O professor Diminoi  pediu para os(as) alunos(as) calcularem a multiplicação de 32 por 64 e expressarem a resposta em forma de potência de base 2. Verifique a resolução dos dois alunos e as estratégias utilizadas em cada caso.
Resolução:
Ambos estão certos!
Amanda decidiu calcular a multiplicação para, depois, fatorar!
Bruno resolveu fatorar primeiro e, depois, utilizar a propriedade de potenciação chamada multiplicação de potências de mesma base!

Multiplicação de potências de mesma base
12) Quanto é 2^{4 .}  2³?
Resolução:
Coloque a resposta numa potência de base 2.
Para não ter que calcular a potência, fazer a multiplicação e, depois, fatorar, temos uma ferramenta muito útil nesse momento, que é a propriedade que diz que, no produto de potências de mesma base, repete-se a base e somam-se os expoentes, ficando:
2⁴ .  2³ = 2 ^{4 + 3} = 2⁷
2⁴  . 2³ = 2 . 2  .  2  . 2  . 2 . 2 . 2 = 2⁷_.
 
13) Complete o quadro abaixo, reduzindo o cálculo a uma só potência.
14) Quanto vale 27 x 81?
(A) 35
(B) 36
(C) 37
(D) 38
Resolução:
Como 27 = 3³ e 81 = 3⁴, temos que 27 x 81 = 3³ . 3⁴ = 3³ + 4 = 3⁷.
Alternativa: C

15) Quanto vale 2²⁰ + 2²⁰?
(A) 2⁴⁰
(B) 2³⁰
() 4¹⁰
(D) 2²¹
Resolução:
Observe que temos 2 parcelas de 2²⁰, ficando:
2  .  2²⁰  = 2¹  . 2²⁰ = 2⁽¹⁺²⁰⁾  =  2²¹
Alternativa: D

16) Quanto vale a potência abaixo?
(A) 0,03125
(B) –0,03125
(C) 32
(D) –32
Resolução:

Alternativa: D

Propriedades das potências: potência de potência
- Recordar a propriedade de potência de potência;
- Resolver problemas usando as propriedades da potência.
 
17) Verdadeiro ou falso?
4⁵ = 2¹⁰
Resolução:
4⁵ = 2¹⁰
É verdadeira essa afirmação, e eu vou resolver de duas maneiras.
4⁵ = 4 . 4 . 4 . 4 . 4 . 4= 256
2¹⁰ = 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2 = 256
Outro modo de resolver é utilizando a propriedade potência de potência, na qual usaremos o fato de 4 ser igual a 2².
4⁵ = (2²)⁵ = 2^2.5 = 2¹⁰

Observe este cálculo!
(3²)⁴ = 3² . 3² . 3² . 3² = 3² = 3^4.2 = 3⁸
Conhecendo a propriedade potência de potência, você poderia reduzir essa resolução, ficando:
(3²)⁴ = 3^2.4 = 3⁸

Observação: note que, na potência de potência, conserva-se a base e multiplicam-se os expoentes.

Propriedade da potenciação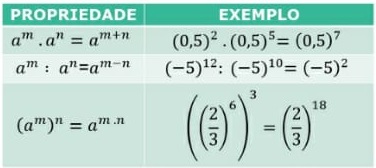
 18) Complete o quadro abaixo, reduzindo o cálculo a uma só potência.
 

19) Qual é a metade de 8²⁰?
(A) 4¹⁰
(B) 8¹⁹
(C) 8¹⁰
(D) 2⁵⁹
Resolução
Como 2³ = 8, temos (2³)²⁰ = 2⁶⁰
A metade de 2⁶⁰ é  2⁶⁰/2 = 2⁵⁹
Alternativa: D

20) 𝑎⁵ . (𝑎⁴ )²  . 𝑎¹  equivale a:
(A) a¹⁴
(B) a³
(C) a¹²
(D) a¹¹
Resolução:
a⁵ . (a^4.5) . a¹ + a⁵ . a⁸ . a¹ = a⁵⁺⁸⁺¹ = a¹⁴
Alternativa: A

21) Qual é a metade de 4¹⁰⁰?
(A) 2¹⁰⁰
(B) 2⁵⁰
(C) 1
(D) 2¹⁹⁹
Resolução:
Como 2² = 4, temos 4¹⁰⁰ = (2²)¹⁰⁰ = 2²⁰⁰
Para calcular a metade, devemos dividir 2²⁰⁰  por 2, ficando:
2²⁰⁰ / 2 = 2²⁰⁰ / 2¹ = 2^{200 -1} = 2¹⁹⁹
Alternativa: D

22) Resolva a expressão abaixo:
(A) -3/5
(B) 27/125
(C) – 27/125
(D) 36/125
Resolução:

Alternativa: C

Potenciação – definição e conceitos básicos
23) 2³ é a mesma coisa que 3²? Por quê?
Resolução:
2³ = 2 . 2 . 2 . 3 = 8
3² =  3 . 3  = 9
Portanto, 2³ é diferente 3².

24) Calcule e escreva como se lê as seguintes potências:
a) 3⁴ = 3 . 3 . 3 . 3 = 81 (três elevado a quarta potência)
b) 12² = 12 . 12 = 144 (doze ao quadrado)

25) Qual é o valor de 12² - 5³ + 3³?
(A) 17
(B) 24
(C) 42
(D) 46
Resolução:
12 x 12 – 5 x 5 x 5 + 3 x 3 x 3 =
144 – 125 + 27 =
46

Potências de um número real com expoente inteiro

Objetivo:
- Verificar a propriedade da potência de um número real com expoente inteiro;
- Resolver problemas aplicando a propriedade da potência de um número real com expoente inteiro

26) “Em 2016, pesquisadores descobriram o maior vírus conhecido até então. Os Pandoravírus foram encontrados no Chile (Pandoravirus salinus) e na Austrália (Pandoravirus dulcis) e têm cerca de 10^-4 cm.”
Resolução:

27) Sabendo que a = 𝟐^−𝟐 e b = 𝟑^−𝟑, calculem, em seu caderno, os valores de:
Resolução: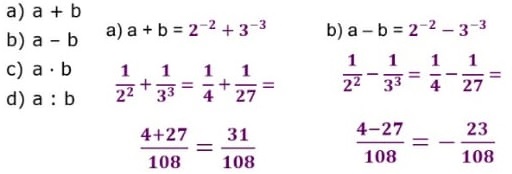


Sabendo que a = 𝟐^−𝟐 e b = 𝟑^−𝟑, calculem, em seu caderno, os valores de:

28) O tamanho esférico da partícula de um vírus SARS-COV-2 é 0,00000005. Esse número em notação científica corresponde a:
(A) 5 . 10^-5 m
(B) 5  . 10^-6 m
(C) 5 . 10^-7 m
(D) 5 . 10^-8 m
Resolução:
Observem que, para 0,00000005 equivaler a 5, temos que deslocar a vírgula para a direita em 8 casas decimais. Portanto, a resposta é:
5  . 10^-8 m.

Até agora, aprendemos como aplicar a propriedade da potência de um número real com expoente inteiro. Agora, vamos trabalhar com mais atividades envolvendo essa propriedade.

Observação:
Verificamos a propriedade da potência de um número real com expoente inteiro negativo: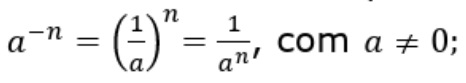
Resolvemos atividades aplicando a propriedade de potência de um número real com expoente inteiro.
 
Potências de um número real com expoente inteiro

Objetivo:
- Relembrar a propriedade da potência de um número real com expoente inteiro;
- Resolver problemas aplicando a propriedade da potência de um número real com expoente inteiro.

29) 2^-3 = - 8 Verdadeiro ou falso?
Resolução:
- 2 . -2 . – 2 = - 8. Verdadeiro

Exemplo:
Quando o expoente for negativo, fazemos: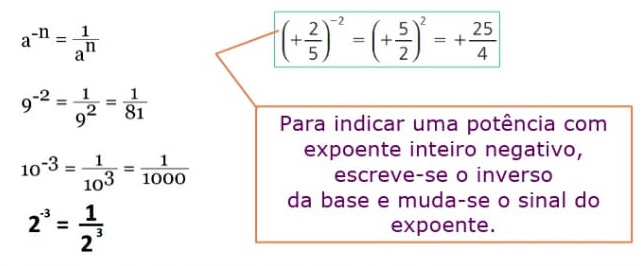

Um número real diferente de zero (ℝ^∗) elevado a um expoente inteiro negativo, é igual ao inverso desse número elevado ao oposto desse expoente.
 
30) Vamos aplicar a propriedade nos dois itens a seguir:


31) Observa as potências abaixo e, calcule em seu caderno os valores de: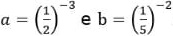

Resolução:


32) Observa as potências abaixo e, calcule em seu caderno os valores de: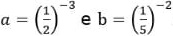
Resolução:


33) Observa as potências abaixo e encontre o produto entre x e y será igual a:
Resolução:
 

Propriedades das potências: multiplicação e divisão de potências de mesma base

Objetivo: Resolver problemas utilizando a propriedade do produto e divisão de potências de mesma base.

34) Vocês sabem quanto é 2⁴  . 2³?
Resolução:
Coloquem a resposta em uma potência de base 2.
Para não ter que calcular a potência, fazer a multiplicação e depois fatorar, temos uma ferramenta muito útil neste momento: a propriedade que diz que, no produto de potências de mesma base, repete-se a base e soma-se os expoentes, ficando:
2⁴ . 2³ = 24+3 = 2⁷
2 . 2 . 2 . 2 . 2 . 2 . 2 =  2⁷

35) Vocês sabem quanto é 2⁶ / 2²? Coloquem a resposta em uma potência de base 2.
Para não ter que calcular a potência, fazer a divisão e depois fatorar, temos uma ferramenta muito útil neste momento: a propriedade que diz que, na divisão de potências de mesma base, repete-se a base e subtrai-se os expoentes, ficando:
Resolução:
 

Quando o expoente for negativo, fazemos:
Para indicar uma potência com expoente inteiro negativo, escreve-se o inverso da base e muda-se o sinal do expoente.
 Um número real diferente de zero (ℝ^∗), elevado a um expoente inteiro negativo, é igual ao inverso desse número elevado ao oposto desse expoente.

36) Completem o quadro abaixo, reduzindo o cálculo a uma só potência.


37) Completem o quadro abaixo, reduzindo o cálculo a uma só potência.


38) Quanto vale  3²⁰ + 3²⁰ + 3²⁰?
(A) 9⁶⁰
(B) 3²⁰
(C) 9
(D) 3²¹
Resolução:
Observem que temos três parcelas de 3²⁰, ficando:
3  . 3²⁰ = 3¹ . 3²⁰ = 3¹⁺²⁰ = 3²¹

39) Quanto vale 1/3 de 3³⁰⁰?
Resolução:
Para calcular 1÷ 3, dividimos 3³⁰⁰ por 3, ficando:
3³⁰⁰ ÷  3 = 3³⁰⁰ ÷  3¹ = 3^300-1 = 3²⁹⁹

40) Quanto vale (3⁶ . 3^-2) ÷  3⁴??
(A) 3^-3
(B) 3^-8
(C) 1
(D) 0
Resolução:
(3⁶ . 3^-2) ÷  3⁴ =
(3^6-2) ÷  3⁴ =
3⁴ ÷ 3⁴
3^4-4 =
0

Propriedades das potências: potência de potência

Objetivos:
- Recordar a propriedade da divisão de potências de mesma base;
- Resolver problemas usando as propriedades da potência.

41) 4⁵ = 2¹⁰ Verdadeiro ou falso?
Resolução:


Potência de potência


Termos de uma potência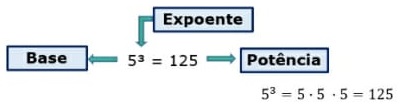

Base: fator que se repete de acordo com o expoente.

Expoente: determina a quantidade de vezes que o fator vai se repetir.

Potência: resultado da potenciação.

Vamos retomar as três propriedades de potências aprendidas até agora?
42)
 
43) Qual é a metade de 16²⁰?
(A) 8¹⁰
(B) 16¹⁹
(C) 2⁴⁰
(D) 2⁷⁹
Resolução:


44) 𝑎⁵ . (𝑎⁴ )²  . 𝑎¹  equivale a:
(A) a¹⁴
(B) a³
(C) a¹²
(D) a¹¹
Resolução:
a⁵ . (a^4.5) . a¹ + a⁵ . a⁸ . a¹ = a⁵⁺⁸⁺¹ = a¹⁴
Alternativa: A

45) a⁵  . (a⁴)² . a¹equivale a:
(A) a¹⁴
(B) a¹³
(C) a¹²
(D) a¹¹
Resolução:
a⁵  . (a⁴)² . a¹ =
a⁵ . a⁸ . a¹ =
a⁵⁺⁸⁺¹
a¹⁴

46) (x²y⁴)² equivale a:
(A) x⁴y⁶
(B) x²y⁸
(C) x⁴y⁸
(D) (xy)⁸
Resolução:
(x²y⁴)² = (x²)² . (y⁴)² = x⁴y⁸

Potências de números racionais na forma fracionária

Objetivo: Compreender as potências com expoente racional na forma fracionária.

Números racionais são aqueles que podemos escrever na forma de fração entre números inteiros, com o denominador diferente de zero.
Vamos ver como simplificar essas expressões nesta aula.
 A propriedade de potência que resolverá expressões do tipo abaixo está relacionada com a operação inversa, ou seja, com a radiciação.

Potências com expoente fracionário

Números racionais são aqueles que podemos escrever na forma de fração entre números inteiros, com o denominador diferente de zero.

A propriedade de potência que resolverá expressões do tipo abaixo está relacionada com a operação inversa, ou seja, com a radiciação.

Potências com expoente fracionário
Para transformar uma potência com expoente fracionário em raiz, seguimos os passos:

A base da potência transforma-se na base do radicando (o número na raiz);

O numerador da fração transforma-se no expoente do radicando;

O denominador transforma-se no índice da raiz.

47) Escreva as potências abaixo como raízes:


48) Escreva as potências abaixo como raízes:


49) Em uma aula de Matemática, a professora Ana resolveu fazer uma gincana na sala de aula e, para isso, dividiu a turma em duas equipes (A e B). Uma das provas dessa gincana foi um Desafio Matemático.
Para resolução desse desafio, cada equipe tinha um limite de tempo de 60 minutos para resolver um total de 6 questões desafiadoras.
Para calcular a pontuação final desse desafio, a professora propôs a seguinte expressão:
Resolução:
O total de pontos é igual a 25^n/6, sendo n o total de questões resolvidas corretamente pela equipe.
a) Qual foi a pontuação da equipe A, já que acertou todas as 6 questões no tempo disponibilizado?


 

b) Qual foi a pontuação que a equipe B ganhou, já que acertou metade das questões no tempo disponibilizado? Pode-se usar a calculadora para esse cálculo.

 

c) Qual seria a pontuação, caso uma equipe tenha zerado nesse desafio? Justifique sua solução.


 
Discuta com os estudantes o porquê de um número elevado a zero resultar em 1.     

Potências de números racionais na forma fracionária

Objetivo: Compreender as potências com expoente racional na forma fracionária.

50) 

Números racionais são aqueles que podemos escrever na forma de fração entre números inteiros, com o denominador diferente de zero.
A propriedade de potência que resolverá expressões do tipo abaixo está relacionada com a operação inversa, ou seja, com a radiciação.

Potências com expoente fracionário
Para transformar uma potência com expoente fracionário em raiz, seguimos os passos:
A base da potência transforma-se na base do radicando (o número na raiz);
O numerador da fração transforma-se no expoente do radicando;
O denominador transforma-se no índice da raiz.
51)
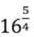equivale a:
(A) 16
(B) 32
(C)  2√2
(D) 2√5
Resolução: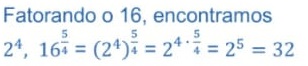


52) O resultado da expressão numérica do quadro é:
(A) 12
(B) 9
(C) 5
(D) 2
Resolução: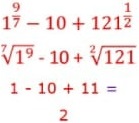


Potências com expoente fracionário
Para transformar uma potência com expoente fracionário em raiz, seguimos os passos:
A base da potência transforma-se na base do radicando (o número na raiz);
O numerador da fração transforma-se no expoente do radicando;
O denominador transforma-se no índice da raiz.

Potências com expoente decimal
53) Simplifique as potências abaixo:
a) 81^0,25
b) 36^0,5
c) 64^0,5
Resolução

54) Dizer “número X elevado a 0,5” tem o mesmo significado de:
Resolução:

55) (Uneb-BA) A expressão P(t) = K · 2^0,05t fornece o número P de milhares de habitantes de uma cidade, em função do tempo t, em anos. Se, em 1990, essa cidade tinha 300.000 habitantes, quantos habitantes, aproximadamente, espera-se que ela tenha no ano 2000?
Use: √2 = 1,41.
(A) 352.000
(B) 401.000
(C) 439.000
(D) 441 000
Resolução:

Potências com expoente racional: situações-problema 

Objetivo: Resolver situações-problema usando potências com expoente racional e suas propriedades.
Há uma diversidade de aplicações de situações-problema envolvendo potências no cotidiano, presentes em diversas ciências: na Matemática financeira, é utilizada na capitalização de capitais, pelo método do juro composto; na Geografia, está relacionada a expressões responsáveis por explicar os crescimentos populacionais; na Química, é utilizada em situações envolvendo decaimento radioativo; na Biologia, está ligada ao desenvolvimento de bactérias em culturas e crescimento de determinadas plantas; na Psicologia, expressa as curvas de aprendizagem, entre outras inúmeras aplicações.
 
Potências com expoente decimal
Como resolvemos um problema?

56) Uma planta aquática circular, com 1 cm de diâmetro, foi colocada em uma estufa até atingir o tamanho ideal para ser comercializada. Sabendo que seu diâmetro dobra a cada dois meses e que a planta sairá da estufa daqui a um ano, quanto deve medir seu diâmetro para que essa planta tenha a dimensão ideal para comercialização?
Resolução:
Dados: planta circular com 1 cm de diâmetro; diâmetro dobra a cada 2 meses; sairá da estufa em 1 ano = 12 meses.
Qual o diâmetro do tamanho ideal?
Se, a cada 2 meses, o diâmetro dobra, então, em 12 meses, estará com 64 cm de diâmetro, que é o tamanho ideal.

57) Ao ser modelada e resolvida uma situação real, chegou-se à conclusão de que y = 64^1,5 . Sendo assim, o valor de y é:
Resolução:

58) Em uma colônia de bactérias, a cada 30 minutos, o número de micro-organismos é multiplicado por 100. Se, na primeira vez em que foi observada, a colônia tinha 1.000 bactérias, a ordem de grandeza de bactérias, após 2 horas, é:
Resolução:
 

Continua...