PP-M-2ºBim-3ª-2023
Professor Diminoi
2º BIMESTRE 2023 MATEMÁTICA - 3ª série – ENSINO MÉDIO
01) (Prova Paulista – 3EM – 1ºBim/2023) Analisando a figura abaixo, podemos afirmar que a razão de Homotetia para o triângulo B’C’D’, em relação ao triângulo BCD, é de:
 (A) 2
(A) 2
(B) 1
(C) 0
(D) -1
(E) - 2
02) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2018) Isometria é uma transformação geométrica que, aplicada a uma figura, mantém as distâncias entre pontos. Duas das transformações isométricas são a reflexão e a rotação. A reflexão ocorre por meio de uma reta chamada eixo. Esse eixo funciona como um espelho, a imagem refletida é o resultado da transformação. A rotação é o “giro” de uma figura ao redor de um ponto chamado centro de rotação. A figura sofreu cinco transformações isométricas, nessa ordem:
 1ª) Reflexão no eixo x;
1ª) Reflexão no eixo x;
2ª) Rotação de 90 graus no sentido anti-horário, com centro de rotação no ponto A;
3ª) Reflexão no eixo y;
4ª) Rotação de 45 graus no sentido horário, com centro de rotação no ponto A;
5ª) Reflexão no eixo x.
Qual a posição final da figura?

03) (Prova Paulista – 3EM – 1ºBim/2023) Observando o polígono A’B’C’D’E’ em relação ao polígono ABCDE, podemos dizer que ocorreu uma
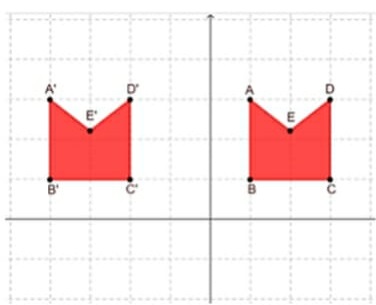 (A) translação aplicada da esquerda para a direita.
(A) translação aplicada da esquerda para a direita.
(B) translação aplicada da direita para a esquerda.
(C) rotação aplicada da direita para a esquerda.
(D) rotação aplicada da esquerda para a direita.
(E) reflexão.
04) (Prova Paulista – 3EM – 1ºBim/2023) Observando o triângulo A’B’C’ em relação ao triângulo ABC, ocorreu uma
 (A) reflexão considerando o eixo vertical.
(A) reflexão considerando o eixo vertical.
(B) reflexão considerando o eixo horizontal.
(C) rotação considerando o eixo vertical.
(D) rotação considerando o eixo horizontal.
(E) translação.
05) (Prova Paulista – 3EM – 1ºBim/2023) Quais foram as transformações geométricas ocorridas na sequência das figuras 1, 2, 3 e 4 respectivamente, que compuseram o ladrilhamento a seguir?
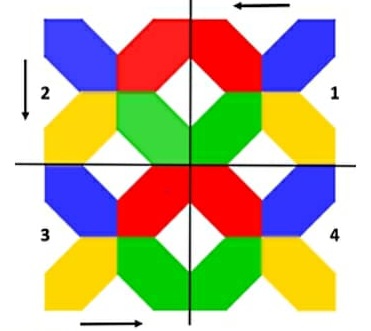 (A) Translação, reflexão e reflexão.
(A) Translação, reflexão e reflexão.
(B) Translação, reflexão e translação.
(C) Reflexão, reflexão e reflexão.
(D) Reflexão, reflexão e translação.
(E) Reflexão, translação e reflexão.
06) (Prova Paulista – 3EM – 1ºBim/2023) Willian desenhou um retângulo medindo 15,5 cm de comprimento e 8,5 cm de largura. Se ele aplicar uma transformação geométrica homotética direta de razão de K = 3, o novo retângulo terá as medidas de
(A) 46,5 cm de comprimento e 25,5 cm de largura.
(B) 25,5 cm de comprimento e 46,5 cm de largura
(C) 18,5 cm de comprimento e 11,5 cm de largura.
(D) 15,8 cm de comprimento e 8,8 cm de largura.
(E) 5,16 cm de comprimento e 2,83 cm de largura.
07) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2015) Um pesquisador, ao explorar uma floresta, fotografou uma caneta de 16,8 cm de comprimento ao lado de uma pegada. O comprimento da caneta ( c ), a largura (L) e o comprimento (C ) da pegada, na fotografia, estão indicados no esquema
 A largura e o comprimento reais da pegada, em centímetros, são, respectivamente, iguais a
A largura e o comprimento reais da pegada, em centímetros, são, respectivamente, iguais a
(A) 4,9 e 7,6.
(B) 8,6 e 9,8.
(C) 14,2 e 15,4.
(D) 26,4 e 40,8.
(E) 27,5 e 42,5.
08) (Prova Paulista – 3EM – 1ºBim/2023) Qual é a soma das medidas dos ângulos X e Y indicados nos polígonos regulares do mosaico abaixo? Dica: 𝑆𝑛 = (𝑛 − 2). 180°
 (A) 90°
(A) 90°
(B) 120°
(C) 135°
(D) 225°
(E) 360°
09) (Prova Paulista – 3EM – 1ºBim/2023) Na figura, há três tipos de ladrilhos com formatos de polígonos regulares. Para que um ladrilhamento usando esses formatos seja possível, a medida do ângulo "a" do ladrilho hexagonal corresponde a:
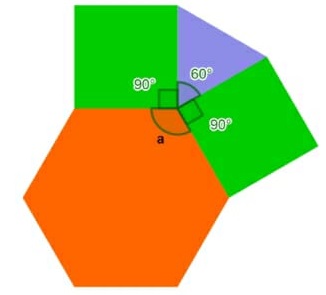 (A) 60°
(A) 60°
(B) 90º
(C) 120°
(D) 135°
(E) 180°
10) (Prova Paulista – 3EM – 1ºBim/2023 - SARESP 2008/2009) O retângulo ABCD da figura abaixo foi obtido a partir de um mosaico de hexágonos regulares, de modo que os pontos A, B, C e D correspondem aos centros dos hexágonos em cujo interior se encontram.
 Assim, admitindo que o retângulo seja pavimentado com partes de hexágonos recortados, sem perdas, o menor número de hexágonos que possibilita essa pavimentação é:
Assim, admitindo que o retângulo seja pavimentado com partes de hexágonos recortados, sem perdas, o menor número de hexágonos que possibilita essa pavimentação é:
(A) 2
(B) 4
(C) 6
(D) 8
(E) 10
11) (Prova Paulista – 3EM – 1ºBim/2023) Erika quer construir um mosaico utilizando apenas um tipo de polígono regular. Dos polígonos abaixo, quais ela pode usar.
 (A) 1, 2 e 4
(A) 1, 2 e 4
(B) 1, 3 e 4
(C) 1, 2 e 5
(D) 2, 3 e 4
(E) 1, 3, e 5
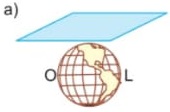
12) (Prova Paulista – 3EM – 1ºBim/2023) Na figura abaixo, as coordenadas geográficas dos pontos E e F são respectivamente:
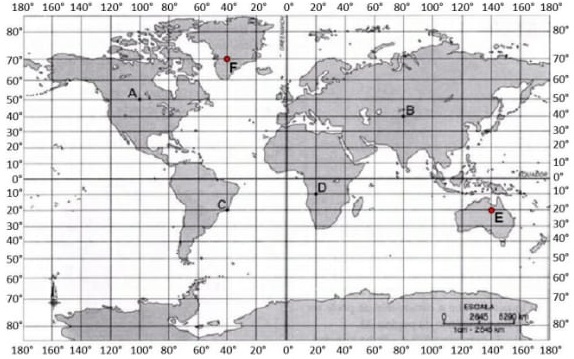 (A) E = 20°O de latitude, 140°S de longitude e F = 70°N de latitude, 40°L de longitude.
(A) E = 20°O de latitude, 140°S de longitude e F = 70°N de latitude, 40°L de longitude.
(B) E = 20°S de latitude, 140°L de longitude e F = 70°S de latitude, 40°L de longitude.
(C) E = 20°S de latitude, 140°L de longitude e F = 70°N de latitude, 40°O de longitude.
(D) E = 20°S de longitude, 140°L de latitude e F = 70°N de longitude, 40°O de latitude.
(E) E = 20°L de longitude, 140°S de latitude e F = 70°O de longitude, 40°N de latitude.
13) (Prova Paulista – 3EM – 1ºBim/2023) Se uma cidade se encontra a - 60° de longitude, qual será o seu fuso horário em relação ao Meridiano de Greenwich?
(A) + 0,25h.
(B) - 0,25h
(C) + 1h
(D) + 4h
(E) - 4h
14) (Prova Paulista – 3EM – 1ºBim/2023) O fuso horário de Brasília em relação ao Meridiano de Greenwich é de -3h. Se adiantarmos em 1h para o horário de verão brasileiro, o novo fuso horário de Brasília será de
(A) -4h em relação ao Meridiano de Greenwich.
(B) 4h em relação ao Meridiano de Greenwich.
(C) 3h em relação ao Meridiano de Greenwich.
(D) -2h em relação ao Meridiano de Greenwich.
(E) 2h em relação ao Meridiano de Greenwich.
15) (Prova Paulista – 3EM – 1ºBim/2023 - Currículo em Ação - ENEM – 2021 – Adaptada) Analise a figura a seguir:
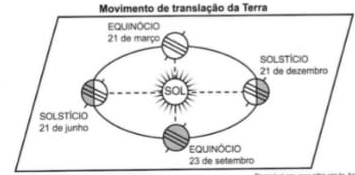 Considerando as informações apresentadas, o prédio do Congresso Nacional, em Brasília, no dia 21 de junho, às 12 horas, projetará sua sombra para a direção
Considerando as informações apresentadas, o prédio do Congresso Nacional, em Brasília, no dia 21 de junho, às 12 horas, projetará sua sombra para a direção
(A) norte.
(B) sul.
(C) leste.
(D) oeste.
(E) nordeste
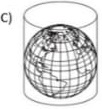
16) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2016) A ONU faz referência a uma projeção cartográfica em seu logotipo. A figura que ilustra o modelo dessa projeção é:





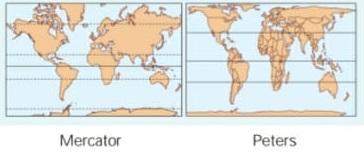
17) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM – 2001) Existem diferentes formas de representação plana da superfície da Terra (planisfério). Os planisférios de Mercator e de Peters são atualmente os mais utilizados. Apesar de usarem projeções, respectivamente, conforme e equivalente, ambas utilizam como base da projeção o modelo:




18) (Prova Paulista – 3EM – 1ºBim/2023) Considerando o sistema Fusos UTM - Sistema Universal Transversa de Mercator, o Brasil está entre os fusos 18 ao 25, conforme a tabela:
 De acordo com UTM, as coordenadas 22°S 49°W está localizada no fuso:
De acordo com UTM, as coordenadas 22°S 49°W está localizada no fuso:
(A) 131
(9) 38
(C) 33
(D) 26
(E) 22
19) (Prova Paulista – 3EM – 1ºBim/2023) Em um sorteio, foram colocadas 6 bolas idênticas numeradas de 1 a 6, em uma caixa. O espaço amostral S desse experimento e o evento A, em que deve ser sorteada uma bola com um número primo, podem ser representados por
(A) S = {1, 2, 3, 4, 5, 6} e A = {2, 3, 5}
(B) S = {2, 3, 5} e A = {1, 2, 3, 4, 5, 6}
(C) S = {1, 2, 3, 4, 5, 6} e A = {1, 2, 3, 5}
(D) S = {1, 2, 3, 5} e A = {1, 2, 3, 4, 5, 6}
(E) S = {1, 2, 3, 4, 5, 6} e A = {3, 5}
20) (Prova Paulista – 3EM – 1ºBim/2023) Uma loja irá sortear um brinde para seus clientes. Para isso, foram entregues 30 números de 1 a 30. Qual é a probabilidade de ser sorteado um número que seja múltiplo de 7 e ímpar?
(A) 1/15
(B) 1/7
(C) 1/2
(D) 2/1
(E) 4/1
21) (Prova Paulista – 3EM – 1ºBim/2023 - Enem 2015) Em uma central de atendimento, cem pessoas receberam senhas numeradas de 1 até 100. Uma das senhas é sorteada ao acaso. Qual a probabilidade de a senha sorteada ser um número de 1 a 20?
(A) 1/100
(B) 19/100
(C) 20/100
(D) 21/100
(E) 80/100
22) (Prova Paulista – 3EM – 1ºBim/2023 - Enem 2010 2ª aplicação) Em uma reserva florestal existem 263 espécies de peixes, 122 espécies de mamíferos, 93 espécies de répteis, 1 132 espécies de borboletas e 656 espécies de aves. Se uma espécie animal for capturada ao acaso, qual a probabilidade de ser uma borboleta?
(A) 63,31%
(B) 70,18%
(C) 56,51%
(D) 49,96%
(E) 43,27%
23) (Prova Paulista – 3EM – 1ºBim/2023 - Enem 2011) O gráfico mostra a velocidade de conexão à internet utilizada em domicílios no Brasil. Esses dados são resultado da mais recente pesquisa, de 2009, realizada pelo Comitê Gestor da Internet (CGI).
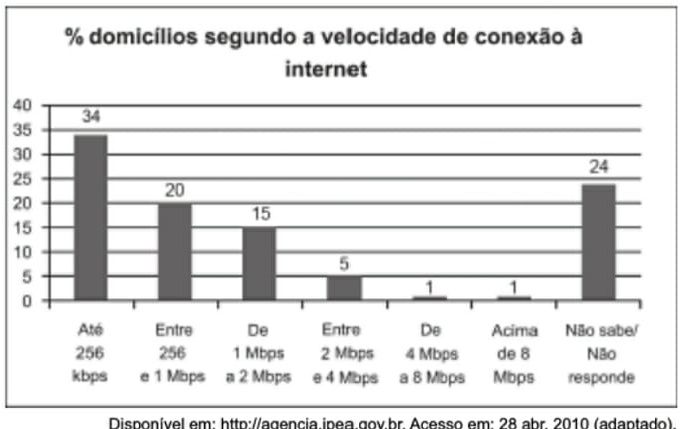 Escolhendo-se, aleatoriamente, um domicílio pesquisado, qual a chance de haver banda larga de conexão de pelo menos 1Mbps neste domicílio?
Escolhendo-se, aleatoriamente, um domicílio pesquisado, qual a chance de haver banda larga de conexão de pelo menos 1Mbps neste domicílio?
(A) 0,45
(B) 0,42
(C) 0,30
(D) 0,22
(E) 0,15
24) (Prova Paulista – 3EM – 1ºBim/2023) No lançamento de um dado não viciado, qual a probabilidade de sair um número maior do 4?
(A) 1/6
(B) 2/6
(C) 3/6
(D) 4/6
(E) 5/6
25) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2020 – PPL – REAPLICAÇÃO) Em uma campanha promocional de uma loja, um cliente gira uma roleta, conforme a apresentada no esquema, almejando obter um desconto sobre o valor total de sua compra. O resultado é o que está marcado na região apontada pela seta, sendo que todas as regiões são congruentes. Além disso, um dispositivo impede que a seta venha a apontar exatamente para a linha de fronteira entre duas regiões adjacentes. Um cliente realiza uma compra e gira a roleta, torcendo para obter o desconto máximo.
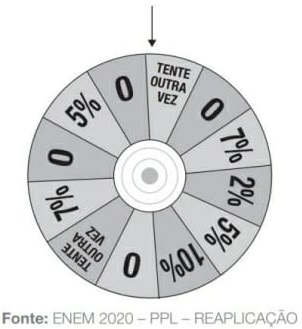 A probabilidade, em porcentagem, de esse cliente ganhar o desconto máximo com um único giro da roleta é melhor aproximada por
A probabilidade, em porcentagem, de esse cliente ganhar o desconto máximo com um único giro da roleta é melhor aproximada por
(A) 8,3.
(B) 10,0.
(C) 12,5.
(D) 16,6.
(E) 50,0.
GABARITO
01E – 02C – 03B – 04B – 05E – 06A – 07D – 08D – 09C -10C – 11A – 12C – 13E – 14C – 15B – 16A – 17C – 18E – 19A – 20A – 21C – 22D – 23D – 24B – 25A.




































