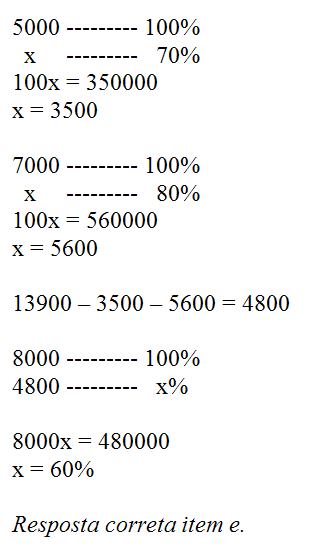PORCENTAGEM
Professor Diminoi
PORCENTAGEM

Porcentagem ou percentagem é usada para calcular descontos, acréscimo de preços, lucros, etc. É uma fração em que o denominador é igual a 100. O símbolo para representar uma porcentagem é % e vem precedido por um número.
Porcentagem envolve diversas situações com que nos deparamos frequentemente em nosso cotidiano, por exemplo em indicadores econômicos, resultados de pesquisas ou promoções. Entendemos porcentagem como sendo a razão entre um número qualquer e 100, sendo representada pelo símbolo %. Utilizamos a ideia de porcentagem para representar partes de algo inteiro.
Sabemos que a porcentagem é uma razão, logo, pode ser representada por uma fração, que, por sua vez, pode ser escrita na forma decimal. De modo geral, se temos um número acompanhado pelo símbolo %, basta dividi-lo por 100, ou seja:
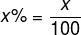
Veja os exemplos seguintes que mostram as diferentes representações de porcentagens. Lembre-se, para “transformar” a porcentagem em fração, basta dividir o número que acompanha o símbolo % por 100 e simplificar a fração; para “transformar” a fração em forma decimal, basta realizar a divisão.
Exemplos
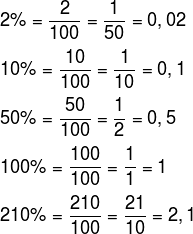
Perceba que quando escrevemos a porcentagem 100% é o mesmo que considerar um inteiro, ou seja, quando consideramos 100% de algo, estamos levando em conta o total daquilo. No caso de 210%, estamos considerando mais que um inteiro, isto é, consideramos 2,1 vezes o total.
Para fazer o caminho de volta, ou seja, dado uma fração ou um número decimal para ser escrito na forma percentual, basta multiplicar o número em questão por 100.
Observe:
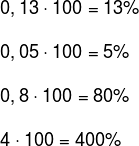
Cálculo de porcentagem com regra de três
01) Determine o valor de 95% de R$ 105,00
Resolução:
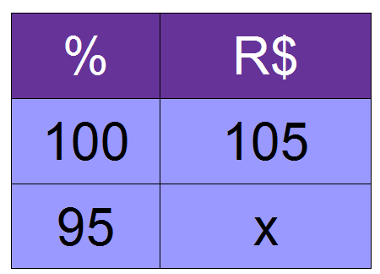
100x = 95 . 105
100x = 9975
x = 9975
100
x = 99,75 reais
Portanto, 95% de R$ 105,00 é igual a R$ 99,75.
02) Em uma sala de 40 alunos, foi realizada uma pesquisa, a qual apontou que 30 alunos gostam de praticar esportes. Qual é a porcentagem de alunos que gostam de esportes?
Resolução:
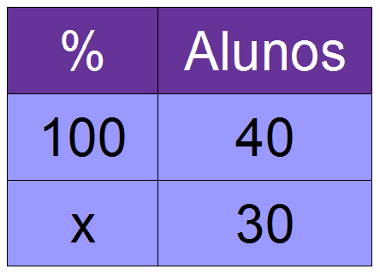
40x = 100 . 30
40x = 3000
x = 3000
40
x = 75%
Temos que 75% dos alunos dessa classe gostam de esportes.
03) Pedro acertou 21 questões de uma prova, que correspondem a 70% do total de questões. Quantas questões tinha a prova?
Resolução:
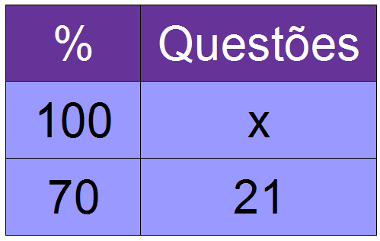
70x = 21 . 100
70x = 2100
x = 2100
70
x = 30
A prova tinha 30 questões.
04) Em uma promoção, o preço de um objeto foi reduzido de R$ 76,00 para R$ 57,00. Calcule o valor do desconto em porcentagem. Devemos primeiramente determinar o valor real do desconto: 76 – 57 = 19. Ao compararmos o valor do desconto com o valor sem o desconto, obtemos o valor percentual.
Resolução:
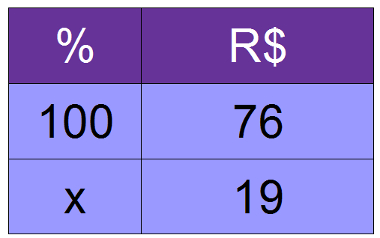
76x = 100 . 19
76x = 1900
x = 1900
76
x = 25%
O desconto dado foi de 25%.
05) Uma conta de restaurante, incluindo os 10% de serviço, ficou em R$ 143,00. Qual o valor da conta sem a taxa de serviço?
Resolução:
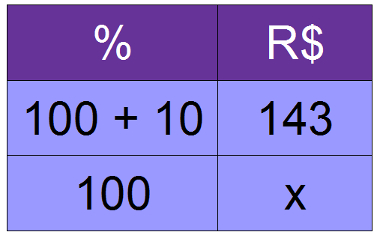
110x = 143 100
110x = 14300
x = 14300
110
x = 130
A conta sem o valor do serviço é de R$ 130,00.
06) Um produto que custava R$ 80,00 foi reajustado em 25%. Determine o novo valor do produto.
Resolução:
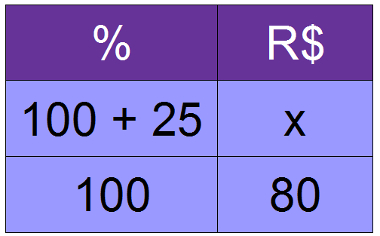
100x = 125 . 80
100x = 10000
x = 100
O preço do produto após o reajuste é de R$ 100,00.
07) O preço de um computador é de R$ 2.200,00. Qual será o preço do computador caso ele sofra um reajuste de 18%?
Resolução:
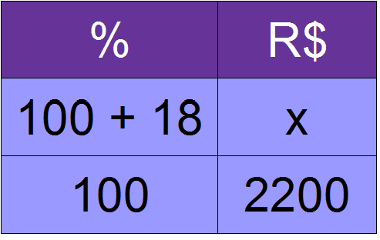
100x = 2200 . 118
100x = 259600
x = 259600
100
x = 2 596
Caso aconteça o reajuste de 18%, o computador passará a custar R$ 2 596,00.
08) Considerando que a população de um país é de cerca de 180 milhões de habitantes e que 38 milhões são considerados fumantes, qual a porcentagem de fumantes no país referido?
Resolução:

180x = 3800
x = 3800
180
x = 21,1
A porcentagem de fumantes no país referido é de aproximadamente 21,1%.
09) Uma pesquisa realizada pelo IBGE constatou que a população de uma cidade havia aumentado de 82.350 para 105.200 habitantes. Calcule o valor desse aumento em índices percentuais.
Resolução:
.gif)
10) Os custos de uma prefeitura com a área da educação aumentaram cerca de 18%. Considerando que a prefeitura destinava a quantia de R$ 900.000,00, qual deverá ser o novo valor destinado para a educação?
Resolução:

11) (Faee) Um funcionário de uma empresa recebeu a quantia de R$ 315,00 a mais no seu salário, referente a um aumento de 12,5%. Sendo assim, o seu salário atual é de:
(A) R$ 2.205,00
(B) R$ 2.520,00
(C) R$ 2.835,00
(D) R$ 2.913,00
(E) R$ 3.050,00
Resolução:

12) (UEMS) Dentro de um recipiente há um líquido que perdeu, por meio de evaporação, 5% de seu volume total, restando 42,75 litros. Qual era o volume total desse líquido?
Resolução:
.gif)
13) (Unifor–CE) Três laboratórios produzem certo medicamento. A tabela abaixo mostra, para um certo mês, o número de unidades produzidas desse medicamento e a porcentagem de vendas dessa produção.
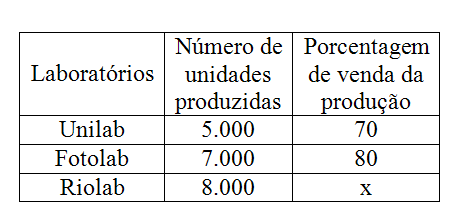 Se, nesse mês, os três laboratórios venderam um total de 13.900 unidades desse medicamento, então o valor de x é:
Se, nesse mês, os três laboratórios venderam um total de 13.900 unidades desse medicamento, então o valor de x é:
(A) 80
(B) 75
(C) 70
(D) 65
(E) 60
Resolução:
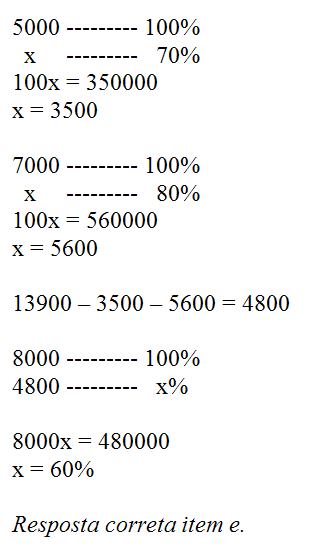
14) Um artigo esportivo teve um aumento de 20%, e agora custa R$ 180,00. Qual era o preço antes desse aumento?
Resolução:
Veja que o problema fala que o novo preço do produto custa agora R$ 180,00 depois de sofrer um reajuste de 20%. Isto quer dizer que o preço antigo correspondia a 100% e o novo preço corresponde a 120%.
Podemos resolver esse problema com regra de três simples. Como o novo preço de R$ 180,00 é 120% e o preço antigo é 100%, mas não sabemos qual é, então colocamos uma variável x.
120% ———- 180
100% ———- x
120x = 180 . 100
120x = 18000
x = 150
Portanto, o preço antes do aumento era de R$ 150,00.
15) Uma loja vendia uma TV por R$ 2.000,00. No dia das mães, a loja anunciou uma promoção oferecendo 20% de desconto em todos os produtos do estoque. Qual o preço final da TV depois do desconto?
Resolução:
Precisamos reduzir o preço de R$ 2000,00 em 20%.
Devemos fazer da seguinte forma:
100% – 20% = 80%
Agora multiplicamos o valor da TV por 80%, ou 0,8.
2000 . 0,8 = 1600
Portanto, o preço da TV com desconto é de R$ 1.600,00.
16) Se 40% de um número qualquer é 20, determine esse número.
Resolução:
Temos que: 40% = 0,40.
Assim,
0,40 . x = 20
x = 20/0,40 = 50
Podemos fazer também da seguinte forma:
40/100 . x = 20
40 . x = 20 . 100
x = 2000/40 = 50
Observação: Fica mais fácil quando não temos calculadora.
17) (OBMEP) Um trabalho de matemática tem 30 questões de aritmética e 50 de geometria. Júlia acertou 70% das questões de aritmética e 80% do total de questões. Qual o percentual das questões de geometria que ela acertou?
Resolução:
Julia acertou 21 questões de aritméticas, pois: 30 . 0,7 = 21;
Júlia acertou 64 questões de 80 (total), pois: 80 . 0,8 = 64;
Em geometria ela acertou 43, pois: 64 – 21 = 43;
Logo, podemos calcular a porcentagem de questões que ela acertou em geometria:
43/50 = 0,86 = 86%
Portanto, Júlia acertou 86% das questões de geometria.
18) Numa padaria, em 60 kg de farinha e fermento, 2% é de fermento. Se acrescentarmos mais 100 gramas de fermento, qual a porcentagem da nova mistura?
Resolução:
Temos que: 2% de 60 kg é 1,2 kg
Assim, considerando a mistura total 60 kg adicionando mais 100 gramas de fermento, temos: 60 kg + 100 g = 60,1 kg
Da mistura total de 60 kg, 1,2 kg corresponde ao fermento, logo adicionando 100 g em 1,2 kg temos:
1,2 kg + 100 g = 1,3 kg
Como 1,3 kg é o total de fermento que temos depois de adicionarmos mais fermento e 60,1 kg o novo total da mistura, precisamos saber quanto 1,3 kg corresponde do total de 60,1 kg em porcentagem.
Para isso fazemos:
1,3/60,1 . 100 = 2,16%
Portanto, a nova mistura possui 2,16% de fermento.
19) Uma mercadoria é vendida em, no máximo, três prestações mensais e iguais, totalizando o valor de R$ 900,00. Caso seja adquirida à vista, a loja oferece um desconto de 12% sobre o valor a prazo. Qual é o preço da mercadoria na compra à vista?
Resolução:
Podemos utilizar a razão centesimal ou o número decimal correspondente:
12% = 12/100 = 0,12
Razão centesimal
12/100 x 900 = 12x900/100 = 1080/100 = 10800/100 = 108 reais
900 – 108 = 792 reais
Número decimal
0,12 x 900 = 108 reais
900 – 108 = 792 reais
A utilização de qualquer procedimento fica a critério próprio, pois os dois métodos chegam ao resultado de forma satisfatória e exata. No caso do exemplo 1, o desconto no pagamento à vista é de R$ 108,00, portanto, o preço é de R$ 792,00.
20) O FGTS (Fundo de Garantia por Tempo de Serviço) é um direito do trabalhador com carteira assinada, no qual o empregador é obrigado por lei a depositar em uma conta na Caixa Econômica Federal o valor de 8% do salário bruto do funcionário. Esse dinheiro deverá ser sacado pelo funcionário na ocorrência de demissão sem justa causa. Determine o valor do depósito efetuado pelo empregador sabendo que o salário bruto do funcionário era R$ 1.200,00.
Resolução:
8% = 8/100 = 0,08
Razão centesimal
8/100 x 1200 = 8x1200 / 100 = 9600 / 100 = 96 reais
Número decimal
0,08 x 1200 = 96 reais
O depósito efetuado foi de R$ 96,00.
21) Em uma sala de aula com 52 alunos, 13 utilizam bicicletas como transporte. Expresse em porcentagem a quantidade de alunos que utilizam bicicleta.
Resolução:
Podemos utilizar uma regra de três simples.
Alunos → 13 ---------- 52
Porcentagem → x ----------- 100%
52*x = 13*100
52x = 1300
x= 1300/52
x = 25%
Portanto, 25% dos alunos utilizam bicicletas.
22) Um jogador de futebol, ao longo de um campeonato, cobrou 75 faltas, transformando em gols 8% dessas faltas. Quantos gols de falta esse jogador fez?
Resolução:
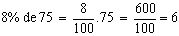 Portanto o jogador fez 6 gols de falta.
Portanto o jogador fez 6 gols de falta.
23) Se eu comprei uma ação de um clube por R$250,00 e a revendi por R$300,00, qual a taxa percentual de lucro obtida?
Resolução:
Montamos uma equação, onde somando os R$250,00 iniciais com a porcentagem que aumentou em relação a esses R$250,00, resulte nos R$300,00.
 Portanto, a taxa percentual de lucro foi de 20%.
Portanto, a taxa percentual de lucro foi de 20%.
24) Determine a área a ser desmatada de uma região de 200 km² de floresta Amazônica, considerando que os órgãos de defesa do meio ambiente permitiram derrubar somente 5% da região citada.
Resolução:
1ª situação
Sabemos que 5% corresponde a 5/100, então podemos realizar a seguinte multiplicação:
5/100 de 200.
5/100 de 200 = (5*200) / 100 = 1000 / 100 = 10
2ª situação
O valor de 5% corresponde a 5/100 que possui representação decimal de 0,05. Então temos que:
5% de 200 = 0,05 * 200 = 10
Portanto, o proprietário deverá desmatar somente 10 km² da região.
25) No intuito de reduzir o consumo de energia elétrica mensal das residências de um determinado país, o governo baixou uma medida provisória decretando que todos reduzam o consumo de energia em até 15%. Essa medida foi criada para que não haja riscos de ocorrerem apagões, em razão da escassez de chuvas que deixaram os reservatórios das hidrelétricas abaixo do nível de segurança. Salvo que a água é utilizada na movimentação das turbinas geradoras de energia elétrica. De acordo com a medida provisória, uma residência com consumo médio de 652 quilowatts–hora mensais, terá que reduzir o consumo em quantos quilowatts–hora mensal?
Resolução:
1º situação
Temos que:
15% de 652 = 15/100 * 652 = (15*652) / 100 = 9780/ / 100 = 97,8
2º situação
15% de 652 = 0,15 * 652 = 97,8
A redução será de 97,8 quilowatts–hora mensal. Assim, o consumo médio cairá de 652 para 554,2 quilowatts–hora mensais aproximadamente.
26) Em uma escola há 800 alunos matriculados, dos quais 60% praticam esportes. Desses 60% temos que: 70% praticam futebol, 20% praticam vôlei e 10% fazem natação. Determine o número de alunos que praticam futebol, vôlei e natação.
Resolução:
Precisamos calcular os 60% dos matriculados na escola:
60% de 800 = 60/100 * 800 = (60*800) / 100 = 48000 / 100 = 480 alunos
Dos 480 alunos vamos calcular:
Praticam futebol
70% de 480 = 70/100 * 480 = (70*480) / 100 = 33600 / 100 = 336 alunos
Praticam vôlei
20% de 480 = 20/100 * 480 = (20*480) / 100 = 9600 / 100 = 96 alunos
Fazem natação
10% de 480 = 10/100 * 480 = (10*480) / 100 = 4800 / 100 = 48 alunos.
27) (ENEM) A taxa anual de desmatamento na Amazônia é calculada com dados de satélite, pelo Instituto Nacional de Pesquisas Espaciais (INPE), de 1º de agosto de um ano a 31 de julho do ano seguinte. No mês de julho de 2009, foi registrado que o desmatamento acumulado nos últimos 12 meses havia sido 64% maior do que no ano anterior, quando o INPE registrou 4.974 km² de floresta desmatada. Nesses mesmos 12 meses acumulados, somente o estado de Mato Grosso foi responsável por, aproximadamente, 56% da área total desmatada na Amazônia.
De acordo com os dados, determine a área desmatada sob a responsabilidade do estado do Mato Grosso, em julho de 2008.
Resolução:
Calcular o aumento da área desmatada:
64% de 4.974 = 64/100 de 4.974 = 0,64 * 4974 = 3.183,36
4.974 + 3.183,36 = 8.157,36
A nova área desmatada corresponde a 8.157,36 km², assim, sob a responsabilidade do Mato Grosso foram desmatados 56%, portanto:
56% de 8157,36 = 56/100 de 8157,36 = 0,56 * 8157,36 = 4.568,12 km².
A área desmatada sob a responsabilidade do estado do Mato Grosso é de 4 568,12 km².
28) (BNB-FGV) Para Hugo, qualquer pessoa com menos de 40 anos é jovem e qualquer pessoa com 40 anos ou mais é velha. Hugo diz que, na empresa em que trabalha 27% das pessoas são velhas. Ele verificou também que entre todas as pessoas da empresa, 20% das mulheres são velhas e 40% dos homens são velhos. Entre as pessoas que trabalham nessa empresa, a porcentagem de homens é de:
(A) 35%
(B) 40%
(C) 45%
(D) 55%
(E) 65%
Resolução:
Na empresa, 27% das pessoas são velhas e 73% são jovens.
Entre as mulheres, 20% são velhas e 80% são jovens.
Entre os homens, 40% são velhos e 60% são jovens.
Sejam: M a quantidade de mulheres e H a quantidade de homens.
Vamos também supor que existem 100 funcionários, ou seja, M + H = 100
Vamos analisar as pessoas velhas:
Representam 27% dos funcionários, 20% da mulheres e 40% dos homens.
0,2M + 0,4H = 27
2M + 4H = 270
M + 2H = 135
Sabendo que M = 100 – H, vamos substituir na equação acima:
100 – H + 2H = 135
H = 135 – 100 = 35
Daí, 35% são homens.
Alternativa: A
29) (Sejus-ES-Vunesp) Perante a lei, quando alguém é preso, é presumidamente inocente, até que os fatos apurados atestem o contrário. Portanto, a princípio, deve aguardar em liberdade seu julgamento, a não ser que se entenda que a pessoa precisa ser presa para que sejam coletadas provas para o inquérito ou processo, a fim de se preservar a ordem pública ou econômica. Em 2005, os presos provisórios no Brasil eram 91 mil, hoje são 173 818, correspondendo a um aumento percentual de, aproximadamente,
(A) 95%.
(B) 91%.
(C) 81%.
(D) 98%.
(E) 85%.
Resolução:
Se o número de presos passou de 91000 para 173818, o aumento foi de:
173818 – 91000 = 82818
Calculando o aumento percentual:
82818/91000 = 0,91 ou 91%
Resposta: B
30) (Correios-Cespe) Além da missão de entregar correspondências, os carteiros são também responsáveis pela difusão de importantes campanhas de conscientização da população e promoção da cidadania. Um exemplo de ação de caráter social que envolve os carteiros e que tem tido grande receptividade é o projeto Papai Noel dos Correios. Em 2009, foram adotados 21% das 1.981.000 cartas recebidas pelos Correios. O projeto contou com o apoio e a participação de 3.818 voluntários internos, 669 voluntários externos e 462 parcerias.
Com base no texto, é correto afirmar que, em 2009, a quantidade de cartas que não foram adotadas pelo projeto Papai Noel dos Correios foi:
superior a 1,2 milhão e inferior a 1,3 milhão.
superior a 1,3 milhão e inferior a 1,4 milhão.
superior a 1,4 milhão e inferior a 1,5 milhão.
superior a 1,5 milhão.
inferior a 1,2 milhão.
Resolução:
Como foram adotados 21% das cartas, então não foram adotados 100 – 21 = 79% das cartas
Logo, 79% de 1.981.000 é 79/100 x 1981000 = 79 x 19810 = 1.564.990
Resposta: D
31) (BB-FCC) Em dezembro de 2007, um investidor comprou um lote de ações de uma empresa por R$ 8 000,00. Sabe-se que: em 2008 as ações dessa empresa sofreram uma valorização de 20%; em 2009, sofreram uma desvalorização de 20%, em relação ao seu valor no ano anterior; em 2010, se valorizaram em 20%, em relação ao seu valor em 2009.
De acordo com essas informações, é verdade que, nesses três anos, o rendimento percentual do investimento foi de:
(A) 20%.
(B) 18,4%.
(C) 18%.
(D) 15,2%.
(E) 15%.
Resolução:
Note que as ações valorizam e desvalorizam em relação ao ano anterior.
Não podemos simplesmente somar ou subtrair as taxas de variação.
Quando valoriza 20%, devemos multiplicar por 1,2.
Quando desvaloriza 20%, devemos multiplicar por 0,8.
Temos:
1,2 x 0,8 x 1,2 = 1,152
Daí, a valorização foi de 15,2%
Resposta: D
32) (BB-Cesgranrio) Um investidor aplicou certa quantia em um fundo de ações. Nesse fundo, 1/3 das ações eram da empresa A, 1/2 eram da empresa B e as restantes, da empresa C. Em um ano, o valor das ações da empresa A aumentou 20%, o das ações da empresa B diminuiu 30% e o das ações da empresa C aumentou 17%. Em relação à quantia total aplicada, ao final desse ano, este investidor obteve:
(A) lucro de 10,3%.
(B) lucro de 7,0%.
(C) prejuízo de 5,5%.
(D) prejuízo de 12,4%.
(E) prejuízo de 16,5%.
Resolução:
Sabendo que 1/3 das ações eram da empresa A, 1/2 eram da empresa B e as restantes, da empresa C, vamos descobrir qual fração representa a quantidade de ações da empresa C:
1/3 + 1/2 = (2 + 3)/6 = 5/6
Logo, 1/6 das ações eram da empresa C.
Se as ações da empresa A subiram 20%:
(1/3).(120/100) = 40/100
Se as ações da empresa B caíram 30%:
(1/2).(70/100) = 35/100
Se as ações da empresa C subiram 17%:
(1/6).(117/100) = 19,5/100
Somando:
40/100 + 35/100 + 19,5/100 = 94,5/100 = 94,5%
Logo, o investidor teve prejuízo de 5,5%.
Resposta: C
33) (BB-Cesgranrio) No Brasil, os clientes de telefonia móvel podem optar pelos sistemas pré-pago ou pós-pago. Em certa empresa de telefonia móvel, 17 em cada 20 clientes utilizam o sistema pré-pago. Sendo assim, o número de clientes que utilizam o sistema pré-pago supera o número de clientes do pós-pago em 24,36 milhões. Quantos milhões de clientes são atendidos por essa empresa?
(A) 29,58
(B) 30,25
(C) 31,20
(D) 32,18
(E) 34,80
Resolução:
Vamos calcular a porcentagem de clientes pré-pago:
17/20 = 0,85 = 85%
Podemos então deduzir que a quantidade de clientes pós-pago é de 15%.
Logo, a diferença entre os dois, que é de 24,36 milhões corresponde a 70%.
O total de linhas é 24,36 / 0,7 = 34,8 milhões.
Resposta: E
34) (RFB-Esaf) Em uma repartição, 3/5 do total dos funcionários são concursados, 1/3 do total dos funcionários são mulheres e as mulheres concursadas correspondem a 1/4 do total dos funcionários dessa repartição. Assim, qual entre as opções abaixo, é o valor mais próximo da porcentagem do total dos funcionários dessa repartição que são homens não concursados?
(A) 21%
(B) 19%
(C) 42%
(D) 56%
(E) 32%
Resolução:
De “3/5 do total dos funcionários são concursados” temos que 60% são concursados e 40% não são concursados.
De “mulheres concursadas correspondem a 1/4 do total dos funcionários” temos que 25% dos funcionários são mulheres concursadas.
De “1/3 do total dos funcionários são mulheres” temos que as mulheres correspondem a aproximadamente 33%.
Daí, a porcentagem de mulheres não concursadas é 33 – 25 = 8%.
Como 40% dos funcionários não são concursados, a porcentagem de homens não concursados é 40 – 8 = 32%
Resposta: E
35) (Sejus-ES) De acordo com relatório da Organização Mundial de Saúde (OMS) acerca do avanço da gripe A ou influenza A, provocada pelo vírus H1N1, inicialmente denominada gripe suína, os dados de maio de 2009, no mundo, eram os seguintes.
I O México, considerado o epicentro da epidemia, era o país mais afetado, com 590 casos confirmados, dos quais 25 resultaram na morte dos pacientes.
II Nos Estados Unidos da América (EUA), segundo país do mundo em número de casos, 226 pessoas tiveram testes com resultado positivo para o vírus H1N1.
III Outros países com casos confirmados da doença, sem nenhuma morte, eram: Canadá (85), Espanha (40), Reino Unido (15), Alemanha (8), Nova Zelândia (4), Israel (3), El Salvador (2), França (2), Áustria (1), China (1), Hong Kong (1), Colômbia (1), Coreia do Sul (1), Costa Rica (1), Dinamarca (1), Irlanda (1), Itália (1), Holanda (1) e Suíça (1).
Com base nos dados do relatório da OMS transcritos acima, julgue os itens I e II a seguir.
Resolução:
I)No México, o número de mortes representa mais de 5% dos casos confirmados da doença em todo o mundo.
ERRADO
Observe que o número de mortes no México foi de 25. Esse número é 5% de 500, ou seja, o número de mortes no México não representa nem 5% dos casos confirmados nesse país, muito menos em todo o mundo.
II)Os países em que foi confirmado apenas um caso da doença representam menos de 2% do número de casos mencionados no relatório.
CERTO
Países com apenas um caso confirmado: Áustria, China, Hong Kong, Colômbia, Coreia do Sul, Costa Rica, Dinamarca, Irlanda, Itália, Holanda e Suíça. Total 11 países. Esse número é 2% de 550. Claramente, foram confirmados mais do que 550 casos, logo 11 representa menos de 2% dos casos.
36) (INSS-Cespe) Um dos indicadores de saúde comumente utilizados no Brasil é a esperança de vida ao nascer, que corresponde ao número de anos que um indivíduo vai viver, considerando-se a duração média da vida dos membros da população. O valor desse índice tem sofrido modificações substanciais no decorrer do tempo, à medida que as condições sociais melhoram e as conquistas da ciência e da tecnologia são colocadas a serviço do homem.
A julgar por estudos procedidos em achados fósseis e em sítios arqueológicos, a esperança de vida do homem pré-histórico ao nascer seria extremamente baixa, em torno de 18 anos; na Grécia e na Roma antigas, estaria entre 20 e 30 anos, pouco tendo se modificado na Idade Média e na Renascença. Mais recentemente, têm sido registrados valores progressivamente mais elevados para a esperança de vida ao nascer. Essa situação está ilustrada no gráfico abaixo, que mostra a evolução da esperança de vida do brasileiro ao nascer, de 1940 a 2000.
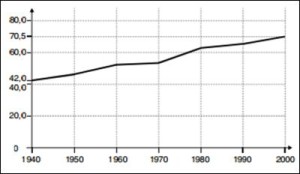 Com base nas informações do texto e considerando os temas a que ele se reporta, julgue os itens I e II seguintes.
Com base nas informações do texto e considerando os temas a que ele se reporta, julgue os itens I e II seguintes.
Resolução:
I) Sabendo-se que, em 1910, a esperança de vida do brasileiro ao nascer era de 34 anos, conclui-se que o valor desse indicador aumentou em mais de 100% em 90 anos, isto é, de 1910 a 2000.
Se duplicarmos a esperança de vida em 1910 teremos 68 anos. Como a expectativa em 2000 era de 70,5 anos, claramente é superior a 100%.
Resposta: Certo
II) Se for mantida, durante o período de 2000-2020, a tendência observada, no gráfico mostrado, no período 1980-2000, a esperança de vida do brasileiro ao nascer será, em 2020, superior a 85 anos.
Analisando o gráfico e sendo bem conservadores, de modo a calcularmos com o maior crescimento possível, vamos considerar que no ano de 1980 a expectativa era de 61 anos, logo, no período 1980-2000 o crescimento foi de 9,5 anos ou 15,57%. Aplicando este percentual sobre 70,5 anos, teremos aproximadamente 81,5 anos.
Resposta: Errado
37) (SAP-SP) Uma pessoa comprou um produto exposto na vitrine por um valor promocional de 20% de desconto sobre o preço P do produto. Como ela pagou em dinheiro, teve mais 10% de desconto sobre o valor promocional. Então, essa pessoa pagou, sobre o preço P do produto, um valor igual a
(A) 0,28P.
(B) 0,03P.
(C) 0,7P.
(D) 0,3P.
(E) 0,72P
Resolução:
Seja P o valor do produto.
Como estava na promoção com 20%, o preço passou a ser de 0,8.P (80% do valor).
Ao pagar em dinheiro, o comprador ganhou mais 10% e o preço passou a ser 0,8P.0,9(90% do valor):
0,8P.0,9 = 0,72.P
Resposta: E
38) (SAP-SP) Em uma academia foi realizada uma enquete em que as pessoas tinham que indicar um setor onde eles mais frequentavam, dentre os três indicados no questionário: musculação, condicionamento físico ou natação. Cada uma dessas pessoas também precisou optar por apenas um tipo de alimentação, a qual acreditava ser mais importante após os treinos, dentre as duas oferecidas: carboidratos ou fibras. Os resultados das escolhas estão na tabela a seguir:
 Nas condições apresentadas na tabela, pode-se afirmar que
Nas condições apresentadas na tabela, pode-se afirmar que
(A) 50% do total de pessoas optaram por Fibras e Natação.
(B) 12% dos que escolheram Fibras optaram por Musculação.
(C) 40% dos que escolheram Carboidratos optaram por Condicionamento Físico.
(D) 30% dos que escolheram Carboidratos optaram por Musculação.
(E) 20% do total de pessoas optaram por Fibras e Condicionamento Físico.
Resolução
Repare que 70 pessoas escolheram carboidratos, e dessas, 28 escolheram condicionamento físico.
28/70 = 0,4 = 40%
Resposta: C
39) (SAP-SP) Uma loja tinha 150 televisões de um modelo que estava para sair de linha. Dessas, foram vendidas 3/5 e para acabar com essa mercadoria foi feita uma promoção de 10% de desconto do valor inicial para as televisões restantes. Foram vendidas todas as televisões e o valor total arrecadado foi de R$ 172.800,00. O preço de cada televisão com o desconto era de
(A) R$ 1.205,00.
(B) R$ 1.080,00.
(C) R$ 1.250,00.
(D) R$ 1.190,00.
(E) R$ 1.100,00.
Resolução:
Das 150 tvs, 3/5 foram vendidas sem desconto:
150.3/5 = 90
Quantidade de tvs vendidas com 10% de desconto:
150 – 90 = 60
Sendo x o preço inicial e cada tv, temos:
90x + 60.x.0,9 = 172800 (utilizamos o 0,9 para representar o desconto de 10%)
90x + 54x = 172800
144x = 172800
x = 172800/144
x = 1200 (esse é o preço inicial de cada tv)
Calculando o preço com o desconto:
1200.0,9 = 1080
Resposta: B
40) (PM-MG) Marque a alternativa CORRETA. Em uma sala de aula, os alunos têm três recipientes de volumes iguais. Um está cheio de líquido A, outro cheio com líquido B e o terceiro vazio. No terceiro recipiente é colocada a metade do volume do líquido A e 30% do volume de B. As percentagens dos líquidos A e B em relação a esta mistura, neste terceiro recipiente, são, respectivamente, iguais a
(A) 62,5% e 37,5%
(B) 50% e 30%
(C) 80% e 20%
(D 40% e 60%
Resolução:
Como todos os recipientes possuem os mesmos volumes, podemos concluir o terceiro recipiente está composto por 50% do líquido A, 30 % do líquido B e 20% sem preenchimento, ou seja, está preenchido em 80%.
Calculando a relação do líquido A com a mistura:
50 / 80
0,625 = 62,5%
Calculando a relação do líquido B com a mistura:
30 / 80
0,375 = 37,5%
Resposta: A
41) (Detran/SP-Vunesp) A parcela do crediário que Carla fez para a compra de um automóvel sofreu um reajuste de 20% no mês anterior. Antes do reajuste, o valor dessa prestação correspondia a 10% do seu salário, o qual também sofreu um aumento de 7% no mesmo mês. Após esses reajustes, a prestação do crediário passou a representar, do salário de Carla, aproximadamente
(A) 13%.
(B) 12%.
(C) 11%.
(D) 15%.
(E) 14%.
Resolução
Considere que o valor da parcela antes do reajuste era de R$ 100,00.
Sabendo que o reajuste da parcela foi de 20%, a nova parcela será de R$ 120,00.
100 . 1,20 = R$ 120,00
A questão também informa que o valor inicial da prestação correspondia a 10% do salário de Carla, ou seja, o salário anterior era de R$ 1.000,00.
Como o salário teve um aumento de 7%, o novo salário passou a ser de R$ 1.070,00.
1000 . 1,07 = R$ 1.070,00
Calculando quanto a nova prestação representa do salário de Carla:
120/1070 ≈ 0,11 = 11%
Resposta: C
42) Determine 25% de 360.

44) Determine 15% de 150.

45) O número 8 representa qual porcentagem de 20?

46) O número 12 representa qual porcentagem de 80?

47) Se 35% dos 40 alunos do 8° ano de um colégio são homens, quantas são as mulheres?

48) Uma bicicleta, cujo preço é R$ 1200,00, pode ser comprada da seguinte maneira:
a) a vista, com 15% de desconto.
b) pagamento para 90 dias, com acréscimo de 25% sobre o preço inicial.
Responda: Qual é a diferença, em reais, entre as duas opções de compra?

49) Na compra de um aparelho obtive desconto de 15% por ter feito o pagamento à vista. Se paguei R$ 102,00 reais pelo aparelho, qual era o seu preço original?

50) (CASA/AgApoioOper (Motorista) Uma fundação que cuida de crianças abandonadas conseguiu, em janeiro, encaminhar 72 crianças para adoção, o que representa 60% das crianças da fundação. Pode-se concluir que o número de crianças dessa fundação que não foram encaminhadas é
(A) 44.
(B) 46.
(C) 47.
(D) 48.
(E) 52.

51) (VNSP-AssistAdmin-I) Um arquiteto projetou uma Escola Infantil, utilizando 45% da área total do terreno para o prédio que continha as salas de aula e 15% para as salas de projeção, biblioteca e laboratórios. Mesmo assim, sobrou uma área de 900 m² para ambientes de lazer. Podemos concluir que o terreno tinha um total, em m², de
(A) 3 250.
(B) 3 000.
(C) 2 750.
(D) 2 450.
(E) 2 250.

52) (PCSP-AgentePolicia) Um produto foi vendido com desconto de 10% sobre o preço normal de venda. Se ele foi vendido por R$ 54,00, o preço normal de venda desse produto é
(A) R$ 59,40.
(B) R$ 58,00.
(C) R$ 60,00.
(D) R$ 59,00.
(E) R$ 58,40.

53) (SOLDADO-PM/PI-NUCEPE) Sobre o preço de uma moto importada incide um imposto de importação de 30%. Em função disso, o seu preço para o importador é de R$ 15.600,00. Supondo que tal imposto passe de 30% para 60%, qual será, em reais, o novo preço da moto, para o importador?
(A) 19.200,00
(B) 22.500,00
(C) 31.200,00
(D) 39.000,00
(E) 21.000,00

54) Um investidor aplicou R$ 2500,00 e após alguns meses ele resgatou 3700,00. Qual foi a porcentagem de lucro?
Resolução:
2500i = 3700
i = 3700 / 2500
i = 1,48
O capital aumentou 1,48 vezes, mas para saber a porcentagem de aumento é preciso subtrair, que representa o capital e depois multiplicar por 100. Portanto a porcentagem de aumento é:
1,48 – 1 = 0,48
0,48 x 100 = 48%
55) Em 2010, determinado produto custava R$ 60,00. Em 2012, esse mesmo produto custa 99,00. Qual a porcentagem do aumento do preço?
Resolução:
60i = 99
i = 99 / 60
i = 1,65
O capital aumentou 1,65 vezes, mas para saber a porcentagem de aumento é preciso subtrair 1, que representa o capital e depois multiplicar por 100. Portanto a porcentagem de aumento é:
1,66 – 1 = 0,66
0,66 x 100 = 65%
56) Ricardo comprou uma geladeira por R$ 2500,00 à vista. No dia seguinte, ele viu uma promoção da loja em que ele comprou a geladeira e ela estava com desconto de 30%. Quanto Ricardo teria pago se tivesse comprado na promoção?
Resolução:
Se o preço que o Ricardo pagou representa 100% do valor e o desconto é de 30%, então na promoção Ricardo pagaria somente 70% do valor pago.
70% de 2500
0,7 x 2500
R$ 1750,00
57) Um comerciante tenta vender um produto para um cliente a R$ 850,00. Sabendo que o cliente pagou somente R$ 700,00 pelo produto, qual foi a porcentagem de desconto?
Resolução:
850i = 700
i = 700 / 850
i = 0,8235
O preço pago foi aproximadamente 0,8235 vezes o preço inicial, mas para calcular a porcentagem de desconto vamos subtrair esse valor de 1 e multiplicar por 100. Portanto a porcentagem de desconto é:
1 – 0,8235 = 0,1765
0,1765 x 100 = 17,65%
58) João comprou um carro por R$ 32000,00. Depois de alguns meses de uso ele bateu o carro. Ao tentar vender o carro, foi lhe oferecido R$ 25500,00 pelo carro. Qual foi a porcentagem de desvalorização do carro?
Resolução:
32000i = 25500
i = 25500 / 32000
i = 0,7968
O preço após a batida aproximadamente 0,7968 vezes o preço inicial. Para calcular a porcentagem de desvalorização vamos subtrair esse valor de 1 e multiplicar por 100. Portanto a porcentagem de desvalorização é:
1 – 0,7968 = 0,2032
0,2032 x 100 = 20,32
59) Uma loja estava oferecendo uma promoção assim: “Leve 13, pague 9.” Qual é a porcentagem de economia nessa promoção?
Resolução:
A melhor maneira de resolver problemas que não informam os valores é dar um valor fictício. Então vamos supor que cada produto custe R$100,00. Nessa lógica, ao invés de pagar R$1300,00 você paga somente R$900,00. A economia nesse caso é de R$400,00. Agora, para calcular a porcentagem da economia basta calcular a razão da economia com o valor que seria pago e multiplicar o resultado por 100.
400 / 1300 = 0,3077
0,3077 x 100 = 30,77
60) Qual o preço de um produto que custava inicialmente R$ 140,00 e sofreu dois reajustes de 12% e 20% respectivamente?
Resolução:
Quando se trata de aumentos consecutivos, devemos passar a porcentagem de aumento para a forma decimal e somar 1. Feito isso, multiplicamos pelo valor que sofrerá o aumento.
P1 = 140 ( 1 + 0,12 )
P1 = 156,80
P2 = 156,80 ( 1 + 0,2 )
P2 = 188,16
61 Um produto que custava R$ 320,00 sofreu um aumento de 18%. Uma cliente foi comprar o produto e obteve um desconto e pagou R$ 350,00. Qual foi a porcentagem de desconto?
Resolução:
Vamos por etapas. Na primeira etapa, o produto teve um aumento de 18%. Calcularemos o valor do produto após o aumento. Na segunda etapa, a cliente teve uma porcentagem de desconto e pagou R$350,00. O valor do desconto é o valor após o aumento menos o valor pago. A porcentagem de desconto é dada pela razão entre o valor do desconto e o valor sem o desconto.
1º passo:
P1 = 350 ( 1 + 0,18 )
P1 = 413,00
2º passo:
D = 63 / 413
D = 15,25%
62) (BB – Fundação Carlos Chagas) O supervisor de uma agência bancária obteve dois gráficos que mostravam o número de atendimentos realizados por funcionários. O Gráfico I mostra o número de atendimentos realizados pelos funcionários A e B, durante 2 horas e meia, e o Gráfico II mostra o número de atendimentos realizados pelos funcionários C, D e E, durante 3 horas e meia.
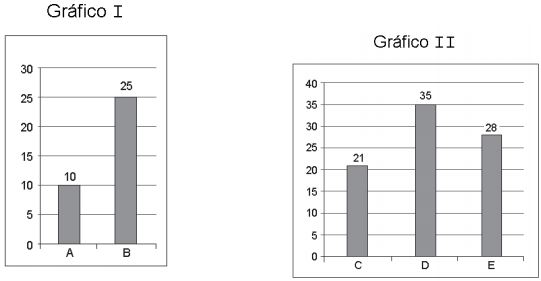 Observando os dois gráficos, o supervisor desses funcionários calculou o número de atendimentos, por hora, que cada um deles executou. O número de atendimentos, por hora, que o funcionário B realizou a mais que o funcionário C é:
Observando os dois gráficos, o supervisor desses funcionários calculou o número de atendimentos, por hora, que cada um deles executou. O número de atendimentos, por hora, que o funcionário B realizou a mais que o funcionário C é:
(A) 4.
(B) 3.
(C) 10.
(D) 5.
(E) 6.
Resolução
Funcionário B
25 atendimentos / 2,5 horas = 10 clientes por hora
Funcionário C
21 atendimentos / 3,5 horas = 6 clientes por hora
Diferença: 10 – 6 = 4
Resposta: A
63) (Sejus-ES-Vunesp) Observe os gráficos e analise as afirmações I, II e III.
Procura por graduação aumenta ano a ano
Explosão do número de inscritos
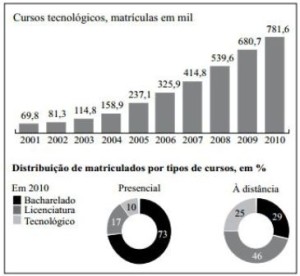 I. Em 2010, o aumento percentual de matrículas em cursos tecnológicos, comparado com 2001, foi maior que 1000%.
I. Em 2010, o aumento percentual de matrículas em cursos tecnológicos, comparado com 2001, foi maior que 1000%.
II. Em 2010, houve 100,9 mil matrículas a mais em cursos tecnológicos que no ano anterior.
III. Em 2010, a razão entre a distribuição de matrículas no curso tecnológico presencial e à distância foi de 2 para 5.
É correto o que se afirma em
(A) I e II, apenas.
(B) II, apenas.
(C) I, apenas.
(D) II e III, apenas.
(E) I, II e III.
Resolução
I. CERTO
Matrículas em 2001: 69800;
Matrículas em 2010: 781600;
Crescimento: 781600 – 69800 = 711800
Crescimento em porcentagem: 711800/69800 = 10,19 ou 1019%
II. CERTO
Matrículas em 2010: 781600
Matrículas em 2009: 680700
Crescimento: 781600 – 680700 = 100900
III. CERTO
Em 2010 tivemos 10 matrículas presenciais e 25 à distância:
10/25 = 2/5
Resposta: E
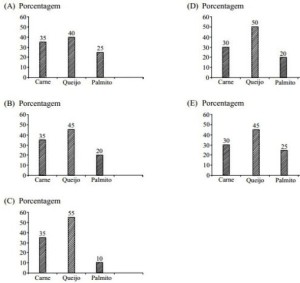
64) (PM SP) Para uma festa junina, foi contratada uma barraca de pastéis, que levou os seguintes tipos de recheios: carne, queijo e palmito. A tabela a seguir mostra a quantidade de pastéis vendidos na festa.
Recheios Número de pastéis vendidos
Carne —— 56
Queijo —– 72
Palmito —- 32
Em relação ao número total de pastéis vendidos na festa, o gráfico que representa essas informações, em porcentagem, é:
 Em relação ao número total de pastéis vendidos na festa, o gráfico que representa essas informações, em porcentagem, é:
Em relação ao número total de pastéis vendidos na festa, o gráfico que representa essas informações, em porcentagem, é:
Resolução
Total de pastéis vendidos: 56 + 72 + 32 = 160
Carne: 56/160 = 0,35 = 35%
Queijo: 72/160 = 0,45 = 45%
Palmito: 0,20 = 20%
Alternativa: B
65) (BB-Cesgranrio) Os gráficos abaixo apresentam dados sobre a produção e a reciclagem de lixo em algumas regiões do planeta.
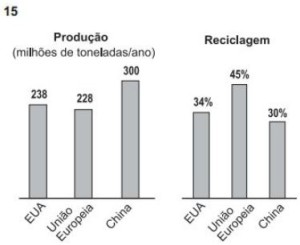 Baseando-se nos dados apresentados, qual é, em milhões de toneladas, a diferença entre as quantidades de lixo recicladas na China e nos EUA em um ano?
Baseando-se nos dados apresentados, qual é, em milhões de toneladas, a diferença entre as quantidades de lixo recicladas na China e nos EUA em um ano?
(A) 9,08
(B) 10,92
(C) 12,60
(D) 21,68
(E) 24,80
Resolução:
A China produz 300 milhões e recicla 30%, ou seja, recicla 90 milhões.
Os EUA produzem 238 milhões e recicla 34%, ou seja, reciclam 80,92 milhões.
China – EUA = 90 – 80,92 = 9,08 milhões de toneladas.
Resposta: A
66) (INSS – Cespe) A tabela abaixo mostra, em porcentagens, a distribuição relativa da população brasileira por grupos etários, de acordo com dados dos censos demográficos de 1940 a 2000.
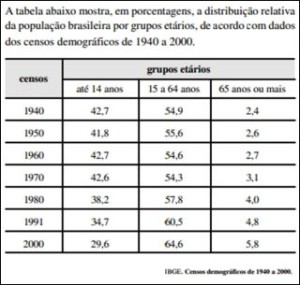 Com base nos dados acerca da evolução da população brasileira apresentados na tabela acima, julgue a afirmação abaixo:
Com base nos dados acerca da evolução da população brasileira apresentados na tabela acima, julgue a afirmação abaixo:
“O gráfico a seguir ilustra corretamente as informações apresentadas na tabela.”
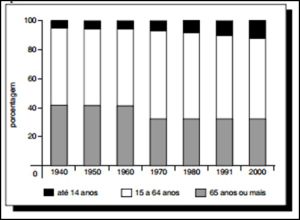 Resolução
Resolução
Observe que o gráfico estaria certo se as cores de “até 14 anos” e “65 anos ou mais” fossem invertidas.
Resposta: Errado
67) (PM Pará) O gráfico abaixo mostra a produção diária de lixo orgânico de duas pessoas. O dia da semana que o gráfico mostra que as produções de lixo das duas pessoas foram iguais é: 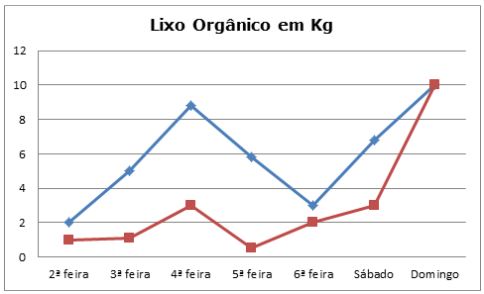 (A) 2ª feira
(A) 2ª feira
(B) 4ª feira
(C) 6ª feira
(D) Sábado
(E) Domingo
Resolução
Repare que existe interseção das linhas azul e vermelha apenas no Domingo, onde cada uma produziu 10 kg de lixo orgânico.
Resposta: E
68) (PM Pará) O gráfico abaixo mostra que no período de 94 a 95 houve um grande aumento no desmatamento da Amazônia. O aumento aproximado, em porcentagem, desse desmatamento no período de 94 a 95 foi de:
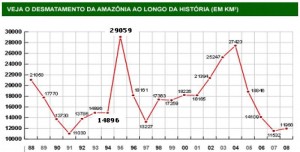 (A) 95
(A) 95
(B) 92
(C) 90
(D) 88
(E) 85
Resolução
Calculando o crescimento do desmatamento:
29059 – 14896 = 14163
Para calcularmos a porcentagem, basta dividir pelo desmatamento de 94:
14163/14896 = 0,95 = 95%
Resposta: A
69) (PM MG) O 150º Batalhão é responsável pela 301ª CIA PM, 302ª CIA PM, 303ª CIA PM e 304ª CIA PM. Nesse Batalhão, no ano de 2017, todas as CIAS PM obtiveram redução percentual (%) nos crimes em relação ao ano de 2016. Com base nas informações contidas no gráfico abaixo, marque a alternativa CORRETA.
GRÁFICO: crimes na área do 150º BPM, por CIA PM – 2016 a 2017:
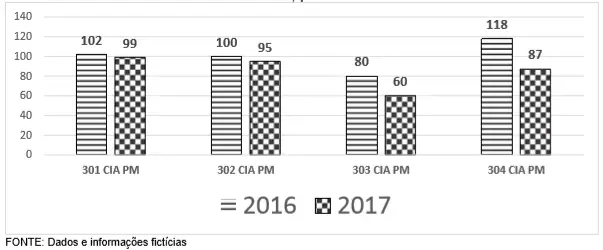 ( ) A 301ª CIA PM obteve maior redução percentual que a 304ª CIA PM.
( ) A 301ª CIA PM obteve maior redução percentual que a 304ª CIA PM.
( ) A 303ª CIA PM conseguiu reduzir os crimes em 25%.
( ) A 303ª CIA PM obteve menor redução percentual que a 302ª CIA PM.
( ) A 302ª CIA PM conseguiu reduzir os crimes em 12%.
Resolução
Calculando o percentual de redução de cada CIA:
301ª CIA: 3/102 = 2,94%
302ª CIA: 5/100 = 5%
303ª CIA: 20/80 = 25%
304ª CIA: 31/118 = 26,2%
Resposta: B
70) (Detran SP – Vunesp) O gráfico apresenta a distribuição de vítimas de trânsito no mês de julho de 2013, segundo o tipo de usuário da via pública em uma determinada cidade brasileira.
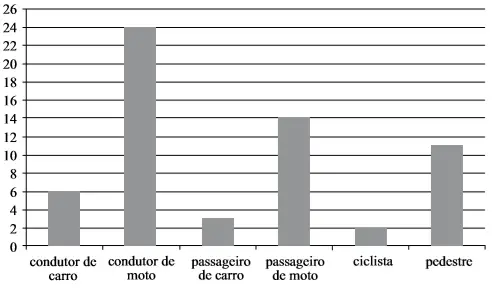 O grupo que corresponde a 2/5 do total de vítimas é o de
O grupo que corresponde a 2/5 do total de vítimas é o de
(A) passageiro de carro.
(B) condutor de carro.
(C) passageiro de moto.
(D) pedestre.
(E) condutor de moto.
Resolução
Analisando o gráfico, a quantidade de vítimas em cada grupo foi:
condutor de carro: 6
condutor de moto: 24
passageiro de carro: 3
passageiro de moto: 14
ciclista: 2
pedestre: 11
Total de vítimas: 6 + 24 + 3 + 14 + 2 + 11 = 60
60 . 2/5 = 120/5 = 24
Resposta: E
Continua...









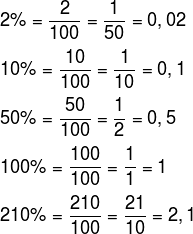
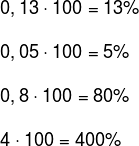








.gif)


.gif)