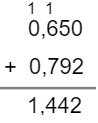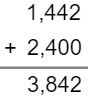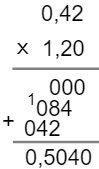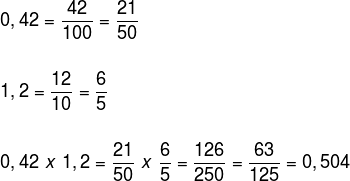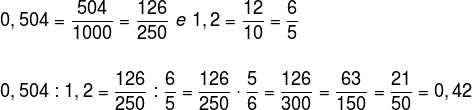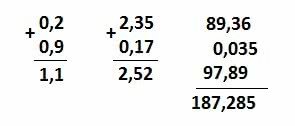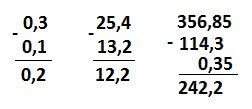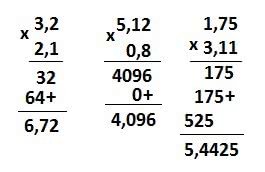Números decimais

Professor Diminoi

O que são números decimais?
Os números decimais têm como principal característica a presença da vírgula. Assim como os números inteiros, os decimais também utilizam o sistema de numeração decimal, ou seja, podemos diferenciar os números pela posição em que os algarismos se encontram.
Os números decimais aparecem com frequência em nosso cotidiano, como ao realizar compras em um supermercado ou abastecer um carro. Assim, é importante entender como funciona o sistema de posição e, consequentemente, a nomenclatura desses números. Veja os exemplos:

Vamos analisar o número 5,4561.
5 → Parte inteira
4 → Décimos
5 → Centésimos
6 → Milésimos
1 → Décimo de Milésimos

Veja que o algarismo 5 aparece duas vezes no número, entretanto, ele representa quantidades diferentes. O 5 (parte inteira) indica 5 unidades, enquanto os números que estão à direita da vírgula representam frações de um inteiro. Assim, a leitura do número deve ser feita da seguinte maneira:

Cinco inteiros, quatro mil, quinhentos e sessenta e um décimo de milésimos

Exemplo 1 – Faça a análise de cada algarismo do número 7,143 e escreva-o por extenso.
7,143 = 7 + 0,1 + 0,04 + 0,003
7 → Parte inteira
0,1 → Décimos
0,04 → Centésimos
0,003 → Milésimos

Portanto, a leitura do número fica:
Sete inteiros e cento e quarenta e três milésimos

Veja que, à esquerda da vírgula, sempre se encontra a parte inteira. Observe agora que, quando o algarismo zero é acrescentado nos décimos, centésimos, milésimos, e assim por diante, não se altera o número, desde que não exista nenhum número à direita desse zero. Veja:
3,000 = 3
5,0 = 5

Para compreender melhor, veja abaixo alguns exemplos:
0,1: um décimo
0,4: quatro décimos
0,01: um centésimo
0,35: trinta e cinco centésimos
0,125: cento e vinte e cinco milésimos
1,50: um inteiro e cinquenta centésimos
2,1: dois inteiros e um décimo
4,8: quatro inteiros e oito décimos

Nomenclatura de números decimais
A fim de facilitar as definições que virão, a seguir estabelecemos algumas nomenclaturas. Um número decimal é formado por sua parte inteira e pela parte decimal. A parte decimal é organizada da seguinte maneira: décimo, centésimo, milésimo, décimo de milésimo, centésimo de milésimo e assim por diante.

Exemplo: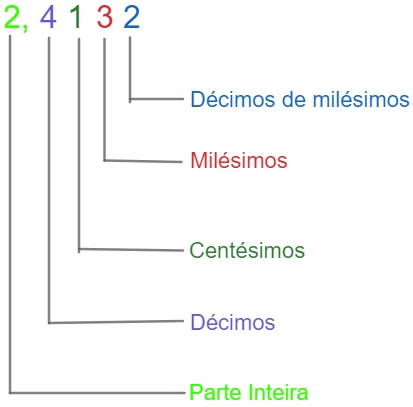
Adição com números decimais
A adição de números decimais é definida de maneira semelhante à adição de números inteiros, nessa operação devemos somar parte inteira com parte inteira, décimos com décimos, centésimos com centésimos, e assim sucessivamente. Em outras palavras, devemos colocar vírgula abaixo de vírgula, veja o exemplo.

Exemplo 1
Vamos determinar a soma dos números 0,65 e 0,792. Lembre-se: o número 0 no final de qualquer número decimal não acresce no valor.

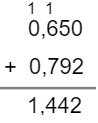
Exemplo - 2
Determine o valor da soma 1,442 + 2,4.

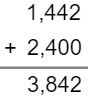
Subtração com números decimais
A subtração entre dois números decimais dá-se do mesmo modo que a sua adição, operamos parte inteira com parte inteira, décimos com décimos, e assim sucessivamente. Veja os exemplos.

Exemplo - 3
Determine a diferença entre os números 3,842 e 1,442.

Multiplicação com números decimais
A multiplicação entre dois números decimais pode ser realizada de duas formas: podemos operar de maneira semelhante à da multiplicação de dois números inteiros, somando, ao final, a quantidade de casas decimais dos dois números e colocando-as no resultado; ou podemos transformar os números decimais em frações e utilizar a multiplicação de fração.

Vamos lembrar como transformar número decimal em fração?

Transformação de número decimal para forma fracionária
Para escrever um número decimal na sua forma fracionária, devemos conservar o número decimal sem a vírgula no numerador da fração, e no denominador colocamos a potência de 10 de acordo com a quantidade de casas decimais que “andamos” para tornar o número decimal em inteiro. 

Exemplo - 1
Vamos escrever o número 0,43 em forma de fração. Para a vírgula desaparecer, devemos “andar” duas casas decimais, ou seja, precisamos multiplicar o número por 100. Assim:

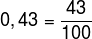
Exemplo - 2
Para escrever o número 0,8 na sua forma fracionária, devemos andar uma casa decimal, logo:
Utilizando os dois métodos, determine o produto entre 0,42 e 1,2. Antes de efetuar a multiplicação, perceba que 0,42 possui duas casas decimais e que o número 1,20 possui duas delas. A soma disso resulta em quatro casas decimais, ou seja, o resultado deverá ter quatro casas decimais.
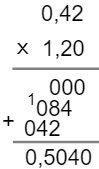Ou seja 0,42 x 1,2 = 0,504.
Agora, transformando os números para sua forma fracionária, temos a seguinte multiplicação:

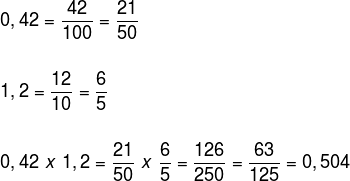
Divisão com números decimais
Na divisão de números decimais também vamos observar dois métodos que podem ser considerados equivalentes. O primeiro método consiste em “andar” a mesma quantidade de casas decimais, ou seja, multiplicar por potências de 10 até que a vírgula não esteja mais presente. O segundo método consiste em representar os números em forma de fração e realizar a divisão de frações.

Exemplo
Vamos realizar a divisão entre os números 0,504 e 1,2.
Com o primeiro método, devemos multiplicar o dividendo e o divisor pelo mesmo número até que a vírgula desapareça.
Para que a vírgula desapareça do denominador, devemos multiplicá-lo por 1000, logo, faremos o mesmo com o divisor.
0,504 · 1000 = 504
1,2 · 1000 = 1200
Armando a conta, temos:
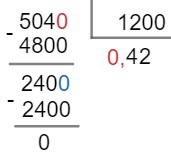Transformando os números decimais em frações, temos:

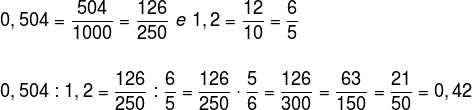
Leitura de números decimais.

Exemplos:
2,1 = dois inteiros e um décimo.
0,36 = trinta e seis centésimos.
2,36 = dois inteiros e trinta e seis centésimos.
14,6 = quatorze inteiros e seis décimos.
0,123 = cento e vinte três milésimos.

Decomposição de número decimal

Dá para quebrar o número decimal também. E decompô-lo também separando os dois lados. Decomponha o número 532,47, por exemplo.
O 5 está na casa das centenas, então, deve ser escrito como: 500
O 3, na das dezenas, então fica: 30
O 2, na das unidades, então fica: 2
O 4, na dos decimais, então fica: 0,4
O 7, na dos centésimos, então fica: 0,07

A resposta final pode ser escrita como: 537,47 = 500 + 30 + 2 + 0,4 + 0,07

Operações com Números Decimais: Adição, Subtração, Multiplicação e Divisão
Para realizar as operações dos números decimais, devemos alinhar os números segundo a vírgula e as casas decimais que possuem.

Adição

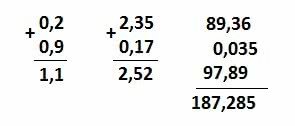
Subtração

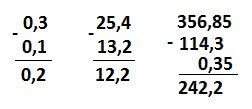
Multiplicação

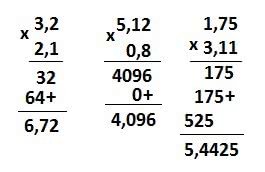
Divisão

Classificação de números decimais

Exemplo -1:


Exemplo -2: