TEOREMA DE TALES & PROPORCIONALIDADE

Professor Diminoi

TEOREMA DE TALES
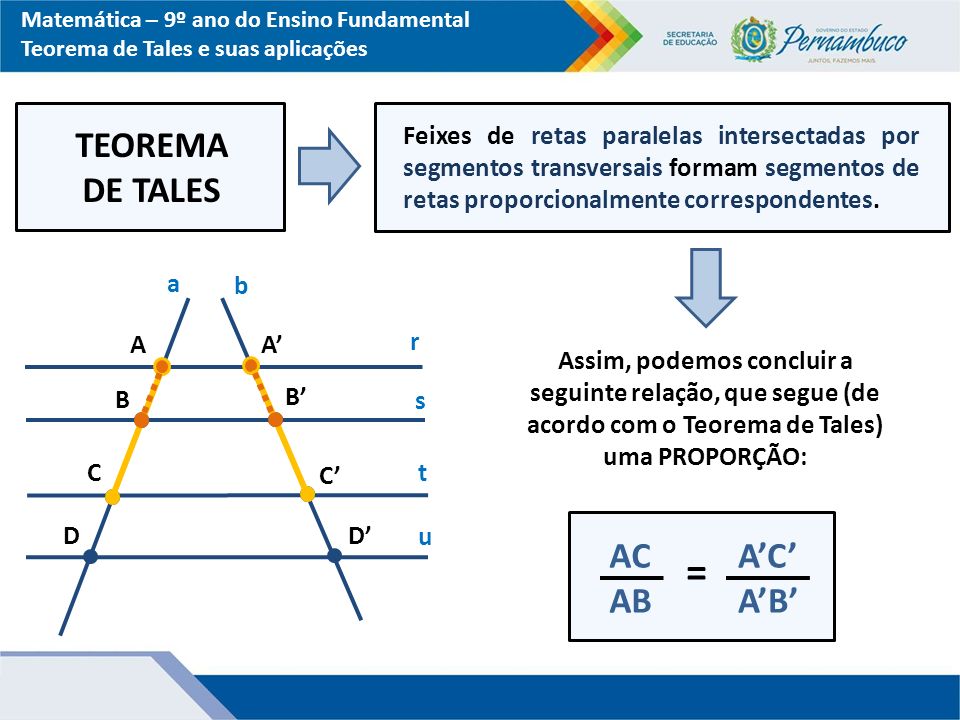
Tales de Mileto foi um matemático e filósofo Grego do período pré-socrático que viveu em meados de 650 A.C. Tales, quando tentava determinar a altura de uma pirâmide, formulou um teorema que afirma:
“Se duas retas são transversais a um conjunto de três ou mais retas paralelas, então a razão entre os comprimentos de dois segmentos quaisquer determinados sobre uma delas é igual a razão entre os comprimentos dos segmentos correspondentes determinados sobre a outra.”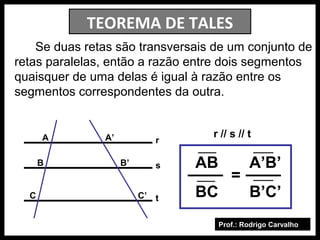

EXERCÍCIOS RESOLVIDOS
01) Observe a imagem abaixo. Nela, pode-se encontrar o valor de x utilizando o Teorema de Tales:
Resolução:
15/5 = 20/x
15x = 100
X=100/15
X = 6,6

02) Seguindo o cálculo do exemplo anterior, vamos encontrar o valor de x:
Resolução:
3x+1 /5x -1 = 4/6
4.(5x – 1) e 6.(3x + 1)
20x – 4 = 18x + 6
20x – 18x = 6 + 4
2x = 10
X = 5

03) Observe a figura baixo e encontre o valor de x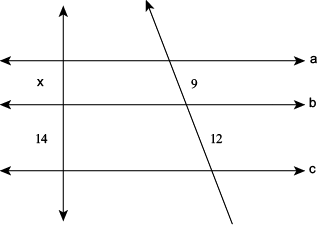
(A) 10
(B) 10,5
(C) 11
(D) 12,5
(E) 13
Resolução:
x / 14 = 9 /2
12x = 14 . 9
12x = 126
x = 126 / 12
x  = 10,5
Alternativa: B

04) Observe a figura baixo e encontre o valor de x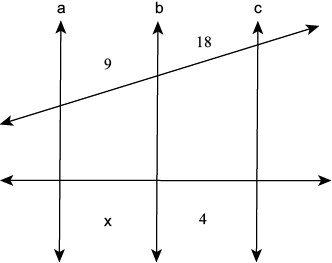
(A) 1
(B) 1,5
(C) 1,8
(D) 2
(E) 2,5
Resolução
9 / x = 18 /4
18x = 9 . 4
18x = 36
x = 36 / 18
x = 2
Alternativa: D

05) A figura abaixo nos mostra duas avenidas que partem de um mesmo ponto A e cortam duas ruas paralelas. Na primeira avenida, os quarteirões determinados pelas ruas paralelas tem 80 m e 90 m de comprimento, respectivamente. Na segunda avenida, um dos quarteirões determinados mede 60 m. Qual o comprimento do outro quarteirão ?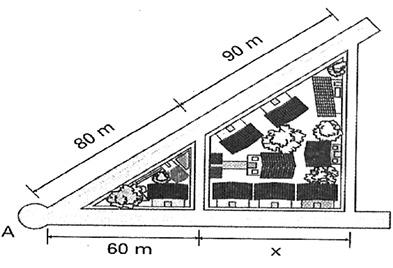
(A) 67,5
(B) 69
(C) 70,5
(D) 72
(E) 75
Resolução
80 / 60 = 90 / x
80x = 60 . 90
80x = 5400
X = 5400 / 80
X = 67,5
Alternativa: A

06) Na figura abaixo, um garoto está em cima de um banco. Qual é a altura desse garoto que projeta uma sombra de 1,2 m, sabendo que o banco de 30 cm projeta uma sombra de 40 cm ?
(A) 75 cm
(B) 80 cm
(C) 0,9 m
(D) 1,10 m
(E) 1,2 m
Resolução:
x / 1,2 = 30 / 40
40x = 1,2 . 30
40x = 36
x = 36 / 40
x = 0,9
Alternativa: C

07) (Caderno Aprender Sempre Volum2 1/Parte 2) (Unirio) Numa cidade do interior, à noite, surgiu um objeto voador não identificado, em forma de disco, que estacionou a 50 m do solo, aproximadamente. Um helicóptero do exército, situado a aproximadamente 30 m acima do objeto, iluminou-o com um holofote, conforme mostra a figura anterior.
Sendo assim, pode-se afirmar que o raio do disco mede, em m, aproximadamente:
(A) 6,0
(B) 5,0
(C) 6,0
(D) 4,0
(E) 3,5 ​
Resolução:
30 / x = 80 / 16
80x = 30 . 16
80 x = 480
x = 480 / 80
x  = 6
Alternativa: C

08) (Caderno Aprender Sempre Volum2 1/Parte 2) (UNESP) A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5m mede 3m.
A altura do prédio é, em metros?
(A) 25.
(B) 29.
(C) 30.
(D) 45.
(E) 75.
Resolução:
Usando a regra de três
5 / 3 = x / 15
5 . 15 = 3 . x
75 = 3x
75/3 = x
25 = x
x = 25
Alternativa: A

09) (SARESP) Para as comemorações de aniversário de uma cidade, foi construído um grande painel de forma triangular na fachada de um edifício, sendo AB paralelo a CD. Dados: VA = 10 m; AC = 5 m; CD = 18 m.
Portanto, AB mede:
(A) 9 m
(B) 12 m
(C) 15 m
(D) 16 m
Resolução:
10 / x = 15 / 18
15x = 10 . 18
15x = 180
x = 180 / 15
x= 12
Alternativa: B

10) (SARESP) Priscila está subindo uma rampa a partir do ponto A em direção ao ponto C. Após andar 5 metros, ela para no ponto B, situado a 3 metros do chão, conforme a figura.
Para que Priscila chegue ao ponto C, situado a 12 metros do chão, ela ainda precisa andar:
(A) 25 m
(B) 20 m
(C) 15 m
(D) 10 m
(E) 5 m
Resolução:
3 / 12 = 5 / 5 + x
15 + 3x = 60
3x = 60 -15
3x = 45
x = 45 / 3
x =15
Alternativa: C

11) Na imagem a seguir, é possível perceber dois triângulos que compartilham parte de dois lados. Sabendo que os segmentos BA e DE são paralelos, qual a medida de x?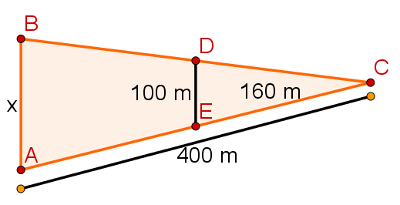
(A) 210 m
(B) 220 m
(C) 230 m
(D) 240 m
(E) 250 m
Resolução:
Quando um triângulo é cortado por um segmento de reta paralelo a um de seus lados, esse segmento forma um segundo triângulo menor e semelhante ao primeiro. É o caso desse exercício. Para resolver essa questão, usaremos apenas a proporção:
400 = 160
  x     100
160x = 400·100
160x = 40000
x = 40000
     160
x = 250 m
Alternativa: E

12) Observe a figura r // s // t. Calcule o valor de x de acordo com o Teorema de Tales.
Resolução:



13) (Fuvest-SP) Três terrenos têm frente para a rua A e para a rua B, como na figura. As divisas laterais são perpendiculares à rua A. Qual a medida de frente para a rua B de cada lote, sabendo que a frente total para essa rua tem 180 m? 
Resolução:

Resposta: a medida da frente dos lotes em relação à rua B são: 80, 60 e 40 metros.

14) No triângulo ABC a seguir, o segmento DE é paralelo ao segmento BC. Determine o valor de x aplicando a proporcionalidade entre segmentos paralelos cortados por segmentos transversais. 
Resolução:
Pelo Teorema de Tales temos:
Resposta: o valor de x corresponde a 9.

15) (MACK-SP) Na figura, sendo a // b //c, o valor de x é:
(A) 3/2
(B) 3
(C) 4/3                                         
(D) 2
(E) 1
Resolução:


16) (UFSM) A crise energética tem levado as médias e grandes empresas a buscarem alternativas na geração de energia elétrica para a manutenção do maquinário. Uma alternativa encontrada por uma fábrica foi a de construir uma pequena hidrelétrica, aproveitando a correnteza de um rio que passa próximo às suas instalações. Observando a figura e admitindo que as linhas retas r, s e t sejam paralelas, pode-se afirmar que a barreira mede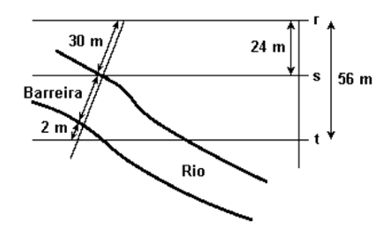
(A) 33
(B) 38
(C) 43
(D) 48
(E) 53
Resolução:
Considerando x como a medida da barreira, pelo teorema de Tales:
   24    =      56     
   30      30 + x + 2
24(30 + x + 2) = 56 · 30
x + 32 = 1680
              24
x + 32 = 70
x = 70 – 32
x = 38
Alternativa: B

17) (Fuvest–SP) A sombra de um poste vertical, projetada pelo sol sobre um chão plano, mede 12 m. Nesse mesmo instante a sombra de um bastão vertical de 1 m de altura mede 0,6 m. Qual a altura do poste?
Resolução:
O modo como o pensamento é organizado para resolver esse exercício geralmente é o seguinte: A sombra do poste está para a sombra do bastão, assim como a altura do poste está para a altura do bastão.
Matematicamente, esse pensamento é escrito da seguinte forma:
x =   1  
12    0,6
0,6x = 12
x = 12
      0,6
x = 20
Resposta: a altura do poste é 20 metros.

18) Calcule o valor de x, sabendo que as retas “e” “f” e “a” são paralelas.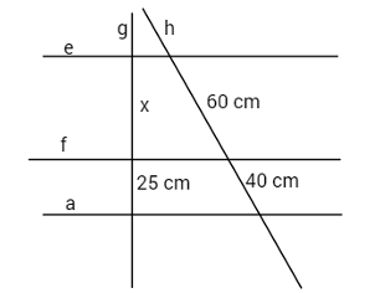
Resolução:
O teorema de Tales garante a seguinte proporcionalidade:
x = x + 25
60  60 + 40
100x = 60(x + 25)
100x = 60x + 60 · 25
100x – 60x = 1500
40x = 1500
x = 1500
      40
x = 37,5 cm

19) Sabendo que as retas “a”, “b” e “c” são paralelas, calcule o valor de y.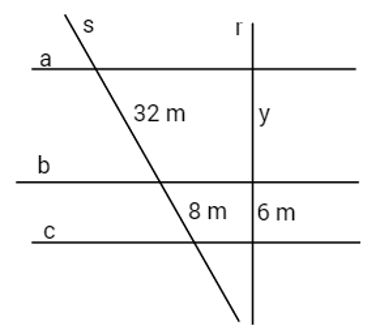
Resolução:
De acordo com o teorema de Tales, essas retas possuem a seguinte proporcionalidade:
32 = y
8     6
8y = 32 · 6
8y = 192
y = 192
     8
y = 24 m

20) Aplicando o Teorema de Tales, encontre o valor de x.
Resolução:

x(x – 2) = (x – 3)  .  (x + 2)
x² – 2x = x² + 2x – 3x – 6
x² – x² – 2x – 2x + 3x = – 6
– 4x + 3x = – 6
– x = – 6
x = 6

21) Sabendo que as retas na horizontal são paralelas, a medida do segmento AC é igual a?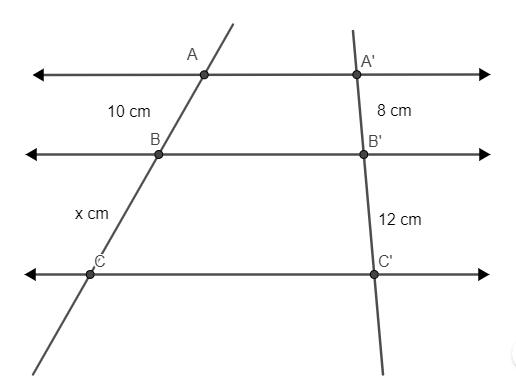
(A) 10 cm
(B) 15 cm
(C) 25 cm
(D) 28 cm
(E) 30 cm
Resolução:
Montando as proporções:
Como queremos o comprimento de AC, basta realizar a soma 15 + 10 = 25 cm.
Alternativa: C

22) (Fuvest–SP) Três terrenos têm frente para a rua A e para a rua B, como na figura. As divisas laterais são perpendiculares à rua A. Qual a medida de x, y e z em metros sabendo que a frente total para essa rua tem 180 m?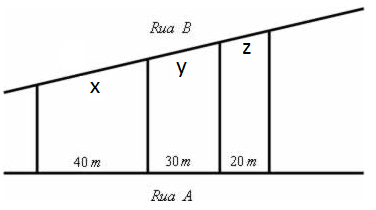
(A) 90, 60 e 30
(B) 40, 60 e 90
(C) 80, 60 e 40
(D) 20 30 e 40
Resolução:
Sabemos que x + y + z = 180. Analisando a rua 1, temos que 40 + 30 + 20 = 90.
Note que o comprimento na rua B é o dobro do comprimento na rua A, então: 180 : 90 = 2.
Sendo 2 a razão de proporção, temos que:
x = 2 · 40 = 80
y = 2 · 30 = 60
z = 2 · 20 = 40
Alternativa: C

23) Para realizar a medição de um prédio, Marcelo decidiu utilizar o teorema de Tales. Ele decidiu observar a sombra que o prédio projetava e a sombra de um poste cuja altura já era conhecida por Marcelo. Ele realizou as medições conforme a imagem a seguir: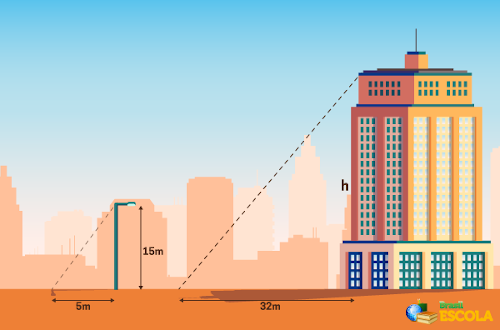
Sabendo que o feixe de luz solar incide de forma paralela sobre o prédio e o poste, então podemos afirmar que a altura h do prédio mede:
(A) 90 m
(B) 92 m
(C) 94 m
(D) 96 m
(E) 98 m
Resolução:
Montando as razões, temos que: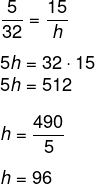

Alternativa: D

24) Na figura a seguir, r//s//t, determine as medidas dos segmentos.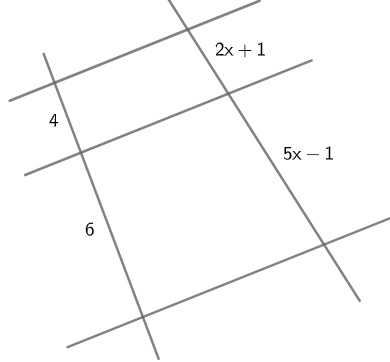
Resolução:
Aplicando o teorema de Tales, temos: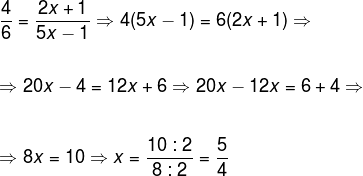

Para determinar a medida dos segmentos, devemos substituir os valores de x.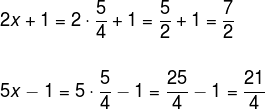


TEOREMA DE TALES NOS TRIÂNGULOS
O teorema de Tales aplicado nos triângulos é mais conhecido por teorema da bissetriz interna. Esse afirma que:
“Em todo triângulo, a bissetriz de qualquer ângulo interno divide o lado oposto a ele em duas partes proporcionais, em relação a seus lados adjacentes.”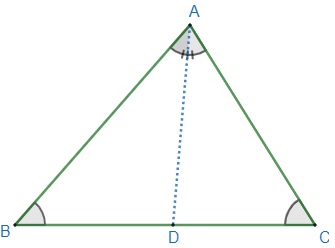
Observe que o segmento AD é a bissetriz do triângulo ABC, visto que ele divide o ângulo BÂC em duas partes iguais. De acordo com o teorema, o segmento de reta AD divide o lado oposto, ou seja, o lado BC, em dois segmentos proporcionais aos lados adjacentes, isto é, os lados AB e AC são proporcionais aos lados BD e DC nessa ordem, e, portanto, podemos escrever:


25) Considere o triângulo seguinte e determine o valor de x, sabendo que o segmento AD é a bissetriz relativa ao lado BC.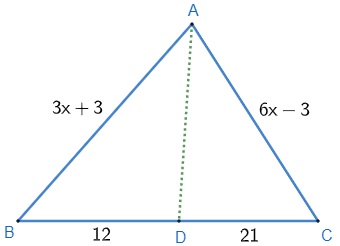
Resolução: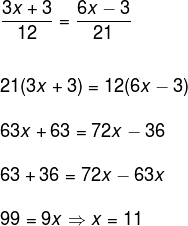


26) (Enem) A planta de determinado bairro de uma cidade apresentou o desenho a seguir. O responsável pelo departamento de obras do município constatou a ausência de algumas medidas nessa planta, as quais ele representou no projeto por x e y.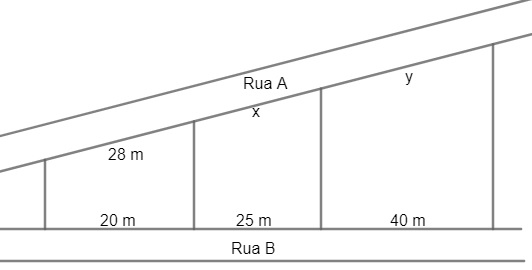
Com base nos dados do projeto, esse responsável pôde calcular corretamente os respectivos valores de x e y:
(A) 35 m e 56 m
(B) 25 m e 40 m
(C) 35 m e 70 m
(D) 56 m e 70 m
(E) 56 m e 84 m
Resolução:
Observando a imagem, temos que o teorema de Tales pode ser aplicado na planta do bairro. Os segmentos que ligam as ruas A e B são paralelos, logo, temos: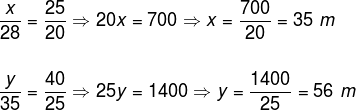

Portanto, os valores de x e y são, respectivamente, 35 m e 56 m.
Alternativa: A

27) – Em um triângulo ABC, o perímetro é 54 cm, BS é a bissetriz, AS = 8 cm, e SC = 10 cm. Determine a medida do lado AB.
Resolução:
Inicialmente vamos ilustrar o triângulo descrito no problema, nomeando x e y os lados dos quais não conhecemos a medida.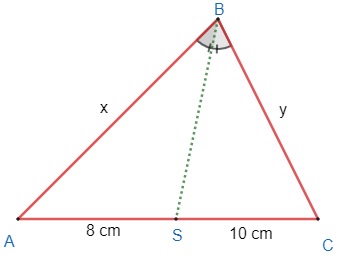
Como foi dado que o perímetro do triângulo ABC é 54 cm, temos que a soma de todos os lados é igual a 54 cm.
x + y + 18 = 54
x + y = 54 -18
x + y = 36
Por outro lado, podemos aplicar o teorema da bissetriz interna no triângulo ABC, tendo que:

Isolando o valor de x na primeira equação, temos que x = 36 – y, e substituindo esse valor na segunda equação, temos que:
10x = 8y
10 · (36 – y) = 8y
360 – 10y = 8y
360 = 8y + 10y
18y = 360
y = 20
Substituindo o valor de y em qualquer uma das equações, temos:
x = 36 – y
x = 36 – 20
x = 16
Portanto, o lado AB mede 16 cm.

28) (IESDE – SAE) Sabendo que r // s // t // u, calcule o valor de x.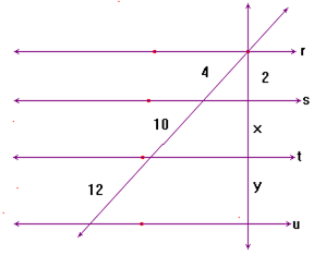
(A) 5
(B) 1
(C) 10
(D) 8
(E) 6
Resolução
Sabendo que as retas r, s e t são paralelas, podemos utilizar o Teorema de Tales, onde teremos a seguinte proporção: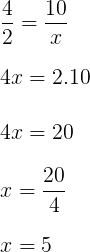

Alternativa: A

29) (IESDE – SAE) A figura abaixo indica dois lotes de terreno com frente para a rua A e para a rua B. As divisas dos lotes são perpendiculares à rua A. As frentes dos lotes 1 e 2 para a rua B medem, respectivamente, 21 m e 28 m. A frente do lote 2 para a rua A mede 20 m. Qual é a medida da frente para a rua A do lote 1?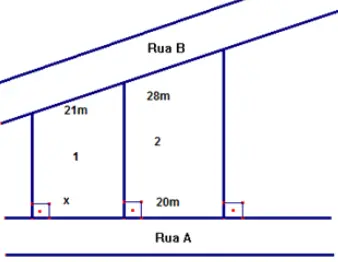
(A) 21 m.
(B) 18 m.
(C) 15 m.
(D) 20 m.
(E) 28 m.
Resolução:
Como as linhas que dividem os lotes são perpendiculares à rua A, podemos concluir que são paralelas, ou seja, podemos utilizar o Teorema de Tales para resolvermos a questão.

Alternativa: C

30) (Inst. Machado de Assis) Utilizando a Teorema de Tales, encontre os valores de x, sabendo que as retas a, b e c são paralelas.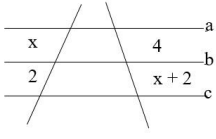
(A) -2, 4
(B) 2, -4
(C) 2, 4
(D) -1, -4
Resolução
Sabendo que as retas a, b e c são paralelas, temos a seguinte proporção: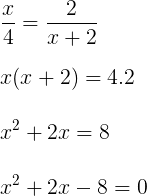

A equação do segundo grau pode ser resolvida através do método da soma e do produto, onde temos:
Soma = -b/a = -2/1 = -2
Produto = c/a = -8/1 = -8
S = {-4, 2}.
Alternativa: B

31) (CEFET MG – 2014) Considere a figura em que r//s//t.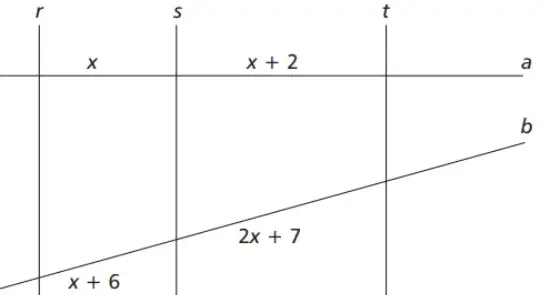
O valor de x é
(A) 3.
(B) 4.
(C) 5.
(D) 6.
Resolução
Considerando o paralelismo das retas r, s e t, temos: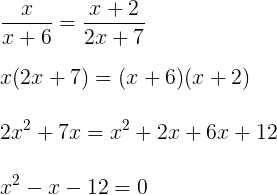

Resolvendo a equação do segundo grau através do método da soma e do produto:
Soma = -b/a = -(-1)/1 = 1
Produto = c/a = -12/1 = -12
S = {-3, 4}.
Como x representa distância, descartamos a raiz negativa.
Alternativa: B


Continua...