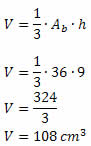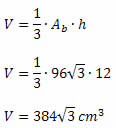GEOMETRIA ESPACIAL II
Professor Diminoi

GEOMETRIA ESPACAL
Conceitos Básicos da Geometria
Os sólidos geométricos ou figuras espaciais são formadas por elementos da geometria que não precisam ser demonstrados ou provados, e portanto são chamados de axiomas.
Assim, para começar a entender algumas das figuras geométricas espaciais, precisamos entender esses conceitos básicos:
Ponto: o ponto é um elemento na geometria que não possui dimensão, é definido como alguma coisa que não possui partes. O ponto é importante pois os planos, retas, e todos os sólidos geométricos são formados por um conjunto de pontos reunidos;
Reta: as retas são pontos alinhados infinitamente, possuindo apenas comprimento. As retas são representadas por letras minúsculas do alfabeto;

Linha: a linha é diferente do conceito de retas. Apesar de ser formada por pontos, a linha pode ser curva ou não. Por exemplo, a circunferência é formada por uma linha curva;
Vértice: o vértice é um ponto que define o encontro de segmentos de retas que formam os lados dos sólidos geométricos;
Plano: planos são regiões infinitas bidimensionais (duas dimensões).
Figuras Geométricas Espaciais
A geometria espacial estuda diversos sólidos geométricos, entre as principais temos: cilindro, cubo, cone, esfera, paralelepípedo e a pirâmide.
As figuras geométrica espaciais são chamadas de poliedros, que são figuras geométricas tridimensionais, e possuem largura, comprimento e altura.
Cilindro
O cilindro é um poliedro com duas bases circulares e congruentes. Além disso, os lados tem formato circular.
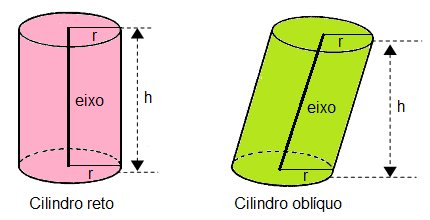 Entre os principais elementos do cilindro, temos:
Entre os principais elementos do cilindro, temos:
Base: duas bases com formato circular e paralelas entre si;
Raio: as bases são círculos que possuem uma medida do centro até a extremidade, chamada de raio;
Geratriz: as geratrizes são segmentos de retas que formam o lado do cilindro;
Diretriz: a diretriz é o ponto na base da geratriz que indica a direção da geratriz.
Cubo
O cubo é um hexaedro regular, ou seja, possuem 6 faces com as mesmas medidas, tanto para área, ângulos e quantidade de arestas.
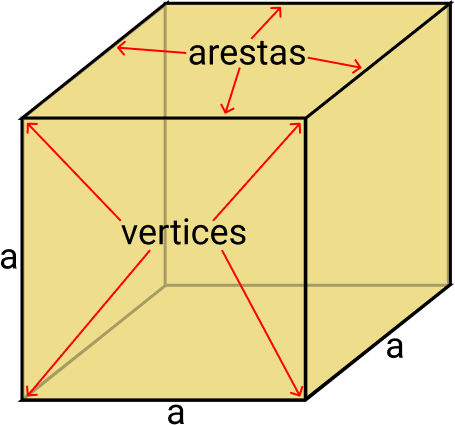 O cubo é formado pelos seguintes elementos:
O cubo é formado pelos seguintes elementos:
Arestas: possui 12 arestas congruentes;
Faces: possui 6 faces quadrangulares;
Diagonais: possui 4 diagonais internamente no cubo;
Vértices: possui 8 vértices;
Ângulos: possui 24 ângulos retos.
Cone
O cone é outro sólido geométrico bem popular, que tem o formato de uma pirâmide.
 O cone possui os seguintes elementos na sua formação:
O cone possui os seguintes elementos na sua formação:
Raio da base: a base é um círculo que possui um raio;
Geratriz: segmentos de retas que formam os lados do cone;
Vértice: ponto que não pertence ao plano da base;
Esfera
A esfera é uma figura geométrica espacial que é limitada por uma superfície esférica. A superfície da esfera é formado por um conjunto de pontos que ficam a uma distância do centro por uma medida que é chamada de raio.
.jpg) A esfera possui algumas partes importantes chamadas de partes da esfera:
A esfera possui algumas partes importantes chamadas de partes da esfera:
Superfície Esférica: é a região superficial da esfera;
Cunha Esférica: a cunha é uma região entre dois semicírculos;
Fuso Esférico: o fuso é uma parte da esfera obtida pelo giro de uma semicircunferência a um certo ângulo;
Calota Esférica: a calota esférica é uma parte da esfera cortada por um plano perpendicular ao eixo de rotação;
Polos: os polos são pontos nas extremidades do eixo de rotação da esfera;
Paralelo: é uma circunferência perpendicular ao eixo de rotação da esfera;
Meridiano: é uma circunferência na superfície na mesma direção do eixo de rotação da esfera.
Paralelepípedo
O paralelepípedo é um poliedro formado por paralelogramos. Suas faces opostas são paralelas, com ângulos retos.
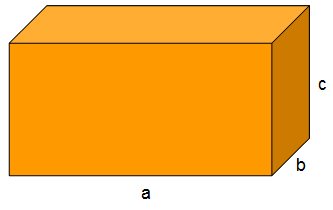 O paralelepípedo possui os seguintes elementos na sua formação:
O paralelepípedo possui os seguintes elementos na sua formação:
Faces: possui 6 faces;
Vértices: possui 8 vértices;
Arestas: possui 12 arestas.
Pirâmide
É um poliedro com base poligonal e os lados são formadas por polígonos triangulares, unidas num vértice que não pertence ao plano da base.
 A pirâmide é formada pelos seguintes elementos:
A pirâmide é formada pelos seguintes elementos:
Arestas laterais: segmentos de retas da base até o vértice;
Faces laterais: formadas por triângulos;
Arestas da base: segmentos de retas ligando os vértices;
Altura da pirâmide: definida pelo vértice;
Apótema da pirâmide: altura da face da pirâmide.
Observação: Na geometria, chama-se aresta o segmento de linha que se encontra com dois vértices em um polígono, poliedro, ou polítopo. Em um poliedro, ou generalizando um polítopo, uma aresta é um segmento de intersecção entre duas faces. Esse segmento comum é o "canto", ou "quina" da figura geométrica. A aresta também possui o nome de "reta".
Poliedros
São aqueles cujas superfícies são formadas apenas por polígonos planos.
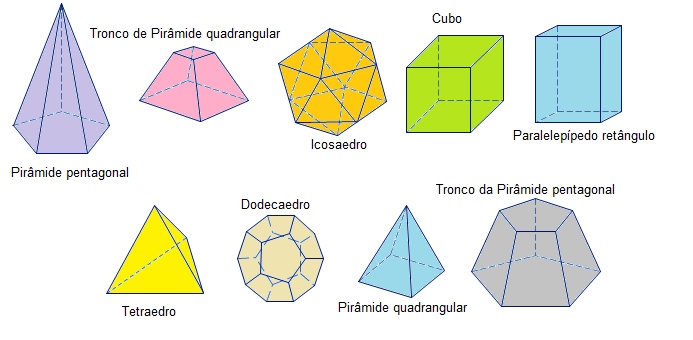
Corpos redondos
São aqueles cujas superfícies têm ao menos uma parte que é arredondada (não plana).
Qualquer poliedro convexo possui a característica de Euler
V + F = A + 2, onde V é o número de vértices, A é o número de arestas e F é o número de faces. Esta equação é conhecida por Fórmula de Euler. Por exemplo, um cubo tem 8 vértices e 6 faces, logo possui 12 arestas
Fórmulas de Área e Volume dos Sólidos

Geometria espacial questões básicas
01) Seja um cilindro circular reto com altura de 10 cm e raio da base de 2 cm. Então, calcule o volume do cilindro.
Resolução:
Dados do problema:
Altura: 10 cm
Raio da base: 2 cm
Volume do cilindro:
V = Ab . h = π . r² . h
V = π . 2² . 10
V = π . 4 . 10
V = 40π
V = 40 . 3,14
V = 125,6 cm³
02) Um barril de petróleo possui altura de 95 cm e 60 cm de largura. Com isso, determine a capacidade do barril.
Resolução:
Dados do problema:
Altura: 95 cm
Raio da base: 30 cm (60 cm equivale ao diâmetro (largura), o diâmetro é o dobro do raio)
Capacidade:
V = Ab . h = π . r² . h
V = π . 30² . 95
V = π . 900 . 95
V = 85.500π
V = 85.500 . 3,14
V = 268.470 cm³
Essa medida é igual a 268,47 litros.
03) Uma lata de cerveja tem 6 cm de diâmetro e 12,5 cm de altura. Qual a quantidade de cerveja que cabe numa lata?
Resolução:
Dados do problema:
Altura: 12,5 cm
Raio da base: 3 cm (6 cm é o diâmetro (r = d/2))
Pelo que sabemos, uma lata de cereja tem capacidade de 350 ml. Além disso, a lata de cerveja tem a forma de um cilindro. Então, para calcular a capacidade dessa lata vamos usar a fórmula do volume:
V = Ab . h = π . r² . h
V = π . 3² . 12,5
V = π . 9 . 12,5
V = 112,5π
V = 112,5 . 3,14
V = 353,25 cm³
Para converter de cm³ para ml vamos usar regra de três simples.
1000 cm³ ————– 1 litro
353,25 cm³ ———— x litro
1000 . x = 353,25 . 1
x = 353,25 / 1000
x = 0,35325 litros ou 353,25 ml (mililitros)
Observação: A unidade de medida do volume é o metro cúbico (m³).
04) (TJ CE – ESAF) Quantos cm³ existem em 10 litros?
(A) 10
(B) 100
(C) 1.000
(D) 10.000
(E) 100.000
Resolução:
Para resolver a questão, o candidato deverá ter conhecimento de que em 10cm³ cabe exatamente 1 litro.
Imagine 10 caixas de 10 cm³ cada uma, lado a lado. O volume, se considerarmos que são apenas um sólido é:
10 cm . 10 cm . 100 cm = 10.000 cm³
Alternativa: D
05) (ENEM) Uma empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugerem que seja adicionado 1,5 ml desse produto para cada 1000 l de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a 1,7 m, com largura e comprimento iguais a 3 m e 5 m, respectivamente. O nível da lâmina d’água dessa piscina é mantido a 50 cm da borda da piscina.
A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é :
(A) 11,25
(B) 27,00
(C) 28,80
(D) 32,25
(E) 49,50
Resolução:
A piscina possui uma profundidade de 1,7 m. Como o nível da água é mantido a 50 cm da borda, podemos concluir que a altura da água é de 1,2 m, ou seja, a água ocupa um paralelepípedo reto de medidas 1,2, 3 e 5 metros.
Calculando o volume:
1,2 . 3 . 5 = 18 m³
Sabendo que a proporção é de 1 m³ de volume para 1000 litros de água, podemos calcular a quantidade de litros de água da piscina:
18 . 1000 = 18.000 litros
Calculando a quantidade de produto:
18 . 1,5 = 27ml
Alternativa B
06) (PM Pará – Fadesp) Sabendo-se que uma pessoa consome aproximadamente 800 metros cúbicos de água por ano e que o planeta dispõe de, no máximo, 9000 quilômetros cúbicos de água para o consumo por ano, pode-se afirmar que a capacidade máxima de habitantes que o planeta suporta, considerando-se apenas a disponibilidade de água para consumo, é aproximadamente:
(A) 11.100.000.000.
(B) 11.150.000.000.
(C) 11.250.000.000.
(D) 11.350.000.000.
Resolução:
Sabe-se que 1 km³ corresponde a 1.000.000.000 m³, daí 9.000 km³ correspondem a 9.000.000.000.000 m³.
9.000.000.000.000 / 800 = 11.250.000.000
Alternativa: C
07) (PM RN – Consultec) Um reservatório, inicialmente vazio, com capacidade para 8000 litros, recebe água à razão de 1600cm³ por segundo.
O tempo decorrido para que ele fique totalmente cheio é de
01) 1h 20min 40s
02) 1h 21min 30s
03) 1h 22min
04) 1h 23min 20s
05) 1h 24min 40s
Resolução:
Para resolvermos a questão, é necessário sabermos que:
– 1 m³ equivale a 1000 litros.
– 0,0016 m³ equivale a 1600 cm³.
O objetivo da questão é encher um reservatório de 8 m³ a uma taxa de 0,0016 m³ por segundo.
8 / 0,0016 = 5000 segundos
Efetuando as devidas transformações, temos que 5000 segundos é equivalente a 1h 23min 20s.
Resposta: 04
08) (Correios – Cespe) Nos Correios, são utilizados vários tipos de caixas para o envio de encomendas, entre elas, a caixa do tipo 4B, um paralelepípedo retângulo, em papel ondulado, com arestas medindo 360 mm, 270 mm e 180 mm. O volume dessa caixa, em dm³, é:
superior a 18 e inferior a 21.
superior a 21 e inferior a 24.
superior a 24.
inferior a 15.
superior a 15 e inferior a 18.
Resolução:
Veja em nossa página sobre unidades e medidas que:
1 m = 10 dm (decímetros)
1 m = 1.000 mm (milímetros)
Transformando as medidas das arestas para dm:
360 mm = 3,6 dm
270 mm = 2,7 dm
180 mm = 1,8 dm
Calculando o volume do paralelepípedo retângulo:
Volume = base x comprimento x altura.
Volume = 3,6 x 2,7 x 1,8
Volume = 17,496dm³
Alternativa: E
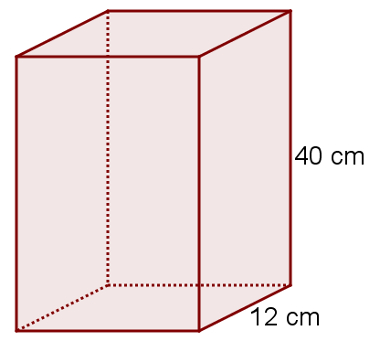
09) Qual é o volume do prisma da imagem a seguir, sabendo que ele é um prisma reto e sua base é quadrada?
 (A) 5760 cm3
(A) 5760 cm3
(B) 5000 cm3
(C) 2500 cm3
(D) 1080 cm3
(E) 480 cm3
Resolução:
O volume do prisma é obtido pelo produto da área da base pela altura. A área da base desse prisma é dada por:
Ab = 12 . 2
Ab = 144 cm2
O produto da área da base pela altura será:
V = Ab·h
V = 144·40
V = 5760 cm3
Alternativa: A
10) Qual o volume de um prisma reto de base hexagonal, sabendo que a base é um polígono regular cujo lado mede 2 centímetros e cujo apótema mede aproximadamente 1,73 centímetros, e que a altura desse prisma é de 25 centímetros.
(A) 10,38 cm3
(B) 259,5 cm3
(C) 129,7 cm3
(D) 20,76 cm3
(E) 40,86 cm3
Resolução:
Não é necessário ter o esboço do prisma para calcular seu volume. Para obter seu volume, basta saber como calcular a área da base e multiplicar o resultado obtido pela altura dele. A área da base desse prisma é dada pela área do hexágono regular, obtida por meio da fórmula:
A = P·a
2
Em que P é o perímetro e a é o apótema. Substituindo os valores, temos:
A = (2·6)·1,73
2
A = 12·1,73
2
A = 20,76
2
A = 10,38 cm2
Para finalizar o exercício, basta multiplicar a área da base pela altura do prisma.
V = Ab·h
V = 10,38·25
V = 259,5 cm3
Alternativa: B
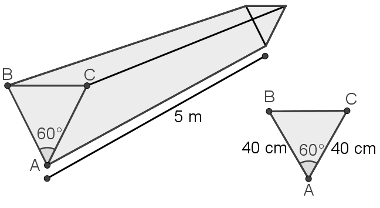
11) (UE-PA/modificada) Uma calha em forma de prisma reto, conforme a figura abaixo, possui 5 m de comprimento e uma secção transversal ABC, na forma de V, tal que AB = AC = 40 cm e BÂC = 60°. Qual o volume que essa calha comporta? (Considere √3 =1,73)
 (A) 300000 cm3
(A) 300000 cm3
(B) 326000 cm3
(C) 346000 cm3
(D) 400000 cm3
(E) 446000 cm3
Resolução:
A base desse prisma é um triângulo isósceles com um ângulo de 60°. Isso significa que os outros dois ângulos também terão essa medida, portanto, esse triângulo também é equilátero. A área do triângulo equilátero é dada pela expressão:
Ab = l2√3
4
Substituindo a medida do lado do triângulo nessa fórmula, temos:
Ab = 402√3
4
Ab = 1600√3
4
Ab = 400√3 cm2
Para finalizar, basta multiplicar a área da base pela altura do prisma. Lembre-se de que 5 m = 500 cm.
V = Ab·h
V = 400√3 . 500
V = 200000 . √3
V = 200000 . 1,73
V = 346000 cm3
Alternativa: C
12) O volume de uma piscina em forma de prisma de base quadrada é 3125 metros cúbicos. Sabendo que a altura dessa piscina é de 5 metros cúbicos, qual é a medida da aresta de sua base em metros?
(A) 5 m
(B) 10 m
(C) 15 m
(D) 20 m
(E) 25 m
Resolução:
O volume do prisma é dado pelo produto da área de sua base pela altura. A área de um quadrado – base desse prisma – é dada pela medida de seu lado elevado ao quadrado. Se o lado desse quadrado é l, podemos substituir os seguintes elementos da fórmula do volume:
V = Ab . h
V = l . l . h
V = l2 . h
3125 = l2·5
3125 = l2
5
l2 = 625
l = √625
l = 25 m
Alternativa: E
13) (ENEM) Uma empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugerem que seja adicionado 1,5 mL desse produto para cada 1 000 L de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a 1,7 m, com largura e comprimento iguais a 3 m e 5 m, respectivamente. O nível da lâmina d’água dessa piscina é mantido a 50 cm da borda da piscina.
A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é
(A) 11,25.
(B) 27,00.
(C) 28,80.
(D) 32,25.
(E) 49,50.
Resolução:
De acordo com o enunciado temos que o volume de água na piscina é igual a:
V = 5.3.1,2
V = 15.1,2
V = 18 m³
ou
V = 18 000 l
Logo, a quantidade de produto será: (18 000.1,5) / 1 000 = 27 ml
Alternativa: B
14) (ENEM) Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.
 Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá
Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá
(A) encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
(B) encher a leiteira toda de água, pois ela tem um volume 20 vezes maior que o volume do copo.
(C) encher a leiteira toda de água, pois ela tem um volume 10 vezes maior que o volume do copo.
(D) encher duas leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
(E) encher cinco leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
Resolução:
O volume do copinho plástico, em centímetros cúbicos, é π . 2² . .4 = 16π
O volume da leiteira, em centímetros cúbicos, é π.4².20 = 320π
(Volume da leiteira) ÷ (volume do copinho) = 320π/16π = 20
Assim, para encher os vinte copinhos plásticos pela metade, é suficiente encher a leiteira até a metade.
Alternativa: A
16) (ENEM) Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19 cm de altura e 6 cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura — 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior —, espaçados de 1 cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.
 Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
(A) 156 cm³.
(B) 189 cm³.
(C) 192 cm³.
(D) 216 cm³.
(E) 540 cm³.
Resolução:
O volume de parafina gasto na nova vela corresponde à subtração do volume da pirâmide maior, com aresta da base de 6 cm e altura de 19 – 3 = 16 cm, pelo volume da pirâmide menor, com 1,5 cm de aresta da base e 4 cm de altura.
Como volume da pirâmide é calculado pela terça parte do produto da área da base pela altura, o volume de parafina, em cm³, é de 1/3.6.6.16 − 1/3.1,5.1,5.4 = 192 – 3 = 189 cm³.
Alternativa: B
17) (PM RJ – Exatus) Sobre retas, planos e suas relações posicionais, Adriana escreveu em seu caderno as seguintes afirmações:
I – Se duas retas distintas são paralelas a um plano, então elas são paralelas entre si.
II – Se uma reta r está contida em um plano α , então existem retas paralelas a r fora de α .
III – Duas retas concorrentes podem ser ortogonais.
IV – Dada uma reta r paralela a um plano α , então r não é paralela a todas as retas de α .
Está correto apenas o que se afirma em:
(A) Apenas as afirmativas I e II.
(B) Apenas as afirmativas II e III.
(C) Apenas as afirmativas II e IV.
(D) Apenas as afirmativas III e IV.
Resolução
Vamos analisar cada uma das afirmações:
I – Se duas retas distintas são paralelas a um plano, então elas são paralelas entre si.
A afirmação está incorreta. Veja na figura um exemplo de duas retas distintas (r, s), paralelas a um plano (em vermelho), e que não são paralelas entre si.
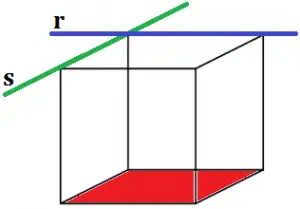
II – Se uma reta r está contida em um plano α , então existem retas paralelas a r fora de α .
A afirmação está correta. Existem infinitas retas paralelas a r (dentro e fora do plano α).
III – Duas retas concorrentes podem ser ortogonais.
A afirmação está correta. Basta que o ângulo entre elas seja de 90º.
IV – Dada uma reta r paralela a um plano α , então r não é paralela a todas as retas de α .
A afirmação está incorreta. Veja na figura que a reta r é paralela a α, porém não é paralela a reta s, que pertence a α.
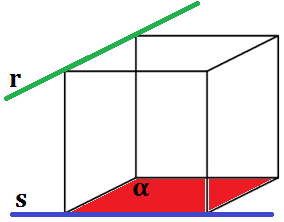
Alternativa: B
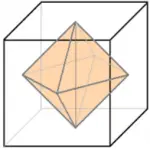
18) (Prefeitura de Ceará Mirim – RN – Comperve) Um brilhante com formato de um octaedro é exibido em uma concorrida exposição. Por medida de segurança, ele foi colocado no interior de um cubo de vidro com seus vértices tocando, precisamente no meio de cada face do cubo, conforme a figura abaixo.
 Se o volume do cubo é 1.728 cm³ , o volume do octaedro, em cm³ , será
Se o volume do cubo é 1.728 cm³ , o volume do octaedro, em cm³ , será
(A) 144.
(B) 288.
(C) 432.
(D) 576.
Resolução
O primeiro passo é determinar a medida das arestas do cubo. Como o volume é igual a 1.728 cm³, podemos afirmar que cada aresta mede 12 cm. Veja:
12³ = 1728
O octaedro pode ser dividido em duas pirâmides. Como os vértices tocam precisamente no meio de cada face do cubo, a base dessas pirâmides é um losango onde as diagonais possuem as mesmas medidas da aresta do cubo. Também é possível observar que a altura é exatamente a metade da aresta do cubo.
Área da base da pirâmide (losango):
A = d1 . d2 / 2
A = 12 . 12 / 2
A = 72 cm²
Volume da pirâmide:
V = Ab . h / 3
V = 72 . 6 / 3
V = 144 cm³
Como o octaedro é composto por duas pirâmides:
2 . 144 = 288 cm³
Alternativa: B
19) (Bombeiros MG – Igetec) O hexaedro regular que inscreve a esfera de volume 9π/2 cm³, tem a medida da diagonal, em centímetros, igual a:
(A) 2,7
(B) √3
(C) 3√3
(D) 3
Resolução
Veja como é um hexaedro e o que seria sua diagonal:
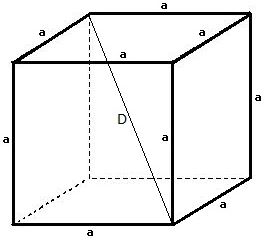
Repare que como o hexaedro está inscrito a uma esfera, a diagonal é o dobro do raio da mesma.
Podemos calcular o raio pela fórmula pois sabemos seu volume:
Volume = π.r³.4/3
9π/2 = π .r ³.4/3
9/2 = r³.4/3
r³ = 9.3/2.4
r³ = 27/8
r = 3/2
Logo, a diagonal é 2.3/2 = 3
Alternativa: D
20) (Vassouras RJ – IBFC) Um poliedro convexo tem 9 faces e 16 arestas. Desse modo, o total de vértices desse poliedro é:
(A) 12
(B) 9
(C) 15
(D) 11
(E) 10
Resolução
Utilizando a relação de Euler:
V + F = A + 2
V + 9 = 16 + 2
V = 18 – 9
V = 9
Alternativa: B
21) (PM ES – Exatus – Geometria Espacial) O volume do sólido gerado pela rotação de um triângulo isósceles de lados congruentes medindo 5 cm e base medindo 6 cm, em torno da base é igual a:
(A) 12π cm³
(B) 13π cm³
(C) 14π cm³
(D) 15π cm³
(E) 16π cm³
Resolução
Veja na figura que após a rotação em torno da base, teremos um sólido formado por dois cones iguais. Basta então calcular o volume de um deles e multiplicar por 2.
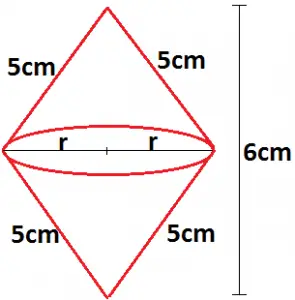
Calculando a altura h do cone através do Teorema de Pitágoras:
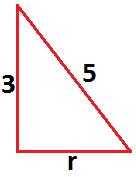
5² = 3² + r²
r² = 25 – 9
r² = 16
r = 4
Calculando o volume do cone:
V = Área da base x altura / 3
V = π . 4² . 3 / 3
V = π . 16
V = 16π cm³
Alternativa: E
22) (TRE PI – FCC) Uma pessoa fez quatro cortes paralelos igualmente espaçados em uma laranja esférica, dividindo-a nas cinco partes indicadas na figura.
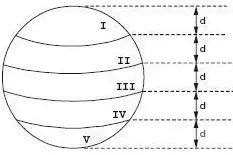
Em relação a essa divisão, é correto afirmar que
(A) todas as partes obtidas têm o mesmo volume.
(B) a parte III é a de maior volume.
(C) o volume da parte I é maior do que o volume da parte II.
(D) não foram obtidas duas partes com o mesmo volume.
(E) a soma dos volumes das partes IV e V é menor do que a soma dos volumes das partes I e II.
Resolução
Como os cortes foram paralelos e igualmente espaçados, a parte que possuirá o maior volume será a que possui o maior raio. Nesta caso, a região de maior volume é a III.
Alternativa: B
23) (EsPCEx) A figura abaixo representa a planificação de um tronco de cone reto com a indicação das medidas dos raios das circunferências das bases e da geratriz.
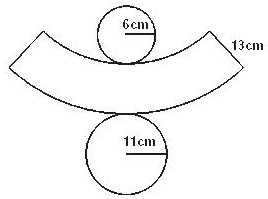 A medida da altura desse tronco de cone é
A medida da altura desse tronco de cone é
(A) 13 cm
(B) 12 cm
(C) 11 cm
(D) 10 cm
(E) 9 cm
Resolução
Veja na figura abaixo o tronco de cone que foi planificado.
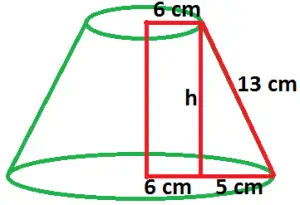
Nela é possível observar que a altura do tronco pode ser calculada através do Teorema de Pitágoras:
13² = h² + 5²
169 = h² + 25
h² = 169 – 25
h² = 144
h = √144
h = 12 cm
Alternativa: B
24) (FUVEST) Os vértices de um tetraedro regular são também vértices de um cubo de aresta 2. A área de uma face desse tetraedro é
(A) 2√3
(B) 4
(C) 3√2
(D) 3√3
(E) 6
Resolução
A parte mais complicada da questão é “enxergar” como os vértices de um tetraedro regular podem ser vértices de um cubo.
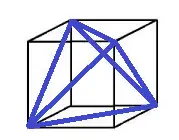
Na figura é possível observar que as arestas do tetraedro regular são diagonais das faces quadradas do cubo. Veja:
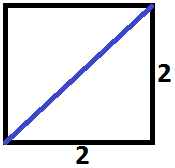
Utilizando o Teorema de Pitágoras para descobrir a medida “a” da aresta do tetraedro:
a² = 2² + 2²
a² = 4 + 4
a² = 8
a = √8
a = 2√2
Agora que sabemos a medida das arestas, basta calcular a área de uma das faces do tetraedro, ou seja, a área do triângulo equilátero de lado 2√2:
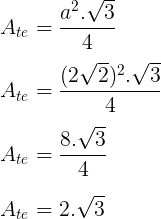
Alternativa: A
25) (EsPCEx – Geometria Espacial) Um reservatório em forma de tronco de pirâmide regular de base quadrada e dimensões indicadas na figura deverá ter suas paredes laterais externas cobertas por uma tinta impermeável, cujo rendimento é de 11m² por galão.
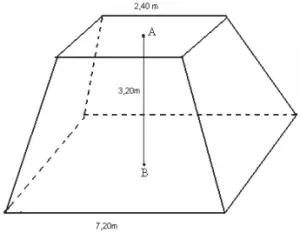 O número mínimo de galões que devem ser adquiridos para tal operação é:
O número mínimo de galões que devem ser adquiridos para tal operação é:
(A) 6
(B) 7
(C) 9
(D) 10
(E) 11
Resolução
Nosso objetivo é calcular a área lateral do tronco de pirâmide regular, ou seja, devemos calcular a área de um dos trapézios e multiplicar por 4.
As medidas da base maior e da base menor já foram informadas na figura.
Vamos descobrir a medida da altura dos trapézios.
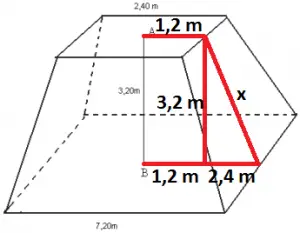
Na figura acima é possível observar que a altura (x) do trapézio pode ser calculada através do Teorema de Pitágoras:
x² = 3,2² + 2,4²
x² = 3,2² + 2,4²
x² = 10,24 + 5,76
x² = 16
x = √16
x = 4 m
Calculando a área do trapézio cuja altura, base menor e base maior medem, respectivamente 4 m, 2,4 m e 7,2 m.
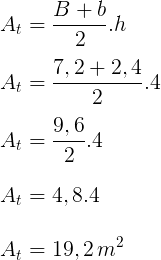
Como cada trapézio possui área de 19,2 m², a área lateral do tronco da pirâmide regular será:
4 . 19,2 = 76,8 m²
Se cada galão pinta uma área de 11 m²:
76,8 / 11 = 6,98
Daí, são necessários 7 galões.
Alternativa: B
26) (SISPREM RS – FUNDATEC) Um enfeite em formato de pirâmide regular e de base quadrada tem o lado da base medindo 10 cm e a altura de 30 cm. Qual é o volume em cm³ dessa pirâmide?
(A) 300.
(B) 690.
(C) 830.
(D) 950.
(E) 1.000.
Resolução:
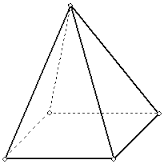
Antes de calcularmos o volume da pirâmide, vamos calcular a área da base (quadrado):
Ab = 10² = 100 cm²
Calculando o volume da pirâmide:
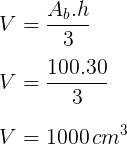
Alternativa: E
27) (AFPR – COPS) A figura, a seguir, mostra um pedaço de cartolina que será dobrado e colado ao longo das bordas para formar uma embalagem na forma de um prisma hexagonal regular reto.
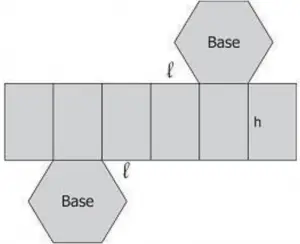 Supondo que l = 2 cm e h = 5 cm, qual é o volume dessa embalagem em cm3?
Supondo que l = 2 cm e h = 5 cm, qual é o volume dessa embalagem em cm3?
(A) √3 cm³
(B) √3/2 cm³
(C) 30√3 cm³
(D) 6√3 cm³
(E) 3√3 cm³
Resolução
O volume de um prisma pode ser calculado multiplicando-se a área da base pela altura.
Como a base é um hexágono regular, podemos calcular a área através da seguinte fórmula:
Ab = 3.l².√3/2
Ab = 3.2².√3/2
Ab = 3.4.√3/2
Ab = 6.√3
Calculando o volume do prisma:
V = h . Ab
V = 5 . 6.√3
V = 30.√3 cm³
lternativa: C
28) (Petrobras – Cesgranrio) Uma fita retangular de 2 cm de largura foi colocada em torno de uma pequena lata cilíndrica de 12 cm de altura e 192π cm³ de volume, dando uma volta completa em torno da lata, como ilustra o modelo abaixo.
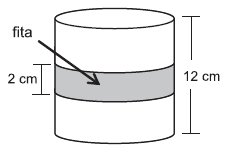 A área da região da superfície da lata ocupada pela fita é, em cm² , igual a
A área da região da superfície da lata ocupada pela fita é, em cm² , igual a
(A) 8π
(B) 12π
(C) 16π
(D) 24π
(E) 32π
Resolução
A informação que ainda não temos para calcular a área pedida é o raio da base do cilindro.
Nosso objetivo inicial será utilizar a medida da altura e do volume para descobrirmos o raio.
Utilizando a fórmula do volume:
V = π.r².h
192π = π . r² . 12
192 = 12r²
r² = 192/12
r² = 16
r = 4 cm
Agora que sabemos a medida do raio, vamos calcular a área lateral ocupada pela fita, cuja altura é de 2 cm.
Al = 2.π.r.h
Al = 2.π.4.2
Al = 16.π cm²
Alternativa: C
29) (SEDUC RJ – COPERJ) A figura abaixo representa uma caixa cúbica onde a distância do ponto A até o ponto B mede 3√5 decímetros:
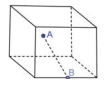 Os pontos A e B são, respectivamente, o centro de uma face e o ponto médio de uma aresta da face oposta. O volume dessa caixa, em dm³ , é igual a:
Os pontos A e B são, respectivamente, o centro de uma face e o ponto médio de uma aresta da face oposta. O volume dessa caixa, em dm³ , é igual a:
(A) 125
(B) 216
(C) 343
(D) 512
(E) 729
Resolução
Precisamos calcular o volume do cubo representado na figura. Nosso primeiro objetivo é calcular a medida da aresta desse cubo, que representaremos inicialmente por x.
Vamos analisar o triângulo retângulo formado pela semi reta AB e pelas semi retas que dividem as faces ao meio.
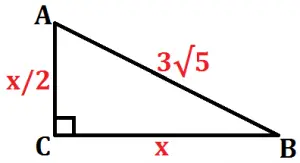
Pelo Teorema de Pitágoras temos:
(3√5)² = x² + (x/2)²
45 = x² + x²/4
45 = 5x²/4
5x² = 4.45
5x² = 180
x² = 180/5
x² = 36
x = 6 dm
Calculando o volume do cubo:
V = x³
V = 6³
V = 216 dm³
30) Calcule o volume de um cilindro cuja altura mede 10 cm e o diâmetro da base mede 6,2 cm. Utilize o valor de 3,14 para π.
Resolução:
Primeiramente, vamos encontrar o valor do raio dessa figura. Lembre-se que o raio é duas vezes o diâmetro. Para tanto, dividimos o valor do diâmetro por 2:
6,2 : 2 = 3,1
r = 3,1 cm
= 10 cm
V = π.r2.h
V = π . (3,1)2 . 10
V = π . 9,61 . 10
V = π. 96,1
V = 3,14 . 96,1
V = 301,7 cm3
31) Um tambor cilíndrico tem uma base de 60 cm de diâmetro e a altura de 100 cm. Calcule a capacidade desse tambor. Utilize o valor de 3,14 para o π.
Resolução:
Primeiramente, vamos encontrar o raio dessa figura, dividindo o valor do diâmetro por 2:
60 : 2 = 30 cm
Assim, basta colocar na fórmula os valores:
V = π . r2 . h
V = π . (30)2 . 100
V = π . 900 . 100
V = 90 . 000 π
V = 282.600 cm3
32) Determine a área e o volume de um cilindro que possui raio da base medindo 5 cm e altura medindo 6 cm.
Resolução:
O exercício forneceu-nos a medida do raio r = 5 cm e altura h = 6 cm.
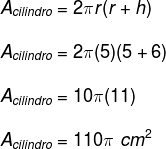

33) (Vunesp) Uma pessoa comprou um litro de leite, e, após beber certa quantidade, colocou o restante dele em uma caneca de alumínio na forma de um cilindro circular reto, com 10 cm de diâmetro interno, conforme ilustra a figura:
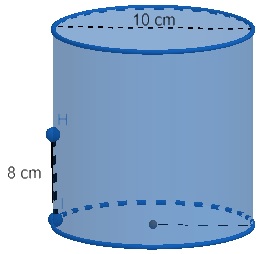 Sabendo-se que o leite, ao ser colocado na caneca, atingiu a altura de 8 cm, pode-se concluir corretamente que a quantidade de leite que a pessoa havia bebido antes de colocá-lo na caneca era:
Sabendo-se que o leite, ao ser colocado na caneca, atingiu a altura de 8 cm, pode-se concluir corretamente que a quantidade de leite que a pessoa havia bebido antes de colocá-lo na caneca era:
(A) 300 ml
(B) 350 ml
(C) 400 ml
(D) 450 ml
(E) 500 ml
(Dado: π = 3)
Resolução:
Vamos determinar o volume de leite no recipiente:
V = π · r2 · h
V = 52 · 8 · 3
V = 25 · 8 · 3
V = 200 · 3
V = 200 ·(3)
V = 600 cm3
Sabemos que 600 cm3 → 0,6 dm3 → 0,6 L. Pelo enunciado, inicialmente tínhamos 1L de leite, como, após beber certa quantidade dele, sobrou 0,6 L, então sabemos que foram bebidos 0,4L de leite, que corresponde a 400ml.
Alternativa: C
34) (PM - ES) Determinado cubo possui volume de 729 cm³. Cada face desse cubo possui área de:
(A) 3 cm2.
(B) 9 cm2.
(C) 27 cm2.
(D) 54 cm2.
(E) 81 cm2.
Resolução:
O objetivo da questão é descobrir a área de cada face do cubo. Para tanto, precisamos descobrir a medida de cada aresta (a).
A única informação que temos é que o volume do cubo é de 729 cm³.
Utilizando a fórmula do volume:
V = a³
729 = a³
a = 9 cm
Calculando a área de cada face, sabendo que as faces têm o formato de um quadrado e que cada aresta do cubo mede 9 cm:
A = a²
A = 9²
A = 81 cm²
Alternativa: E
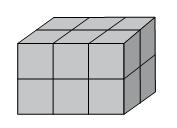
35) (SAP SP – VUNESP) Os produtos de uma empresa são embalados em caixas cúbicas, com 20 cm de aresta. Para transporte, essas embalagens são agrupadas, formando um bloco retangular, conforme mostrado na figura. Sabe-se que 60 desses blocos preenchem totalmente o compartimento de carga do veículo utilizado para o seu transporte. Pode-se concluir, então, que o volume máximo, em metros cúbicos, transportado por esse veículo é
 (A) 4,96.
(A) 4,96.
(B) 5,76.
(C) 7,25.
(D) 8,76.
(E) 9,60.
Resolução:
O primeiro passo é calcular o volume de cada caixa. Como as respostas estão apresentadas em metros cúbicos, vamos considerar que cada aresta mede 0,2 m (20 cm).
Vc = a³
Vc = 0,2³
Vc = 0,008 m³
Pela figura, percebe-se que um bloco retangular contém 12 caixas. Vamos calcular o volume de cada bloco:
Vb = 12 . 0,008 = 0,096 m³
Para finalizar, cabem 60 blocos no caminhão. Calculando o volume total:
Vt = 60 . 0,096 = 5,76 m³
Alternativa: B
36) (PM ES – Exatus) Um estoquista, ao conferir a quantidade de determinado produto embalado em caixas cúbicas de arestas medindo 40 cm, verificou que o estoque do produto estava empilhado de acordo com a figura que segue:
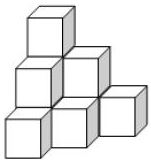 Ao realizar corretamente os cálculos do volume dessa pilha de caixas, o resultado obtido foi:
Ao realizar corretamente os cálculos do volume dessa pilha de caixas, o resultado obtido foi:
(A) 0,64 m³
(B) 1,6 m³
(C) 6,4 m³
(D) 16 m³
(E) 64 m³
Resolução:
Pela figura, é possível observar que existem 10 caixas empilhadas.
Vamos calcular o volume de cada caixa, sabendo que cada aresta mede 0,4 m (40 cm):
V = a³
V = 0,4³
V = 0, 0,064 m³
Como existem 10 caixas:
Vt = 10 . 0,064 = 0,64 m³
Alternativa: A
37) (SES DF – IADES) Sabe–se que o volume de um cubo de aresta α é dado por α³. Considerando que a aresta de um cubo seja multiplicada por 2, em quantas vezes seu volume aumentará?
(A) Duas.
(B) Três.
(C) Quatro.
(D) Seis.
(E) Oito.
Resolução:
Como foi informado, o volume de um cubo de aresta α é igual a α³. Vamos calcular o volume de um cubo de aresta 2α:
V = (2α)³
V = 2³.α³
V = 8.α³
Daí, quando multiplicamos a aresta do cubo por 2, o volume para a ser 8 vezes maior.
Alternativa: E
38) Considere uma caixa de água com formato de um paralelepípedo reto retângulo totalmente cheia, com comprimento de 7 m e largura de 4 m e altura de 2 m.
Calcule:
a) A área da base
Resolução:
A área da base desta caixa é calculada pela fórmula do retângulo, pois a base da caixa é retangular: Ab = comprimento x largura
Ab = 7 . 4 = 28 m²
A área lateral
Resolução:
A área da lateral de um paralelepípedo é calculada pela fórmula:
Al = 2((comprimento x altura) + (largura x altura)) = (7 x 2) + (4 x 2) = 14 + 8 = 22 m²
c) A área total
Resolução:
A área total do paralelepípedo é:
At = 2((comprimento x largura) + (comprimento x altura) + (largura x altura)) = (7 x 4) + (7 x 2) + (4 x 2) = 28 + 14 + 8 = 50 m²
d) O volume de água da caixa
Resolução:
O volume de um paralelepípedo é: V = (comprimento x largura x altura) = 7 x 4 x 2 = 56 m³
39) Um aquário possui o formato de um paralelepípedo com as seguintes dimensões:
.jpg) Determine quantos litros de água são necessários para encher o aquário.
Determine quantos litros de água são necessários para encher o aquário.
Resolução:
V = comprimento x largura x altura
V = 50 cm x 20 cm x 15 cm
V = 15000 cm³ (centímetros cúbicos)
Como foi informado que 1 cm³ corresponde a 1 ml, temos que 15000 cm³ é igual a 15000 ml ou 15 litros.
40) O degrau de uma escada lembra a forma de um paralelepípedo com as seguintes dimensões: 1 m de comprimento, 0,5 m de largura e 0,4 m de altura. Determine o volume total de concreto gasto na construção dessa escada sabendo que ela é constituída de 20 degraus.
.jpg) Resolução:
Resolução:
Volume do degrau
V = 1 m x 0,5 m x 0,4 m
V = 0,20 m³
Volume total da escada
0,20 x 20
4 m³ ou 4 mil litros de concreto.
41) Considere um cone cuja base tem raio 2 m e a altura mede 8 m. Considere π = 3,14. Calculemos o volume do cone:
Resolução:
V = ⅓ π.r2.h
V = 1 . 3,14 . 22 . 8
3
V = 3,14 . 4 . 8
3
V = 100,48
3
V ≈ 33,49 m3
Então o volume do cone é de, aproximadamente, 33,49 m3.
42) Um cone circular reto em que a geratriz mede 5 m e a altura, 4 m.
Resolução:
Para calcularmos o volume desse sólido, precisamos encontrar a medida do raio, para tanto, utilizaremos o Teorema de Pitágoras:
g2 = h2 + r2
r2 = g2 – h2
r2 = 52 – 42
r2 = 25 – 16
r2 = 9
r = 3 m
Agora que temos o valor do raio, podemos calcular o volume do cone utilizando a fórmula:
V = ⅓ π.r2.h
V = 1 . 3,14 . 32 . 4
3
V = 3,14 . 9 . 4
3
V = 113,04
3
V = 37,68 m3
Portanto, o volume desse cone circular reto é 37, 68 m3.
43) Um copo será fabricado no formato de um cone com as seguintes medidas: 4 cm de raio e 12 cm de altura. Qual será a capacidade do copo?
Resolução:
.jpg)
44) Uma fábrica de doces e balas irá produzir chocolates na forma de guarda-chuva, com as seguintes medidas: 8 cm de altura e 3 cm de raio de acordo com a ilustração. Qual a quantidade de chocolate utilizada na produção de 2000 peças?
Resolução:
.jpg) Cada chocolate possui 75,36 cm³ de volume. A fábrica quer produzir 2000 peças, então:
Cada chocolate possui 75,36 cm³ de volume. A fábrica quer produzir 2000 peças, então:
2000 * 75,36 = 150 720 cm³
Lembrando que 1 cm³ = 1 ml, temos 150 720 ml de chocolate que corresponde a 150,72 litros.
45) Uma casquinha de sorvete possui o formato de um cone reto com altura de 10 cm e raio da base medindo 5 cm. Determine o volume da casquinha.
Resolução:
.jpg) O volume da casquinha é de 261,66 cm³, que corresponde a, aproximadamente, 261 ml.
O volume da casquinha é de 261,66 cm³, que corresponde a, aproximadamente, 261 ml.
46) Um reservatório possui volume de aproximadamente 3000 m³ e diâmetro da base medindo 24 metros. Determine a altura deste reservatório.
Resolução:
O valor do raio nesse exemplo é 12, porque o raio é metade do diâmetro, veja:
r = d
2
r = 24
2
r = 12
Agora que já sabemos o valor do raio podemos calcular o volume do reservatório.
.jpg) A altura do reservatório é de aproximadamente 20 metros.
A altura do reservatório é de aproximadamente 20 metros.
47) Uma pirâmide de base quadrangular possui altura medindo 2 metros e cada lado da base com medida igual a 3 metros. Determine o volume dessa pirâmide.
.jpg) Resolução:
Resolução:
.jpg)
48) Uma indústria irá fabricar uma peça no formato de uma pirâmide de base triangular com as medidas indicadas na figura. Sabendo que serão fabricadas 500 peças maciças de aço, determine o volume total de aço que será gasto na produção dessas peças.
.jpg) Resolução:
Resolução:
.jpg)
49) A figura representa uma pirâmide de base pentagonal com lados regulares medindo 12 metros e a apótema da base medindo 8,2 metros, aproximadamente. Sabendo que a altura dessa pirâmide é igual a 20 metros, qual será sua capacidade sabendo que 1 m³ corresponde a 1000 litros?
.jpg) Resolução:
Resolução:
Área da base e Volume
.jpg) Se 1m³ corresponde a 1000 litros, temos que:
Se 1m³ corresponde a 1000 litros, temos que:
1640m³ = 1640 * 1000 = 1 640 000 litros de capacidade.
50) Calcule o volume da pirâmide de base quadrada a seguir:
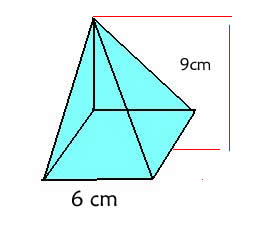 Resolução:
Resolução:
Pela análise da figura, temos que:
h = 9 cm
Ab = 62 = 36 cm2
Assim, o volume da pirâmide será dado por:
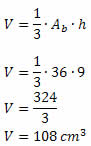
51) Calcule o volume de uma pirâmide regular de base hexagonal sabendo que sua altura é de 12 cm e que cada aresta da base mede 8 cm.
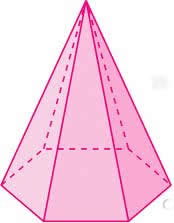 Resolução:
Resolução:
Primeiro, vamos calcular a área da base dessa pirâmide. Sabemos que a base da pirâmide é um hexágono regular de 8 cm de aresta. A área do hexágono regular é dada por:
 Conhecida a medida da área da base da pirâmide, podemos utilizar a fórmula do volume.
Conhecida a medida da área da base da pirâmide, podemos utilizar a fórmula do volume.
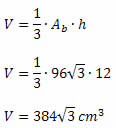
52) (ENEM) Uma empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugerem que seja adicionado 1,5 mL desse produto para cada 1 000 L de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a 1,7 m, com largura e comprimento iguais a 3 m e 5 m, respectivamente. O nível da lâmina d’água dessa piscina é mantido a 50 cm da borda da piscina.
A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é
(A) 11,25.
(B) 27,00.
(C) 28,80.
(D) 32,25.
(E) 49,50.
Resolução:
De acordo com o enunciado temos que o volume de água na piscina é igual a:
V = 5 . 3 . 1,2
V == 15 . 1,2 = 18 m³
ou
V = 18 000 l
Logo, a quantidade de produto será: (18 000 . 1,5) / 1 000 = 27 ml
Alternativa: B
53) Um reservatório em formato cilíndrico possui raio igual a 2 metros e sua altura é de 10 metros, como mostra a imagem a seguir. Qual é o volume desse reservatório? (considere π = 3,14).
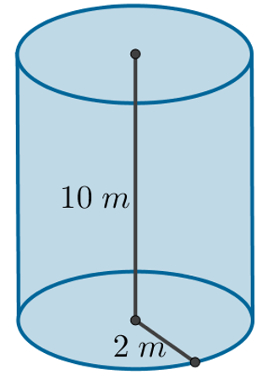 (A) 125,6 m3
(A) 125,6 m3
(B) 115,6 m3
(C) 100,6 m3
(D) 75,6 m3
(E) 15,6 m3
Resolução:
O volume do cilindro é dado pela área da base multiplicada por sua altura. Assim, podemos obter essa medida com a seguinte fórmula:
V = π . r2 . h
Substituindo os valores de π, do raio e da altura desse cilindro, teremos:
V = 3,14 . 22 . 10
V = 31,4 . 4
V = 125,6 m3
Alternativa A
54) Um cilindro possui volume igual a 7850 cm3 e seu diâmetro mede 10 centímetros. Qual é a medida da altura desse cilindro? (Considere π = 3,14).
(A) 50 cm
(B) 100 cm
(C) 120 cm
(D) 150 cm
(E) 200 cm
Resolução:
Para determinar a altura do cilindro, basta usar a fórmula do volume, uma vez que conhecemos seu volume e raio. Para encontrar o raio, lembre-se de que o diâmetro tem o dobro da medida do raio, logo, r = 5 cm.
V = π . r2 . h
7850 = 3,14 . 52 · h
7850 = 3,14 .25h
7850 = 3,14 . 25h
7850 = 78,5h
7850 = h
78,5
h = 100 cm
Alternativa B
55) Qual é o volume de um cilindro cuja altura é igual ao dobro de seu raio.
(A) πr3
(B) 2r3
(C) 2πr
(D) 2π
(E) 2πr3
Resolução:
Se o raio desse cilindro mede x, então sua altura mede 2x. Logo:
V = πr2 . h
V = πx2 . 2x
V = 2π . r3
Alternativa: E
Continua...













.jpg)








 Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?










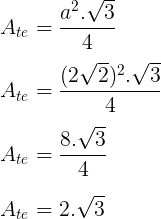


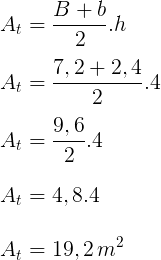

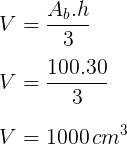




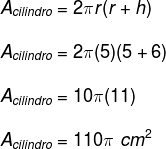




.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)