Professor Diminoi
IMPULSO
O que é impulso na Física?
Impulso é uma grandeza física que mede a mudança da quantidade de movimento sofrida por um corpo sobre o qual atua uma força (F) durante um intervalo de tempo (Δt). O impulso é uma grandeza vetorial, isto é, apresenta módulo, direção e sentido, e sua unidade no Sistema Internacional de Unidades (SI) é o kg.m/s ou, simplesmente, N.s.
Fórmula do Impulso de uma força constante
I = Fm . Δt
I = impulso (kg.m/s ou N.s)
Fm = força média (N)
Δt = intervalo de tempo (s)
O impulso também equivale à mudança da quantidade de movimento de um corpo. Quando aplicamos uma força em um corpo durante certo intervalo de tempo, a velocidade do corpo pode sofrer variações, por isso, o impulso também pode ser definido em relação à mudança da quantidade de movimento de um corpo.
I = ΔQ
I = QF - QI
I = mvF - mvI
I = Impulso (N.s ou kg.m/s)
ΔQ = variação da quantidade de movimento (N.s ou kg.m/s)
QF = quantidade de movimento final (N.s ou kg.m/s)
Qi = quantidade de movimento inicial (N.s ou kg.m/s)
m = massa (kg)
vF = velocidade final (m/s)
vi = velocidade inicial (m/s)
Por fim, podemos dizer que o produto da força pelo intervalo de tempo de aplicação dessa força equivale à variação da quantidade de movimento:
F = Δt . ΔQ
Em resumo, a força média exercida durante uma colisão é inversamente proporcional à sua duração:
I = F . Δt
F = I/Δt
Logo, o tempo de uma colisão e a força exercida sobre o corpo são grandezas inversamente proporcionais.
Impulso e quantidade de movimento
A unidade do impulso é a mesma utilizada na quantidade de movimento: kg.m/s. Além disso, dizemos que o impulso que é aplicado sobre um corpo é igual à variação da quantidade de movimento desse corpo:
I = ΔQ
I = QF – QI
I = mvF - mvI
Onde
I = impulso (N.s ou kg.m/s)
ΔQ = variação da quantidade de movimento (N.s ou kg.m/s)
QF = quantidade de movimento final (N.s ou kg.m/s)
Qi = quantidade de movimento inicial (N.s ou kg.m/s)
m = massa (kg)
vF = velocidade final (m/s)
vi = velocidade inicial (m/s)
QUESTÕES RESOLVIDAS
01) Calcule o módulo do impulso exercido pelo motor de um veículo de 800 kg que acelera de uma velocidade inicial de 20 m/s até 30 m/s.
Resolução
O impulso exercido sobre o veículo pode ser determinado por meio da variação da quantidade de movimento, isto é, equivale à quantidade de movimento final subtraída da quantidade de movimento inicial. Logo, o módulo desse impulso é dado por:
I = QF – QI
I = (800) . (30) – (800) . (20)
I = 24000 – 16000
I = 8000 N.s
ou
8000 kg.m/s
O resultado acima nos indica que, sobre esse veículo, agiu uma força média de 8000 N a cada segundo.
Teorema do impulso
A fórmula utilizada para definir o teorema do impulso é apresentada abaixo:
F . Δt = ΔQ
É importante lembrarmos que impulso e quantidade de movimento são grandezas vetoriais, isto é, ao realizarmos cálculos que envolvam essas grandezas, devemos fazer somas vetoriais, que levam em conta a direção e o sentido do movimento. Para tanto, é possível adotarmos algumas regras simples:
QUESTÕES RESOLVIDAS
02) Uma força de 120,0 N é aplicada em uma pequena bolinha de tênis de 0,050 kg por uma raquete durante um intervalo de tempo igual a 0,01 s. Sabendo que a bolinha movia-se no sentido direita-esquerda e, imediatamente antes de tocar a raquete, encontrava-se com velocidade de 15 m/s, calcule:
a) O módulo do impulso exercido sobre a bola.
Resolução:
Para calcularmos o módulo do impulso exercido sobre a bola, usaremos a fórmula abaixo:
I = Fm . Δt
Logo, teremos um impulso igual a:
I = Fm . Δt
I = (120,0) . (0,01)
I = 1,2 N.s
03) A velocidade final da bola.
Resolução
Para calcularmos a velocidade final da bola, usaremos a seguinte definição de impulso:
I = ΔQ
I = QF – QI
I = mvF - mvI
Devemos ficar atentos ao sentido de movimento da bola: a força exercida sobre ela e sua velocidade final são horizontais no sentido esquerda-direita. Já a velocidade inicial da bola está no sentido direita-esquerda, portanto, deve ter um sinal diferente. Dessa forma, teremos:
I = QF – QI
1,2 = (0,050) . (vF) – (0,050) . (15)
0,050vF = 1,2 + 0,75
vF = 1,95/0,050
vF = 38 m/s
Fórmula do impulso
As fórmulas do impulso estão resumidas abaixo:
I = Fm . Δt
Relação do impulso com a variação da quantidade de movimento
I = Δt
I = QF – QI
I = mvF - mvI
Gráfico para cálculo do impulso de uma força variável
É comum encontrarmos exercícios que envolvam forças variáveis. Nesses casos, podemos determinar o impulso exercido sobre um corpo por meio da área do gráfico da força pelo intervalo de tempo de aplicação dessa força:
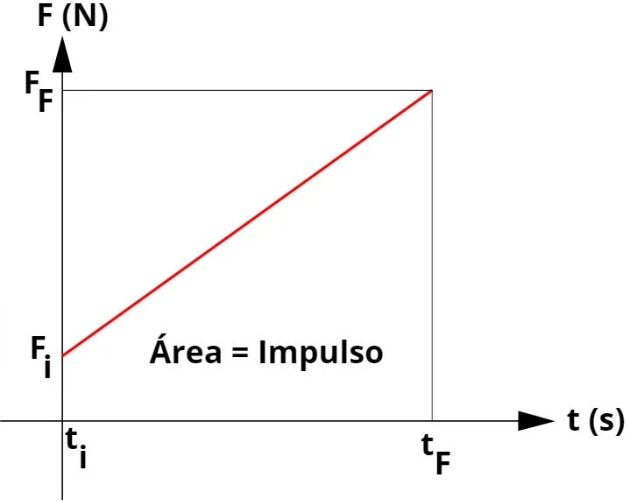
FF = força final (N)
Fi = força inicial (N)
ti = instante inicial (s)
tF = instante final (s)
Para determinarmos o módulo do impulso sofrido pelo corpo, basta calcularmos a área do gráfico.
04) Uma partícula recebe um impulso externo de uma força segundo o gráfico apresentado abaixo:

Considere que, após a aplicação da força, a velocidade da partícula seja mantida na mesma direção e no mesmo sentido. Determine a quantidade de movimento adquirida pelo corpo.
Resolução
Como sabemos, a área do gráfico de força por tempo fornece-nos o impulso exercido sobre o corpo. Dessa forma, temos que:
I = b . h
I = 10 . 5
I = 50N.s
Como o teorema do impulso informa que o impulso exercido sobre um corpo é igual à sua variação de quantidade de movimento, logo, essa variação é de 50 N.s.
05) (FUVEST) Após o chute para a cobrança de uma penalidade máxima, uma bola de futebol de massa igual 0,40 kg sai com velocidade igual a 24 m/s. O tempo de contato entre o pé do jogador e a bola é de 3,0.10-2 s.
a) Qual é a quantidade de movimento adquirida pela bola com o chute?
Resolução
Vamos calcular a quantidade de movimento que foi adquirida pela bola. Para tanto, consideramos que, durante a cobrança de pênalti, a bola encontrava-se em repouso. Portanto, o impulso adquirido por ela pode ser calculado da seguinte forma:
I = QF - QI
I = (0,40) . (24) – (0,40) . 0
I = 9,6kg.m/s
b) Qual é a força média aplicada pelo pé do jogador sobre a bola?
Resolução
Para calcular a força média aplicada durante o chute, utilizaremos a equação a seguir:
I = F . Δt
9,6 = F . (0,03)
F = 9,6/0,03
F = 320N
06) Durante um jogo de futebol, um jogador chuta a bola, aplicando sobre ela uma força de intensidade igual a 5 . 102 N durante um intervalo de tempo de 0,1s. Calcule o impulso da força aplicada pelo jogador.
Resolução:
F = 5 . 102 N
t = 0,1s
I = F . t
I = 5 . 102 . 0,1
I = 50 N.s
07) (PUC – MG) Uma força de 6 N atuando sobre um objeto em movimento altera sua quantidade de movimento em 3kg . m/s. Durante quanto tempo essa força atuou sobre esse objeto?
(A) 1s
(B) 2s
(C) 0,25
(D) 0,50
Resolução:
F = 6 N
ΔQ = 3Kg . m/s
Utilizamos a equação do teorema do impulso e quantidade de movimento:
ΔQ = I
ΔQ = F.t
3 = 6 . t
3 = t
6
t = 0,50 s
Alternativa: D
08) O gráfico a seguir representa a variação da intensidade da força F em função do tempo:

Gráfico da força aplicada sobre uma partícula em função do tempo
Calcule o impulso da força no intervalo de 15s.
Resolução:
O impulso da força F é igual à área sob a curva do gráfico da força x tempo.
A área desse gráfico é igual à soma da área do retângulo, de 0 a 8 s, com a área do triângulo no intervalo de 8 a 15 s.
A área do retângulo é calculada pelo produto entre a sua base e altura:
Ar = b . h
Ar = 8 . 15
Ar = 120
A área do triângulo é dada pelo produto entre a base e a altura dividido por 2:
At = b . h
2
At = 7 . 15/2
At = 105/2
At = 52,5
I = Atotal
I = Ar + At
I = 120 + 52,5
I = 172,5 N.s
09) (UNIFOR – CE) Uma bola de massa 0,5 kg é chutada para o gol, chegando ao goleiro com velocidade de 40m/s e, rebatida por ele, sai com velocidade de 30 m/s numa direção perpendicular à do movimento inicial. O impulso que a bola sofre graças à intervenção do goleiro, tem módulo, em N.s:
(A) 15
(B) 20
(C) 25
(D) 30
(E) 35
Resolução:
m = 0,5 kg
v1 = 40 m/s
v2 = 30 m/s (perpendicular à v0)
Como as duas velocidades são perpendiculares entre si, para encontramos a velocidade resultante, devemos utilizar o teorema de Pitágoras:
v2 = v12 + v22
v2 = 402 + 302
v2 = 1600 + 900
v2 = 2.500
v = √2.500
v = 50 m/s
Agora podemos utilizar o teorema do impulso e quantidade de movimento:
I = mv
I = 0,5 . 50
I = 25 kg. m/s
Alternativa: C
10) (PUC-RJ) Um garoto de massa 30 kg está parado sobre uma grande plataforma de massa 120 kg também em repouso em uma superfície de gelo. Ele começa a correr horizontalmente para a direita, e um observador, fora da plataforma, mede que sua velocidade é de 2,0 m/s. Sabendo que não há atrito entre a plataforma e a superfície de gelo, a velocidade com que a plataforma se desloca para a esquerda, para esse observador, é, em m/s:
(A) 1,0
(B) 2,0
(C) 0,5
(D) 8,0
(E) 4,0
Resolução:
A quantidade de movimento do garoto para a direita deve ser igual à quantidade de movimento da plataforma para a esquerda:
m . v = M . V
30 . 2 = 120 . V
60 = 120 . V
V = 60
120
V = 6
12
V = 0,5 m/s
Alternativa: C
11) (FAMEMA-SP) Um brinquedo consiste em um fole acoplado a um tubo plástico horizontal que se encaixa na traseira de um carrinho, inicialmente em repouso. Quando uma criança pisa no fole, comprimindo-o até o final, o ar expelido impulsiona o carrinho.

Considere que a massa do carrinho seja de 300 g, que o tempo necessário para que a criança comprima completamente o fole seja de 0,2 s e que, ao final desse intervalo de tempo, o carrinho adquira uma velocidade de 8 m/s. Admitindo desprezíveis todas as forças de resistência ao movimento do carrinho, o módulo da força média (FMÉD) aplicada pelo ar expelido pelo tubo sobre o carrinho, nesse intervalo de tempo, é igual a
(A) 10 N.
(B) 14 N.
(C) 12 N.
(D) 8 N.
(E) 16 N.
Resolução:
A partir do teorema do impulso, podemos escrever:
I = ΔQ
F.Δt = QFINAL – QINICIAL
Inicialmente o carrinho está em repouso, portanto, a quantidade de movimento inicial é nula:
F.Δt = QFINAL
F.Δt = m.v
F . 0,2 = 0,3 . 8
F = 2,4
0,2
F = 12 N
Alternativa: C
12) Uma força de 5000 N é aplicada a um objeto de forma indefinida, produzindo um impulso de módulo 1000 N.s. Sabendo que a força é horizontal e para a direita, determine o tempo de contato da força sobre o corpo e a direção do impulso.
(A) 0,2 s e horizontal para a direita
(B) 0,4 s horizontal para a esquerda
(C) 0,2 s horizontal para a esquerda
(D) 0,6 s vertical para cima
(E) 0,5 horizontal para a direita
Resolução:
A partir da definição de impulso, podemos escrever:
I = F . Δt
Δt = I
F
Δt = 1000
5000
Δt = 0,2 N.s
O impulso possui a mesma direção e o mesmo sentido da força; nesse caso, horizontal e para a direita.
Alternativa: A
13) Marque a alternativa correta a respeito da relação entre energia cinética e quantidade de movimento.
(A) Tanto quantidade de movimento quanto energia cinética são grandezas escalares.
(B) A quantidade de movimento é a razão da energia cinética pela velocidade de um corpo.
(C) Essas duas grandezas não possuem nenhuma relação, pois uma é escalar e a outra é vetorial.
(D) A energia cinética pode ser definida por meio da razão do quadrado da quantidade de movimento pelo dobro da massa do objeto.
(E) A energia cinética pode ser definida por meio do produto do quadrado da quantidade de movimento pelo dobro da massa do objeto.
Resolução:
A partir da definição de energia cinética e quantidade de movimento, podemos escrever que:
Q = m.v >> v = Q
m
Ec = m.v2
2
Ec = m . Q2
2 m2
Ec = Q2
2m
Alternativa: D
QUANTIDADE DE MOVIMENTO
Quantidade de movimento é o produto entre a massa de um corpo e sua velocidade. Trata-se de uma grandeza vetorial cuja unidade de medida, de acordo com o Sistema Internacional de Unidades (SI), tanto pode ser o kg.m/s quanto o N.s.

A fórmula utilizada para calcular a quantidade de movimento é a seguinte:
Q = m . v
Q = quantidade de movimento (kg.m/s)
m = massa (kg)
v = velocidade (m/s)
A quantidade de movimento é uma grandeza particularmente útil para o estudo das colisões, uma vez que, em colisões elásticas, a quantidade total de movimento deve ser mantida constante.
QUESTÕES RESOLVIDAS
14) Uma bola de 400 g se movimenta num dado instante, conforme figura abaixo, com velocidade de módulo igual a 2 m/s. Qual o módulo, a direção e o sentido da quantidade de movimento da bola no referido momento?
Resolução:
Para calcular a quantidade de movimento, basta multiplicar a velocidade da bola, por sua massa. Entretanto, devemos transformar as unidades para o sistema internacional.
m = 400 g = 0,4 kg
Substituindo, temos:
Q = m . v
Q = 0,4 . 2
Q = 0,8 kg.m/s
A direção e o sentido da quantidade de movimento serão os mesmos da velocidade, ou seja, direção horizontal e sentido da esquerda para a direita.
15) Uma bola de futebol tem massa 1,2kg e se desloca com velocidade igual a 15m/s. Qual a quantidade de movimento dela?
Resolução:
Q = m . v
Q = 1,2 . 15
Q = 18kg.m/s
16) Acerca da grandeza física conhecida como quantidade de movimento, são feitas as seguintes afirmações:
I – A quantidade de movimento é uma grandeza física escalar.
II – A unidade de medida da quantidade de movimento é o kg.m/s.
III – A quantidade de movimento é definida pelo produto entre massa e velocidade.
São verdadeiras:
(A) I e II
(B) II e III
(C) I, II e III
(D) Somente I
(E) Somente III
Resolução:
A quantidade de movimento pode ser calculada multiplicando-se a massa de um corpo por sua velocidade. Essa grandeza física é vetorial, e sua unidade de medida, de acordo com o SI, é o kg.m/s. Dessa maneira, são corretas as afirmações II e III.
Alternativa: B
17) (Uerj) O gráfico abaixo indica a variação da aceleração a de um corpo, inicialmente em repouso, e da força F que atua sobre ele.

Quando a velocidade do corpo é de 10 m/s, sua quantidade de movimento, em kg.m/s corresponde a:
(A) 50
(B) 30
(C) 25
(D) 15
Resolução:
Primeiramente, é necessário descobrir qual é a massa do corpo a partir do gráfico e por meio da fórmula da força resultante.
F = m . a
6 = m . 2
m = 6/2
m = 3 kg
Por fim, o exercício pede que calculemos a quantidade de movimento quando a velocidade do corpo for de 10 m/s. Para tanto, basta fazermos o seguinte cálculo:
Q = m . v
Q = 3 . 10
Q = 30 kg.m/s
Alternativa: B
18) (Uece) Considere um vagão com uma carga líquida que é puxado por uma locomotiva em uma via reta horizontal. Despreze os atritos e considere que a força aplicada pela locomotiva ao vagão seja constante. Caso haja vazamento dessa carga, o momento linear do conjunto formado pelo vagão e a carga no seu interior:
(A) varia somente pela aplicação da força.
(B) varia pela aplicação da força e pela variação na massa.
(C) varia somente pela perda de massa do vagão.
(D) não varia mesmo com mudança na massa.
Resolução:
Como já vimos, a força resultante aplicada sobre um corpo depende da variação da quantidade de movimento, que, por sua vez, depende tanto da massa quanto da velocidade do corpo. A relação entre a força e a quantidade de movimento:
Alternativa: B
19) Determine o módulo da quantidade de movimento de um veículo automotivo de 900 kg que se desloca com velocidade de 72 km/h e assinale a alternativa correta:
(A) 1800 kg.m/s
(B) 19.600 kg.m/s
(C) 64.800 kg.m/s
(D) 8.000 kg.m/s
(E) 18.000 kg.m/s
Resolução:
Para calcularmos o módulo da quantidade de movimento, é necessário que se multiplique a massa do corpo por sua velocidade, mas também é necessário que as unidades de medida estejam definidas de acordo com as unidades do SI. Dessa maneira, é preciso dividir a velocidade, que está em km/h, por 3,6. Confira o cálculo:
Q = m . v
Q = 900 . 72/3,6
Q = 18000 kg.m/s
Alternativa: E
20) (ENEM) Durante um reparo na estação espacial internacional, um cosmonauta, de massa 90 kg, substitui uma bomba do sistema de refrigeração, de massa 360 kg, que estava danificada. Inicialmente, o cosmonauta e a bomba estão em repouso em relação à estação. Quando ele empurra a bomba para o espaço, ele é empurrado no sentido oposto. Nesse processo, a bomba adquire uma velocidade de 0,2 m/s em relação à estação.
Qual é o valor da velocidade escalar adquirida pelo cosmonauta, em relação à estação, após o empurrão?
(A) 0,05 m/s
(B) 0,20 m/s
(C) 0,40 m/s
(D) 0,50 m/s
(E) 0,80 m/s
Resolução:
Usando a conservação da quantidade de movimento, temos que Qf = Qi = 0, como adquirem velocidades com sentidos opostos, então:
M.V - m.v = 0
360.0,2 - 90.v = 0
90.v = 72
v = 72/90
v = 0,80 m/s
Alternativa: E
IMPULSO E QUANTIDADE DE MOVIMENTO
21) (Udesc) O airbag e o cinto de segurança são itens de segurança presentes em todos os carros novos fabricados no Brasil. Utilizando os conceitos da Primeira Lei de Newton, de impulso de uma força e variação da quantidade de movimento, analise as proposições.
I. O airbag aumenta o impulso da força média atuante sobre o ocupante do carro na colisão com o painel, aumentando a quantidade de movimento do ocupante.
II. O airbag aumenta o tempo da colisão do ocupante do carro com o painel, diminuindo assim a força média atuante sobre ele mesmo na colisão.
III. O cinto de segurança impede que o ocupante do carro, em uma colisão, continue se deslocando com um movimento retilíneo uniforme.
IV. O cinto de segurança desacelera o ocupante do carro em uma colisão, aumentando a quantidade de movimento do ocupante.
Assinale a alternativa correta:
(A) Somente as afirmativas I e IV são verdadeiras.
(B) Somente as afirmativas II e III são verdadeiras.
(C) Somente as afirmativas I e III são verdadeiras.
(D) Somente as afirmativas II e IV são verdadeiras.
(E) Todas as afirmativas são verdadeiras.
Resolução:
I] - Falsa. O airbag reduz a força aplicada sobre o corpo, aumentando o tempo de aplicação da força.
[II] - Verdadeira.
[III] - Verdadeira.
[IV] – Falsa. A quantidade de movimento do ocupante é reduzida.
Alternativa: B
22) (PUC-RJ) Um jogador de tênis, durante o saque, lança a bola verticalmente para cima. Ao atingir sua altura máxima, a bola é golpeada pela raquete de tênis e sai com velocidade de 108 km/h na direção horizontal.
Calcule, em kg.m/s, o módulo da variação de momento linear da bola entre os instantes logo após e logo antes de ser golpeada pela raquete.
Dado: considere a massa da bola de tênis igual a 50 g.
(A) 1,5
(B) 5,4
(C) 54
(D) 1500
(E) 5400
Resolução:
Para resolver o exercício, é necessário escrever a massa, que está em gramas, em quilogramas (m = 50.10-3 kg). Além disso, a velocidade, que está em km/h, deve ser expressa em m/s.
ΔQ = mvF – mvI
ΔQ = 50 . 10-3 . (30 - 0)
ΔQ = 1,5 gk.m/s
Alternativa: A
33) (UECE) Considere uma esfera muito pequena de massa igual a 1 kg deslocando-se a uma velocidade de 2 m/s sem girar durante 3 s. Nesse intervalo de tempo, o momento linear dessa partícula é:
(A) 2 kg.m/s
(B) 3 s
(C) 6 kg.m/s
(D) 6 m
Resolução:
Para resolver o exercício, basta que se multiplique a massa e a velocidade do corpo, mas também é necessário recordar a unidade de medida da quantidade de movimento, o kg.m/s.
Q = m . v
Q = 1 . 2
Q = 2 kg.m/s
Alternativa: A
COLISÃO

Colisões elásticas e inelásticas
As colisões elásticas e inelásticas são interações entre corpos em que um exerce força sobre o outro, sendo a classificação feita de acordo com a conservação da energia.
A colisão entre as bolas de bilhar é um exemplo de colisão elástica, pois não há deformação dos corpos
As colisões são interações entre corpos em que um exerce força sobre o outro.
Características inerentes às colisões elásticas e inelásticas.
Colisões elásticas
A colisão é denominada elástica quando ocorre conservação da energia e do momento linear dos corpos envolvidos. A principal característica desse tipo de colisão é que, após o choque, a velocidade das partículas muda de direção, mas a velocidade relativa entre os dois corpos mantém-se igual. Para compreender melhor, observe o exemplo da figura:

Velocidade dos corpos A e B antes e depois de uma colisão elástica
Podemos observar na figura acima que, após o choque, as esferas passaram a mover-se em sentido contrário ao que tinham antes de colidirem.
Equações para a energia cinética e para o momento linear:
Como já citado anteriormente, nesse tipo de colisão, ocorre a conservação da energia e do momento linear. Essa conservação pode ser descrita pelas equações:
Para conservação do momento linear:
Qi = Qf —> mA . VIA + mB . VIB = mA . VFA + mB . VFB
Para a conservação da energia cinética:
EI = EF —> 1 mA . VIA2 + 1 mB . VIB2 = 1 mA . VFA2 + 1 mB . VFB2
2 2 2 2
Sendo que:
mA e mB = massas dos corpos A e B respectivamente;
VI = velocidade inicial;
VF = velocidade final.
Colisões inelásticas
Se, ao ocorrer uma colisão, não houver conservação da energia cinética, ela será denominada colisão inelástica. Nesse tipo de colisão, a energia pode ser transformada em outra forma, por exemplo, em energia térmica, ocasionando o aumento da temperatura dos objetos que colidiram. Dessa forma, apenas o momento linear é conservado.
As colisões inelásticas podem ser classificadas de duas formas: perfeitamente inelásticas e parcialmente inelásticas.
Colisões perfeitamente inelásticas: quando ocorre a perda máxima de energia cinética. Após esse tipo de colisão, os objetos seguem unidos como se fossem um único corpo com massa igual à soma das massas antes do choque.

Após um choque perfeitamente inelástico, os dois objetos seguem juntos na mesma direção como se fossem um único objeto
Como citado anteriormente, nesse caso, ocorre apenas a conservação do momento linear. Podemos obter uma expressão para a velocidade final VF dos objetos. Veja as equações a seguir:
Qi = Qf —> mA . VIA + mB . VIB = (mA + mB) VF
Isolando VF, temos:
VF = mA . VIA + mB . VIB
mA + mB
Colisões parcialmente inelásticas: ocorre conservação de apenas uma parte da energia cinética de forma que a energia final é menor do que a energia inicial. Constituem a maioria das colisões que ocorre na natureza. Nesse caso, após o choque, as partículas separam-se, e a velocidade relativa final é menor do que a inicial.

Após uma colisão parcialmente inelástica, as esferas afastam-se com velocidade relativa diferente da velocidade de aproximação
A figura acima mostra o comportamento de duas esferas antes e depois de uma colisão parcialmente inelástica. Para compreender melhor, utilizamos valores numéricos para as velocidades. A velocidade relativa antes da colisão é dada pela diferença entre as duas velocidades:
Vrel = VIA - VIB
Substituindo os valores, temos:
Vrel = 6 – (-4) = 10 m/s
Depois da colisão, temos a seguinte situação:
Vrel = VFA - VFB
Vrel = 3 - (- 4) = 7m/s
Podemos ver que a velocidade relativa antes da colisão é diferente da velocidade relativa depois da colisão. É isso que caracteriza essa colisão como parcialmente inelástica, mas que também pode ser chamada de parcialmente elástica.
QUESTÕES RESOLVIDAS
24) Quando uma pessoa dispara uma arma vemos que ela sofre um pequeno recuo. A explicação para tal fenômeno é dada:
(A) pela conservação da energia.
(B) pela conservação da massa.
(C) pela conservação da quantidade de movimento do sistema.
(D) pelo teorema do impulso.
(E) pelo teorema da energia cinética.
Resolução:

Como a troca de forças acontece internamente, ou seja, entre os corpos do sistema, (arma e bala), o sistema é mecanicamente isolado, portanto, a quantidade de movimento deste se conserva.
Alternativa: C
25) Supondo que uma arma de massa 1kg dispare um projétil de massa 10g com velocidade de 400 m/s, calcule a velocidade do recuo dessa arma.
(A) -2 m/s
(B) -4 m/s
(C) -6 m/s
(D) -8 m/s
(E) -10 m/s
Resolução:

Alternativa: B
26) (Cesgranrio-RJ) Um carrinho de massa m1 = 2,0 kg, deslocando-se com velocidade V1 = 6,0 m/s sobre um trilho horizontal sem atrito, colide com outro carrinho de massa m2 = 4,0 kg, inicialmente em repouso sobre o trilho. Após a colisão, os dois carrinhos se deslocam ligados um ao outro sobre esse mesmo trilho. Qual a perda de energia mecânica na colisão?
(A) 0 J
(B) 12 J
(C) 24 J
(D) 36 J
(E) 48 J
Resolução:
Alternativa: C
27) (FUVEST) Uma partícula se move com velocidade uniforme V ao longo de uma reta e choca-se frontalmente com outra partícula idêntica, inicialmente em repouso. Considerando o choque elástico e desprezando atritos, podemos afirmar que, após o choque:
(A) as duas partículas movem-se no mesmo sentido com velocidade V/2.
(B) as duas partículas movem-se em sentidos opostos com velocidades – V e + V.
(C) a partícula incidente reverte o sentido do seu movimento, permanecendo a outra em repouso.
(D) a partícula incidente fica em repouso e a outra se move com velocidade v.
(E) as duas partículas movem-se em sentidos opostos com velocidades – v e 2v.
Resolução:
Em um choque perfeitamente elástico com partículas idênticas há troca de velocidades.
Alternativa: D
28) (Udesc) Em uma colisão elástica frontal (em uma dimensão) entre duas partículas de massas m1 e m2, a partícula 2 estava em repouso antes da colisão. Analise as proposições em relação à colisão.
I. A quantidade de movimento e a energia cinética do sistema se conservam.
II. Se as massas são iguais, a magnitude da velocidade adquirida pela partícula 2, após a colisão, é igual à magnitude da velocidade da partícula 1, antes da colisão.
III. Se m1 é maior que m2, a magnitude da velocidade adquirida pela partícula 2, após a colisão, será maior que a magnitude da velocidade da partícula 1, antes da colisão.IV. Se m1é menor que m2, o vetor velocidade da partícula 1, após a colisão, é igual ao vetor velocidade que ela tinha antes da colisão.
Assinale a alternativa correta:
(A) Somente as afirmativas I e III são verdadeiras.
(B) Somente as afirmativas I, III e IV são verdadeiras.
(C) Somente as afirmativas I, II e III são verdadeiras.
(D) Somente a afirmativa II é verdadeira.
(E) Somente a afirmativa IV é verdadeira.
Resolução:
I: VERDADEIRA
II: VERDADEIRA
III: VERDADEIRA
IV: FALSA. Em relação ao módulo e à direção, a velocidade não sofre alteração, mas o sentido é oposto, logo, os vetores velocidade antes e depois da colisão não são iguais.
Alternativa: C
29) (ESPCEX) Dois caminhões de massa m1=2,0 ton e m2=4,0 ton, com velocidades v1=30 m/s e v2=20 m/s, respectivamente, e trajetórias perpendiculares entre si, colidem em um cruzamento no ponto G e passam a se movimentar unidos até o ponto H, conforme a figura abaixo. Considerando o choque perfeitamente inelástico, o módulo da velocidade dos veículos imediatamente após a colisão é:

(A) 30 km/h
(B) 40 km/h
(C) 60 km/h
(D) 70 km/h
(E) 75 km/h
Resolução:
As quantidades de movimento de cada caminhão serão calculadas por:
Q1 = m1 . V1
Q1 = 2 . 103 . 30
Q1 = 6 . 104 kgm/s
Q2 = m2 . V2
Q2 = 4 . 103 . 20
Q2 = 8 . 104 kgm/s
Há um ângulo de 90° entre as quantidades de movimento dos caminhões. Sendo essa uma grandeza vetorial, a quantidade de movimento resultante (QR) advém de uma soma vetorial:
QR2 = Q12 + Q22
QR2 = ( 6 . 104)2 + (8 . 104 )2
QR2 = 36 . 108 + 64 . 108
QR2 = 100 . 108
QR2 = 102 . 108
QR2 = 1010
QR = (1010)1/2
QR= 105 kgm/s
Como a colisão é do tipo perfeitamente inelástica, após sua ocorrência, os corpos permanecem grudados. Sendo assim, podemos determinar a quantidade de movimento resultante como:
QR= (m1 + m2) . V
105 = ( 2 . 103 + 4 . 103 ) . V
105 = 6 . 103 .V
V = (105 ÷ 6 . 103)
V = 102 ÷ 6
Para transformar em km/h, deve-se multiplicar o valor por 3,6:
V = 3,6 (102 ÷ 6)
V = 360 ÷ 6
V = 60 km/h
Alternativa: C
30) Um objeto de massa m movimenta-se com velocidade V. Em certo instante, ele colide contra outro objeto de mesma massa que estava inicialmente em repouso. Após a colisão, os dois objetos movimentam-se juntos. Marque a opção que indica a velocidade do conjunto formado pelos dois corpos após a colisão e o coeficiente de restituição dessa colisão.
(A) 0,5v e 0,8
(B) v e 1
(C) 0,5 v e 1
(D) 0,75 v e 0
(E) 0,5 v e 0.
Resolução:
A velocidade do conjunto pode ser determinada pela conservação da quantidade de movimento:
QINICIAL = Q FINAL
m.v = (m+m).V
m.v = 2m . V
v = 2.V
V = v / 2
V = 0,5 v
Os objetos permanecem grudados após a colisão, o que indica uma colisão perfeitamente inelástica. Sendo assim, o valor do coeficiente de restituição é zero, uma vez que não há velocidade relativa de afastamento entre os objetos.
Alternativa: E
31) A respeito dos tipos de colisão e de seus valores de coeficiente de restituição, marque o que for correto.
(A) O coeficiente de colisão para um choque parcialmente elástico será sempre maior que 0 e menor ou igual a 1.
(B) Na colisão parcialmente elástica, sempre haverá conservação parcial da quantidade de movimento, portanto, o coeficiente de restituição será sempre 0,5.
(C) Na colisão inelástica, não há velocidade relativa de aproximação entre os corpos, o que faz com que o coeficiente de restituição dessa colisão seja nulo.
(D) A energia cinética é totalmente conservada na colisão do tipo perfeitamente elástica.
(E) Na colisão perfeitamente elástica, há conservação total da energia cinética e conservação parcial da quantidade de movimento.
Resolução:
a) ERRADA. Nas colisões parcialmente elásticas, o coeficiente de restituição será sempre maior que zero e menor que um (0 < e < 1), mas nunca será igual a um.
b) ERRADA: Na colisão parcialmente elástica, o coeficiente de restituição pode assumir qualquer valor entre 0 e 1.
c) ERRADA: Na colisão perfeitamente inelástica, não há velocidade relativa de afastamento entre os objetos que colidem.
d) CORRETA.
e) ERRADA: Na colisão perfeitamente elástica, a energia cinética e a quantidade de movimento sempre serão conservadas.
Alternativa: D
EXERCÍCIOS SOBRE CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
32) (UNICAMP-SP) Tempestades solares são causadas por um fluxo intenso de partículas de altas energias ejetadas pelo Sol durante erupções solares. Esses jatos de partículas podem transportar bilhões de toneladas de gás eletrizado em altas velocidades, que podem trazer riscos de danos aos satélites em torno da Terra. Considere que, em uma erupção solar em particular, um conjunto de partículas de massa total mp = 5 kg, deslocando-se com velocidade de módulo vp = 2x105 m/s, choca-se com um satélite de massa Ms = 95 kg que se desloca com velocidade de módulo igual a Vs = 4x103 m/s na mesma direção e em sentido contrário ao das partículas. Se a massa de partículas adere ao satélite após a colisão, o módulo da velocidade final do conjunto (VCONJ) será de:
(A) 102.000 m/s.
(B) 14.000 m/s.
(C) 6.200 m/s.
(D) 3.900 m/s.
Resolução:
Adotando o sentido de movimento do conjunto de partículas como positivo, podemos igualar as quantidades de movimento antes e depois do choque.
QINICIAL = QFINAL
A quantidade de movimento é fruto do produto da massa pela velocidade do corpo. A massa a ser considerada após a colisão é a soma da massa do conjunto de partículas com a massa do satélite, uma vez que os corpos permanecem grudados.
mp . Vp - MS . VS = (mP + MS) . VCONJ
5 . 2 x 105 – 95 . 4 x 103 = (5 + 95) . VCONJ
10 x 105 - 380 x 103 = 100 . VCONJ
1000 x 103 - 380 x 103 = 100 . VCONJ
- 620 x 103 = 102 . VCONJ
VCONJ = - 6200 m/s
Em módulo: VCONJ = 6200 m/s
Alternativa: C
33) (UDESC) Um foguete, durante a sua subida, queima combustível a uma taxa de 2,8 kg/s. Sabendo-se que o foguete expele os gases da queima a uma velocidade constante de 3,50 km/s e que a massa inicial do conjunto é de 800 kg, então a aceleração inicial do foguete é de:
(A) 12,25 x 10–3 m/s2
(B) 12,25 m/s2
(C) 12,25 x 10–6 m/s2
(D) 640 m/s2
(E) 81,63 m/s2
Resolução:
Ao igualar a quantidade de movimento do gás com a quantidade de movimento do foguete, considerando um intervalo de tempo de 1s, teremos:
QGÁS = QFOGUETE
2,8 kg. 3500 m/s = 800 . v
9800 = 800 . v
98 = v
8
v = 12,25 m/s
A velocidade do foguete variou de 0 a 12,25 m/s em 1 segundo. Sendo assim, podemos concluir que a aceleração inicial do foguete é 12,25 m/s2.
Alternativa: B
34) Um patinador desatento, de massa igual a 60 kg, movimenta-se a 2 m/s. Em um determinado instante, ele se choca com um latão de lixo completamente cheio. Após a colisão, o latão é arrastado por alguns metros. Sabendo que a massa do latão de lixo é de 20 kg, determine a velocidade do conjunto (patinador + latão) após a colisão.
(A) 1,80 m/s
(B) 1,75 m/s
(C) 1,30 m/s
(D) 1,50 m/s
(E) 1,60 m/s
Resolução:
Igualando as quantidades de movimento antes e depois do choque, teremos:
QANTES = QDEPOIS
QPATINADOR = QCONJUNTO
60 . 2 = (60 + 20) . V
120 = 90 . V
V = 120
80
V = 12
8
V = 1,5 m/s
Alternativa: D
35) Determine a velocidade de recuo (VREC) de um canhão com massa de 400 kg, que, após o tiro, libera uma bala de massa de 8 kg a uma velocidade de 300 m/s.
(A) 2 m/s
(B) 3 m/s
(C) 4 m/s
(D) 5 m/s
(E) 6 m/s
Resolução:
A quantidade de movimento deve ser considerada antes e após o tiro:
QANTES = QDEPOIS
Antes do tiro, bala e canhão estão em repouso, portanto, a quantidade de movimento é nula. Após o disparo, bala e canhão adquirem velocidades de sentidos opostos. O sentido da velocidade do canhão será adotado como negativo.
0 = 8 . 300 – 400 . VREC
400 . VREC = 2400
VREC = 2400
400
VREC = 6 m/s
Alternativa: E
Conservação da energia nas colisões elásticas
Colisão entre dois automóveis

Nas colisões do tipo elástica, a energia mecânica total do sistema tem sempre o mesmo valor. Se uma das partes aumenta sua energia mecânica, alguma outra parte terá sua energia reduzida.
Emecânica total antes da colisão = Emecânica total depois da colisão
É importante salientarmos que a energia total, isto é, a soma de todas as energias envolvidas no sistema se conserva. Portanto, na maioria das situações que envolvem colisões elásticas, a energia potencial do sistema permanece a mesma e, portanto, a única forma de energia que devemos levar em consideração é a energia cinética.
Sendo assim, temos:
ECtotal antes = ECtotal depois

Para a equação acima estamos supondo apenas dois objetos envolvidos na colisão.
A conservação da energia mecânica só se aplica a colisões elásticas, mas a conservação da quantidade de movimento aplica-se a qualquer tipo de colisão. Supondo uma colisão em uma dimensão, temos:
Ptotal antes = Ptotal depois
m1.v1 antes+m2.v2 antes = m1.v1 depois)+m2.v2 depois
Se as massas dos objetos e as velocidades antes da colisão forem conhecidas, temos duas equações com duas incógnitas. Para simplificar a resolução das duas equações de conservação podemos fazer o seguinte:
m1 (v1 antes-v1 depois ) = m2 (v2 depois-v2 antes)
m1 (v12antes-v12depois ) = m2(v22depois -v22antes)
Fazendo a divisão da segunda equação pela primeira teremos:
v1 antes+v1 depois = v2 depois-v2 antes
Que também pode ser escrita da seguinte forma:
v1 antes-v2 antes = v2 depois-v1 depois
Esta equação expressa que a velocidade relativa de aproximação é igual à velocidade relativa de afastamento.
EXERCÍCIOS SOBRE VELOCIDADE RELATIVA
36) (IFBA) Dois veículos A e B trafegam em uma rodovia plana e horizontal, obedecendo às seguintes equações horárias cujas unidades estão expressas no Sistema internacional de medidas (S.I.):
XA = 200,0 + 10,0t e XB = 1000,0 – 30,0t
Ao analisar esses movimentos, pode-se afirmar que a velocidade relativa de afastamento dos veículos, em km/h, vale:
(A) 20,0
(B) 40,0
(C) 80,0
(D) 100,0
(E) 144,0
Resolução:
Pela equação, pode-se perceber que as posições iniciais dos veículos A e B são, respectivamente, 200 km e 1000 km. Ainda por meio da observação das funções horárias da posição, podemos verificar que a velocidade do veículo B é maior que a do veículo A. A velocidade relativa de afastamento é a soma das velocidades dos móveis, uma vez que o sinal das velocidades nas equações é diferente, indicando que o movimento ocorre em sentido oposto.
VA = 10 m/s = 36 km/h
VB = 30 m/s = 108 km/h
VREL = 108 + 36 = 144 km/h
Alternativa: E
37) (PUC-RS) Analise a situação a seguir:
Duas esferas – A e B – de massas respectivamente iguais a 3 kg e 2 kg estão em movimento unidimensional sobre um plano horizontal perfeitamente liso, como mostra a figura 1.

Inicialmente as esferas se movimentam em sentidos opostos, colidindo no instante t1. A figura 2 representa a evolução das velocidades em função do tempo para essas esferas imediatamente antes e após a colisão mecânica.

Sobre o sistema formado pelas esferas A e B, é correto afirmar:
(A) Há conservação da energia cinética do sistema durante a colisão.
(b) Há dissipação de energia mecânica do sistema durante a colisão.
(C) A quantidade de movimento total do sistema formado varia durante a colisão.
(D) A velocidade relativa de afastamento dos corpos após a colisão é diferente de zero.
(E) A velocidade relativa entre as esferas antes da colisão é inferior à velocidade relativa entre elas após colidirem.
Resolução:
a) Errado. Haveria conservação de energia cinética se a velocidade das esferas permanecesse igual após a colisão.
b) Correto. A prova disso é que não houve conservação da velocidade das esferas, indicando perda de energia cinética.
c) Errado. A quantidade de movimento para sistemas desse tipo sempre é conservada.
d) Errado. O gráfico indica que, após a colisão, a velocidade das esferas possui mesmo valor.
e) Errado. A velocidade relativa após a colisão é nula, pois as esferas movimentam-se no mesmo sentido e com velocidades iguais.
Alternativa: B
38) Marque a alternativa correta a respeito do conceito de velocidade relativa.
(A) A velocidade relativa é o conjunto de valores que representa o movimento relativo entre dois móveis.
(B) Se dois objetos aproximam-se, movimentando-se em sentido oposto e com velocidades iguais a 20 m/s e 30 m/s, a velocidade relativa de aproximação entre eles é de 10 m/s.
(C) A velocidade relativa entre dois móveis sempre é a soma das velocidades individuais.
(D) Se dois objetos afastam-se, movimentando-se em sentido oposto e com velocidades iguais a 20 m/s e 30 m/s, a velocidade relativa de afastamento entre eles é de 50 m/s.
(E) A velocidade relativa entre dois móveis sempre é a diferença das velocidades individuais.
Resolução:
No caso do afastamento de dois móveis que se deslocam em sentido oposto, a velocidade relativa é a soma das velocidades individuais (20 + 30 = 50 m/s).
Alternativa: D
39) Leia as afirmações a seguir sobre o conceito de velocidade relativa.
I – A velocidade relativa é o valor único de velocidade que representa o movimento relativo entre objetos quaisquer.
II – A velocidade relativa na colisão frontal entre dois veículos que se movimentavam em sentidos opostos é a soma das velocidades de cada um dos automóveis antes da colisão.
III – Não há um caso em que a velocidade relativa seja a soma das velocidades dos móveis.
Está correto o que se afirma
(A) em I, II e III.
(B) em I e II
(C) apenas em II
(D) apenas em I
(E) apenas em III.
Resolução:
I – Verdadeira.
II – Verdadeira.
III – Falsa. Nos casos em que os sentidos dos móveis são opostos, a velocidade relativa sempre é a soma das velocidades individuais.
Alternativa: B
40) (Unitau) Uma motocicleta com velocidade constante de 20 m/s ultrapassa um trem de comprimento 100 m e velocidade 15 m/s. A duração da ultrapassagem é:
(A) 5 s
(B) 15 s
(C) 20 s
(D) 25 s
(E) 30 s
Resolução:
O movimento dos móveis ocorre no mesmo sentido, logo, pode-se determinar a velocidade relativa da moto em relação ao trem como sendo a subtração entre os módulos das velocidades dos dois veículos:
VREL = 20 – 15 = 5 m/s
Podemos concluir que a moto movimenta-se a 5 m/s em relação ao trem. Por meio da definição de velocidade média, e sabendo que o trem possui 100 m de comprimento, temos:
V = Δs ÷ Δt
5 = 100 ÷ Δt
Δt = 100 ÷ 5
Δt = 20 s.
Alternativa: C
41) Dois móveis movimentam-se de acordo com as seguintes funções horárias:
SA = 15 + 25.t
SB = 20 + 30.t
Marque a alternativa correta a respeito do movimento desses objetos:
(A) A velocidade relativa de aproximação dos móveis é de 5 m/s.
(B) Não há movimento relativo de aproximação ou afastamento dos móveis.
(C) O móvel A afasta-se de B com uma velocidade de 5 m/s
(D) O móvel B afasta-se de A com uma velocidade de 5 m/s.
(E) O movimento do móvel A é classificado como retrógrado.
Resolução:
A função horária utilizada foi: S = S0 + v.t, portanto, os valores 25 e 30 correspondem, respectivamente, às velocidades dos objetos A e B em m/s. As velocidades possuem o mesmo sinal, logo o movimento dos móveis ocorre no mesmo sentido, e a velocidade relativa entre os móveis será dada pela subtração das velocidades de cada um:
VREL = 30 – 25 = 5 m/s
O corpo B afasta-se de A com uma velocidade de 5 m/s.
Alternativa: D
42) Um ônibus e uma moto movimentam-se, no mesmo sentido, com velocidades de 20 m/s e 30 m/s, respectivamente. Sentado a uma das janelas do ônibus, um passageiro marca um tempo de 3 s para que a moto ultrapasse o ônibus. Determine o tamanho do ônibus.
(A) 30 m
(B) 25 m
(C) 15 m
(D) 10 m
(E) 12 m
Resolução:
Como o movimento dos móveis ocorre no mesmo sentido e a velocidade da moto é maior, podemos concluir que a velocidade relativa de aproximação será dada pela subtração das velocidades dos móveis.
VREL = 30 – 20 = 10 m/s
Pode-se concluir que a moto tem uma velocidade de 10 m/s em relação ao ônibus. Por meio da definição de velocidade média, podemos determinar o tamanho do ônibus:
V = Δs ÷ Δt
10 = Δs ÷ 3
Δs = 3 . 10 = 30 m
Alternativa: A








