PA & PG
Professor Diminoi

PROGRESSÃO ARITMÉTICA (PA)
A ideia de progressão está relacionada com avanço e sucessão. Na Matemática, caracterizamos a progressão como uma série numérica de quantidades, ou seja, que ocorre de forma sucessiva, uma após a outra. Ela sempre é estabelecida por uma lei de formação, que é uma fórmula matemática.
No Ensino Médio, estudamos dois tipos de progressão, a aritmética e a geométrica.
Progressão Aritmética
Na progressão aritmética (PA), cada termo a partir do segundo é determinado pela soma do anterior por uma constante chamada de razão. Para determinar os termos da sequência, aplica-se a seguinte fórmula:
an = a1 + (n – 1) . r
an = n-ésimo termo da sequência
a1 = primeiro termo
n = posição do termo na sequência
r = razão
Ainda em relação a PA, temos a fórmula que fornece a soma dos n primeiro termos, que é a seguinte:
Sn= n . (a1 + an)
2
Sn = soma dos n primeiros termos de uma PA
n = posição do termo na sequência
a1 = primeiro termo da sequência
an = n-ésimo termo da sequência
Soma dos N termos da PA.
Nessa progressão, também temos a fórmula da soma dos n primeiros termos, que é dada por:
Sn = a1 . (qn – 1)
q - 1
Sn = soma dos n primeiros termos de um PG
a1 = primeiro termo da sequência
q = razão
n = posição do termo na sequência
PROGRESSÃO GEOMÉTRICA (PG)
Já a progressão geométrica (PG) pode ser entendida como qualquer sequência de números em que, a partir do segundo termo, a sequência é dada por meio da multiplicação do termo anterior pela razão.
an = a1 . qn – 1
an = n-ésimo termo da sequência
a1 = primeiro termo da sequência
q = razão
n = posição do termo da sequência
Soma dos termos de uma P.G finita
Progressão geométrica finita é uma PG que tem um número determinado de elementos. Por exemplo, a seqüência (3,6,12,24,48) é uma PG de razão igual a q = 2.
A soma dos temos dessa PG será 3 + 6 + 12 + 24 + 48 = 93. Fazer essa soma é fácil, pois ela possui apenas cinco elementos, caso seja necessário somar os termos de uma PG com mais de dez elementos, o que é mais complicado, é preciso utilizar uma fórmula. Veja a sua demonstração:
Dada uma PG finita qualquer com n elemento, ou seja, com a quantidade de elementos indefinida. PG finita (a1, a2, a3, ... , an). A soma desses n elementos será feita da seguinte forma:
Sn = a1 + a2 + a3 + ... + an
Sabendo que;
a2 = a1 . q
a3 = a1 . q2
an = a1 . qn – 1
Podemos dizer que a soma dessa PG será:
Sn = a1 + a1 . q + a1 . q2 + a1 . q3 + ... + a1 . qn – 2 + a1 . qn – 1.
Como se trata de uma equação, se multiplicar um membro é preciso multiplicar o outro, por isso é necessário multiplicar os dois termos da última equação por q:
q . Sn = (a1 + a1 . q + a1 . q2 + a1 . q3 + ... + a1 . qn – 1)
q . Sn = a1 . q + a1 . q2 + a1 . q3 + a1 . q4 + ... + a1 . qn – 1 + a1 . qn
Fazendo a subtração:
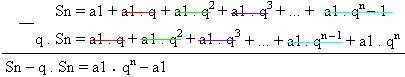
Colocando em evidência os termos semelhantes, temos:
q . Sn – q . Sn = a1 . qn – a1
Sn (q - 1) = a1 (qn – 1)
Isolando o termo Sn (soma dos elementos), iremos obter a seguinte fórmula:
Sn = a1 (qn – 1)
q - 1
Portanto, a fórmula para obter a soma dos n elementos de uma PG finita é:
Sn = a1 (qn 1)
q 1
Questões resolvidas:
01) Dê a soma dos termos da seguinte PG (7,14,28, ... , 3584).
Resolução:
Para utilizarmos a fórmula da soma é preciso saber quem é o 1º termo, a razão e a quantidade de elementos que essa PG possui.
a1 = 7
q = 2
n = ?
Sn = ?
Portanto, é preciso que encontremos a quantidade de elementos que possui essa PG, utilizando a fórmula do termo geral.
an = a1 . qn – 1
3584 = 7 . 2n – 1
3584 : 7 = 2n – 1
512 = 2n – 1
29 = 2n – 1
n – 1 = 9
n = 10
Sn = a1 (qn – 1)
q - 1
S10 = 7 (210 – 1)
2 – 1
S10 = 7 (1024 – 1)
2 – 1
S10 = 7 . 1023
S10 = 7161
02) Encontre o vigésimo termo da sequência (1, 3, 5, 7 . . .) e calcule a soma dos 20 primeiros termos.
Resolução:
a1 = 1
r = 2 → Para descobrir r, observe a progressão. O próximo número é sempre o anterior mais 2: 1 + 2 = 3; 3 + 2 = 5 …
n = 20
a20 = ?
an = a1 + (n – 1) . r
a20 = 1 + (20 – 1) . 2
a20 = 1 + (19) . 2
a20 = 1 + 38
a20 = 39
O vigésimo termo da sequência é o número 39.
Sn= n . ( a1 + an )
2
S20 = 20 . ( 1 + 39 )
2
S20 = 20 . ( 40)
2
S20 = 20 . 20
S20 = 400
Resposta: a soma dos vinte primeiros termos da sequência é 400.
03) Determine o sexto termo da progressão geométrica (2, 6, 18, 54...) e, em seguida, calcule a soma dos seis primeiros termos.
Resolução:
Para resolver esse exercício, devemos calcular a razão (q). Para isso, efetue as divisões:
6 = 3
2
18 = 3
6
54 = 3
18
Com isso, verificamos que a razão da PG é 3. Sabendo que a1 = 2 e n = 6, substitua os valores na fórmula:
a6 = a1 . qn – 1
a6 = 2 . ( 3)6 -1
a6 = 2 . (3)5
a6 = 2 . 243
a6 = 486
O sexto termo da PG é o número 486. Vamos agora calcular a soma dos seis primeiros termos da sequência.
Sn = a1 . (qn - 1)
q – 1
Sn = 2 . (36 - 1)
3 – 1
Sn = 2 . (729 - 1)
3 – 1
Sn = 2 . (728)
2
Sn = 1456
2
Sn = 728
Resposta: a soma dos seis primeiros termos da progressão geométrica é igual a 728.
04) Calcule o 10° termo da P.A.: (26, 31, 36, 41, ...)
Resolução:
Primeiro, devemos identificar que a1 = 26, r = 31 - 26 = 5 e n = 10 (10º termo). Substituindo esses valores na fórmula do termo geral, temos:
an = a1 + (n - 1) . r
a10 = 26 + (10-1) . 5
a10 = 26 + 9 .5
a10 = 71
Resposta: o décimo termo da progressão aritmética indicada é igual a 71.
05) Encontre o termo geral da progressão aritmética (PA) abaixo:
A = (3, 7, ...)
Resolução:
Apesar de a sequência apresentar apenas dois elementos, já podemos destacar dois termos importantes. Temos o primeiro elemento (a1 = 3) e ainda a razão, que é dada pela diferença de um termo pelo termo imediatamente anterior. Portanto, a razão r é dada por r = 7 – 3 = 4. Dessa forma, é possível determinar a fórmula de seu termo geral:
an = a1 + (n – 1).r
an = 3 + (n – 1).4
an = 3 + 4n – 4
an = 4n – 1
Resposta: o termo geral da PA (3, 7, …) é an = 4n – 1.
06) A soma dos 20 termos de uma PA é 500. Se o primeiro termo dessa PA é 5, qual é a razão r dessa PA?
Resolução:
As informações das quais dispomos são que n = 20, Sn = 500 e a1 = 5. Vamos utilizar a fórmula da soma dos termos de uma progressão aritmética para encontrar o último termo dessa sequência:
Sn = (a1 + an).n
2
500 = (5 + a20).20
2
500.2= (5 + a20).20
1000 = 100 + 20.a20
1000 – 100 = 20.a20
900 = 20.a20
a20 = 900
20
a20 = 45
Vamos agora utilizar a fórmula do termo geral para encontrar o valor da razão r:
an = a1 + (n – 1).r
45 = 5 + (20 – 1).r
45 – 5 = 19.r
r = 40 ≈ 2
19
Resposta: a razão dessa PA é de aproximadamente 2 cm.
07) (UF – CE) A soma dos 15 primeiros termos de uma progressão aritmética é 150. O 8° termo dessa PA é:
(A) 10
(B) 15
(C) 20
(D) 25
(E) 30
Resolução:
Se a soma dos 15 primeiros termos é 150, na fórmula da soma de uma PA, teremos que Sn = 150 e n = 15. Logo:
Sn = (a1 + an).n
2
150 = (a1 + a15).15
2
300 = (a1 + a15).15
300 = a1 + a15
15
a1 + a15 = 20
Nesse exercício, não temos determinada a razão da progressão aritmética. Portanto, utilizaremos uma ideia que pode facilmente ser demonstrada em uma progressão aritmética qualquer. Um elemento da sequência é igual à média aritmética do elemento que o antecede e do elemento que o sucede. Por exemplo, dada a progressão aritmética An = (a1, a2, …, an-1, an, an+1), temos que:
An = an-1 + an-2
2
Sendo assim, podemos dizer que:
A8 = a7 + a9
2
Além disso, em uma progressão aritmética, a soma dos termos equidistantes é igual. Para esse exercício, temos a sequência:
An = (a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11, a12, a13, a14, a15)
a1 + a15 = a2 + a14 = a3 + a13 = … = a7 + a9
Retornando às equações anteriores, podemos então reescrever o termo A8, substituindo a soma “a7 + a9” por “a1 + a15”, que é equivalente, portanto:
A8 = a1 + a15
2
A8 = 20
2
A8 = 10
Alternativa: A
08) (Osec – SP) Um jardim tem uma torneira e dez roseiras dispostas em linha reta. A torneira dista 50 m da primeira roseira e cada roseira dista 2 m da seguinte. Um jardineiro, para regar as roseiras, enche um balde na torneira e despeja seu conteúdo na primeira. Volta à torneira e repete a operação para cada roseira seguinte. Após regar a última roseira e voltar à torneira para deixar o balde, ele terá andado:
(A) 1200 m.
(B) 1180 m.
(C) 1130 m.
(D) 1110 m.
(E) 1000 m.
Resolução:
Para regar a primeira roseira, o jardineiro está próximo à torneira e precisa andar 50 m para chegar à roseira e outros 50 m para retornar à torneira, andando nesse primeiro momento 100 metros.
Novamente, o jardineiro sairá de próximo da torneira e andará 50 m até a primeira roseira e mais dois metros até a segunda roseira para então retornar, andando assim outros 52 metros de volta, o que totaliza 104 metros de caminhada.
Para regar a terceira roseira, o jardineiro fará o mesmo percurso que acabara de fazer com o acréscimo de dois metros na ida e dois metros na volta, em decorrência da distância entre a segunda e a terceira roseira, totalizando 108 metros de percurso.
O trajeto percorrido pelo jardineiro pode ser considerado uma progressão aritmética de razão 4, observe:
A10 = (100, 104, 108, …, a10)
Vamos identificar o último termo dessa sequência, que corresponde ao trajeto do jardineiro ao regar a décima roseira. Utilizaremos a fórmula do termo geral para encontrar o a10.
an = a1 + (n – 1).r
a10 = a1 + (10 – 1).r
a10 = 100 + 9.r
a10 = 100 + 9.4
a10 = 100 + 36
a10 = 136
Se queremos saber o percurso total percorrido pelo jardineiro, podemos calcular a soma dos termos dessa progressão aritmética:
S10 = (a1 + a10).10
2
S10 = (100 + 136).10
2
S10 = 236.5
S10 = 1180
Alternativa: B
09) (Vunesp) Várias tábuas iguais estão em uma madeireira. A espessura de cada tábua é 0,5 cm. Forma-se uma pilha de tábuas colocando-se uma tábua na primeira vez e, em cada uma das vezes seguintes, tantas quantas já estejam na pilha.

a) Se nós organizarmos a quantidade de madeiras em cada pilha, teremos formada uma progressão geométrica (1, 2, 4,...). Vamos identificar a razão dessa PG:
Resolução:
q = a2
a1
q = 2/1
q = 2
Agora que já identificamos que a razão da PG é 2, podemos utilizar a fórmula do termo geral para saber quantas tábuas haverá na nona pilha:
an = a1.qn – 1
a9 = a1.q8
a9 = 1 . 28
a9 = 256
Resposta: a nona pilha será composta por 256 tábuas.
b) a altura, em metros, da pilha.
Resolução:
Se cada tábua possui 0,5 cm de espessura, basta multiplicar esse valor pela quantidade de tábuas da nona pilha. Portanto, 0,5 . 256 = 128 cm ou 1,28 m.
09) Determine a soma dos 10 primeiros termos da PG (1, 3, 9, 27).
Resolução:
Identificando a razão q dessa PG:
q = a2
a1
q = 3
1
q = 3
Identificada a razão q = 3, vamos utilizar a fórmula da soma dos n primeiros termos:
Sn = a1(qn – 1)
q – 1
S10 = 1(310 – 1)
3 – 1
Sn = 59049 – 1
3 – 1
Sn = 59048
2
10) (FUVEST/01) Uma progressão aritmética e uma progressão geométrica têm, ambas, o primeiro termo igual a 4, sendo que os seus terceiros termos são estritamente positivos e coincidem. Sabe-se ainda que o segundo termo da progressão aritmética excede o segundo termo da progressão geométrica em 2. Então, o terceiro termo das progressões é:
(A) 10
(B) 12
(C) 14
(D) 16
(E) 18
Resolução:
Sejam (a1, a2, a3, …) a PA de razão r e (g1, g2, g3, …) a PG de razão q. Temos como condições iniciais:
(1) a1 = g1 = 4
(2) a3 > 0, g3 > 0 e a3 = g3
(3) a2 = g2 + 2
Reescrevendo (2) e (3) utilizando as fórmulas gerais dos termos de uma PA e de uma PG e (1) obtemos o seguinte sistema de equações:
(4)
a3 = a1 + 2r
e
g3 = g1.q2
4 + 2r = 4q2
(5)
a2 = a1 + r e g2
g1.q
4 + r = 4q + 2
Expressando, a partir da equação (5), o valor de r em função de q e substituindo r em (4) vem:
(5)
r = 4q + 2 – 4
r = 4q – 2
(4) => 4 + 2(4q – 2) = 4q2
4 + 8q – 4 = 4q2
4q2 – 8q = 0
q(4q – 8) = 0
q = 0 ou 4q – 8 = 0 > q = 2
Como g3 > 0, q não pode ser zero e então q = 2. Para obter r basta substituir q na equação (5):
r = 4q – 2
r = 8 – 2
r = 6
Para concluir calculamos a3 e g3:
a3 = a1 + 2r
a3 = 4 + 12 = 16
g3 = g1.q2
g3 = 4.4 = 16
Alternativa: D
11) (ITA/2000) O valor de n que torna a sequência (2 + 3n; –5n; 1 – 4n) uma progressão aritmética pertence ao intervalo:
(A) [– 2, –1]
(B) [– 1, 0]
(C) [0, 1]
(D) [1, 2]
(E) [2, 3]
Resolução:
Para que a sequência se torne uma PA de razão r é necessário que seus três termos satisfaçam as igualdades (aplicação da definição de PA):
(1) -5n = 2 + 3n + r
(2) 1 – 4n = -5n + r
Determinando o valor de r em (1) e substituindo em (2):
(1)
r = 5n – 2 – 3n = -8n – 2
(2)
1 – 4n = -5n – 8n – 2
1 – 4n = -13n – 2
13n – 4n = -2 – 1
9n = -3
n = -3/9 = -1/3
Ou seja,
-1 < n < 0
Alternativa: B
12) (PUC-SP/2003) Os termos da sequência (10; 8; 11; 9; 12; 10; 13; …) obedecem a uma lei de formação. Se an, em que n pertence a N*, é o termo de ordem n dessa sequência, então a30 + a55 é igual a:
(A) 58
(B) 59
(C) 60
(D) 61
(E) 62
Resolução:
Primeiro, observe que os termos ímpares da sequência é uma PA de razão 1 e primeiro termo 10 – (10; 11; 12; 13; …). Da mesma forma os termos pares é uma PA de razão 1 e primeiro termo igual a 8 – (8; 9; 10; 11; …) . Assim, as duas PA têm como termo geral o seguinte formato:
(1) ai = a1 + (i – 1).1 = a1 + i – 1
Para determinar a30 + a55 precisamos estabelecer a regra geral de formação da sequência, que está intrinsicamente relacionada às duas progressões da seguinte forma:
Se n (índice da sucessão) é impar temos que n = 2i – 1, ou seja, i = (n + 1)/2;
se n é par temos n = 2i ou i = n/2.
Daqui e de (1) obtemos que:
an = 10 + [(n + 1)/2] – 1 se n é ímpar
an = 8 + (n/2) – 1 se n é par
Logo:
a30 = 8 + (30/2) – 1 = 8 + 15 – 1 = 22
e
a55 = 10 + [(55 + 1)/2] – 1 = 37
E portanto:
a30 + a55 = 22 + 37 = 59
13) (UFLA/99) A soma dos elementos da sequência numérica infinita (3; 0,9; 0,09; 0,009; …) é:
(A) 3,1
(B) 3,9
(C) 3,99
(D) 3,999
(E) 4
Resolução:
Sejam S a soma dos elementos da sequência e S1 a soma da PG infinita (0,9; 0,09; 0,009; …) de razão q = 10-1 = 0,1. Assim:
S = 3 + S1
Como -1 < q < 1 podemos aplicar a fórmula da soma de uma PG infinita para obter S1:
S1 = 0,9/(1 – 0,1)
0,9/0,9 = 1
S = 3 + 1
S = 4
Alternativa: E
14) (STA. CASA) A soma dos vinte primeiros termos de uma progressão aritmética é -15. A soma do sexto termo dessa P.A., com o décimo quinto termo, vale:
(A) 3,0
(B) 1,0
(C) 1,5
(D) -1,5
(E) -3,0
Resolução:
Aplicando a fórmula da soma dos 20 primeiros termos da PA:
S20 = 20( a1 + a20)/2 = -15
Na PA finita de 20 termos, o sexto e o décimo quinto são equidistantes dos extremos, uma vez que:
15 + 6 = 20 + 1 = 21
E, portanto:
a6 + a15 = a1 + a20
Substituindo este valor na primeira igualdade vem:
20(a6 + a15) / 2 = -15
10(a6 + a15) = -15
a6 + a15 = -15/10
-1,5
Alternativa: B
15) (MACK) O sexto termo de uma PG, na qual dois meios geométricos estão inseridos entre 3 e -24, tomados nessa ordem, é:
(A) -48
(B) -96
(C) 48
(D) 96
(E) 192
Resolução:
Para determinar os dois meios geométricos da PG cujos extremos são 3 e -24 precisamos calcular, primeiro, sua razão q, com n = 4. Pela fórmula do termo geral temos que:
a4 = a1.q4-1
-24 = 3q3
q3 = -24/3 = -8
q = -2
Logo a PG é (3; -6; 12; -24; …) e seu sexto termo é obtido, também, através da fórmula do termo geral:
a6 = a1q6-1
a6 = 3(-2)5
-3.32 = -96
Alternativa: B
16) (ENEM) Uma professora realizou uma atividade com seus alunos utilizando canudos de refrigerante para montar figuras, onde cada lado foi representado por um canudo. A quantidade de canudos (C) de cada figura depende da quantidade de quadrados (Q) que formam cada figura. A estrutura de formação das figuras está representada a seguir:

 Que expressão fornece a quantidade de canudos em função da quantidade de quadrados de cada figura?
Que expressão fornece a quantidade de canudos em função da quantidade de quadrados de cada figura?
(A) C = 4Q.
(B) C = 3Q + 1.
(C) C = 4Q – 1
(D) C = Q + 3.
(E) C = 4Q – 2.
Resolução:
Para formar um quadrado, é necessário utilizar quatro canudos. Para formar dois quadrados, sete canudos e, para formar três quadrados, 10 canudos. Vejamos na tabela a seguir a distribuição dos canudos em relação à quantidade de quadrados:
N° de quadrados (Q) Quantidade de Canudos (C)
1 4
2 7
3 10
Os números que identificam a quantidade de canudos descrevem uma progressão aritmética de razão 3. Utilizaremos aqui a fórmula do termo geral, que nos ajudará a caminhar para a solução. Vamos identificar o n-ésimo termo da PA (4, 7, 10):
an = a1 + (n – 1).r
an = 4 + (n – 1).3
Mas de acordo com o problema, podemos reescrever essa fórmula. Considerando que Q representa as posições n da progressão e C representa cada termo an da PA, temos:
C = 4 + (Q – 1).3
C = 4 + 3Q – 3
C = 3Q + 1
Alternativa: B
17) (ENEM) As projeções para a produção de arroz no período de 2012-2021, em uma determinada região produtora, apontam para uma perspectiva de crescimento constante da produção anual. O quadro apresenta a quantidade de arroz, em toneladas, que será produzida nos primeiros anos desse período, de acordo com essa projeção.
Ano Projeto da Produção (t)
2012 50,25
2013 51,50
2014 52,75
2015 54,00
A quantidade total de arroz, em toneladas, que deverá ser produzida no período de 2012 a 2021 será de
(A) 497,25.
(B) 500,85.
(C) 502,87.
(D) 558,75.
(E) 563,25.
Resolução:
Através do quadro, podemos identificar uma progressão aritmética formada pelos números que compõem a coluna “Projeto da Produção (t)”. O a1 = 50,25 e o a2 = 51,50, sendo que o a1 refere-se ao ano de 2012, o a2, ao ano de 2013 e assim por diante. Precisamos identificar o 10° termo, aquele que se refere ao ano de 2021. Vamos procurar a razão (r) dessa PA:
r = a2 – a1
r = 51,50 – 50,25
r = 1,25
Agora que conhecemos a razão, vamos identificar o termo a10 através da fórmula do termo geral:
an = a1 + (n – 1).r
a10 = 50,25 + (10 – 1).1,25
a10 = 50,25 + 9.1,25
a10 = 50,25 + 11,25
a10 = 61,50
Identificado que o a10 é 61,50, podemos utilizar a fórmula da soma dos termos de uma PA finita para saber a produção total do período 2012 – 2021:
Sn = (a1 + an).n
2
S10 = (50,25 + 61,50).10
2
S10 = 111,75.10
2
S10 = 1117,5
2
S10 = 558,75
Alternativa: D
18) (ENEM) Jogar baralho é uma atividade que estimula o raciocínio. Um jogo tradicional é a Paciência, que utiliza 52 cartas. Inicialmente são formadas sete colunas com as cartas. A primeira coluna tem uma carta, a segunda tem duas cartas, a terceira tem três cartas, a quarta tem quatro cartas, e assim sucessivamente até a sétima coluna, a qual tem sete cartas, e o que sobra forma o monte, que são as cartas não utilizadas nas colunas. A quantidade de cartas que forma o monte é
(A) 21
(B) 24
(C) 26
(D) 28
(E) 31.
Resolução:
Para resolver essa questão, vamos identificar a progressão arimética que nos é dada no problema. Podemos considerar que cada coluna corresponde a um termo da sequência numérica, portanto, o primeiro termo é 1 (a1 = 1), o segundo é 2 (a2 = 2), o terceiro termo é 3 (a3 = 3) e assim sucessivamente até o sétimo e último termo da sequência numérica (a7 = 7). Sabemos que a progressão possui sete elementos (n = 7) e temos conhecidos o primeiro e o último termo, logo, podemos usar a fórmula da soma dos elementos de uma PA:
Não pare agora... Tem mais depois da publicidade ;)
Sn = (a1 + an). n
2
S7 = (a1 + a7). 7
2
S7 = (1 + 7). 7
2
S7 = (1 + 7). 7
2
S7 = 8 . 7
2
S7 = 56
2
S7 = 28
Então há 28 cartas distribuídas nas fileiras. Como no baralho há 52 cartas, fazendo 52 – 28 = 24, descobrimos que há 24 cartas no monte.
Alternativa: B
19) (ENEM) O número mensal de passagens de uma determinada empresa aérea aumentou no ano passado nas seguintes condições: em janeiro foram vendidas 33.000 passagens; em fevereiro, 34.500; em março, 36.000. Esse padrão de crescimento se mantém para os meses subsequentes. Quantas passagens foram vendidas por essa empresa em julho do ano passado?
(A) 38.000
(B) 40.500
(C) 41.000
(D) 42.000
(E) 48.000
Resolução:
Se considerarmos as quantidades de passagens vendidas como elementos de uma sequência numérica, podemos escrevê-los como:
janeiro: a1 = 33.000
fevereiro: a2 = 34.500
março: a3 = 36.000
Se fizermos a diferença entre os termos subsequentes, teremos a3 – a2 = 1.500, e a2 – a1 = 1500. Podemos então afirmar que essa é uma progressão arimética de razão 1500. Como consideramos que cada mês corresponde a um elemento da progressão aritmética e partindo da ideia de que janeiro corresponde ao primeiro elemento, podemos dizer que julho seria representado pelo termo a7. Sendo assim, podemos identificar o sétimo elemento da sequência numérica através da fórmula:
an = a1 + (n - 1) . r
a7 = 33.000 + (7 - 1) . 1.500
a7 = 33.000 + 6 . 1.500
a7 = 33.000 + 9.000
a7 = 42.000
Portanto, foram vendidas 42.000 passagens em julho.
Alternativa: D
Continua...









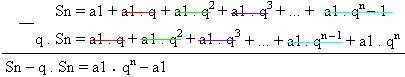


 Que expressão fornece a quantidade de canudos em função da quantidade de quadrados de cada figura?
Que expressão fornece a quantidade de canudos em função da quantidade de quadrados de cada figura?