POLINÔMIOS E PRODUTAS NOTÁVEIS

POLINÔMIOS E PRODUTAS NOTÁVEIS

Professor Diminoi

EXPRESSÕES ALGÉBRICAS
As expressões algébricas são aquelas expressões matemáticas que possuem números e letras, também conhecidas como variáveis. Utilizamos as letras para representar valores desconhecidos ou até mesmo para analisar o comportamento da expressão de acordo com o valor dessa variável.
As expressões algébricas são bastante comuns no estudo das equações e na escrita de fórmulas da Matemática e áreas afins. Caso a expressão algébrica possua um único termo algébrico, ela é conhecida como monômio; quando possui mais de um, é chamada de polinômio. É possível também calcular operações algébricas, que são as operações entre expressões algébricas.

POLINÔMIOS
Os polinômios são expressões algébricas formadas por números (coeficientes) e letras (partes literais). As letras de um polinômio representam os valores desconhecidos da expressão.
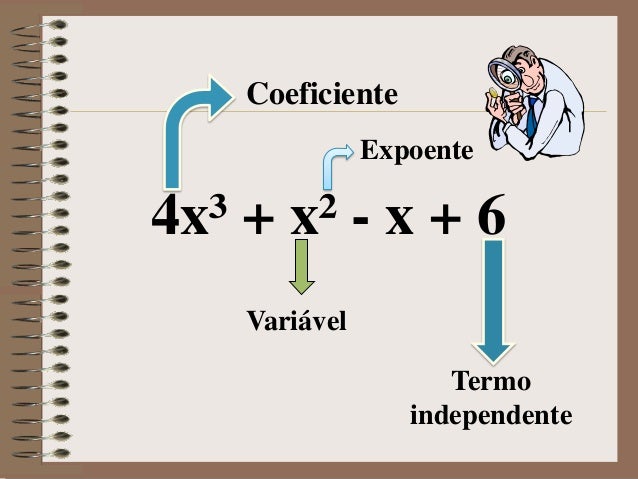
Exemplos:
a) 3ab + 5
b) x³+ 4xy - 2x²y³
c) 25x²- 9y²

Monômio, Binômino e Trinômio
Os polinômios são formados por termos. A única operação entre os elementos de um termo é a multiplicação. Quando um polinômio possui apenas um termo, ele é chamado de Monômio.

Exemplos:
a) 3x
b) 5abc
c) x²y³z⁴

Os chamados Binômios são polinômios que possuem somente dois monômios (dois termos), separados por uma operação de soma ou subtração.

Exemplos:
a) a²- b²
b) 3x + y
c) 5ab + 3cd²

Já os Trinômios são polinômios que possuem três monômios (três termos), separados por operações de soma ou subtração.

Exemplos:
a) x²+ 3x + 7

b) 3ab - 4xy - 10y

c) m³n + m²+ n⁴

Grau dos Polinômios
O grau de um monômio é a soma dos expoentes da sua parte literal;
9x⁵ possui apenas um expoente, então o monômio é do 5º grau.
8x² y⁴ possui dois expoentes, então devemos somá-los 2 + 4 = 6, portanto esse polinômio é de 6º grau.
19abc possui três expoentes, devemos somá-los 1 + 1 + 1 = 3, portanto esse polinômio é de 3º grau.

Observação: Num polinômio que possui mais de 2 monômios, para encontrarmos o seu grau é preciso observar se ele está com os termos semelhantes reduzidos se estiver escrito na forma reduzida, o grau que ele irá assumir é o do monômio que tiver o grau maior.

5x⁴+ 3x²– 5 está escrito na forma reduzida e o monômio de maior grau é o 5x⁴, então o polinômio será do 4º grau.
x² + 4x – x² + 10, possui termo semelhante (x2), então a sua forma reduzida ficará
4x + 10, o monômio de maior grau é 4x, portanto o grau do polinômio será de 1º grau.

Observação: o polinômio nulo é aquele que possui todos os coeficientes iguais a zero. Quando isso ocorre, o grau do polinômio não é definido.

Adição de Polinômios
Fazemos essa operação somando os coeficientes dos termos semelhantes (mesma parte literal).
(- 7x³ + 5 x²y - xy + 4y) + (- 2x²y + 8xy - 7y)
- 7x³+ 5x²y - 2x²y - xy + 8xy + 4y - 7y
- 7x³ + 3x²y + 7xy - 3y

Subtração de Polinômios
O sinal de menos na frente dos parênteses inverte os sinais de dentro dos parênteses. Após eliminar os parênteses, devemos juntar os termos semelhantes.
(4x² - 5xk + 6k) - (3x - 8k)
4x² - 5xk + 6k - 3xk + 8k
4x²- 8xk + 14k

Multiplicação de Polinômios
Na multiplicação devemos multiplicar termo a termo. Na multiplicação de letras iguais, repete-se e soma-se os expoentes.
(3x² - 5x + 8) . (-2x + 1)
-6x³ + 3x² + 10x² - 5x - 16x + 8
-6x³ + 13x² - 21x +8

Divisão de Polinômios

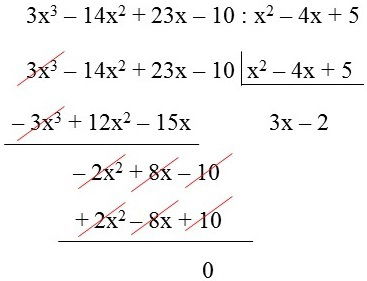
Observação: Na divisão de polinômios utilizamos o método chave. Primeiramente realizamos a divisão entre os coeficientes numéricos e depois a divisão de potências de mesma base. Para isso, conserva-se a base e subtraia os expoentes.

Fatoração de Polinômios

Fator Comum em Evidência
ax + bx = x (a + b)
Exemplo:
4x + 20 = 4 (x + 5)

Agrupamento
ax + bx + ay + by
x . (a + b) + y . (a + b)
(x + y) . (a + b)

Exemplo:
8ax + bx + 8ay + by
x (8a + b) + y (8a + b)
(8a + b) . (x + y)

Trinômio Quadrado Perfeito (Adição)
a² + 2ab + b² = (a + b)²

Exemplo:
x² + 6x + 9 = (x + 3)²

Trinômio Quadrado Perfeito (Diferença)
a² - 2ab + b² = (a - b)²

Exemplo:
x² - 2x + 1 = (x - 1)²

Diferença de Dois Quadrados
(a + b) . (a - b) = a² - b²

Exemplo:
x² - 25
(x + 5) . (x - 5)

Cubo Perfeito (Adição)
a³ + 3a²b + 3ab² + b³ = (a + b)³

Exemplo:
x³ + 6x² + 12x + 8
x³ + 3 . x² . 2 + 3 . x . 2² + 2³
(x + 2)³

Cubo Perfeito (Diferença)
a³ - 3a²b + 3ab² - b³ = (a - b)³

Exemplo:
y³ - 9y² + 27y - 27
y³ - 3 . y² . 3 + 3 . y . 3² - 3³
(y - 3)³

PRODUTUDOS NOTÁVEIS
Os produtos notáveis são expressões algébricas utilizadas em muitos cálculos matemáticos, por exemplo, nas equações de primeiro e de segundo grau.
O termo "notável" refere-se à importância e notabilidade desses conceitos para a área da matemática.
Revisão de conceitos básicos:
- Quadrado: elevado a dois
- Cubo: elevado a três
- Diferença: subtração
- Produto: multiplicação

Existem cinco propriedades dos produtos notáveis mais relevantes:
(a + b)² → quadrado da soma de dois termos
(a – b)² → quadrado da diferença de dois termos
(a + b) . (a – b) → produto da soma pela diferença de dois termos
(a + b)³ → cubo da soma de dois termos
(a – b)³ → cubo da diferença de dois termos

Quadrado da Soma de Dois Termos: (a + b)²

O quadrado da soma dos dois termos é representado pela seguinte expressão:
(a + b)² = a² + 2ab + b²

Assim, o quadrado do primeiro termo é somado ao dobro do primeiro termo pelo segundo termo, e por fim, somado ao quadrado do segundo termo.

Os produtos entre polinômios conhecidos como quadrados da soma são os do tipo:
(x + a)² = x² + 2xa + a²

Quadrado do primeiro termo mais duas vezes o primeiro vezes o segundo mais o quadrado do segundo termo

Exemplo:
(x + 7)²
x² + 2x7 + 49
x² + 14x + 49

Quadrado da diferença de dois termos: (a – b)²
(a – b)² = a² - 2ab + b²
Logo, o quadrado do primeiro termo é subtraído ao dobro do produto do primeiro termo pelo segundo termo e, por fim, somado ao quadrado do segundo termo.
(x – a)²
x² – 2xa + a²
Quadrado do primeiro termo menos duas vezes o primeiro vezes o segundo mais o quadrado do segundo termo.

Produto da soma pela diferença de dois termos: ( a + b) . (a – b)
a² - b² = (a + b) . (a – b)

Nota-se que ao aplicar a propriedade distributiva da multiplicação, o resultado da expressão é a subtração do quadrado do primeiro e do segundo termo.

Exemplo:
(x + a)(x – a)
x² – a²

Exemplo:
(xy + 4)(xy – 4)
(xy)² – 16²

Quadrado do primeiro termo menos o quadrado do segundo termo.

Cubo da soma de dois termos: (a + b)³
O cubo da soma de dois termos é representado pela seguinte expressão:
(a + b)³ = (a + b) . (a + b) . (a + b)

Logo, ao aplicar a propriedade distributiva temos:
a³ + 3a²b + 3ab² + b³

Dessa forma, o cubo do primeiro termo é somado ao triplo do produto do quadrado do primeiro termo pelo segundo termo e o triplo do produto do primeiro termo pelo quadrado do segundo termo. Por fim, ele é somado ao cubo do segundo termo.
Com a propriedade distributiva, é possível criar uma “fórmula” também para produtos com o seguinte formato:
(x + a)(x + a)(x + a)

Na notação de potência, ele é escrito da seguinte maneira:
(x + a)³

Exemplo:
(x + a)³
x³ + 3x²a + 3xa² + a³

Assim, em vez de fazer um cálculo extenso e cansativo, podemos calcular (x + 5)³, por exemplo, facilmente da seguinte maneira:
(x + 5)³
x³ + 3x²5 + 3x5² + 5³
x³ + 15x² + 75x + 125

Cubo da diferença de dois termos: (a – b)³
O cubo da diferença de dois termos é representado pela seguinte expressão:
(a – b)³ = (a – b) . (a – b) . (a – b)

Logo, ao aplicar a propriedade distributiva temos:
a³ - 3a²b + 3ab² - b³

Assim, o cubo do primeiro termo é subtraído ao triplo do produto do quadrado do primeiro termo pelo segundo termo. Por conseguinte, ele é somado ao triplo do produto do primeiro termo pelo quadrado do segundo termo. E, por fim, é subtraído ao cubo do segundo termo.
Exemplo:
(x – a)(x – a)(x – a)

Por meio da propriedade distributiva e simplificando os resultados, encontraremos o seguinte resultado para esse produto:
(x – a)³
x³ – 3x²a + 3xa² – a³

Exemplo:
(x – 2y)³
x³ – 3x²2y + 3x(2y)² – (2y)³
x³ – 3x²2y + 3x4y² – 8y³
x³ – 6x²y + 12xy² – 8y³

QUESTÕES RESOLVIDAS
01) Dada a expressão x³ + 4x² + 3x – 5, qual é o valor numérico da expressão quando x = 2. Para calcular o valor da expressão, vamos substituir o x por 2.
(A) 10
(B) 15
(C) 20
(D) 25
Resolução:
2³ + 4 · 2² + 3 · 2 – 5
8 + 4 · 4 + 6 – 5
8 + 16 + 6 – 5
30 – 5
25
Alternativa: D

02) Calcule o polinômio (x + 7)²
(A) x² + 14x² + 49
(B) x² + 14 + 49
(C) x + 14x + 49
(D) x² + 14x + 49
Resolução:
(x + 7)²
x² + 2x7 + 49
x² + 14x + 49
Alternativa: D

03) Calcule o polinômio (x + 7)²
(A) x² + 14x + 49
(B) -x² + 14x + 49
(C) x² + 14x + 9
(D) x²+ x² + 49
Resolução:
(x + 7)²
x² + 2x7 + 49
x² + 14x + 49
Alternativa: A

04) Efetuando a multiplicação do polinômio (3x² – 5x + 8) . (-2x + 1) temos:
(A) 6x³ + 13x² – 21x + 8
(B) – 6x³ + 13x² – 21x + 8
(C) – 6x³ + 13x2 – 21x -8
(D) – 6x² + 13x² – 21x + 8
Resolução:
(3x² – 5x + 8) . (-2x + 1)
– 6x³ + 3x² + 10x² – 5x – 16x + 8
– 6x³ + 13x² – 21x +8
Alternativa: B

05) Efetuando a multiplicação do polinômio (2x + a) . (2x -4a) temos:
(A) 4x – 6xa – 4a²
(B) - 4x² – 6xa – 4a²
(C) 4x² – 6xa – 4a²
(D) 4x² – 6xa – 4a
Resolução:
(2x + a) . (2x -4a)
2x . 2x – 2x . 4a + a . 2x – a . 4a
4x² – 6xa – 4a²
Alternativa: C

06) A expressão algébrica que representa o perímetro do retângulo a seguir é: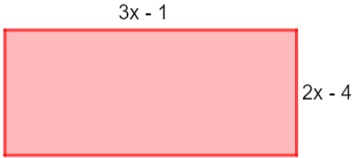
(A) 5x – 5
(B) 10x – 10
(C) 5x + 5
(D) 8x – 6
(E) 3x – 2
Resolução:
Para calcular o perímetro, vamos somar os quatro lados. Sabendo que os lados paralelos são iguais, temos que:
P = 2(2x – 4) + 2 (3x – 1)
P = 4x – 8 + 6x – 2
P = 10x – 10
Alternativa: B

07) A respeito dos produtos notáveis, assinale a alternativa correta.
(A) (x + a)² = x² + a²
(B) (x + a)² = x² + xa + a²
(C) (x – a)² = x² – a²
(D) (x – a)² = x² – 2x – a²
(E) (x – a)² = x² – 2x + a²
Resolução:
Os três casos mais comuns de produtos notáveis são:
(x + a)² = x² + 2ax + a²
(x – a)² = x² – 2ax + a²
e x² – a² = x² – a²
A alternativa correta é aquela que representa um desses três casos.
Alternativa: E

08) (IMNEC) A diferença entre o quadrado da soma e o quadrado da diferença entre dois números reais é igual a:
(A) a diferença dos quadrados dos dois números.
(B) a soma dos quadrados dos dois números.
(C) a diferença dos dois números.
(D) ao dobro do produto dos números.
(E) ao quádruplo do produto dos números.
Resolução:
Sejam x e y os dois números em questão, a diferença entre o quadrado da soma e o quadrado da diferença desses dois números, bem como a simplificação desse cálculo, é:
(x + y)² – (x – y)²
x² + 2xy + y² – (x² – 2xy + y²)
x² + 2xy + y² – x² + 2xy – y²
2xy + 2xy
4xy
Esse resultado pode ser lido como “o quádruplo do produto dos números”.
Alternativa: E

09) Seja x² + y² = 60. Qual é o valor positivo de x + y, sabendo que xy = 20?
(A) 5
(B) 10
(C) 15
(D) 20
Resolução:
Primeiramente, observe que:
xy = 20
2xy = 2·20
2xy = 40
Somando 40 em ambos os lados da equação e substituindo 40 por 2xy no primeiro membro, teremos:
x² + y² = 60
x² + y² + 40 = 60 + 40
x² + y² + 2xy = 100
Observe que, agora, o primeiro membro é um produto notável que pode ser reescrito da seguinte maneira:
x² + y² + 2xy = 100
(x + y)² = 100
Fazendo a raiz quadrada em ambos os membros, teremos:
√(x + y)² = √100
x + y = 10 ou
x + y = – 10
Alternativa: B

10) O resultado y²x² – 4a² é obtido por meio de qual dos produtos notáveis abaixo?
(A) (yx + 2a)(yx – 2a)
(B) (yx + 2a)(yx + 2a)
(C) (x + a)(y – 2)
(D) (y + a)(x + 2)
(E) (yx + 2a)²
Resolução:
Fazendo o caminho inverso, da fatoração de polinômios, poderemos descobrir qual é o produto notável que gerou a expressão acima. A diferença de dois quadrados sempre é resultado do produto da soma pela diferença. O primeiro termo desse produto é a raiz do primeiro termo da expressão do exercício. O segundo termo é a raiz do segundo elemento da expressão do exercício, por isso, teremos:
y²x² – 4a² = (yx + 2a)(yx – 2a)
Alternativa: A

11) (3x + y)²
(3x + y)²
(3x)² + 2.3x.y + y²
9x² + 6xy + y²

12) (2x + 3y)³
(2x + 3y)³
(2x)³ + 3.(2x)².3y + 3.2x.(3y)² + (3y)³
8x³ + 36x²y + 54xy² + 27y³

13) (5 + x)²
(5 + x)²
5² + 2.5.x + x²
25 + 10x + x²

14) Realize o produto entre (√5 – 2).(√5 + 2)
Resolução:
(√5 – 2).(√5 + 2)
√5.√5 + √5 . 2 – 2 . √5 – 2 . 2
√(5.5) + 2√5 – 2√5 – 4
√25 – 4
5 – 4
1

15) Desenvolva o polinômio: (x + 3)²
Resolução:
(x + 3)²
x² + 2 . 3x + 3²
x² + 6x + 9

Simplifique as expressões:
16) (x + y)² – x² – y²
Resolução:
(x + y)² – x² – y²
x² + 2xy + y² – x² – y²
2xy

17) (x – y)² – (x + y)²
Resolução:
Primeiramente:
(x – y)²
x² – 2xy + y²
(x + y)²
x² + 2xy + y²
Assim,
(x – y)² – (x + y)²
x² – 2xy + y² – (x² + 2xy + y²)
x² – 2xy + y² – x² – 2xy – y²
x² – x² – 2xy – 2xy + y² – y²
-2xy – 2xy
-4xy

Efetue as multiplicações:
18) (x – 2) . (x – 5)
Resolução:
(x – 2).(x-5)
xx + x(-5) + (-2)x + (-2).(-5)
x² + ((-2) + (-5))x + (-2).(-5)
x² – 7x + 10

19) (x + 15) . (x – 4)
Resolução:
(x + 15)(x – 4)
xx + x(-4) + 15x + 15(-4)
x² + (15 + (-4))x + 15.(-4)
x² + 11x – 60

20) Encontre o quadrado da soma de (x + 7)²
Resolução:
(x + 7)²
x² + 2x7 + 49
x² + 14x + 49

21) Encontre o quadrado da diferença de (x – a)²
^Resolução:
^{(x – a)2}
x² – 2xa + a²

22) Calcule o produto da soma pela diferença (xy + 4)(xy – 4).
Resolução:
(xy + 4)(xy – 4)
(xy + 4)(xy – 4) = (xy)² – 16²

23) Qual o cubo da soma (x + 5)³
Resolução:
(x + 5)³
x³ + 3x²5 + 3x5² + 5³
x³ + 15x² + 75x + 125

24) Qual o cubo da diferença de (x – 2y)³
Resolução:
(x – 2y)³
x³ – 3x²2y + 3x(2y)² – (2y)³
x³ – 3x²2y + 3x4y² – 8y³
x³ – 6x²y + 12xy² – 8y³

25) (3x + y)²
Resolução:
(3x + y)²
(3x)² + 2.3x.y + y²
9x² + 6xy + y²

26) (2x + 3y)³
Resolução:
(2x + 3y)³
(2x)³ + 3.(2x)².3y + 3.2x.(3y)² + (3y)³
8x³ + 36x²y + 54xy² + 27y³

27) (5 + x)²
Resolução:
(5 + x)²
5² + 2.5.x + x²
25 + 10x + x²

Simplifique as expressões:
28) (x + y)² – x² – y²
Resolução:
(x + y)² – x² – y²
x² + 2xy + y² – x² – y²
2xy

29) (x – y)² – (x + y)²
Resolução:
Primeiramente:
(x – y)²
x² – 2xy + y²
(x + y)²
x² + 2xy + y²
Assim,
(x – y)² – (x + y)²
x² – 2xy + y² – (x² + 2xy + y²)
x² – 2xy + y² – x² – 2xy – y²
x² – x² – 2xy – 2xy + y² – y²
-2xy – 2xy
-4xy

Efetue as multiplicações:
30) (x – 2).(x – 5)
Resolução:
(x – 2).(x-5)
xx + x(-5) + (-2)x + (-2).(-5)
x² + ((-2) + (-5))x + (-2).(-5)
x² – 7x + 10

31) (x + 15).(x – 4)
Resolução:
(x + 15)(x – 4)
xx + x(-4) + 15x + 15(-4)
x² + (15 + (-4))x + 15.(-4)
x² + 11x – 60

32) Desenvolva o polinômio: (x + 3)²
Resolução:
(x + 3)²
x² + 2 . 3x + 3²
x² + 6x + 9

33) Desenvolva o polinômio: (3x – 4z)²
Resolução:
(3x – 4z)²
(3x)² – 2 . 3x . 4z + (4z)²
9x² – 24xz + 16z²

34) Desenvolva o cubo (2 + x)³ e (2 – x)³
Resolução:
(2 + x)³
2³ + 3 . 2² . x + 3 . 2 . x² + x³
8 + 12x + 6x² + x³
x³ + 6x² + 12x + 8

35) Cubo da diferença: (2 – x)³
Resolução:
(2 – x)³
2³ – 3 . 2² . x + 3 . 2 . x² – x³
8 – 12x + 6x² – x³
– x³ + 6x² – 12x + 8

36) Qual é a forma fatorada do produto entre os polinômios x² + 14x + 49 e x² – 14x + 49?
(A) (x + 7)² . (x – 7)²
(B) (x² + 14x + 49) . (x² – 14x + 49)
(C) (x + 7) . (x – 7)²
(D) (x + 7)² . x – 7²
(E) x + 7² . (x – 7)²
Resolução:
Como estamos buscando a forma fatorada do produto, não é necessário multiplicar os polinômios, basta fatorá-los e escrever o produto entre as formas fatoradas. Observe:
A forma fatorada de x² + 14x + 49, seguindo o método do trinômio quadrado perfeito, é:
x² + 14x + 49 = (x + 7)²
Já a forma fatorada de x² – 14x + 49, seguindo o mesmo método, é:
x² – 14x + 49 = (x – 7)²
Portanto, o produto entre as formas fatoradas é:
(x + 7)²·(x – 7)²
Alternativa: A

37) Qual é a forma simplificada da expressão algébrica abaixo?
(x² + 14x + 49) . ( x² – 49)
       x² – 14x + 49
(A) (x + 7)·(x + 7)
             x – 7
(B) x + 7
x – 7
(C) (x + 7)³
  x – 7
(D) (x + 7)²
x – 7
(E) (x² + 14x + 49)
           x – 7
Resolução:
Observe que existem três polinômios que podem ser fatorados nessa expressão algébrica. Para fatorá-los, utilizaremos os casos de trinômio quadrado perfeito e diferença de dois quadrados.
Observe:
(x² + 14x + 49) . ( x² – 49)
x² – 14x + 49
(x + 7)² . (x – 7) . (x + 7)
(x – 7)²
(x + 7) . x + 7) . (x – 7) . (x + 7)
(x – 7)·(x – 7)
Agora basta “cortar” os termos idênticos no numerador e denominador. Nessa questão, existe apenas um termo idêntico, a saber (x – 7). O resultado final será:
(x + 7) . (x + 7) . (x + 7)
x – 7
Esse resultado pode ser reescrito da seguinte maneira:
(x + 7)³
x – 7
Alternativa: C

38) A razão entre as formas fatoradas dos polinômios ax + 2a + 5x + 10 e a² + 10a + 25 é:
(A) (a + 5)(x – 2)
      (a + 5)(a + 5)
(B) a + 5
(C) a – 5
(D) x – 2
    a + 5
(E) x + 2
a + 5
Resolução:
No numerador, utilizaremos o método de fatoração por agrupamento, que faz uso da fatoração por fator comum em evidência repetidas vezes. Já no denominador, utilizaremos o método de fatoração do trinômio quadrado perfeito. Escrevendo a razão proposta, obteremos:
ax + 2a + 5x + 10
a² + 10a + 25
a(x + 2) + 5(x + 2)
(a + 5)(a + 5)
(a + 5)(x + 2)
(a + 5)(a + 5)
gora vamos dividir os termos idênticos presentes na expressão algébrica acima:
x + 2
a + 5
Alternativa: E

39) A forma simplificada da razão entre os polinômios x³ – 8y³ e x² – 4xy + 4y² é:
(A) (x + 4y)²
     x – 4y
(B) (x² + 2xy + 4y²)
x – 2y
(C) (x + y)²
     x – y
(D) (2x + 2)²
      x – y
(E) (x + y)²
     2x – y
Resolução:
Para resolver essa questão, devemos escrever a razão entre os polinômios:
x³ – 8y³
x² – 4xy + 4y²
Agora utilize o método de fatoração da diferença entre dois cubos no numerador e do trinômio quadrado perfeito no denominador.
(x – 2y)(x² + 2xy + 4y²)
            (x – 2y)²
Escrevendo o denominador em forma de produto teremos:
(x – 2y)(x² + 2xy + 4y²)
        (x – 2y)(x – 2y)
Agora basta “cortar” os fatores idênticos que aparecem tanto no numerador quanto no denominador:
(x² + 2xy + 4y²)
         x – 2y
Alternativa: B

APROFUNDANADO O CONHAMECIMENTO
Divisão de polinômio - Continuação:
Ao dividir um polinômio P (x) por um polinômio D (x) não nulo, em que o grau de P é maior que D (_P> _D), quer dizer que devemos encontrar um polinômio Q (x) e R (x), de modo que:
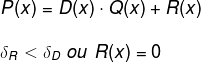
Note que esse processo é equivalente a escrever:
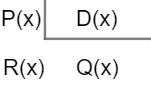P (x) → dividendo
D (x) → divisor
Q (x) → quociente
R (x) → resto

Das propriedades da potenciação, temos que o grau do quociente é igual à diferença entre os graus do dividendo e divisor.
_{Q = P – D}
Ainda, quando o resto da divisão entre P (x) e D (x) é igual a zero, dizemos que P (x) é divisível por D (x).

Regras da divisão de polinômios

Método dos coeficientes a determinar — método de Descartes
Para realizar a divisão entre os polinômios P (x) e D (x), com grau de P maior que o grau de D, seguimos os passos:
Passo 1 - Determinar o grau do polinômio quociente Q (x);
Passo 2 - Tomar o maior grau possível para o resto da divisão R (X) (Lembre-se: R (x) = 0 ou _R< _D);
Passo 3 - Escrever os polinômios Q e R com coeficientes literais, de forma que P (x) = D (x) · Q (x) + R (x).

Exemplo:
Sabendo-se que P (x) = 4x³– x² + 2 e que D (x) = x² + 1, determina-se o polinômio quociente e o resto.
O grau do quociente é 1, pois:
_Q=_{P – D}
_Q=3 – 2
_Q= 1
Assim no polinômio Q (x) = a·x +b, o resto R (x) é um polinômio cujo maior grau pode ser 1, logo: R (x) = c ·x +d. Substituindo os dados na condição do passo 3, temos: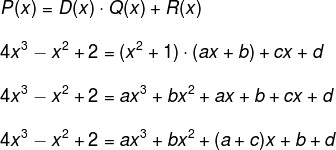

Comparando os coeficientes dos polinômios, temos: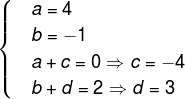

Logo, o polinômio Q (x) = 4x-1 e R (x) = -4x + 3.

Método da chave
Consiste em realizar a divisão entre polinômios seguindo a mesma ideia da divisão entre dois números, o chamado algoritmo da divisão. Veja o exemplo a seguir.
Novamente vamos considerar os polinômios P (x) = 4x³– x² + 2 e D (x) = x² + 1, e agora vamos dividi-los utilizando o método da chave.
Passo 1 - Completar o polinômio dividendo com coeficientes nulos, caso necessário.
P (x) = 4x³– x² + 0x + 2
Passo 2 - Dividir o primeiro termo do dividendo pelo primeiro termo do divisor e, em seguida, multiplicar o quociente por todo divisor. Veja: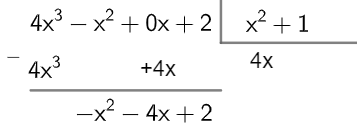

Passo 3 - Dividir o resto do passo 2 pelo quociente e repetir esse processo até que o grau do resto seja menor que o grau do quociente.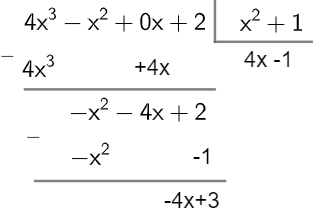

Logo, Q (x) = 4x-1 e R (x) = -4x +3.

Dispositivo prático de Briot-Ruffini
Utilizado para dividir polinômios por binômios.
Vamos considerar os polinômios: P (x) = 4x³+ 3 e D (x) = 2x + 1.
Esse método consiste em desenhar dois segmentos, um horizontal e outro vertical, e nesses segmentos colocamos o coeficiente do dividendo e a raiz do polinômio divisor, além disso, repete-se o primeiro coeficiente.
Exemplo: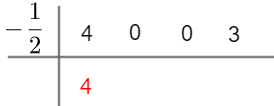

Perceba que o menor meio é a raiz do divisor e que o primeiro coeficiente foi divido.
Agora, devemos multiplicar a raiz do divisor pelo termo repetido e somá-lo ao próximo.

Exemplo: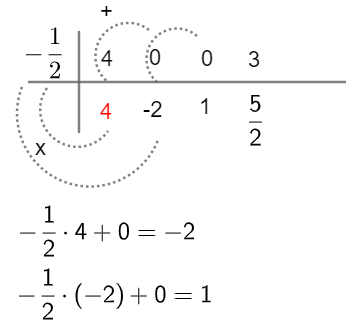

O último número encontrado no dispositivo prático é o resto, e os demais são os coeficientes do polinômio quociente. Devemos dividir esses números pelo primeiro coeficiente do divisor, nesse caso por 2. Assim:
Para saber mais sobre esse método de divisão de polinômios,

Fator comum em evidência
Esse tipo de fatoração é usado quando existe um fator recorrente em todos os termos do polinômio. Pode conter números e letras, sendo assim colocado à frente dos parênteses. Dentro desses parênteses, fica o resultado da divisão de cada termo pelo fator comum.

Observação: o “passo a passo” desse tipo de fatoração se dá em 3 etapas, sendo:
Identificar algum número que divida todos os coeficientes do polinômio e as letras que se repetem em cada um dos termos;

Colocar os fatores comuns, sejam eles números ou letras, na frente dos parênteses, em evidência;
Colocar dentro dos parênteses o resultado da divisão de cada fator identificado do polinômio pelo que está na frente dos parênteses. Para letras, utiliza-se a regra da divisão de potências que possuem mesma base.

Exemplos - 1:
Como expressar a forma fatorada de 12x + 6y – 9z?
Primeiramente, identificamos que todos os coeficientes podem ser divididos por 3 e que não há nenhuma letra repetida. Na sequência, coloca-se 3 na frente dos parênteses, dividindo todos os termos por esse número e colocando o resultado da operação dentro dos parênteses.
Assim, temos que:
12x + 6y – 9z = 3(4x +2y – 3z)
Como fatorar o polinômio 2a²b + 3a³c – a⁴?
Na primeira etapa, verificamos que não há nenhum número que seja capaz de dividir, ao mesmo tempo, 2, 3 e 1. Assim, nenhum número é colocado à frente dos parênteses.
Na sequência, podemos perceber que a letra “a” se repete em cada um dos termos do polinômio. Portanto, o fator comum será a², já que este é o menor expoente de “a” no polinômio. Assim, dividimos cada termo do polinômio por a², tendo como:
2a² b : a² = 2a² – 2 b = 2b
3a³c : a² = 3a³ – 2 c = 3ac
a⁴: a² = a²
Por fim, coloca-se a² na frente dos parênteses e o resultado da divisão dentro deles, tendo como resultado da fatoração:
2a²b + 3a³c – a⁴ = a² (2b + 3ac – a²)
Exemplo -2:

Considere o retângulo:
Observe que a área do retângulo azul mais a área do retângulo verde resultam no retângulo maior. Vamos analisar cada uma dessas áreas:
A_AZUL= b · x
A_VERDE = b · y
A_MAIOR = b · (x + y)
Assim, temos que:
A_MAIOR= A_AZUL+ A_VERDE
b (x + y) = bx + by

03) Para fatorar a expressão: 12x + 24y.
Resolução:
Nota-se que 12 é o fator em evidência, uma vez que ele aparece em ambas as parcelas, assim, para determinar os números que vão no interior dos parênteses, basta dividir cada parcela pelo fator em evidência.
12x / 12 = x
24y / 12 = 2y
12x + 24y = 12 . (x + 2y)

13) Para fatorar a expressão 21ab²– 70a²b.
Resolução:
Do mesmo modo, inicialmente, determina-se o fator em evidência, isto é, o fator que se repete nas parcelas. Veja que da parte numérica temos o 7 como fator comum, uma vez que ele é o único que divide ambos os números. Agora, em relação à parte literal, veja que se repete somente o fator ab, logo, o fator em evidência é: 7ab.
21ab²– 70a²b = 7ab (3b – 10^a)

Fatoração por agrupamento
A fatoração por agrupamento é decorrente da fatoração por evidência, a única diferença é que, em vez de termos um monômio como fator comum ou fator em evidência, teremos um polinômio.

Exemplo:
Considere a expressão (a + b) · xy + (a + b) · wz²
Resolução:
Observe que o fator comum é o binômio (a + b), logo, a forma fatorada da expressão anterior é:
(a + b) · (xy + wz²)

Diferença entre dois quadrados
Considere dois números a e b, quando temos a diferença do quadrado desses números, isto é, a² – b², então podemos escrevê-los como sendo o produto da soma pela diferença, ou seja:
a² – b²= (a + b) · (a – b)

03) Para fatorar a expressão x² – y².
Resolução:
Podemos utilizar a diferença entre dois quadrados, logo:
x² – y²= (x + y) · (x – y)

14) Para fatorar 2.020² – 2.019².
Resolução:
Podemos utilizar a diferença entre dois quadrados, logo:
2.020² – 2.019²
(2.020 + 2.019) · (2.020 – 2.019)
2.020² – 2.019²
4.039 · 1
2.020² – 2.019²
4.039

Trinômio do quadrado perfeito
Considere o quadrado seguinte de lado (a + b) e observe as áreas dos quadrados e retângulos formados em seu interior.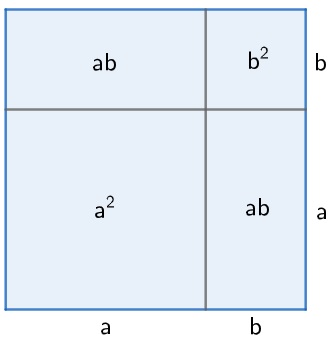
Veja que a área do quadrado maior é dada por (a + b)², mas, por outro lado, a área do quadrado maior pode ser obtida pela soma dos quadrados e retângulos do seu interior, assim:
(a + b)² = a² + ab + ab + b²
(a + b)² = a² + 2ab + b²
(a + b)² = a² + 2ab + b²
De maneira análoga, temos que:
(a – b)² = a² – 2ab + b²

15) Considere a expressão x² + 12x + 36.
Resolução:
Para fatorar uma expressão desse tipo, basta identificar o coeficiente da variável x e o coeficiente independente, e comparar com a fórmula dada, veja:
x² + 12x + 36
a² + 2ab + b²
Fazendo as comparações, veja que x = a, 2b = 12 e b² = 36; das igualdades, temos que b = 6, assim a expressão fatorada é:
x² + 12x + 36 = (x + 6)²

Trinômio do segundo grau
Considere o trinômio ax² + bx + c. A sua forma fatorada pode ser encontrada utilizando suas raízes, ou seja, os valores de x que zeram tal expressão. Para determinar os valores que zeram tal expressão, basta resolver a equação ax² + bx + c = 0 utilizando o método que achar conveniente. Aqui ressaltamos o método mais conhecido como Método de Bhaskara .

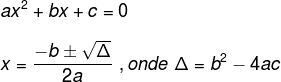
A forma fatorada do trinômio ax² + bx + c é:
ax² + bx + c
a · (x – x₁) · (x – x₂)

16) Considere a expressão x² + x – 20.
Resolução:
O primeiro passo é determinar as raízes da equação x² + x – 20 = 0.
Assim a forma fatorada da expressão x² + x – 20 é:
(x – 4) · (x + 5) cubo da diferença entre dois números
O cubo da diferença entre dois números a e b é dado por:
(a – b)³ = (a – b) · (a – b)²
(a – b)³ = (a – b) · (a² – 2ab + b²) cubo da soma de dois números
De maneira análoga, temos que (a + b)³ = (a + b) · (a + b)², logo:
(a + b)³ = (a + b) · (a²+ 2ab + b²)

A fatoração é um instrumento que facilita a resolução das expressões algébricas.

17) (UFMG) O polinômio P (x) = 3x⁵ - 3x⁴ -2x³ + mx² é divisível por D (x) = 3x² - 2x. O valor de m é:
Resolução:
Como o polinômio P é divisível por D, então podemos aplicar o algoritmo da divisão. Assim,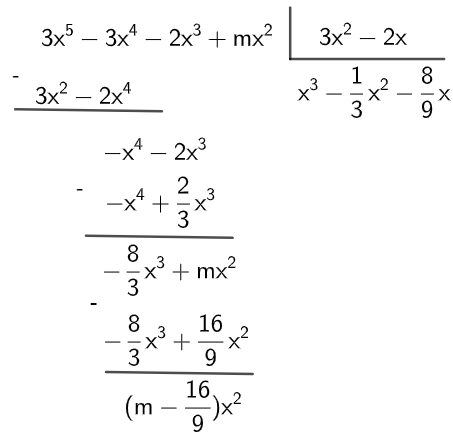

Como foi dado que os polinômios são divisíveis, então o resto é igual a zero. Logo,

18) Para fatorar a expressão x² – y².
(A) (x + y) · (x – y)
(B) (x + y) · (x + y)
(C) (x - y) · (x – y)
(D) x² + y² · (x – y)
(E) x² + y² · x² + y²
Resolução:
x² – y²= (x + y) · (x – y)
Alternativa: A

02) A expressão algébrica que representa o perímetro do retângulo a seguir é:
(A) 5x – 5
(B) 10x – 10
(C) 5x + 5
(D) 8x – 6
(E) 3x – 2
Resolução:
Para calcular o perímetro, vamos somar os quatro lados. Sabendo que os lados paralelos são iguais, temos que:
P = 2(2x – 4) + 2 (3x – 1)
P = 4x – 8 + 6x – 2
P = 10x – 10
Alternativa: B

03) qual é o produto entre 3 e o polinômio P(x) = 2x⁹ + 3x² – 8?
(A) 6x⁹ + 3x² – 24
(B) 6x⁹ + 9x² – 24
(C) 2x⁹ + 9x² – 24
(D) 6x⁹ + 9x²
Resolução:
3·(2x⁹ + 3x² – 8)
3·2x⁹ + 3·3x² + 3·(– 8)
6x⁹ + 9x² – 24
Alternativa: B

04) Qual é o produto entre 3x² e 2x⁶ + 3x² – 2x?
(A) 6x⁸+ x⁴– 6x³
(B) 6x⁸ + 6x⁴ – 6x³
(C) 6x⁸ + 9x⁴ – 6x³
(D) x⁸ + 9x⁴ – 6x³
Resolução:
3x²·(2x⁶ + 3x² – 2x)
3x²·2x⁶ + 3x²·3x² + 3x²·(– 2x)
6x^{6 + 2} + 9x^{2 + 2} – 6x^{2 + 1}
6x⁸ + 9x⁴ – 6x³
Alternativa: C

05) Qual é o produto entre os polinômios 2x² + 4x³ – 2x e 3x⁹ – 2x³ – 8?
(A) 12x12 + 6x11 – 6x10 – 8x6 – 4x5 – 28x4 + 16x2 + 32x
(B) 12x12 + 6x11 – 6x10 – 8x6 – 4x5 – 28x4 + 16x2 + x
(C) x¹² + 6x¹¹ – 6x¹⁰ – 8x⁶ – 4x⁵ – 28x⁴ + 16x² + 16x
(D) 12x¹² + 6x¹¹ – 6x¹⁰ – 8x⁶ – 4x⁵ – 28x⁴ + 16x² + 16x
Resolução:
(2x² + 4x³ – 2x)·(3x⁹ – 2x³ – 8)
2x²·(3x⁹) + 2x²·(– 2x³) + 2x² ·(– 8) + 4x³·(3x⁹) + 4x³·(– 2x³) + 4x³·(– 8) – 2x·3x⁹ –2x(– 2x³) – 2x(– 8)
6x²⁺⁹ – 4x³⁺² – 16x² + 12x³⁺⁹ – 8x³⁺³ – 32x³ – 6x⁹ + 4x³ + 16x
6x²⁺⁹ – 4x³⁺² – 16x² + 12x³⁺⁹ – 8x³⁺³ – 32x³ – 6x⁹⁺¹ + 4x³⁺¹ + 16x
6x¹¹ – 4x⁵ – 16x² + 12x¹² – 8x⁶ – 32x³ – 6x¹⁰ + 4x⁴ + 16x
12x¹² + 6x¹¹ – 6x¹⁰ – 8x⁶ – 4x⁵ – 28x⁴ + 16x² + 16x
Alternativa: D

06) No retângulo a seguir as medidas dos lados estão na mesma unidade de medida. Escreva a expressão que representa a área da região.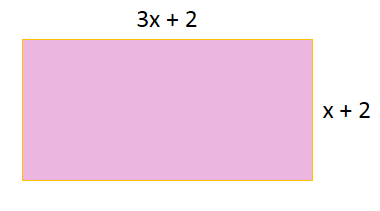
A área de um retângulo é dada pelo produto do comprimento pela largura.
A(x) = (3x + 2).(x + 2)
(3x).(x) + (3x).(2) + (2).(x) + (2).(2)
3x² + 6x + 2x + 4
3x² + 8x + 4