LOGARITMO
Professor Diminoi
Logaritmo (log)
Definição de logaritmo:
Logaritmo é uma função matemática que está baseada nas propriedades da potenciação e exponenciação.
O valor do logaritmo corresponde ao expoente que se deve elevar uma determinada base, positiva e diferente de 1, para que o resultado seja igual a um número positivo b.
Para melhor compreender o conceito do logaritmo, faz-se necessário a observação da fórmula da equação logarítmica:
Originalmente, o conceito do logaritmo foi criado pelo matemático escocês John Napier (1550 – 1617), no século XVII, com o propósito de simplificar os cálculos trigonométricos complexos. O matemático inglês Henry Briggs (1561 – 1630) também contribuiu com os estudos sobre o logaritmo, considerado um dos responsáveis por aprimorar esta função e criar a sua atual lei de formação.
Etimologicamente, a palavra “logaritmo” é formada pela junção de dois termos gregos: lógos e arithmós, que significam, respectivamente, “razão” e “número”.
Definição de logaritmo
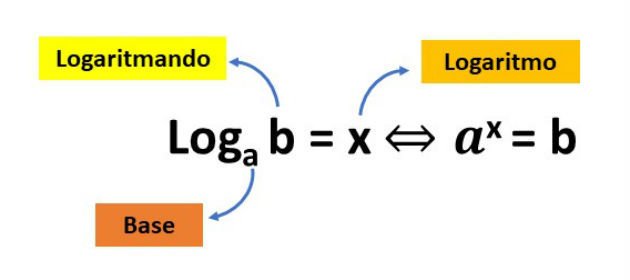 Temos:
Temos:
a = base do logaritmo
b = logaritmando
x = logaritmo
O logaritmo de b na base a é o expoente que devemos atribuir ao número a para obter b.
Exemplos:
log24 = 2, pois 2² = 4
log327 = 3, pois 3³ = 27
log12144 = 2, pois 12² = 144
Definições:
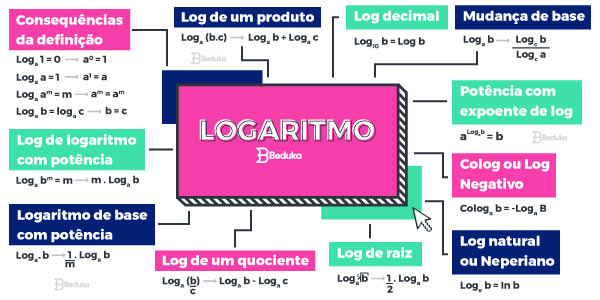
Propriedades do logaritmo
Algumas das principais regras do logaritmo são:
1ª propriedade - Quando o logaritmando é igual à base, o logaritmo será sempre igual a 1.
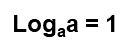 1ª propriedade - Logaritmo de qualquer base, cujo logaritmando seja igual a 1, terá sempre o resultado igual a 0.
1ª propriedade - Logaritmo de qualquer base, cujo logaritmando seja igual a 1, terá sempre o resultado igual a 0.
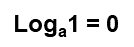 3ª propriedade - Dois logaritmos com a mesma base são iguais quando os logaritmandos também são iguais.
3ª propriedade - Dois logaritmos com a mesma base são iguais quando os logaritmandos também são iguais.
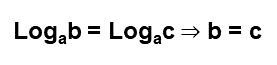 4ª propriedade - Uma potência de base a e expoente igual a logaritmo de b na base a, é igual a b.
4ª propriedade - Uma potência de base a e expoente igual a logaritmo de b na base a, é igual a b.
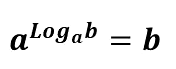 5ª propriedade - Quando o logaritmando é composto por uma multiplicação de números, podemos separá-los numa soma de logaritmos com a mesma base para ambos.
5ª propriedade - Quando o logaritmando é composto por uma multiplicação de números, podemos separá-los numa soma de logaritmos com a mesma base para ambos.
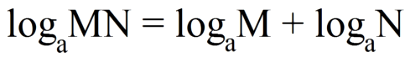 6ª propriedade - Quando o logaritmando é composto por uma divisão de números, podemos separá-los numa subtração de logaritmos, com a mesma base para ambos.
6ª propriedade - Quando o logaritmando é composto por uma divisão de números, podemos separá-los numa subtração de logaritmos, com a mesma base para ambos.
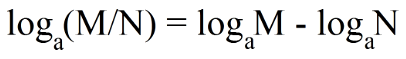 7ª propriedade - A regra da potência: o logaritmo de uma potência simplifica-se multiplicando o expoente pelo logaritmo, mantendo a mesma base e o logaritmando.
7ª propriedade - A regra da potência: o logaritmo de uma potência simplifica-se multiplicando o expoente pelo logaritmo, mantendo a mesma base e o logaritmando.
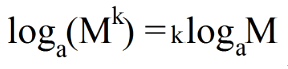 Exemplo
Exemplo
Log 1000. Para calcular esse logaritmo, devemos encontrar um número que, elevado a 10, seja igual a 1000, isto é, 10x = 1000.
Resolvendo a equação exponencial, temos:
10x =1000
10x = 103
x = 3
Portanto,
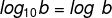
Exemplo
Calcule o logaritmo:
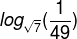 Devemos encontrar um número que, elevado à raiz de 7, seja igual a um quarenta e nove avos. Resolvendo a equação, temos:
Devemos encontrar um número que, elevado à raiz de 7, seja igual a um quarenta e nove avos. Resolvendo a equação, temos:
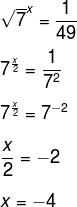
Condição de existência do logaritmo
Considere o logaritmo a seguir:
logb = x
A expressão só está definida para quando a base for maior que zero e diferente de um e quando o logaritmando for maior que zero, ou seja:
a > 0 e a ≠ 1
b > 0
Logaritmo como expoente

Observação: observe na imagem, que quando um número a é elevado a um logaritmo de base a, o resultado dessa potenciação será igual ao logaritmando do expoente, como demonstra a justificativa (marcada em vermelho).
Logaritmando é uma multiplicação
log a D.E = loga D + loga E
Uma das mais importantes propriedades logarítmicas, a expressão acima mostra que, quando o logaritmando é uma multiplicação, é possível separar cada um dos fatores.
Para isso, utilizam-se logaritmos de mesma base inicial somados.
Observe uma aplicação prática. Sabendo que log 2 = 0,3, qual o valor de y na equação abaixo?
log 160 = y
log 16 . 10 = y
log 2 . 2 . 2 . 2 . 10 = y
log 2 + log 2 + log 2 + log 2 + log 10 = y
0,3 + 0,3 + 0,3 + 0,3 + 1 = y
y = 2,2
Lembre-se, log 10 = 1 porque a base é igual ao logaritmando, como vimos acima.
Logaritmando é uma divisão
log a (D/E) = loga D – loga E
No extremo oposto da propriedade anterior, e tão importante quanto ela, está a regra que dita como resolver uma equação em que o logaritmando pode ser fracionado, como mostra o exemplo acima.
Logaritmando com expoente
log ak = k . log a
Quando o logaritmando possui um expoente, teremos a conhecida “regra do tombo”. Isso significa que você pode multiplicar o logaritmo pela potência k, como descreveu a equação anterior.
Como calcular logaritmos?
A partir da expressão log4 256 = y, você deve adicionar a pergunta base do cálculo logarítmico “Qual o valor de y para que 4y = 256?”.
Resolucao
Com isso, você pode fatorar o número 256 com números primos, até que o resultado das divisões seja igual a 1. Assim:

Observe que, com a fatoração adequada, obtém-se que o logaritmo de 256 na base 4 é igual a 4 (log4 256 = y → y = 4) , já que 44 = 256.
QUESTOES RESOLVIDAS
01) (UDESC) Se loga b = 3 e logab c = 4, então loga c é:
(A) 12
(B) 16
(C) 24
(D) 8
(E) 6
Resolucao
Podemos manipular cada uma das expressões fornecidas:
loga b = 3
a3 = b
logab c = 4
(ab)4 = c
(a.a3)4 = c
(a4)4 = c
a16 = c
loga c = x
ax = c
x = 16
Alternativa B
Logaritmos: o que são, propriedades e como calcular
Os logaritmos são ferramentas matemáticas que se relacionam intimamente com a exponenciação e potenciação dos números.
A representação da função logarítmica considera uma base e um logaritmando, como mostra a figura:
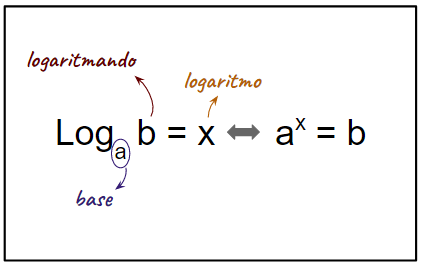 Observe a igualdade apresentada no lado direito da figura: a base elevada ao valor logaritmo, fornece o logaritmando (ax = b).
Observe a igualdade apresentada no lado direito da figura: a base elevada ao valor logaritmo, fornece o logaritmando (ax = b).
Para que a afirmação anterior seja verdadeira, é necessário que b > 0, uma vez que todo número real, quando elevado a x, não pode resultar em 0 (ax > 0).
Além disso, a base deve ser positiva e diferente de um (a > 0 e a≠1), visto que 1x = 1.
Logaritmo decimal
Em termos práticos, você pode imaginar o logaritmo como uma pergunta: “a que potência a base ‘a’ precisa ser elevada para que ‘b’ seja igual a ela? (ax = b)
Exemplo
log10 100 = x
Resolucao
A que potência o número 10 (base) precisa ser elevado para que seja igual a 100 (logaritmando)?
10x. = 100
10.10 = 100
102 = 100
x = 2
Por definição, quando o log aparece sem a base no canto inferior direito, entende-se que a base = 10. Nesse caso, trata-se de um logaritmo decimal.
Exemplo
log 10000 = log10 10000
Logaritmo neperiano (log e)
Como o sistema numérico ocidental é decimal, é muito comum que o log apareça na base 10. Mas outro valor de grande importância para a resolução de equacoes logarítmicas é o número de euler (e), que é aproximadamente igual a 2,718281…
Propriedades dos logaritmos
No estudo dos logaritmos, foi percebido certos padrões que se repetem continuamente. Quando observados junto às regras da potenciação, notou-se que a equação logarítmica possui algumas propriedades, que serão abordadas nos tópicos a seguir.
Condição de existência do logaritmo - Considere o logaritmo a seguir:
A expressão só está definida para quando a base for maior que zero e diferente de um e quando o logaritmando for maior que zero, ou seja:
a > 0 e a ≠ 1
b > 0
Propriedade dos logaritmos
As principais propriedades dos logaritmos. Todos os logaritmos aqui citados satisfazem a condição de existência.

MUDANÇA DE BASE
É possível trocar a base de um logaritmo quando observada a fórmula abaixo:
log b c = log a c / log a b
Você deve adicionar logaritmos da base desejada no denominador e no divisor da fração. Depois, a base “original” (b) vira logaritmando da parte de baixo, e o logaritmando “original” (c) fica na parte de cima.
02) Determine o número que se obtém ao se escrever o número 3 no sistema de numeração de base 2.
(A) (111)
(B) (101)
(C) (10)
(D) (01)
(E) (11)
Resolucao
Temos que 3 = 1 . 2 + 1.1
Logo, 3 na base 2 é 11
03) (Prova Resolvida PM Acre Músico – Funcab) Considere A = (11000) e B = (10001) , números escritos no sistema de numeração de base 2. Escreva-os no sistema de numeração de base 10 e determine o valor de A- B.
(A) -7
(B) 41
(C) -17
(D) 0
(E) 7
Resolucao
Passando para a base 10:
11000 = 1.16 + 1.8 + 0.4 + 0.2 + 0.1 = 24
10001 = 1.16 + 0.8 + 0.4 + 0.2 + 1.1 = 17
24 – 17 = 7
04) (UDESC) Se loga b = 3 e logab c = 4, então loga c é:
(A) 12
(B) 16
(C) 24
(D) 8
(E) 6
Resolucao
Podemos manipular cada uma das expressões fornecidas:
loga b = 3a3 = b
logab c = 4
(ab)4 = c
(a.a3)4 = c
(a4)4 = c
a16 = c
loga c = x
ax = c
x = 16
Alternativa B
05) Seja f(x) = log2x e g(x) = log3 x a lei de formação de duas funções f(x) e g(x), então o valor de f(8) – g (9) é igual a:
(A) 0.
(B) 1.
(C) 2.
(D) –1.
(E) – 2.
Resolucao
Calculando f(8), temos que:
f(8) = log2 8
f(8) = 3
Agora calculando g(9):
g(9) = log39
g(9) = 2
Por fim, a diferenca entre elas é 3 – 2 = 1.
Alternativa B
06) Sobre a função logarítmica, julgue as afirmativas a seguir:
I - O domínio da função logarítmica é o conjunto dos números reais.
II - A função logarítmica é crescente quando a sua base é maior que 1.
III - A função logarítmica é decrescente quando sua base é negativa.
(A) Somente a I é verdadeira.
(B) Somente a II é verdadeira.
(C) Somente a III é verdadeira.
(D) Somente a II e a III são verdadeiras.
(E) Somente a I e a II são verdadeiras.
Resolucao
I → Falsa, pois o domínio é formado pelos numeros reais positivos.
II → Verdadeira. Se a base é maior que 1, a função é crescente.
III → Falsa. A base não pode ser negativa. Para que a função seja decrescente, sua base precisa ser um número maior que 0 e menor que 1.
Alternativa B
07) Durante os estudos sobre o crescimento de uma determinada árvore, foi possível modelar o crescimento dela no decorrer do tempo por meio da função A(t) = 1 + log3 (5 + t), em que t é o tempo em anos e A(t) é a altura em metros. Sendo assim, podemos afirmar que altura dessa árvore, após 4 anos, será de:
(A) 1 metro.
(B) 2 metros.
(C) 2 metros e meio.
(D) 3 metros.
(E) 3 metros e meio.
Resolucao
A(t) = 1 + log3 (5 + t)
A(4) = 1 + log3 (5 + 4)
A(4) = 1 + log3 (9)
A(4) = 1 + 2
A(4) = 3 metros
Alternativa D
08) Em uma determinada cidade, o número de nascimentos, no decorrer dos anos, está sempre crescendo. Para compreender melhor essa relação, os matemáticos modelaram uma função que dá a expectativa da quantidade que crianças que vão nascer para um determinado ano.
N(t) = 900 . log2 (t – 1999)3 , em que t > 1999. De acordo com essa função, supondo que o comportamento seja exatamente o previsto, nascerão 5.400 crianças no ano de:
(A) 2002.
(B) 2003.
(C) 2004.
(D) 2005.
(E) 2006.
Resolucao
Dada a função:
N(t) = 900 ·log2 (t – 1999)3
Queremos que:
900 ·log2 (t – 1999)3 = 5400
Utilizando a propriedade do logaritmo:
900 ·3 log2 (t – 1999) = 5400
2700 log2 (t – 1999) = 5400
log2(t – 1999) = 5400 : 2700
log2 (t – 1999) = 2
Utilizando a definição de logaritmo:
2² = t – 1999
4 = t – 1999
4 + 1999 = t
2003 = t
Alternativa B
09) (Unesp) A expectativa de vida em anos, em uma região, de uma pessoa que nasceu a partir de 1900 no ano x ( x ≥ 1900) é dada por L(x) = 12 . (199log10x - 651). Considerando Log2 = 0,3, uma pessoa dessa região que nasceu no ano 2000 tem expectativa de viver:
(A) 48,7 anos.
(B) 54,6 anos.
(C) 64,5 anos.
(D) 68,4 anos.
(E) 72,3 anos.
Resolucao
L(x) = 12·(199log10x – 651)
L(2000) = 12·(199log10 2000 - 651)
L(2000) = 12·[199log10 (1000·2) - 651]
L(2000) = 12 . [199(log10 1000 + log102) - 651]
L(2000) = 12·[199·(3 + 0,3) - 651]
L(2000) = 12·[199·(3,3) - 651]
L(2000) = 12·[656,7 - 651]
L(2000) = 12·5,7
L(2000) = 68,4 anos
Alternativa D
10) Seja f(x) = log2x e g(x) = log3 x a lei de formação de duas funções f(x) e g(x), então o valor de f(8) – g (9) é igual a:
(A) 0.
(B) 1.
(C) 2.
(D) –1.
(E) – 2.
Resolucao
Calculando f(8), temos que:
f(8) = log2 8
f(8) = 3
Agora calculando g(9):
g(9) = log39
g(9) = 2
Por fim, a diferenca entre elas é 3 – 2 = 1.
Alternativa B
11) (Enem) A Escala e Magnitude de Momento (abreviada como MMS e denotada como MW), introduzida em 1979 por Thomas Haks e Hiroo Kanamori, substituiu a Escala de Richter para medir a magnitude dos terremotos em termos de energia liberada. Menos conhecida pelo público, a MMS é, no entanto, a escala usada para estimar as magnitudes de todos os grandes terremotos da atualidade. Assim como a escala Richter, a MMS é uma escala logarítmica. MW e M0 se relacionam pela fórmula:
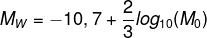 Onde M0 é o momento sísmico (usualmente estimado a partir dos registros de movimento da superfície, através dos sismogramas), cuja unidade é o dina⋅cm. O terremoto de Kobe, acontecido no dia 17 de janeiro de 1995, foi um dos terremotos que causaram maior impacto no Japão e na comunidade científica internacional. Teve magnitude MW = 7,3.
Onde M0 é o momento sísmico (usualmente estimado a partir dos registros de movimento da superfície, através dos sismogramas), cuja unidade é o dina⋅cm. O terremoto de Kobe, acontecido no dia 17 de janeiro de 1995, foi um dos terremotos que causaram maior impacto no Japão e na comunidade científica internacional. Teve magnitude MW = 7,3.
Mostrando que é possível determinar a medida por meio de conhecimentos matemáticos, qual foi o momento sísmico M0?
(A) 10-5,10
(B)10-0,73
(C)1012,00
(D)1021,65
(E)1027,00
Resolucao
Como Mw = 7,3, substituindo na lei de formação, temos que:
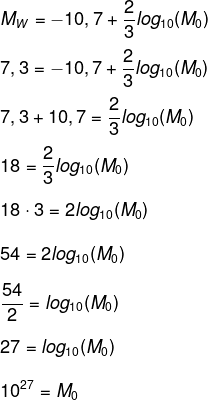
Alternativa E
12) Analisando o gráfico da função:
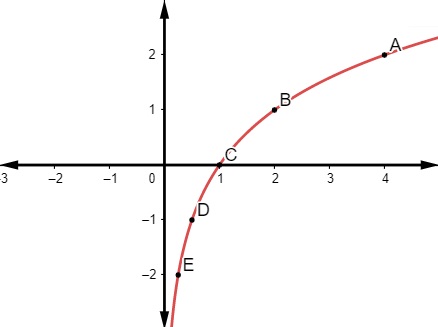 Podemos afirmar que a sua lei de formação é:
Podemos afirmar que a sua lei de formação é:
(A) f(x) = 2x
(B) f(x) = logx + 2
(C) f(x) = log2x
(D)f(x) = – 2x
(E) f(x) = log x²
Resolucao
Analisando o comportamento da função, ela é uma funcao logaritmica. Note que o ponto (2,1) pertence ao gráfico, então:
f(x) = logax
f(2) = loga2
1 = loga2
Aplicando a definição de logaritmo, temos que:
a1= 2
a = 2
Como a base é 2, então a funcao é:
f(x) = log2x
Alternativa C
13) Podemos ver a seguir a representação de uma função logarítmica:
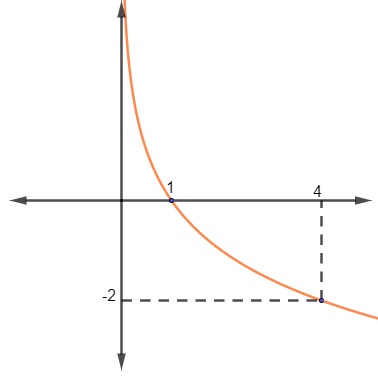 Com base em seu gráfico, sabendo que essa função é uma função do tipo f(x) = logb x, então o valor da base b é:
Com base em seu gráfico, sabendo que essa função é uma função do tipo f(x) = logb x, então o valor da base b é:
(A) 1
(B) 2
(C) 4
(D) -2
(E) 1/2
Resolucao
Analisando o gráfico, sabemos que f(4) = – 2. Então, temos que:
f(4) = logb 4
– 2 = logb 4
Aplicando a definição de logaritmo:
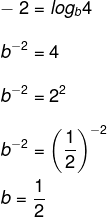
Alternativa E
14) Sobre a função logarítmica, julgue as afirmativas a seguir:
I → O domínio da função logarítmica é o conjunto dos números reais.
II → A função logarítmica é crescente quando a sua base é maior que 1.
III → A função logarítmica é decrescente quando sua base é negativa.
(A) Somente a I é verdadeira.
(B) Somente a II é verdadeira.
(C) Somente a III é verdadeira.
(D) Somente a II e a III são verdadeiras.
(E) Somente a I e a II são verdadeiras.
Resolucao
I → Falsa, pois o domínio é formado pelos numeros reais positivos.
II → Verdadeira. Se a base é maior que 1, a função é crescente.
III → Falsa. A base não pode ser negativa. Para que a função seja decrescente, sua base precisa ser um número maior que 0 e menor que 1.
Alternativa B
15) Durante os estudos sobre o crescimento de uma determinada árvore, foi possível modelar o crescimento dela no decorrer do tempo por meio da função A(t) = 1 + log3 (5 + t), em que t é o tempo em anos e A(t) é a altura em metros. Sendo assim, podemos afirmar que altura dessa árvore, após 4 anos, será de:
(A) 1 metro.
(B) 2 metros.
(C) 2 metros e meio.
(D) 3 metros.
(E) 3 metros e meio.
Resolucao
A(t) = 1 + log3 (5 + t)
A(4) = 1 + log3 (5 + 4)
A(4) = 1 + log3 (9)
A(4) = 1 + 2
A(4) = 3 metros
Alternativa D
16) (UFSM) A partir de dados do Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep), o índice de Desenvolvimento da Educação Básica (Idep) para as séries iniciais do Ensino Fundamental da escola Estadual Básica Professora Margarida Lopes (Santa Maria, RS) pode ser representada pela expressão:
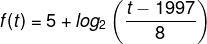 Considere que f(t) representa o Ideb em função do ano t em que o dado foi coletado. Diante dessas informações, pode-se afirmar que o acréscimo do Ideb previsto para essa escola, de 2005 a 2013, é de:
Considere que f(t) representa o Ideb em função do ano t em que o dado foi coletado. Diante dessas informações, pode-se afirmar que o acréscimo do Ideb previsto para essa escola, de 2005 a 2013, é de:
(A) 5
(B) 1
(C) 1/2
(D) 1/4
(E) 0
Resolucao
Queremos encontrar a diferença: f(2013) – f(2005).
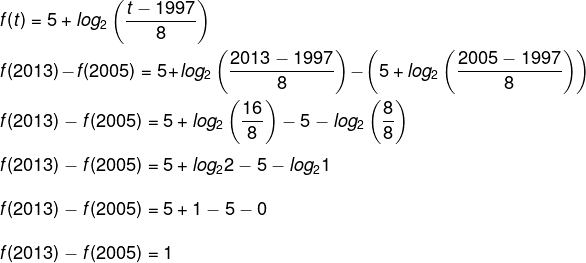 Alternativa B
Alternativa B
17) Em uma determinada cidade, o número de nascimentos, no decorrer dos anos, está sempre crescendo. Para compreender melhor essa relação, os matemáticos modelaram uma função que dá a expectativa da quantidade que crianças que vão nascer para um determinado ano.
N(t) = 900 ·log2 (t – 1999)3 , em que t > 1999. De acordo com essa função, supondo que o comportamento seja exatamente o previsto, nascerão 5.400 crianças no ano de:
(A) 2002.
(B) 2003.
(C) 2004.
(D) 2005.
(E) 2006.
Resolucao
Dada a função:
N(t) = 900 ·log2 (t – 1999)3
Queremos que:
900 ·log2 (t – 1999)3 = 5400
Utilizando a propriedade do logaritmo:
900 ·3 log2 (t – 1999) = 5400
2700 log2 (t – 1999) = 5400
log2(t – 1999) = 5400 : 2700
log2 (t – 1999) = 2
Utilizando a definição de logaritmo:
2² = t – 1999
4 = t – 1999
4 + 1999 = t
2003 = t
Alternativa B
18) O tempo, em minutos, que um medicamento leva para fazer efeito em uma pessoa é dado pela função:
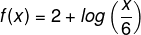 Considere que x é a idade e f(x) é o tempo em minutos.
Considere que x é a idade e f(x) é o tempo em minutos.
Em um paciente que possui 30 anos, o tempo necessário para que esse remédio faça efeito é de:
(Use log 2 = 0,3.)
(A) 2 minutos e 70 segundos.
(B) 2 minutos e 42 segundos.
(C) 3 minutos e 26 segundos.
(D) 5 minutos.
(E) 7 minutos e 30 segundos.
Resolucao
Calculando f(30):
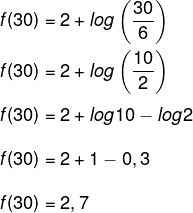 Agora vamos converter a parte decimal em segundos. Sabemos que 0,7 · 60 = 42, ou seja, 2 minutos e 42 segundos.
Agora vamos converter a parte decimal em segundos. Sabemos que 0,7 · 60 = 42, ou seja, 2 minutos e 42 segundos.
Alternativa B
19) O volume de um reservatório em função do tempo é dado em litros pela função:
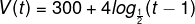 Considere que t ≥ 1, e t é dado em dias e V(t) é dado em litros. Sendo assim, após quantos dias o volume da piscina será de 284 litros?
Considere que t ≥ 1, e t é dado em dias e V(t) é dado em litros. Sendo assim, após quantos dias o volume da piscina será de 284 litros?
(A) 12 dias
(B) 14 dias
(C) 15 dias
(D) 16 dias
(E) 17 dias
Resolucao
Sabemos que V(t) = 284, então:
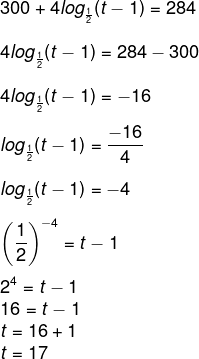 Alternativa E
Alternativa E
20) (PM ES-Funcab) Sendo log 2 = 0,30 e log 3 = 0,47, qual o conjunto solução da expressão abaixo?
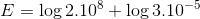 (A) S = {6,17}
(A) S = {6,17}
(B) S = {5,33}
(C) S = {4,37}
(D) S = {3,91}
(E) S = {3,77}
Resolução
A questão é relativamente simples para os alunos que já dominam as propriedades dos logaritmos.
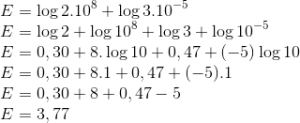 Alternativa E
Alternativa E
21) Qual é o valor da expressão
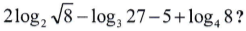
(A) 2/7
(B) -7/2
(C) – 2/7
(D) 7/2
Resolução
Calcularemos separadamente o valor de cada logaritmo, considerando:
log2√8 = x
log327 = y
log48 = z
Analisando o primeiro logaritmo, temos:
2x = √8 = 81/2 = (23)1/2 = 23/2
Conclusão: x = 3/2
Analisando o segundo logaritmo, temos:
3y = 27 = 33
Conclusão: y = 3
Analisando o terceiro logaritmo, temos:
22z = 4z = 8 = 23
Conclusão: 2z = 3 e z = 3/2
Finalizando:
2.log2√8 – log327 – 5 + log48
2.(3/2) – 3 – 5 + 3/2
3 – 3 – 5 + 3/2
-5 + 3/2
-7/2
Alternativa: B
23) (TJ SC) Sabendo que log 123 = 2,09, assinale a alternativa que contém o valor de log 1,23.
(A) 0,09
(B) 0,0209
(C) 0,209
(D) 1,09
(E) 1,209
Resolução
Como log 123 = 2,09, temos:
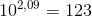 Dividindo ambos os membros por 100:
Dividindo ambos os membros por 100:
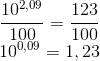 Pela definição de logaritmos:
Pela definição de logaritmos:
log 1,23 = 0,09
Alternativa A
24) (PM Acre-IBADE) A febre amarela é uma doença infecciosa aguda, de curta duração (no máximo 10 dias), gravidade variável, causada pelo vírus da febre amarela, que ocorre na América do Sul e na África. A única forma de evitar a febre amarela silvestre é a vacinação contra a doença. A vacina é gratuita e está disponível nos postos de saúde em qualquer época do ano.
Um posto de saúde iniciou a vacinação contra a febre amarela com um lote de x doses. Sabe-se que o planejado é que o número de doses produzidas dobre a cada ano. Dessa maneira, após quanto tempo esse número passará a ser igual a 20 vezes o inicial? (Use: log2 = 0,3).
(A) 4 anos e 4 meses
(B) 10 anos e 3 meses
(C) 3 anos e 4 meses
(D) 4 anos e 1 mês
(E) 13 anos e 3 meses
Resolução
Sendo x a quantidade inicial de doses e considerando que o número deve dobrar a cada ano, podemos montar a equação abaixo, onde n é a quantidade de anos.
2n.x = 20.x
2n = 20
log(2n) = log20
n.log2 = log2 + log10
n.0,3 = 0,3 + 1
0,3n = 1,3
n = 1,3/0,3
n = 4,33…
n = 4 anos e 4 meses
Alternativa A
25) (Vunesp-PM-SP) Ao resolver certo problema, encontramos a equação exponencial ax = 100.
Sabendo que o logaritmo decimal de “a” é igual a 0,54, o valor de “x” é, aproximadamente,
(A) 2,8.
(B) 3,1.
(C) 3,4.
(D) 3,7.
(E) 4,2.
Resolução
Aplicando o logaritmo decimal em ambos os lados da equação:
log(ax) = log100
x.loga = 2
x.0,54 = 2
x = 2/0,54
x = 3,7
Alternativa D
26) (PM AL-CESPE) Um corpo com temperatura inicial de 36°C está em um ambiente cuja temperatura é de 20°C. Nesse ambiente, vão demorar 20 minutos para que a temperatura inicial do corpo caia para 28°C. Sabendo-se que o resfriamento de um corpo pode ser modelado pela lei do resfriamento de Newton, conforme a qual a temperatura do corpo T, em função do tempo t, em horas, é dada pela função exponencial T(t) = (Tc−Ta)10-kt + Ta, em que Tc é a temperatura inicial do corpo e Ta é a temperatura ambiente, é correto afirmar que a constante k é igual a log10(27).
CERTO ou ERRADO?
Resolução
Considerando que 20 minutos é 1/3 de uma hora, podemos utilizar a função exponencial:
T(t) = (Tc − Ta)10-kt + Ta
28 = (36 − 20)10-k/3 + 20
28 – 20 = 16.10-k/3
8 = 16.10-k/3
10-k/3 = 8/16
10-k/3 = 1/2
Aplicando log em ambos os lados da igualdade:
log(10-k/3) = log(1/2)
(-k/3).log10 = log1 – log2
(-k/3).1 = 0 – log2
k/3 = log2
k = 3log2
Resposta errada
EQUACOES LOGARITMICAS
27) (UP) A solução da equação logarítmica log10 (x-4) = 2 é:
(A) x = 6.
(B) x = 10.
(C) x = 50.
(D) x = 100.
(E) x = 104.
Resolução
Pela definição de logaritmos, temos:
10² = x – 4
100 = x – 4
x = 100 + 4
x = 104
Alternativa E
28) (CETREDE) Pode-se afirmar que o conjunto verdade da equação logarítmica log x + log (x+1) – log 6 = 0 é
(A) {3}.
(B) {2, –3}.
(C) {2}.
(D) {–2, 3}.
(E) {2, 3}.
Resolução
Aplicando as propriedades de adição e subtração de logaritmos, temos:
log x + log (x+1) – log 6 = 0
log[ x.(x + 1) / 6 ] = 0
Pela definição de logaritmos:
x.(x + 1) / 6 = 100 = 1
x.(x + 1) / 6 = 1
x.(x + 1) = 6
x² + x – 6 = 0
Temos uma equação do segundo grau que pode ser resolvida através do método da soma e do produto:
S = -b/a = -1/1 = -1
P = c/a = -6/1 = -6
Os dois números cuja soma é igual a -1 e o produto é igual a -6 são -3 e 2. Como o logaritmando deve ser maior que zero, descartamos o -3.
Alternativa C
FUNÇÃO LOGARÍTMICA
29) A função logarítmica na base 2, para x > 0 é sempre positiva.
II- A função logarítmica natural f(x) = ln(x), para x > 0 é sempre crescente.
III- A função cosseno f(x) = cos(x), para x > 0, é sempre positiva.
IV- A função tangente, f(x) = tg(x), para 0 < x < π/2, é sempre crescente.
Quais as únicas alternativas corretas?
(A) I e II
(B) II e IV
(C) III e IV
(D) I, II e III
(E) I, III e IV
Resolução
I) Falsa. Será negativa quando 0 < x < 1.
II) Verdadeira. O número de Euler é aproximadamente 2,718 > 1, fazendo com que a função seja crescente para x > 0.
III) Falsa. A função Cosseno varia entre 1 e -1
IV) Verdadeira. A função tangente é sempre crescente para x > 0.
Alternativa B
30) (Fuvest - SP) Se x5 = 1000 e b3 = 100, então o logaritmo de x na base b vale:
(A) 0,5
(B) 0,9
(C) 1,2
(D) 1,5
(E) 2,0
Resolucao
Como os números 1000 e 100 podem ser escritos na base 10, temos:
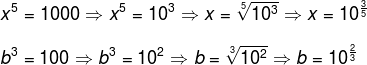 Substituindo no logaritmo de x na base b e aplicando a definição, temos:
Substituindo no logaritmo de x na base b e aplicando a definição, temos:
.jpg)
31) (Enem) Define-se o potencial hidrogeniônico (pH) de uma solução como o índice que indica sua acidez, neutralidade ou alcalinidade. É encontrado da seguinte maneira:
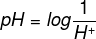
Sendo H+ a concentração de íons de hidrogênio nessa solução. O pH de uma solução, em que H+ = 1,0 ·10-9, é:
Resolucao
Substituindo o valor do H+ na fórmula do pH, temos:
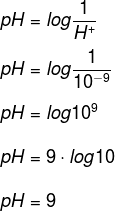
Continua...










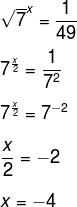
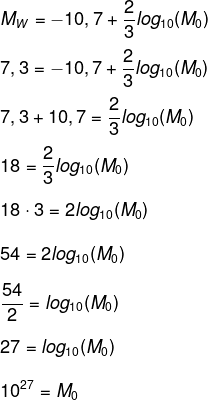


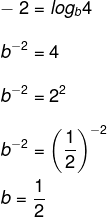
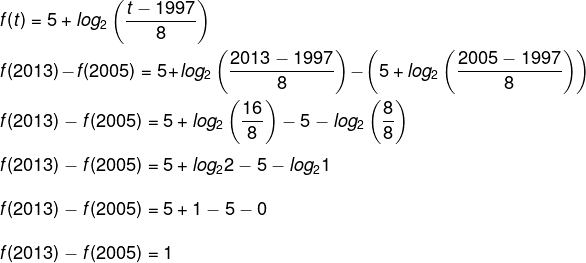
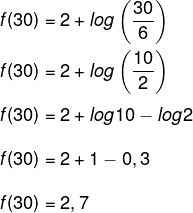
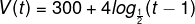
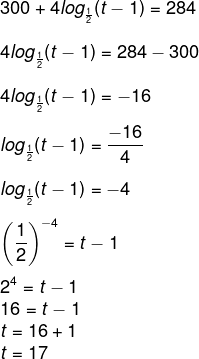
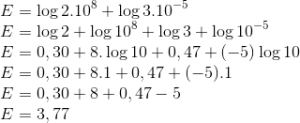
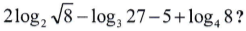
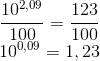
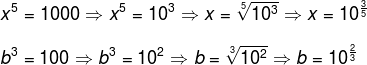
.jpg)