PP-M-3ª-1ºBIM-2023
Professor Diminoi
1º BIMESTRE 2023 MATEMÁTICA - 3ª série –ENSINO MÉDIO
01) (Prova Paulista – 3EM – 1ºBim/2023 - SEED/PR) Uma pessoa tem um terreno quadrado de 30m por 30 m. O proprietário pretende construir uma casa e gramar a área restante. As dimensões da casa são x metros de largura por 2x metros de comprimento.
Qual a expressão que representa a parte que terá grama ?
(A) A = 30x - 2x²
(B) A = 900 - 2x²
(C) A = 30x² + 2x
(D) A = 900 + 2x²
(E) A = 900x² + 2x²
02) (Prova Paulista – 3EM – 1ºBim/2023 - SEED/PR) O retângulo e o quadrado representados abaixo têm a mesma área.
 A medida do lado do quadrado e a medida do comprimento do retângulo são respectivamente:
A medida do lado do quadrado e a medida do comprimento do retângulo são respectivamente:
(A) 12 e 24
(B) 10 e 14
(C) 8 e 16
(D) 6 e 12
(E) 4 e 8
03) (Prova Paulista – 3EM – 1ºBim/2023 - UFMG) Um certo reservatório, contendo 72𝑚³ de água, deve ser drenado para limpeza. Decorridas t horas após o início da drenagem, o volume de água que saiu do reservatório, em 𝑚³, é dado por 𝑉(𝑡) = 24𝑡 − 2𝑡² . Sabendo-se que a drenagem teve início às 10 horas, o reservatório estará completamente vazio às:
(A) 14 horas
(B) 16 horas
(C) 19 horas
(D) 22 horas
(E) 25 horas
04) (Prova Paulista – 3EM – 1ºBim/2023 - UFSM/2014) Ao descartar detritos orgânicos nos lagos, o homem está contribuindo para a redução da quantidade de oxigênio destes. Porém, com o passar do tempo, a natureza vai restaurar a quantidade de oxigênio até o seu nível natural. Suponha que a quantidade de oxigênio, t dias após os detritos orgânicos serem despejados no lago, é expressa por:
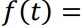
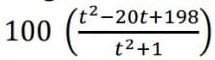
Por cento (%) de seu nível normal. Se 𝑡1 e 𝑡2, com 𝑡1 < 𝑡2, representam o número de dias para que a quantidade de oxigênio seja 50% de seu nível normal, então 𝑡2 – 𝑡1 é igual a
(A) −4√5.
(B) −2√5.
(C) 2√5.
(D) 4√5.
(E) 40.
05) (Prova Paulista – 3EM – 1ºBim/2023 - SEED/PR) A função que descreve a simetria dessa figura abaixo é dada por 𝑦 = 3𝑥2 − 3.
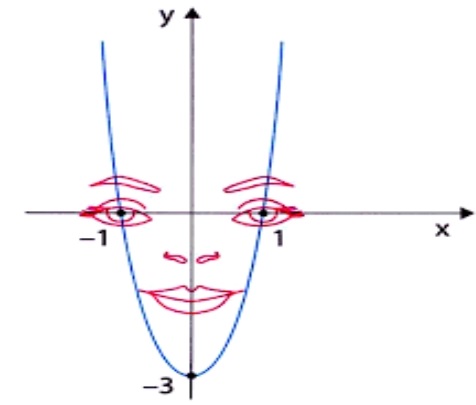 Quais pares ordenados desse gráfico são os pontos de zero da função ?
Quais pares ordenados desse gráfico são os pontos de zero da função ?
(A) (0 , -1) e (0 , 1)
(B) (-1 , 0) e (0 , -3)
(C) (0 , -3) e (1 , 0)
(D) (-1 , 0) e (1 , 0)
(E) (-1 , 1) e (1 , -1)
06) (Prova Paulista – 3EM – 1ºBim/2023 - SEED/PR) O gráfico a seguir está representando qual função?
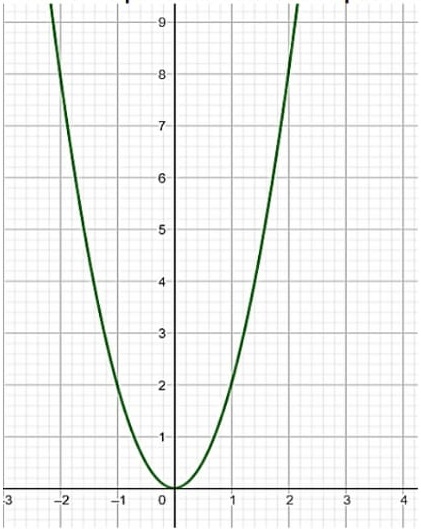 (A) f(x) = 𝑥² 2
(A) f(x) = 𝑥² 2
(B) f(x) = 2x²
(C) f(x) = x²
(D) f(x) = 4x²
(E) f(x) = 2x
07) (Prova Paulista – 3EM – 1ºBim/2023 - SEED/PR) Uma parte do gráfico da função f(x) = ax² + bx + c está representado a seguir.
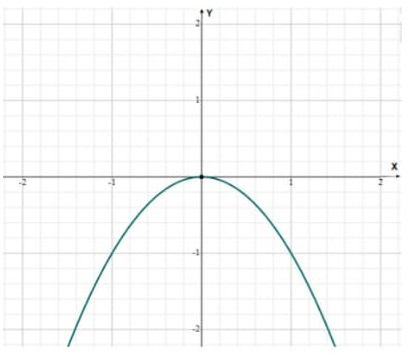 Considerando essa afirmação, é correto afirmar que:
Considerando essa afirmação, é correto afirmar que:
(A) a > 0 e b . c = 0
(B) a = 0 e b . c > 0
(C) a < 0 e b . c = 0
(D) a < 0 e b . c < 0
(E) a = 0 e b . c = 0
08) (Prova Paulista – 3EM – 1ºBim/2023 - SEED/PR) Observando os gráficos abaixo e suas respectivas funções podemos concluir que:
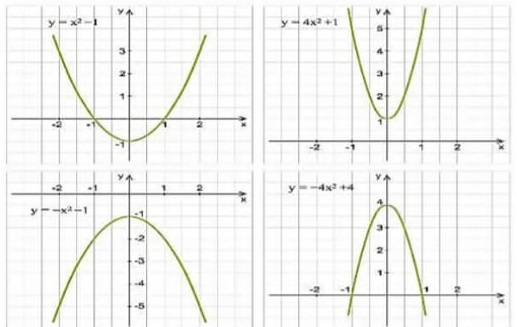 (A) As funções não apresentam raízes.
(A) As funções não apresentam raízes.
(B) O eixo de simetria está deslocado 1 unidade para cima ou para baixo.
(C) As concavidades das parábolas estão relacionadas com o sinal de “c” das funções.
(D) O ponto de intersecção do gráfico com o eixo das ordenadas é o valor de “c” na função.
(E) Ao menos uma função tem “a” igual a 0.
09) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2016) Um senhor, pai de dois filhos, deseja comprar dois terrenos, com áreas de mesma medida, um para cada filho. Um dos terrenos visitados já está demarcado e, embora não tenha um formato convencional (como se observa na Figura B), agradou ao filho mais velho e, por isso, foi comprado. O filho mais novo possui um projeto arquitetônico de uma casa que quer construir, mas, para isso, precisa de um terreno na forma retangular (como mostrado na Figura A) cujo comprimento seja 7m maior do que a largura.
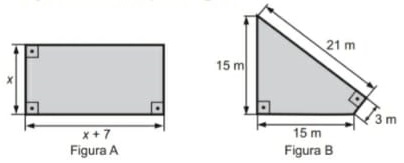 Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metros, do comprimento e da largura sejam iguais, respectivamente, a
Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metros, do comprimento e da largura sejam iguais, respectivamente, a
(A) 7,5 e 14,5.
(B) 9,0 e 16,0.
(C) 9,39,3 e 16,3.
(D) 10,0 e 17,0.
(E) 13,5 e 20,5.
10) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2013) Para o reflorestamento de uma área, deve-se cercar totalmente, com tela, os lados de um terreno, exceto o lado margeado pelo rio, conforme a figura. Cada rolo de tela que será comprado para confecção da cerca contém 48 metros de comprimento.
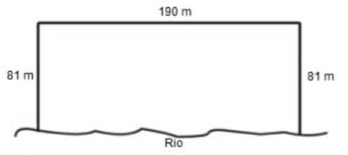 A quantidade mínima de rolos que deve ser comprada para cercar esse terreno é
A quantidade mínima de rolos que deve ser comprada para cercar esse terreno é
(A) 6.
(B) 7.
(C) 8.
(D) 11.
(E) 12.
11) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2010) Em canteiros de obras de construção civil é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo, conforme pode ser visto na figura, em que as estacas foram indicadas por letras.
 A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto. Nessas condições, a área a ser calçada corresponde:
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto. Nessas condições, a área a ser calçada corresponde:
(A) à mesma área do triângulo AMC.
(B) à mesma área do triângulo BNC.
(C) à metade da área formada pelo triângulo ABC
(D) ao dobro da área do triângulo MNC.
(E) ao triplo da área do triângulo MNC.
12) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2015) Para uma alimentação saudável, recomenda-se ingerir, em relação ao total de calorias diárias, 60% de carboidratos, 10% de proteínas e 30% de gorduras. Uma nutricionista, para melhorar a visualização dessas porcentagens, quer dispor esses dados em um polígono. Ela pode fazer isso em um triângulo equilátero, um losango, um pentágono regular, um hexágono regular ou um octógono regular, desde que o polígono seja dividido em regiões cujas áreas sejam proporcionais às porcentagens mencionadas. Ela desenhou as seguintes figuras:
 Entre esses polígonos, o único que satisfaz as condições necessárias para representar a ingestão correta de diferentes tipos de alimentos é o
Entre esses polígonos, o único que satisfaz as condições necessárias para representar a ingestão correta de diferentes tipos de alimentos é o
(A) triângulo.
(B) losango.
(C) pentágono.
(D) hexágono.
(E) octógono.
13) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2016) Pretende-se construir um mosaico com o formato de um triângulo retângulo, dispondo-se de três peças, sendo duas delas triângulos retângulos congruentes e a terceira um triângulo isósceles. A figura apresenta cinco mosaicos formados por três peças.
 Na figura, o mosaico que tem as características daquele que se pretende construir é o
Na figura, o mosaico que tem as características daquele que se pretende construir é o
(A) 1.
(B) 2.
(C) 3.
(D) 4.
(E) 5
14) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2021) O instrumento de percussão conhecido como triângulo é composto por uma barra fina de aço, dobrada em um formato que se assemelha a um triângulo, com uma abertura e uma haste, conforme ilustra a Figura 1.
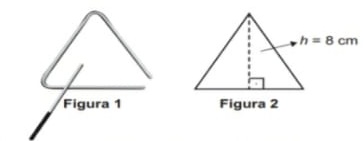 Uma empresa de brindes promocionais contrata uma fundição para a produção de miniaturas de instrumentos desse tipo. A fundição produz, inicialmente, peças com o formato de um triângulo equilátero de altura h, conforme ilustra a Figura 2. Após esse processo, cada peça é aquecida, deformando os cantos, e cortada em um dos vértices, dando origem à miniatura. Assuma que não ocorram perdas de material no processo de produção, de forma que o comprimento da barra utilizada seja igual ao perímetro do triângulo equilátero representado na Figura 2.
Uma empresa de brindes promocionais contrata uma fundição para a produção de miniaturas de instrumentos desse tipo. A fundição produz, inicialmente, peças com o formato de um triângulo equilátero de altura h, conforme ilustra a Figura 2. Após esse processo, cada peça é aquecida, deformando os cantos, e cortada em um dos vértices, dando origem à miniatura. Assuma que não ocorram perdas de material no processo de produção, de forma que o comprimento da barra utilizada seja igual ao perímetro do triângulo equilátero representado na Figura 2.
Considere 1,7 como valor aproximado para √3 para a fórmula ℎ = 𝑙√3/2. Nessas condições, o valor que mais se aproxima da medida do comprimento da barra, em centímetro, é
(A) 9,07.
(B) 13,60.
(C) 20,40.
(D) 27,18.
(E) 36,24.
15) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2008) O tangram é um jogo oriental antigo, uma espécie de quebra-cabeça, constituído de sete peças: 5 triângulos retângulos e isósceles, 1 paralelogramo e 1 quadrado. Essas peças são obtidas recortando-se um quadrado de acordo com o esquema da figura 1. Utilizando-se todas as sete peças, é possível representar uma grande diversidade de formas, como as exemplificadas nas figuras 2 e 3.
 Se o lado AB do hexágono mostrado na figura 2 mede 2 cm, então a área da figura 3, que representa uma “casinha”, é igual a
Se o lado AB do hexágono mostrado na figura 2 mede 2 cm, então a área da figura 3, que representa uma “casinha”, é igual a
(A) 4 cm2.
(B) 8 cm2.
(C) 12 cm2.
(D) 14 cm2.
(E) 16 cm2.
16) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2022) O professor de artes orientou seus estudantes a realizarem a seguinte sequência de atividades:
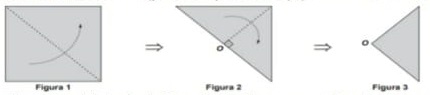 Dobrar uma folha de papel em formato quadrado duas vezes, em sequência, ao longo das linhas tracejadas, conforme ilustrado nas figuras 1 e 2, para obter o papel dobrado, conforme Figura 3.
Dobrar uma folha de papel em formato quadrado duas vezes, em sequência, ao longo das linhas tracejadas, conforme ilustrado nas figuras 1 e 2, para obter o papel dobrado, conforme Figura 3.
Em seguida, no papel dobrado da Figura 3, considerar o ponto R, sobre o segmento 𝑂𝑀, sendo o ponto médio do lado do quadrado original, de modo que 𝑂𝑅 = 1/4 𝑂𝑀, traçar um arco de circunferência de raio medindo 1/2 𝑂𝑀 com centro no ponto R, obtendo a Figura 4. Por último, recortar o papel ao longo do arco de circunferência e excluir a parte que contém o setor circular, obtendo o papel dobrado, conforme Figura 5.

Após desdobrado o papel que restou na Figura 5, a figura plana que os estudantes obterão será
(A) 
(B) 
(C) 
(D) 
(E) 
17) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2022) Uma empresa de engenharia projetou uma casa com a forma de um retângulo para um de seus clientes. Esse cliente solicitou a inclusão de uma varanda em forma de L. A figura apresenta a planta baixa desenhada pela empresa, já com a varanda incluída, cujas medidas, indicadas em centímetro, representam os valores das dimensões da varanda na escala de 1 : 50.
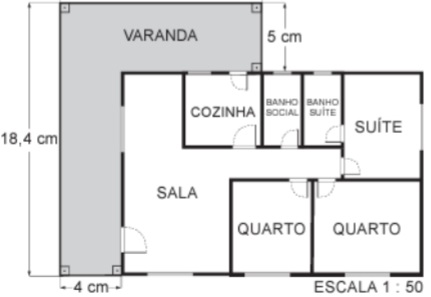
A medida real da área da varanda, em metro quadrado, é
(A) 33,40
(B) 66,80
(C) 89,24
(D) 133,60
(E) 534,40
18) (Prova Paulista – 3EM – 1ºBim/2023) O número de erros na página de um site de grande acesso, em 200 dias pesquisados, está no gráfico a seguir:
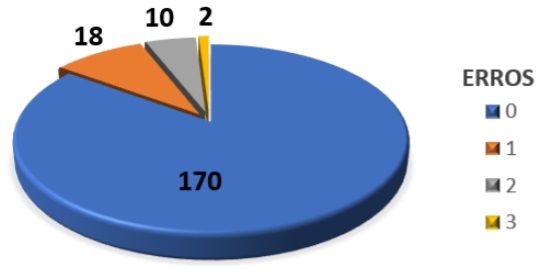
Qual é a porcentagem referente a 1 erro?
(A) 1%
(B) 9%
(C) 10%
(D) 18%
(E) 20%
19) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2010) O gráfico expõe alguns números da gripe A-H1N1. Entre as categorias que estão em processo de imunização, uma já está completamente imunizada, a dos trabalhadores da saúde.
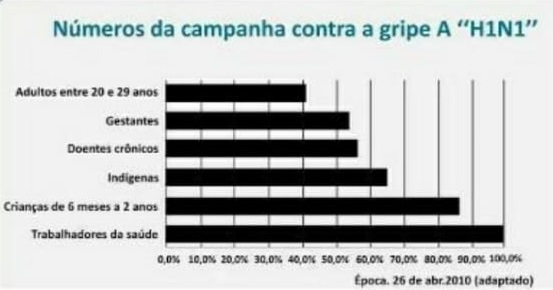
De acordo com o gráfico, entre as demais categorias, a que está mais exposta ao vírus da gripe A-H1N1 é a categoria de
(A) indígenas.
(B) gestantes.
(C) doentes crônicos.
(D) adultos entre 20 e 29 anos.
(E) crianças de 6 meses a 2 anos.
20) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2020) Os gráficos representam a produção de peças em uma indústria e as horas trabalhadas dos funcionários no período de cinco dias. Em cada dia, o gerente de produção aplica uma metodologia diferente de trabalho. Seu objetivo é avaliar a metodologia mais eficiente para utilizá-la como modelo nos próximos períodos. Sabe-se que, neste caso, quanto maior for a razão entre o número de peças produzidas e o número de horas trabalhadas, maior será a eficiência da metodologia.
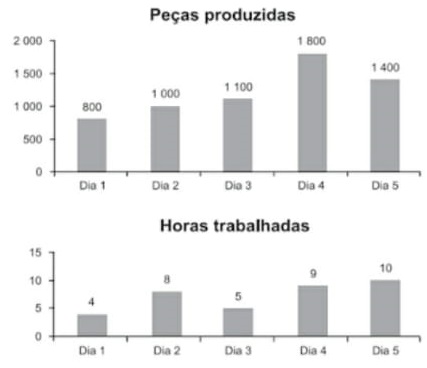
Em qual dia foi aplicada a metodologia mais eficiente?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
21) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2022) Nos cinco jogos finais da última temporada, com uma média de 18 pontos por jogo, um jogador foi eleito o melhor do campeonato de basquete. Na atual temporada, cinco jogadores têm a chance de igualar ou melhorar essa média. No quadro estão registradas as pontuações desses cinco jogadores nos quatro primeiros jogos das finais deste ano.
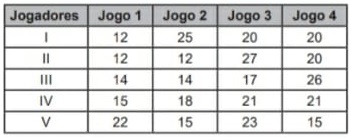
O quinto e último jogo será realizado para decidir a equipe campeã e qual o melhor jogador da temporada.
O jogador que precisa fazer a menor quantidade de pontos no quinto jogo, para igualar a média de pontos do melhor jogador da temporada passada, é o
(A) I.
(B) II.
(C) III.
(D) IV.
(E) V.
22) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2021) O quadro apresenta o número de terremotos de magnitude maior ou igual a 7, na escala de Richter, ocorridos em nosso planeta nos anos 2000 e 2011.

Um pesquisador acredita que a mediana representa bem o número anual típico de terremotos em um período. Segundo esse pesquisador, o número anual típico de terremotos de magnitude maior ou igual a 7 é
(A) 11.
(B) 15.
(C) 15,5.
(D) 15,7.
(E) 17,5.
23) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM - 2014 - 2º Aplicação) Um construtor pretende murar um terreno e, para isso, precisa calcular o seu perímetro. O terreno está representado no plano cartesiano, conforme a figura, no qual foi usada a escala 1 : 500. Use 2,8 como aproximação para √8.
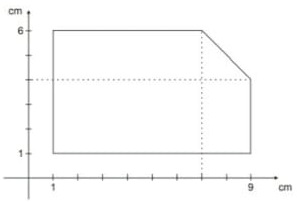
De acordo com essas informações, o perímetro do terreno, em metros, é
(A) 110.
(B) 120.
(C) 124.
(D) 130.
(E) 144.
24) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2015) Devido ao aumento do fluxo de passageiros, uma empresa de transporte coletivo urbano está fazendo estudos para a implantação de um novo ponto de parada em uma determinada rota. A figura mostra o percurso, indicado pelas setas, realizado por um ônibus nessa rota e a localização de dois de seus atuais pontos de parada, representados por P e Q.
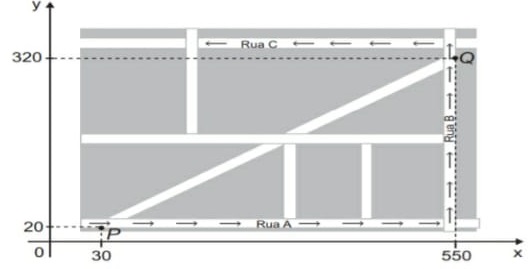
Os estudos indicam que o novo ponto T deverá ser instalado, nesse percurso, entre as paradas já existentes P e Q, de modo que as distâncias percorridas pelo ônibus entre os pontos P e T e entre os pontos T e Q sejam iguais. De acordo com os dados, as coordenadas do novo ponto de parada são
(A) (290 ; 20).
(B) (410 ; 0).
(C) (410 ; 20).
(D) (440 ; 0).
(E) (440 ; 20).
25) (Prova Paulista – 3EM – 1ºBim/2023 - ENEM 2013) Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:

A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas
(A) (65 ; 35).
(B) (53 ; 30).
(C) (45 ; 35).
(D) (50 ; 20).
(E) (50 ; 30).
GABARITO
01B – 02C – 03B – 04C – 05D – 06B – 07C – 08D – 09B -10C – 11E – 12C – 13B – 14D – 15B – 16C – 17A – 18B – 19D – 20C – 21A – 22C – 23C – 24E – 25E.




































