GEOMETRIA GERAL - EF
Professor Diminoi
9º ANO – 4º BIMESTRE
Geometria Geral
Relações entre arcos e ângulos na circunferência de um círculo.
Polígonos regulares.
Vistas ortogonais de figuras espaciais.
Volume de prismas e cilindros.
Probabilidade e Estatística
Análise de probabilidade de eventos aleatórios: eventos dependentes e independentes.
Análise combinatória
GEOMETRIA
Relações entre arcos e ângulos na circunferência de um círculo.
Ângulos no Círculo - Revisão
A Circunferência - É a linha azul que envolve a região cinza, enquanto o círculo é toda a região pintada de cinza reunida com a circunferência.
Círculo - É a reunião azul da circunferência com o conjunto de pontos localizados dentro da mesma.
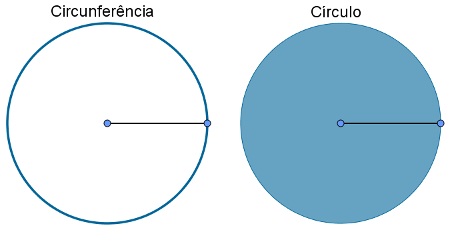
Elementos do círculo e da circunferência
Raio - É a distância entre um ponto de uma circunferência e seu centro. O raio do círculo é a distância entre a borda do círculo e seu centro.

O comprimento da circunferência
C = 2πr
C = comprimento da circunferência
r = raio da circunferência
Π = 3,1416
Área do círculo
A = πr2
A = área da circunferência
r = raio da circunferência
Π = 3,1416
Cordas - Em uma circunferência, a corda é qualquer segmento de reta que liga dois de seus pontos. Ou seja, segmentos de reta que ligam dois pontos distintos de sua borda.

Diâmetro - O diâmetro é uma corda da circunferência que contém o centro e sua medida é igual a duas vezes o raio.
d = 2 . r
d = diâmetro
r = ario
Arco - Considere os pontos A e B sobre uma circunferência. As duas partes formadas que vão de A até B são chamadas de arcos da circunferência, como demonstrado na figura a seguir:
 Observação: m outras palavras, o arco é uma parte de uma circunferência limitada por dois pontos.
Observação: m outras palavras, o arco é uma parte de uma circunferência limitada por dois pontos.
Setor circular - É o equivalente ao arco, porém para o círculo. Em dados dois raios distintos de um círculo, o setor circular é a parte limitada por eles.

Observação: o setor circular é algo que se parece com uma fatia de pizza e a parte restante também é chamada de setor circular.
Ângulo central - É um ângulo cujo vértice está no centro de um círculo e os lados são seus raios. Um ângulo central está ligado a um arco no círculo onde foi definido.

Coroa circular - É uma figura geométrica limitada por dois círculos que possuem o mesmo centro (concêntricos) de raios diferentes e se assemelha a um anel.
.jpg) Relações entre arcos e ângulos na circunferência de um círculo.
Relações entre arcos e ângulos na circunferência de um círculo.
A relação entre ângulos e círculo é muito importante no estudo da geometria. Diversos assuntos ligados à astronomia possuem relações estreitas com ângulos no círculo ou na circunferência. Podemos ter ângulos com vértice no centro, no interior ou no exterior de um círculo, cada um apresentando características e propriedades diferentes.
Existem vário tipos de ângulos tais como:
- Ângulo ao Centro
- Ângulo Inscrito
- Ângulo Externo
- Ângulo Interno
- Ângulo de Segmento
Observação: cada um dos ângulos no círculo apresenta propriedades e características diferentes veja alguns exemplos.
Ângulo ao Centro

Características: corresponde a um ângulo (também conhecido como ângulo central) cujo vértice se encontra no centro da circunferência. Os lados do ângulo são secantes à circunferência. Neste ângulo, a sua amplitude é igual à amplitude do arco correspondente, isto é,
AÔB =AB
Ângulo Inscrito

Características: corresponde a um ângulo cujo vértice se encontra na circunferência. Os lados do ângulo são secantes à circunferência. Neste ângulo, a sua amplitude é igual a metade da amplitude do arco correspondente (é de salientar, que uma consequência desta particularidade, resulta no facto de um ângulo inscrito numa semicircunferência ser reto). Esta é a fórmula de cálculo da sua amplitude:
AÔB = AB/2
Ângulo Externo

Características: corresponde a um ângulo (também conhecido como ângulo excêntrico exterior) cujo vértice se encontra no exterior da circunferência. Os lados do ângulo são secantes ou tangentes à circunferência. Neste ângulo, a sua amplitude pode ser calculada através da seguinte fórmula:
AÔB = AB − CD/2
Ângulo Interno

Corresponde a um ângulo (também conhecido como ângulo excêntrico interior) cujo vértice se encontra no interior da circunferência, mas afastado do centro. Os lados do ângulo são secantes à circunferência.
AÔB= AB + CD/2
Ângulo de Segmento

Características: corresponde a um ângulo (também conhecido como ângulo semi-inscrito) cujo vértice se encontra na circunferência. Um dos lados é secante e o outro tangente à circunferência. Neste ângulo, a sua amplitude é igual a metade da amplitude do arco correspondente (é de salientar, que uma consequência desta particularidade, resulta no facto de um ângulo que tenha como lado secante um dos diâmetros da circunferência, ser um ângulo reto). Aqui fica a fórmula:
AÔB = AO/2
Medidas de Arcos de Circunferência
Dada uma circunferência qualquer de centro O e raio r, marcamos dois pontos A e B, os quais dividem a circunferência em duas partes denominadas de arco de circunferência. Os pontos A e B são os extremos dos arcos. Caso as extremidades sejam coincidentes, temos um arco com uma volta completa.
Figura 1
.jpg)
Podemos notar nessa circunferência a existência do arco AB e de um ângulo central representado por α. Para cada arco existente na circunferência, temos um ângulo central correspondente, ou seja: med(AÔB) = med(AB). Portanto, o comprimento de um arco depende do valor do ângulo central.
Na medição de arcos e ângulos, usamos duas unidades:
- Grau
- Radiano
Medidas em grau
Sabemos que uma volta completa na circunferência corresponde a 360º. Se a dividirmos em 360 arcos, teremos arcos unitários medindo 1 grau. Dessa forma, enfatizamos que a circunferência é simplesmente um arco de 360º com o ângulo central medindo uma volta completa, ou 360º. Também podemos dividir o arco de 1 grau em 60 arcos de medidas unitárias iguais a 1’ (arco de um minuto). Da mesma forma, podemos dividir o arco de 1’ em 60 arcos de medidas unitárias iguais a 1” (arco de um segundo).
Medidas em radianos
Dada uma circunferência de centro O e raio R, com um arco de comprimento s e α o ângulo central do arco.
Figura 2
.jpg)
Dizemos que o arco mede um radiano se o comprimento do arco for igual à medida do raio da circunferência. Assim, para sabermos a medida de um arco em radianos, devemos calcular quantos raios da circunferência são precisos para se ter o comprimento do arco.
Fórmulas
.jpg) R = raio
R = raio
α = ângulo
S = comprimento do arco
O = ângulo central
.jpg) R = raio
R = raio
α = ângulo
S = comprimento do arco
O = ângulo central
De acordo com as relações entre as medidas em grau e radiano de arcos, vamos destacar uma regra de três capaz de converter as medidas dos arcos.
360º = 2π radianos (aproximadamente 6,28)
180º = π radiano (aproximadamente 3,14)
90º = π/2 radiano (aproximadamente 1,57)
45º = π/4 radiano (aproximadamente 0,785)
REGRA DE TRÊS SIMPLES

Exemplo 1
Ou seja, a medida do ângulo α é o comprimento do arco definido como l sobre o comprimento do raio r.
As medidas de arcos em uma circunferência em graus e radianos são diretamente proporcionais, dessa forma podemos converter uma media em outra através de uma regra de três simples.
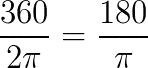 Logo, se quisermos converter uma medida em graus para radianos, por exemplo, devemos proceder da seguinte forma:
Logo, se quisermos converter uma medida em graus para radianos, por exemplo, devemos proceder da seguinte forma:
Graus Radianos
a ——————– α
180 —————— π
Observação:
α é a medida do ângulo em radianos
a é a medida do ângulo em graus
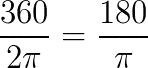
Observação: a conversão é feita multiplicando em cruz.
EXERCÍCIOS RESOLVIDOS
01) Faça a conversão 270º em radianos
Resolução:
270° ––––– α
180° ––––– π
180α = 270 π
α = 270π
180
α = 3π
2
02) Sabemos que a medida de 180° equivale a π radianos. Determine qual valor em radianos corresponde a 1° e também qual valor em graus é correspondente ao valor de 1 radiano.
Resolução:
Primeiramente, vamos utilizar regra de três simples para fazer a transformação de 1° em radianos:
180° ––––– π rad
1° ––––– x
180.x = 1 . π
x = π
180
Podemos ainda estabelecer um valor aproximado se considerarmos que π ≈ 3,1415...:
x = 3,1415
180
x ≈ 0,01745 rad
Novamente utilizando regra de três, vamos verificar qual é a medida em graus que corresponde ao valor de 1 rad:
180° ––––– π rad
x ––––– 1 rad
π.x = 180
x = 180
π
x = 180
3,1415
x ≈ 57,29°
Em cada caso a seguir faça a conversão:
03) 120° em radianos
Resolução:
Para converter 120° em radianos, vamos utilizar regra de três simples:
180° ––––– π rad
120° ––––– x
180.x = 120 . π
x = 120 π
180
Simplificando a fração obtida por 60, teremos:
x = 2 π rad
3
04) 2π em graus
7
Resolução:
Para transformar a medida de radianos para graus, basta substituir o π por 180°:
x = 2 π
7
x = 2.180
7
x = 360
7
x = 51,43°
05) 234° em radianos
Resolução:
Utilizaremos regra de três para fazer a transformação para radianos:
180° ––––– π rad
234° ––––– x
180.x = 234 . π
x = 234 π
180
Simplificando o numerador e o denominador da fração por 18, teremos:
x = 13 π rad
10
06) 3π em graus
5
Resolução:
Basta substituir o π por 180°:
x = 3 π
5
x = 3.180
5
x = 540
5
x = 108°
07) (FUVEST) Quantos graus mede aproximadamente um ângulo de 0,105 radianos?
(A) 2
(B) 4
(C) 6
(D) 8
(E) 10
Resolução:
Sabemos que π rad equivale a 180°:
180° ––––– π rad
x ––––– 0,105 rad
π.x = 180 . 0,105
Podemos utilizar que π ≈ 3,1415...:
3,1415 . x = 18,9
x = 6,02°
Portanto, um ângulo que mede 0,105 radianos equivale a, aproximadamente, 6,02°.
Alternativa: C
08) (Unifor) Reduzindo-se ao primeiro quadrante um arco de medida 7344°, obtém-se um arco, cuja medida, em radianos, é:
(A) π
3
(B) π
2
(C) 2π
3
(D) π
5
(E) 9π
10
Resolução:
Primeiramente, precisamos verificar qual é o ângulo correspondente a 7344° no primeiro quadrante. Para isso, nós calculamos o quociente entre 7344° e 360°, obtendo 20 como resultado e um resto de 144°. Para reduzir 144° ao primeiro quadrante faremos:
180° – 144° = 36°
Vamos agora utilizar regra de três para verificar a medida em radianos que corresponde ao ângulo de 36°:
180° ––––– π rad
36° ––––– x
180.x = 36 . π
x = 36 π
180
Simplificando a fração obtida por 36, encontramos:
x = π
5
Alternativa: D
09) Transformar 60º em radianos.
Resolução:
.jpg)
11) Converter 50º em radianos.
Resolução:
Utilizando a regra de três:
180º ————– π rad
50º ————— x
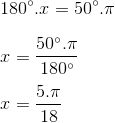
12) Converter 20º em radianos.
Resolução:
Utilizando a regra de três:
180º ————– π rad
20º ————— x
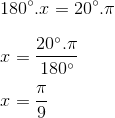
13) Converter 3π/4 rad em graus.
Resolução:
Utilizando a regra de três, onde x é a medida em graus:
180º ———– π rad
x ———– 3π/4
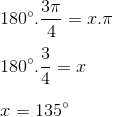
14) Converter π/7 rad em graus.
Resolução:
Utilizando a regra de três, onde x é a medida em graus:
180º ———– π rad
x ———– π/7
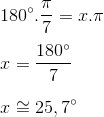
Comprimento de um Arco
Dada uma circunferência de centro O, raio r e dois pontos A e B pertencentes à circunferência, temos que a distância entre os pontos assinalados é um arco de circunferência. O comprimento de um arco é proporcional à medida do ângulo central, quanto maior o ângulo, maior o comprimento do arco; e quanto menor o ângulo, menor o comprimento do arco.
.jpg) Para determinarmos o comprimento de uma circunferência utilizamos a seguinte expressão matemática: C = 2 . π . r. A volta completa em uma circunferência é representada por 360º. Vamos realizar uma comparação entre o comprimento da circunferência em medida linear (ℓ) e medida angular (α).
Para determinarmos o comprimento de uma circunferência utilizamos a seguinte expressão matemática: C = 2 . π . r. A volta completa em uma circunferência é representada por 360º. Vamos realizar uma comparação entre o comprimento da circunferência em medida linear (ℓ) e medida angular (α).
Dados importantes
Comprimento de uma circunferência
C = 2 . π .r
Observação: uma volta completa em uma circunferência é representada por 360º
Quando o ângulo for em Graus
Quando o ângulo central α é dado em graus, podemos calcular o comprimento do arco através da fórmula:
C = α.π.r / 180º
C = comprimento do arco da circunferência
α = ângulo
π = 3,14
r = raio
Quando o ângulo for em Radianos
Quando o ângulo central α é dado em radianos, podemos calcular o comprimento do arco através da seguinte fórmula:
C = α.r
C = comprimento do arco da circunferência
α = ângulo
r = raio
Observação: devemos utilizar π = 3,14 (valor aproximado).
EXERCÍCIOS RESOLVIDOS
15) Determine o comprimento de um arco onde o ângulo central é 60º, onde o raio da circunferência é igual a 5 cm.
Resolução
c = α.π.r / 180º
c = 60º . 3,14 . 5 / 180º
c = 942 / 180
c = 5,23 cm
16) Determine o comprimento do arco cujo ângulo central é 1,2π e o raio da circunferência é igual a 10 cm.
Resolução
C = α.r
C = 1,2π . 10
C = 1,2 . 3,14 . 10
C = 37,68 cm
17) Determine o comprimento do arco:
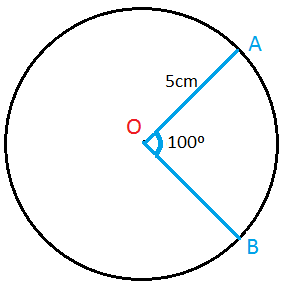 Resolução
Resolução
c = α.π.r / 180º
c = 100º . 3,14 . 5 / 180º
c = 1570 / 180
c = 8,72 cm
18) Determine o comprimento do arco:
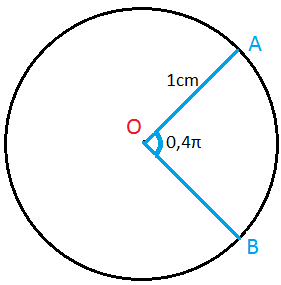 Resolução
Resolução
C = α.r
C = 0,4π . 1
C = 0,4 . 3,14 . 1
C = 1,25 cm
19) A roda de uma motocicleta possui o raio medindo 50 centímetros. Determine a distância que a motocicleta percorre quando a roda dá 500 voltas. Utilize π = 3,14.
Resolução:
C = 2 . π . r
C = 2 . 3,14 . 50
C = 314 cm
500 voltas
C = 314 . 500
C = 157.000 cm ou 1,5 km.
20) (Cefet–MG) A medida do menor ângulo central formado pelos ponteiros de um relógio que está marcando 9h 30min, em grau, é:
(A) 90
(B) 105
(C) 110
(D) 120
(E) 150
Resolução:
Em qualquer relógio analógico o ponteiro das horas percorre um ângulo de 30º em exatamente 1 hora. Dessa forma, em 30 minutos percorre 15º. Então:
3 . 30º + 15º = 90º + 15º = 105º
Alternativa: B
21) Determine o comprimento de um arco com ângulo central igual a 30º contido numa circunferência de raio 2 cm.
Resolução:
ℓ = α . π . r / 180º
ℓ = 30º . 3,14 . 2 / 180º
ℓ = 188,40 / 180
ℓ = 1,05 cm
Resposta: o comprimento do arco será de 1,05 centímetros.
22) O ponteiro dos minutos de um relógio de parede mede 10 cm. Qual será o espaço percorrido pelo ponteiro após 30 minutos?
Resolução:
Observa a figura do relógio:
.jpg)
ℓ = α . π . r / 180º
ℓ = 180º . 3,14 . 10 / 180º
ℓ = 5652 / 180
ℓ = 31,4 cm
Resposta: o espaço percorrido pelo ponteiro dos minutos será de 31,4 centímetros.
23) Determine o comprimento de um arco com ângulo central medindo π/3 contido numa circunferência de 5 cm de raio.
Resolução:
ℓ = α . r
ℓ = π/3 . 5
ℓ = 5π/3
ℓ = 5*3,14 / 3
ℓ = 15,7 / 3
ℓ = 5,23 cm
04) Um pêndulo de 15 cm de comprimento oscila entre A e B descrevendo um ângulo de 15º. Qual é o comprimento da trajetória descrita pela sua extremidade entre A e B?
.jpg) Resolução:
Resolução:
ℓ = α . π . r / 180º
ℓ = 15º . 3,14 . 15 / 180º
ℓ = 706,5 / 180
ℓ = 3,9 cm
Resposta: o comprimento da trajetória entre A e B é de 3,9 centímetros.
Polígonos

 São linhas fechadas formadas apenas por segmentos de reta que não se cruzam e que estão no mesmo plano. Em outras palavras, um polígono é uma figura geométrica limitada por lados. Os polígonos são chamados regulares quando são convexos, possuem todos os lados com a mesma medida e todos os ângulos internos congruentes.
São linhas fechadas formadas apenas por segmentos de reta que não se cruzam e que estão no mesmo plano. Em outras palavras, um polígono é uma figura geométrica limitada por lados. Os polígonos são chamados regulares quando são convexos, possuem todos os lados com a mesma medida e todos os ângulos internos congruentes.
O polígono a seguir é um exemplo de hexágono regular. Observe as medidas de seus lados e ângulos:
Polígonos convexos e regulares
Para serem considerados convexos e regulares, os polígonos devem cumprir alguns pré-requisitos.
Polígono é uma figura geométrica plana formada por diversos elementos. Todavia, apenas um desses elementos é responsável pela definição dessas figuras: o lado.
O lado de um polígono é um segmento de reta qualquer pertencente ao seu contorno. Os triângulos, por exemplo, possuem três lados; os retângulos possuem quatro lados, e os pentágonos possuem cinco lados, exatamente a mesma quantidade de segmentos de reta do contorno desses polígonos.
Os outros elementos presentes nos polígonos são:
Ângulos internos
Ângulos externos
Diagonais
Vértices.
Para ser considerada polígono, uma figura geométrica precisa ser formada por uma linha única, fechada e formada apenas por segmentos de reta. Além disso, esses segmentos de reta não podem cruzar-se.
A figura abaixo apresenta alguns exemplos de polígonos:
Os polígonos A, B e C são formados por 4, 5 e 6 segmentos de reta, respectivamente. Note que esses segmentos, em cada polígono, formam uma linha fechada e não se cruzam de forma alguma. A imagem seguinte apresenta alguns exemplos de figuras geométricas que não são polígonos.

As figuras geométricas A, B e C não são fechadas, portanto, não podem ser consideradas polígonos. Já a figura D possui um cruzamento de segmentos de reta e, por essa razão, também não pode ser considerada polígono.
Polígonos convexos:
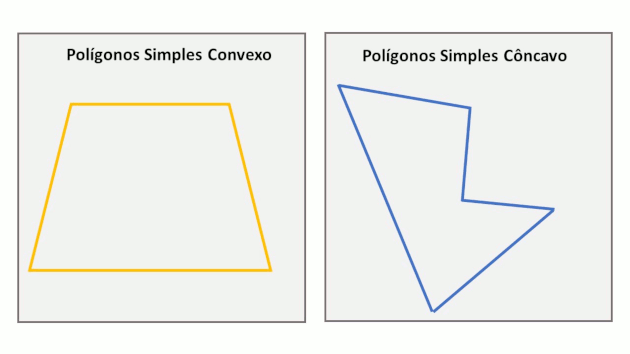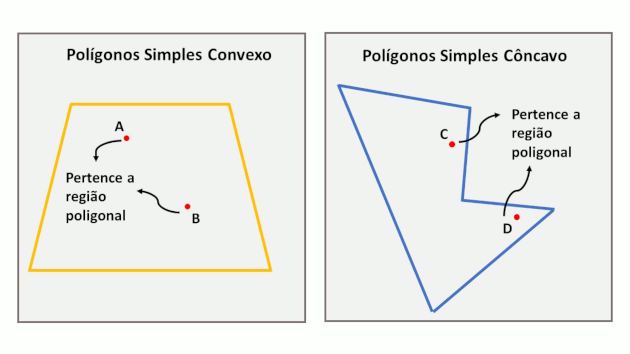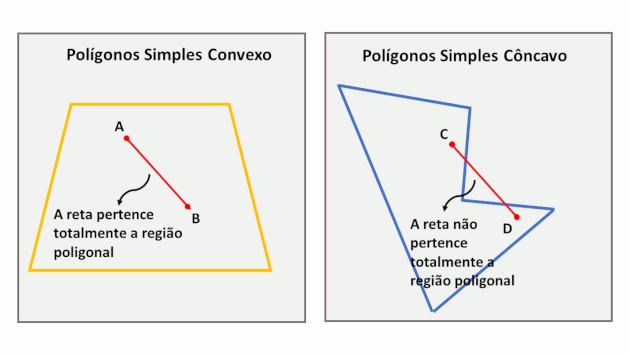
Dados dois pontos A e B quaisquer interiores a um polígono, se o segmento de reta determinado por esses dois pontos estiver inteiramente contido no interior do polígono, então esse polígono será convexo.
A figura abaixo apresenta alguns exemplos de polígonos convexos.
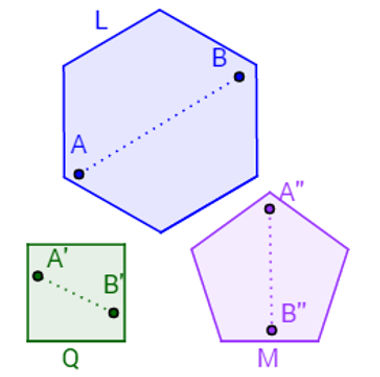 Note que, independentemente da posição dos pontos A e B, A' e B' ou A'' e B'', o segmento determinado por esses pontos sempre estará inteiramente contido no interior de seus respectivos polígonos. Por outro lado, a imagem abaixo representa um polígono não convexo. Isso acontece porque o segmento AB não está totalmente contido no interior do polígono, mesmo que os pontos A e B estejam.
Note que, independentemente da posição dos pontos A e B, A' e B' ou A'' e B'', o segmento determinado por esses pontos sempre estará inteiramente contido no interior de seus respectivos polígonos. Por outro lado, a imagem abaixo representa um polígono não convexo. Isso acontece porque o segmento AB não está totalmente contido no interior do polígono, mesmo que os pontos A e B estejam.
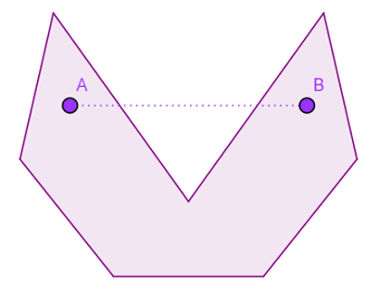 Observação: Os polígonos que têm um vértice voltado para dentro, formando uma espécie de “boca”, não são convexos.
Observação: Os polígonos que têm um vértice voltado para dentro, formando uma espécie de “boca”, não são convexos.
Polígonos Regulares:
Um polígono é considerado regular quando ele é convexo e possui todos os lados e ângulos com a mesma medida.
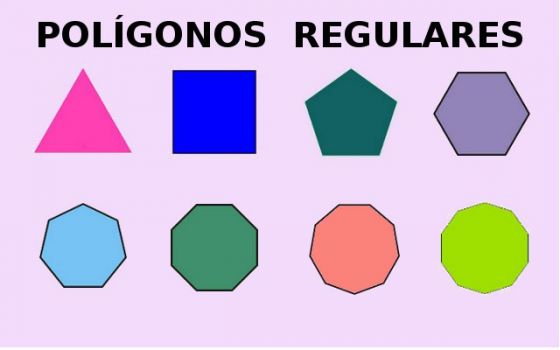 Observação: na imagem abaixo alguns exemplos de polígonos regulares.
Observação: na imagem abaixo alguns exemplos de polígonos regulares.
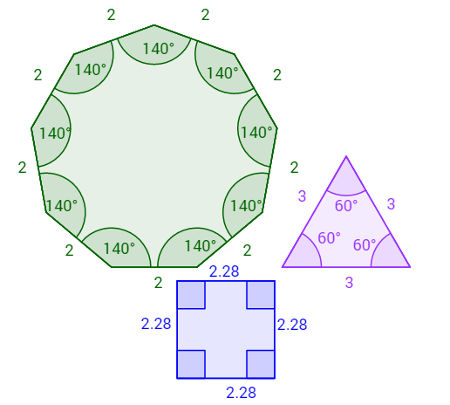 Observe que, em cada polígono da imagem acima, todos os lados e ângulos têm a mesma medida. Observe também que um polígono regular de quatro lados é sempre um quadrado e um polígono regular de três lados é sempre um triângulo equilátero.
Observe que, em cada polígono da imagem acima, todos os lados e ângulos têm a mesma medida. Observe também que um polígono regular de quatro lados é sempre um quadrado e um polígono regular de três lados é sempre um triângulo equilátero.
 Polígono formado por outros polígonos com número de lados em progressão aritmética
Polígono formado por outros polígonos com número de lados em progressão aritmética
Propriedades dos polígonos regulares
1ª Propriedade
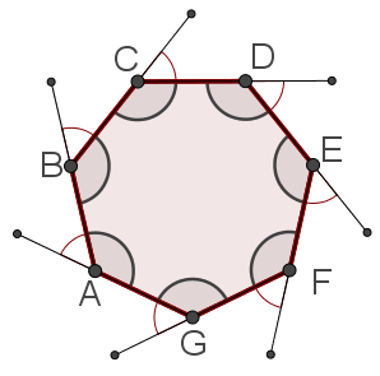
Todo polígono regular possui o mesmo número de vértices, lados, ângulos internos e ângulos externos. Para verificar isso, observe no exemplo a seguir um heptágono regular com sete lados, sete vértices, sete ângulos internos e sete ângulos externos.
 2ª Propriedade
2ª Propriedade
A medida de cada ângulo interno de um polígono regular.
S = (n – 2)180
n
S = som dos lados
n = quantidade ledos
Essa fórmula é usada para encontrar a soma das medidas dos ângulos internos de um polígono convexo dividido pelo número de lados que o polígono possui.
Como exemplo, temos que cada ângulo interno de um octógono regular mede 135°, pois:
a = (n – 2)180
n
a = (8 – 2)180
8
a = (6)180
8
a = 1080
8
a = 135°
3ª Propriedade
A medida de cada ângulo externo de um polígono regular é obtida pela seguinte fórmula:
e = 360
n
Nessa fórmula, n é o número de lados do polígono.
Assim, cada ângulo externo de um hexágono regular mede 60°, pois:
e = 360
n
e = 360
6
e = 60°
 OBSERVAÇÃO: a somo ao ângulos externos de um polígono qualquer (independente da quantidade de lados) é sempre igual a 360º.
OBSERVAÇÃO: a somo ao ângulos externos de um polígono qualquer (independente da quantidade de lados) é sempre igual a 360º.
FÓRMULAS

EXERCÍCIOS RESOLVIDOS
01) Qual a soma dos ângulos internos de um icoságono convexo?
Resolução:
Os icoságonos são polígonos que possuem 20 lados. A soma dos ângulos internos é:
S = (n – 2)180
S = (20 – 2)180
S = 18 .180
S = 3280°
Qual é a medida de cada ângulo interno de um icoságono regular?
Polígonos regulares possuem ângulos congruentes. Assim, já sabendo que a soma dos ângulos internos do icoságono é 3280°, cada ângulo dele é igual a:
3280 = 162°
20
Resposta: 162º
02) Qual é a soma dos ângulos internos de um heptágono regular?
Resolução:
O heptágono possui 7 lados.
S = (n – 2) . 180º
S = (7 – 2) . 180º
S = 5 . 180º
S = 900º
A soma dos ângulos internos de um heptágono é 900º.
03) Qual a soma dos ângulos internos de um icoságono (20 lados)?
Resolução:
Aplicando a fórmula:
S = (n – 2) . 180º
S = (20 – 2) . 180º
S = 18 . 180º
S = 3240º
A soma dos ângulos internos de um icoságono é 3240º.
Observação: podemos utilizar a fórmula da soma dos ângulos internos para calcular o número de lados de qualquer polígono, desde que a soma dos ângulos internos seja dada.
04) Quantos lados possui um polígono cuja soma dos ângulos internos é igual a 2340º?
Resolução:
S = (n – 2) . 180º
2340º = (n – 2) . 180º
2340º = 180n – 360º
2340 + 360 = 180n
2700 = 180n
180n = 2700
n = 2700/180
n = 15
O polígono possui 15 lados.
Observação: a soma dos ângulos externos de qualquer polígono regular é 360º. Para calcular a medida do ângulo externo de um polígono é preciso dividir 360º pelo número de lados da figura poligonal.
04) Quanto mede o ângulo externo do hexágono?
Resolução:
O hexágono possui seis lados, então:
ai = 360º / 6
ai = 60º
Resposta: cada ângulo externo de um hexágono mede 60º.
05) A respeito das classificações que os polígonos podem sofrer, assinale a alternativa que for correta:
(A) Um polígono é chamado convexo quando, dados os pontos A e B em seu interior, existe um único segmento que liga esses pontos.
(B) Um polígono é chamado não convexo quando, dados os pontos A e B, nem todos os pontos do segmento AB estão no interior do polígono.
(C) Um polígono é chamado regular quando todos os seus ângulos possuem a mesma medida.
(D) Um polígono é chamado regular quando todos os seus lados possuem a mesma medida.
(E) Um polígono convexo não pode ser regular.
Resolução:
a) Incorreta!
No plano, sempre existirá um segmento de reta que ligará dois pontos. Portanto, a afirmativa é inconclusiva. Apenas com essa afirmativa é impossível determinar se um polígono é convexo ou não, pois, para que um polígono seja convexo, é necessário que nenhum dos pontos do segmento AB seja exterior ao polígono, quando os pontos A e B estiverem em seu interior.
b) Correta!
c) Incorreta!
Um polígono é regular quando seus ângulos internos têm a mesma medida e, ao mesmo tempo, seus lados são todos congruentes.
d) Incorreta!
Os ângulos desse polígono precisam ter a mesma medida para que ele seja regular.
e) Incorreta!
Para que um polígono seja regular, ele precisa obrigatoriamente ser convexo.
Alternativa: B
06) Todo polígono é composto por elementos que são outras figuras geométricas e que recebem um nome especial por causa de sua função, definição e propriedades. A respeito desses elementos dos polígonos, assinale a alternativa correta:
(A) Os triângulos não possuem diagonais.
(B) Uma diagonal de um polígono é qualquer segmento de reta que liga dois de seus vértices.
(C) Um ângulo externo de um polígono é qualquer ângulo que pertença a ele e que não seja um ângulo interno.
(D) Os quadrados possuem apenas uma diagonal.
(E) Os retângulos e os quadrados possuem um número diferente de diagonais.
Resolução:
a) Correta!
As diagonais são segmentos de reta que ligam dois vértices não consecutivos de um polígono. Não existem vértices que não sejam consecutivos em um triângulo, por isso não existem diagonais nele.
b) Incorreta!
Para ser diagonal, o segmento de reta precisa ligar dois vértices não consecutivos do polígono.
c) Incorreta!
Um ângulo externo é a abertura entre um lado e o prolongamento do lado adjacente a ele. Portanto, não é qualquer ângulo que pode ser considerado um ângulo externo de um polígono.
d) Incorreta!
Os quadrados possuem duas diagonais.
e) Incorreta!
Quadrados e retângulos possuem o mesmo número de diagonais.
Alternativa: A
07) Um polígono convexo que possua exatamente 170 diagonais é formado por quantos lados?
(A) 10 lados
(B) 13 lados
(C) 15 lados
(D) 17 lados
(E) 20 lados
Resolução:
Para descobrir o número de lados de um polígono convexo, sabendo-se seu número de diagonais, basta usar a fórmula da soma das diagonais de um polígono convexo. Substituindo nessa fórmula o número de diagonais desse polígono, teremos:
S = n(n – 3)
2
170 = n(n – 3)
2
170·2 = n(n – 3)
340 = n2 – 3n
n2 – 3n – 340 = 0
Δ = b2 – 4·a·c
Δ = (– 3)2 – 4·1·(– 340)
Δ = 9 + 1360
Δ = 1369
n = – b ± √Δ
2a
n = – (– 3) ± √1369
2
n = 3 ± 37
2
n’ = 3 + 37 = 40 = 20
2 2
n’’ = 3 – 37 = – 34 = – 17
2 2
Como não pode existir um polígono com – 17 lados, então essa figura tem exatamente 20 lados.
Alternativa: E
08) Qual é a medida de um ângulo interno de um eneágono regular?
(A) 100°
(B) 110°
(C) 120°
(D) 140°
(E) 150°
Resolução:
Um eneágono é um polígono que possui nove lados. A medida de cada um dos ângulos internos dessa figura é dada pela seguinte expressão:
A = (n – 2)180
n
A = (9 – 2)180
9
A = (7)180
9
A = 1260
9
A = 140°
Cada ângulo interno de um polígono convexo que possua nove lados mede 140°.
Alternativa: D
09) Os polígonos podem ser classificados como convexos ou não convexos, regulares ou não regulares. A respeito dessa classificação, assinale a alternativa correta:
(A) Um polígono é dito convexo quando possui todos os lados iguais.
(B) Um polígono é dito convexo quando possui todos os ângulos iguais.
(C) Um polígono é regular quando possui lados congruentes.
(D) Um polígono é convexo quando qualquer segmento de reta, que possui extremidades em seu interior, não possui pontos fora dele.
(E) Um polígono é dito regular quando um segmento de reta, que possui extremidades em seu interior, possui pontos fora dele.
Resolução:
Um polígono é dito convexo quando não existe nenhum segmento de reta com extremidades em seu interior com pontos fora dele. Um polígono é dito regular quando seus lados são congruentes e todos os seus ângulos internos têm a mesma medida. Assim, as alternativas a, b, c e e estão incorretas.
Alternativa: D
10) Considerando os elementos dos polígonos convexos e suas definições básicas, assinale a alternativa correta:
(A) Os lados de um polígono são segmentos de reta que podem cruzar-se em qualquer ponto.
(B) O vértice de um polígono é o ponto de encontro entre seus dois maiores lados.
(C) Os ângulos externos de um polígono são a abertura entre dois lados consecutivos, só que pelo lado externo do polígono.
(D) Os ângulos internos do polígono são a abertura entre dois lados consecutivos do polígono, em seu interior.
(E) As diagonais de um polígono são segmentos de reta que ligam dois de seus vértices.
Resolução:
a) Incorreta!
Os lados de um polígono são segmentos de reta que não se cruzam. Esses elementos encontram-se apenas em suas extremidades.
b) Incorreta!
Os vértices de um polígono são todos os pontos de encontro entre seus lados.
c) Incorreta!
Os ângulos externos de um polígono são a abertura entre um lado e o prolongamento do lado adjacente.
d) Correta!
e) Incorreta!
As diagonais de um polígono são segmentos de reta que ligam dois de seus vértices, com a condição de que esses vértices não sejam consecutivos. O segmento de reta que liga dois vértices consecutivos de um polígono é o lado.
Alternativa D
11) A soma dos ângulos internos de um polígono convexo é igual a 2340°. Quantos lados esse polígono possui?
(A) 13 lados
(B) 15 lados
(C) 17 lados
(D) 19 lados
(E) 21 lados
Resolução:
Para fazer esse cálculo, basta usar a fórmula:
S = (n – 2)180
Em que S é a soma dos ângulos internos do polígono e n é seu número de lados. Substituindo 2340° nessa fórmula, teremos:
2340 = (n – 2)180
2340 = n – 2
180
13 = n – 2
n = 13 + 2
n = 15
O polígono possui 15 lados.
Alternativa B
12) Um polígono convexo possui 25 lados. Qual é o número total de diagonais que esse polígono possui?
(A) 200
(B) 225
(C) 250
() 260
(E) 275
Resolução:
Para encontrar o número de diagonais de um polígono convexo, basta usar a fórmula:
d = n(n – 3)
2
Na qual n é o número de lados do polígono. Substituindo n por 25, teremos:
d = n(n – 3)
2
d = 25(25 – 3)
2
d = 25(22)
2
d = 25·11
d = 275
Alternativa E
13) Calcule a soma dos ângulos internos de um triângulo qualquer e de um retângulo qualquer.
Resolução:
Independentemente do polígono a que o exercício ou situação se refira, a soma dos seus ângulos internos tem valor fixo e é dada pela fórmula S = (n – 2)·180, em que n é o número de lados do polígono. Logo,
Soma dos ângulos internos do triângulo:
S = (3 – 2)·180
S = 1·180
S = 180°
Qualquer que seja o triângulo, a soma de seus ângulos internos sempre será igual a 180°. Isso pode ser usado quando conhecemos as medidas de dois dos ângulos internos de um triângulo e é necessário calcular o valor da última.
Soma dos ângulos internos de um retângulo:
S = (4 – 2)·180
S = 2·180
S = 360°
Observação: não só retângulos, mas qualquer que seja o quadrilátero, a soma de seus ângulos internos será 360°.
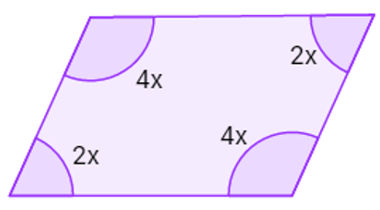
14) Calcule o valor de cada ângulo do quadrilátero seguinte:
 Resolução:
Resolução:
A soma dos ângulos internos de um quadrilátero é dada por:
S = (n – 2)·180
Sabendo que o número de lados da figura é 4, basta substituir n por 4:
S = (4 – 2)·180
S = 2·180
S = 360°
Agora some os ângulos internos dessa figura e iguale o resultado a 360°:
2x + 4x + 2x + 4x = 360
12x = 360
x = 360
12
x = 30
Agora basta substituir x em cada ângulo para descobrir os seus valores.
4x = 4·30 = 120° e
2x = 2·30 = 60°
Os ângulos são 120° e 60°.
15) (UNIFESP - 2003) Pentágonos regulares congruentes podem ser conectados lado a lado, formando uma estrela de cinco pontas, conforme destacado na figura a seguir
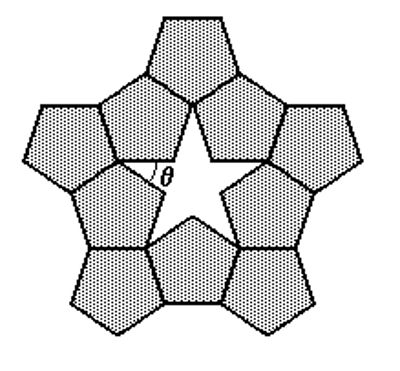 Nessas condições, o ângulo θ mede:
Nessas condições, o ângulo θ mede:
(A) 108°.
(B) 72°.
(C) 54°.
(D) 36°.
(E) 18°.
Resolução:
Na ponta da estrela onde está destacado o ângulo θ, temos o encontro de três ângulos internos de pentágonos regulares. Para descobrir a medida de cada um desses ângulos, basta calcular a soma dos ângulos internos do pentágono e dividir por 5.
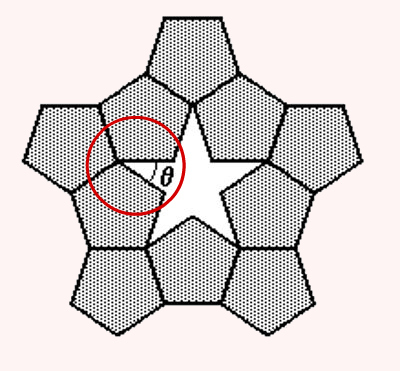
A fórmula para calcular a soma dos ângulos internos de um polígono é:
S = (n – 2)·180
*n é o número de lados do polígono. No caso desse exercício:
S = (5 – 2)·180
S = 3·180
S = 540
Dividindo a soma dos ângulos internos por 5, pois um pentágono possui cinco ângulos internos, encontraremos 108° como medida de cada ângulo interno.
Observe na imagem anterior que a soma de três ângulos internos do pentágono com o ângulo θ tem como resultado 360°.
108 + 108 + 108 + θ = 360
324 + θ = 360
θ = 360 – 324
θ = 36°
Alternativa: D
16) (FAAP-97) A medida mais próxima de cada ângulo externo do heptágono regular da moeda de R$ 0,25 é:
.jpg) (A) 60°
(A) 60°
(B) 45°
(C) 36°
(D) 83°
(E) 51°
Resolução:
Heptágonos são figuras geométricas que possuem sete lados, sete vértices e sete ângulos. Como esse heptágono é regular, então todos os seus ângulos e lados possuem a mesma medida.
A soma dos ângulos internos do heptágono é:
S = (n – 2)·180
S = (7 – 2)·180
S = 5·180
S = 900°
Cada ângulo interno do heptágono regular mede a soma dos ângulos internos dividida por 7.
900 = 128,57
7
Agora, resta apenas descobrir o valor de um ângulo externo. Os ângulos externos de um polígono são suplementares aos ângulos internos respectivos. Portanto, a soma entre um ângulo interno e seu ângulo externo tem como resultado 180°. Dessa forma, os ângulos externos da moeda de 25 centavos medem:
128,57 + x = 180
x = 180 – 128,57
x = 51,43°
Alternativa: E
Vistas ortogonais de figuras espaciais.
Projeções ortogonais
A projeção ortogonal das figuras geométricas sobre um plano pode ser comparada à sombra desse mesmo objeto no horário em que o sol está mais alto no dia. Nesse horário, a sombra possui dimensões iguais às do objeto, mas não possui profundidade alguma.
As projeções ortogonais sempre são exploradas nas avaliações porque a única forma de resolver problemas sobre o possível formato de uma projeção é por meio de raciocínio lógico.
Projeção do ponto sobre o plano
A figura formada pela projeção ortogonal de um ponto P sobre o plano é o ponto P'. Essa projeção é definida como a extremidade do segmento de reta perpendicular ao plano cuja outra extremidade seja o ponto P.
Observe que um segmento de reta é perpendicular a um plano quando, dado o ponto P' de intersecção entre os dois, todas as retas pertencentes a esse plano que passam por esse ponto P' são perpendiculares ao segmento de reta dado. Para verificar isso, é suficiente observar duas retas perpendiculares contidas no plano.

Projeção ortogonal P' do ponto P sobre o plano
Projeção da reta sobre o plano
A figura formada pela projeção ortogonal de uma reta r sobre o plano é outra reta s. Essa projeção é definida como a intersecção entre o plano que contém a reta r e o plano que contém a reta s quando os dois são perpendiculares.
No caso particular em que a reta r já é perpendicular ao plano, a sua projeção sobre esse plano é apenas um ponto.
 Projeção ortogonal da reta r sobre um plano
Projeção ortogonal da reta r sobre um plano
Projeção do segmento de reta sobre o plano
A figura formada pela projeção ortogonal de um segmento de reta sobre o plano é outro segmento de reta. Essa projeção é definida como o segmento de reta cujas extremidades são as projeções ortogonais dos pontos extremos do segmento de reta inicial. A imagem a seguir ilustra essa situação.
Os segmentos de reta também possuem uma particularidade: se o segmento for perpendicular ao plano, sua projeção ortogonal será apenas um ponto.

Projeção de uma figura sobre o plano
A projeção ortogonal de uma figura geométrica qualquer sobre o plano é o conjunto das projeções ortogonais de seus pontos sobre o plano. Sendo assim, cada ponto dessa figura representa a extremidade de um segmento de reta. A outra extremidade está no plano, e a figura formada por todas essas últimas é a projeção ortogonal da figura geométrica.
Revisão

Teorema de Euler
Válido somente para os Polígonos Regulares, o teorema desenvolvido pelo matemático Euler relaciona os três principais componentes dos poliedros: as faces, os lados e os vértices.
V + F = A + 2
V = número de vértices
F = número de faces
A = número de arestas
EXERCÍCIOS RESOLVIDOS
01) (Vassouras RJ – IBFC) Um poliedro convexo tem 9 faces e 16 arestas. Desse modo, o total de vértices desse poliedro é:
(A) 12
(B) 9
(C) 15
(D) 11
(E) 10
Resolução:
Utilizando a relação de Euler:
V + F = A + 2
V + 9 = 16 + 2
V = 18 – 9
V = 9
Alternativa: B
02) (SISPREM RS – FUNDATEC) Um enfeite em formato de pirâmide regular e de base quadrada tem o lado da base medindo 10 cm e a altura de 30 cm. Qual é o volume em cm³ dessa pirâmide?
(A) 300.
(B) 690.
(C) 830.
(D) 950.
(E) 1.000.
Resolução:
 Antes de calcularmos o volume da pirâmide, vamos calcular a área da base (quadrado):
Antes de calcularmos o volume da pirâmide, vamos calcular a área da base (quadrado):
Ab = 10² = 100 cm²
Calculando o volume da pirâmide:
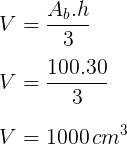
Alternativa: E
04) (ENEM) Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura. Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a
(A) 5 cm.
(B) 6 cm.
(C) 12 cm.
(D) 24 cm.
(E) 25 cm.
Resolução:
Sendo a a aresta do cubo, temos:
a3 = 4 . 18 . 3
a3 = 216
a = 6
09) (ENEM) Considere um caminhão que tenha uma carroceria na forma de um paralelepípedo retângulo, cujas dimensões internas são 5,1 m de comprimento, 2,1 m de largura e 2,1 m de altura. Suponha que esse caminhão foi contratado para transportar 240 caixas na forma de cubo com 1 m de aresta cada uma e que essas caixas podem ser empilhadas para o transporte. Qual é o número mínimo de viagens necessárias para realizar esse transporte?
(A) 10 viagens.
(B) 11 viagens.
(C) 12 viagens.
(D) 24 viagens.
(E) 27 viagens.
Resolução:
No comprimento conseguiremos colocar 5 caixas, na largura 2 caixas e na altura 2 caixas. Total de caixas 5 . 2 . 2 = 20 caixas.
Número mínimo de viagens é 240/20 = 12
11) (ENEM) Das alternativas a seguir sobre os poliedros, assinale aquela que for correta:
(A) Um poliedro é um sólido geométrico limitado por qualquer tipo de superfície.
(B) Os elementos dos poliedros são os mesmos elementos dos polígonos, uma vez que ambos possuem vértices.
(C) Prismas são poliedros que possuem duas bases poligonais e todas as faces laterais com formato de paralelogramo.
(D) Prismas e pirâmides são os únicos exemplos de poliedros existentes.
(E) As esferas são poliedros.
Resolução:
a) Incorreta!
Um poliedro é um sólido geométrico limitado por polígonos, ou seja, por figura planas. Os poliedros não podem ser limitados por curvas.
b) Incorreta!
Os poliedros e polígonos possuem em comum os vértices e os segmentos de reta. Entretanto, nos polígonos, esses segmentos são chamados de lados e, nos poliedros, de arestas. Além disso, os polígonos não possuem faces, que são elementos dos poliedros.
c) Correta!
d) Incorreta!
Existe uma terceira classe de poliedros, que são aqueles que não são prismas nem pirâmides. Um exemplo deles são os troncos de pirâmides.
e) Incorreta!
As esferas não são poliedros porque não são limitadas por polígonos.
Alternativa: C
12) Observe o sólido geométrico a seguir e assinale a alternativa correta:
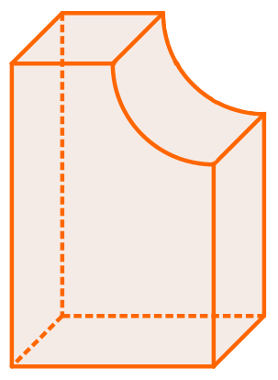 (A) É um prisma, pois possui duas bases e faces laterais planas.
(A) É um prisma, pois possui duas bases e faces laterais planas.
(B) É uma pirâmide, pois afunila em sua parte superior.
(C) É um cilindro, pois possui uma parte arredondada.
(D) É um corpo redondo, pois possui uma parte arredondada.
(E) Nenhuma das alternativas anteriores está correta.
Resolução:
O sólido em questão não é prisma nem pirâmide, pois possui uma parte arredondada, o que não é encontrado nos sólidos. Também não é cilindro, uma vez que as “bases” de um cilindro são círculos. Além disso, não é um corpo redondo, pois esse tipo de sólido possui a característica de rolar se colocado em uma superfície plana levemente inclinada. O sólido em questão não rola, independentemente do modo como for colocado.
Assim, nenhuma das alternativas está correta.
Alternativa: E
13) (ENEM) Maria quer inovar em sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas estão as planificações dessas caixas.
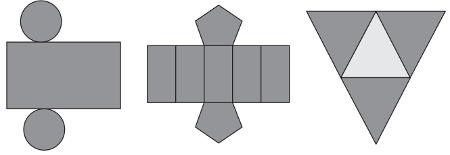 Quais serão os sólidos geométricos que Maria obterá a partir dessas planificações?
Quais serão os sólidos geométricos que Maria obterá a partir dessas planificações?
(A) Cilindro, prisma de base pentagonal e pirâmide.
(B) Cone, prisma de base pentagonal e pirâmide.
(C) Cone, tronco de pirâmide e pirâmide.
(D) Cilindro, tronco de pirâmide e prisma.
(E) Cilindro, prisma e tronco de cone.
Resolução:
Todo cilindro é formado por duas “bases” com formato de círculo. A parte curva do cilindro, ao ser planificada, gera um retângulo. Por isso, a primeira imagem é a planificação de um cilindro. A segunda imagem possui duas bases poligonais congruentes e cinco faces retangulares, justamente o necessário para a construção de um prisma pentagonal reto. Por fim, temos quatro triângulos regulares e congruentes, o número de faces necessárias para construção de um tetraedro, que é uma pirâmide.
Assim, os sólidos obtidos serão um cilindro, um prisma de base pentagonal e uma pirâmide.
Alternativa: A
14) (UF – PI) Em um poliedro convexo, o número de arestas excede o número de faces em 18. O número de vértices desse poliedro é:
(A) 10
(B) 20
(C) 24
(D) 30
(E) 32
Resolução:
Através do enunciado recebemos a informação de que F + 18 é igual ao número de arestas, ou seja, o número de arestas é igual ao número de faces mais 18 unidades.
A = F + 18
Após desenvolvermos essa igualdade, devemos substituí-la dentro da Relação de Euler e descobrir o valor que a questão pede, ou seja, o número de vértices.
V + F = A + 2
V + F – A = 2
V + F –(F + 18) = 2
V + F – F -18 = 2
V = 2 + 18
V = 20
O valor de vértices é 20
Alternativa: B
15) (Fuvest – SP) O número de faces triangulares de uma pirâmide é 11. Pode-se, então, afirmar que esta pirâmide possui:
(A) 33 vértices e 22 arestas.
B) 12 vértices e 11 arestas.
(C) 22 vértices e 11 arestas.
(D) 11 vértices e 22 arestas.
(E) 12 vértices e 22 arestas.
Resolução:
Como foi informado que temos 11 faces nessa pirâmide, concluindo que existe mais uma face que compõe a base chegamos a um valor de 12 faces no total. Sendo 12 faces triangulares, logo teremos também 12 vértices.
Nesse primeiro momento podemos eliminar as alternativas a, c e d, uma vez que sabemos que o número de vértices é 12 e apenas as opções b e e apresentam essa informação.
Sabendo que essa pirâmide possui 12 faces e 12 vértices devemos inserir essas informações na relação de Euler e descobrir o número de arestas e resolver a questão.
V + F = A + 2
12 + 12 = A + 2
24 = A + 2
A = 24 – 2
A = 22
Se possuímos 12 vértices e 22 arestas
Alternativa: E
Volume de Prismas e Cilindros

GEOMETRIA ESPACAL
Conceitos Básicos da Geometria
Os sólidos geométricos ou figuras espaciais são formadas por elementos da geometria que não precisam ser demonstrados ou provados, e portanto são chamados de axiomas.
Assim, para começar a entender algumas das figuras geométricas espaciais, precisamos entender esses conceitos básicos:
Ponto: o ponto é um elemento na geometria que não possui dimensão, é definido como alguma coisa que não possui partes. O ponto é importante pois os planos, retas, e todos os sólidos geométricos são formados por um conjunto de pontos reunidos;
Reta: as retas são pontos alinhados infinitamente, possuindo apenas comprimento. As retas são representadas por letras minúsculas do alfabeto;

Linha: a linha é diferente do conceito de retas. Apesar de ser formada por pontos, a linha pode ser curva ou não. Por exemplo, a circunferência é formada por uma linha curva;
Vértice: o vértice é um ponto que define o encontro de segmentos de retas que formam os lados dos sólidos geométricos;
Plano: planos são regiões infinitas bidimensionais (duas dimensões).
Figuras Geométricas Espaciais
A geometria espacial estuda diversos sólidos geométricos, entre as principais temos: cilindro, cubo, cone, esfera, paralelepípedo e a pirâmide.
As figuras geométrica espaciais são chamadas de poliedros, que são figuras geométricas tridimensionais, e possuem largura, comprimento e altura.
Cilindro
O cilindro é um poliedro com duas bases circulares e congruentes. Além disso, os lados tem formato circular.
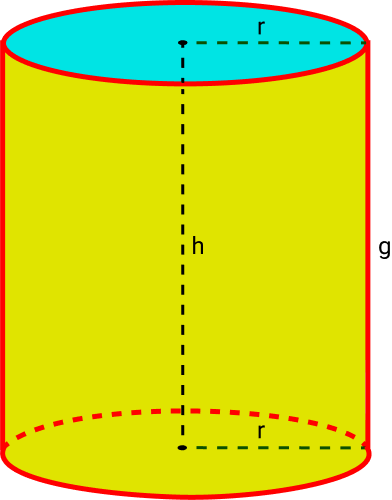
Entre os principais elementos do cilindro, temos:
Base: duas bases com formato circular e paralelas entre si;
Raio: as bases são círculos que possuem uma medida do centro até a extremidade, chamada de raio;
Geratriz: as geratrizes são segmentos de retas que formam o lado do cilindro;
Diretriz: a diretriz é o ponto na base da geratriz que indica a direção da geratriz.
Cubo
O cubo é um hexaedro regular, ou seja, possuem 6 faces com as mesmas medidas, tanto para área, ângulos e quantidade de arestas.

O cubo é formado pelos seguintes elementos:
Arestas: possui 12 arestas congruentes;
Faces: possui 6 faces quadrangulares;
Diagonais: possui 4 diagonais internamente no cubo;
Vértices: possui 8 vértices;
Ângulos: possui 24 ângulos retos.
Cone
O cone é outro sólido geométrico bem popular, que tem o formato de uma pirâmide.
 O cone possui os seguintes elementos na sua formação:
O cone possui os seguintes elementos na sua formação:
Raio da base: a base é um círculo que possui um raio;
Geratriz: segmentos de retas que formam os lados do cone;
Vértice: ponto que não pertence ao plano da base;
Esfera
A esfera é uma figura geométrica espacial que é limitada por uma superfície esférica. A superfície da esfera é formado por um conjunto de pontos que ficam a uma distância do centro por uma medida que é chamada de raio.
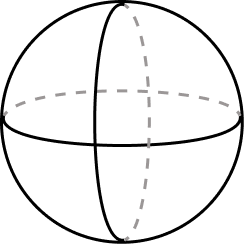
A esfera possui algumas partes importantes chamadas de partes da esfera:
Superfície Esférica: é a região superficial da esfera;
Cunha Esférica: a cunha é uma região entre dois semicírculos;
Fuso Esférico: o fuso é uma parte da esfera obtida pelo giro de uma semicircunferência a um certo ângulo;
Calota Esférica: a calota esférica é uma parte da esfera cortada por um plano perpendicular ao eixo de rotação;
Polos: os polos são pontos nas extremidades do eixo de rotação da esfera;
Paralelo: é uma circunferência perpendicular ao eixo de rotação da esfera;
Meridiano: é uma circunferência na superfície na mesma direção do eixo de rotação da esfera.
Paralelepípedo
O paralelepípedo é um poliedro formado por paralelogramos. Suas faces opostas são paralelas, com ângulos retos.
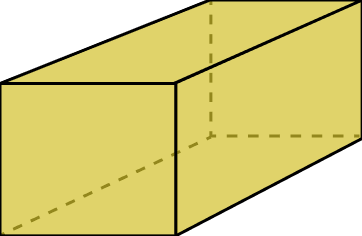 O paralelepípedo possui os seguintes elementos na sua formação:
O paralelepípedo possui os seguintes elementos na sua formação:
Faces: possui 6 faces;
Vértices: possui 8 vértices;
Arestas: possui 12 arestas.
Pirâmide
É um poliedro com base poligonal e os lados são formadas por polígonos triangulares, unidas num vértice que não pertence ao plano da base.
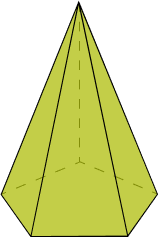 A pirâmide é formada pelos seguintes elementos:
A pirâmide é formada pelos seguintes elementos:
Arestas laterais: segmentos de retas da base até o vértice;
Faces laterais: formadas por triângulos;
Arestas da base: segmentos de retas ligando os vértices;
Altura da pirâmide: definida pelo vértice;
Apótema da pirâmide: altura da face da pirâmide.
Observação: Na geometria, chama-se aresta o segmento de linha que se encontra com dois vértices em um polígono, poliedro, ou polítopo. Em um poliedro, ou generalizando um polítopo, uma aresta é um segmento de intersecção entre duas faces. Esse segmento comum é o "canto", ou "quina" da figura geométrica. A aresta também possui o nome de "reta".
Poliedros
São aqueles cujas superfícies são formadas apenas por polígonos planos.
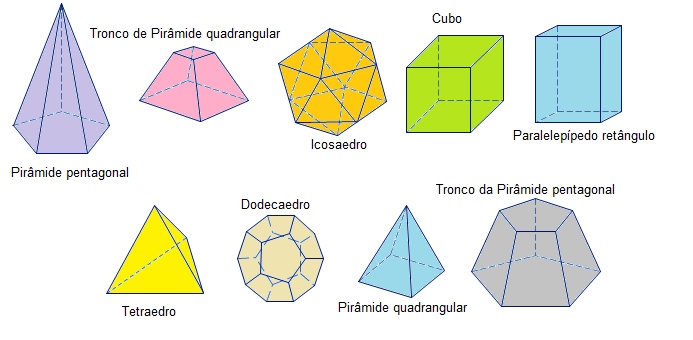
Corpos redondos
São aqueles cujas superfícies têm ao menos uma parte que é arredondada (não plana).
Qualquer poliedro convexo possui a característica de Euler
V + F = A + 2
V = número de vértices
A = número de arestas
F = número de faces.
Observação: Esta equação é conhecida por Fórmula de Euler.
Exemplo.
Um cubo tem 8 vértices e 6 faces, logo possui 12 arestas
Fórmulas de Área e Volume dos Sólidos

 EXERCÍCIOS RESOLVIDOS
EXERCÍCIOS RESOLVIDOS
01) Calcule o volume de um cilindro cuja altura mede 10 cm e o diâmetro da base mede 6,2 cm. Utilize o valor de 3,14 para π.
Resolução:
Primeiramente, vamos encontrar o valor do raio dessa figura. Lembre-se que o raio é duas vezes o diâmetro. Para tanto, dividimos o valor do diâmetro por 2:
6,2 : 2 = 3,1
r: 3,1 cm
h: 10 cm
V = π.r2.h
V = π . (3,1)2 . 10
V = π . 9,61 . 10
V = π. 96,1
V = 3,14 . 96,1
V = 301,7 cm3
02) Um tambor cilíndrico tem uma base de 60 cm de diâmetro e a altura de 100 cm. Calcule a capacidade desse tambor. Utilize o valor de 3,14 para o π.
Resolução:
Primeiramente, vamos encontrar o raio dessa figura, dividindo o valor do diâmetro por 2:
60 : 2 = 30 cm
Assim, basta colocar na fórmula os valores:
V = π . r2 . h
V = π . (30)2 . 100
V = π . 900 . 100
V = 90 . 000 π
V = 282.600 cm3
03) Determine a área e o volume de um cilindro que possui raio da base medindo 5 cm e altura medindo 6 cm.
Resolução:
O exercício forneceu-nos a medida do raio r = 5 cm e altura h = 6 cm.
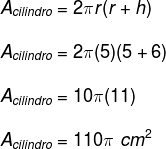

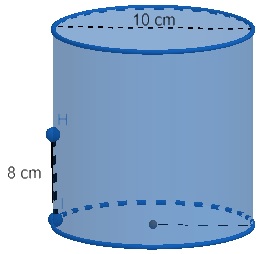
04) (Vunesp) Uma pessoa comprou um litro de leite, e, após beber certa quantidade, colocou o restante dele em uma caneca de alumínio na forma de um cilindro circular reto, com 10 cm de diâmetro interno, conforme ilustra a figura:
05) (PM - ES) Determinado cubo possui volume de 729 cm³. Cada face desse cubo possui área de:
(A) 3 cm2.
(B) 9 cm2.
(C) 27 cm2.
(D) 54 cm2.
(E) 81 cm2.
Resolução:
O objetivo da questão é descobrir a área de cada face do cubo. Para tanto, precisamos descobrir a medida de cada aresta (a).
A única informação que temos é que o volume do cubo é de 729 cm³.
Utilizando a fórmula do volume:
V = a³
729 = a³
a = 9 cm
Calculando a área de cada face, sabendo que as faces têm o formato de um quadrado e que cada aresta do cubo mede 9 cm:
A = a²
A = 9²
A = 81 cm²
Alternativa: E
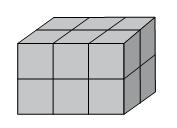
06) (SAP SP – VUNESP) Os produtos de uma empresa são embalados em caixas cúbicas, com 20 cm de aresta. Para transporte, essas embalagens são agrupadas, formando um bloco retangular, conforme mostrado na figura. Sabe-se que 60 desses blocos preenchem totalmente o compartimento de carga do veículo utilizado para o seu transporte. Pode-se concluir, então, que o volume máximo, em metros cúbicos, transportado por esse veículo é
 (A) 4,96.
(A) 4,96.
(B) 5,76.
(C) 7,25.
(D) 8,76.
(E) 9,60.
Resolução:
O primeiro passo é calcular o volume de cada caixa. Como as respostas estão apresentadas em metros cúbicos, vamos considerar que cada aresta mede 0,2 m (20 cm).
Vc = a³
Vc = 0,2³
Vc = 0,008 m³
Pela figura, percebe-se que um bloco retangular contém 12 caixas. Vamos calcular o volume de cada bloco:
Vb = 12 . 0,008 = 0,096 m³
Para finalizar, cabem 60 blocos no caminhão. Calculando o volume total:
Vt = 60 . 0,096 = 5,76 m³
Alternativa: B
07) (PM ES – Exatus) Um estoquista, ao conferir a quantidade de determinado produto embalado em caixas cúbicas de arestas medindo 40 cm, verificou que o estoque do produto estava empilhado de acordo com a figura que segue:
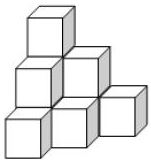 Ao realizar corretamente os cálculos do volume dessa pilha de caixas, o resultado obtido foi:
Ao realizar corretamente os cálculos do volume dessa pilha de caixas, o resultado obtido foi:
(A) 0,64 m³
(B) 1,6 m³
(C) 6,4 m³
(D) 16 m³
(E) 64 m³
Resolução:
Pela figura, é possível observar que existem 10 caixas empilhadas.
Vamos calcular o volume de cada caixa, sabendo que cada aresta mede 0,4 m (40 cm):
V = a³
V = 0,4³
V = 0, 0,064 m³
Como existem 10 caixas:
Vt = 10 . 0,064 = 0,64 m³
Alternativa: A
08) (SES DF – IADES) Sabe–se que o volume de um cubo de aresta α é dado por α³. Considerando que a aresta de um cubo seja multiplicada por 2, em quantas vezes seu volume aumentará?
(A) Duas.
(B) Três.
(C) Quatro.
(D) Seis.
(E) Oito.
Resolução:
Como foi informado, o volume de um cubo de aresta α é igual a α³. Vamos calcular o volume de um cubo de aresta 2α:
V = (2α)³
V = 2³.α³
V = 8.α³
Daí, quando multiplicamos a aresta do cubo por 2, o volume para a ser 8 vezes maior.
Alternativa: E
00) Considere uma caixa de água com formato de um paralelepípedo reto retângulo totalmente cheia, com comprimento de 7 m e largura de 4 m e altura de 2 m.
Calcule:
a) A área da base
Resolução:
A área da base desta caixa é calculada pela fórmula do retângulo, pois a base da caixa é retangular: Ab = comprimento x largura
Ab = 7 x 4 = 28 m²
b) A área lateral
Resolução:
A área da lateral de um paralelepípedo é calculada pela fórmula: Al = 2((comprimento x altura) + (largura x altura)) = (7 x 2) + (4 x 2) = 14 + 8 = 22 m²
c) A área total
Resolução:
A área total do paralelepípedo é: At = 2((comprimento x largura) + (comprimento x altura) + (largura x altura)) = (7 x 4) + (7 x 2) + (4 x 2) = 28 + 14 + 8 = 50 m²
d) O volume de água da caixa
Resolução:
O volume de um paralelepípedo é: V = (comprimento x largura x altura) = 7 x 4 x 2 = 56 m³
10) Uma fábrica produz tijolos no formato de paralelepípedos e de cubos, com volume igual. Sabendo que os tijolos no formato de paralelepípedo têm 5 cm de largura, 20 cm de comprimento e 2 cm de altura. A medida dos lados dos tijolos que têm o formato de cubo é igual a:
(A) 4,64 cm
(B) 7,1 cm
(C) 10 cm
(D) 20,4 cm
(E) 35 cm
Resolução:
O volume do paralelepípedo é: Volume paralelepípedo = 50 x 5 x 2= 100 cm³
Como a questão diz que o paralelepípedo e o cubo possui volume igual, então:
Volume paralelepípedo = Volume cubo
Considerando a como a medida da aresta do cubo, então:
Volume cubo = a³
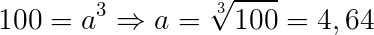
Logo, as arestas dos tijolos com formato de cubo possui um tamanho aproximado de 4,64 cm.
Alternativa: A
11) Um aquário possui o formato de um paralelepípedo com as seguintes dimensões:
.jpg) Determine quantos litros de água são necessários para encher o aquário.
Determine quantos litros de água são necessários para encher o aquário.
Resolução:
V = comprimento x largura x altura
V = 50 cm x 20 cm x 15 cm
V = 15000 cm³ (centímetros cúbicos)
Como foi informado que 1 cm³ corresponde a 1 ml, temos que 15000 cm³ é igual a 15000 ml ou 15 litros.
12) O degrau de uma escada lembra a forma de um paralelepípedo com as seguintes dimensões: 1 m de comprimento, 0,5 m de largura e 0,4 m de altura. Determine o volume total de concreto gasto na construção dessa escada sabendo que ela é constituída de 20 degraus.
.jpg) Resolução:
Resolução:
Volume do degrau
V = 1 m x 0,5 m x 0,4 m
V = 0,20 m³
Volume total da escada
0,20 x 20
4 m³ ou 4 mil litros de concreto.
13) Considere um cone cuja base tem raio 2 m e a altura mede 8 m. Considere π = 3,14. Calculemos o volume do cone:
Resolução:
V = ⅓ π.r2.h
V = 1 . 3,14 . 22 . 8
3
V = 3,14 . 4 . 8
3
V = 100,48
3
V ≈ 33,49 m3
Então o volume do cone é de, aproximadamente, 33,49 m3.
14) Um cone circular reto em que a geratriz mede 5 m e a altura, 4 m.
Resolução:
Para calcularmos o volume desse sólido, precisamos encontrar a medida do raio, para tanto, utilizaremos o Teorema de Pitágoras:
g2 = h2 + r2
r2 = g2 – h2
r2 = 52 – 42
r2 = 25 – 16
r2 = 9
r = 3 m
Agora que temos o valor do raio, podemos calcular o volume do cone utilizando a fórmula:
V = ⅓ π.r2.h
V = 1 . 3,14 . 32 . 4
3
V = 3,14 . 9 . 4
3
V = 113,04
3
V = 37,68 m3
Portanto, o volume desse cone circular reto é 37, 68 m3.
15) Um copo será fabricado no formato de um cone com as seguintes medidas: 4 cm de raio e 12 cm de altura. Qual será a capacidade do copo?
Resolução:
.jpg)
16) Uma fábrica de doces e balas irá produzir chocolates na forma de guarda-chuva, com as seguintes medidas: 8 cm de altura e 3 cm de raio de acordo com a ilustração. Qual a quantidade de chocolate utilizada na produção de 2000 peças?
Resolução:
.jpg)
Cada chocolate possui 75,36 cm³ de volume. A fábrica quer produzir 2000 peças, então:
2000 * 75,36 = 150 720 cm³
Lembrando que 1 cm³ = 1 ml, temos 150 720 ml de chocolate que corresponde a 150,72 litros.
17) Uma casquinha de sorvete possui o formato de um cone reto com altura de 10 cm e raio da base medindo 5 cm. Determine o volume da casquinha.
Resolução:
.jpg)
O volume da casquinha é de 261,66 cm³, que corresponde a, aproximadamente, 261 ml.
18) Um reservatório possui volume de aproximadamente 3000 m³ e diâmetro da base medindo 24 metros. Determine a altura deste reservatório.
Resolução:
O valor do raio nesse exemplo é 12, porque o raio é metade do diâmetro, veja:
r = d
2
r = 24
2
r = 12
Agora que já sabemos o valor do raio podemos calcular o volume do reservatório.
.jpg)
A altura do reservatório é de aproximadamente 20 metros.
19) Uma pirâmide de base quadrangular possui altura medindo 2 metros e cada lado da base com medida igual a 3 metros. Determine o volume dessa pirâmide.
.jpg) Resolução:
Resolução:
.jpg)
20) Uma indústria irá fabricar uma peça no formato de uma pirâmide de base triangular com as medidas indicadas na figura. Sabendo que serão fabricadas 500 peças maciças de aço, determine o volume total de aço que será gasto na produção dessas peças.
.jpg) Resolução:
Resolução:
.jpg)
21) A figura representa uma pirâmide de base pentagonal com lados regulares medindo 12 metros e a apótema da base medindo 8,2 metros, aproximadamente. Sabendo que a altura dessa pirâmide é igual a 20 metros, qual será sua capacidade sabendo que 1 m³ corresponde a 1000 litros?
.jpg) Resolução:
Resolução:
Área da base e Volume
.jpg)
Se 1m³ corresponde a 1000 litros, temos que:
1640m³ = 1640 * 1000 = 1 640 000 litros de capacidade.
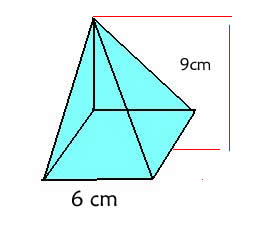
22) Calcule o volume da pirâmide de base quadrada a seguir:
 Resolução:
Resolução:
Pela análise da figura, temos que:
h = 9 cm
Ab = 62 = 36 cm2
Assim, o volume da pirâmide será dado por:
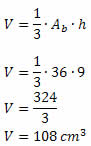
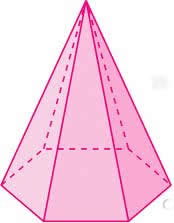
23) Calcule o volume de uma pirâmide regular de base hexagonal sabendo que sua altura é de 12 cm e que cada aresta da base mede 8 cm.
 Resolução:
Resolução:
Primeiro, vamos calcular a área da base dessa pirâmide. Sabemos que a base da pirâmide é um hexágono regular de 8 cm de aresta. A área do hexágono regular é dada por:

Conhecida a medida da área da base da pirâmide, podemos utilizar a fórmula do volume.
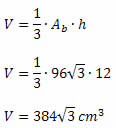
24) (ENEM) Uma empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugerem que seja adicionado 1,5 mL desse produto para cada 1 000 L de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a 1,7 m, com largura e comprimento iguais a 3 m e 5 m, respectivamente. O nível da lâmina d’água dessa piscina é mantido a 50 cm da borda da piscina.
A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é
(A) 11,25.
(B) 27,00.
(C) 28,80.
(D) 32,25.
(E) 49,50.
Resolução:
De acordo com o enunciado temos que o volume de água na piscina é igual a:
V = 5 . 3 . 1,2 = 15 . 1,2 = 18 m³ = 18 000 l
Logo, a quantidade de produto será: (18 000 . 1,5) / 1 000 = 27 ml
Alternativa: B
25) Um reservatório em formato cilíndrico possui raio igual a 2 metros e sua altura é de 10 metros, como mostra a imagem a seguir. Qual é o volume desse reservatório? (considere π = 3,14).
 (A) 125,6 m3
(A) 125,6 m3
(B) 115,6 m3
(C) 100,6 m3
(D) 75,6 m3
(E) 15,6 m3
Resolução:
O volume do cilindro é dado pela área da base multiplicada por sua altura. Assim, podemos obter essa medida com a seguinte fórmula:
V = π . r2 . h
Substituindo os valores de π, do raio e da altura desse cilindro, teremos:
V = 3,14 . 22 . 10
V = 31,4 . 4
V = 125,6 m3
Alternativa A
26) Um cilindro possui volume igual a 7850 cm3 e seu diâmetro mede 10 centímetros. Qual é a medida da altura desse cilindro? (Considere π = 3,14).
(A) 50 cm
(B) 100 cm
(C) 120 cm
(D) 150 cm
(E) 200 cm
Resolução:
Para determinar a altura do cilindro, basta usar a fórmula do volume, uma vez que conhecemos seu volume e raio. Para encontrar o raio, lembre-se de que o diâmetro tem o dobro da medida do raio, logo, r = 5 cm.
V = π . r2 . h
7850 = 3,14 . 52·h
7850 = 3,14 .25h
7850 = 3,14 . 25h
7850 = 78,5h
7850 = h
78,5
h = 100 cm
Alternativa B
27) (ENEM) Uma artesã confecciona dois diferentes tipos de vela ornamental a partir de moldes feitos com cartões de papel retangulares de 20 m x 10 cm (conforme ilustram as figuras abaixo). Unindo dois lados opostos do cartão, de duas maneiras, a artesã forma cilindros e, em seguida, os preenche completamente com parafina.
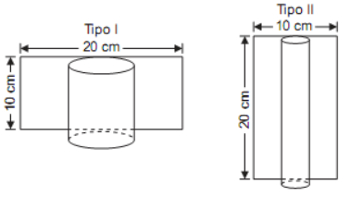 Supondo que o custo da vela seja diretamente proporcional ao volume da parafina empregado, o custo da vela do tipo I, em relação ao custo da vela do tipo II, será:
Supondo que o custo da vela seja diretamente proporcional ao volume da parafina empregado, o custo da vela do tipo I, em relação ao custo da vela do tipo II, será:
(A) o triplo.
(B) o dobro.
(C) igual.
(D) a metade.
(E) a terça parte.
Resolução:
Será preciso encontrar o volume de cada um dos cilindros, mas, para isso, é preciso encontrar primeiramente seus raios. Para tanto, basta notar que o comprimento da circunferência é igual ao comprimento do lado maior do retângulo no cilindro I e no cilindro II é igual ao lado menor desse mesmo retângulo. Usando a fórmula do comprimento da circunferência, encontraremos os raios:
CI = 2π . r . I
20 = 2π . r . I
20 = r . I
2π
10 = r . I
π
CII = 2π . R . II
10 = 2π . r . II
10 = r . II
2π
5 = rII
π
O volume do primeiro cilindro é:
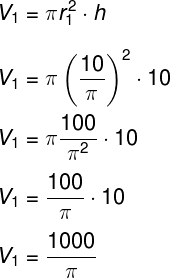
Já o volume do segundo cilindro é:
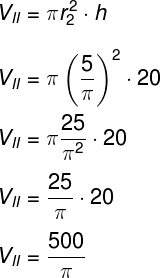
Portanto, o volume do cilindro 1 é o dobro do volume do cilindro 2.
Alternativa B
28) Qual é o volume de um cilindro cuja altura é igual ao dobro de seu raio.
(A) πr3
(B) 2r3
(C) 2πr
(D) 2π
(E) 2πr3
Resolução:
Se o raio desse cilindro mede x, então sua altura mede 2x. Logo:
V = πr2 . h
V = πx2 . 2x
V = 2π . r3
Alternativa: E
29) (ENEM) Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.
 Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá
Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá
(A) encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
(B) encher a leiteira toda de água, pois ela tem um volume 20 vezes maior que o volume do copo.
(C) encher a leiteira toda de água, pois ela tem um volume 10 vezes maior que o volume do copo.
(D) encher duas leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
(E) encher cinco leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
Resolução:
O volume do copinho plástico, em centímetros cúbicos, é π . 2² . 4 = 16π
O volume da leiteira, em centímetros cúbicos, é π . 4² . 20 = 320π
(Volume da leiteira) ÷ (volume do copinho) = 320π/16π = 20
Assim, para encher os vinte copinhos plásticos pela metade, é suficiente encher a leiteira até a metade.
Alternativa: A
31) (ENEM) Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19 cm de altura e 6 cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura — 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior —, espaçados de 1 cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.
 Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
(A) 156 cm³.
(B) 189 cm³.
(C) 192 cm³.
(D) 216 cm³.
(E) 540 cm³.
Resolução:
O volume de parafina gasto na nova vela corresponde à subtração do volume da pirâmide maior, com aresta da base de 6 cm e altura de 19 – 3 = 16 cm, pelo volume da pirâmide menor, com 1,5 cm de aresta da base e 4 cm de altura.
Como volume da pirâmide é calculado pela terça parte do produto da área da base pela altura, o volume de parafina, em cm³, é de 1/3 . 6 . 6 . 16 − 1/3 . 1,5 . 1,5 . 4 = 192 – 3 = 189 cm³.
Alternativa: B
32) (Prefeitura de Ceará Mirim – RN – Comperve) Um brilhante com formato de um octaedro é exibido em uma concorrida exposição. Por medida de segurança, ele foi colocado no interior de um cubo de vidro com seus vértices tocando, precisamente no meio de cada face do cubo, conforme a figura abaixo.
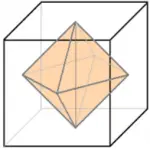 Se o volume do cubo é 1.728 cm³ , o volume do octaedro, em cm³ , será
Se o volume do cubo é 1.728 cm³ , o volume do octaedro, em cm³ , será
(A) 144.
(B) 288.
(C) 432.
(D) 576.
Resolução
O primeiro passo é determinar a medida das arestas do cubo. Como o volume é igual a 1.728 cm³, podemos afirmar que cada aresta mede 12 cm. Veja:
12³ = 1728
O octaedro pode ser dividido em duas pirâmides. Como os vértices tocam precisamente no meio de cada face do cubo, a base dessas pirâmides é um losango onde as diagonais possuem as mesmas medidas da aresta do cubo. Também é possível observar que a altura é exatamente a metade da aresta do cubo.
Área da base da pirâmide (losango):
A = d1 x d2 / 2
A = 12 x 12 / 2
A = 72 cm²
Volume da pirâmide:
V = Ab x h / 3
V = 72 x 6 / 3
V = 144 cm³
Como o octaedro é composto por duas pirâmides:
2 x 144 = 288 cm³
Alternativa: B
33) (Bombeiros MG – Igetec) O hexaedro regular que inscreve a esfera de volume 9π/2 cm³, tem a medida da diagonal, em centímetros, igual a:
(A) 2,7
(B) √3
(C) 3√3
(D) 3
Resolução:
Veja como é um hexaedro e o que seria sua diagonal:
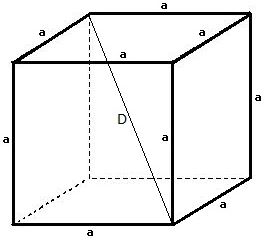
Repare que como o hexaedro está inscrito a uma esfera, a diagonal é o dobro do raio da mesma.
Podemos calcular o raio pela fórmula pois sabemos seu volume:
Volume = π . r³ . 4/3
9π/2 = π . r³ . 4/3
9/2 = r³ . 4/3
r³ = 9 . 3/2.4
r³ = 27/8
r = 3/2
Logo, a diagonal é 2 . 3/2 = 3
Alternativa: D
34) (Vassouras RJ – IBFC) Um poliedro convexo tem 9 faces e 16 arestas. Desse modo, o total de vértices desse poliedro é:
(A) 12
(B) 9
(C) 15
(D) 11
(E) 10
Resolução
Utilizando a relação de Euler:
V + F = A + 2
V + 9 = 16 + 2
V = 18 – 9
V = 9
Alternativa: B
35) (PM ES – Exatus – Geometria Espacial) O volume do sólido gerado pela rotação de um triângulo isósceles de lados congruentes medindo 5 cm e base medindo 6 cm, em torno da base é igual a:
(A) 12π cm³
(B) 13π cm³
(C) 14π cm³
(D) 15π cm³
(E) 16π cm³
Resolução:
Veja na figura que após a rotação em torno da base, teremos um sólido formado por dois cones iguais. Basta então calcular o volume de um deles e multiplicar por 2.
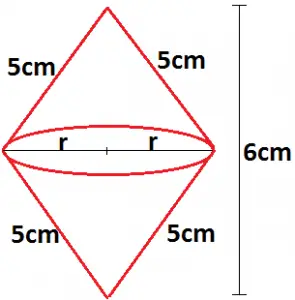
Calculando a altura h do cone através do Teorema de Pitágoras:
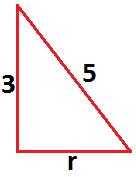
5² = 3² + r²
r² = 25 – 9
r² = 16
r = 4
Calculando o volume do cone:
V = Área da base x altura / 3
V = π . 4² . 3 / 3
V = π . 16
V = 16π cm³
Alternativa: E
36) (SISPREM RS – FUNDATEC) Um enfeite em formato de pirâmide regular e de base quadrada tem o lado da base medindo 10 cm e a altura de 30 cm. Qual é o volume em cm³ dessa pirâmide?
(A) 300.
(B) 690.
(C) 830.
(D) 950.
(E) 1.000.
Resolução:

Antes de calcularmos o volume da pirâmide, vamos calcular a área da base (quadrado):
Ab = 10² = 100 cm²
Calculando o volume da pirâmide:
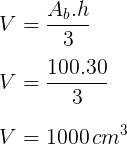
Alternativa: E
37) (AFPR – COPS) A figura, a seguir, mostra um pedaço de cartolina que será dobrado e colado ao longo das bordas para formar uma embalagem na forma de um prisma hexagonal regular reto.
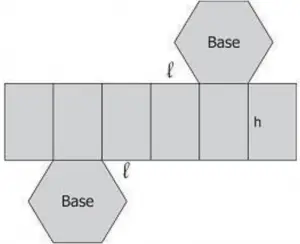 Supondo que l = 2 cm e h = 5 cm, qual é o volume dessa embalagem em cm3?
Supondo que l = 2 cm e h = 5 cm, qual é o volume dessa embalagem em cm3?
(A) √3 cm³
(B) √3/2 cm³
(C) 30√3 cm³
(D) 6√3 cm³
(E) 3√3 cm³
Resolução
O volume de um prisma pode ser calculado multiplicando-se a área da base pela altura.
Como a base é um hexágono regular, podemos calcular a área através da seguinte fórmula:
Ab = 3 . l² . √3/2
Ab = 3 . 2² . √3/2
Ab = 3 . 4 . √3/2
Ab = 6 . √3
Calculando o volume do prisma:
V = h . Ab
V = 5 . 6 . √3
V = 30 . √3 cm³
Alternativa: C
38) (Petrobras – Cesgranrio) Uma fita retangular de 2 cm de largura foi colocada em torno de uma pequena lata cilíndrica de 12 cm de altura e 192π cm³ de volume, dando uma volta completa em torno da lata, como ilustra o modelo abaixo.
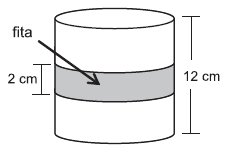 A área da região da superfície da lata ocupada pela fita é, em cm², igual a
A área da região da superfície da lata ocupada pela fita é, em cm², igual a
(A) 8π
(B) 12π
(C) 16π
(D) 24π
(E) 32π
Resolução
A informação que ainda não temos para calcular a área pedida é o raio da base do cilindro.
Nosso objetivo inicial será utilizar a medida da altura e do volume para descobrirmos o raio.
Utilizando a fórmula do volume:
V = π . r² . h
192π = π . r² . 12
192 = 12r²
r² = 192/12
r² = 16
r = 4 cm
Agora que sabemos a medida do raio, vamos calcular a área lateral ocupada pela fita, cuja altura é de 2 cm.
Al = 2 . π . r . h
Al = 2 . π . 4 . 2
Al = 16π cm²
Alternativa: C
39) (SEDUC RJ – COPERJ) A figura abaixo representa uma caixa cúbica onde a distância do ponto A até o ponto B mede 3√5 decímetros:
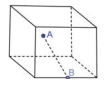 Os pontos A e B são, respectivamente, o centro de uma face e o ponto médio de uma aresta da face oposta. O volume dessa caixa, em dm³, é igual a:
Os pontos A e B são, respectivamente, o centro de uma face e o ponto médio de uma aresta da face oposta. O volume dessa caixa, em dm³, é igual a:
(A) 125
(B) 216
(C) 343
(D) 512
(E) 729
Resolução:
Precisamos calcular o volume do cubo representado na figura. Nosso primeiro objetivo é calcular a medida da aresta desse cubo, que representaremos inicialmente por x.
Vamos analisar o triângulo retângulo formado pela semi reta AB e pelas semi retas que dividem as faces ao meio.
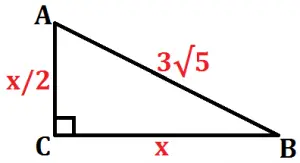
Pelo Teorema de Pitágoras temos:
(3√5)² = x² + (x/2)²
45 = x² + x²/4
45 = 5x²/4
5x² = 4 . 45
5x² = 180
x² = 180/5
x² = 36
x = 6 dm
Calculando o volume do cubo:
V = x³
V = 6³
V = 216 dm³
Alternativa: B
Probabilidade, Permutação e Arranjos
Probabilidade
Probabilidade é o estudo das chances de ocorrência de um resultado, que são obtidas pela razão entre casos favoráveis e casos possíveis.
Para compreender esse ramo, é extremamente importante conhecer suas definições mais básicas, como a fórmula para o cálculo de probabilidades em espaços amostrais equiprováveis, probabilidade da união de dois ou mais eventos, probabilidade do evento etc.
Experimento aleatório
É qualquer experiência cujo resultado não seja conhecido. Por exemplo: ao jogar uma moeda e observar a face superior, é impossível saber qual das faces da moeda ficará voltada para cima, exceto no caso em que a moeda seja viciada (modificada para ter um resultado mais frequentemente).
Suponha que uma sacola de supermercado contenha maçãs verdes e vermelhas. Retirar uma maçã de dentro da sacola sem olhar também é um experimento aleatório.
Ponto amostral
Um ponto amostral é qualquer resultado possível em um experimento aleatório. Por exemplo: no lançamento de um dado, o resultado (o número que aparece na face superior) pode ser 1, 2, 3, 4, 5 ou 6. Então, cada um desses números é um ponto amostral desse experimento.
Espaço amostral
O espaço amostral é o cunjunto formado por todos os pontos amostrais de um experimento aleatório, ou seja, por todos os seus resultados possíveis. Dessa maneira, o resultado de um experimento aleatório, mesmo que não seja previsível, sempre pode ser encontrado dentro do espaço amostral referente a ele.
Como os espaços amostrais são conjuntos de resultados possíveis, utilizamos as representações de conjuntos para esses espaços. Por exemplo: O espaço amostral referente ao experimento “lançamento de um dado” é o conjunto Ω, tal que:
Ω = {1, 2, 3, 4, 5, 6}
Esse conjunto também pode ser representado pelo Diagrama de Venn ou, dependendo do experimento, por alguma lei de formação.
O número de elementos dos espaços amostrais é representado por n(Ω). No caso do exemplo anterior, n(Ω) = 6. Lembre-se de que os elementos de um espaço amostral são pontos amostrais, ou seja, resultados possíveis de um experimento aleatório.
Evento
Os eventos são subconjuntos de um espaço amostral. Um evento pode conter desde zero a todos os resultados possíveis de um experimento aleatório, ou seja, o evento pode ser um conjunto vazio ou o próprio espaço amostral.
No primeiro caso, ele é chamado de evento impossível.
No segundo, é chamado de evento certo.
Ainda no experimento aleatório do lançamento de um dado, observe os seguintes eventos:
A = Obter um número par:
A = {2, 4, 6} e n(A) = 3
B = Sair um número primo:
B = {2, 3, 5} e n(B) = 3
C = Sair um número maior ou igual a 5:
C = {5, 6} e n(C)= 2
D = Sair um número natural:
D = {1, 2, 3, 4, 5, 6} e n(D) = 6
Espaços equiprováveis
Um espaço amostral é chamado equiprovável quando todos os pontos amostrais dentro dele têm a mesma chance de ocorrer. É o caso de lançamentos de dados ou de moedas não viciados, escolha de bolas numeradas de tamanho e peso idênticos etc.
Observação: um exemplo de espaço amostral que pode ser considerado não equiprovável é o formado pelo seguinte experimento: escolher entre tomar sorvete ou fazer caminhada.
Cálculo de probabilidades
As probabilidades são calculadas dividindo-se o número de resultados favoráveis pelo número de resultados possíveis:
P = n(E)
n(Ω)
Nesse caso, E é um evento que se quer conhecer a probabilidade, e Ω é o espaço amostral que o contém.
Por exemplo, no lançamento de um dado, qual a probabilidade de sair o número um?
Exemplo 1
Sair o número um é o evento E. Assim, n(E) = 1. O espaço amostral desse experimento contém seis elementos: 1, 2, 3, 4, 5 e 6. Logo, n(Ω) = 6.
Resolução:
P = n(E)
n(Ω)
P = 1
6
P = 0,1666…
P = 16,6%
Exemplo 2
Qual a probabilidade de obtermos um número par no lançamento de um dado?
Resolução:
Os números pares possíveis em um dado são 2, 4 e 6. Logo, n(E) = 3.
P = n(E)
n(Ω)
P = 3
6
P = 0,5
P = 50%
Observação:
As probabilidades sempre resultarão em um número dentro do intervalo 0 ≤ x ≤ 1. Isso acontece porque E é um subconjunto de Ω. Dessa maneira, E pode conter desde zero até, no máximo, o mesmo número de elementos que Ω.
Fórmula e cálculo da probabilidade
A probabilidade de acontecer determinado evento A, representado por P(A), é a divisão entre o número de casos favoráveis e o número de casos possíveis. Podemos representar, então, a chance de ocorrer o evento A por:
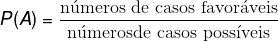 A regra do “ou”
A regra do “ou”
Outro princípio de probabilidade diz que a ocorrência de dois eventos que se excluem mutuamente é igual à soma das probabilidades com que cada evento ocorre. Esse princípio é conhecido popularmente como regra do “ou”, pois corresponde à pergunta: qual é a probabilidade de ocorrer um evento OU outro?
Exemplo 1
A probabilidade de obter “cara” ou “coroa”, ao lançarmos uma moeda, é igual a 1, porque representa a probabilidade de ocorrer “cara” somada à probabilidade de ocorrer “coroa” (1/2 + 1/2 =1).
Resolução:
Para calcular a probabilidade de obter “face 1” ou “face 6” no lançamento de um dado, basta somar as probabilidades de cada evento: 1/6 + 1/6 = 2/6.
Em certos casos precisamos aplicar tanto a regra do “e” como a regra do “ou” em nossos cálculos de probabilidade.
Exemplo 2
No lançamento de duas moedas, qual a probabilidade de se obter “cara” em uma delas e “coroa” na outra?
Resolução:
Para ocorrer “cara” na primeira moeda E “coroa” na segunda, OU “coroa” na primeira e “cara” na segunda. Assim nesse caso se aplica a regra do “e” combinada a regra do “ou”. A probabilidade de ocorrer “cara” E “coroa” (1/2 X 1/2 = 1/4) OU “coroa” e “cara” (1/2 X 1/2 = 1/4) é igual a 1/2 (1/4 + 1/4).
Eventos Independentes
Dizemos que E1 e E2 e ...En-1, En são eventos independentes quando a probabilidade de ocorrer um deles não depende do fato de os outros terem ou não terem ocorrido.
Fórmula da probabilidade dos eventos independentes:
P(E1 e E2 e E3 e ...e En-1 e En) = P(E1).P(E2).p(E3)...P(En)
Exemplo 1
Uma urna tem 30 bolas, sendo 10 vermelhas e 20 azuis. Se sortearmos 2 bolas, 1 de cada vez e repondo a sorteada na urna, qual será a probabilidade de a primeira ser vermelha e a segunda ser azul?
Resolução:
Como os eventos são independentes, a probabilidade de sair vermelha na primeira retirada e azul na segunda retirada é igual ao produto das probabilidades de cada condição:
P(A e B) = P(A).P(B).
Ora, a probabilidade de sair vermelha na primeira retirada é 10/30 e a de sair azul na segunda retirada 20/30. Daí, usando a regra do produto, temos:
10/30 . 20/30 = 2/9
Observação: na segunda retirada forma consideradas todas as bolas, pois houve reposição. Assim, P(B/A) = P(B), porque o fato de sair bola vermelha na primeira retirada não influenciou a segunda retirada, já que ela foi reposta na urna.
EXERCÍCIOS DE EVENTOS INDEPENDENTES
01) Em uma gaveta temos 12 camisas, das quais, quatro são de gola polo e o restante, de gola normal. Retirando duas camisas sucessivamente ao acaso e sem reposição, qual é a probabilidade de as duas camisas serem de gola polo?
Resolução:

02) Em uma cesta, temos oito bombons de morango, dez bombons de maracujá e quatro bombons de uva. Determine a probabilidade de retiramos sucessivamente com reposição, três bombons de maracujá.
Resolução:

03) Sabemos que um baralho é composto de 52 cartas, onde temos a representação de quatro naipes: copas, ouro, paus e espadas. Dessa forma, cada naipe é representado por 13 cartas. Determine a probabilidade de escolhermos ao acaso e sucessivamente, três cartas de um mesmo naipe sem reposição.
Resolução:
.gif)
04) Em relação ao enunciado da questão 03, determine a probabilidade de retirarmos ao acaso e sucessivamente quatro cartas, considerando uma de cada naipe e sem reposição, isto é: 1 carta de ouro, 1 carta de copas, 1carta de paus e 1 carta de espadas.
Resolução:
.gif)
05) (Cesgranrio – RJ) Um juiz de futebol possui três cartões no bolso. Um é todo amarelo, outro é todo vermelho e o terceiro é vermelho de um lado e amarelo do outro. Num determinado lance, o juiz retira ao acaso, um cartão do bolso mostrando-o a um jogador. Qual é a probabilidade de a face que o juiz vê ser vermelha, e de a outra face mostrada ao jogador, ser amarela?
Resolução:

Eventos Dependentes
Exemplos de eventos dependentes
A Faculdade de Educação da Universidade da Georgia define um evento dependente como duas variáveis em uma probabilidade de que se influenciam mutuamente. Por exemplo: existem apenas 52 cartas em um baralho, e todas são pretas ou vermelhas, têm números, imagens de reis e rainhas e símbolos como espadas, ases, ouros e paus. Assim, caso alguém pegue duas cartas em um jogo, essa pessoa pode calcular a probabilidade de quais cartas tirou.
Eventos Mutuamente Exclusivos
Dizemos que dois ou mais eventos são mutuamente exclusivos quando a realização de um, exclui a realização do(s) outro(s). Se dois eventos são mutuamente exclusivos, a probabilidade de que um ou outro ocorra é igual à soma das probabilidades de que cada um deles se realize, ou seja, os elementos desses eventos não se repetem.
P (A U B) = P(A) + P(B)
Considerando dois eventos A e B contidos num mesmo espaço amostral, existirá a presença de elementos repetidos. Sendo assim:
P(A U B) = P(A) + P(B) – P (A ∩ B)
Exemplo 1
Uma urna contém 20 bolas idênticas numeradas de 1 a 20. Extraindo-se uma bola ao acaso dessa urna, qual a probabilidade de o número da bola sorteada ser:
a) múltiplo de 2 ou 3?
Resolução:
Consideramos os seguintes eventos:
A → o número múltiplo de 2:
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
A = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20} →
B → o número múltiplo de 3:
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
B = {3, 6, 12, 15, 18} →
A ∩ B = {6, 12, 18} →
Como ou 65%.
b) múltiplo de 5 ou 7?
Resolução:
Consideramos os seguintes eventos:
A → o número é múltiplo de 5:
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
A = {5, 10, 15, 20} =
B → o número é múltiplo de 7:
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
B = {7, 14} =
Como A ∩ B = ?, então P (A U B) = P(A) + P(B). Assim:
ou 30%
Probabilidade de Eventos Simultâneos
O cálculo da probabilidade de eventos simultâneos determina a chance de dois eventos ocorrerem simultânea ou sucessivamente.
A fórmula para o cálculo dessa probabilidade decorre da fórmula da probabilidade condicional. Assim, teremos:
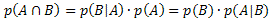
Se os eventos A e B forem independentes, ou seja, se o fato de ocorrer o evento B não alterar a probabilidade de ocorrer o evento A, a fórmula para o cálculo da probabilidade condicional será:
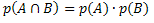
Vamos fazer alguns exemplos para explorar o uso da fórmula e a maneira correta de interpretar os problemas relacionados à probabilidade de eventos simultâneos.
Exemplo 1
Em dois lançamentos sucessivos de um mesmo dado, qual a probabilidade de ocorrer um número maior que 3 e o número 2?
Resolução:
A ocorrência de um evento não influencia a probabilidade de outro ocorrer, portanto são dois eventos independentes. Vamos distinguir os dois eventos:
A: sair um número maior que 3 → temos como possíveis resultados os números 4, 5 ou 6.
B: sair o número 2
Vamos calcular a probabilidade de ocorrência de cada um dos eventos. Observe que no lançamento de um dado, temos 6 valores possíveis.
Assim:
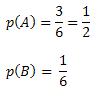
Dessa forma, teremos:
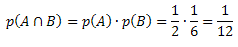
Exemplo 2
Numa urna há 30 bolinhas numeradas de 1 a 30. Serão retiradas dessa urna duas bolinhas, ao acaso, uma após a outra, sem reposição. Qual a probabilidade de sair um múltiplo de 10 na primeira e um número ímpar na segunda?
Resolução:
O fato de a retirada das bolinhas ocorrer sem reposição, implica que a ocorrência do primeiro evento interfere na probabilidade do segundo ocorrer. Portanto, esses eventos não são independentes. Vamos determinar cada um dos eventos.
A: sair um múltiplo de 10 → {10, 20, 30}
B: sair um número ímpar → {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29}
A probabilidade de ocorrer os dois eventos sucessivamente será dada por:
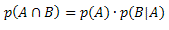
Faremos os cálculos separadamente:
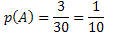
Para o cálculo de p(B|A) é preciso notar que não teremos mais 30 bolinhas na urna, pois uma foi retirada e não houve reposição, restando 29 bolinhas na urna. Assim,
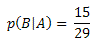
Logo,
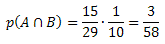
Exemplo 3
Uma moeda e um dado são lançados simultaneamente. Qual a probabilidade de ocorrer coroa e número primo?
Resolução:
Primeiro, vamos determinar o espaço amostral S, que é o conjunto com todos os possíveis resultados. Para melhor compreensão, iremos denominar cara de C e coroa de K.
Assim:
S = {(C, 1); (C; 2); (C, 3); (C, 4); (C, 5); (C, 6); (K; 1), (K, 2); (K, 3); (K, 4); (K, 5); (K, 6)} à n(S) = 12
Vamos descrever os eventos A e B.
A: ocorrer coroa
B: ocorrer número primo
É fácil ver que esses dois eventos são independentes, um pode ocorrer sem a interferência do outro. Dessa forma, para resolução, utilizaremos a fórmula:
P(A∩B) = p(A) . p(B)
p(A) = 1/2, pois no lançamento de uma moeda há metade de chance de sair cara e metade de sair coroa.
p(B) = 3/6 = 1/2, pois dos 6 possíveis resultados no lançamento de um dado, três deles são números primos.
Logo,
P(A∩B) =1/2 .1/2 = 1/4
Exemplo 4
Uma urna contém 10 etiquetas identificadas pelas letras A, B, C, D, ..., I, J. Duas delas são retiradas ao acaso, sucessivamente. Qual a probabilidade de saírem duas vogais, se a extração é feita sem reposição?
Resolução:
amos determinar os dois eventos envolvidos.
Evento A: sair uma vogal
Evento B: sair uma vogal
O fato de não haver reposição das etiquetas indica que a ocorrência de um evento interfere na ocorrência do outro, pois não haverá a mesma quantidade de etiquetas após a ocorrência de um deles. Dessa forma, utilizaremos a expressão:
P(A∩B) = p(A│B) . p(B)
Vamos então calcular p(B) e p(A|B).
p(B)= 3/10, pois, das dez letras, apenas 3 são vogais.
p(A│B)= 2/9, pois, se B ocorreu, restaram 9 letras e, dessas, apenas 2 são vogais.
Logo,
P(A∩B) = 2/9 . 3/10 = 6/90 = 1/15
EXERCÍCIOS RESOLVIDOS DIVERSOS
06) Vamos determinar a probabilidade de tirarmos uma bola branca em uma urna com 10 bolas brancas e 20 bolas vermelhas.
Resolução:
Para isso, vamos inicialmente determinar o número de casos favoráveis e o número de casos possíveis.
Casos favoráveis = 10 (bolas brancas)
Casos possíveis = 10 + 20 (bolas brancas + bolas vermelhas)
Veja que os casos favoráveis são os casos que nos interessam – nesse caso, a quantidade de bolas brancas – e casos possíveis representam o total de elementos do espaço amostral. Vamos chamar de A o evento em questão, assim:
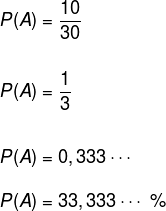
A chance de tirar uma bola branca é, portanto, de 33,33%.
07) (UFPE) Uma letra é escolhida ao acaso dentre as que formam a palavra PERNAMBUCO. Qual a probabilidade de ser uma consoante?
Resolução:
Observe que o total de letras na palavra PERNAMBUCO é igual a 10. O caso favorável nesse problema é a quantidade de consoantes, que são 6. Logo, a probabilidade de escolhermos uma consoante é de:
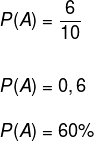
08) Qual é a probabilidade de, no lançamento de 4 moedas, obtermos cara em todos os resultados?
(A) 2%
(B) 2,2%
(C) 6,2%
(D) 4%
(E) 4,2%
Resolução:
Primeiramente, é necessário encontrar o número total de possibilidades de resultados:
2 . 2 . 2 . 2 = 16
Posteriormente, devemos encontrar o número de possibilidades de obter cara em todos os resultados. Na realidade, só existe uma possibilidade de que isso aconteça.
Por fim, basta dividir o segundo pelo primeiro:
1 = 0,0625
16
Multiplicando 6,25 por 100, para obter um percentual, teremos: 6,25%
Alternativa: C
08) Duas moedas e dois dados, todos diferentes entre si, foram lançados simultaneamente. Qual é o número de possibilidades de resultados para esse experimento?
(A) 146
(B) 142
(C) 133
(D) 144
(E) 155
Resolução:
Para calcular o número de possibilidades de resultados de um experimento nesses moldes, multiplique o número de resultados possíveis de cada objeto em observação. No caso de cada moeda, 2 resultados, e de cada dado, 6 resultados:
2 .2 . 6 . 6 = 4 . 36 = 144
Alternativa: D
09) Qual é o número total de possibilidades de resultado no lançamento de 5 moedas?
(A) 2
(B) 5
(C) 10
(D) 24
(E) 32
Resolução:
O número total de resultados que pode ser obtido no lançamento de duas moedas é encontrado multiplicando-se a quantidade de resultados da primeira moeda pela quantidade da segunda e assim por diante. Observe:
2 . 2 . 2 . 2 . 2 = 32
Portanto, são 32 possibilidades diferentes.
Alternativa: E
10) No lançamento de dois dados, qual é o número total de possibilidades de resultados e qual é a probabilidade de obtermos soma igual a 8?
(A) 36 e 5%
(B) 36 e 14%
(C) 6 e 5%
(D) 5 e 6%
(E) 36 e 6%
Resolução:
Primeiramente, vamos descobrir o número total de possibilidades, pois ele será usado para descobrirmos a probabilidade de obter soma 8:
São dois dados com seis resultados possíveis cada. As combinações entre esses resultados podem ser calculadas multiplicando-se o número de resultados do primeiro pelo do segundo:
6 . 6 = 36
Também poderíamos ter escrito todas as possibilidades e contado-as, mas esse procedimento gasta mais tempo. Portanto, o número total de possibilidades de resultados é 36.
Para calcular a probabilidade de sair soma 8, devemos procurar as possibilidades de obter tal soma. São elas:
2,6; 3,5; 4,4; 5,3 e 6,2
Sendo 5 o número de possibilidades de obter soma 8, divida esse número pelo número total de possibilidades de resultados:
5 = 0,14
36
Para transformar isso em porcentagem, basta multiplicar por 100:
0,14 . 100 = 14%
A probabilidade de sair soma 8 é 14%.
Alternativa: B
11) (PM PE – IAUPE) Dos 500 aprovados em um concurso, 205 falam inglês, 210, espanhol, e 65, ambos os idiomas. Escolhendo ao acaso um dos aprovados, qual a probabilidade de ele não falar nenhum desses idiomas?
(A) 40%
(B) 25%
(C) 30%
(D) 45%
(E) 35%
Resolução:
Total de alunos que falam algum idioma:
205 + 210 – 65 = 350
Veja que subtraímos os 65 alunos que falam os dois idiomas e estavam sendo contados duas vezes quando consideramos os 205 que falam inglês e os 210 que falam espanhol.
Total de estudantes que não falam nenhum idioma:
500 – 350 = 150
Probabilidade do estudante não falar nenhum idioma:
150/500 = 0,3 = 30%
Alternativa: C
12) (BB – Cesgranrio) Uma moeda não tendenciosa é lançada até que sejam obtidos dois resultados consecutivos iguais. Qual a probabilidade de a moeda ser lançada exatamente três vezes?
(A) 1/8
(B) 1/4
(C) 1/3
(D) 1/2
(E) 3/4
Resolução:
Primeira jogada: qualquer resultado serve (probabilidade igual a 1)
Segunda jogada: só serve o resultado que não aconteceu da primeira vez (probabilidade igual a 1/2)
Terceira jogada: só serve o mesmo resultado que aconteceu na segunda jogada (probabilidade igual a 1/2)
Logo: 1 , 1/4 . 1/4 = 1/4
Alternativa: B
13) Em um grupo de pessoas, as idades são: 10, 12, 15 e 17 anos. Caso uma pessoa de 16 anos junte-se ao grupo, o que acontece com a média das idades do grupo?
Resolução:
.gif)
14) A distribuição de salários de uma empresa é fornecido pela tabela a seguir:
.gif) Calcule a média salarial dessa empresa.
Calcule a média salarial dessa empresa.
Resolução:
.gif)
15) (Unicamp-SP) Para votar, cinco eleitores demoraram, respectivamente, 3min 38s, 3min 18s, 2min 46s, 2min 57s e 3min 26s. Qual foi a média do tempo de votação (em minutos e segundos) desses eleitores?
Resolução:
.jpg)
16) (Unifor-CE) Em certa eleição municipal foram obtidos os seguintes resultados:
.gif) O número de votos obtido pelo candidato vencedor foi:
O número de votos obtido pelo candidato vencedor foi:
(A) 178
(B) 182
(C) 184
(D) 188
(E) 191
Resolução:
Calcular o índice percentual de votos nulos e brancos:
x + 26% + 24% + 22% = 100%
x = 100% – 72%
x = 28%
Calcular o total de votos com base nos votos nulos e brancos:
28% de x = 196
0,28x = 196
x = 196/0,28
x = 700
O total de votos é igual a 700, e o candidato vencedor teve 26% desses votos, então:
26% de 700 → 0,26 * 700 → 182 votos
Alternativa: B
17) (FGV-SP) A tabela abaixo representa a distribuição de frequência dos salários de um grupo de 50 empregados de uma empresa, em certo mês. O salário médio desses empregados, nesse mês, foi de:
.gif) (A) R$ 2 637,00
(A) R$ 2 637,00
(B) R$ 2 520,00
(C) R$ 2 500,00
(D) R$ 2 420,00
(E) R$ 2 400,00
Resolução:
.jpg)
Eventos Aleatórios
Fatorial
É importante falarmos sobre fatorial pois na análise combinatória é comum o uso de fatorial nas fórmulas.
Seja n um número natural, maior que 1, definimos fatorial de n como o produto de todos os números naturais de n até 1.
Simbolicamente, o fatorial de n é: n!
n! = n(n – 1).(n – 2) . … . 3 . 2 . 1
Exemplo 1
3! = 3 . 2 . 1 = 6
10! = 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 3.628.800
Princípio Fundamental da Contagem
O princípio fundamental da contagem nos permite definir uma regra de forma que possamos determinar o número de possibilidades de ocorrência de um evento, para que não precisamos reproduzir todas as possibilidades de ocorrência do evento.
Exemplo 2
Maria foi a uma loja comprar um par de sapatos. A loja possui três pares de sapatos que interessavam à Maria, em 2 cores diferentes, preto e branco. Quantas possibilidades de escolhas Maria tinha para comprar 1 par de sapatos?
Resolução:
Podemos utilizar um diagrama chamado de diagrama de árvore para descrever todas as possibilidades que Maria disponha para comprar 1 par de sapatos.
 No entanto, descrever todas as possibilidades que Maria possui pode ser um pouco mais complexo. Por exemplo, se ampliássemos as possibilidades para duas ou mais lojas, ou simplesmente a loja disponibilizasse mais opções de cores e modelos à Maria.
No entanto, descrever todas as possibilidades que Maria possui pode ser um pouco mais complexo. Por exemplo, se ampliássemos as possibilidades para duas ou mais lojas, ou simplesmente a loja disponibilizasse mais opções de cores e modelos à Maria.
Podemos então utilizar do princípio fundamental da contagem para simplificar o problema.
Para cada par de sapato, Maria possui duas possibilidades de escolhas: preto ou branco. Então, vamos chamar de p o número de pares sapatos e c o número de cores disponível.
p = 3
c = 2
Assim, fazendo o produto temos o total de possibilidades que Maria possui para comprar 1 par de sapatos.
p . c = 3 . 2 = 6 possibilidades
Permutação simples
Definimos permutação simples como o número de possibilidades que podemos organizar n elementos distintos em n posições, de forma que cada possibilidade seja diferente da ordem em que os elementos aparecem.
Permutação simples
Pn = n!
Exemplo 3
Em uma eleição para prefeito existem 3 candidatos. Quais as possibilidades dos três candidatos no resultado da eleição?
Resolução:
Cada candidato na eleição pode ocupar três posições no resultado da eleição: eleito (primeiro lugar), segundo lugar e terceiro lugar.
Assim, trata-se de um problema de permutação simples.
P3 = 3! = 3 . 2 . 1 = 6
Resposta: 6 possibilidades que podem ocorrer no resultado da eleição.
Permutação com repetição
Na permutação com repetição, na análise combinatória, os elementos do evento são repetidos, diferentemente da permutação simples.
Permutação com repetição
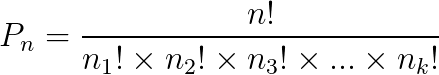 Pn = é a permutação
Pn = é a permutação
N = total de elementos do evento
n1! . n2! . n3! . … . nk! = elementos repetidos no evento
Exemplo 4
Quantos anagramas possuem a palavra CARRO?
Resolução:
Podemos ver que duas letras se repetem. Então, tempos os seguintes dados no problema:
N = 5 letras;
n1 = 2 letras que se repetem.
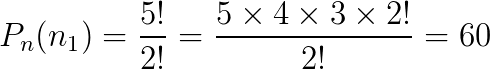
Resposta: a palavra carro possui 60 anagramas.
Exemplo 5
Dado o conjunto B = {5,6,7}, veja os possíveis agrupamentos formados com 2 elementos de B.
Resolução:
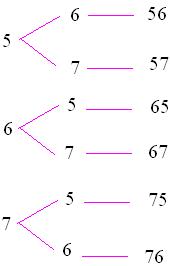 Então, os agrupamentos formados com 2 elementos do conjunto b são: 56,5 7, 65, 67,75, 76. Esse agrupamento é formado por arranjos simples pelos elementos do conjunto B.
Então, os agrupamentos formados com 2 elementos do conjunto b são: 56,5 7, 65, 67,75, 76. Esse agrupamento é formado por arranjos simples pelos elementos do conjunto B.
Arranjo simples
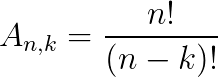 An, k = é o arranjo
An, k = é o arranjo
N = total de elementos do evento
K = total de agrupamentos, com k ≤ n
Exemplo 6
Quantos números de 3 algarismos podemos formar com o conjunto abaixo:
A = {1, 2, 3, 5, 7 e 9}
Resolução:
Temos os seguintes dados:
N = números de elementos;
k = quantidades de algarismos por número.
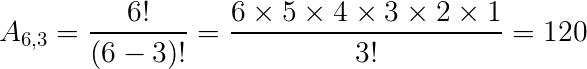
Resposta: podemos formar até 120 número de três algarismos.
Arranjo com repetição
Arranjo com repetição é utilizado quando a ordem dos elementos do evento é importante, sendo que cada elementos pode ser contado mais de uma vez.
Arranjo com repetição
An,k = nk
An,k = é o arranjo com repetição
N = total de elementos do evento
K = número de elementos escolhidos no evento
Exemplo 7
Seja o conjunto das vogais: A = {a, e, i, o, u}
Se tomarmos o agrupamento de dois em dois, sendo um arranjo com repetição, quantos agrupamentos poderíamos fazer com as vogais do conjunto A?
Resolução:
A = {a, e, i, o, u}
n = 5
k = 2
A5,2 = 52 = 25
Resposta: poderíamos fazer 25 combinações diferentes.
Combinação simples
Utilizamos combinação simples quando a ordem dos elementos no evento não importa, porém cada elementos pode ser contado somente uma vez.
Combinação simples
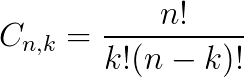 Cn,k = é a combinação simples
Cn,k = é a combinação simples
N = total de elementos do eventos
k = total de agrupamentos do evento, com k ≤ n
Exemplo 8
De quantas maneiras diferentes podemos separar 12 bolas de gudes de cores diferentes, colocando 3 bolas de gudes por pote?
Resolução:
Dados:
n = 12 bolas de gudes
k = 3 bolas de gudes por pote
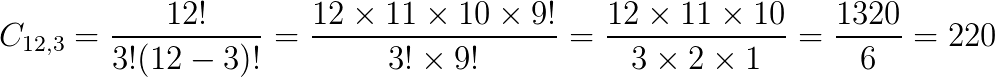
Resposta: podemos separar as 12 bolas de gudes distintas, com três em cada pote, de 220 formas diferentes.
Combinação com repetição
Utilizamos a combinação com repetição quando a ordem dos elementos do evento não importa, porém, podemos escolher cada elementos mais de uma vez.
Combinação com repetição
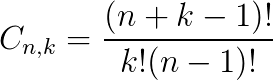 Cn,k = é a combinação com repetição
Cn,k = é a combinação com repetição
N = é o total de elementos do evento
k = total de elementos escolhidos do evento
Exemplo 9
Uma loja decide sortear para os clientes 3 pares de sapatos das 10 melhores marcas do mercado. De quantas formas o ganhador do prêmio pode escolher os três pares de sapatos da lista das 10 melhores marcas, sendo permitido repetições?
Resolução:
N = 10 marcas
k = 3 pares de sapatos
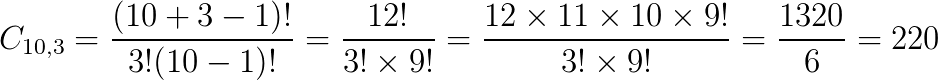
Resposta: o ganhador do prêmio poderá escolher de 220 maneiras distintas os três pares de sapatos das 10 melhores marcas.
FATORIAL - EXERCÍOCIOS RESOLVIDOS
0! (lê-se 0 fatorial)
0! = 1
1! (lê-se 1 fatorial)
1! = 1
2! (lê-se 2 fatorial)
2! = 2 . 1 = 2
3! (lê-se 3 fatorial)
3! = 3 . 2 . 1 = 6
4! (lê-se 4 fatorial)
4! = 4. 3 . 2 . 1 = 24
5! (lê-se 5 fatorial)
5! = 5 . 4 . 3 . 2 . 1 = 120
6! (lê-se 6 fatorial)
6! = 6 . 5 . 4 . 3 . 2 . 1 = 720
7! (lê-se 7 fatorial)
7! = 7 . 6 . 5 . 4. 3 . 2 . 1 = 5040
8! (lê-se 8 fatorial)
8! = 8 . 7 . 6 . 5 . 4. 3 . 2 . 1 = 40320
9! (lê-se 9 fatorial)
9! = 9 . 8 . 7 . 6 . 5 . 4. 3 . 2 . 1 = 362.880
10! (lê-se 10 fatorial)
10! = 10 . 9 . 8 . 7 . 6 . 5 . 4. 3 . 2 . 1 = 3.628.800
Obs: O número fatorial também pode ser representado da seguinte maneira:
5!
5 . 4!;
5 . 4 . 3!;
5 . 4 . 3 . 2!
Observação: esse processo é muito importante quando se utiliza a simplificação de números fatoriais.
01) Calcule o valor das frações abaixo:
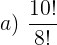
Resolução:
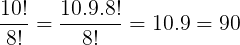
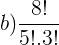
Resolução:
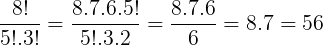
02) Simplifique as expressões abaixo:
Resolução:
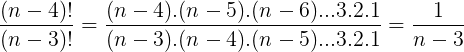
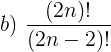
Resolução:
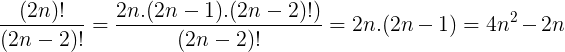
EXERCÍCIOS RESOLVIDOS
04) Uma lanchonete vende uma promoção de lanche a um preço único. No lanche, estão incluídos um sanduíche, uma bebida e uma sobremesa. São oferecidos três opções de sanduíches: hambúrguer especial, sanduíche vegetariano e cachorro-quente completo. Como opção de bebida pode-se escolher 2 tipos: suco de maçã ou guaraná. Para a sobremesa, existem quatro opções: cupcake de cereja, cupcake de chocolate, cupcake de morango e cupcake de baunilha. Considerando todas as opções oferecidas, de quantas maneiras um cliente pode escolher o seu lanche?
Resolução:
Podemos começar a resolução do problema apresentado, construindo uma árvore de possibilidades, conforme ilustrado abaixo:
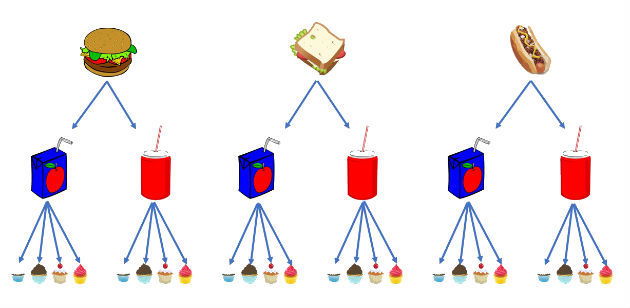 Acompanhando o diagrama, podemos diretamente contar quantos tipos diferentes de lanches podemos escolher. Assim, identificamos que existem 24 combinações possíveis.
Acompanhando o diagrama, podemos diretamente contar quantos tipos diferentes de lanches podemos escolher. Assim, identificamos que existem 24 combinações possíveis.
Podemos ainda resolver o problema usando o princípio multiplicativo. Para saber quais as diferentes possibilidades de lanches, basta multiplicar o número de opções de sanduíches, bebidas e sobremesa.
Total de possibilidades: 3 . 2 . 4 = 24
Resposta: temos 24 tipos diferentes de lanches para escolher na promoção.
05) Quantos anagramas podemos formar com a palavra GATO?
Resolução:
Podemos variar as letras de lugar e formar vários anagramas, formulando um caso de permutação simples.
P = 4! = 24
.jpg)
06) De quantas maneiras distintas podemos organizar as modelos Ana, Carla, Maria, Paula e Silvia para a produção de um álbum de fotografias promocionais
Resolução:
Note que o princípio a ser utilizado na organização das modelos será o da permutação simples, pois formaremos agrupamentos que se diferenciarão somente pela ordem dos elementos.
P = n!
P = 5!
P = 5 . 4 . 3 . 2 .1
P = 120
Portanto, o número de posições possíveis é 120.
07) De quantas maneiras distintas podemos colocar em fila indiana seis homens e seis mulheres:
a) em qualquer ordem
Resolução:
Podemos organizar as 12 pessoas de forma distinta, portanto utilizamos
12! = 12 .11 .10 .9 . 8 .7 . 6 . 5 . 4 . 3 . 2 . 1 = 479.001.600 possibilidades
b) iniciando com homem e terminando com mulher
Resolução:
Ao iniciarmos o agrupamento com homem e terminarmos com mulher teremos:
Seis homens aleatoriamente na primeira posição.
Seis mulheres aleatoriamente na última posição.
.jpg) P = (6 . 6) . 10!
P = (6 . 6) . 10!
P = 36 .10!
P = 130.636.800 possibilidades
08) Os resultados do último sorteio da Mega-Sena foram os números 04, 10, 26, 37, 47 e 57. De quantas maneiras distintas pode ter ocorrido essa sequência de resultados?
Resolução:
Os números sorteados da mega sena formam uma sequência de seis números. Para calcular as formas distintas que esse resultado pode ter sido sorteado, basta calcular: P6 = 6! = 6 . 5 . 4 . 3 . 2 . 1 = 720.
09) Na palavra NORTE, quantos anagramas podem ser formados? Quantos começam com vogal?
Resolução:
Na palavra NORTE, temos 5 letras e a quantidade de anagramas distintos é dada por P5 = 5! = 5 . 4 . 3 . 2 . 1 = 120. Para sabermos quantos começam com vogal, sabemos que, fixado que a primeira letra é uma vogal, restam apenas quatro posições a serem permutadas. Então temos 4! = 4 . 3 . 2 . 1 = 24. Como temos duas vogais, basta multiplicar 2 . 2 4 = 48. Assim, dos 120 anagramas que podem ser formados, apenas 48 começam com vogais.
10) Se considerarmos o conjunto B = {A, B, C, D} formados por 4 pontos não colineares (que não pertence a mesma reta), qual a quantidade de triângulos que podemos formar?
Resolução:
Considerando o exemplo acima veja todas as possibilidades de triângulos formados com os quatro pontos não colineares:
ABC, BAC, CAB, DAB
ABD, BAD, CAD, DAC
ACB, BCA, CBA, DBA
ACD, BCD, CBD, DBC
ADB, BDA, CDA, DCA
ADC, BDC, CDB, DCB
Percebemos que há vários agrupamentos que se diferem pela ordem de seus elementos, esses representam o mesmo triângulo, por isso que consideramos esse exercício como sendo uma combinação simples, assim a quantidade de combinações simples que os 4 pontos não colineares (A,B,C,D), tomados 3 a 3 irão formar será 4, pois os seus agrupamentos se diferem pela natureza de seus elementos e não pela ordem.
Para encontrar essa quantidade de agrupamentos formados em uma combinação simples utilizamos a seguinte fórmula:
Cn,p = n!
p! (n – p)!
n é a quantidade de elementos de um conjunto
p é um número natural menor ou igual a n, que representa a quantidade de elementos que irão formar os agrupamentos.
Substituindo os dados acima na fórmula teremos:
n = 4
p = 3
C4,3 = 4!
3! (4-3)!
C4,3 = 4 . 3!
3! . 1
C4,3 = 4
11) O presidente de uma grande empresa reserva todas as segundas-feiras de manhã para realizar uma reunião com todos os diretores. Considerando que existem cinco diretores nas mais diversas áreas dessa empresa, calcule de quantas maneiras essas seis pessoas (presidente e diretores) podem ser dispostos numa mesa não redonda. Esse é um típico caso de permutação simples.
Resolução:
P6 = 6 . 5 . 4 . 3 . 2 . 1 = 720
Resposta: o presidente e os diretores podem ser dispostos em uma mesa não redonda de 720 maneiras distintas.
12) Quantos anagramas podem ser formados com a palavra MATEMÁTICA?
Resolução:
Observe que são dez letras das quais uma delas se repete três vezes, caso da letra A, e outra que se repete duas vezes, o da letra T. Realizando o cálculo, tem-se:
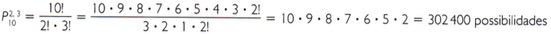
Resposta: com a palavra MATEMÁTICA podem ser formados 302400 anagramas.
Continua...














.jpg)





.jpg)
.jpg)
.jpg)
.jpg)

.jpg)
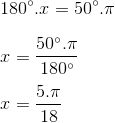
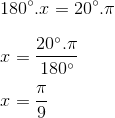
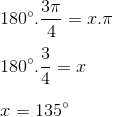
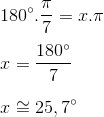
.jpg)


.jpg)
.jpg)














.jpg)






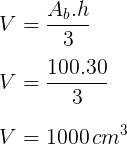












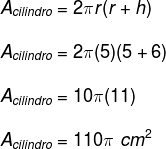




.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)

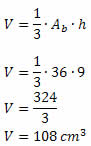


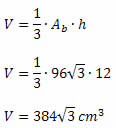


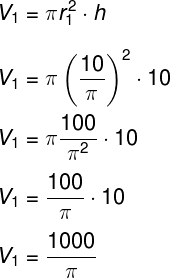
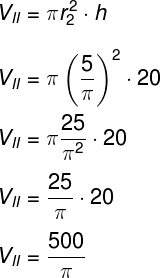












.gif)
.gif)

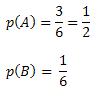
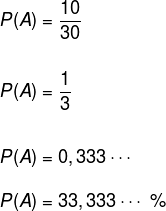
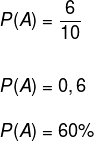
.gif)
.gif)
.gif)
.jpg)
.gif)
.gif)
.jpg)
 No entanto, descrever todas as possibilidades que Maria possui pode ser um pouco mais complexo. Por exemplo, se ampliássemos as possibilidades para duas ou mais lojas, ou simplesmente a loja disponibilizasse mais opções de cores e modelos à Maria.
No entanto, descrever todas as possibilidades que Maria possui pode ser um pouco mais complexo. Por exemplo, se ampliássemos as possibilidades para duas ou mais lojas, ou simplesmente a loja disponibilizasse mais opções de cores e modelos à Maria.
 Acompanhando o diagrama, podemos diretamente contar quantos tipos diferentes de lanches podemos escolher. Assim, identificamos que existem 24 combinações possíveis.
Acompanhando o diagrama, podemos diretamente contar quantos tipos diferentes de lanches podemos escolher. Assim, identificamos que existem 24 combinações possíveis..jpg)
.jpg) P = (6 . 6) . 10!
P = (6 . 6) . 10!