PLANO CARTSIANO I
Professor Diminoi
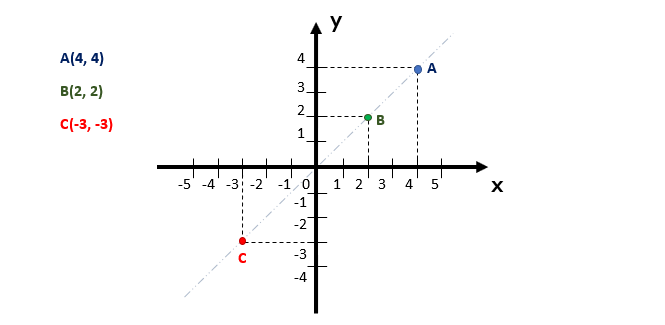
Plano cartesiano
Sistema de orientação e localização
Plano cartesiano, também conhecido como sistema cartesiano, é um traçado de retas perpendiculares onde perpassa outra, sendo uma na horizontal e outra na vertical, formando quadrantes de 90°. Esse esquema serve para variados cálculos.
Quem teorizou e desenvolveu o plano foi René Descartes. Ele simplificou a álgebra através da geometria euclidiana, fazendo cálculos em um pressuposto plano. Para entender do que se trata o sistema de orientação e cálculos de Descartes é importante aprender sobre as retas e infinidade dos números.

Propriedades
Entende-se que uma reta, além de ser o caminho mais curto de um ponto a outro, não possui nem início nem fim (infinita). Como não existe um início ou final, foi-se estabelecido que para criar um norte é necessário um ponto de origem. Esse tal ponto conta sempre como 0, sendo também o eixo e o meio.
Cada ponto que a reta segue para cima ou à direita os valores passam a ser positivos. Já os pontos para baixo ou à esquerda os números passam a ser negativos.
Os eixos do plano cartesiano
Uma das principais partes que formam o plano cartesiano são os eixos, que são chamados de abscissas e ordenadas. Servem para ajudar na orientação dos cálculos, principalmente na identificação das direções corretas.
Abscissa significa cortada, em latim. É uma coordenada na horizontal. Ela é geralmente denominada como X. A ordenada, que é o contrário da abscissa, é a linha vertical nomeada de Y.

Localização de pontos no plano cartesiano
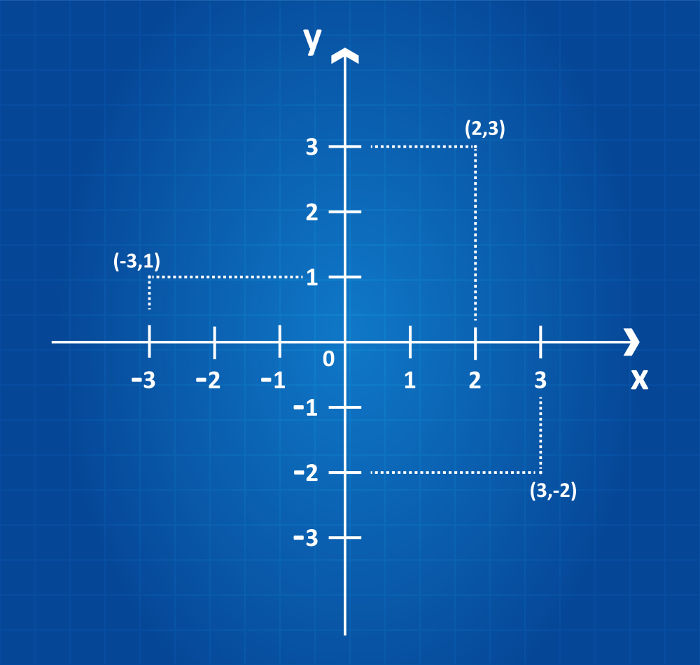
Quadrantes
Os quadrantes são numerados no sentido anti-horário. Começa pelo lado em que as abscissas e ordenadas são coordenadas positivas. Vejamos o exemplo:
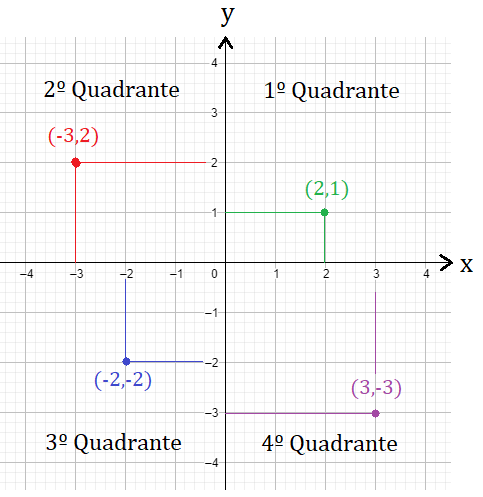 A relação dos quadrantes é dada por:
A relação dos quadrantes é dada por:
(I) Quadrante: positivo, positivo;
(II) Quadrante: negativo, positivo;
(III) Quadrante: negativo, negativo;
(IV) Quadrante: positivo negativo.
Distância entre dois pontos
Para determinarmos a distância entre dois pontos quaisquer no plano cartesiano podemos utilizar o teorema de Pitágoras.
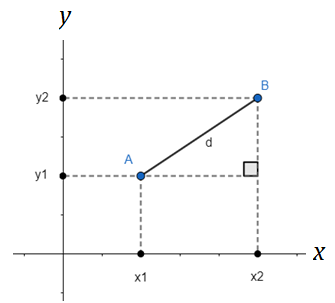 dAB = √(x2 – x1)2 + (y2 – y1)2
dAB = √(x2 – x1)2 + (y2 – y1)2
Espaço entre três dimensões
O espaço em três dimensões tem algumas diferenças em relação ao de duas dimensões. 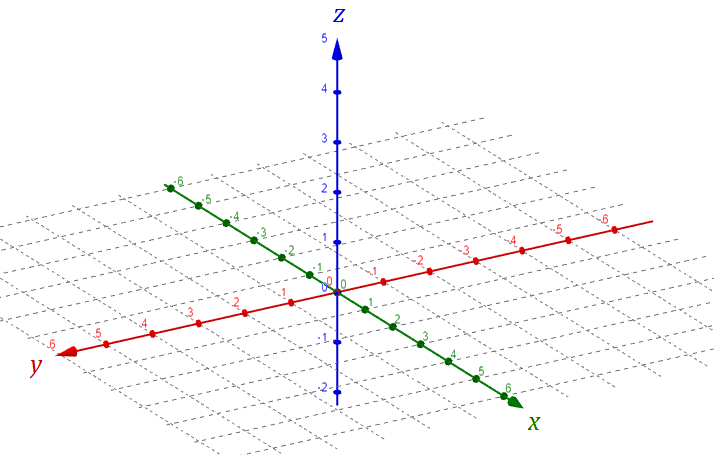
Agora, um novo eixo aparece, perpendicular ao plano cartesiano (x, y), o eixo z. Ele também é uma reta real e o seu marco zero é coincidente com o ponto (0,0) no plano (x, y). Agora, para determinarmos um ponto neste espaço devemos acrescentar uma nova coordenada, o que nos leva a representação de qualquer ponto no espaço como (x, y, z).
Distância entre três pontos
A distância entre dois pontos no espaço continua seguindo a mesma regra do teorema de Pitágoras, porém com uma coordenada a mais:
 d = √(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
d = √(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
Questões resolvidas
01) Um triângulo equilátero tem seus vértices com as seguintes coordenadas no plano cartesiano:
A(2, 1), B(5, 1) e C(2, 4)
Quais são as coordenadas do baricentro desse triângulo?
(A) G = (3, 2)
(D) G = (2, 3)
(C) G = (3, 3)
(D) G = (2, 2)
(E) G = (1, 2)
Resolução:
Para responder a essa questão, basta usar a fórmula a seguir para determinar as coordenadas do baricentro do triângulo:
G = (x1 + x2 + x3, y1 + y2 + y3)
3 3
G = (2 + 5 + 2, 1 + 1 + 4)
3 3
G = (3, 2)
Alternativa: A
02) Qual é o ponto de encontro entre as retas: x – y = 0 e x + y – 4 = 0
(A) (2, 0)
(B) (0, 2)
(C) (2, 2)
(D) (0, 0)
(E) (1, 1)
Resolução:
Para determinar o ponto de encontro entre duas retas, deve-se isolar uma de suas incógnitas, descobrir o valor de uma delas e depois encontrar o valor da outra, por processos de substituição. Observe:
x – y = 0
logo, x = y
x + y – 4 = 0
y + y – 4 = 0
2y = 4
y = 2
Assim:
x – y = 0
x – 2 = 0
x = 2
O ponto de encontro entre essas duas retas tem as seguintes coordenadas (2, 2).
Alternativa: C
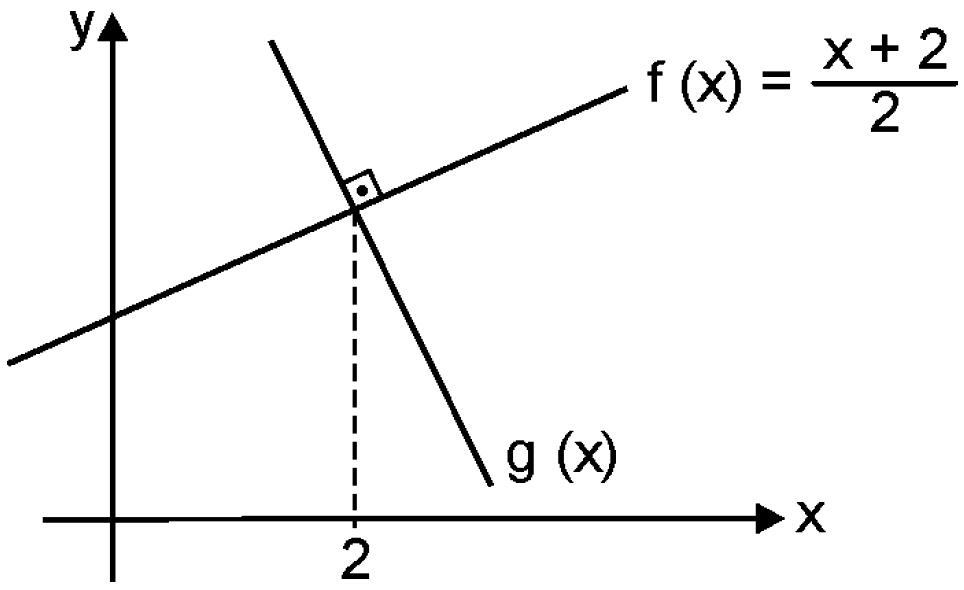
03) A figura abaixo mostra os gráficos das funções do 1º grau f(x) e g(x) no plano cartesiano. A função gof(x) pode ser representada por uma reta cujo coeficiente angular (ou declividade) é igual a:
 (A) 4
(A) 4
(B) 2
(C) 1
(D) –1
(E) –2
Resolução:
Primeiro, determinamos as coordenadas do ponto de encontro entre f e g:
f(x) = x + 2
2
f(2) = 2 + 2
2
f(2) = 4/2
f(2) = 2
As coordenadas do ponto de encontro são (2, 2).
Agora, é necessário encontrar a equação da equação g(x). Para tanto, seu coeficiente angular a é:
a = – 1/m
Em que m é o coeficiente angular de f, pois f e g são perpendiculares.
a = – 1
½
a = – 1·2
a = – 2
Por fim, sabendo o coeficiente angular e um dos pontos pertencentes à reta g, podemos escrever sua equação. Lembre-se, é claro, de que essa equação pode ser entendida como função.
y – yo = m(x – xo)
y – 2 = – 2(x – 2)
y = 2 – 2x + 4
y = – 2x + 6
Em seguida, basta fazer a composição das funções, simplificar o resultado e observar o valor do coeficiente angular da reta que a composição representa.
gof(x) = g(f(x)) = – 2(x + 2) + 6
2
gof(x) = g(f(x)) = – (x + 2) + 6
gof(x) = g(f(x)) = – x – 2 + 6
gof(x) = g(f(x)) = – x + 4
Alternativa: D
04) Qual é a distância entre o ponto de coordenadas (2, – 1) e a reta
y = – 3x + 1?
4
(A) 1/5
(B) ¼
(C) 1/3
(D) ½
(E) 2/5
Resolução:
Primeiramente, é necessário escrever a reta na forma geral:
y = – 3x + 1
4
y – 1= – 3x
4
4y + 3x – 4 = 0
Agora, basta substituir os valores dos coeficientes da reta e as coordenadas do ponto na fórmula:
D = | axo + byo + c |
√(a2 + b2)
D = | 3∙2 + 4∙(– 1) – 4 |
√(32 + 42)
D = | 6 – 4 – 4 |
√(9 + 16)
D = | – 2 |
√(25)
D = 2
5
Alternativa: E
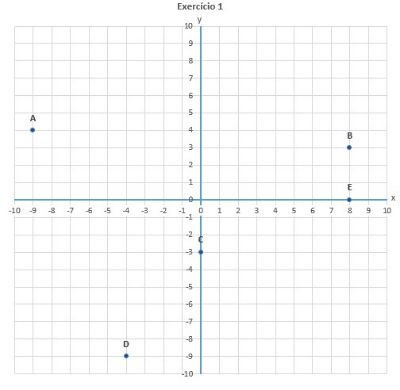
05) Marque os pontos A (2, 3), B (-2,5), C (-3, -2) e D (1, -4) no plano cartesiano.
Resolução:
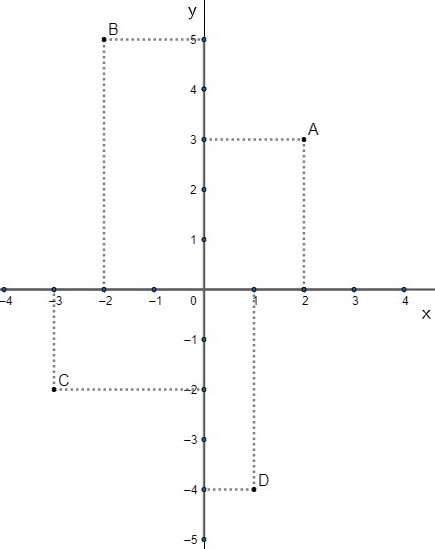
07) Localize os pares ordenados no plano cartesiano:
(A) (-9, 4)
(B) (8, 3)
(C) (0, -3)
(D) (-4, -9)
(E) (8, 0)
Resolução:
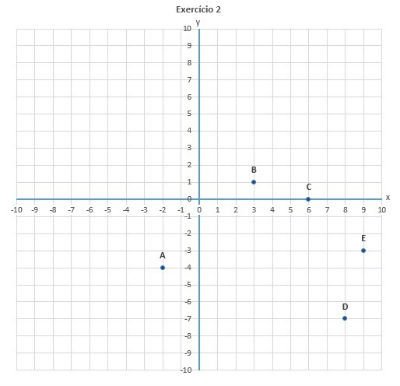
08) Em quais quadrantes estão localizados os pontos:
(A) (-2, -4)
(B) (3, 1)
(C) (0, 6)
(D) (8, -7)
(E) (9, -3)
Resolução:
a) 3.° quadrante
b) 1.° quadrante
c) 1.° quadrante
d) 4.° quadrante
e) 4.° quadrante
09) Qual par ordenado não está representado no plano cartesiano?
(A) (3, -4)
(B) (4, -3)
(C) (-8, -9)
(D) (8, 9)
(E) (9, -8)
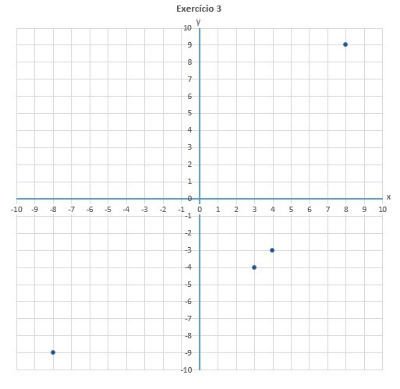
Alternativa: E
10) (PM ES 2013 – Exatus) Clarence desenhou o triângulo determinado pelas coordenadas dos pontos cartesianos A(7;5), B(3;2) e C(7;2). Ao calcular a área e o perímetro desse triângulo, os valores obtidos foram, respectivamente:
(A) 3 e 3
(B) 3 e 6
(C) 6 e 6
(D) 6 e 12
(E) 12 e 12
Resolução:
Desenhando o triângulo:
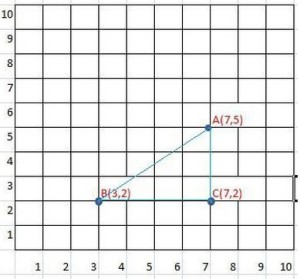
Pela figura, temos um triângulo retângulo com BC = 4 e AC = 3. Vamos descobrir AB usando teorema de Pitágoras:
AB² = 4² + 3²
AB² = 16 + 9
AB² = 25
AB = 5
Perímetro = AB + BC + CA
Perímetro = 5 + 4 + 3 = 12
Área = 3×4/2 = 6
Alternativa: D
11) (PM Pará 2012) Os pontos (2,3), (5,3) e (2,7) são vértices de um triângulo retângulo. A área desse triângulo é:
(A) 5 u.a
(B) 6 u.a
(C) 7 u.a
(D) 8 u.a
(E) 9 u.a
Resolução:
Desenhando o triângulo do plano cartesiano:
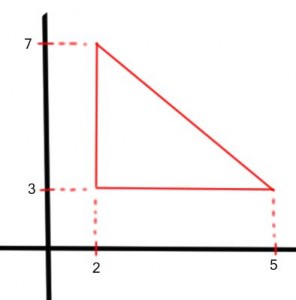
Nele é possível observar que:
A altura mede 7 – 3 = 4
A base mede 5 – 2 = 3
Calculando a área do triângulo:
A = base x altura / 2
A = 3 . 4/2
A = 6
Alternativa: B
12) Um triângulo equilátero tem seus vértices com as seguintes coordenadas no plano cartesiano:
A(2, 1), B(5, 1) e C(2, 4)
Quais são as coordenadas do baricentro desse triângulo?
(A) G = (3, 2)
(B) G = (2, 3)
(C) G = (3, 3)
(D) G = (2, 2)
(E) G = (1, 2)
Resolução:
Para responder a essa questão, basta usar a fórmula a seguir para determinar as coordenadas do baricentro do triângulo:
G = (x1 + x2 + x3, y1 + y2 + y3)
3 3
G = (2 + 5 + 2, 1 + 1 + 4)
3 3
G = (3, 2)
Alternativa A
13) (Pucsp) Os pontos A=(-1; 1), B=(2; -1) e C=(0; -4) são vértices consecutivos de um quadrado ABCD. A equação da reta suporte da diagonal BD, desse quadrado, é:
(A) x + 5y + 3 = 0.
(B) x – 2y – 4 = 0.
(C) x – 5y – 7 = 0.
(D) x + 2y – 3 = 0.
(E) x – 3y – 5 = 0.
Resolução:
No quadrado, as diagonais são perpendiculares, desta maneira, BD⊥AC. Sendo r a reta suporte de AC, sabemos que r: y = ax + b, A (-1,1) e C (0,-4). Logo, -4 = 0a + b ⇔ b = -4 e 1 = -a + b ⇔ a = b – 1 = -4 – 1 ⇔ a = -5 e, por isso, r: y = -5x – 4. Sendo s a reta suporte de BD, sabemos que ms.mr = -1 ⇒ ms.(-5) =-1 ⇔ ms = 1/5. Por conseguinte, s: y = x/5 + b, mas B (2,-1) é um ponto de s, então: -1 = 2/5 + b ⇒ b = -1 – 2/5 = (-5-2)/5 ⇔ b = -7/5 e, enfim, s: y = x/5 – 7/5 ⇔ s: x – 5y -7 = 0.
Alternativa: C
14) Demonstre que o triângulo de vértices A(8 , 2), B(3 , 7) e C(2 , 1) é isósceles. Em seguida, calcule seu perímetro.
Resolução:
Para demonstrar que o triângulo ABC é isósceles se faz necessário mostrar que ele possui dois lados com a mesma medida. Assim, vamos calcular a distância entres seus vértices, que será a medida de cada lado.
.gif)
Agora, vamos calcular o seu perímetro. Lembrando que perímetro é a soma das medidas dos lados e é representado por 2P, temos:
.gif)
15) Quais são os possíveis valores de c para que os pontos (c , 3), (2 , c) e (14, -3) sejam colineares?
Resolução:

16) Determine o valor de x para que o ponto M(2 , 3) seja o ponto médio do segmento de extremos A(x , 5) e B(3 , x).
Resolução:

17) (Fuvest-SP) Se (m+2n , m – 4) e (2 – m , 2n) representam o mesmo ponto do plano cartesiano, então mn é igual a:
(A) – 2
(B) 0
(C) √2
(D) 1
(E) ½
Resolução:
.gif)
18) (FEI-SP) Num sistema de coordenadas cartesianas são dados os pontos A(0 , 0) e P(3 , h). Assinale a alternativa cuja expressão representa a distância do ponto P ao ponto A em função de h.
(A) d = √(9 + h2)
(B) d = h + 3
(C) d = 3h
(D) d = √(9 + 6h + h2)
(E) d = 9 + h
Resolução:
.gif)
Continua...























.gif)


.gif)
.gif)
