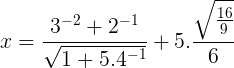EXPRESSÕES NUMÉRICAS I

EXPRESSÕES NUMÉRICAS I

Professor Diminoi

EXPRESSÕES NUMÉRICAS
São formadas pelas operações matemáticas aplicadas a números conhecidos e cumprem determinada ordem.

COMO RESOLVER UMA EXPRESSÃO NUMÉRICA

Quanto a prioridade dos sinais gráficos:
1º Parênteses ( )

2º Colchetes [ ]
3º Chaves { }

Quanto a prioridade das operações:
1º Potências ou Raízes
2º Multiplicações ou Divisões
3º Adições ou Subtrações

Caso apareçam essas duas operações ao mesmo tempo dentro de uma mesma expressão algébrica, calculamo-las na ordem em que aparecerem.

Da mesma forma, operações com mesmo grau de prioridade são sempre calculadas na ordem em que aparecem, o que acontece com a multiplicação e a divisão.

Na ausência de multiplicação e divisão na expressão numérica, calculamos, então, a adição e a subtração dos termos. Caso exista as duas operações, calculamo-las na ordem em que aparecerem até encontrarmos um resultado final.

Dada a expressão abaixo resolva:

5 + 2 . √9 – 4 : 2 – 1 + 3²

Primeiramente calcularemos a radiciação ou a potenciação:

5 + 2 . √9 – 4 : 2 – 1 + 3²
5 + 2 . 3 – 4 : 2 – 1 + 9

Calculamos a multiplicação ou a divisão na ordem em que elas parecem
5 + 2 . 3 – 4 : 2 – 1 + 9
5 + 6 – 2 – 1 + 9

Agora realizaremos as adições e subtrações na ordem em que elas parecem:
5 + 6 – 2 – 1 + 9
11 – 2 – 1 + 9
9 – 1 + 9
8 + 9
17

EXERCÍCIOS RESOLVIDOS

01) {[2 + (5 + 4) : 3 – √4 + 9] : 4}²

Para calcular a expressão quando ela possui símbolos, começamos sempre resolvendo as operações que estão dentro do parêntese.
{[2 + (5 + 4) : 3 – √4 + 9] : 4}²
{[2 + 9 : 3 – √4 + 9] : 4}²

Agora que não há nenhuma operação entre parênteses, vamos buscar eliminar os colchetes. Dentro deles, é importante respeitar a ordem de prioridade das operações, começando, então, nesse caso, pela radiciação.
{[2 + 9 : 3 – √4 + 9] : 4}²
{[2 + 9 : 3 – 2 + 9] : 4}²

Ainda com o objetivo de eliminar o colchete, realizaremos agora a divisão, já que ela possui prioridade em relação à adição e subtração.
{[2 + 9 : 3 – 2 + 9] : 4}²
{[2 + 3 – 2 + 9] : 4}²

Para eliminar o colchete, calcularemos as adições e a subtração, na ordem em que essas operações aparecem.
{[2 + 3 – 2 + 9] : 4}²
{[5 – 2 + 9] : 4}²
{[3 + 9] : 4}²
{12 : 4}²
Agora que eliminamos o parêntese, por fim, vamos eliminar as chaves, e, para isso, vamos calcular a divisão:
{12 : 4}²
3²
Por fim, só nos resta calcular a potência:
3²
9

02)
8 ÷ 2(2 + 2) =
8 ÷ 2 . 4 =
4 . 4 = 16

03)

– 8 + { – 5 + [ (8 – 12) + (13 + 12) ] – 10 } =
– 8 + { – 5 + [ – 4 + 25] – 10 } =
– 8 + { – 5 + 21 – 10 } =
– 8 + 6 = – 2

04)
{ [ (8 . 4 + 3) ÷ 7 + (3 + 15 ÷ 5) ‧ 3] . 2 – (19 – 7) ÷ 6 } . 2 + 12 =
{ [ (32 + 3) ÷ 7 + (3 + 3) ‧ 3 ] . 2 – 12 ÷ 6} ‧ 2 + 12 =
{ [ 35 ÷ 7+ 6 . 3] . 2 – 2 } . 2 + 12 =
{ [ 5 + 18 ] . 2 – 2 } . 2 + 12 =
{ 23 ‧ 2– 2 } . 2 + 12 =
{ 46 – 2 } ‧ 2 + 12 =
44 . 2 + 12 =
88 + 12 = 100

05)
[ √100– (2⁴– 8) . 2 – 24 ] ÷ (2²– 3 + 2) =
[ 10 – (16 – 8) . 2 – 24 ] ÷ (4 – 3 + 2) =
[ 10 – 8 . 2– 24 ] ÷ 3 =
[ 10 – 16 – 24 ] ÷ 3 =
– 30 ÷ 3 = – 10

06) Qual é o resultado da expressão: 20 ÷ {√4 . [-9 + 17 ÷ (-2 + 5)]} – [7 . (-3) – 16 ÷ (-2) + 2]
(A) 9
(B) 10
(C) 11
(D) 12
(E) 13
Resolução
Primeiro vamos eliminar o parêntese:
20 ÷ {√4 . [-9 + 12 ÷ (-2 + 5)]} – [7 · (-3) – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 12 ÷ (-2 + 5)]} – [7 · (-3) – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 12 ÷ 3]} – [7 · (-3) – 16 ÷ (-2) + 2]
Agora eliminaremos os colchetes:
20 ÷ {√4 . [-9 + 12 ÷ 3]} – [7 . (-3) – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 4]} – [7 . (-3) – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 4]} – [7 . (-3) – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 4]} – [-21 – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 4]} – [-21 – 16 ÷ (-2) + 2]
20 ÷ {√4 . [-9 + 4]} – [-21 + 8 + 2]
20 ÷ {√4 . [-9 + 4]} – [-21 + 8 + 2]
20 ÷ {√4 . (-5)} – [-21 + 8 + 2]
20 ÷ {√4 . (-5)} – [-21 + 8 + 2]
20 ÷ {√4 . (-5)} – [-13 + 2]
20 ÷ {√4 · (-5)} – [-13 + 2]
20 ÷ {√4 . (-5)} – [-11]
20 ÷ {√4 . (-5)} + 11
Agora eliminaremos as chaves, respeitando a ordem de prioridade entre as operações:
20 ÷ {√4 . (-5)} + 11
20 ÷ {2 . (-5)} + 11
20 ÷ {2 . (-5)} + 11
20 ÷ (-10) + 11
Eliminando todos os símbolos, realizaremos, primeiro, a divisão e, depois, a adição:
20 ÷ (-10) + 11
-2 + 11
9
Alternativa: A

07) Analisando as expressões:
I. [8 : (8 × (-2) + 18)] – √16
II. [8 × (9 : 3 + 1)] + 2
III. {3² – [4 + (3 – 6 : 2)²]} – 5
As expressões que têm como resultado zero são:
(A) I, II e III
(B) somente I e II
(C) somente I e III
(D) somente II e III
(E) Nenhuma delas
Resolução
Resolvendo cada uma delas, temos que:
I.
[8 : (8 × (-2) + 18)] – √16
[8 : (-16 + 18)] – √16
[8 : 2] – √16
4 – √16
4 – 4
0

II.
[8 × (9 : 3 + 1)] + 2
[8 × (3 + 1)] + 2
[8 × 4] + 2
32 + 2
34

III.
{3² – [4 + (3 – 6 : 2)²]} – 5
{3² – [4 + (3 – 3)²]} – 5
{3² – [4 + 0²]} – 5
{3² – [4 + 0]} – 5
{3² – 4} – 5
{9 – 4} – 5
5 – 5
0
Alternativa: C

SITUAÇÕES PROBLEMAS
01) Gustavo comprou pela internet 4 camisetas: uma vermelha de R$ 45 cada; uma azul de R$ 38 cada, uma preta de R$ 42 cada e uma branca de R$ 28 cada.
Qual foi o valor total pago por Gustavo pelas camisetas?
(A) Gustavo pagou um total de R$ 53 nas camisetas.
(B) Gustavo pagou um total de R$ 153 nas camisetas.
(C) Gustavo pagou um total de R$ 253 nas camisetas.
(D) Gustavo pagou um total de R$ 353 nas camisetas.
Resolução:
Somar o total pago pelas camisetas:
45 + 38 + 42 + 28 = 153
Alternativa: B

02) Gustavo comprou pela internet 4 camisetas: uma vermelha de R$ 45 cada; uma azul de R$ 38 cada, uma preta de R$ 42 cada e uma branca de R$ 28 cada.
E se ele parcelar sua compra em 3 vezes no cartão, qual será o valor de cada parcela?
(A) Cada parcela terá o valor de R$ 51.
(B) Cada parcela terá o valor de R$ 81.
(C) Cada parcela terá o valor de R$ 70.
(D) Cada parcela terá o valor de R$ 90.
Resolução:
Somar o total pago pelas camisetas:
45 + 38 + 42 + 28 = 153
Dividir o total pago por 3
153/3 = 51
Alternativa: A

03) Mariana comprou 3 canetas e uma lapiseira, gastando ao todo 60 reais. A lapiseira custou 24 reais. Quanto custou cada caneta, se elas tem o mesmo preço?
(A) Cada caneta custou 12 reais
(B) Cada caneta custou 14 reais
(C) Cada caneta custou 16 reais
(D) Cada caneta custou 18 reais
Resolução:
60 - 24 = 36
36 : 3 = 12
Cada caneta custou 12 reais
Alternativa:

04) Para uma excursão a um museu, um colégio alugou 4 ônibus. Em cada ônibus foram colocados 35 alunos . Além dos alunos 10 professores acompanham esses alunos na excursão. Quantas pessoas ao todo participaram dessa excursão ?
(A) Participaram dessa excursão 100 pessoas
(B) Participaram dessa excursão 50 pessoas
(C) Participaram dessa excursão 150 pessoas
(D) Participaram dessa excursão 100 pessoas
Resolução:
4 . 35 = 140
140 + 10 = 150
Participaram dessa excursão 150 pessoas
Alternativa:

05) Resolvendo expressão numérica: 30 ÷ [10 + (2 + 3)] temos:
(A) 1
(B) 2
(C) 3
(D) 4
Resolução:
Devemos começar a resolver esta expressão resolvendo as prioridades. No caso desta expressão, resolveremos primeiro os parênteses e colchetes primeiro.
30 ÷ [10 + (2 + 3)]
30 ÷ [10 + 5]
30 ÷ 15
2
Alternativa: B

06) Resolva a expressão dada: 7² – 3 ÷ 2 + √16
(A) 25,5
(B) 14,1
(C) 39
(D) 51,1
Resolução:
NestA expressão, as prioridades são as potências e radiciação, a divisão e, finalmente, a adição.
Então:
7² – 3 ÷ 2 + √16
49 – 3 ÷ 2 + 4
49 – 1,5 + 4
47,5 + 4
51,5
Alternativa: D

07) Resolva a expressão: 6 + 20 – 12 . 2
(A) 2
(B) 4
(C) 6
(D) 8
Resolução:
6 + 20 – 12 . 2
6 + 20 – 24
26 – 24
2
Alternativa: A

08) Resolva a expressão a seguir: 3 x 8 – √25 + 3
(A) 25
(B) 46
(C) 36
(D) 7
Resolução:
Aqui as prioridades são: radiciação e potenciação e, por fim, a multiplicação.
3 x 8 – √25 + 3³
3 x 8 – 5 + 27
24 – 5 + 27
24 + 22
46
Alternativa: B

09) (PM AC – Funcab) Determine o valor da expressão: -1 + 6 x (7 – 4 ÷ 2)
(A) 7,5
(B) 29
(C) 8,5
(D) 24
(E) 32,5
Resolução
-1 + 6 x (7 – 4 ÷ 2)
-1 + 6 x (7 – 2)
-1 + 6 x 5
-1 + 30
29
Resposta: B

10) (TJ CE – ESAF) Simplifique: ( (0 ÷ 3) + (0,75 x 4) ) / ( 1 + 0,5).
(A) 1,5
(B) 2
(C) 4
(D) 5,5
(E) 6
Resolução:
( (0 ÷ 3) + (0,75 x 4) ) / ( 1 + 0,5)
( 0 + 3) ) / 1,5
3 / 1,5
2
Resposta: B

PROBLEMAS MATEMÁTICOS
Os problemas matemáticos são resolvidos utilizando inúmeros recursos matemáticos, destacando, entre todos, os princípios algébricos, os quais são divididos de acordo com o nível de dificuldade e abordagem dos conteúdos. Nas séries iniciais os cálculos envolvem adições e subtrações; posteriormente, multiplicações e divisões.

Na 2ª fase do Ensino Fundamental os problemas são resolvidos com a utilização dos fundamentos algébricos, isto é, criamos equações matemáticas com valores desconhecidos (letras). Observe algumas situações que podem ser descritas com utilização da álgebra.

O dobro de um número adicionado com 4 → 2x + 4.

A soma de dois números consecutivos → x + (x + 1)

O quadrado de um número mais 10 → x² + 10

O triplo de um número adicionado ao dobro do número → 3x + 2x

A metade da soma de um número com 15 → (x + 15)/2

A quarta parte de um número → x/4

SITUAÇÕES PROBLEMAS RESOLVIDOS
01) A soma de três números pares consecutivos é igual a 96. Determine-os.
1º número: x
2º número: x + 2
3º número: x + 4
( x )+(x + 2) + (x + 4) = 96
Resolução:
x + x + 2 + x + 4 = 96
3x = 96 – 4 – 2
3x = 96 – 6
3x = 90
x = 90/3
x = 30
1º número: x → 30
2º número: x + 2 → 30 + 2 = 32
3º número: x + 4 → 30 + 4 = 34
Os números procurados são 30, 32 e 34.

02) O triplo de um número natural somado a 4 é igual ao quadrado de 5. Calcule-o:
(A) 13
(B) 7
(C) 9
(D) 13
Resolução:
3x + 4 = 5²
3x = 25 – 4
3x = 21
x = 21/3
x = 7
O número procurado é igual a 7.
Alternativa: B

03) A idade de um pai é o quádruplo da idade de seu filho. Daqui a cinco anos, a idade do pai será o triplo da idade do filho. Qual é a idade atual de cada um?
Resolução:
Atualmente
Filho: x
Pai: 4x
Futuramente
Filho: x + 5
Pai: 4x + 5
4x + 5 = 3 . (x + 5)
4x + 5 = 3x + 15
4x – 3x = 15 – 5
x = 10
Pai: 4x → 4 . 10 = 40
O filho tem 10 anos e o pai tem 40.

04) O dobro de um número adicionado ao seu triplo corresponde a 20. Qual é o número?
Resolução:
2x + 3x = 20
5x = 20
x = 20/5
x = 4
O número corresponde a 4.

05) Em uma chácara existem galinhas e coelhos totalizando 35 animais, os quais somam juntos 100 pés. Determine o número de galinhas e coelhos existentes nessa chácara.
Resolução:
Galinhas: g
Coelhos: c
g + c = 35
Cada galinha possui 2 pés e cada coelho 4, então:
2g + 4c = 100
Sistema de equações
Isolando c na 1ª equação:
g + c = 35
c = 35 – g
8Substituindo c na 2ª equação:
2g + 4c = 100
2g + 4 . (35 – g) = 100
2g + 140 – 4g = 100
2g – 4g = 100 – 140
– 2g = – 40
g = 40/2
g = 20
Calculando c
c = 35 – g
c = 35 – 20
c = 15

06) Carlos comprou uma televisão no valor de R$ 950,00, dividida em 10 prestações iguais. Ao pagar a 4º prestação, recebeu de presente de seu avô, o restante do dinheiro para a quitação do aparelho. Quanto Carlos recebeu?
(A) R$ 270,00
(B) R$ 570,00
(C) R$ 70,00
(D) R$ 370,00
Resolução:
O valor do aparelho é igual a R$ 950,00.
Carlos resolveu dividir o televisor em 10 prestações iguais, então devemos realizar uma operação de divisão: 950: 10 = 95 reais.
Carlos efetuou o pagamento de 4 prestações, dessa forma, ainda faltam 6. São as prestações restantes que o avô de Carlos resolveu pagar. Portanto, 95 . 6 = 570 reais.
Carlos recebeu R$ 570,00 de seu avô.
Alternativa: B

07) João tinha uma quantia, gastou 35% e ainda ficou com R$ 97,50. Qual o valor que João tinha inicialmente?
(A) R$ 150,00
(B) R$ 1350,00
(C) R$ 10,00
(D) R$ 200,00
Resolução:
Quando trabalhamos com porcentagem, sempre precisamos nos lembrar de que o valor corresponde a 100%. Dos 100%, João gastou 35%, então: 100% – 35% = 65%. Os 65% restante, correspondem a R$ 97,50. Dessa forma, temos que:

João tinha o valor inicial de R$ 150,00.
Alternativa: A

08) O preço de uma geladeira, à vista, é R$ 1 200,00. No pagamento em três prestações ocorre um acréscimo de 10% de juros. Qual será o valor da prestação no pagamento parcelado?
(A) R$ 140,00
(B) R$ 340,00
(C) R$440,00
(D) R$ 250,00
Resolução:
Veja que no pagamento parcelado, o preço da televisão aumenta de acordo com o juro de 10%. Vamos calcular 10% do valor à vista da geladeira:

A geladeira sofrerá um aumento de R$ 120,00 R$ 1.200,00 + R$ 120,00 = R$ 1320,00
O preço final para o financiamento é de R$ 1 320,00, que será dividido em três prestações:
1 320 : 3 = 440 reais.
Na compra da geladeira a prazo, o valor de cada prestação será de R$440,00.
Alternativa: C

09) O dobro de um número adicionado ao seu triplo, é igual ao próprio número adicionado a 168. Qual é o número?
(A) 35
(B) 40
(C) 42
(D) 55
Resolução:
Como você não conhece o número, deverá representá-lo por “x”.
Dobro de x = 2 . x = 2x
Triplo de x = 3 . x = 3x
2x + 3x = x + 168
2x + 3x – x = 168
4x = 168
x = 168/4
x = 42
Alternativa: C

Exercícios resolvidos
01) Resolva a expressão numérica 7 -3 + 1 – 2 =
Resolução:
4 + 1 -2 =
5 – 2 =
3

02) Resolva a expressão numérica 15 -1 -2 + 5 =
Resolução:
14 -2 + 5 =
12 + 5 =
7

03) Resolva a expressão numérica 8 – [– (6 + 4) + (3 – 2 – 1)] =
Resolução:
8 – [– (6 + 4) + (3 – 2 – 1)] = resolva primeiro os parênteses.
8 – [– 10 + (1 – 1)] =
8 – [– 10 + 0 ] = resolva os colchetes.
8 – [– 10] = faça o jogo de sinais para eliminar o colchete.
8 + 10 = 18
Conclusão: o valor numérico da expressão é 18.

04) Resolva a expressão numérica – 62 : (– 5 + 3) – [– 2 . (– 1 + 3 – 1)² – 16 : (– 1 + 3)²]
Resolução:
– 62 : (– 5 + 3) – [– 2 . (– 1 + 3 – 1)² – 16 : (– 1 + 3)²] = elimine os parênteses.
– 62 : (– 2) – [– 2 . (2 – 1)² – 16 : 2²] = continue eliminando os parênteses.
– 62 : (– 2) – [– 2 . 1 – 16 : 2²] = resolva as potências dentro do colchetes.
– 62 : (– 2) – [– 2 . 1 – 16 : 4] = resolva as operações de multiplicação e divisão nos colchetes.
– 62 : (– 2) – [– 2 – 4] =
– 62 : (– 2) – [– 6] = elimine o colchete.
– 62 : (– 2) + 6 = efetue a potência.
31 + 6 = 37 efetue a adição.
Conclusão: o valor numérico da expressão é 37.

05) Resolva a expressão 25 + {14 – [25 x 4 + 40 – (20 ÷ 2 + 10)]}
Resolução:
25 + {14 – [25 x 4 + 40 – (20 ÷ 2 + 10)]} → primeiro resolveremos a divisão interna aos parênteses.
25 + {14 – [25 x 4 + 40 – (10 + 10)]} → resolveremos a adição interna aos parênteses.
25 + {14 – [25 x 4 + 40 – (20)]} → eliminaremos os parênteses, como o sinal que os antecede é negativo, inverteremos o sinal interno.
25 + {14 – [25 x 4 + 40 – 20]} → resolveremos a multiplicação interna aos colchetes.
25 + {14 – [100 + 40 – 20]} → resolveremos a adição e subtração, em qualquer ordem, internas aos colchetes.
25 + {14 – [120]} → eliminaremos os colchetes, como o sinal que os antecede é negativo, inverteremos o sinal interno.
25 + {14 – 120} → resolveremos a subtração interna aos colchetes.
25 + {- 106} → eliminaremos as chaves, como o sinal que as antecede é positivo, manteremos o sinal interno original.
25 – 106 → resolveremos a subtração
- 81 (Resultado Final)

06) Resolva a expressão numérica – 8 + { – 5 + [ (8 – 12) + (13 + 12) ] – 10 } =
Resolução:
– 8 + { – 5 + [ (8 – 12) + (13 + 12) ] – 10 } =
– 8 + { – 5 + [ – 4 + 25] – 10 } =
– 8 + { – 5 + 21 – 10 } =
– 8 + 6 = – 2

07) Resolva a expressão numérica { [ (8 ‧ 4 + 3) ÷ 7 + (3 + 15 ÷ 5) ‧ 3] ‧ 2 – (19 – 7) ÷ 6 } ‧ 2 + 12 =
Resolução:
{ [ (8 ‧ 4 + 3) ÷ 7 + (3 + 15 ÷ 5) ‧ 3] ‧ 2 – (19 – 7) ÷ 6 } ‧ 2 + 12 =
{ [ (32 + 3) ÷ 7 + (3 + 3) ‧ 3 ] ‧ 2 – 12 ÷ 6} ‧ 2 + 12 =
{ [ 35 ÷ 7+ 6 ‧ 3] ‧ 2 – 2 } ‧ 2 + 12 =
{ [ 5 + 18 ] ‧ 2 – 2 } ‧ 2 + 12 =
{ 23 ‧ 2 –2 } ‧ 2 + 12 =
{ 46 –2 } ‧ 2 + 12 =
44 ‧ 2 + 12 =
88 + 12 = 100

08) Resolva a expressão numérica [ √100 –(2⁴– 8) · 2 –24 ] ÷ (2²– 3 + 2) =
Resolução:
[ √100 –( 2⁴– 8 ) · 2 –24 ] ÷ ( 2²– 3 + 2 ) =
[ 10 –( 16 – 8 ) · 2 –24 ] ÷ ( 4 – 3 + 2 ) =
[ 10 – 8 · 2 –24 ] ÷ 3 =
[ 10 – 16 –24 ] ÷ 3 =
– 30 ÷ 3 = – 10

09) Resolva a expressão numérica 15 + [( 3 . 6 -2 ) - (10 -6 : 2 ) + 1 ] =
Resolução:
15 + [ ( 18 -2 ) -( 10 -3 ) + 1 ] =
15 + [ 16 -7 + 1 ]=
15 + [ 9 + 1 ] =
15 + 10 =
25

10) Resolva a expressão numérica 50 -{ 40 – 3 x [ 5 - ( 10 -7 ) ] }=
Resolução:
50 -{ 40 - 3x [ 5 – 3 ] }=
50 -{ 40 -3x2 } =
50 -{ 40 -6 } =
50 -34 =
16

11) Calcule o valor numérico da expressão [(18 + 3 · 2) ÷ 8 + 5 · 3] ÷ 6
Resolução:
A ordem em que uma expressão deve ser calculada é a seguinte: primeiro as operações dentro dos parênteses; depois, dentro dos colchetes e, por fim, dentro das chaves. Quanto às operações, o correto é realizar primeiramente as multiplicações e divisões e, posteriormente, as adições e subtrações. Portanto:
[ ( 18 + 3 . 2 ) ÷ 8 + 5 · 3 ] ÷ 6
[ ( 18 + 6 ) ÷ 8 + 5 . 3 ] ÷ 6
[ ( 24 ) ÷ 8 + 5 . 3 ] ÷ 6
Quando sobrar apenas um número dentro dos parênteses, colchetes ou chaves, elimine essas marcações.
[ ( 24 ) ÷ 8 + 5 . 3 ] ÷ 6
[ 24 ÷ 8 + 5 . 3] ÷ 6
[ 3 + 15 ] ÷ 6
[ 18 ] ÷ 6
18 ÷ 6
3
Conclusão: o valor numérico dessa expressão é 3.

12) Calcule o valor numérico da expressão {[(8 · 4 + 3) ÷ 7 + (3 + 15 ÷ 5) · 3] · 2 – (19 – 7) ÷ 6} · 2 + 12.
Resolução:
Primeiramente, devem ser calculadas as operações dentro dos parênteses. Mesmo dentro dos parênteses, a ordem correta de operações é multiplicação e divisão, depois adição e subtração.
{ [ ( 8 . 4 + 3 ) ÷ 7 + ( 3 + 15 ÷ 5 ) . 3 ] . 2 – ( 19 – 7 ) ÷ 6} . 2 + 12
{ [ ( 32 + 3 ) ÷ 7 + ( 3 + 3 ) . 3] . 2 – ( 12 ) ÷ 6} . 2 + 12
Agora realizaremos as somas dentro dos parênteses e eliminaremos os parênteses desnecessários.
{ [ ( 32 + 3 ) ÷ 7 + ( 3 + 3 ) . 3 ] . 2 –( 12 ) ÷ 6} . 2 + 12
{ [ 35 ÷ 7 + 6 . 3 ] . 2 –12 ÷ 6 } . 2 + 12
Eliminados os parênteses, partiremos para os cálculos dos colchetes:
{ [ 35 ÷ 7 + 6 . 3 ] . 2 –12 ÷ 6 } . 2 + 12
{ [ 5 + 18 ] . 2 –12 ÷ 6 } . 2 + 12
{ [ 23 ] . 2 –12 ÷ 6 } . 2 + 12
{ 23 . 2 –12 ÷ 6 } . 2 + 12
Sem colchetes, realizaremos as operações presentes nas chaves, respeitando a ordem de operações:
{ 23 . 2 –12 ÷ 6 } . 2 + 12
{ 46 –2 } . 2 + 12
{ 44 } . 2 + 12
44 . 2 + 12
Basta finalizar a expressão respeitando apenas a ordem entre as operações.
44 . 2 + 12
88 + 12
100
Conclusão: o valor numérico da expressão é 100.

13) (UniCESUMAR - SP) Escrever um número na notação científica significa expressá-lo como o produto de dois números reais x e y, tais que: 1 ≤ x < 10 e y é uma potência de 10.
Assim, por exemplo, as respectivas expressões dos números 0,0021 e 376,4 na notação científica são 2,1 x 10^–3 e 3,764 x 10².
Com base nessas informações, a expressão do número N na notação científica é:
N =   14,4·0,072
      0,16·0,000027
(A) 7,2 x 10³
(B) 2,4 x 10⁴
(C) 2,4 x 10⁵
(D) 3,6 x 10⁴
(E) 3,6 x 10³
Resolução:
N = 1,44·10¹·7,2·10^-2
      1,6·10^-1·2,7·10^-5
N = 1,44·7,2·10¹·10^-2
       1,6·2,7·10^-1·10^-5
N = 10,368·10^1-2
       4,32·10^-1-5
N = 10,368·10^-1
       4,32·10^-6
N = 2,4·10⁵
Alternativa: C

14) (UNAERP - SP) Analisando as expressões:
I. [(+2)(– 3/4):(–2/3)]
II. (+2–3+1):(–2+2)
III. (+4–9):(–5+3)
IV. (2–3+1):(–7)
podemos afirmar que zero é o valor de:
(A) somente I, II e IV
(B) somente I e III
(C) somente IV
(D) somente II e IV
(E) somente II
Resolução:
Para resolver essa questão, é necessário resolver antes todas as expressões numéricas presentes.
I: [(+2)(–3)]:(–2)
4 3
(–6):(–2)
4    3
(–6) · 3
4   –2
18
8
Como 18 divido por 8 é um número próximo de 2, então a expressão I é diferente de zero.
II: (+2 – 3 + 1):(–2 + 2) = 0:0
Como não é possível dividir números por 0, então 0:0 não existe e, por isso, a expressão é diferente de zero.
III: (+ 4 – 9):(– 5 + 3) = (– 5):(– 2) = 2,5
2,5 é diferente de zero.
IV: (2 – 3 + 1):(–7) = 0:(–7) = 0
Essa expressão é a única que tem 0 como resultado.
Alternativa C

15) Resolva a expressão numérica {15 + [(7 – 100:10²) + (16:√4 – 4)]² + 10}·3
Resolução:
Assim, para os primeiros parênteses, faremos a potência; depois, a divisão e, por fim, a subtração:
{15 + [(7 – 100:10²) + (16:√4 – 4)]² + 10}·3
{15 + [(7 – 100:100) + (16:√4 – 4)]² + 10}·3
{15 + [(7 – 1) + (16:√4 – 4)]² + 10}·3
{15 + [(6) + (16:√4 – 4)]² + 10}·3
Nesse caso, os parênteses podem ser eliminados.
{15 + [6 + (16:√4 – 4)]² + 10}·3
Agora os parênteses seguintes. Primeiro, a raiz quadrada; depois, divisão e subtração.
{15 + [6 + (16:2 – 4)]² + 10}·3
{15 + [6 + (8 – 4)]² + 10}·3
{15 + [6 + (4)]² + 10}·3
{15 + [6 + 4]² + 10}·3
Note que, dentro dos colchetes, sobrou apenas uma adição. Depois de realizá-la, o número que sobrar deverá ser elevado ao quadrado. Assim, obteremos:
{15 + [10]² + 10}·3
{15 + 100 + 10}·3
Agora, falta apenas realizar os cálculos dentro das chaves e multiplicar o resultado por 3:
{15 + 100 + 10}·3
125·3
375

16) A respeito da resolução de expressões numéricas, assinale a alternativa correta:
(A) As operações devem ser feitas na ordem em que aparecem.
(B) É necessário calcular primeiro todas as operações no interior dos parênteses na ordem em que elas aparecem.
(C) A pessoa que realiza os cálculos escolhe a ordem mais oportuna para eles.
(D) Não existe ordem para realização dos cálculos em uma expressão numérica.
(E) As adições e subtrações são os últimos cálculos na lista de prioridades das expressões numéricas.
Resolução:
a) Falsa!
As operações devem ser feitas na seguinte ordem: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
b) Falsa!
Embora realmente seja necessário calcular primeiro as operações no interior de parênteses, a ordem de realização das operações é: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
c) Falsa!
A ordem para realização das operações é predefinida: potências e raízes, multiplicações e divisões e, por fim, adições e subtrações.
d) Falsa!
Na realidade, existe uma ordem de realização dos cálculos, como já dito.
e) Verdadeira!
Alternativa: E

17) Qual das alternativas a seguir representa um quinto do resultado desta expressão numérica:
[(64 – 16·4) + (48·10 – 180)]·5
(A) 270
(B) 300
(C) 350
(D) 400
(E) 410
Resolução:
Para resolver esse problema, lembre-se da ordem de resolução das expressões numéricas. Primeiramente, deve-se resolver o interior dos parênteses; em seguida, os colchetes e, nos casos em que aparecerem, as chaves. Já as operações matemáticas devem ser resolvidas com a seguinte prioridade: primeiramente, as raízes e potências (na ordem em que aparecerem); depois, multiplicações e divisões (na ordem em que aparecerem) e, por fim, adições e subtrações (na melhor ordem possível). Dessa maneira, faremos:
[ ( 64 – 16 . 4 ) + ( 48 . 10 – 180 ) ] . 5 =
[ ( 64 – 64 ) + ( 480 – 180 ) ] . 5 =
[ 0 + 300 ] . 5 =
300 . 5 =
1500
Como o exercício pede um quinto desse resultado, será necessário dividi-lo por 5:
1500:5 = 300
Alternativa: B

18) Analise a solução da expressão algébrica abaixo e assinale a alternativa correta:
{ ( 10 · 10 + 4 . 11 ) : 12 – [ ( 20 + 19 . 10 ) :39 + 15 ] } + 50 =
{ ( 100 + 44 ) : 12 – [ (39 .10 ) : 39 + 15 ] } + 50 =
{ 144 : 12 – [ 390 : 39 + 15 ] } + 50 =
{ 12 – [ 10 + 15 ] } + 50 =
{ 12 – 25 } + 50 =
– 13 + 50 = 37
(A) A resolução está correta, nenhum erro foi cometido.
(B) A resolução está correta, mas por coincidência, pois alguns erros foram cometidos.
(C) A resolução está incorreta, o verdadeiro resultado é 50.
(D) A resolução está incorreta, pois foi feita uma soma em vez de dar prioridade a uma multiplicação.
(E) A resolução está incorreta, pois as multiplicações devem ser feitas sempre depois das divisões.
Resolução:
a) Incorreta!
A resolução está incorreta e um erro foi cometido.
b) Incorreta!
A resolução está incorreta.
c) Incorreta!
O resultado não é 50.
d) Correta!
Observe que, logo no início, houve esta soma: 20 + 19 = 39. O correto seria primeiramente multiplicar 19·10 e, depois, somar 20 ao resultado.
e) Incorreta!
Não existe prioridade entre multiplicações e divisões.
Alternativa: D

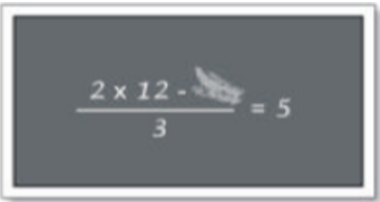
19) Margarida viu no quadro-negro algumas anotações da aula anterior um pouco apagadas, conforme mostra a figura a seguir. Qual número foi apagado?
(A) 9
(B) 10
(C) 12
(D) 13
(E) 15
Resolução:
Primeiramente, trocaremos x por ·, para representar a multiplicação, e o espaço apagado por y, para representar o número que queremos descobrir. Posteriormente, multiplicaremos ambos os lados da igualdade pelo mesmo número para obter:
2 . 12 – x = 5
3
2 . 12 – x = 5·3
2 . 12 – x = 15
24 – x = 15
Agora, pense em um número que subtraído de 24 resulte em 15, ou seja, um número que somado com 15 resulte em 24. Esse número é 9.
Alternativa: A

20) (CREF SC – Quadrix) Qual é o valor da expressão numérica abaixo?
[- (-2)³ – 2³]
(A) 0
(B) 1
(C) 8
(D) -8
(E) -16
Resolução:
[- (-2)³ – 2³]
[- (-8) – 2³]
[8 – 2³]
[8 – 8]
0
Alternativa: A

21) (Bombeiros AC – Funcab) Calcule o valor da expressão [2 + 3 . 4] ÷ 7 + 7.
(A) 9
(B) 7
(C) 4
(D) 12
(E) 1
Resolução:
[2 + 3 x 4] ÷ 7 + 7
[2 + 12] ÷ 7 + 7
14 ÷ 7 + 7
2 + 7
9
Alternativa: A

22) (PM AC – Funcab) Determine o valor da expressão -1 + 6 x (7 – 4 ÷ 2)
(A) 7,5
(B) 29
(C) 8,5
(D) 24
(E) 32,5
Resolução:
-1 + 6 x (7 – 4 ÷ 2)
-1 + 6 x (7 – 2)
-1 + 6 x 5
-1 + 30
29
Alternativa: B

23) (Guarda Civil SP) Qual o valor de x na expressão abaixo?
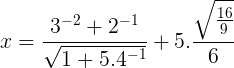(A) 1/27
(B) 41/27
(C) 1/17
(D) 11/18
(E) 41/17
Resolução:
Vamos calcular por partes:
3-² + 2-¹ = 1/9 + 1/2 = (2 + 9)/18 = 11/18
√( 1 + 5 . 4-¹ ) = √( 1 + 5/4 ) = √ [ ( 4 + 5 ) /4 ] = √(9/4) = 3/2
5.√( 16/9 ) / 6 = 5.( 4/3 ) / 6 = 5 . 4/6 . 3 = 20 / 18 = 10/9
( 11/18 ) / ( 3/2 ) = 11 . 2/18 . 3 = 22/54 = 11/27
11/27 + 10/9 = ( 11 + 30 )/27 = 41/27
Alternativa: E

24) (TJ CE – ESAF) Simplifique: ( (0 ÷ 3) + (0,75 . 4) ) / ( 1 + 0,5)
(A) 1,5
(B) 2
(C) 4
(D) 5,5
(E) 6
Resolução:
( (0 ÷ 3) + (0,75 x 4) ) / ( 1 + 0,5)
( 0 + 3) ) / 1,5
3 / 1,5
2
Alternativa: B

25) Resolva expressão { 100 – [25 . (35 : 7) ] . 2} =
Resolução:
1º – Resolvemos as raízes e potências; nesse caso não há.
2º – Resolvemos as divisões e multiplicações :
{ 100 – [25 . (35 : 7) ] . 2} = ?
{ 100 – [25 . 5 ] . 2} = ?
{ 100 – [125] . 2} = ?
3º – Resolvemos as somas e subtrações.
{ 100 – 250 } = – 150

26) (UNAERP SP) Analisando as expressões:
I. [(+2)(–3/4)]:(–2/3)
II. (+2 – 3 + 1):(–2+2)
III. (+4–9):(–5+3)
IV (2–3+1):(–7)
Podemos afirmar que zero é o valor de:
(A) somente I, II e IV
(B) somente I e III
(C) somente IV
(D) somente II e IV
(E) somente II
Resolução:
A única forma de ter certeza do resultado é resolvendo todas as expressões numéricas presentes no exercício.
Lembre-se da ordem de resolução das expressões: primeiramente o que está no interior de parênteses, depois dentro de colchetes e, por fim, dentro de chaves. As operações encontradas devem ser feitas na seguinte ordem: radiciação ou potenciação, depois multiplicação ou divisão e, por fim, as adições ou subtrações.
I. Primeiramente o que está no interior dos parênteses:
[(+2)(–3/4)]:(–2/3)
[(+2)(–0,75)]:(–0,666...)
Observe que os parênteses dentro dos colchetes servem apenas para dizer que se trata de uma multiplicação entre um número positivo e um número negativo. Sendo assim, o resultado dessa multiplicação será negativo também. Portanto, teremos:
–1,5:(–0,666...)
Fazendo o jogo de sinais para a divisão acima, teremos:
1,5:0,666...
O resultado dessa divisão é 2,25, que é diferente de zero.
II. Primeiramente, devemos resolver o que está no interior dos parênteses. É aconselhável somar números de sinais iguais quando a soma envolve três ou mais parcelas.
(+2 – 3 + 1):(–2+2)
(+3 – 3):(– 2+2)
0:0
A divisão encontrada, de zero por zero, não pode existir, pois, em uma divisão, o divisor é obrigatoriamente diferente de zero. Portanto, o resultado dessa divisão não é zero.
III. Novamente, é preciso fazer os cálculos no interior dos parênteses primeiro.
(+4–9):(–5+3)
(– 5):(– 2)
Fazendo o jogo de sinais, teremos:
5:2 = 2,5
Esse resultado é diferente de zero.
IV. Primeiramente, resolva as operações no interior dos parênteses.
(2–3+1):(–7)
(3 – 3):(–7)
0:(–7)
0
O único item que resulta em zero é o IV, logo
Alternativa: C

27) (UEL PR) Considere dois números inteiros, a e b, consecutivos e positivos. Qual das expressões abaixo corresponde necessariamente a um número par?
(A) a + b
(B) 1 + ab
(C) 2 + a + b
(D) 2a + b
(E) 1 + a + b
Resolução:
Se a e b são consecutivos, um deles tem que ser par, e o outro, ímpar. Números pares podem ser escritos na forma 2n, e números ímpares, na forma 2n + 1. Supondo que a = 2n, b obrigatoriamente deve ser igual a 2n+1, pois 2n+1 é consecutivo de a.
Agora, é preciso analisar cada alternativa da questão.

a) a + b =
2n + 2n + 1 =
4n + 1 =
2·(2n) + 1
É um número ímpar, pois é o sucessor de um número par.

b) 1 + ab
O produto entre um número par e um número ímpar é um número par. Somando esse resultado a um, obtemos um número ímpar.

c) 2 + a + b
A soma de um número par com um número ímpar sempre tem um número ímpar como resultado. Assim, 2 + a é um número par que, somado a b (ímpar), resulta em um número ímpar.

d) 2a + b
Qualquer multiplicação por 2 tem como resultado um número par. A soma de um número par (2a) com um número ímpar sempre resulta em um número ímpar.

e) 1 + a + b
A soma entre um número par e um número ímpar é igual a um número ímpar. Somando um número ímpar com um número ímpar, o resultado sempre será um número par. Logo, o resultado da soma acima será um número par.
Alternativa: E

28) Os professores de determinada escola precisavam fazer a contagem dos alunos vencedores dos jogos internos a fim de adquirir as medalhas para premiação. No sexto ano, são 50 alunos no total. Apenas a quinta parte deles recebeu medalhas no vôlei, e a metade recebeu medalhas no futebol. No sétimo ano, com 30 alunos, apenas as meninas, que representam um terço dos alunos da sala, foram premiadas no vôlei e todos os meninos foram premiados no futebol. Já no oitavo ano, foram 7 medalhas de ouro, 4 de prata e 3 de bronze. Por fim, o nono ano não participou da competição.
Quantas medalhas foram compradas?
(A) 79
(B) 80
(C) 78
(D) 77
(E) 81
Resolução:
Primeiramente, é necessário montar a expressão numérica que representa a situação. A quinta parte de 50 é representada pela divisão 50:5 e a metade é 50:2. A situação do sétimo é de 30:3 meninas premiadas e 30-30:3 meninos premiados. Por fim, basta somar 7, 4 e 3 alunos do oitavo ano. Observe:
(50:5 + 50:2) + (30:3 + 30 – 30:3) + 7 + 4 + 3
Faça primeiro o interior dos parênteses, dando prioridade para multiplicações e divisões.
(50:5 + 50:2) + (30:3 + 30 – 30:3) + 7 + 4 + 3
(10 + 25) + (10 + 30 – 10) + 7 + 4 + 3
35 + 30 + 7 + 4 + 3
Agora realize as operações que sobraram.
35 + 30 + 7 + 4 + 3
65 + 7 + 4 + 3
72 + 4 + 3
76 + 3
79
O número de alunos premiados foi 79.
Alternativa: A

29) Que número representa metade do resultado da expressão numérica [(4·5 – 6·3):(5·13 – 9·7)]:[(12²:6·4):(6·8 – 6·7)]
(A) 1
(B) 2
(C) 0,5
(D) 1,5
(E) 2,5
Resolução:
A hierarquia de realização dos cálculos começa com o interior dos parênteses para depois o interior dos colchetes. Nas operações, a ordem correta é potenciação e radiciação, depois multiplicação e divisão e, por fim, adições e subtrações.
Seguindo essa ordem, teremos o seguinte:
[(4·5 – 6·3):(5·13 – 9·7)]:[(12²:6·4):(6·8 – 6·7)]
[(20 – 18):(65 – 63)]:[(144:24):(48 – 42)]
[2:2]:[6:6]
1:1
1
O resultado da expressão numérica é 1, mas a questão pede metade desse resultado.
1/2 = 0,5
Alternativa: C

Continua...