Professor Diminoi
Fração geratriz é um tipo de fração que, ao dividir o seu numerador pelo denominador, é obtido uma dízima periódica (número decimal infinito). Esse número pertence ao conjunto dos números racionais (Q).
Encontrar a fração que gera a dízima nem sempre é uma tarefa fácil. Precisamos dividir em dois casos: quando a dízima é simples e quando ela é composta. Para encontrar a fração geratriz, utilizamos uma equação.
Fração geratriz de uma dízima periódica simples
Exemplo:
Vamos encontrar a fracao geratriz da dízima 1,353535…
Seja x = 1,353535…, como essa dízima possui 2 números no seu período (35), vamos multiplicar x por 100. Então,
100x = 135,3535…
Agora realizando a subtração,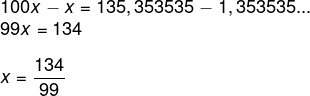
Existe um método prático para encontrarmos a fração geratriz de uma dízima periódica simples que evita a construção de equações. Vamos encontrar novamente a fração geratriz da dízima 1,353535…, porém pelo método prático.
1º passo: identificar período e parte inteira.
Parte inteira = 1
Período = 35
2º passo: encontrar o numerador.
O numerador é o número formado pela parte inteira e o período (no exemplo, é 135) menos a parte inteira, ou seja:
135 – 1 = 134
3º passo: encontrar o denominador.
Para isso, vamos avaliar quantos números têm no período da dízima, e, para cada número, acrescentaremos o número 9 no denominador. Como nesse caso há dois números, o denominador é 99. Logo, a fração geratriz é:![]()
Fração geratriz de uma dízima periódica composta
Um pouco mais complicada de se encontrar, a fração geratriz de uma dízima periódica composta pode ser determinada também por meio de uma equacao.
Exemplo:
Vamos encontrar a fração geratriz da dízima 2,13444...
Seja x = 2,13444…. vamos multiplicar por 100 para que, após a vírgula, fique somente a parte periódica. Então,
100x = 213,444….
Por outro lado, sabemos que 1000x= 2134,444….
Agora faremos a subtração: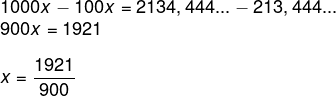
Para a dízima periódica composta, também existe um método prático, que vamos usar para encontrar a fração geratriz da dízima periódica composta 2,13444…
1º passo: identificar as partes da dízima periódica.
Parte inteira = 2
Parte não periódica = 13
Período = 4
2º passo: encontrar o numerador.
Para calcular o numerador, vamos escrever o número formado pela parte inteira, parte não periódica e período, ou seja, 2134 menos a parte inteira e a parte não periódica, ou seja, 213.
2134 – 213 = 1921
3º passo: encontrar o denominador.
No denominador, para cada número no período, acrescentamos um 9 e, para cada número na parte não periódica, um 0. No exemplo, o denominador é 900.
A fração geratriz é:![]()
EXERCICIOS RESOLVIDOS
00) Dos números a seguir, assinale aquele que corresponde a uma dízima periódica composta.
(A) 3,14159284…
(B) 2,21111
(C) 0,3333….
(D) 1,21111….
Resolução:
Analisando as alternativas, temos que:
a) É uma dízima não periódica. Perceba que, por mais que seja infinita, não há como prever os próximos números.
b) Não é uma dízima.
c) É uma dízima periódica simples.
d) Verdadeira, pois é uma dízima periódica composta.
Alternativa D.
00) A fração geratriz da dízima 12,3727272… é ?
(A) 1372/9999
(B) 12249/990
(C) 12/999
(D) 123/990
Resolução:
Pelo método prático, temos que: 12372 – 123= 12249, que será o numerador.
Analisando a parte decimal:
3 = parte não periódica
72 = período
990 = denominador
A fração que melhor representa é 12249/990
Alterntiva B
A fração geratriz é a representação fracionária de uma dízima periódica. Ela é utilizada para facilitar as operações básicas envolvendo dízimas periódicas.
A fração geratriz é a representacao fracionaria de uma dízima periódica. Essa representação é uma estratégia importante na resolução de problemas sobre operações básicas da Matemática que envolvem dízimas periódicas. Para encontrá-la, podemos utilizar técnicas de equação e também um método prático.
O que é uma dízima periódica?
Antes de entender o que é uma fração geratriz, é fundamental compreender o que é uma dízima periódica. Existem dois casos possíveis de dízimas periódicas: a dízima periódica simples e a dízima periódica composta. Uma dízima periódica é um número decimal que possui parte decimal infinita e periódica.
Dízima periódica simples
A dízima periódica simples é composta pela parte inteira e parte decimal. A parte decimal é a repetição do seu período, conforme os exemplos a seguir.
Exemplos - 1:
a) 1,2222…
Parte inteira =1
Parte decimal = 0,2222…
Período = 2
b) 3,252525…
Parte inteira = 3
Parte decimal = 0,252525…
Período = 25
c) 0,8888…
Parte inteira = 0
Parte decimal = 0,8888
Período = 8
Dízima periódica composta
A dízima periódica composta é uma dízima que possui parte inteira, parte decimal e, em sua parte decimal, uma parte não periódica — conhecida como antiperíodo — e o período.
Exemplos - 2:
a) 2,0666…
Parte inteira = 2
Parte decimal = 0,0666…
Antiperíodo = 0
Período = 6
b) 13,518888…
Parte inteira = 13
Parte decimal = 0,51888…
Antiperíodo = 51
Período = 8
c) 0,109090909…
Parte inteira = 0
Parte decimal = 0,10909090
Antiperíodo = 1
Período = 09
O que é fração geratriz?
Fração geratriz é a representação fracionária da dízima periódica, seja ela simples, seja composta. Como o nome sugere, a fração geratriz gera a dízima quando dividimos o numerador pelo denominador da representação fracionária.
Método Prático
Para encontrar a fração geratriz de uma dízima periódica, podemos também utilizar um método prático.
Quando a dízima for simples, o numerador será igual a parte inteira com o período menos a parte inteira, e no denominador, a quantidades de "noves" igual ao número de algarismo do período.
Exemplos 1
Qual a fração geratriz da dízima periódica 0,222...?
Resolução
Método prático para dízima periódica simples adotamos o seguinte: parte inteira e período menos a parte inteira dividido pelo período (para algarismo que compõem o período substitui-se por 9).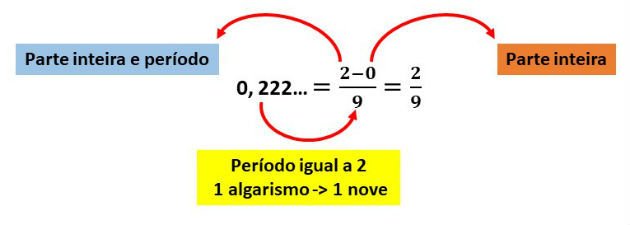 Exemplos 2
Exemplos 2
Qual a fração geratriz da dízima periódica 34,131313...?
Resolução
Método prático para dízima periódica simples adotamos o seguinte: parte inteira e período menos a parte inteira dividido pelo período (para algarismo que compõem o período substitui-se por 9).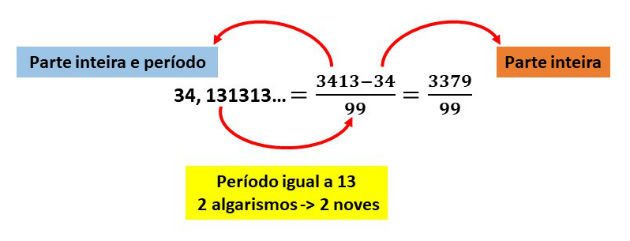
Exemplos 3
Qual a fração geratriz da dízima periódica 6,3777...?
Resolução
Método prático para dízima periódica composta adotamos o seguinte: parte inteira e números que não se repetem e período menos a parte inteira e número que não se repetem dividido pelo período (para algarismo que compõem o período substitui-se por 9) e para cada número que não se repete adote zero.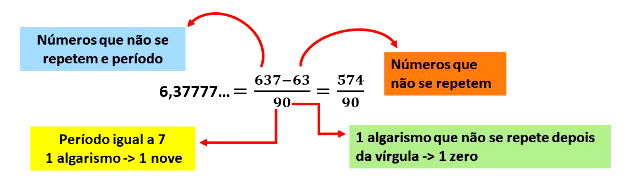
Exemplos:
a) 0,11111...
b) 1,3535...
c) 0,3177...
d) 2,5555...
Exemplos - 3: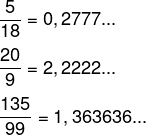
Passo a passo para calcular a fração geratriz
Passo a passo para a dízima periódica simples e para a dízima periódica composta.
Como achar a fração geratriz de uma dízima periódica.
Dízimas periódicas simples
Para encontrar a fração geratriz de uma dízima periódica simples, é necessário seguir alguns passos, sendo eles:
1º passo: igualar a dízima periódica a x.
2º passo: de acordo com a quantidade de algarismos do período, multiplicar os dois lados da equação por:
10 → se houver 1 algarismo no período;
100 → se houver 2 algarismos no período;
1000 → se houver 3 algarismos no período; e assim sucessivamente.
3º passo: calcular a diferença entre a equação encontrada no 2º passo e a equação igualada a x no 1º passo, e resolver a equação.
Os números decimais periódicos possuem um ou mais algarismos que se repetem de forma infinita.
Exemplos:
a) 0,11111...
b) 1,3535...
c) 0,3177...
d) 2,5555...
Exemplo - 4:
Encontre a fração geratriz da dízima 1,444…
x = 1,4444…
O período é 4 e, como há apenas um algarismo no período, multiplicaremos por 10 dos dois lados:
10x = 1,444… · 10
10x = 14,444…
10x – x = 14,444.. – 0,444…
9x = 14
x = 14/9
Então, a fração geratriz da dízima é:![]()
Exemplo - 5:
Encontre a fração geratriz da dízima periódica 3,252525…
x = 3,252525…
O período é 25 e, como possui 2 algarismos, multiplicaremos por 100.
100x = 3,252525… · 100
100x = 325,252525…
Agora calculando a diferença entre 100x e x:
100x – x = 325,2525… – 3,252525…
99x = 322
x = 322/99
Então, a fração geratriz da dízima é:![]()
Dízima periódica composta
Quando a dízima periódica é composta, o que muda é que acrescentamos um novo passo na resolução para encontrar a fração geratriz.
1º passo: igualar a dízima periódica a x.
2º passo: transformar a dízima periódica composta em uma dízima periódica simples multiplicando por:
10, se houver 1 algarismo no antiperíodo;
100, se houver 2 algarismos no antiperíodo; e assim sucessivamente.
3º passo: de acordo com a quantidade de algarismos do período, multiplicar os dois lados da equação por:
10 = se houver 1 algarismo no período;
100 = se houver 2 algarismos no período;
1000 = se houver 3 algarismos no período; e assim sucessivamente.
4º passo: calcular a diferença entre a equação encontrada no 3º passo e 2º passo, e resolver a equação.
Exemplo - 6:
Encontre a fração geratriz da dízima 5,0323232…
x = 5,0323232…
Note que há 1 algarismo no antiperíodo, que é o 0. Multiplicaremos por 10 para que ela vire uma dízima periódica.
10x = 5,0323232… · 10
10x = 50,323232…
Agora vamos identificar o período, que é 32. Como há 2 algarismos, multiplicaremos a dízima por 100.
1000x = 5032,323232…
Agora calculamos a diferença entre 1000x e 10x:
1000x – 10x = 5032,323232… – 50,323232…
990x = 4982
x=4982/990
Então, a fração geratriz é:![]()
Método prático
Utilizamos o método prático para facilitar o processo de encontrar a fração geratriz da dízima periódica. Vamos analisar dois casos diferentes: quando a dízima periódica é simples e quando ela é composta.
Método prático para dízimas periódicas simples
Em uma dízima periódica simples, o método prático consiste em:
1º passo: escrever a soma entre a parte inteira e a parte decimal da dízima periódica;
2º passo: transformar a parte decimal em fração, da seguinte maneira: o numerador sempre será o período e o denominador será:
9 = se houver 1 algarismo no período;
99 = se houver 2 algarismos no período;
999 = se houver 3 algarismos no período; e assim sucessivamente.
3º passo: realizar a soma da parte inteira com a fração encontrada.
Exemplo - 7:
5,888…
5,888… = 5 + 0,888…
Transformando 0,888… em fração, temos numerador igual a 8, pois 8 é o período da fração, e denominador igual a 9, pois há somente 1 algarismo no período, logo: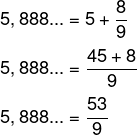
Método prático para dízimas periódicas compostas
Exemplo -8
Encontraremos a fração geratriz da dízima 4,1252525…
Primeiro identificamos a parte inteira, o antiperíodo e o período da dízima composta:
Parte inteira: 4
Antiperíodo: 1
Período: 25
O numerador da dízima composta é a diferença entre o número formado pelos algarismos da parte inteira, antiperíodo e período, com o número formado pela parte inteira e antiperíodo.
4125 – 41 = 4084
No denominador, para cada número no período, acrescentamos um 9 e, na sequência, para cada número na parte não periódica, um 0.
O período é 25, então acrescentamos 99; o antiperíodo é 1, então acrescentamos 0, logo o denominador é 990.
A fração geratriz da dízima é:![]()
EXERCICIOS RESOLVIDOS
01) Ao realizar a divisão entre dois números naturais, foi encontrada a dízima periódica 1,353535… A fração geratriz dessa dízima é: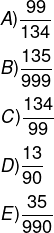
Resolução
Faremos x = 1,353535…
Multiplicando por 100 dos dois lados, temos que:
100 x = 135,3535…
Agora calcularemos a diferença entre 100x e x.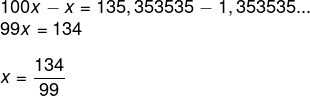 Alternativa C.
Alternativa C.
00) Se x = 0,151515… e y = 0,242424…, a divisão y : x é igual a?![]()
Resolução
Encontrando as frações geratrizes pelo método prático, temos que:
x = 0,151515…
A dízima possui período igual a 15, logo seu numerador é 15, e o denominador, 99.![]() Com o mesmo raciocínio para y = 0,242424…, o numerador é 24, e o denominador, 99.
Com o mesmo raciocínio para y = 0,242424…, o numerador é 24, e o denominador, 99.![]() Alternativa A.
Alternativa A.
QUESTOES RESOLVIDAS
01) Ao realizar a divisão entre dois números naturais, foi encontrada a dízima periódica 1,353535… A fração geratriz dessa dízima é:
(A) 99/134
(B) 135/999
(C) 134/99
(D) 13/90
(E) 35/900
Resolução
Faremos x = 1,353535…
Multiplicando por 100 dos dois lados, temos que:
100 x = 135,3535…
Agora calcularemos a diferença entre 100x e x.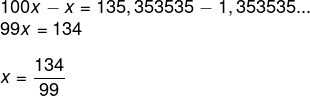 Alterntiva C
Alterntiva C
02) Se x = 0,151515… e y = 0,242424…, a divisão y : x é igual a?
(A) 8/5
(B) 15/17
(C) 10/16
(D) 1/ 4
(E) 9/5
Resolução
Encontrando as frações geratrizes pelo método prático, temos que:
x = 0,151515…
A dízima possui período igual a 15, logo seu numerador é 15, e o denominador, 99.
15 / 99
Com o mesmo raciocínio para y = 0,242424…, o numerador é 24, e o denominador, 99.
24 / 99
Alternativa A
03) Dos números a seguir, assinale aquele que corresponde a uma dízima periódica composta.
(A) 3,14159284…
(B) 2,21111
(C) 0,3333….
(D) 1,21111….
Resolução
Analisando as alternativas, temos que:
a) É uma dízima não periódica. Perceba que, por mais que seja infinita, não há como prever os próximos números.
b) Não é uma dízima.
c) É uma dízima periódica simples.
d) Verdadeira, pois é uma dízima periódica composta.
Alternativa D
04) A fração geratriz da dízima 12,3727272… é ?
(A) 1372/9999
(B) 12249/990
(C) 12/999
(D) 123/990
Resolução:
Pelo método prático, temos que: 12372 – 123= 12249, que será o numerador.
Analisando a parte decimal:
3 → parte não periódica
72 → período
990 → denominador
Alternativa B
05) (TJ CE – ESAF) Qual a fração que dá origem à dízima 2,54646… em representação decimal?
(A) 2.521 / 990
(B) 2.546 / 999
(C) 2.546 / 990
(D) 2.546 / 900
(E) 2.521 / 999
Resolução
Note que temos uma sequência infinita de “46” a partir da segunda casa decimal.
2,54646… = 2,5 + 0,04646…
2,54646… = 2,5 + 0,4646…/10
2,54646… = 2,5 + (46/99)/10
2,54646… = 25/10 + 46/990
2,54646… = (2475 + 46)990
2,54646… = 2521/990
Alternativa A
06) (SUSEP – ESAF) Indique qual o número racional geratriz da dízima periódica 7,233…
(A) 723/99
(B) 723/90
(C) 716/99
(D) 716/90
(E) 651/90
Resolução
Veja que o algarismo 3 é repetido infinitamente a partir da segunda casa decimal
7,233… = 7,2 + 0,033…
7,233… = 72/10 + 0,33…/10
7,233… = 36/5 + (1/3)/10
7,233… = 36/5 + 1/30
7,233… = (216 + 1)/30
7,233… = 217/30
7,233… = 651/90
Alternativa E
07) (PM SC – CESIEP) Leia as afirmações a seguir:
I. Os números Naturais são aqueles inteiros não positivos mais o zero.
II.Os números Irracionais são aqueles que representam dízimas periódicas.
III. Os números Reais representam a soma dos números Racionais com os Irracionais.
Assinale a alternativa correta:
(A) Somente a assertiva II está correta.
(B) Somente a assertiva III está correta.
(C) Somente a assertiva I está correta.
(D) Somente as assertivas II e III estão corretas.
Resolução
I. Falsa – Os números Naturais são os inteiros positivos mais o zero.
II. Falsa – Os números representados por dízimas periódicas pertencem ao conjunto dos números Racionais.
III. Correto – Os Reais é a união dos irracionais com os racionais.
Alternativa B
08) (TRT 15 – FCC) Renato dividiu dois números inteiros positivos em sua calculadora e obteve como resultado a dízima periódica 0,454545… . Se a divisão tivesse sido feita na outra ordem, ou seja, o maior dos dois números dividido pelo menor deles, o resultado obtido por Renato na calculadora teria sido
(A) 0,22.
(B) 0,222…
(C) 2,22.
(D) 2,222…
(E) 2,2.
Resolução
O “45” está sendo repetido infinitamente.
0,454545… = 45/99
0,454545… = 5/11
Descobrimos os números que geram a dízima periódica. Basta agora inverter a ordem e dividir novamente.
11/5 = 2,2
Alternativa E
09) (UFAC – MS Concursos) Sejam x e y dois números reais. Sendo x = 2,333… e y = 0,1212…, dízimas periódicas. A soma das frações geratrizes de x e y é:
(A) 7/3.
(B) 4/33.
(C) 27/11.
(D) 27/33.
(E) 27/3.
Resolução
Calculando a fração geratriz de x:
2,333… = 2 + 0,333…
2,333… = 2 + 1/3
2,333… = (6 + 1)/3
2,333… = 7/3
Calculando a fração geratriz de y:
0,1212… = 12/99
0,1212… = 4/33
Somando as frações geratrizes:
7/3 + 4/33
(77 + 4)/33
81/33
27/11
Alternativa C
EXERCÍCIOS SOBRE FRAÇÃO GERATRIZ
01) Sobre as dízimas, julgue as afirmativas a seguir:
I. A representação fracionária da dízima periódica é chamada de fração geratriz.
II. As dízimas não periódicas possuem fração geratriz.
III. Toda dízima periódica é um número racional.
Marque a alternativa correta:
(A) Somente a afirmativa I é verdadeira.
(B) Somente a afirmativa II é verdadeira.
(C) Somente a afirmativa III é verdadeira.
(D) Somente a afirmativa II é falsa.
(E) Todas as afirmativas são verdadeiras.
Resolucao
I → Verdadeira, pois a fração geratriz é a representação fracionária da dizima.
II → Falsa, pois a dízima não periódica não possui representação fracionária, somente dízimas periódicas possuem.
III → Verdadeira, pois um número racional é aquele que possui representação fracionária, e a fração geratriz é essa representação.
Alternativa D
02) Seja x = 1,123123… A diferença entre o numerador e o denominador da sua representação fracionária é:
(A) 123.
(B) 999.
(C) 321.
(D) 112.
(E)1122.
Resolucao
Primeiro encontraremos a fração geratriz de x:
x = 1,123123…
x = 1+ 0,123123…
Na dízima periódica 0,123123…, 123 é o período e será o numerador da fracao. Já o denominador será 999, pois há três algarismos no período.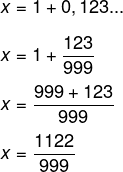 Com a fração geratriz, a diferenca entre o numerador e o denominador será de:
Com a fração geratriz, a diferenca entre o numerador e o denominador será de:
1122 – 999 = 123
Alternativa A
03) A fração geratriz de dízima periódica 3,151515… é igual a:
(A) 104/33
(B) 15/99
(C) 5/33
(D)115/99
(E) 18/00
Resolucao
Seja x = 3,1515…, temos que: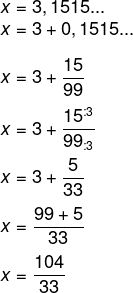 Alternativa A
Alternativa A
04) (TRT) Renato dividiu dois números inteiros positivos em sua calculadora e obteve como resultado a dízima periódica 0,454545… Se a divisão tivesse sido feita na outra ordem, ou seja, o maior dos dois números dividido pelo menor deles, o resultado obtido por Renato na calculadora teria sido:
(A) 0,22.
(B) 0,222…
(C) 2,22.
(D) 2,222…
(E) 2,2.
Resolucao
Primeiro vamos encontrar a fração geratriz da dízima 0,454545… Como o período é 45 e é composto por dois algarismos, ele será o numerador, e o denominador será 99. O exercício propõe uma divisão entre o denominador e o numerador, logo:
99 : 45 = 2,2
Alterntiva E
05) Durante os estudos dos números racionais, Eduardo encontrou como resultado de uma divisão o número 3,0121212… Com base no resultado encontrado por ele, julgue as afirmativas a seguir:
I. O resultado é um número racional.
II. O resultado é uma dízima periódica composta.
III. O resultado não pode ser representado como uma fração.
Marque a alternativa correta:
(A) Somente a afirmativa I é falsa.
(B) Somente a afirmativa II é falsa.
(C) Somente a afirmativa III é falsa.
(D) Todas as afirmativas são verdadeiras.
(E) Todas as afirmativas são falsas.
Resolucao
I → Verdadeira, pois as dízimas periódicas são numeros racionais.
II → Verdadeira, pois é possível perceber que, em sua parte decimal, há uma parte não periódica.
III → O resultado não pode ser representado como uma fração.
Alternativa C
07) A fração geratriz da dízima 1,52222… é ?
(A) 133/99
(B) 90/134
(C) 137/9
(D) 135/90
(E) 2/9
Resolucao
Seja x = 1,5222…, temos que:
10x = 15,222…
10x = 15 + 0,222…
A fração geratriz de 0,222… possui numerador igual a 2 e denominador igual a 9, então: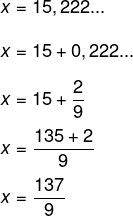 Alternativa C
Alternativa C
08) Sobre as dízimas, julgue as afirmativas a seguir:
I. Toda dízima possui uma fração geratriz.
II. Uma dízima pode ser um número racional ou irracional.
III. A representação decimal do número π é uma dízima periódica
Marque a alternativa correta:
(A) Somente a afirmativa I é verdadeira.
(B) Somente a afirmativa II é verdadeira.
(C) Somente a afirmativa III é verdadeira.
(D) Somente a afirmativa I e II são verdadeiras.
(E) Somente as afirmativas II e III são verdadeiras.
Resolucao
I → Falsa, pois as dízimas não periódicas não podem ser representadas como fração.
II → Verdadeira, pois as dízimas periódicas são números racionais, e as dízimas não periódicas são Numeros irracionais.
III → Falsa, pois π = 3,14159265…, que é uma dízima não periódica.
Alternativa B
09) Calcule a fração geratriz de cada uma das dízimas periódicas simples:
a) 3,21212121…
b)1,888888…
c) 0,26262626…
d) 12,33333…
e) 17,89898989…
Resolucao 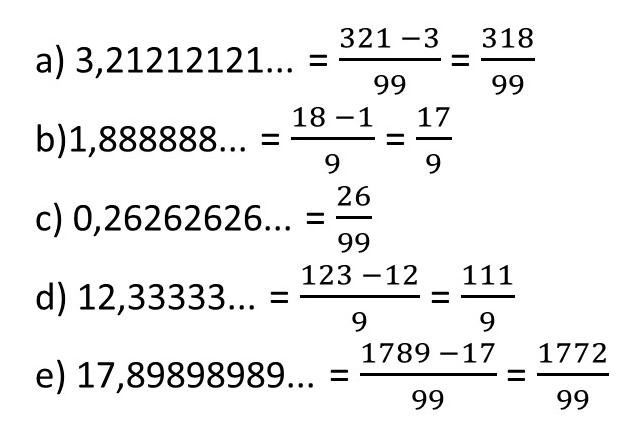
10) Calcule a fração geratriz de cada uma das dízimas periódicas compostas:
a) 1,133333….
b) 3,563636363…
c) 17,415151515…
d) 0,244444…
e) 5,01209209209…
Resolucao 
11) Encontre a fração geratriz para realizar as seguintes operações entre números decimais:
a) 1,1212121212… + 1,17
b) 23,012121212… + 1,14141414…
Resolucao 
12) Utilizando fração geratriz, encontre o resultado da seguinte operação:
(1,0131313… – 0, 0141414…)
Resolucao 
13) Por meio de fração geratriz, encontre o resultado da seguinte operação:
0,54 + 3/5 – 1,22222… + 1,133333…
Resolucao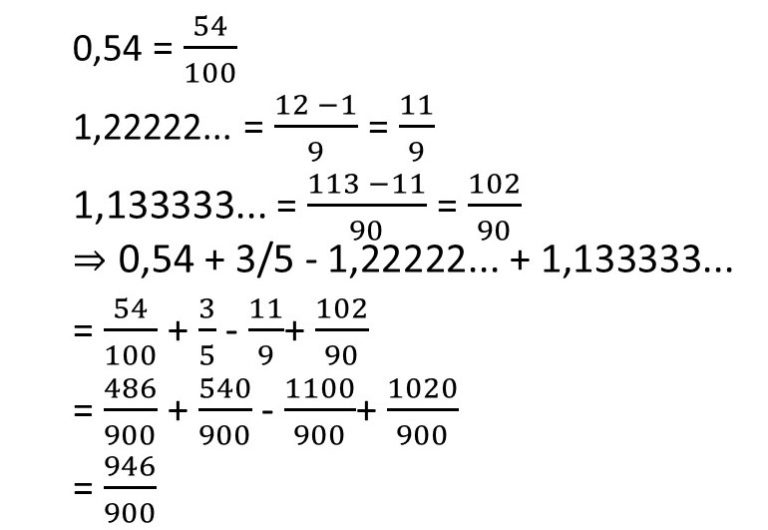
Continua...







