OPERACOES COM RADICAIS

Professor Diminoi
Operações com radicais
As operações com radicais, envolvendo adição e subtração, são solucionadas identificando os radicais semelhantes e operando os coeficientes.
- Obter o resultado referente à adição de raízes só é possível quando os radicais são semelhantes
Quando falamos de raízes na matemática, sempre devemos nos lembrar que o índice da raiz muda, pois ela pode ser do tipo quadrada, cúbica e de muitos outros tipos.

Observação: para que possamos realizar operações com radicais na adição e na subtração, é necessário que o radical seja o mesmo.

Para realizar operações com radicais na adição e na subtração devemos, primeiramente, verificar se os radicais são semelhantes.
Para que o radical de duas ou mais raízes sejam semelhantes é preciso que:
- o índice e o radicando sejam idênticos.
- a única parte que pode ser diferente é o coeficiente que acompanha o radical.

Leitura de radical
Exemplo

Partes de um radical
E fundamental conhecer a estrutura e a nomenclatura das partes de uma raiz
Exemplo
Exemplo
Operações com radicais
As operações com radicais, envolvendo adição e subtração, são solucionadas identificando os radicais semelhantes e operando os coeficientes.
Quando falamos de raízes na matemática, sempre devemos nos lembrar que o índice da raiz muda, pois ela pode ser do tipo quadrada, cúbica e de muitos outros tipos.
Para que possamos realizar operações com radicais na adição e na subtração, é necessário que o radical seja o mesmo. Sendo assim, torna-se fundamental conhecer a estrutura e a nomenclatura das partes de uma raiz.

Propriedades da Radiciação
As propriedades da radiciação são muito úteis quando necessitamos simplificar radicais. Confira a seguir.

Propriedade 1
Já que a radiciação é a operação inversa da potenciação, todo radical pode ser escrito na forma de potência.
Exemplo

Propriedade 2
Multiplicando-se ou dividindo-se índice e expoente pelo mesmo número, a raiz não se altera.
Exemplo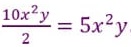
Exemplo

Propriedade 3
Na multiplicação ou divisão com radiciais de mesmo índice realiza-se a operação com os radicandos e mantém-se o índice do radical.
Exemplo
Propriedade 4
A potência da raiz pode ser transformada no expoente do radicando para que a raiz seja encontrada.
Exemplo
Quando o índice e a potência apresentam o mesmo valor: 
Exemplo
Exemplo
Propriedade 5
A raiz de outra raiz pode ser calculada mantendo-se o radicando e multiplicando-se os índices.
Exemplo

Radiciação e Potenciação
A radiciação é a operação matemática inversa da potenciacao. Desta forma, podemos encontrar o resultado de uma raiz buscando a potenciação, que tem como resultado a raiz proposta.
Observacao: 
Note que se o radicando (x) é um número real e o índice (n) da raiz é um número natural, o resultado (a) é a raiz enésima de x se aⁿ = x.

Exemplos

Racionalização de Denominadores
A racionalização de denominadores consiste em transformar uma fração, que apresenta um número irracional no denominador, em uma fração equivalente com denominador racional.

Raiz quadrada no denominador
Neste caso, o quociente com o número irracional √5  no denominador foi transformado em um número racional ao utilizarmos o fator racionalizante √5.

Raiz com índice maior que 2 no denominador
Neste caso, o quociente com o número irracional  ⁵√9 no denominador foi transformado em um número racional ao utilizarmos o fator racionalizante ⁵√3³, cujo expoente (3) foi obtido pela subtração do índice (5) do radical pelo expoente (2) do radicando.

Adição ou subtração de radicais no denominador
Neste caso, utilizamos o fator racionalizante √3 + √3 para eliminar a radical do denominador temos:
(a + b) . (a – b) = a² – b²

Soma e Subtração
Para somar ou subtrair devemos identificar se os radicais são semelhantes, ou seja, se apresentam índice e radicando iguais.

Radicais semelhantes
Para somar ou subtrair radicais semelhantes, devemos repetir o radical e somar ou subtrair seus coeficientes.
Exemplos
Exemplos

Radicais semelhantes após simplificação
Neste caso, devemos inicialmente simplificar os radicais para se tornarem semelhantes. Depois, faremos como no caso anterior.
Exemplo 1
Assim, 
Exemplo 2
Assim,

Radicais não são semelhantes
Calculamos os valores dos radicais e depois efetuamos a soma ou a subtração.
Exemplos
(valores aproximados, pois a raiz quadrada de 5 e de 2 são números irracionais)

Multiplicação e Divisão
Radicais com mesmo índice
Repete a raiz e realiza a operação com os radicandos.
Exemplos

Radicais com índices diferentes
Primeiro, devemos reduzir ao mesmo índice, depois realizar a operação com os radicandos.
Exemplo 1
Assim, 
Exemplo 2
Assim, 

OUTROS EXEMPLOS
Operações com radicais
As operações com radicais, envolvendo adição e subtração, são solucionadas identificando os radicais semelhantes e operando os coeficientes.
Quando falamos de raízes na matemática, sempre devemos nos lembrar que o índice da raiz muda, pois ela pode ser do tipo quadrada, cúbica e de muitos outros tipos.
Para que possamos realizar operações com radicais na adição e na subtração, é necessário que o radical seja o mesmo. Sendo assim, torna-se fundamental conhecer a estrutura e a nomenclatura das partes de uma raiz.

Propriedades da radiciação
As propriedades da radiciação servem para simplificar e solucionar cálculos que envolvem raízes.

1 - Raízes de mesmo índices

Essa propriedade mostra que a raiz de um produto é o produto das raízes.

2 -  Cálculo de Raiz da raiz
Para calcular a raiz da raiz, conserve o radicando e multiplique o índice.

3 -  Potenciação de raiz
4 -  Divisão de raízes de mesmo índice


Para realizar operações com radicais na adição e na subtração devemos, primeiramente, verificar se os radicais são semelhantes.
Para que o radical de duas ou mais raízes sejam semelhantes.
- é preciso que o índice e o radicando sejam idênticos.
- a única parte que pode ser diferente é o coeficiente que acompanha o radical.

Exemplos de operações de adição e subtração com radicais: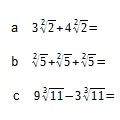


 

 

 

Resolucao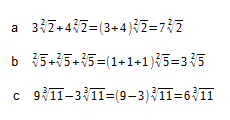


 

 

 

d) Resolva a seguinte expressão numérica com radicais: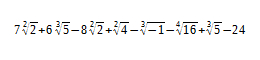

Resolucao

 
Exemplos resolvidos
e) Resolva a expressao abaixo

Resolucao:
Como dito acima, operaremos apenas os coeficientes: – 2 + 1 – 3 = – 4.


f) Resolva a expressao abaixo

Resolucao:
Subtrairemos os coeficientes 3 e – 1/2 para determinar a diferença dos radicais:


g) Resolva a expressao abaixo

Resolucao:
Operaremos os coeficientes fracionários:


h) Resolva a expressao abaixo

Resolucao:
Como já vimos, só podemos somar ou subtrair radicais de mesmo radicando e mesmo índice. Por essa razão, vamos organizar a expressão, colocando em evidência cada radical semelhante:


i) Resolva a expressao abaixo

Resolucao:
Reorganizaremos também a expressão, agrupando radicais semelhantes e operando seus respectivos coeficientes:


Exercícios sobre raiz quadrada
01) Um terreno possui área igual a 196 m². Sabendo que esse terreno tem formato de um quadrado, então os seus lados possuem medida igual a:
(A) 12 m.
(B) 13 m.
(C) 14 m.
(D) 15 m.
(E) 16 m.
Resolucao
A área de um quadrado é igual ao lado ao quadrado, então, para encontrar o valor do lado, vamos calcular a raiz quadrada da área do terreno.
Para calcular a raiz quadrada de 196, vamos fatorar esse número: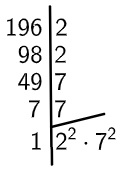

Então, temos que:
Alternativa C

02) Dos números abaixo, marque aquele que possui uma raiz quadrada exata.
(A) 600
(B) 215
(C) 144
(D) 110
(E) 70
Resolucao
Analisando as alternativas, a única que é formada por um quadrado perfeito é a alternativa “c”, pois temos que 12² = 144, ou seja, √144 = 12. As demais alternativas não são raízes exatas.
Alternativa C

03) O valor da expressão algébrica a seguir é:
√4+√16 – √25 ×√9
(A) – 9.
(B) – 6.
(C) – 5.
(D) – 4.
(E) – 2.
Resolucao
Resolvendo a expressão, temos que:
√4+√16 – √25 ×√9
2 + 4 – 5 × 3
6 – 15
– 9
Alternativa A

04) (Cefet/RJ 2014) Por qual número devemos multiplicar o número 0,75 de modo que a raiz quadrada do produto obtido seja igual a 45?
(A) 2700
(B) 2800
(C) 2900
(D) 3000
Resolucao
Seja x o número procurado, temos que: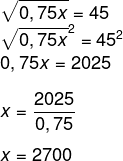

Alternativa A

05) O valor da expressão numérica a seguir é:

(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
Resolucao
Realizando o produto, temos que: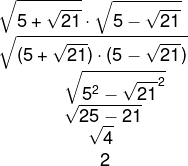

Alternativa A

06) Qual é a raiz quadrada de 5184?
(A) 42
(B) 58
(C) 68
(D) 72
(E) 88
Resolucao
Fatorando 5184, temos que:

Então, podemos fazer o seguinte cálculo: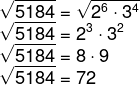

Alternativa D

07) Analise as afirmativas a seguir:
I - A raiz quadrada de 1500 é menor que 38.
II – A raiz quadrada de 190 é maior que 13.
III – A raiz quadrada de 0 é igual a 0.
Marque a alternativa correta.
(A) Somente a afirmativa I é verdadeira.
(B) Somente a afirmativa II é verdadeira.
(C) Somente a afirmativa III é verdadeira.
(D) Somente as afirmativas I e II são verdadeiras.
(E) Somente as afirmativas II e III são verdadeiras.
Resolucao
I → Falsa, pois sabemos que 38 · 38 = 1.444, logo a raiz de 1500 é maior que 38.
II → Verdadeira, pois sabemos que 13 · 13 = 169, logo a raiz de 190 é maior que 13.
III → Verdadeira, pois a raiz de 0 é 0.
Alternativa E

08) (Ethos concursos) A raiz quadrada de um número é uma importante operação matemática, assim como a adição, a subtração, a multiplicação e a divisão. Somente alguns números possuem raiz quadrada, são aqueles considerados quadrados perfeitos. Sendo assim, calcule a raiz quadrada de 625 e assinale a alternativa CORRETA.
(A) 35
(B) 24
(C) 25
(D) 17
(E) 49
Resolucao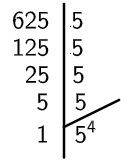

Então, temos que:
√625 = √5⁴
√625 = 5²
√625 = 25
Alternativa C

09) Qual é o valor da simplificação da expressão a seguir?

(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Resolucao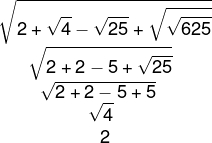

Alternativa C

10) Sabendo que √x = 9, então o valor da terça parte de x é:
(A) 81
(B) 72
(C) 36
(D) 27
(E) 9
Resolucao
√x = 9
√x² = 9²
x = 81
Como queremos a terça parte de x então 81: 3 = 27.
Alternativa D

11) Sobre a raiz quadrada, julgue as afirmativas a seguir.
I → Não é possível calcular a raiz quadrada de número negativo.
II → Os números 0, 1, 4, 9 e 16 são todos os quadrados perfeitos menores que 20.
III → A raiz quadrada de 8 é igual a 4.
As afirmativas são, respectivamente:
(A) V, V e V.
(B) F, F e F.
(C) F, F e V.
(D) V, V e F.
(E) V, F e V.
Resolucao
I → Verdadeira.
II → Verdadeira.
II → Falsa, pois 4 é raiz quadrada de 16, e não de 8.
Alternativa D

12) (IFG 2019) Os babilônicos talvez tenham usado a fórmula abaixo para obter aproximações interessantes de raízes quadradas de números não quadrados perfeitos.

Atribuindo a = 4/3 e b = 2/9 nessa fórmula, é correto afirmar que obtemos a aproximação: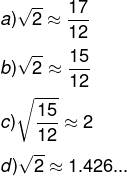

Resolucao
Vamos substituir o valor de a e b: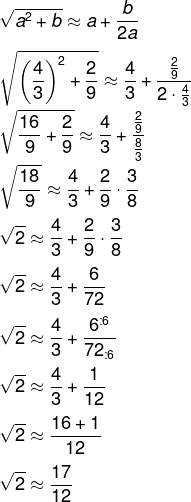

Alternativa A

Exercícios sobre cálculo de raízes por meio de fatoração
13) Qual é a raiz cúbica de 3375?
(A) 12
(B) 13
(C) 14
(D) 15
(E) 16
Resolucao
Para calcular essa raiz, utilizaremos o método da fatoração:

Em vez de multiplicar todos os fatores obtidos, como é feito para encontrar o mínimo múltiplo comum, reescreva esses fatores agrupando-os em potências de 3 sempre que possível, como foi feito acima.
Para finalizar, substitua 3375 por 33·53 no radical para obter a seguinte raiz e prossiga utilizando as propriedades dos radicais.

Alternativa D

14) Em função de √2, qual é o resultado da expressão a seguir?

(A) 22√2
(B) 16√2
(C) 32√2
(D) 21√2
(E) 18√2
Resolucao
Primeiramente, decomponha 2048 e 512. Após isso, reescreva os fatores primos em potências de 2, se possível.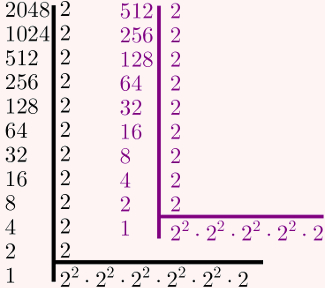

Por fim, utilize as mesmas propriedades do exercício anterior para simplificar os cálculos e subtraia os resultados.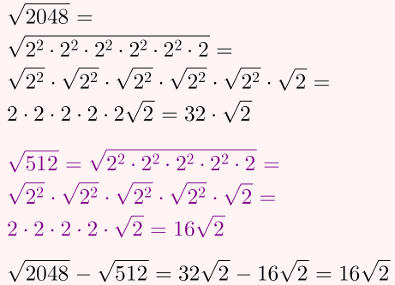

Alternativa B

15) Quais são as raízes da equação x² + 16x – 36 = 0?
(A) 2 e 3
(B) 20 e 20
(C) 2 e 20
(D) 20 e – 20
(E) 2 e – 18
Resolucao
Utilizando o método de Bhaskara, calcularemos o discriminante: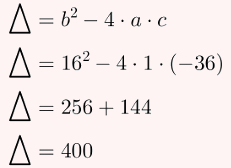

Tendo em vista que precisaremos calcular a raiz de 400 para usar seu resultado na fórmula de Bhaskara, seguem os respectivos cálculos: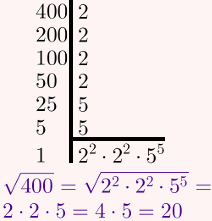

Agora resta apenas calcular as raízes: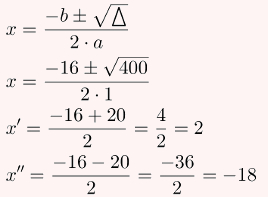

Dessa maneira, as raízes são 2 e –18.
Alternativa E

16) Um lote quadrado possui 1600 m² de área. Qual é a medida do comprimento desse lote quadrado?
(A) 40 m
(B) 42 m
(C) 44 m
(D) 46 m
(E) 48 m
Resolucao
A medida do lado de um quadrado sempre pode ser obtida a partir da raiz quadrada de sua área. Portanto, basta calcular a raiz quadrada de 1600 para obter a medida em questão. Utilizando o método da fatoração, teremos: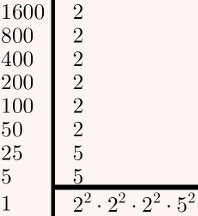

Para finalizar, substitua 1600 no radical pelo produto encontrado na fatoração anterior, como ilustrado na imagem seguinte:

Portanto, o comprimento do lote é 40 m.
Alternativa A


Continua ....