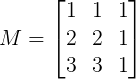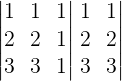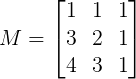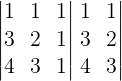PONTO/RETA/ALINHAMENTO
Professor Diminoi

DISTÂNCIA ENTRE DOIS PONTOS
A distância permeia todos os conceitos da Geometria Analítica, pois, nessa área da Matemática, temos a relação de elementos geométricos com os algébricos, e o elemento básico da Geometria é o ponto.
Um dos conceitos básicos da Geometria é que a menor distância entre dois pontos é dada por uma reta. Na Geometria Analítica, esses pontos recebem coordenadas no plano cartesiano e, por meio dessas coordenadas, podemos encontrar o valor da distância entre dois pontos.
Distância entre dois pontos: representação geométrica
Vamos representar dois pontos quaisquer no plano cartesiano.
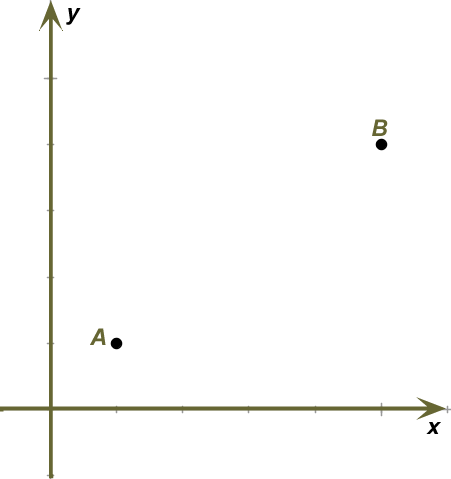
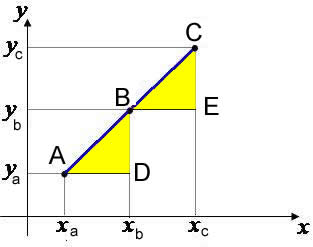
A distância entre os pontos A e B é a medida do segmento que tem os dois pontos como extremidade. Por se tratar de dois pontos quaisquer, representaremos as coordenadas desses pontos de maneira genérica.
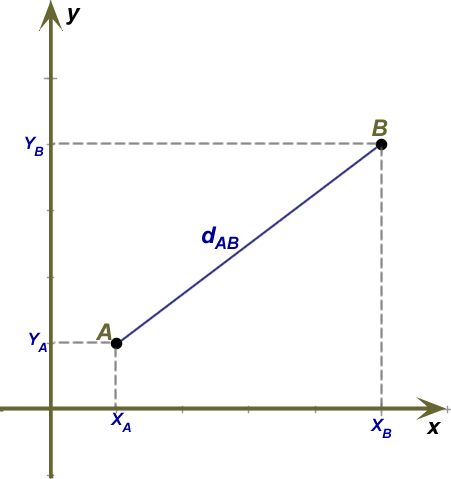
Sabe-se que os eixos coordenados do plano cartesiano são ortogonais, portanto, podemos construir um triângulo retângulo utilizando os pontos A e B, como mostra a figura a seguir.
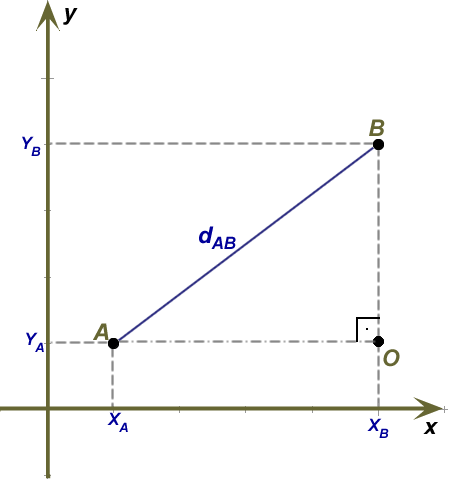
A menor distância entre dois pontos em um segmento de reta pode ser calculado a partir de uma fórmula desenvolvida, com bases nas regras do Teorema de Pitágoras, principalmente quando os pontos marcados no plano cartesiano formam um triângulo retângulo.
Fórmula da distância entre dois pontos no plano
Para dois pontos quaisquer, tais como A (x1,y1) e B (x2, y2), temos:
Fórmula da distância entre dois pontos


Exercícios Resolvidos
01) Dados os pontos A (2,-3) e B (4,5), determine a distância entre eles.
Resolução:
xa: 2
xb: 4
ya: -3
yb: 5

02) Determine a distância entre os pontos traçados a seguir, sendo eles: P(-2,3) e Q(-5,-9).
Resolução:
xa: -2
xb: -5
ya: 3
yb: -9

02) Calcule a distância entre os pontos A (1,1) e B(4,5) e represente-os geometricamente.
Como vimos anteriormente, basta aplicar a expressão para o cálculo da distância entre dois pontos. Sendo assim:
Resolução:
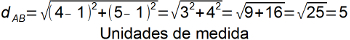
03) (ENEM – 2013) Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:
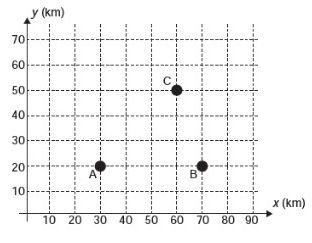 A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas
A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas
(A) (65 ; 35)
(B) (53 ; 30)
(C) (45 ; 35)
(D) (50 ; 20)
(E) (50 ; 30)
Alternativa: D
04) Qual é a distância entre os pontos A e B, em centímetros, sabendo que suas coordenadas são A = (2,3) e B = (-2,-2)?
(A) 41 cm
(B) 6 cm
(C) 49 cm
(D) 41,5 cm
(E) 6,4 cm
Resolução:
Basta utilizar a fórmula para distância entre dois pontos.
 Alternativa: E
Alternativa: E
05) Determine a área, em metros quadrados, do triângulo a seguir, sabendo que ele é retângulo em B.
Triângulo retângulo em B
.jpg) (A) 2 m2
(A) 2 m2
(B) 5,66 m2
(C) 2,83 m2
(D) 8 m2
(E) 9 m2
Resolução:
Calcule as distâncias entre B e C (dBC) e entre B e A (dBA), que são a base e a altura desse triângulo, uma vez que ele é retângulo em B.
Primeiramente, calcularemos dBC:
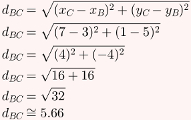 Agora, calcularemos dBA:
Agora, calcularemos dBA:
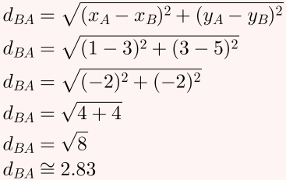 Para finalizar o exercício, basta calcular a área desse triângulo, lembrando que a área de um triângulo pode ser calculada multiplicando sua base por sua altura e dividindo o resultado por 2:
Para finalizar o exercício, basta calcular a área desse triângulo, lembrando que a área de um triângulo pode ser calculada multiplicando sua base por sua altura e dividindo o resultado por 2:
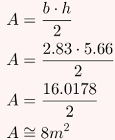 Alternativa: D
Alternativa: D
06) (Cesgranrio) A área do triângulo, cujos vértices são (1, 2), (3, 4) e (4, -1), é igual a:
(A) 6.
(B) 8.
(C) 9.
(D) 10.
(E) 12.
Resolução:
Primeiro, desenharemos o triângulo e mostraremos que um de seus ângulos é reto. Caso um dos ângulos do triângulo não seja reto, é necessário descobrir sua altura, o que pode ser feito utilizando distância entre ponto e reta.
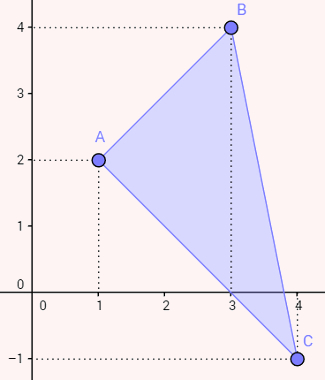 Observe que possivelmente o ângulo A é um ângulo reto. Caso isso ocorra, AB já é a altura do triângulo com relação à base AC. Para garantir isso, basta calcular os coeficientes angulares de AB e de AC. Caso o coeficiente angular de AB seja o (inverso do oposto" do coeficiente angular de AC, então AC e AB são perpendiculares e A é um ângulo reto.
Observe que possivelmente o ângulo A é um ângulo reto. Caso isso ocorra, AB já é a altura do triângulo com relação à base AC. Para garantir isso, basta calcular os coeficientes angulares de AB e de AC. Caso o coeficiente angular de AB seja o (inverso do oposto" do coeficiente angular de AC, então AC e AB são perpendiculares e A é um ângulo reto.
Primeiramente, o coeficiente angular de AC:
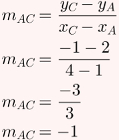 Agora, o coeficiente angular de AB:
Agora, o coeficiente angular de AB:
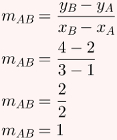 Os coeficientes angulares são inversos e opostos. Logo, AC é perpendicular a AB. Assim, AB é a altura do triângulo ABC, enquanto AC é a base. Para calcular a área desse triângulo, é necessário calcular antes os comprimentos de sua base e altura, que são os segmentos perpendiculares AC e AB. Para tanto, utilizaremos a fórmula da distância entre dois pontos. Observe:
Os coeficientes angulares são inversos e opostos. Logo, AC é perpendicular a AB. Assim, AB é a altura do triângulo ABC, enquanto AC é a base. Para calcular a área desse triângulo, é necessário calcular antes os comprimentos de sua base e altura, que são os segmentos perpendiculares AC e AB. Para tanto, utilizaremos a fórmula da distância entre dois pontos. Observe:
Cálculo da altura do triângulo ABC:
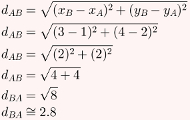 Cálculo da base do triângulo ABC:
Cálculo da base do triângulo ABC:
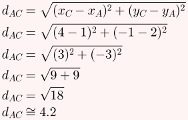 Agora, basta calcular a área do triângulo ABC, sabendo que sua base mede aproximadamente 4,2 e sua altura mede aproximadamente 2,8.
Agora, basta calcular a área do triângulo ABC, sabendo que sua base mede aproximadamente 4,2 e sua altura mede aproximadamente 2,8.
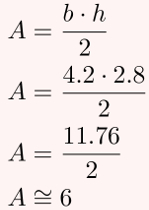 Como os valores das distâncias foram arredondados para baixo, então o valor obtido na área é um pouco menor que 6. Logo, conforme as alternativas de resposta, a área desse triângulo é 6.
Como os valores das distâncias foram arredondados para baixo, então o valor obtido na área é um pouco menor que 6. Logo, conforme as alternativas de resposta, a área desse triângulo é 6.
Alternativa: A
07) (PUC) O ponto B = (3, b) é equidistante dos pontos A = (6, 0) e C = (0, 6). Logo, o ponto B é:
(A) (3, 1).
(B) (3, 6).
(C) (3, 3).
(D) (3, 2).
(E) (3, 0).
Resolução:
Para resolver esse exercício, basta resolver a equação dAB = dBC. Antes disso, porém, calcularemos dAB e dBC separadamente e elevaremos seus resultados ao quadrado. Primeiramente, a distância entre A e B:
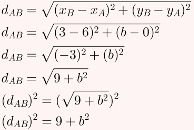 Agora, a distância entre B e C:
Agora, a distância entre B e C:
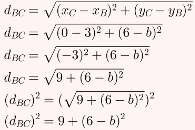 O resultado final é obtido resolvendo a equação gerada por (dAB)2 = (dBC)2. Observe:
O resultado final é obtido resolvendo a equação gerada por (dAB)2 = (dBC)2. Observe:
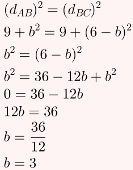 Alternativa: C
Alternativa: C
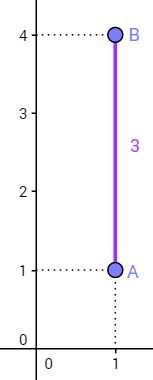
08) Calcule a distância entre os pontos A(1,1) e B(1,4).
Primeiramente, mostraremos por meio do plano cartesiano que dAB = 3. Observe a figura a seguir:
 Resolução:
Resolução:
Agora, vamos mostrar que, utilizando a fórmula para o cálculo de distância entre dois pontos, encontraremos que a distância entre A e B (dAB) é igual a 3. Observe:
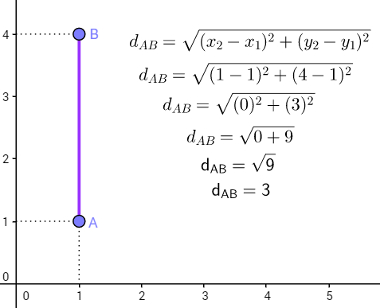
09) Calcule a distância entre os pontos A(– 2, 4) e B(2,2).
Resolução:
Não é necessário fazer qualquer desenho para calcular a distância entre dois pontos, pois basta ter em mãos as coordenadas de dois pontos quaisquer do plano e utilizar a fórmula proposta acima. Observe:
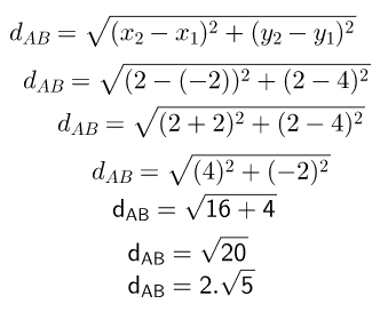
10) Calcule a distância entre os pontos A = (4, -8, -9) e B = (2, -3, -5).
Resolução:
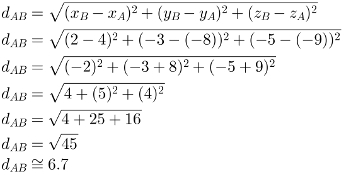
Ponto médio de um segmento no plano
O segmento de reta é um subconjunto da reta, é parte da reta.
Ao contrário da reta, o segmento é finito, possuindo começo e fim, podendo ser medido. Mesmo sendo finito, ele possui infinitos pontos e o ponto que divide o segmento de reta em duas partes de mesmo tamanho é chamado de ponto médio.
.jpg) Vamos determinar as coordenadas do ponto médio do segmento PQ da figura.
Vamos determinar as coordenadas do ponto médio do segmento PQ da figura.
 Assim, o ponto médio tem coordenadas:
Assim, o ponto médio tem coordenadas:

11) Determine as coordenadas do ponto médio do segmento AB de extremos A(1, 9) e B(7, 5).
Resolução:
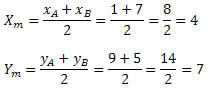 Portanto, o ponto médio do segmento AB tem coordenadas M(4 , 7)
Portanto, o ponto médio do segmento AB tem coordenadas M(4 , 7)
12) O ponto médio do segmento PQ tem coordenadas M(5, 5). Sabendo que o ponto P tem coordenadas P(3, 4), quais são as coordenadas do ponto Q?
Resolução:
Sabemos que
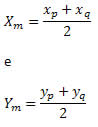 Segue que
Segue que
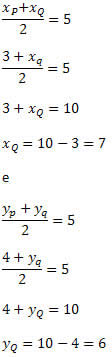 Portanto, o ponto Q tem coordenadas (7, 6).
Portanto, o ponto Q tem coordenadas (7, 6).
13) Determine as coordenadas do ponto médio do segmento AM, sabendo que M é o ponto médio do segmento AB, sendo A(0, 0) e B(– 12, 20).
Resolução:
Primeiro determinaremos as coordenadas do ponto M. Como M é ponto médio do segmento AB, temos que:
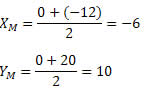 Logo, M tem coordenadas (– 6, 10).
Logo, M tem coordenadas (– 6, 10).
Queremos determinar o ponto médio do segmento AM. Vamos chamar esse ponto de N. Assim,
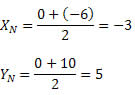 Portanto, o ponto médio do segmento AM tem coordenadas N(– 3, 5).
Portanto, o ponto médio do segmento AM tem coordenadas N(– 3, 5).
Espaço entre três dimensões
O espaço em três dimensões tem algumas diferenças em relação ao de duas dimensões.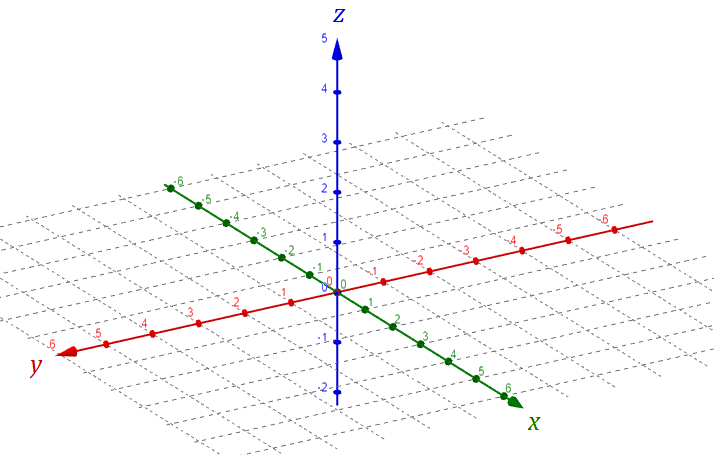
Agora, um novo eixo aparece, perpendicular ao plano cartesiano (x, y), o eixo z. Ele também é uma reta real e o seu marco zero é coincidente com o ponto (0,0) no plano (x, y). Agora, para determinarmos um ponto neste espaço devemos acrescentar uma nova coordenada, o que nos leva a representação de qualquer ponto no espaço como (x, y, z).
Distância entre três pontos
A distância entre dois pontos no espaço continua seguindo a mesma regra do teorema de Pitágoras, porém com uma coordenada a mais:
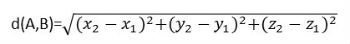
DISTÂNCIA ENTRE PONTO E RETA
Seja P um ponto qualquer no plano cartesiano e r uma reta representada em sua forma geral pela equação ax + by + c = 0.
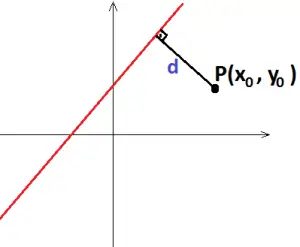
A distância de um ponto a uma reta é a medida do segmento que parte do ponto e forma com a reta um ângulo de 90º.
FÓRMULA DA DISTÂNCIA ENTRE PONTO E RETA
Sendo d a distância entre o ponto P e a reta r: ax + by + c = 0, podemos calcular o valor de d através da seguinte fórmula:
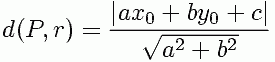
.JPG) Essa expressão surge de uma generalização feita, podendo ser utilizada nas situações em que envolve o cálculo da distância entre um ponto qualquer e uma reta.
Essa expressão surge de uma generalização feita, podendo ser utilizada nas situações em que envolve o cálculo da distância entre um ponto qualquer e uma reta.
Exercícios resolvidos
14) Dado o ponto A(3, -6) e r: 4x + 6y + 2 = 0. Estabeleça a distância entre A e r utilizando a expressão dada anteriormente.
Resolução:
x: 3
y: -6
a: 4
b: 6
c: 2
.jpg) Calcule a distância da reta P à reta r, nas questões 09 e 10:
Calcule a distância da reta P à reta r, nas questões 09 e 10:
15) P(1,3) e r: 5x + 12y – 2 = 0
Resolução:
Iremos substituir 1 = x0; 3 = y0; a = 5; b = 12; c = -2.
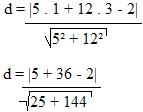 d = 39
d = 39
13
16) P(-2,-4) e r: y = x – 8
Resolução:
Nesse caso a reta está na forma reduzida, portanto é preciso transformá-la para a forma geral.
y = x – 8 → x – y – 8 = 0
Assim, iremos substituir -2 = x0; -4 = y0; a = 1; b = -1; c = -8.
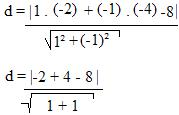 d = |-6|
d = |-6|
√2
d = 6 . √2 = 6√2 = 6√2 = 3 √2
√2 . √2 (√2)2 2
17) Sabendo que os vértices de um triângulo são A(1,3), B(5,0) e C(0,5), responda:
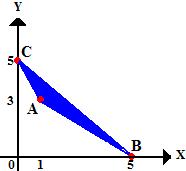
a) Qual é a equação geral da reta AB?
Resolução:
Os pontos A(1,3) e B(5,0) pertencem à reta AB e com eles podemos encontrar o coeficiente angular dessa reta e aplicá-lo na equação fundamental.
mAB= 0 – 3 = - 3
5–1 4
y – y0 = m (x – x0)
y – 0 = -3/4 (x – 5)
y = -3/4x + 15/4
4y = - 3x + 15
4
3x + 4y – 15 = 0
b) Calcule a medida da altura relativa ao vértice C.
Resolução:
Nesse caso iremos calcular a distância do ponto C à reta AB. Substituindo os valores 0 = x0; 5 = y0; a = 3; b = 4; c = -15 na fórmula:
d = |ax0 + by0 + c|
√(a2 + b2)
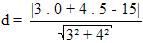
d = |20 – 15|
√25
d = 5 = 1
5
18) Qual é a distância, por exemplo, do ponto P(-1,2) à reta r: x - 2y + 1 = 0.
Resolução:
Temos P(-1, 2) = P(x1, y1), a = 1, b= - 2 e c=1. Assim:
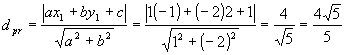
19) Dado o ponto B com coordenadas (2, 6) e reta s: 2x + 4y – 1 = 0, determine a distância entre eles de acordo com os conceitos e fundamentos da Geometria Analítica.
Resolução:
.gif)
20) Considerando que a distância entre ponto P(k, 4) e a reta r, de equação 6x + 8y – 80 = 0, é igual a 6 unidades, calcule o valor da coordenada k.
Resolução:
.gif)
22) (Fuvest-SP) Calcule a distância entre a reta r1, de equação 3y = 4x – 2, e a reta r2, de equação 3y = 4x + 8, sabendo que r1//r2.
Resolução:

25) Calcular a distância do ponto P(1,2) a reta r: 2x + 3y + 4 = 0
Resolução:
Antes de utilizarmos a fórmula que aprendemos, devemos identificar as informações necessárias para utilizá-la.
Como o ponto é P(1, 2), temos que:
xo = 1
yo = 2
Como a equação da reta é 2x + 3y + 4 = 0, temos que:
a = 2
b = 3
c = 4
Utilizando a fórmula:
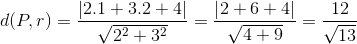
26) Calcular a distância do ponto P(2, 3) à reta r: 4x – y + 7 = 0.
Resolução:
Identificando as informações fornecidas pela questão:
xo = 2
yo = 3
a = 4
b = -1
c = 7
Utilizando a fórmula:
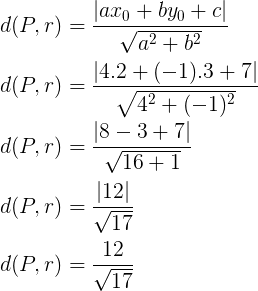
27) (ENEM – 2011) Um bairro de uma cidade foi planejado em uma região plana, com ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho. No plano de coordenadas cartesianas seguinte, esse bairro localiza-se no segundo quadrante, e as distâncias nos
eixos são dadas em quilômetros.
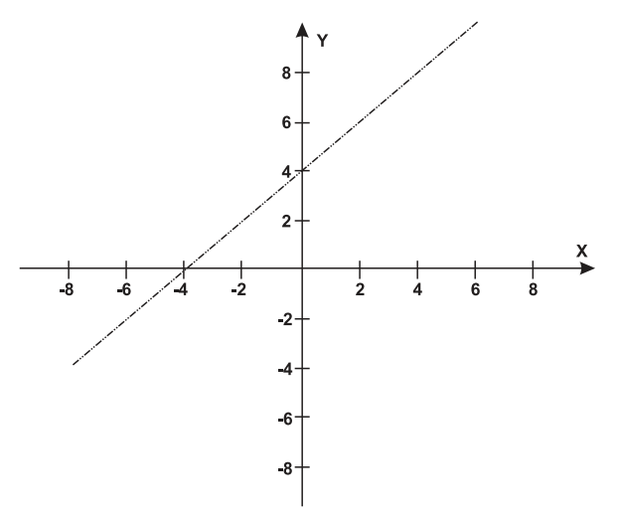
A reta de equação y = x + 4 representa o planejamento do percurso da linha do metrô subterrâneo que atravessará o bairro e outras regiões da cidade.
No ponto P = (-5,5), localiza-se um hospital público. A comunidade solicitou ao comitê de planejamento que fosse prevista uma estação do metrô de modo que sua distância ao hospital, medida em linha reta, não fosse maior que 5 km.
Atendendo ao pedido da comunidade, o comitê argumentou corretamente que isso seria automaticamente satisfeito, pois já estava prevista a construção de uma estação no ponto
(A) (-5,0)
(B) (-3,1)
(C) (-2,1)
(D) (0,4)
(E) (2,6)
Resolução:
Usando a reta da equação fornecida, vamos procurar por pontos no 2º quadrante, segundo as características fornecidas. Vamos tentar usando os seguintes pontos:

Alternativa: B
CONDIÇÃO DE ALINHAMENTO ENTRE TRÊS PONTOS
Três pontos estão alinhados se, e somente se, pertencerem à mesma reta.
.jpg)
O alinhamento de três pontos pode ser determinado aplicando o cálculo do determinante de uma matriz de ordem 3x3. Ao calcular o determinante da matriz construída utilizando as coordenadas dos pontos em questão e encontrando valor igual a zero, podemos afirmar que existe colinearidade dos três pontos.
.jpg)
As coordenadas dos pontos A, B e C são:
Ponto A (x1,y1)
Ponto B (x2,y2)
Ponto C (x3,y3)
Para verificarmos se os pontos estão alinhados, podemos utilizar a construção gráfica determinando os pontos de acordo com suas coordenadas posicionais. Outra forma de determinar o alinhamento dos pontos é através do cálculo do determinante pela regra de Sarrus envolvendo a matriz das coordenadas.
.jpg)
Exercícios resolvidos
28) Dados os pontos A (2, 5), B (3, 7) e C (5, 11), vamos determinar se estão alinhados.
Resolução:
.jpg) Diagonal principal
Diagonal principal
2 . 7 . 1 = 14
5 . 1 . 5 = 25
1 . 3 . 11 = 33
Diagonal secundária
1 . 7 . 5 = 35
2 . 1 . 11 = 22
5 . 3 . 1 = 15
Somatório diagonal principal – Somatório diagonal secundária
(14 + 25 + 33) – (35 + 22 + 15)
72 – 72 = 0
Conclusão: Os pontos somente estarão alinhados se o determinante da matriz quadrada calculado pela regra de Sarrus for igual a 0.
29) Considerando os pontos A(2, 2), B(–3, –1) e C(–3, 1), verifique se eles estão alinhados.
Resolução:
.jpg)
Diagonal principal
2 . (–1) . 1 = –2
2 . 1 . (–3) = –6
1 . (–3) . 1 = –3
Diagonal secundária
1 . (–1) . (–3) = 3
2 . 1 . 1 = 2
2 . (–3) . 1 = –6
(– 2 – 6 – 3) – (3 + 2 – 6)
– 11 – (–1)
– 11 + 1 = – 10
Conclusão: pelo resultado do determinante da matriz verificamos que os pontos não estão alinhados.
30) Verifique se os pontos P(2,1), Q(0,-3) e R(-2,-7) estão alinhados.
Resolução:
Vamos construir a matriz através das coordenadas dos pontos P, Q e R e aplicar Sarrus.
2 . (–3) . 1 + 1 . 1 . (–2) + 1 . (–7) . 0 – [1 . (–3) . ( –2) + 1. 0 . 1 + 2 . (–7) . 1] = 0
– 6 – 2 – 0 – [6 + 0 – 14] = 0
– 8 – 6 +14 = 0
–14 + 14 = 0
0 = 0
Conclusão: podemos verificar que os pontos estão alinhados, pois o determinante da matriz das coordenadas dos pontos é nulo.
31) Verifique se os pontos A(0, 4), B(–6, 2) e C(8, 10) estão alinhados.
Resolução:
Diagonal principal
0 . 2 . 1 = 0
4 . 1 . 8 = 32
1 * (–6) * 10 = –60
32 + (– 60)
32 – 60
–28
Diagonal secundária
4 . (–6) . 1 = –24
0 . 1 . 10 = 0
1 . 2 . 8 = 16
–24 + 16
–8
Determinante
–28 – (–8)
–28 + 8
– 20
Conclusão: temos que o determinante é diferente de zero. Dessa forma, os pontos não estão alinhados.
32) Determine o valor de y de maneira que os pontos P(1, 3), Q(3, 4) e R(y, 2) sejam os vértices de um triângulo qualquer.
Resolução:
Para que os pontos P, Q e R sejam os vértices de um triângulo qualquer, eles não podem estar alinhados. Dessa forma, o valor do determinante da matriz formada pelas coordenadas dos pontos dados deverá ser diferente de zero.
Diagonal principal
1 . 4 . 1 = 4
3 . 1 . y = 3y
1 . 3 . 2 = 6
Diagonal secundária
1 . 4 . y = 4y
1 .1 . 2 = 2
3 . 3 . 1 = 9
4 + 3y + 6 – (4y + 2 + 9) ≠ 0
4 + 3y + 6 – 4y – 2 – 9 ≠ 0
3y – 4y + 4 + 6 – 2 – 9 ≠ 0
–y + 10 – 11 ≠ 0
–y ≠ 11 – 10
–y ≠ 1
y ≠ –1
Conclusão: temos que valor de y que torna o problema verdadeiro corresponde a –1.
33) (UFMG) Determine o valor de m para que os pontos A(2m+1, 2), B(–6, –5) e C(0, 1) sejam colineares.
Resolução:
Diagonal principal
(2m+1) . (–5) . 1 = –10m – 5
2 . 1 . 0 = 0
1 * (–6) * 1 = –6
Diagonal secundária
1 . (–5) . 0 = 0
(2m + 1) . 1 . 1 = 2m + 1
2 * (–6) . 1 = –12
–10m – 5 – 6 – (2m + 1 – 12) = 0
–10m – 5 – 6 – 2m – 1 + 12 = 0
– 12m – 12 + 12 = 0
–12m = 0
m = 0
Conclusão: Para que os pontos sejam colineares, o valor de m deve ser igual a 0.
34) Utilize a condição de alinhamento de três pontos para verificar se os pontos A(1, 1), B(2, 2) e C(3,3) pertencem à mesma reta.
Resolução:
Calculando o determinante da matriz M abaixo através da regra de Sarrus:
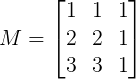
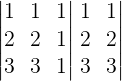 DetM = 1.2.1 + 1.1.3 + 1.2.3 – 3.2.1 – 3.1.1 – 1.2.1
DetM = 1.2.1 + 1.1.3 + 1.2.3 – 3.2.1 – 3.1.1 – 1.2.1
DetM = 2 + 3 + 6 – 6 – 3 – 2
DetM = 0
Conclusão: Os pontos A, B e C estão alinhados.
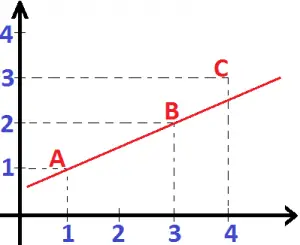
27) Utilize a condição de alinhamento de três pontos para verificar se os pontos A(1, 1), B(3, 2) e C(4, 3) são colineares.
Resolução:
Utilizando a regra de Sarrus para calcular o determinante da matriz M abaixo:
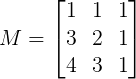
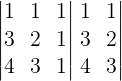 DetM = 1.2.1 + 1.1.4 + 1.3.3 – 4.2.1 – 3.1.1 – 1.3.1
DetM = 1.2.1 + 1.1.4 + 1.3.3 – 4.2.1 – 3.1.1 – 1.3.1
DetM = 2 + 4 + 9 – 8 – 3 – 3
DetM = 1
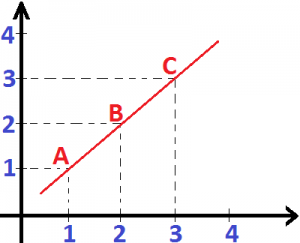
Conclusão: Os pontos A, B e C não estão alinhados. Veja:
Continua...















 A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas
A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas.jpg) (A) 2 m2
(A) 2 m2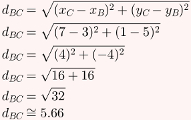
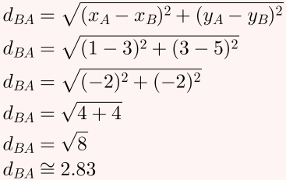
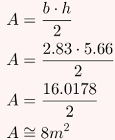

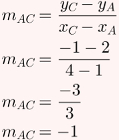
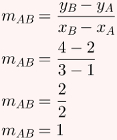
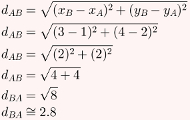
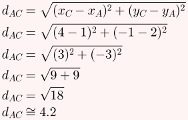
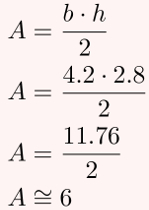
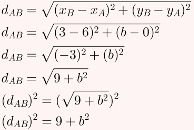
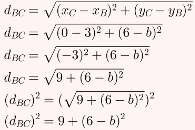
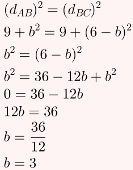

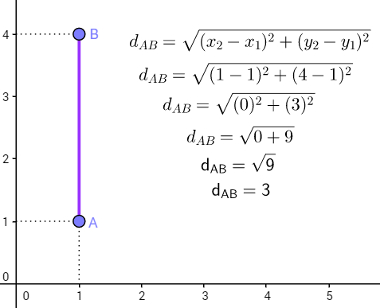
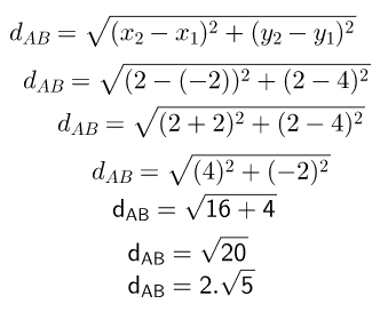
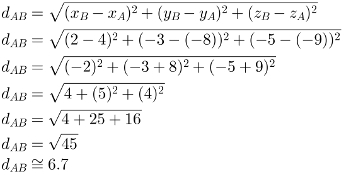
.jpg)

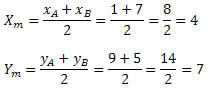
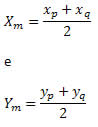
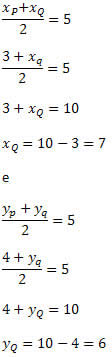
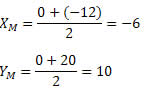
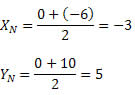



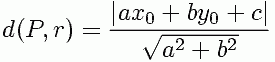
.jpg)
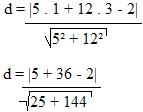
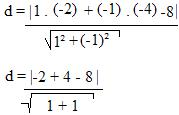

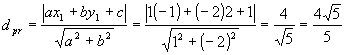
.gif)
.gif)

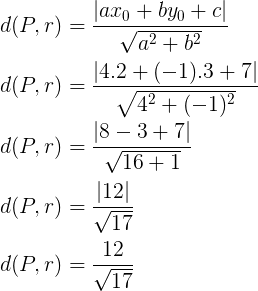


.jpg)
.jpg)
.jpg)
.jpg)
.jpg)