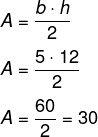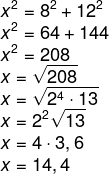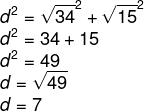TEOREMA DE PITÁGORAS

Professor Diminoi

Teorema de Pitágoras
O teorema de Pitágoras relaciona as medidas dos lados de um triângulo retângulo da seguinte maneira:
 “Em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.”

O teorema de Pitágoras é muito importante para a Matemática, tendo influenciado outros grandes resultados matemáticos.

Fórmula do teorema de Pitágoras
Para aplicação do teorema de Pitágoras, é necessário compreender as nomenclaturas dos lados de um triângulo retângulo. O maior lado do triângulo fica sempre oposto ao maior ângulo, que é o ângulo de 90°. Esse lado recebe o nome de hipotenusa e será representado aqui pela letra a.
Os demais lados do triângulo são chamados de catetos e serão aqui representados pelas letras b e c.
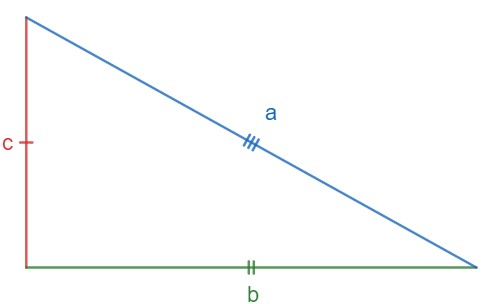O teorema de Pitágoras afirma que é válida a relação a seguir:

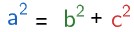
01) Um terreno retangular será dividido ao meio, pela sua diagonal, formando dois triângulos retângulos. A metade desse terreno será cercada com 4 fios de arame farpado. Sabendo que as dimensões desse terreno são de 20 metros de largura e 21 metros de comprimento, qual será a metragem mínima gasta de arame?
(A) 300 metros
(B) 280 metros
(C) 140 metros
(D) 70 metros
(E) 29 metros
Resolução:
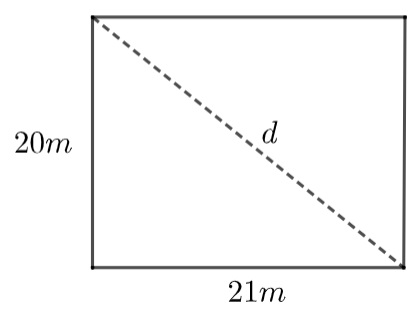Para encontrar a hipotenusa, que é diagonal d desse retângulo, aplicamos o Teorema de Pitágoras.
d² = 20² + 21²
d² = 400 + 441
d² = 841
d = √841
d = 29
Sabendo que as dimensões do triângulo são 20, 21 e 29, vamos calcular seu perímetro.
P = 20 + 21 + 29 = 70 metros
Como haverá 4 fios de arame farpado, multiplicativo o perímetro por 4, encontraremos a metragem de arame necessária.
70 × 4 = 280 metros
Alternativa: B

02) A área do triângulo retângulo que possui base medindo 5 cm e hipotenusa medindo 13 cm é igual a:
(A) 30 cm²
(B) 60 cm²
(C) 24 cm²
(D) 16 cm²
(E) 12 cm²
Resolução:
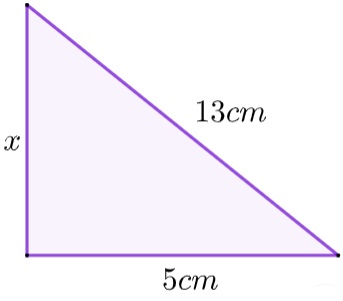Como o triângulo é retângulo, seja x a sua altura, que coincide com o cateto que não conhecemos, aplicando o teorema de Pitágoras, temos que:
x² + 5² = 13²
x² + 25 = 169
x² = 169 – 25
x² = 144
x = √144
x = 12
Para calcular a área do triângulo, temos que:

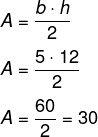
Alternativa: A

03) Uma represa no formato retangular possui dimensões de 30 metros por 40 metros. Qual será a distância percorrida por uma pessoa que atravessa essa represa pela sua diagonal?
(A) 45 metros
(B) 50 metros
(C) 65 metros
(D) 70 metros
(E) 80 metros
Resolução:
Desenhando a situação, temos que:
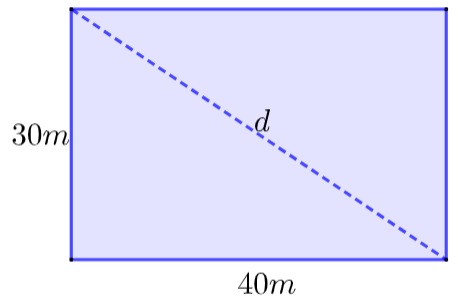Pelo teorema de Pitágoras, temos que:
d² = 30² + 40²
d² = 900 + 1600
d² = 2500
d = √2500
d = 50 metros
Alternativa: B

04) (Fundatec) O famoso teorema de Pitágoras nos permite calcular o valor da hipotenusa e dos catetos formadores do triângulo retângulo. Sabendo que a hipotenusa de um determinado triângulo mede 10 cm e o cateto oposto mede 6 cm, assinale a alternativa que contém a medida do cateto adjacente:
(A) 7
(B) 8
(C) 9
(D) 10
(E) 11
Resolução:
Aplicando o teorema de Pitágoras, temos que:
10² = 6² + x²
100 = 36 + x²
100 – 36 = x²
64 = x²
x = √64
x = 8
Alternativa: B

05) (IFG 2019) Considere que o tamanho de uma televisão, dado em polegadas, corresponde ao comprimento da sua diagonal e que, no caso de televisores de tamanho normal, a largura e a altura seguem, ordenadamente, a relação 4:3. Observe a figura abaixo e considere 1 polegada = 2,5 cm.
Com relação a uma televisão plana de 40 polegadas, é correto afirmar que sua largura e sua altura são, respectivamente:
(A) 60 cm e 45 cm                  
(B) 80 cm e 60 cm
(C) 64 cm e 48 cm                   
(D) 68 cm e 51 cm
Resolução:
Sabendo que a TV tem dimensões proporcionais a 3 e 4, seja 3k e 4k o comprimento e a altura respectivamente, temos que:
40² = (3k)² + (4k)²
1600 = 9k² + 16k²
1600 = 25k²
1600/25 = k²
64 = k²
k = √64
k = 8
Sabendo que k = 8, então as dimensões da TV em polegadas são:
4k → 4 × 8 = 32
3k → 4 × 3 = 24
Para transformar em centímetros, basta multiplicar por 2,5, já que uma polegada equivale a 2,5 cm.
32 . 2,5 = 80 cm
24 . 2,5 = 60 cm
Alternativa: B

06) (IBEG) Um empresário adquiriu um terreno comercial em formato triangular. As medidas perpendiculares são de 120 metros e 160 metros. Após a limpeza do terreno, o proprietário decidiu construir uma cerca de arame liso com 8 fios em volta de todo o perímetro do terreno. Cada metro do fio de arame custa R$ 1,50. Diante das informações apresentadas, calcule o perímetro total do terreno utilizando o teorema de Pitágoras, a quantidade de metros de arames a ser utilizado e o valor do custo com a aquisição dos fios de arame.
(A) Perímetro total de 280 metros; 2.240 metros de fios; custo de R$ 3.360.
(B) Perímetro total de 300 metros; 2.400 metros de fios; custo de R$ 3.600.
(C) Perímetro total de 350 metros; 2.800 metros de fios; custo de R$ 4.200.
(D) Perímetro total de 480 metros; 3.840 metros de fios; custo de R$ 5.760.
(E) Perímetro total de 400 metros; 3.200 metros de fios; custo de R$ 4.800.
Resolução:
Primeiro encontraremos a hipotenusa x.
x² = 120 ² + 160²
x² = 14.400 + 25.600
x² = 40.000
x = √40.000
x = 200
gora calculando o perímetro, temos que:
200 + 120 + 160 = 480 metros
Como serão dadas 8 voltas, então:
480 . 8 = 3840
Sabendo que o metro custa R$1,50, então:
1,50 . 3.840 = 5760,00
Alternativa: D

07) (IFG 2020) O desmatamento tem sido uma problemática crescente no Brasil. Supondo que, ao efetuar o desmatamento de uma determinada área, um madeireiro se depara com uma árvore que já se encontra quebrada; parte do tronco da árvore que se manteve fixa ao solo mede 3 m e forma com este um ângulo de 90⁰; a ponta da parte quebrada que toca o solo encontra-se a 4 m de distância da base da árvore. Qual era a altura da árvore antes de se quebrar:
(A) 5 m
(B) 7 m
(C) 8 m
(D) 9 m
Resolução:
Para encontrar o valor da parte da árvore que quebrou, basta aplicar o teorema de Pitágoras.
x² = 3² + 4²
x² = 9 + 16
x² = 25
x = √25
x = 5
Como ainda há 3 metros que ficaram fixos no solo, a altura da árvore é de 5 + 3 = 8 metros.
Alternativa: C

08) Um carro se desloca por uma rampa inclinada. Essa rampa possui 60 metros de comprimento e altura máxima de 10 metros, conforme a imagem:
A distância x entre o ponto A e B é de aproximadamente:
(A) 45 metros
(B) 50 metros
(C) 55 metros
(D) 58 metros
(E) 59 metros
Resolução:
Aplicando o teorema de Pitágoras, temos que:
60² = 10² + x²
3600 = 100 + x²
3600 – 100 = x²
x² = 3500
x = √3500
x = 59,16 metros
Alternativa: E

09) Em seu quintal, Sara decidiu criar um jardim no formato de um triângulo retângulo. Para isso é importante que ela saiba as dimensões dos lados desse triângulo. Analisando a imagem, podemos afirmar que o valor da hipotenusa é: (Use √13 = 3,6)
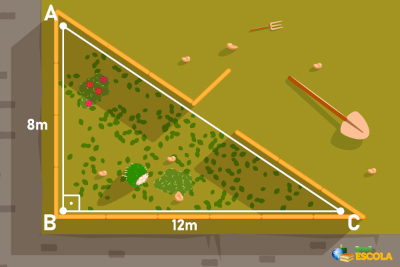(A) 10 cm
(B) 13,4 cm
(C) 15,2 cm
(D) 16 cm
(E) 14,4 cm
Resolução:
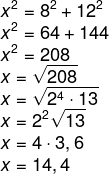Alternativa: E

10) Analisando os triângulos a seguir, podemos afirmar que a soma x + y é igual a:
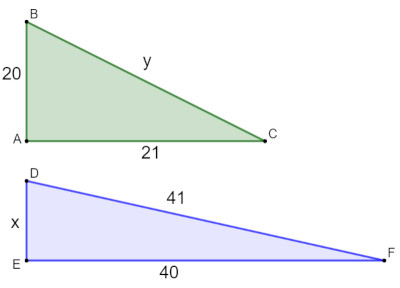(A) 29
(B) 9
(C) 30
(D) 38
(E) 40
Resolução:
Encontrando o valor de x, temos que:
41² = x² + 40²
1681 = x² + 1600
x² = 1681 – 1600
x² = 81
x = √81
x = 9
Encontrando o valor de y:
y² = 21² + 20²
y² = 441 + 400
y² = 841
y = √841
y = 29
x + y = 9 + 29 = 38
Alternativa: D

11) Ao encerrar o expediente de trabalho, Sunara chamou um táxi para retornar à sua casa. No caminho, o semáforo sinalizou a cor amarela, mas o motorista ainda estava muito distante. Em seguida, foi sinalizado vermelho, e o motorista parou a uma distância horizontal de 3 m de um semáforo que possui 4 m de altura. Analisando a imagem, qual é o comprimento representado por x:
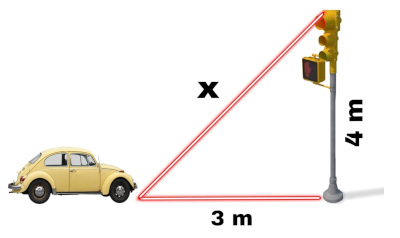(A) 2 m
(B) 3 m
(C) 4 m
(D) 5 m
(E) 6 m
Resolução:
x²  = 3² + 4²
x² = 9 + 16
x² = 25
x = √25
x = 5
Alternativa: D

12) Utilize a relação pitagórica para encontrar a diagonal.
(A) 5
(B) 6
(C) 7
(D) 42
(E) 49
Resolução:
Aplicando o teorema de Pitágoras, temos que:
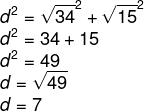Alternativa:
 
13) A distância entre os muros laterais de um lote retangular é exatamente 12 metros. Sabendo que uma diagonal desse lote mede 20 metros, qual é a medida do portão até o muro do fundo?
(A) 8 metros
(B) 10 metros
(C) 12 metros
(D) 14 metros
(E) 16 metros
Resolução:
A diagonal de um retângulo sempre determina dois triângulos retângulos. Portanto, os muros frontal e lateral desse lote podem ser considerados catetos, e a diagonal é a hipotenusa. Sabendo que a medida do muro lateral de um lote é justamente a distância do portão até o muro do fundo, utilizaremos o Teorema de Pitágoras para calculá-la.
Seja o comprimento do muro lateral igual a x, pelo teorema de Pitágoras,
20² = 12² + x²
400 = 144 + x²
400 – 144 = x²
x² = 256
x = √256
x = 16 metros
Alternativa: E

14) Um garoto observa uma coruja no alto de um poste de 8 metros de altura. A sombra projetada desse poste no chão possui comprimento de 6 metros naquele horário. Sabendo que o poste forma um ângulo de 90° com o solo, qual é a distância do garoto até a coruja?
(A) 6 metros
(B) 8 metros
(C) 10 metros
(D) 12 metros
(E) 14 metros
Resolução:
A distância do garoto até a coruja é exatamente a hipotenusa do triângulo cujos catetos são o próprio poste e sua sombra. Desse modo, sendo essa distância igual a x, pelo Teorema de Pitágoras, teremos:
x² = 8² + 6²
x² = 64 + 36
x² = 100
x = √100
x = 10 metros
Alternativa: C

15) (IFSC/2015) Para acessar o topo de uma plataforma de saltos a 400 cm de altura, um atleta deve subir uma escadaria que possui 8 degraus no primeiro lance e 6 degraus no segundo lance de escada, conforme mostra a figura ao lado. Sabendo que cada degrau possui 30 cm de profundidade, é CORRETO afirmar que o comprimento, em cm, da haste metálica AB utilizada para dar sustentação à plataforma é:
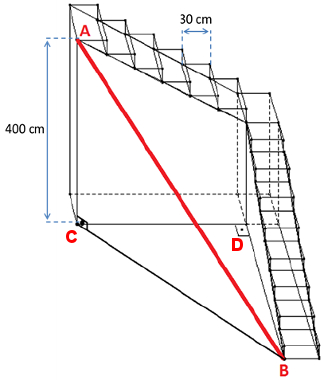(A) 300
(B) 400
(C) 500
(D) 200
(E) 100
Resolução:
Para calcular o comprimento da barra AB, é necessário descobrir primeiro o comprimento da barra BC.
Para descobrir o comprimento da barra BC, utilizaremos o Teorema de Pitágoras no triângulo BCD. Note que os catetos BD e CD medem, respectivamente, 8 · 30 e 6 · 30, isto é, 240 cm e 180 cm. Logo:
BC² = 240² + 180²
BC² = 57600 + 32400
BC² = 90000
BC = √90000
BC = 300
Considerando o triângulo ABC, cujos catetos, agora conhecidos, medem 400 cm e 300 cm, poderemos utilizar o Teorema de Pitágoras para calcular o comprimento da haste AB.
Antes disso, existe um resultado que diz o seguinte: quando um triângulo retângulo possui catetos múltiplos de 3 e 4 por um fator comum, sua hipotenusa será múltiplo de 5 pelo mesmo fator.
Assim, a haste AB, hipotenusa do triângulo ABC, mede 500 cm, pois seus catetos medem 300 cm e 400 cm, que são múltiplos de 3 e 4 por 100.
Caso haja dúvida, segue a solução utilizando o teorema de Pitágoras diretamente:
AB² = 400² + 300²
AB² = 160000 + 90000
AB² = 250000
AB = √250000
AB = 500 cm
Alternativa: C

16) (IFSP/2015) O transporte alternativo é uma maneira de se locomover usando um meio diferente dos mais tradicionais. A bicicleta é um exemplo disso. Em alguns lugares, ela é usada porque é mais barata, como no interior do Brasil e em países como a Índia e China. Outras pessoas escolhem andar de bicicleta por uma questão ideológica, porque elas não agridem o meio ambiente e não causam tantos transtornos quanto os carros. Usando uma bicicleta, uma pessoa sai do ponto A e se dirige ao ponto B. O percurso, dado em km, representado pelos segmentos AC, CD e DB está esboçado no gráfico abaixo.
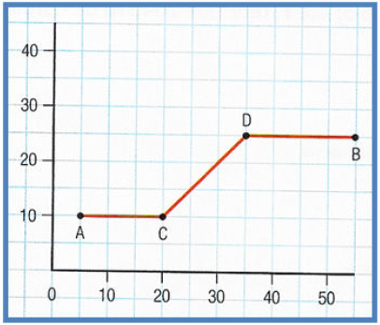Considerando √2 = 1,4, assinale a alternativa que apresenta a distância percorrida pela pessoa do ponto A ao ponto B.
(A) 56 km.
(B) 21 km.
(C) 20 km.
(D) 15 km.
(E) 10 km.
Resolução:
Observe o triângulo retângulo construído na imagem abaixo para o cálculo da distância CD.

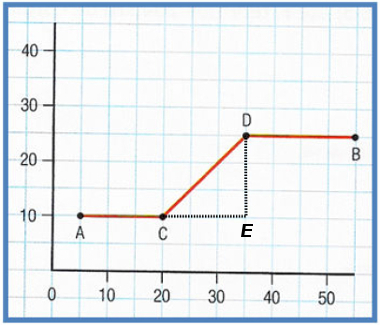
Observe que ambos os segmentos CE e ED medem 15 km. Utilizando o teorema de Pitágoras, calcularemos o comprimento do segmento CD:
CD² = 15² + 15²
CD² = 225 + 225
CD² = 450
CD = √450
Simplificando √450 pelo processo de fatoração, obtemos:
√450 = √(2·3²·5²) = 3·5√2 = 15·√2 = 15·1,4 = 21
Para descobrir a distância percorrida entre os pontos A e B, basta somar os comprimentos dos segmentos AC, CD e DB:
AC + CD + DB = 15 + 21 + 20 = 56 km
Alternativa: A

17) (PM ES 2013 – Exatus) A diagonal de um retângulo mede 10 cm, e um de seus lados mede 8 cm. A superfície desse retângulo mede:
(A) 40 cm²
(B) 48 cm²
(C) 60 cm²
(D) 70 cm²
(E) 80 cm²
Resolução:
Desenhando o retângulo com as características informadas:

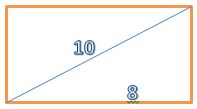
Para calcular a área precisamos saber a medida do outro lado, que pode ser descoberto pelo teorema de Pitágoras:
10² = 8² + x²
100 = 64 + x²
100 – 64 = x²
36 = x²
x = 6
Calculando a área do retângulo:
Área = 8.6 = 48 cm²
Alternativa: B

18) (Bombeiros ES 2011 – Cespe) Considerando que a área de um triângulo retângulo é igual a 30 cm² e a média aritmética das medidas de seus lados é igual a 10 cm, a afirmação abaixo está certa ou errada?
“O maior lado desse triângulo mede menos que 13,5 cm.”
Resolução:
Desenhando o triângulo com as características informadas:

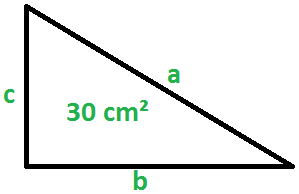
Como a média aritmética dos lados é igual a 10 cm:
(a + b + c) /3= 10
a + b + c = 30
Utilizando a fórmula da área do triângulo retângulo:
A = base x altura / 2
30 = b . c/2
b . c = 60
Pelo Teorema de Pitágoras:
a² = b² + c²
Temos
a + b + c = 30
30 – a = b + c
(30 – a)² = (b + c)²
30² – 2.30.a + a² = b² +2bc + c²
900 – 60a + a² = b² +2bc + c²
Sabendo do teorema de pitágoras podemos eliminar a² = b² + c². Vamos também substituir bc = 60:
900 – 60a = 2.60
60a = 900 – 120
60a = 780
a = 780/60
a = 13

19) (PM SP 2014 – Vunesp)  Duas estacas de madeira, perpendiculares ao solo e de alturas diferentes, estão distantes uma da outra, 1,5 m. Será colocada entre elas uma outra estaca de 1,7 m de comprimento, que ficará apoiada nos pontos A e B, conforme mostra a figura.
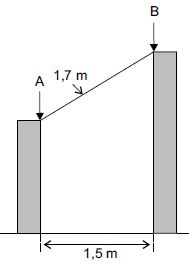A diferença entre a altura da maior estaca e a altura da menor estaca, nessa ordem, em cm, é:
(A) 95.
(B) 75.
(C) 85.
(D) 80.
(E) 90.
Resolução:
Para resolvermos a questão, vamos localizar um triângulo retângulo na figura. Veja:

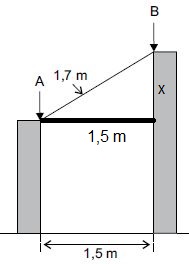
Note que x é exatamente a diferença que queremos, e podemos calculá-lo através do Teorema de Pitágoras:
1,7² = 1,5² + x²
2,89 = 2,25 + x²
x² = 2,89 – 2,25
x² = 0,64
x = 0,8 m ou 80 cm
Alternativa: D

20) (SAP SP 2013) Roberto irá cercar uma parte de seu terreno para fazer um canil. Como ele tem um alambrado de 10 metros, decidiu aproveitar o canto murado de seu terreno (em ângulo reto) e fechar essa área triangular esticando todo o alambrado, sem sobra. Se ele utilizou 6 metros de um muro, do outro muro ele irá utilizar, em metros,
(A) 7.
(B) 5.
(C) 8.
(D) 6.
(E) 9.
Resolução:
A questão fala em cercar um canto murado, utilizando 10m de tela. Temos claramente um triângulo retângulo. Veja a figura:

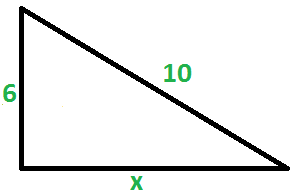
Basta utilizarmos o teorema de pitágoras, onde 10 é a hipotenusa, um cateto é 6 e o outro vamos chamar de x:
10² = 6² + x²
100 = 36 + x²
x² = 100 – 36
x² = 64
x = 8
Alternativa: C

21) (PM Pará 2007 – Fadesp) Uma praça tem a forma de um triângulo ABC, retângulo em A, cuja hipotenusa a mede 250 metros e o cateto c mede 200 metros. Para garantir a execução de um serviço, houve necessidade de se interditar uma parte da praça com uma corda MN perpendicular à hipotenusa, distando 150 metros do vértice B, com M na hipotenusa e N no cateto c. O comprimento dessa corda, em metros, é
(A) 112,5.
(B) 125,5.
(C) 150,5.
(D) 175,5.
Resolução:
Com as informações do enunciado, o formato da praça pode ser representado pela figura abaixo:

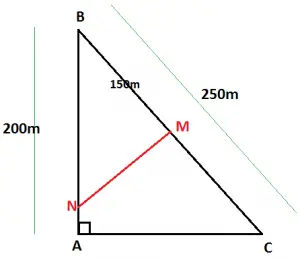
Nosso primeiro passo é acharmos o valor de AC através do teorema de Pitágoras:
BC² = AB² + AC²
250² = 200² + AC²
62500 = 40000 + AC²
AC² = 62500 – 40000
AC² = 22500
AC = 150
Pela semelhança dos triângulos ABC e MBN:
Aternativa: A

22) (IBGE 2016 – Cesgranrio) Na Figura a seguir, PQ mede 6 cm, QR mede 12 cm, RS mede 9 cm, e ST mede 4 cm.
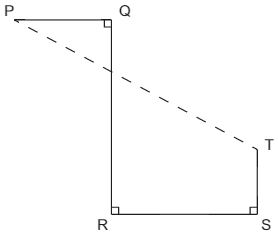A distância entre os pontos P e T, em cm, mede
(A) 17
(B) 21
(C) 18
(D) 20
(E) 19
Resolução:
Vamos marcar na figura as distâncias fornecidas e um ponto Z, de modo que tenhamos um triângulo retângulo onde PT é a medida da hipotenusa.

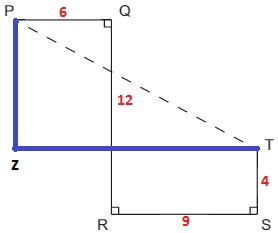
Como temos um triângulo retângulo iremos utilizar o famoso teorema de Pitágoras, onde:
PT = hipotenusa
PZ = 12 – 4 = 8
ZT = 6 + 9 = 15
PT² = 8² + 15²
PT² = 64 + 225
PT² = 289
PT = 17
Alternativa: A

23) (TJ SP 2015 – Vunesp) Em um jardim, um canteiro de flores, formado por três retângulos congruentes, foi dividido em cinco regiões pelo segmento AB, conforme mostra a figura.
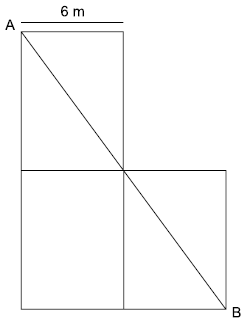Se AB mede 20 m, então a área total desse canteiro é, em m², igual a
(A) 162.
(B) 126.
(C) 135.
(D) 153.
(E) 144.
Resolução;
Sabendo que os retângulos são congruentes e que AB = 20, vamos aplicar o teorema de pitágoras no triângulo abaixo:

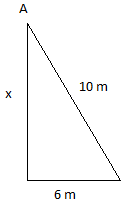
Onde 6 e x são as medidas do retângulo.
10² = x² + 6²
100 = x² + 36
x² = 100 – 36
x² = 64
x = 8 m
Calculando a área do retângulo:
A = 6 . 8 = 48 m²
Como o canteiro é formado por 3 desses retângulos:
At = 3 . 48 = 144 m²
Alternativa: E