QUESTÕES DO SARESP

Professor Diminoi
SARESP

01) (SARESP) Para garantirmos que dois polígonos sejam semelhantes é necessário que:
I. Possuam o mesmo número de lados.
II. Os lados correspondentes sejam proporcionais.
III. Os ângulos internos correspondentes sejam congruentes.
IV. O número de lados seja proporcional.
A alternativa que garante a proporcionalidade é:
(A) I, II e III
(B) II, III e IV
(C) I, III e IV
(D) I, II e IV
Resolução:
Para que dois polígonos sejam semelhantes, deve existir proporcionalidade entre seus lados correspondentes, além de ângulos correspondentes congruentes.
Alternativa: A

02) (SARESP) Observe a figura, desenhada no quadriculado 1 x 1
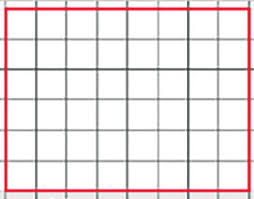Das figuras reduzidas abaixo (desenhada no quadriculado 1 x 1), a semelhante à figura acima é:
(A) Figura I
(B) Figura II
(C) Figura III
(D) Figura IV
Resolução:
Uma figura é reduzida ou ampliada em relação a outra quando ela é reduzida ou ampliada na mesma proporção
Alternativa: V

03) (SARESP) Observe os triângulos A e B a seguir:
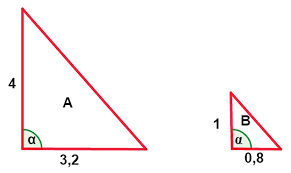Sabendo que os triângulos A e B são semelhantes, a constante de proporcionalidade k que gerou o triângulo B é:
(A) k = 0,2
(B) k = 0,25
(C) k = 2,4
(D) k = 3
Resolução:
Basta achar a razão entre os lados do triângulo B e seus correspondentes no triângulo A é a constante de proporcionalidade procurada.
k = 0,8/3,2 = 1/4
0,25
k = 1/4
0,25
Alternativa: B 

04) (SARESP) (Adaptada - Nova Escola) Na figura abaixo cada lado do quadradinho mede 1u.
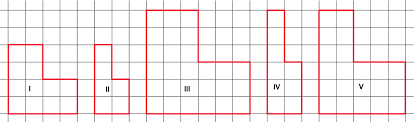
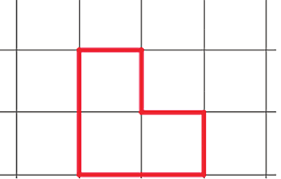As figuras a seguir (cada lado do quadradinho mede 1 u) que tiveram suas dimensões ampliadas em 2 e 3 vezes respectivamente, em relação a figura acima, são:
(A) Figura I e Figura II
(B) Figura I e Figura III
(C) Figura II e Figura IV
(D) Figura III e Figura V
Resolução:
A figura I duplicou (2)
A figura III triplicou (3)
Alternativa: B
Observação: quando no enunciado do problema estiver a palavra “respectivamente”. Isso quer dizer que a resposta deve está na ordem da pergunta. Nesse caso, primeiro a figura que foi ampliada em 2 e depois a figura que foi ampliada em 3.

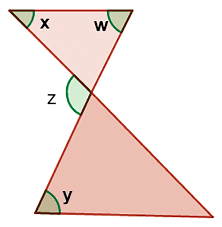
05) (SARESP) Na figura a seguir temos dois triângulos semelhantes nos quais os ângulos x e y medem respectivamente 45° e 55°. Calcule a medida dos ângulos w e z, respectivamente.
(A) 55° e 45°
(B) 55° e 80°
(C) 55° e 100°
(D) 80° e 100°
Resolução:
A soma dos ângulos internos em qualquer triângulo é sempre 180°, então podemos afirmar que o ângulo AÔB é = 180° - 45° – w°
180° - 45° – 55°
AÔB = 80° e este ângulo é suplementar de ẑ.
Com isto podemos concluir que
ẑ = 180° – 80°
ẑ = 100°
ŵ = 55°
ẑ = 100°
Alternativa: C

06) (SARESP) Observe as figuras abaixo:
O triângulo SOL é uma ampliação do triângulo TEU. As medidas x, y, z e w dos ângulos indicados são:
(A) x = 22°, y = 60°, z = 22° e w = 98°
(B) x = 60°, y = 22°, z = 98° e w = 22°
(C) x = 60°, y = 32°, z = 98° e w = 32°
(D) x = 60°, y = 38°, z = 98° e w = 38°
Resolução:
Em uma ampliação ou redução os ângulos internos são congruente (iguais)
Alternativa: D

07) (SARESP) Um lado de um triângulo mede 45 m. Num triângulo semelhante, o lado correspondente mede 30 m. Se o perímetro do primeiro é de 120 m, o do segundo será de:
(A) 45 m
(B) 75 m
(C) 80 m
(D) 180 m
Resolução:
Temos então dois triângulos semelhantes, conforme o enunciado. Perímetro é a soma das medidas de todos os lados, como os lados correspondentes são proporcionais (apresentam uma constante de proporcionalidade), logo os perímetros também serão, isto é, a razão entre os perímetros terá a mesma constante de proporcionalidade apresentada entre os lados correspondentes.
45/30 = 120/P
45P = 120 . 30
P = 3600/45
P = 80 m
Alternativa: C

08) (SARESP) Rodrigo observou que em determinada hora do dia, o Edifício “Conquista” projeta uma sombra de 20 metros ao mesmo tempo em que uma árvore de 9 metros projeta uma sombra de 4 metros (O edifício e a arvore estão na vertical, apoiados na mesma horizontal). Se mais tarde a sombra da árvore diminuir 1 metro a sombra do edifício passará a medir:
(A) 45 m
(B) 22,5 m
(C) 19 m
(D) 15 m
Resolução:
Precisamos primeiramente encontrar a altura do prédio em questão. Pela semelhança de triângulos podemos escrever a razão entre as alturas e a razão entre as sombras projetadas e igualá-las.
H/S = h/s
H = altura do maior
S = sombra do maior
h = altura do menor
s = sombra do menor
20/4 = h/9
h = 20 . 9/4
h = 45 metros
Como o enunciado nos traz que em outro momento a sombra da árvore diminuiu em um metro, passando então para 3m, logo houve também neste instante a redução da sombra do prédio.
S/3= 45/9
S = (45 . 3)/9
S = 15 metros
Alternativa: D

09) (SARESP) A figura a seguir representa o perfil de uma escada. Cada degrau tem a mesma extensão (d) e a mesma altura. Sabendo que o lado BC mede 4 m e que AC mede 5 m determine, em centímetros, a extensão (d) de cada degrau:
(A) 20
(B) 40
(C) 60
(D) 80
Resolução:
Aplicando uma das relações métricas do triângulo retângulo que é:
hipotenusa² = cateto² + cateto²
Assim temos:
(A C)² = (AB)² + (BC)²
5² = (AB)² + (4)²
(AB)² = 25 – 16
AB = √9
AB = 3 m
Conforme explicado acima devemos dividir BC por 5:
4 ÷ 5 = 0,80 m = 80 cm
Alternativa: D

10) (SARESP) (PC MA – FGV 2012) A figura abaixo mostra uma viga AB de 4 m de comprimento presa no ponto A de uma parede vertical. A viga é mantida na posição horizontal pelo cabo de aço PQ de forma que P está fixo na parede, AP é vertical e Q está no meio da viga AB. Sabe-se que o ângulo APQ mede 40^o.
Dados: sen 40^o = 0,64; cos 40^o = 0,77; tg 40^o = 0,84
(A) 2,38 m
(B) 2,60 m
(C) 3,13 m
(D) 4,76 m
Resolução:
A viga na horizontal, um cabo fixado na parede vertical formando o triângulo PAQ retângulo em A com o P̂= 40° e AB = 4 m. Para encontrar o valor de AQ, basta que cateto oposto seja dividido pelo cateto adjacente.
Alternativa: A

11) (SARESP) (Adaptada da Revista Nova Escola) Adriana alugou um espaço de 100 m² e dividiu essa área, conforme a figura:
A equação que corresponde à área total alugada por Adriana é:
(A) x² + 3² = 100
(B) x + 3² = 100
(C) x² + 3x + 9 = 100
(D) (x + 3)² = 100
Resolução:

O espaço alugado por Adriana é de formato quadrado cujo lado é (x + 3) e área 100 m². Podemos então escrever que: (x + 3)² = 100; essa equação representa a área total.
Alternativa: D

12) (SARESP) O produto das idades de dois irmãos, Antônio e Rafael é 70. Sabe-se que Antônio é três anos mais velho que Rafael. A equação que nos permite calcular a idade de Rafael é:
(A) x (x + 3) = 70
(B) x (x + 3) + 70 = 0
(C) x (3x) = 70
(D) x + x³ = 70
Resolução:

Podemos dizer que Rafael tem x anos e o enunciado nos diz que Antônio é 3 anos mais velho, então tem (x + 3) anos e que o produto das idades é 70. Logo, podemos escrever que x (x + 3) é igual a 70.
Alternativa: A

13) (SARESP) A soma das raízes da equação 4x² + 4x − 8 = 0, é igual a:
(A) - 4
(B) - 1
(C) 1
(D) 4
Resolução:
As Relações de Girard para resolução da equação 4x² + 4x − 8 = 0, pode ser um dos métodos utilizados para obter rapidamente a resposta.
a = 4
b = 4
c = - 8
Soma das raízes = −b/a
S = −4/4
S  = -1
Alternativa: B

14) (SARESP) As raízes da equação (x + 2)² = 9, são:
(A) -3 e 3
(B) -1 e 1
(C) 1 e − 5
(D) 7 e − 11
Resolução:

Para a resolução da equação (x + 2)² = 9, alguns alunos conseguem fazer a seguinte pergunta: que número (x + 2) que ao ser elevado ao quadrado resulta em 9? A resposta a sua pergunta será 3 ou – 3 e resolvem as igualdades:
x + 2 = 3
x = 3 – 2
x = 1
x + 2 = − 3
x = − 3 – 2
x = − 5
Obtendo as raízes 1 e – 5.
Alternativa: C

15) (SARESP) Luís quer cercar sua horta de formato retangular com duas voltas de arame. As dimensões da horta são expressas por (x – 5) e (x + 5) e sua área total é 56 m². A metragem de arame que Luís precisa comprar é de:
(A) 81 m
(B) 72 m
(C) 36 m
(D) 18 m
Resolução:

Com as informações que temos da horta: formato retangular de dimensões (x – 5) por (x + 5) e área 56 m², podemos afirmar que: (x – 5) (x + 5) = 56.
Utilizando a propriedade distributiva ou o produto da soma pela diferença, temos:
x² – 25 = 56
Resolvendo:
x² = 56 + 25
x² = 81
x = ± √81
x = ± 9
Com isto podemos encontrar as dimensões da horta.
Se x = 9
O lado (x − 5)
(9 − 5) = 4 m
O lado (x + 5)
(9 + 5) = 14 m
Se x = −9
O lado (x − 5)
(-9 − 5) = −14 m (absurdo!)
Para luís cercar a sua horta de dimensões 4 por 14 precisamos encontrar o perímetro.
Perímetro = 4 + 4 + 14 + 14 = 36 m
Como Luís deseja contornar a horta com duas voltas de arame, precisará de: 36 . 2 = 72 m
Alternativa: B

16) (SARESP) Analise as afirmações.
(A) A quantidade de questões erradas em uma prova (prova formada por questões de mesmo valor) e a nota obtida são grandezas inversamente proporcionais.
(B) A massa de uma pessoa e a sua idade são grandezas que não envolvem proporcionalidade.
(C) A quantidade de litros de combustível e o valor pago são grandezas inversamente proporcionais.
(D) A velocidade de um automóvel e o tempo gasto em um determinado percurso são grandezas diretamente proporcionais.
Classifique-as, respectivamente, em Verdadeira (V) ou Falsa (F).
(A) F, F, V, V
(B) V, F, V, F
(C) F, V, F, V
(D) V, V, F, F
Resolução:
a) Quanto mais questões estiverem erradas, menor será a nota obtida e as questões possuem o mesmo valor (constante proporcionalidade), temos então grandezas inversamente proporcionais.
Logo, o item a) é verdadeiro (V).
b) Não existe proporcionalidade entre massa de uma pessoa e a sua idade.
Logo, o item b) é verdadeiro (V).
c) Quanto mais litros de combustível maior será o valor a ser pago e a constante de proporcionalidade é o preço do litro do combustível, temos então grandezas diretamente proporcionais.
Logo, o item c) é falso (F).
d) Se dobrarmos a velocidade de um automóvel ele chegará ao seu destino na metade do tempo. Do mesmo modo, se reduzirmos a velocidade desse automóvel pela metade ele levará o dobro do tempo para chegar ao mesmo destino. A constante de proporcionalidade em questão é o determinado percurso, temos então grandezas inversamente proporcionais.
Logo, o item d) é falso (F).
Observação: Para que grandezas sejam inversamente proporcionais não basta uma aumentar e a outra diminuir, é preciso que o aumento e a diminuição estejam ligados por uma relação multiplicativa do tipo k . x.
Alternativa: D

17) (SARESP) Uma máquina de xerox tira 280 cópias em 7 minutos. Em um quarto de hora essa máquina tirará:
(A) 40
(B) 160
(C) 600
(D) 1 000
Resolução:
Quanto mais cópias forem tiradas, maior será o tempo gasto para isto. Portanto as grandezas, número de cópias (n) e tempo gasto (t) são grandezas diretamente proporcionais.
Usamos Regra de três simples
7          280
15        x
7x = 15 . 280
7x  = 4200
x = 4200/7
x = 600
Alternativa: C

18) (SARESP) Patrícia está programando viajar com o seu carro para a praia no próximo feriado. A cada 80 km rodados, seu carro consome 10 litros de combustível. A distância que Patrícia irá percorrer nesta viagem é de 480 km e o preço do litro de combustível é de R$ 2,80. O gasto que Patrícia terá com o combustível será de:
(A) R$ 168,00
(B) R$ 224,00
(C) R$ 1 344,00
(D) R$ 1 680,00
Resolução:
Quanto mais km foram percorridos (e) maior será o consumo de combustível (c). Portanto as grandezas km percorridos e litros de combustível são grandezas diretamente proporcionais.  Primeiro vamos achar quantos litros ela gastará para percorrer 480km
Usando Regra de Três Simples
80        10
480      x
80x =  480 . 10
80x = 4800
x = 4700/80
x  = 60
Para saber quantos litros ela precisa para percorrer 480km é só multiplicar 60 por 2,58.
60 . 2,80 = 158
Alternativa: A

19) (SARESP) Sabendo que a área total da moldura é de 7 m², calcule a medida x do lado dos quadrados nos cantos da moldura, tendo em vista que os quatro cantos da moldura são quadrados idênticos.
(A) 0,2 m.
(B) 0,3 m.
(C) 0,4 m.
(D) 0,5 m.
Resolução:
Tem-se inicialmente que, a área do vitral (4m . 2m) é 8m².
A dimensão dos lados da figura retangular com a moldura ficará acrescida de 2x. Sendo (4 + 2x) e (2 + 2x).
A outra informação é que a área da moldura é 7m².
Ao subtrair a área do vitral (8m²) da área total da figura (4 + 2x) . (2 + 2x), tem-se a área da moldura que é 7m².

Assim:
[(4 + 2x)  . (2 + 2x) – 8] = 7
8 + 12x + 4x² – 8 = 7
4x² + 12x = 7
x2 + 12x – 7 = 0
Na equação, temos que:
a = 4
b = 12
c = −7
Δ = √b² – 4 ∙ a ∙ c
Δ =  √122 –4 ∙ 4 . (–7)
Δ = √144 + 112
Δ = √256
Δ = 16
As raízes da equação serão:
x = –12 ± 16 8
x₁ = 0,5
x₂ = –28 8
Observação: neste caso não se considera a raiz positiva (+) que é x = 0,5m.
Alternativa: D

20)  (SARESP) Observe os números apresentados nos itens a seguir.
I. 1/√5
II. 4,121212 ...
III. π/2
IV. 0,11223344...
V. 17/8
Os números irracionais estão apresentados nos itens:
(A) I, II e III
(B) II, III e V
(C)II e V
(D)I, III e IV
Resolução:
Os números irracionais são aqueles que não podem ser representados por uma fração. Eles têm números decimais infinitos mas não forma uma dízima periódica.
Alternativa: D

21) (SARESP)  Dentre os números abaixo, indique aquele que pode ser chamado de Natural, Inteiro, Racional e Real:
(A) 4,1
(B) 14/7
(C) – 2
(D) √8
Resolução:
Nesse caso o único valor -2
Alternativa: B

22) (SARESP) A fração geratriz da dízima periódica 7,4343434... é:
(A) 736/99
(B) 743/99
(C) 736/9
(D) 43/9
Resolução:
Fração geratriz é aquela que quando dividimos seu numerador pelo denominador, o resultado será uma dízima periódica (número decimal periódico). Portanto, Basta saber realizar a conversão, ou seja fazer a divisão a seguir.   
7 . 43/99 = 736/99
7, 4343434 ...
Alternativa: A

23) (SARESP) A fração 8/9 é a geratriz da dízima periódica:
(A) 0,898989...
(B) 0,99999...
(C) 0,88888...
(D) 0,11111...
Resolução:
Quando a fração é dada e precisamos achar a dízima periódica, basta fazer a divisão da fração
9/9 = 0,88888...
Alternativa: C

24) (SARESP) A parte não periódica da dízima que tem como fração geratriz 37/45 é:
(A) 3
(B) 4
(C) 7
(D) 8
Resolução:
Nesse caso é preciso encontrar a dízima correspondente e dela reconhecer a parte não periódica. Ou seja:
37/45 = 0, 82222 ... Percebe-se que aparte não periódica é a que não se repete e nesse caso é o 8.
Alternativa: D

25) (SARESP) Observe os números abaixo.
I. 254,56565...
II. 6,4198476321...
III. − π
IV. √3
V. – 0,5
Os números racionais e os irracionais estão representados nos itens
(A) Racionais: I e V; Irracionais: II e IV
(B) Racionais: I, II e V; Irracionais: III e IV
(C)Racionais: I e V; Irracionais: II, III e IV
(D)Racionais: I e II; Irracionais: III, IV e V
Resolução:
Para optou por esta alternativa é necessário saber distinguir entre um número racional e um irracional.
- Os números irracionais são aqueles que não podem ser representados por uma fração. Eles têm números decimais infinitos mas não forma uma dízima periódica.
- Números racionais são todos os números que podem ser expressos em forma de fração.
Alternativa: C

26) (SARESP) Dentre as opções abaixo indique a que representa um número racional.
(A) √17¹
(B)√4⁴
(C)√10² + 3²
(D)√2² . 6
Resolução:
Números racionais são todos os números que podem ser expressos em forma de fração.
Alternativa: B

27) (SARESP) Observe a construção geométrica abaixo.
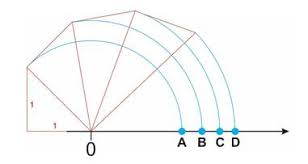Os pontos A, B, C e D correspondem, respectivamente, a:
(A)√2, √3, 2 e √5
(B) 1, √2, √3 e √5
(C)√5, 2 , √3 e √2
(D)√2, 2, 3 e 4
Resolução:
Basta identificar a hipotenusa dos triângulos retângulos como os segmentos correspondentes aos números indicados na reta real.
Alternativa: A

28) (SARESP) Observe a construção abaixo.
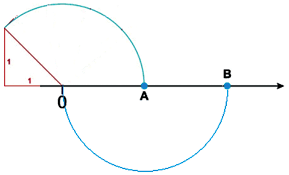Podemos afirmar que o ponto B indica a posição do número:
(A)√2
(B)√3
(C)2√2
(D)2√3
Resolução:
É necessário saber interpretar construções geométricas para a localização de números reais na reta.
Alternativa: C

29) (SARESP) A ONU estima que em 2030 a população mundial chegará a 8,6 bilhões de pessoas. A representação desse número em notação científica é:
(A) 8,6 . 10¹⁰
(B) 8, 6 . 10⁹
(C) 8,6 . 10⁸
(D) 8,6 . 10⁷
Resolução:
Nesse caso é necessário saber escrever 6,8 bilhões (8 600 000 000) e também saber as regras para números em notação científica.
Alternativa: B

30) (SARESP) Usando um microscópio eletrônico, um pesquisador mediu o diâmetro de uma partícula obtendo 3943,57 fentômetros de diâmetro. Observe o quadro com as unidades de medida menores que o milímetro.
Prefixos do Sistema Internacional de Medidas Prefixo
Nome              Símbolo (m)      10ⁿ        Equivalência numérica
milímetro        mm                     10⁻³     0,001
micrômetro    μm                      10⁻⁶      0,000 001
nanômetro      nm                     10⁻⁹      0,000 000 001
picômetro       pm                     10⁻¹²     0,000 000 000 001
fentômetro      fm                      10⁻¹⁵     0,000 000 000 000 001
A alternativa que mostra a medida do diâmetro, em metros, encontrado pelo pesquisador, representada na norma de escrita da notação científica, é:
(A) 3, 94357 . 10⁻¹²m
(B) 3,94357 . 10⁻¹⁴m
(C) 3943,57 . 10⁻¹⁵m
(D) 3,94357 . 10⁻¹⁸m
Resolução:
Basta utilizar a notação científica e fazer sua representação correta 3943, 57 fentômetros = 3, 94357 . 10³ . 10⁻¹⁵ m = 3, 94357. 10⁻¹² m
Alternativa: A

31)  (SARESP) Um ano-luz, em notação científica, corresponde a 9,461 x 1012 km, esse número em sua representação extensa é:
(A) 9.461.000.000
(B) 940.610.000.000
(C)9.461.000.000.000
(D)946.100.000.000.000
Resolução:
Nesse caso é necessário saber as regras para números em notação científica.
Alternativa: C

32) (SARESP) Observe os triângulos ABC e XYZ representados a seguir.
Podemos afirmar que esses triângulos:
(A) são semelhantes porque a medida do lado XY é o dobro da medida do lado AB.
(B) são semelhantes porque a medida do ângulo X é o dobro da medida do ângulo A.
(C) não são semelhantes porque não são dadas as medidas de todos os lados de cada triângulo.
(D) não são semelhantes porque as medidas dos ângulos dos triângulos não são iguais.
Resolução:
Triângulos congruentes todos os seus ângulos internos tem a mesma medida.
Alternativa: D

33) (SARESP) Observe a figura abaixo e as afirmações feitas sobre ela.
I. O trapézio TICOé isósceles
II.O trapézio NEMO é uma redução do trapézio TICO, pois ambos têm a mesma forma.
III. Os trapézios TICO e NEMO são semelhantes, pois são mantidos os paralelismos dos lados.
IV. O trapézio NEMO não é redução do trapézio TICO, pois o fator de redução não se mantém.
São verdadeiras apenas as afirmações:
(A) I e III.
(B) I e IV.
(C) II e III.
(D) II e IV.
Resolução:
O trapézio TICO é isósceles e a não semelhante, porque o fator de redução 1/3 das bases dos trapézios não se mantém para as alturas.
Alternativa: B

34) (SARESP) Péricles é um arquiteto e, num projeto que está desenvolvendo, deve ampliar um retângulo em 3,5 vezes. O retângulo original tem lados de 7cm e 5cm. Escolha o retângulo ampliado por Péricles.

Resolução:
Por esta alternativa é necessário saber identificar e utilizar o fator de ampliação, calculando o valor dos dois lados do retângulo: 7cm x 3,5 = 24,5cm e 5cm x 3,5 = 17,5cm.
Alternativa: A

35) (SARESP) A razão de proporcionalidade que deve ser usada para que, a partir do hexágono regular A, se obtenha o hexágono regular B é:
(A) 4,0
(B) 2,5
(C) 0,8
(D) 0,4
Resolução:
A razão de A por B é a divisão de A/B
A = 32
B = 80
A/B
32/80 = 0, 4
Alternativa: D

36) (SARESP) Na figura a seguir, observe os diferentes triângulos.
Considerando as medidas dos ângulos de cada triângulo, podemos afirmar que um par de triângulos semelhantes é:
(A) ABC e CHI.
(B) ECF e FCG.
(C) ECF e ABC.
(D) ACD e ECG.
Resolução:
Os triângulos semelhantes que têm como ângulos internos 60^o,30^o e 90^o
Alternativa: C

37) (SARESP) Na figura a seguir os triângulos ABC e ADE são semelhantes.
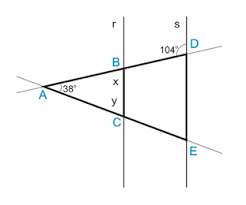As medidas x e y dos ângulos indicados são, respectivamente:
(A) 104⁰ e 76⁰
(B) 66⁰ e 104⁰
(C) 66⁰ e 76⁰
(D) 76⁰ e 66⁰
Resolução:
Analisando a imagem fornecida, é necessário saber que a soma dos ângulos internos de um triando é igual a 180º. Também é necessário lembrar a relação entre ângulos complementares e ângulos suplementares e realizar os cálculos de modo adequado:
Alternativa: D

38) (SARESP)  Observe os triângulos da figura.
A razão entre as áreas dos triângulos ABC e CDE é:
(A) 2
(B) 4
(C) 8
(D) 16
Resolução:
Basta calcular as áreas dos dois triângulos chegando corretamente e à razão entre suas áreas. Reconhecendo que ambos os triângulos, ABC e CDE são retângulos e isósceles e obteve as áreas:
AABC = (2x)²/2 = 2x²
ACDE = x2/2²
A razão entre elas R = AABC/ACDE
2x²/ x2/² = 4
Alternativa: B

39) (SARESP) Em uma construção um pedreiro transporta massa de cimento por uma rampa como a indicada abaixo.
A altura dessa construção, em metros, é:
(A) 3
(B) 3 √2
(C) √27
(D) 5
Resolução:
Aplicando o teorema de Pitágoras obteve:
x² = 6² – (3√3)2
x² = 36 – 27
x = 3m
Alternativa: A

40) (SARESP) Para a construção de um móvel, que deverá ficar encaixado no canto de um quarto, um marceneiro dispõe de uma placa retangular de madeira cujos lados medem 80 cm e 60 cm. Ele precisa cortar essa placa conforme o desenho abaixo.
A medida a ser usada para o corte do segmento AM, em centímetros, é
(A) 64
(B) 48
(C) 36
(D) 32
Resolução:
Basta calculado a medida da diagonal AC aplicando o teorema de Pitágoras:
d² = 60² + 80²
d = 100 e, em seguida, usando a relação b² = am, chamando a medida do segmento AM de m
60² = 100m
m = 36.
Alternativa: C

41) (SARESP) Determine a equação de 2^o grau, cuja soma de suas raízes é 1 e o produto das raízes é – 12.
(A) – x² + x - 12 = 0
(B) – x² – x + 12 = 0
(C) x² – x – 12 = 0
(D) x² – x + 12 = 0
Resolução:
Quando se multiplica todos os termos por (- 1): Se um dos números é x, o outro será 1 – x e o produto dos dois será dado por x (1 – x) = - 12.
Logo a equação será: x – x² + 12 = 0 ou x² – x – 12 = 0
Alternativa: C

42) (SARESP)  Pedro vai pintar uma parede cuja área é 18 m². O comprimento dessa parede é o dobro da altura. A equação que permite obtermos o comprimento (C) e a altura (h) da parede é:
(A) h² − 9 = 0 ou C² + 36 = 0
(B) h² − 9 = 0 ou C² − 9 = 0
(C) h²  − 9 = 0 ou C² + 9 = 0
(D) h² − 9 = 0 ou C² − 36 = 0
Resolução:
Uma das possibilidades de representação por uma equação é considerando que a área procurada é dada por C . h = 18 e que C = 2h, chega-se à equação 2h . h = 18 ou h²= 9.
A outra é a possibilidade de tomar h = 1⁄2 C, chegando à equação C . 1⁄2 C = 18 ou C² = 36.
Alternativa: D

43) (SARESP) As raízes da equação 4x² − 81 = 0 são:
(A) ± 81/4
(B) 81/4
(C) ± 9/2
(D) 9/2
Resolução:

Outra possibilidade por ser uma equação de 2^o grau, pode-se usar o procedimento da fatoração, usando a fórmula ou, “isolando” x.
Alternativa: C

44) (SARESP) Os valores de x que tornam a equação −x² + 6x − 5 = 0 verdadeira são:
(A) 1 e 5
(B) – 1 e – 5
(C) – 1 e 5
(D) 1 e – 5
Resolução:

a = -1
b = 6
c = -5
Aplicando Baskara teremos e as relações de Girard:
Soma = -b/a = 6
Produto = c/a =5
Alternativa: A

45) (SARESP) Sabendo que a área da figura abaixo é 48 cm², podemos afirmar que as medidas dos lados, em cm, são:
(A) 6 e 8
(B) 12 e 13
(C) 3 e 16
(D) 2 e 24
Resolução:
A área do retângulo é dada pelo produto dos lados, sabe calcular o produto de binômios e resolver corretamente uma equação de 2^o grau, uma vez que a solução é dada por:
(x – 2) (3x + 1) = 48
3x² – 5x – 50 = 0
Suas raízes são 5 e – 10/3. Como se trata das medidas dos lados de um retângulo, descarta-se a raiz negativa.
Assim sendo x = 6
3x + 1 = 3 . 5 +1 = 16
5 – 2 = 3
Alternativa: C

46) (SARESP) Pensei em um número positivo, calculei o seu dobro, somei 24 e obtive o quadrado do número que pensei. O número que pensei foi:
(A) 24
(B) 12
(C) 6
(D) 4
Resolução:

x₁ = 6
x₂ = −4
Observação: nesse caso o problema não pede ser um número negativo.

47) (SARESP) As tabelas abaixo mostram sequências de valores que podem ser proporcionais ou não. Analise cada uma delas e indique a alternativa correta.
(A) I é diretamente proporcional; II não é proporcional; III é inversamente proporcional.
(B) I não é proporcional; II é diretamente proporcional; III é inversamente proporcional.
(C) I não é proporcional; II é inversamente proporcional; III é diretamente proporcional.
(D) I é diretamente proporcional; II é inversamente proporcional; III não é proporcional.
Resolução:
Para que grandezas sejam inversamente proporcionais não basta uma aumentar e a outra diminuir, é preciso que o aumento e a diminuição estejam ligados por uma relação multiplicativa do tipo k x.
Alternativa: B
Observação: para que grandezas sejam inversamente proporcionais não basta uma aumentar e a outra diminuir, é preciso que o aumento e a diminuição estejam ligados por uma relação multiplicativa do tipo k . x.

48) (SARESP) Dentre as situações apresentadas a seguir, assinale aquela em que se tem uma relação de proporcionalidade inversa.
(A) Uma máquina embala 1.800 bombons por hora, 4 dessas máquinas embalam 1.800 bombons em 15 minutos.
(B) Para ir de sua casa ao estádio de futebol Vanderley demora 2 horas de ônibus, se for de metrô demora meia hora a menos.
(C) Para ir de uma cidade A até uma cidade B, usando seu carro, uma pessoa gastou R$ 120,00 de combustível, uma outra pessoa, também usando seu carro, gastou R$ 60,00
(D) A produção diária de pães de certa padaria é de 500 pães, em uma semana sua produção é de 3.500 pães.
Resolução:
Para que grandezas sejam inversamente proporcionais não basta uma aumentar e a outra diminuir, é preciso que o aumento e a diminuição estejam ligados por uma relação multiplicativa do tipo k x.
Alternativa: A
Observação: ou vice-versa

49) (SARESP) A empresa Aroma Perfumaria está armazenando sua produção de sabonetes em caixas. Sabe-se que grupos de 20 caixas do mesmo tipo pesam, em média, 60 kg. Se já têm em estoque 75 dessas caixas, a quantidade de quilos de sabonete armazenada é de:
(A) 245
(B) 235
(C) 225
(D) 215
Resolução:
Calculando quanto pesa cada caixa para chegar ao resultado, que 75 caixas correspondem a 3 grupos de 20 mais um grupo de 15 caixas, que 75 caixas correspondem a 4 grupos de 20 menos 5 caixas.
Alternativa: C

49) (SARESP) Uma caixa d’água, com um furo no fundo, está perdendo 1,7 litros de água a cada 3 horas. A quantidade de água, em litros, desperdiçada por esta caixa em 24 horas é:
(A) 12
(B) 13,4
(C) 13,44
(D) 13,6
Resolução:
Existe a relação de proporcionalidade direta que existe entre os elementos da situação porque quanto maior o tempo maior será o desperdícios de água, e nesse caso podemos aplicar regra de três simples.
1,7       3
x          24
3x = 1,7 . 24
3x = 40,8
x = 40,8/3
x = 13,6
Alternativa: D
Observação: para que grandezas sejam inversamente proporcionais não basta uma aumentar e a outra diminuir, é preciso que o aumento e a diminuição estejam ligados por uma relação multiplicativa do tipo k . x.

50) (SARESP) Observe as afirmativas:
(I) 3/4 é um número racional.
(II) 11/7 é um número irracional.
(III) 20⁄5 é um número natural.
(IV) 1/3 é um número inteiro.
São verdadeiras as afirmativas
(A) (I) e (II).
(B) (I) e (III).
(C) (III) e (IV).
(D) (II) e (III).
Resolução:
(I) 3/4  é um número racional;
VERDADEIRA - pois, todo número que possa ser escrito na forma de fração, em que o numerador e o denominador são números inteiros (com o denominador diferente de zero), é chamado de número racional.
(II) 11/7 é um número irracional;
FALSA – pois, o número apresentado, representa um número racional, e não um irracional, que é definido da seguinte maneira: “número irracional é todo Real, que não pode ser escrito como uma fração com numerador e
denominador, compostos por números inteiros”.
(III) 20/5 é um número natural;
VERDADEIRA – pois, apesar de ser representado em forma de uma fração imprópria, é equivalente ao número natural 4.
(IV) 1/3  é um número inteiro.
FALSA – pois, apesar do numerador e denominador serem números inteiros, os quocientes entre eles não resultam em um número inteiro, portanto trata-se de um número racional, com dízima periódica constante (0,3333...).
Alternativa: B

51) (SARESP) Dentre as alternativas a seguir, a correta é
(A) A divisão entre dois números naturais, diferentes de zero, sempre resultará em número natural.
(B) A divisão entre dois números inteiros diferentes de zero, sempre resultará em um número inteiro.
(C) A divisão entre dois números racionais, sempre resultará em um número racional.
(D) A divisão entre dois números irracionais, sempre resultará em um número irracional.
Resolução:
O conjunto dos Números Naturais é fechado somente para as operações de adição e multiplicação.
O conjunto dos Números Inteiros é fechado somente para as operações de adição, subtração e multiplicação.O conjunto dos Números Racionais é fechado para as quatro operações, para a divisão (Q∗).
O conjunto dos Números Irracionais não é fechado para as quatro operações.
Sendo assim, a alternativa que atende a um dos tópicos acima descritos na:
Alternativa C

52) (SARESP) A fração geratriz que representa 5,3333... é
(A) 33/90
(B) 3/9
(C) 53/9
(D) 16/3
Resolução:
Fração geratriz é aquela que quando dividimos seu numerador pelo denominador, o resultado será uma dízima periódica (número decimal periódico). Portanto, Basta saber realizar a conversão, ou seja fazer a divisão a seguir.  
16/3 = 5,3333...
Alternativa: D

53) (SARESP) Se x = 0,22222... e y = 0,11111..., as frações geratrizes de x e y são
(A) 1/3 e 1/1
(B) 2/9 e 1/9
(C) 2/1 e 1/2
(D) 2/10 e 1/10
Resolução:
Fração geratriz é aquela que quando dividimos seu numerador pelo denominador, o resultado será uma dízima periódica (número decimal periódico). Portanto, Basta saber realizar a conversão, ou seja fazer a divisão a seguir.  
2/9 = 0,2222...
x = 0,2222...
y = 0,1111...
1/9 = 0,1111...
Alternativa: B

54) (SARESP) As frações geratrizes das dízimas periódicas 3,59999... e 3,595959... são
(A) 324/90 e 356/99
(B) 35/9 e 35/99
(C) 36/10⁄ e 360/100
(D) 3/6 e 3/59
Resolução:
Fração geratriz é aquela que quando dividimos seu numerador pelo denominador, o resultado será uma dízima periódica (número decimal periódico). Portanto, Basta saber realizar a conversão, ou seja fazer a divisão a seguir.  
324/90 = 0,2222...
359/99 = 3,59595...
Alternativa: A

55) (SARESP) Na tabela seguinte, apresentam-se os três primeiros termos de uma sequência de números em que cada termo, a exceção do primeiro termo é um décimo do anterior.
1º Turno        2º Turno        3º Turno        ...         10º Turno
0,2                  0,02                 0,002                       0,0000000002
Em notação científica o décimo termo da sequência, será
(A) 2 ∙ 10^-10
(B) 2 ∙ 10¹⁰
(C) 2 ∙ 10^-3
(D) 2 ∙ 10^-2
Resolução:
Apenas escrever um valor em notação científica.
Alternativa: A

56) (SARESP) A distância entre o Sol e a Lua é de aproximadamente 149.600.000 km. A representação deste número em notação científica equivale a
(A) 1,496 ∙ 10^-9
(B) 1,496 ∙ 10^-8
(C) 1,496 ∙ 10⁸
(D) 1,496 ∙ 10⁹
Resolução:
Apenas escrever um valor em notação científica.
Alternativa: C

57) (SARESP) Observe a figura a seguir
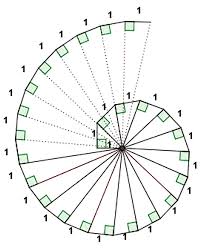A alternativa VERDADEIRA é
(A) Todas as medidas dos segmentos da figura pertencem ao conjunto dos números Naturais.
(B) Existem segmentos cujas medidas não pertencem ao conjunto dos números Reais.
(C) Existem segmentos cujas medidas pertencem ao conjunto dos números irracionais e outros ao conjunto dos números Naturais.
(D) Todas as medidas dos segmentos da figura pertencem ao conjunto dos números racionais.
Resolução:
Encontramos medidas de segmentos pertencentes ao conjunto dos números irracionais e outros ao conjunto dos números naturais
Alternativa: C

59) (SARESP) Na construção geométrica a seguir
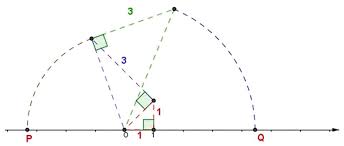Os pontos P e Q, representam os números reais:
(A) - 3 e 4
(B) √-11 e 20
(C) -3,5 e 4,5
(D) -√11 e √20
Resolução:
Alternativa: D

59) (SARESP) Dadas as figuras a seguir
As medidas dos lados do quadrado AOCB, pertencem ao conjunto dos números naturais. Utilizando o diagrama que representa os conjuntos numéricos, a diagonal OB do quadrado e o arco AC, pertencem respectivamente, ao conjunto dos números:
(A) Naturais e Naturais.
(B) Irracionais e Irracionais.
(C) Racionais e Racionais.
(D) Naturais e Irracionais.
Resolução:
Alternativa: B

60) (SARESP)
(A) 50.
(B) 46.
(C) 18.
(D) 16.
Resolução:
Uso do Teorema de Tales os lados HI e GF são paralelos, então:
EI/ HG = EH/IF
10/6 = 30/y
10y = 180
y = 180/10
y = 18
Alternativa: C

61) (SARESP) Observe as afirmativas:
(I) 3/4 é um número racional.
(II) 11/7 é um número irracional.
(III) 20/5 é um número natural.
(IV) 1/3⁄ é um número inteiro.
São verdadeiras as afirmativas
(A) (I) e (II).
(B) (I) e (III).
(C) (III) e (IV).
(D) (II) e (III).
Resolução:
(I) 3/4 é um número racional;
VERDADEIRA - pois, todo número que possa ser escrito na forma de fração, em que o numerador e o denominador são números inteiros (com o denominador diferente de zero), é chamado de número racional.
(II) 11/7⁄ é um número irracional;
FALSA – pois, o número apresentado, representa um número racional, e não um irracional, que é definido da seguinte maneira: “número irracional é todo Real, que não pode ser escrito como uma fração com numerador e denominador, compostos por números inteiros”.
(III) 20/5⁄ é um número natural;
VERDADEIRA – pois, apesar de ser representado em forma de uma fração imprópria, é equivalente ao número natural 4.
(IV) 1/3 é um número inteiro.
FALSA – pois, apesar do numerador e denominador serem números inteiros, os quocientes entre eles não resultam em um número inteiro, portanto trata-se de um número racional, com dízima periódica constante (0,3333...).
Alternativa B

62) (SARESP) Dentre as alternativas a seguir, a correta é
(A) A divisão entre dois números naturais, diferentes de zero, sempre resultará em número natural.
(B) A divisão entre dois números inteiros diferentes de zero, sempre resultará em um número inteiro.
(C) A divisão entre dois números racionais, sempre resultará em um número racional.
(D) A divisão entre dois números irracionais, sempre resultará em um número irracional.
Resolução:

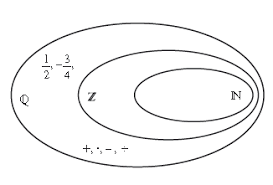
“Dizemos que um conjunto numérico C é fechado, se, e somente se, para todos os elementos de C, dois a dois, o resultado da operação é um elemento pertencente a C.”
Então podemos destacar que:
O conjunto dos Números Naturais é fechado somente para as operações de adição e multiplicação.
O conjunto dos Números Inteiros é fechado somente para as operações de adição, subtração e multiplicação.
O conjunto dos Números Racionais é fechado para as quatro operações, para a divisão (Q∗).
O conjunto dos Números Irracionais não é fechado para as quatro operações.
Sabendo-se disto, a alternativa que atende a um dos tópicos acima descritos, é a alternativa C, destacaremos a seguir, o motivo que sustenta tal proposição, a relação de inclusão do conjunto dos números racionais.
Alternativa: C

63) (SARESP) Ana precisa digitar a fração 8/10 na calculadora, mas não consegue. Ela poderá substituir a fração por outras representações. Indique a alternativa que apresenta duas possibilidades que Ana poderá usar:
(A) 0,8 e 80%
(B) 0,08 e 80%
(C) 0,8 e 8%
(D) 0,08 e 8%
Resolução:
A identificou que 8/10 = 0,8. Para transforma em porcentagem basta multiplicação o resultado da divisão por 100. 0,8 . 100 = 80
Alternativa: A

64) (SARESP) Observe os números representados por letras na reta numérica a seguir:
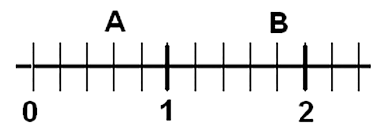(A) 0,3 e 1,4
(B) 0,6 e 1/8
(C) 6/10 e 18/10
(D) 1/3 e 1,9
Resolução:
A unidade de medida é de 2mm e identifica corretamente os números representados pelas letras.
Alternativa: C

65) (SARESP) Observe os números que aparecem na reta abaixo.
O número indicado pela seta é
(A) 0,9.               
(B) 0,54.                
(C) 0,8.                
(D) 0,55
Resolução:
A reta está graduada em 0,01
Alternativa: B

66) (SARESP) Ao resolver corretamente a expressão -1 - (-5).(-3) + (-4).3 : (-4), o resultado é
(A) -13.                 
(B) -2.               
(C) 0.               
(D) 30.
Resolução:
-1 - (-5) . (-3) + (-4) . 3 : (-4)
-1 - (-5) . (-3) + (-4) . 3 : (-4)
-1 +5 . -3 -4 . 3 : -4
-1 – 15 -12 : -4
-16 + 13
-13
Alternativa: A

67) (SARESP) Pedro e João jogaram uma partida de bolinhas de gude. No final, João tinha 20 bolinhas, que correspondiam a 8 bolinhas a mais que Pedro. João e Pedro tinham juntos
(A) 28 bolinhas.
(B) 32 bolinhas.
(C) 40 bolinhas.
(D) 48 bolinhas.
Resolução:
João tem 20 bolinhas e ele tem 8 a mais que Pedro.
Pedro tem 8 a menos que João, fazendo 20 -8 = 12
Pedro tem 12 bolinhas, somando os dois fica 20 + 23 = 32
Alternativa: B

68) (SARESP) Cíntia conduzia um carrinho de brinquedo por controle remoto em linha reta. Ela anotou em uma tabela os metros que o carrinho andava cada vez que ela acionava o controle. Escreveu valores positivos para as idas e negativos para as vindas.
Após Cíntia acionar o controle pela sexta vez, a distância entre ela e o carrinho era de
(A) -11 m.                   
(B) 11 m.                   
(C) -27 m.                     
(D) 27 m.
Resolução:
1º: 17
2º: 17 -8 = 9
3º: 9 + 13 = 22
4º: 22 + 4 = 26
5º: 26 – 22 = 4
1º: 4 + 7 = 11
Alternativa: B

69) (SARESP) A fração 3/100 corresponde ao número decimal
(A) 0,003.               
(B) 0,3.                 
(C) 0,03.                
(D) 0,0003.
Resolução:
Basta dividir o numerado pelo denominador
3/100 = 0,03
Alternativa: C

70) (SARESP) Nas figuras abaixo, as áreas escuras são partes tiradas do inteiro. A parte escura que equivale aos 3/5 tirados do inteiro é
(A) 
(B) 
(C) 
(D) 

Resolução:
Alternativa: C   

71) (SARESP) Observe as figuras:
Pedrinho e José fizeram uma aposta para ver quem comia mais pedaços de pizza. Pediram duas pizzas de igual tamanho. Pedrinho dividiu a sua em oito pedaços iguais e comeu seis. José dividiu a sua em doze pedaços iguais e comeu nove.
Então,
(A) Pedrinho e José comeram a mesma quantidade de pizza.
(B) José comeu o dobro do que Pedrinho comeu.
(C) Pedrinho comeu o triplo do que José comeu.
(D) José comeu a metade do que Pedrinho comeu.
Resolução:
Observando as figuras percebemos que as pizzas tem o mesmo tamanho, elas apenas foram divididas em pedações de tamanho diferentes
Alternativa: A

72) (SARESP) O número decimal que é decomposto em 5 + 0,06 + 0,002 é
(A) 5,62.               
(B) 5,602.               
(C) 5,206.                
(D) 5,062.
Resolução:
5,000
0,060
0,002
---------
5,062
Alternativa: D

73) (SARESP) O número irracional 7 está compreendido entre os números
(A) 2 e 3          
(B) 13 e 15         
(C) 3 e 4          
(D) 6 e 8
Resolução:
√7 = 2,6457
Alternativa: A

74) (SARESP) Distribuímos 120 cadernos entre as 20 crianças da 1ª série de uma escola. O número de cadernos que cada criança recebeu corresponde a que porcentagem do total de cadernos?
(A) 5%                   
(B) 10%                   
(C) 15%                   
(D) 20%
Resolução:
Primeiro vamos calcular quantos cadernos cada um recebeu
120/20 = 6
Achado quanto é 6% de 120
120      100
6          x
120x = 6 . 100
120x = 600
x = 600/120
x = 5
Alternativa: A

75) (SARESP)  O desenho de um colégio foi feito na seguinte escala: cada 4cm equivalem a 5m. A representação ficou com 10 m de altura. Qual é a altura real, em metros, do colégio?
(A) 2,0.                    
(B) 12,5.                   
(C) 50,0.                 
(D) 125,0.
Resolução:
Usando regra de três simples
4          5
10        x
4x = 5 . 10
4x = 50
x = 50/4
x = 12,5
Alternativa: B

76) (SARESP) Dada a expressão:  
Sendo a = 1, b = -7 e c = 10, o valor numérico de x é
(A) -5.                    
(B) -2.                   
(C) 2.                   
(D) 5.
Resolução:
Aplicando a fórmula dada na questão
-(-7) + √(-7)2 – 4 . 1 . 10 / 2 . 1
7 +√49 – 40 / 2
7 + √9 / 2
7 + 3 / 2
10 / 25
5
Alternativa: D

77) (SARESP) Lucas comprou 3 canetas e 2 lápis, pagando R$ 7,20. Danilo comprou 2 canetas e 1 lápis, pagando R$ 4,40. O sistema de equações do 1º grau que melhor representa a situação é
Resolução:
Analisando as alternativas observa-se que o primeiro sintema representa  um enunciado do problema
Caneta = x
Lápis = y
3x + 2y = 7,20
Alternativa: A

78) (SARESP) Observe o gráfico abaixo.
O gráfico representa o sistema
Resolução:
O ponto está nas coordenadas x = 2 e y = 1
x  =2
y = 1
substituindo o x por 2
y = -2x + 5
y = -2 . 2 = 5
y = -4 + 5
y = 1 (verdadeiro
Substituindo o y por 1
y = -2x + 5
1 = -2x + 5
1 -5 = 2x
4 = 2x
4/2 =x
x = 2
Alternativa: B

79) (SARESP) Resolva a expressão: 20 – √4 + 3² x 3 – 2 ÷ 2
Resolução:
20 – √4 + 3² x 3 – 2 ÷ 2
20 – 2 + 9 x 3 – 2 ÷ 2
20 – 2 + 27 – 1
18 + 27 – 1
45 – 1
44

80) (SARESP) Resolva a expressão: 10² x [20 ÷ (2 + 2) – 4]
Resolução:
10² x [20 ÷ (2 + 2) – 4]
10² x [20 ÷ 4 – 4]
10² x [5 – 4]
10² x 1
100 x 1
100

81) (Avaliação da Aprendizagem em Processo – AAP) Em uma campanha de vacinação, os 450 frascos de vacina permitiram vacinar 1575 crianças. A secretária de saúde do município informou que receberão mais 200 frascos. Neste caso, quantas crianças aproximadamente poderiam ser vacinadas com este novo lote?​
(A) 3545 crianças
(B) 900 crianças
(C) 700 crianças
(D) 650 crianças
Resolução:
450 -- 1575
200 --- x
450x = 200 . 1574
200x = 315 000
x 0 315000 / 450
x = 700
Alternativa: C

82) (Avaliação da Aprendizagem em Processo – AAP) Um livro foi publicado por uma editora contendo 120 páginas com 20 linhas escritas em cada página. Para atrair mais leitores, diminuindo o preço, a editora começou a confeccionar o livro com 24 linhas por páginas. Neste caso, quantas páginas terá o livro?
(A) 100
(B) 140
(C) 144
(D) 164
Resolução:
120 --- 20
X   ---- 24
Invertendo: grandeza inversamente proporcional
120 --- 24
X  ---- 20
24x = 120 . 20
24x = 240
x = 240 / 24
x = 100
Alternativa: A

83) (Avaliação da Aprendizagem em Processo – AAP) Em uma pista de corrida de kart, um dos veículos, correndo a 12 m/s, levou 80 segundos para dar uma volta na pista. Outro veículo que partiu junto ao primeiro e correu com velocidade de 10 m/s, após dar também uma volta na pista, quanto tempo chegou depois?
(A) 13 segundos
(B) 16 segundos
(C) 67 segundos
(D) 96 segundos
Resolução:
Assim, x = 96 segundos, o que equivale a 16 segundos depois do veículo mais rápido..
Alternativa: B

85) (SARESP) 

 

 

 

 

 

 

 

 

 

 

Resolução:
O ponto está nas coordenadas x = 2 e y = 1
x  =2
y = 1
substituindo o x por 2
y = -2x + 5
y = -2 . 2 = 5
y = -4 + 5
y = 1 (verdadeiro
Substituindo o y por 1
y = -2x + 5
1 = -2x + 5
1 -5 = 2x
4 = 2x
4/2 =x
x = 2
Alternativa: B