PP-M-2ª-2ºBIM-2023

Professor Diminoi
PROVA PAULISTA - MATEMÁICA - 2º BIM - 2ª SÉRIE EM/2023

01) (Prova Paulista – 1ª Serie EM)  Quando o Sol se encontra a 60° acima do horizonte, um prédio projeta sua sombra no chão com o comprimento de 20 m. Assim, a altura do prédio será de:
(A) 40 m
(B) 20√3 m
(C) 10√3 m
(D) 10 m
(E) 20√3 / 3m

 02) (Prova Paulista – 1ª Serie EM)  Uma pessoa de 1,70m de altura observa o pássaro no topo de uma árvore formando um ângulo de 30° com a horizontal, como mostra a figura.
Sabendo que ele está a 10m de distância da árvore, determine a altura da árvore.
(A) 2,20 m
(B) 5,80 m
(C) 7,50 m
(D) 8,70 m
(E) 10,40 m

03) (Prova Paulista – 1ª Serie EM)  Das alternativas abaixo, assinale a resposta que corretamente representa o valor do seno de 300°.
(A) √2 / 2, porque seno 300º = sem 45º
(B) 1 / 2, porque seno 300º =  - sem 305º
(C) 1 / 2, porque seno 300º =  sem 305º
(D) - √3/ 2, porque seno 300º =  - sem 60º
(E) √3/ 2, porque seno 300º =  sem 60º

04) (Prova Paulista – 1ª Serie EM)  A professora Sandra pediu a seus alunos que verificassem se o sinal da tangente 350° é positivo ou negativo, justificando a resposta. Das respostas dadas, qual foi a correta?
(A) O sinal da tangente é negativo porque 350° está no terceiro quadrante.
(B) O sinal da tangente é positivo porque 350° está no terceiro quadrante.
(C) O sinal da tangente é negativo porque 350° está no primeiro quadrante.
(D) O sinal da tangente é positivo porque 350° está no quarto quadrante.
(E) O sinal da tangente é negativo porque 350° está no quarto quadrante.

05) (Prova Paulista – 1ª Serie EM)  Dada a função abaixo:
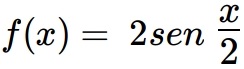Podemos afirmar que esta função possui
(A) amplitude 1 e perˊıodo π.
(B) amplitude 1 e perˊıodo 2 π.
(C) amplitude 2 e perˊıodo 2 π.
(D) amplitude 2 e perˊıodo 4 π.
(E) amplitude 4 e perˊıodo 2 π.

06) (Prova Paulista – 1ª Serie EM)  Analisando o gráfico da função trigonométrica abaixo:
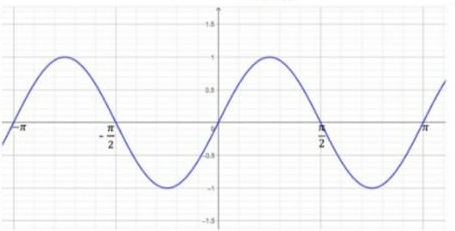A função representada pelo gráfico é descrita por:
(A) f(x) = sen (x)
(B) f(x) = cos (x)
(C) f(x) = tg (x)
(D) f(x) = sen(2x)
(E) f(x) = cos (2x)

07) (Prova Paulista – 1ª Serie EM)  Analisando o gráfico da função f(x)= 3 cos x, assinale a alternativa que representa, respectivamente, amplitude e período dessa função:
(A) Amplitude = 3 e Período = 2 π
(B) Amplitude = 3 e Período = 4 π
(C) Amplitude = 6 e Período = 2 π
(D) Amplitude = 6 e Período = 4 π
(E) Amplitude = 3 e Período = π

08) (Prova Paulista – 1ª Serie EM)  Assinale a alternativa que representa a função do gráfico
(A) f(x) sem 1/2x
(B) f(x) = cos 1/2x
(C) f(x) = cos x
(D) f(x) = sem x
(E) f(x) = cos 2x

09) (Prova Paulista – 1ª Serie EM)  A área, em metros quadrados, do polígono ABCDE representado na figura a seguir é:
(A) 19√5
(B) 29
(C) 32,5
(D) 19 + √5
(E) 43

10) (Prova Paulista – 1ª Serie EM)  Na figura, temos um círculo com raio de 5 cm e que corresponde a mesma altura do triângulo.
A área da região azul em cm² será de:
(A) 25(1 –x)
(B) 24(4π -1)
(C) 25(1 - 4π)
(D) 25(π – 2)
(E) 25(π – 1)

11) (Prova Paulista – 1ª Serie EM)  Os números de faces, vértices e arestas de um prisma de base hexagonal são, respectivamente
(A) 8, 18 e 12.
(B) 12, 8 e 18
(C) 8, 12 e 18
(D) 12, 18 e 8
(E) 18, 12 e

12) (Prova Paulista – 1ª Serie EM)  A professora de Manoel pediu para que ele preenchesse uma tabela com o número de vértices, faces e arestas de cinco poliedros de sua preferência. Então, ele montou a seguinte tabela:
Ao corrigir a tabela, a professora notou que em duas linhas havia um erro, e que em todas as linhas o número de faces estava correto. A fim de ajudar Manoel, a professora recordou com ele a relação de Euler que estabelece uma relação entre número de vértices (V), de arestas (A) e de faces (F), descrita por V + F = A + 2. Com isso, Manoel verificou corretamente que havia erro apenas nas linhas
(A) do cubo e do prisma hexagonal
(B) do cubo e da pirâmide hexagonal
(C) do paralelepípedo e da pirâmide quadrangular
(D) do paralelepípedo e da pirâmide hexagonal
(E) da pirâmide hexagonal e do prisma hexagona

13) (Prova Paulista – 1ª Serie EM)  Considere um poliedro regular com 8 vértices, 6 faces, 12 arestas. Esse poliedro pode ser um(a):
(A) cubo.
(B) tetraedro
(C) pirâmide de base quadrada.
(D) prisma de base triangular.
(E) octaedro.

14) (Prova Paulista – 1ª Serie EM)  Um poliedro convexo possui 16 faces e 18 vértices. Qual é o número de arestas desse poliedro ?
(A) 18
(B) 20
(C) 32
(D) 34
(E)36

15) (Prova Paulista – 1ª Serie EM)  Para presentear alguns amigos, Joana irá confeccionar algumas caixas com formato de prisma de base quadrada, onde colocará a lembrança que irá dar. Usará nessas embalagens, papelão que é comercializado por m².
As dimensões da caixa se encontram na figura. Joana fará 20 caixas, quantos m² de papelão, no mínimo, irá precisar?
(A) 1600
(B) 320
(C) 240
(D) 3,2
(E) 0,24

16) (Prova Paulista – 1ª Serie EM)  A área da base de um bloco retangular é de 100 cm² e o seu volume é de 550 cm³. Qual a altura desse bloco ?
(A) 650 m
(B) 450 m
(C) 65 m
(D) 55 m
(E) 5,5 m

17) (Prova Paulista – 1ª Serie EM)  Um cubo possui a soma das medidas de suas arestas igual a 36 cm. Qual o volume desse cubo?
(A) 27 cm²
(B) 9 cm²
(C) 216 cm²
(D) 243 cm²
(E) 20,45 cm²

18) (Prova Paulista – 1ª Serie EM)  Uma fábrica produz velas em formato de pirâmides de base quadrada medindo 8cm de lado e 12 cm de altura.
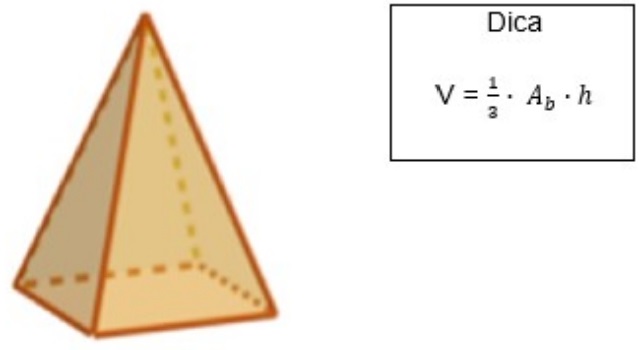Determine o volume, em centímetros cúbicos de parafina, que é utilizado para fabricar cada vela
(A) 32
(B) 64
(C) 96
(D) 128
(E) 256

19) (Prova Paulista – 1ª Serie EM) Uma industria produz latas de alumínio no format cilíndrico reto conforme as medidas dadas na figura abaixo.
Determine a área total dessa lata de alumínio. Considere 𝝅 = 3,14.
(A) 628 cm²
(B) 549,5 cm²
(C) 533,8 cm²
(D) 307 cm²
(E) 200 cm²

20) (Prova Paulista – 1ª Serie EM)  O reservatório de água do bairro, onde Isaac mora, possui um formato cilíndrico, com 5 metros de altura e 4 metros de diâmetro. Qual a capacidade máxima desse reservatório? Considere: π = 3, 14 e lembre-se que 1m³ = 1000 litros.
(A) 12 560 litros
(B) 20 000 litros
(C) 62 800 litros
(D) 80 000 litros
(E) 251 200 litros

GABARITO
01B – 02C – 03D – 04E – 05D – 06D – 07A – 08E – 09B – 10E – 11C – 12C – 13A – 14C – 15D – 16E – 17A – 18E – 19A – 20C.