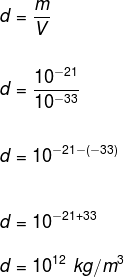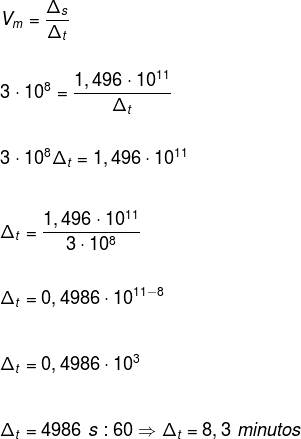NOTACAO CIENTIFICA 1

Professor Diminoi
MATEMATICA
A notação científica é uma ferramenta bastante utilizada não só na Matemática, mas também na Física e Química. Ela nos permite escrever e operar números que, quando escritos em sua forma original, exigem grande paciência e esforço, já que, ou são números muito grandes, ou muito pequenos. Imagine, por exemplo, você escrevendo a distância entre o planeta Terra e o Sol em quilômetros ou escrevendo a carga de um próton em coulomb.
Ou seja, é uma maneira de escrever um número muito grande ou muito pequeno de modo a facilitar sua multiplicação, divisão, soma ou subtração.

Exemplos
A massa de um elétron é de cerca de 0.000 000 000 000 000 000 000 000 000 000 910 938 22 kg.
Escrito em notação científica =  9,109 382 2.10^-31kg.
- A massa da Terra é de cerca de 5 973 600 000 000 000 000 000 000 kg.

Escrito em notação científica = 5,9736 . 10²⁴kg.
- A circunferência da Terra é de aproximadamente 40 000 000 m. Escrito em notação científica =  4 . 10⁷ m.
Em notação de engenharia, é de 40 .10⁶ m.

No estilo de representação do SI =  40 Mm (40 megametro).
- A carga elementar do próton ou elétron é cerda de 0,00000000000000000016C
Escrito em notação científica = 1,6 . 10^-19C

Observação: quando usa-se Notação Científica, o “ideal” e deixar apenas uma  casa antes da vírgula e essa casa deve ser diferente de zero.
Se o numero aumente o expoente da potência diminoi.
Se o número diminoi o expoente da potência aumenta.

Exemplos:
a) 238 . 10⁷= 2,38 . 10⁹

b) 0,238 . 10⁷= 2,38 . 10⁶

c) 238 . 10^-7= 2,38 . 10^-5

d) 0,238 . 10^-7= 2,38 . 10^-8

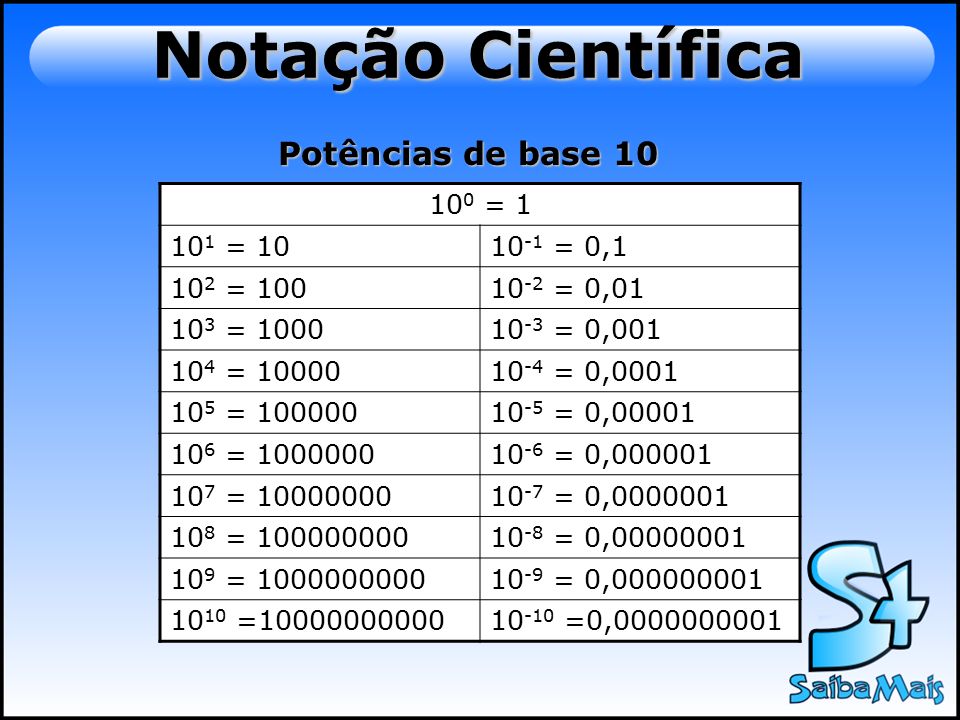
Também podemos representar as potências de base 10 de expoentes negativos.
A visualização será a seguinte:

10^-1 = 0,1

10^-2 = 10 / 10 = 0,01

10^-3 = 10 / 10 / 10 = 0,001

10^-4 = 10 / 10 / 10 / 10 = 0,0001

10^-5 = 10 / 10 / 10 / 10 / 10 = 0,00001


Exercícios de fixação 

01) Escreva os valores em notação científica (resolvidos)

a) 200 = 2 . 10²

d) 200000 = 2 . 10⁵

c) 200 000 000 = 2 . 10⁸

d) 200 000 000 000 000 000 = 2 . 10¹⁷

e) 1 200 000 000 000 = 1,2 . 10¹²

f) 0,02 = 2 . 10^-2

g) 0,002 = 2 . 10^-3

h) 0,000 000 002 = 2 . 10^-9

i) 0,00000000000000000016 = 1,6 . 10^-19

Multiplicação com Notação Científica
Observação:
- Multiplica-se os valores de base dez.
- Soma-se ou subtrai os expoentes.

02) Efetue as multiplicações

a)10². 3.10² = 6 . 10⁴

b)6.10⁵.12.10⁹ = 72 . 10¹⁴ = 7,2 . 10¹⁵

c)10². 3.10^-2= 24 . 10⁰ = 24 . 1  =  24

d)10⁹. 2.10⁹= 18 . 10⁹ . 10⁹ = 18 . 10¹⁸  =  1,8 . 10¹⁹

e)109 . 2.10¹³=10 . 10⁹ . 10¹³ = 10 . 10²²

f)10⁹. 2.10^-4. 0,5.10³= 9 . 10⁹ . 10^-4 . 10³ = 9 . 10¹² . 10^-4 = 19 . 10⁸

g)10⁹. 2 . 10⁵. 12,5.10^-6 = 225 . 10⁹ . 10⁵ . 10^-6 = 225 .10¹⁴ . 10^-6 = 225 .10⁸ = 2,25 . 10¹⁰

h)10^-9. 2 . 10^-9. 12 . 10⁴ = 360 . 10^-9 . 10^-9 . 10⁴ = 360 . 10^-18 .  10⁴  = 360 . 10^-14  = 3,6 . 10^-12

 
Divisão com Notação Científica

No Numerado e no Denominador
- Multiplica-se os valores que não tem base dez (se for o caso)
- Divide-se os valores que não tem base dez (se for o caso)
- Soma-se ou subtrai os expoentes.
- A base dez que esta dividindo passa multiplicando trocando o sinal de expoente (- passar para +) e (+ passa para -)
- Soma-se ou subtrai os expoentes.

03) Efetue as divisões.

a) 6 . 10⁸/ 3 .10³= 3 . 10⁸ / 10³ =    3 .10⁸ . 10^-3    =  3 .10⁵

b) 9 .10⁸/ 3 . 10^-3= 3 . 10⁸ / 10^-3 =   3 . 10⁸ . 10³  = 3 . 10¹¹

c) 9 . 10⁸/ 2 . 10⁵= 4,5 . 10⁸ / 10⁵  =   4,5 . 10⁸ . 10^-5  =  4,5 . 10³

d)10⁸/ 2.10⁸= 12,5.10⁸ / 10⁸  = 12,5 . 10⁸.10^-8  =  12,5 . 10⁰  = 12,5 . 1 =  12,5

e)10⁸/ 18.10^-3.0,5. 0⁸= 9.10⁸ /9.10^-3 .10⁸  =  10⁸ / 10^-3.10⁸  =  10⁸ / 10⁵  = 10⁸.10^-5 = 10³

f) 2 . 10^-3/ 20 . 10³= 0,5 . 10^-3 / 10³  =  0,5 . 10^-3 . 10³  =   0,5 .10⁰  → 0,5 . 1  =  0,5

g) 99 . 10^-8/ 99 . 10^-8= 10^-8 / 10^-8  =   10^-8 . 10⁸  =  10⁰  =  1


A adição na Notação Científica
Nesses casos, podemos somar os coeficientes e conservar a potência de base dez.

Fórmula Geral para adição na notação científica
(x . 10^a) + ( y . 10^a) = (x + y) . 10^a

Observação: é necessário deixar os expoentes com os mesmos valores.

Exemplo: 
1,28 . 10⁸ + 4 . 10⁵

1º passo: igualar os expoentes 1280. 10⁵ . 4.10⁵

2º passo: somar ou subtrair as bases diferentes de dez =  (1280 + 4 ) . 10⁵ = 1284 . 10⁵

3º paso deixar de modo ideal  =  1,284 . 10⁸


Exemplo: Efetue a adição das notações científicas abaixo:

a) 1,2 . 10 ²+ 11,5 . 10² =  (1, 2 + 11. 5) . 10²=  12,7 . 10²  =  1,27.10³

b) 0,23 . 10^-3 + 0,4 . 10^-3 =  (0,23 + 0,4) . 10^-3 =  0,63 . 10^-3 =  6,3.10^-4

c) 200 + 3,5 . 10²  = 2 . 10² + 3,5 . 10²=  (2 + 3,5) . 10²  =  5,5 . 10² 

Nesse exemplo, tivemos que transformar 200 para 2. Ao fazer isso, obtemos a mesma ordem de grandeza para as duas notações científicas.

 
A subtração na Notação Científica

Subtraímos os coeficientes na notação cientifica quando as ordens de grandeza da base dez são iguais.


Fórmula Geral para subtração na notação científica

(x . 10^a) – ( y . 10^a) = (x – y) . 10^a

Exemplo: Obtenha os resultados das subtrações abaixo:

a) 34,567 . 10³– 5,6 . 10³= (34,567 – 5,6) . 10³  =  28,967 . 10³  =  2,8967 . 10⁴

b) 1,14 . 10^-2 – 0,26 . 10^-2  = (1,14 – 0.26) . 10^-2=  0,88 . 10^-2  =  8,8 . 10^-3

c) 25,4 . 10² – 12,3 . 10³ = 25,4 . 10² – 123 . 10² =  (25,4 – 123) . 10²  =  – 97,6 . 10²  =  – 9,76 . 10³ 

Tivemos que transformar 12,3 para 123 pois a ordem de grandeza escolhida para a base dez foi o número 2.

 
ALGARISMO SIGNIFICATIVO
Os algarismos significativos são os algarismos que têm importância na exatidão de um número, por exemplo, o número 2,67 tem três algarismos significativos. 
Se expressarmos o número como 2,6700, entretanto, temos cinco algarismos significativos, pois os zeros à direita dão maior exatidão para o número.

Os exemplos abaixo têm 4 algarismos significativos:

Algarismos Duvidosos
Ao realizar a medição de algum objeto, nunca teremos a medida exata do objeto, utilizando uma régua, por mais precisa que seja. Isso porquê o último algarismo dessa medição, será duvidoso.
Uma régua comum tem divisões de centímetros e milímetros. Ao medir um lápis, por exemplo, nota-se que o comprimento dele tem 13,5 cm, pois aparentemente ele fica em cima dessa medida.
Porém não podemos ter certeza quanto ao algarismo 5 desse número. Poderia ser 13,49 ou 13,51. Então este último algarismo é chamado de duvidoso, e representamos com um traço em cima: 13,5.

Observação: Em qualquer número, o algarismo duvidoso será o último algarismo significativo, contando da esquerda para direita.

9,9999998 = o algarismo duvidoso é o 8

14,79234320 = o algarismo duvidoso é o 0

1,00000 = o algarismo duvidoso é o último zero
 

ORDEM DE GRANDEZA
Ordem de grandeza de uma medida é uma estimativa de potência de base 10 mais próxima de uma determinada medida.
Geralmente quando estudamos alguns exercícios envolvendo cálculos sobre questões de Física, Química ou Matemática, optamos pelo valor aproximado de uma grandeza.

Essa opção ocorre por diversos motivos, pois, em alguns casos, faltam-nos dados para a realização correta dos cálculos e, em outros, não há um valor exato.
Imagine que você e mais três amigos resolveram acampar em uma mata por um período de sete dias. Sem ter a certeza de que encontrariam água limpa para beber, vocês resolveram levar água em quantidade suficiente para toda a viagem. Então, qual é a quantidade de água que vocês devem levar?

Em geral, para fazermos cálculos aproximados, precisamos de certa dose de intuição e algum conhecimento referente à situação estudada. No nosso exemplo, podemos partir do fato de que devemos beber cerca de dois litros de água por dia. Como são quatro escoteiros, são necessários pelo menos oito litros de água por dia. Em uma semana, o número de litros de água que cada pessoa necessitará é 56.

Para dar certa margem de segurança, podemos arredondar esse número para 60. Assim, o ideal é que as pessoas levem pelo menos 60 litros de água. Esse é um exemplo básico do caso em que não existe um valor exato, pois o que se pode fazer é um cálculo aproximado.

Quando nossos cálculos são aproximados, costumamos dar o resultado final, ou seja, a resposta expressa em potência de 10 mais próxima do resultado encontrado. A resposta dada dessa maneira costuma ser chamada de ordem de grandeza. 

Utilizamos a notação científica para escrever números reais em produto de potência de base dez. A estrutura utilizada é a seguinte:
a . 10^b
a = coeficiente, também chamado de mantissa;
b = expoente, que é a ordem de grandeza.

Qualquer número pode ser escrito como notação científica. Para isso, basta transformá-lo em um produto que possua os elementos mantissa e ordem de grandeza.

Podemos dividir a ordem de grandeza em dois casos:

Caso 1: O deslocamento da vírgula é para a esquerda quando o valor do número é muito grande. A ordem de grandeza é a quantidade de posições deslocadas e, nesse caso, é positiva.
Exemplos:
34578 = 34578,0 → A vírgula deve ser deslocada para a esquerda e ficará à direita do primeiro algarismo significativo (termo numérico que expressa a exatidão do número). Assim, ela estará entre os números 3 e 4578.
Como a vírgula foi deslocada quatro casas à esquerda, a representação da notação científica é a seguinte:
34578,0 = 3,4578 . 10⁴

Isso porque:
3,4578 . 10⁴ 
3,4578 . 10000
4578

Caso 2: a vírgula será deslocada para a direita quando o valor do número for muito pequeno. A ordem de grandeza da potência de base dez será negativa.

Exemplos:
0,000036 → Como a vírgula será deslocada para a direita, a ordem de grandeza será negativa. O número possui dois algarismos significativos, e a vírgula deve ficar à direita do primeiro algarismo significativo; logo, estará entre os números 3 e 6.
Como a vírgula foi deslocada cinco casas à direita, a notação científica desse número é a seguinte:
0,000036 = 3,6 . 10^-5

Isso porque:
3,6 . 10^-5 
3,6 . 1 = 10⁵
3,6 . 1 = 100000
3,6 = 100000
0,000036

Mantissa: é obtida pelo posicionamento da vírgula à direita do primeiro algarismo significativo (termo numérico que expressa a exatidão do número).

Exemplos:
0,0034 → Possui dois algarismos significativos, que são 3 e 4. Devemos deslocar a vírgula para o primeiro algarismo mais significativo e, em seguida, representar o número como um produto de base 10.
Desloque a vírgula da esquerda para a direita até o primeiro algarismo mais significativo, que é o 3.
0003,4
Da origem de onde estava a vírgula até o número 3, foram deslocadas três casas. Por esse motivo, a ordem de grandeza da base 10 é - 3.
3,4 . 10^-3
7456,35 → Possui seis algarismos significativos, que são: 7, 4, 5, 6, 3 e 5. A vírgula deve ser deslocada para que possamos representar o número como um produto de base 10 com expoente.
Desloque a vírgula da direita para a esquerda até o primeiro algarismo mais significativo, que é o 7.
7,45635
Da origem de onde estava a vírgula até o número 7, deslocamos três casas. Por esse motivo, a ordem de grandeza da base 10 é + 3.
7,45635 . 10⁺³
0,0678 → Possui três algarismos significativos, que são 6, 7 e 8. A vírgula deve ser deslocada para que o número seja representado em termos de potência de base 10.
Desloque a vírgula da esquerda para a direita até o primeiro algarismo mais significativo.
6,78

Da origem de onde estava a vírgula até o número 6, deslocamos duas casas. Por esse motivo, a ordem de grandeza da base 10 é -2.

Exemplos

Mil = 1000 = 10³

Milhão = 1 000 000 = 10⁶

Bilhão = 1 000 000 000 = 10⁹

Trilhão = 1 000 000 000 000 = 10¹²

Quatrilhão = 1000 000 000 000 000 = 10¹⁵


Notação Científica - Resolvidos
01) Considere o número 0,00000000000002, converta-o em notação científica.
Resolução:
Primeiro encontramos o número significativo, deslocando a vírgula até o número 2. O expoente é o total de vezes que deslocamos a vírgula, 14, e é negativo pois temos um número decimal menor que 0.
Resposta: 2  . 10^-14

02) O número 349000 em notação científica corresponde a:
Resolução:
O primeiro número significativo é 3, então temos: 3,49000
O valor do expoente é a quantidade de vezes que deslocamos a vírgula para a esquerda até encontrar um número significativo, pois temos: 349000,0 Então, como deslocamos 5 vezes, temos a seguinte notação:
Resposta: 3,49 . 10⁵

03) Escreva o número 0,0004 em notação científica.
Resolução:
Devemos primeiro deslocar a vírgula para depois do número 4, então temos: 4 ,0 Como deslocamos 4 vezes a vírgula até o número 4, assim o valor do expoente da notação científica será -4, pois se trata de um número decimal menor que 0.
Resposta: 4 . 10^-4

04) Como escrevemos 5 . 10³ na forma decimal?
Resolução:
Como o valor do expoente é positivo, temos que adicionar após o número 5, três zeros.
Portanto, 5 .  10³ = 5000
Curiosidade:
Se o expoente fosse negativo seria deslocar a vírgula para a esquerda, então teríamos: 0,005.

05) Faça a adição e subtração 6,5 . 10³ e 2,3 . 10³.
Resolução:
Adição:
6,5 . 10³ + 2,3 . 10³
(6,5 + 2,3) . 10³
8,8 . 10³
Subtração
6,5 . 10³ – 2,3 .10³
(6,5 – 2,3) . 10³
4,2 . 10³
Observação: Lembrando que na adição e subtração os expoentes das notações devem ser iguais.

06) Realize a divisão e multiplicação das notações científicas: 5 . 10³ e 2,3 . 10².
Resolução:
Divisão:
5 .10³ ÷ 2,3 . 10²
(5 ÷ 2,3) . 10^{3 - 2}
2,17 . 10¹

Na divisão realizamos a divisão dos coeficientes, repetimos a base 10 e subtraímos os expoentes.
Multiplicação: na multiplicação realizamos o produto dos coeficientes, repetimos a base 10 e somamos os expoentes.
(5 . 10³) . (2,3 .10²)
( 5 .2,3) . 10³⁺²
11,5 .10⁵
Neste caso, 11, 5 . 10⁵ não está na forma padronizada, a mantissa deve ser igual ou maior que 1 e menor que 10. Portanto, temos que fazer um ajuste.
Então, vamos deslocar a vírgula uma casa à esquerda e somar 1 ao expoente. Portanto e resposta final assim:
1,5 . 10⁶

07) Representar o número 0,00000000000000000016 C (Coulomb) em notação científica.
Resolução:
Este número representa o valor da carga do elétron. É um número menor que 1. Existem 19 zeros neste número. Para facilitar a representação deste número vamos usar potências de dez (com expoente negativo, pois os zeros estão à esquerda do 16), ou seja, vamos representá-lo em notação científica. Neste caso:
1º passo: quais são os algarismos diferentes de zero? 16;
2° passo: quantos algarismos têm depois da vírgula, contando com os zeros e com o 16? 20 algarismos. Representamos por -20, pois os zeros estão à esquerda do 16;
3° passo: representá-lo em notação científica:
Multiplicamos o número diferente de zero (16) por 10 elevado a quantidade de algarismos que existem depois da vírgula (contando com os zeros e com o 16), ou seja, -20. Assim:
16 . 10^-20C
Para que o 1 fique na frente da vírgula, vamos deslocá-la 1 casa decimal para esquerda do 16. Mas, se deslocarmos a vírgula uma casa decimal para a esquerda, o expoente negativo de base 10 aumenta (lembrando que -19 é maior que -20) de um número, ou seja,
1,6 . 10^-19C

08) Expressar 567,9 em notação científica
Resolução:
Neste caso, sabemos que
567,9 = 567, 0 .10⁰
Observação: todo número elevado a zero é 1, portanto 10 elevado a zero é igual a 1.
5,679 = 567, 0 .10²
Para que o 5 fique na frente da vírgula, vamos deslocá-la 2 casas decimais para esquerda do 567,9. Mas, se deslocarmos a vírgula duas casas decimais para a esquerda, o expoente de base 10 aumenta de dois números, ou seja,

09) Expressar 3456,9 em notação científica.
Resolução:
Sabemos que
3456,9 = 3456,9 . 10⁰
Observação: todo número elevado a zero é 1, portanto 10 elevado a zero é igual a 1.
3456,9 = 3,4569 . 10³

10) Expressar  414,8 . 10⁴  em notação científica.
Resolução:
Para que o 4 fique na frente da vírgula, vamos deslocá-la 2 casas decimais para esquerda do 414,8. Mas, se deslocarmos a vírgula duas casas decimais para a esquerda, o expoente de base 10 aumenta de dois números, ou seja,
4,148 . 10⁶ 

11) Expressar 0,000566 em notação científica
Resolução:
1º passo: quais são os algarismos diferentes de zero? 566;
2° passo: quantos algarismos têm depois da vírgula, contando com os zeros e com o 566?
6 algarismos. Representamos por -6, pois os zeros estão à esquerda do 566.
3° passo: representa-lo em notação científica:
É um número menor que 1. Multiplicamos os número diferente de zero (566) por 10 elevado a quantidade de algarismos que existem depois da vírgula (contando com os zeros e com o 566), ou seja, -6. Assim:
566 . 01^-6
Para que o 5 fique na frente da vírgula, vamos deslocá-la 2 casas decimais para esquerda. Mas, se deslocarmos a vírgula duas casas para a esquerda, o expoente negativo (-6) de base 10 aumenta de dois números (lembrando que -4 é maior que -6), ou seja,
5,66 . 01^-4

12) Expressar 0,00033 em notação científica
Resolução:
1º passo: quais são os algarismos diferentes de zero? 33;
2° passo: quantos algarismos têm depois da vírgula, contando com os zeros e com o 33?
5 algarismos. Representamos por -5, pois os zeros estão à esquerda do 33.
3° passo: representá-lo em notação científica:
É um número menor que 1. Multiplicamos os número diferente de zero (33) por 10 elevado a quantidade de algarismos que existem depois da vírgula (contando com os zeros e com o 33), ou seja, -5.
Assim:
33 . 10^-5
Para que o 3 fique na frente da vírgula, vamos deslocá-la 1 casa decimal para esquerda do 33. Mas, se deslocarmos a vírgula uma casa para a esquerda, o expoente negativo (-5) de base 10 aumenta de um número (lembrando que -4 é maior que -5), ou seja,
3,3 . 10^-4

13) Expressar 0,000000651 em notação científica
Resolução:
1º passo: quais são os algarismos diferentes de zero? 651;
2° passo: quantos algarismos têm depois da vírgula, contando com os zeros e com o 651?
9 algarismos. Representamos por -9, pois os zeros estão à esquerda do 651.
3° passo: representá-lo em notação científica:
É um número menor que 1. Multiplicamos os número diferente de zero (651) por 10 elevado a quantidade de algarismos que existem depois da vírgula (contando com os zeros e com o 651), ou seja, -9. Assim:
651 . 10^-9
Para que o 6 fique na frente da vírgula, vamos deslocá-la 2 casas decimais para esquerda do 651. Mas, se deslocarmos a vírgula duas casas para a esquerda, o expoente negativo (-9) de base 10 aumenta de dois números (lembrando que -7 é maior que -9), ou seja,
651 . 10^-7

14) (PM-ES-Exatus) Sabe-se que a população de determinada cidade é de 5.000.000 habitantes, e que 35% dessa população tomou a vacina contra gripe, sendo que 60% das pessoas vacinadas eram crianças. Portanto, o número de crianças que tomaram a vacina contra gripe é igual a:
(A) 1,05 x 10⁴
(B) 1,05 x 10⁵
(C) 1,05 x 10⁶
(D) 1,75 x 10⁵
(E) 1,75 x 10⁶
Resolução:
5000000 . 35/100
175000000/100
1750000
1750000 . 60/100
1050000
1,05 . 10⁶

15)  Em notação científica, a massa de um elétron em repouso corresponde a 9,11 x 10⁻³¹ kg e um próton, nessa mesma condição, tem massa de 1,673 x 10^-27 kg. Quem possui maior massa?
Resolução:
O próton possui maior massa.
Escrevendo os dois números em forma decimal, temos:
Massa do elétron 
9,11 x 10^-31 = 0,000000000000000000000000000000911
Massa do próton 
1,673 x 10^-27 = 0,000000000000000000000000001673
Observe que quanto maior o expoente da potência de 10, maior o número de casas decimais que compõem o número.
O sinal de menos (-) indica que a contagem deve ser feita da esquerda para direita e de acordo com os valores apresentados a maior massa é a do próton, pois seu valor está mais próximo de 1.

16) (ENEM) As exportações de soja no Brasil totalizaram 4,129 milhões em toneladas no mês de julho de 2012 e registraram um aumento em relação ao mês de julho de 2011, embora tenha havido uma baixa em relação ao mês de maio de 2012
A quantidade, em quilogramas, de soja exportada pelo Brasil no mês de julho de 2012 foi de:
(A) 4,129 x 10³
(B) 4,129 x 10⁶
(C) 4,129 x 10⁹
(D) 4,129 x 10¹²
(E) 4,129 x 10¹⁵
Resolução:
4,129 x 10⁹
Podemos dividir a quantidade de soja exportada em três partes:
4,129 milhões toneladas
A exportação é dada em toneladas, mas a resposta deve estar em quilogramas e, por isso, o primeiro passo para resolver a questão é fazer a conversão de toneladas para quilogramas.
1 tonelada = 1 000 kg = 10³ kg
São milhões de toneladas exportadas, sendo assim, devemos multiplicar quilogramas por 1 milhão.
1 milhão = 10⁶
10⁶ x 10³ 
10⁶⁺³ 
10⁹
Escrevendo o número de exportações em notação científica, temos 4,129 x 10⁹ quilogramas de soja exportada.

17) (ENEM) Uma das principais provas de velocidade do atletismo é a prova dos 400 metros rasos. No Campeonato Mundial de Sevilha, em 1999, o atleta Michael Johnson venceu essa prova, com a marca de 43,18 segundos. Esse tempo, em segundo, escrito em notação científica é
(A) 0,4318 x 10²
(B) 4,318 x 10¹
(C) 43,18 x 10⁰
(D) 431,8 x 10^-1
(E) 4 318 x 10^-2
Resolução:
Embora todos os valores das alternativas sejam formas de representar a marca de 43,18 segundos, apenas a alternativa b está correta, pois obedece as regras da notação científica.
O formato utilizado para representar os números é N . 10ⁿ, onde:
N representa um número real maior ou igual a 1 e menor que 10.
O n é um número inteiro que corresponde ao número de casas decimais que a vírgula "andou".
A notação científica 4,318 x 10¹ representa 43,18 segundos, pois a potência elevada a 1 tem como resultado a própria base.
4,318 x 10¹ = 4,318 x 10 = 43,18 segundos.

18) Representar a massa da Terra em notação científica
Resolução:
A massa da Terra é dada por 5 960 000 000 000 000 000 000 000 kg. É um número maior que 1. Existem 22 zeros à direita do número. Para facilitar a representação deste número vamos usar potências de dez (com expoente positivo, pois os zeros estão à direita do 596), ou seja, vamos representá-lo em notação científica. Assim:
1º passo: quais são os algarismos diferentes de zero? 596;
2° passo: quantos zeros tem o número? 22 zeros;
3° passo: representá-lo em notação científica:
Multiplicamos o número diferente de zero (596) por 10 elevado a quantidade de zeros (+22) que existem no número, ou seja,
596 .10²²kg
Para que o 5 fique na frente da vírgula, vamos deslocá-la 2 casas decimais para esquerda do 596. Mas, se deslocarmos a vírgula duas casas para a esquerda, o expoente positivo de base 10 aumenta de dois números, ou seja,
5,96 .10²⁴kg

19) (PM ES – Exatus) Sabe-se que a população de determinada cidade é de 5.000.000 habitantes, e que 35% dessa população tomou a vacina contra gripe, sendo que 60% das pessoas vacinadas eram crianças. Portanto, o número de crianças que tomaram a vacina contra gripe é igual a:
(A) 1,05 x 10⁴
(B) 1,05 x 10⁵
(C) 1,05 x 10⁶
(D) 1,75 x 10⁵
(E) 1,75 x 10⁶
Resolução
5000000 . 35/100 = 175000000/100 = 1750000
1750000 . 60/100 = 1050000 = 1,05 . 10⁶
Alternativa C

20) (ETEC) A Estrela da Morte é uma arma ícone da série cinematográfica Star Wars. De formato esférico ela era considerada similar a uma Lua. Essa arma/estação espacial podia se locomover pelo espaço na velocidade da luz, ou seja, 3,0 ×10⁵ km/s. Admita que a Estrela da Morte precisasse se posicionar de maneira a realizar um ataque de máxima eficiência ao Planeta C. Inicialmente, a estação espacial encontrava-se no ponto A e, entre ela e o Planeta C, havia um grande asteroide, por isso necessitou ir para o ponto B, de modo a poder visualizar perfeitamente o Planeta C, conforme a figura.
Assinale a alternativa que contém o tempo que a Estrela da Morte demorou para se locomover do ponto A para o B.
(A) 5,0 ×10⁴ s
(B) 15,0 ×10⁴ s
(C) 45,0 ×10⁴ s
(D) √353 x 10⁴s
(E) √353/3 x 10⁴s
Resolução:
h² = a² + b²
(1,7.10¹⁰)² = AB² + (8,0.10⁹)²
2,89.10²⁰ = AB² + 64.10¹⁸
289.10¹⁸ = AB² + 64.10¹⁸
AB² = 289.10¹⁸ - 64.10¹⁸
AB² = 10¹⁸(289 - 64)
AB² = (√225.10¹⁸)
AB = 15 . 10⁹ km.
Velocidade média:
Vm = ∆S / ∆t
3,0.10⁵ = 15.10⁹/t
t = 15.10⁹/3,0.10⁵
t = 5.10⁴ segundos.
Alternativa: A

21) (ETEC) Admita que a área da superfície do planeta Terra seja de 500 milhões de km². Logo, pode-se estimar que o tamanho médio de cada hotspot identificado em 1999 seria, em km²,
(A) 28 . 10⁶
(B) 28 . 10⁴
(C) 28 . 10³
(D) 28 . 10¹
(E) 28 . 10⁰
Resolução:
1 milhão = 1.000.000
500 milhões = 500 000 000
Calculando a porcentagem
500      100
1,4       x
500x = 1,4 . 100
500x = 140
x = 140/500
x = 0,28
Lembramos que um milhão tem sies zero: 000000, portanto, temos que multiplicar 0,28 . 1000000 x = 280000 em notação científica podemos escrever 0,28 . 10⁶ ou 28 . 10⁴ nesse caso a correta é:
Alternativa: B

Observação: 
Em questões dissertativas não essa maneira de escrever notação científica não é usual. O “ideal” é deixar apenas uma casa antes da vírgula e essa casa deve ser diferente de zero. (0,28 . 10⁶ = 28 . 10⁴).

Leia o texto para responder às questões de números 26 e 27.
Para reduzir o consumo de derivados de petróleo, os fabricantes de produtos de plásticos iniciaram a produção de suas peças utilizando bioplástico, material biodegradável e/ou produzido a partir de fontes renováveis. A Xplástico, indústria há 20 anos no mercado, usa 6 000 toneladas de plástico comum para fabricar 20 bilhões de peças todos os anos. Essa empresa, no início do ano de 2018, começou a produzir a linha eco-copos com bioplástico. Essa linha representa algo em torno de 2% do número total de peças plásticas produzidas por ano nessa empresa.

22) (ETEC) Suponha que a razão anual entre as quantidades de eco-copos e o total de peças plásticas produzidas seja constante até 2030, e que a quantidade de massa plástica utilizada na confecção de cada peça seja sempre igual. O número de toneladas de plástico comum que deixarão de ser utilizadas pela Xplástico, de 2018 a 2 030, ao produzir as peças de eco-copos, é
(A) 10.
(B) 120.
(C) 1 320.
(D) 1 440.
(E) 1 560.
Resolução:
Primeiro vamos calcular 2% de 6000 para descobri a massa usada por ano na produção de eco-copos.
6000    100
x          2
100x = 6000 . 2
100x = 12000
x = 12000/100
x =120
Por ano são utilizados 120 toneladas de plásticos comum para fabricação de eco-copos.
Fazendo a multiplicação pelo período solicitado temos
120 . 12 = 1440
Observação: no texto fala a parti de 2018, já na questão diz: de 2018 a 2030. Nesse caso são 13 anos portanto será 1440 + 120 = 1560.
Alternativa: E

23) (ETEC) De acordo com o texto, pode-se concluir corretamente que o número de peças produzidas pela Xplástico por hora, em média, está mais próximo de
(A) 2,0 × 10¹²
(B) 2,0 × 10⁹
(C) 2,0 × 10⁶
(D) 2,0 × 10³
(E) 2,0 × 10⁰
Resolução:
Em notação científica ao “ideal” e deixar apenas uma casa antes da vírgula. Quando esse número aumenta o expoente diminui e quando o número diminui o expoente amenta. Para cada casa que a vírgula corre acrescenta-se ou subterra-se um zero.
Vinte milhões 20 000 000 =  2,0 . 10⁷
Alternativa: C

24) (ETEC) No século XVI, divertidos duelos intelectuais entre professores das academias contribuíram para o avanço da Matemática. Motivado por um desses duelos, o matemático italiano Niccólo Fontana (Tartaglia) (1500 – 1557) encontrou uma fórmula para resolver equações polinomiais de terceiro grau. No entanto, os outros matemáticos da época não tinham acesso a tal descoberta, tendo que encontrar formas alternativas para resolver aqueles problemas. Uma dessas formas alternativas é a fatoração, que facilita a observação das raízes (soluções), pois transforma a adição dos termos da equação em uma multiplicação igualada a zero.
Observe o exemplo
x³ + 6x² + 5x – 12 = 0 <=> (x – 1) ∙ (x + 3) ∙ (x + 4) = 0
Analisando o exemplo dado, é correto afirmar que essa equação
(A) possui três raízes naturais distintas.
(B) possui três raízes inteiras distintas.
(C) possui duas raízes naturais distintas e uma raiz irracional.
(D) possui duas raízes irracionais distintas e uma raiz inteira.
(E) não possui raízes reais.
Resolução:
Cubo da soma
Com a propriedade distributiva, é possível criar uma “fórmula” também para produtos com o seguinte formato:
(x + a)(x + a)(x + a)
Na notação de potência, ele é escrito da seguinte maneira:
(x + a)³
Por meio da propriedade distributiva e simplificando o resultado, encontraremos o seguinte para esse produto notável:
(x + a)³ = x³ + 3x²a + 3xa² + a³
Alternativa: B

25) (Enem) Pesquisadores da Universidade de Tecnologia de Viena, na Áustria, produziram miniaturas de objetos em impressoras 3D de alta precisão. Ao serem ativadas, tais impressoras lançam feixes de laser sobre um tipo de resina, esculpindo o objeto desejado. O produto final da impressão é uma escultura microscópica de três dimensões, como visto na imagem ampliada.
A escultura apresentada é uma miniatura de um carro de Fórmula 1, com 100 micrômetros de comprimento. Um micrômetro é a milionésima parte de um metro. Usando notação científica, qual é a representação do comprimento dessa miniatura, em metro?
(A) 1,0 × 10⁻¹
(B) 1,0 × 10⁻³
(C) 1,0 × 10⁻⁴
(D) 1,0 × 10⁻⁶
(E) 1,0 × 10^–7
Alternativa C
 
26) (Enem) A gripe é uma infecção respiratória aguda de curta duração causada pelo vírus influenza. Ao entrar no nosso organismo pelo nariz, esse vírus multiplica-se, disseminando-se para a garganta e demais partes das vias respiratórias, incluindo os pulmões.
O vírus influenza é uma partícula esférica que tem um diâmetro interno de 0,00011 mm.
Em notação científica, o diâmetro interno do vírus influenza, em mm, é
(A) 1,1 × 10^-1
(B) 1,1 × 10^-2
() 1,1 × 10^-3
(D) 1,1 × 10^-4
(E) 1,1 × 10^-5
Alternativa D

27) (Enem) A volemia (V) de um indivíduo é a quantidade total de sangue em seu sistema circulatório (coração, artérias, veias e capilares). Ela é útil quando se pretende estimar o número total (N) de hemácias de uma pessoa, a qual é obtida multiplicando-se a volemia (V) pela concentração (C) de hemácias no sangue, isto é, N = V x C. Num adulto normal essa concentração é de 5 200 000 hemácias por mL de sangue, conduzindo a grandes valores de N. Uma maneira adequada de informar essas grandes quantidades é utilizar a notação científica, que consiste em expressar N na forma N = Q x 10n, sendo 1 ≤ Q < 10 e n um número inteiro.
Considere um adulto normal, com volemia de 5 000 mL. Qual a quantidade total de hemácias desse adulto, em notação científica?
(A) 2,6 x 10^-10
(B) 2,6 x 10^-9
(C) 2,6 X 10⁹
(D) 2,6 x 10¹⁰
(E) 2,6 x 10¹¹
Alternativa  D

28) (UFRGS) Considerando um próton como um cubo de aresta 10^–11 m e massa 10^–21 kg, qual a sua densidade?
Resolucao
Sabemos que a densidade é a razão entre massa e volume, logo é necessário calcular o volume desse próton. Como a forma do próton segundo o enunciado é um cubo, o volume é determinado por: V = a³, em que a é a medida da aresta.
V = (10 – 11)³
V = 10 – 33 m³
A densidade é, portanto:


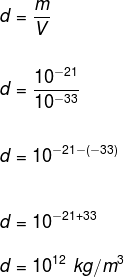
29) A velocidade da luz é de 3,0 . 10⁸ m/s. A distância entre a Terra e o Sol é de 149.600.000km. Quanto tempo a luz do sol gasta para chegar até a Terra?
Resolucao
Sabemos que a relação entre distância, velocidade e tempo é determinada por:

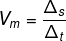
Antes de substituir os valores na fórmula, note que a velocidade da luz está em metros por segundo, e a distância entre a Terra e o Sol, em quilômetros, ou seja, é necessário escrever essa distância em metros. Para isso, vamos multiplicar a distância por 1000.
149.600.000 · 1000
1,496 · 108 · 103
1,496 · 108+3
1,496 · 1011 m
Agora, substituindo os valores na fórmula, temos:
 

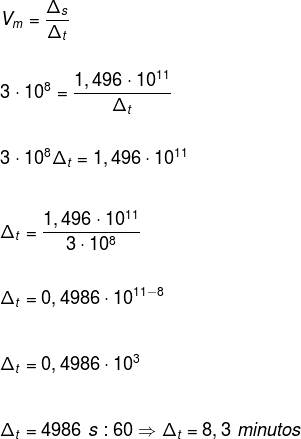
30) (Enem) Um asteroide batizado de 2013-TV135 passou a aproximadamente 6,7 × 10⁶ quilômetros da Terra. A presença do objeto espacial nas proximidades da Terra foi detectada por astrônomos ucranianos, que alertaram para uma possível volta do asteroide em 2032.
O valor posicional do algarismo 7, presente na notação científica da distância, em quilômetro, entre o asteroide e a Terra, corresponde a
(A) 7 décimos de quilômetro.
(B) 7 centenas de quilômetros.
(C) 7 dezenas de milhar de quilômetros.
(D) 7 centenas de milhar de quilômetros.
(E) 7 unidades de milhão de quilômetros
Resolução
6,7 . 10⁶ = 6.700.000
Então o 7 corresponde à centena de milhar.
Alternativa D

31) (Enem) A Agência Espacial Norte Americana (NASA) informou que o asteroide YU 55 cruzou o espaço entre a Terra e a Lua no mês de novembro de 2011. A ilustração a seguir sugere que o asteroide percorreu sua trajetória no mesmo plano que contém a órbita descrita pela Lua em torno da Terra. Na figura, está indicada a proximidade do asteroide em relação à Terra, ou seja, a menor distância que ele passou da superfície terrestre.
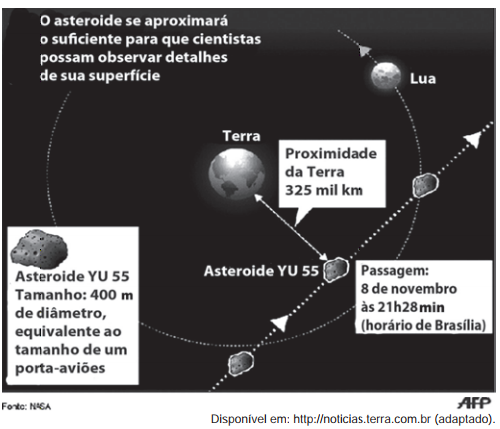Com base nessas informações, a menor distância que o asteroide YU 55 passou da superfície da Terra é igual a:
(A) 3,25 × 10² km
(B) 3,25 × 10³ km
(C) 3,25 × 10⁴ km
(D) 3,25 × 10⁵ km
(E) 3,25 × 10⁶ km
Resolução
Queremos representar 325 mil em notação científica:
325000
Ao colocar a vírgula entre 3 e 2, teremos 5 números após ela. Então, esse número em notação científica será 3,25 × 10⁵ km.
Alternativa D


Continua....