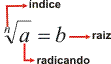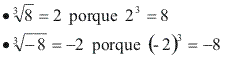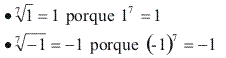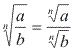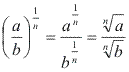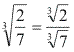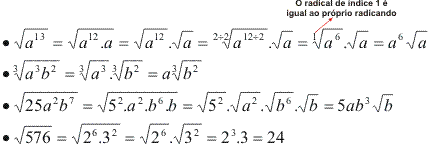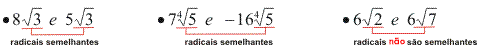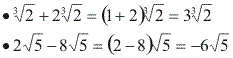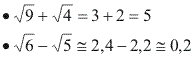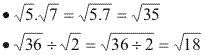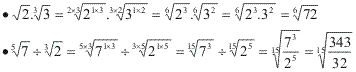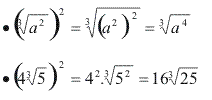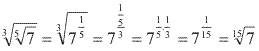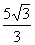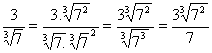EF II - RADICIACAO

Professor Diminoi
RADICIACAO

O que é radiciação?
Já sabemos que 6² = 36. Aprenderemos agora a operaçao que nos permite determinar qual o número que elevado ao quadrado equivale a 36.
²√36 = 6, pois 6 elevado ao quadrado é 36.

Essa operaçao é a inversa da potenciação e denomina-se radiciação.

Exemplos


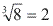
pois 2³ = 8.


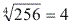
pois 
4⁴ = 256

Sendo assim:
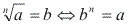Notaçao
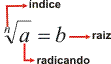Leitura
√82 (lê-se “raiz quadrada de 81”)
³√64 (lê-se “raiz cúbica de 64”)
⁴√16 (lê-se “raiz quarta de 16”)

Observaçao: Na indicaçao de raiz quadrada, podemos omitir o índice 2.

Exemplo
²√81 = √81

Raízes de índice par
Quando elevamos um número positivo ou um número negativo a um expoente par, o resultado sempre é um número positivo.

Exemplo
(-4)² = (-4)(-4) = 16
(+4)² = (+4)(+4) = 16
Porém, como em matemática o resultado de uma operaçao deve ser único, fica definido que:


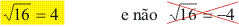
Genericamente:
Qualquer raiz de índice par de um número positivo é o número positivo que elevado ao expoente correspondente a esse indíce equivale ao número dado.

Observaçao: Não existe raiz real de um número negativo se o índice for par.

Exemplo
√-4 nao existe, pois nao há nenhum número real que elevado ao quadrado dê - 4.

Raízes de índice ímpar
Quando o índice de uma raiz é ímpar e o radicando é positivo, a raiz é positiva.
Quando o índice de uma raíz é ímpar e o radicando é negativo, a raiz é negativa.

Exemplos:



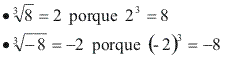
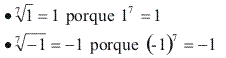
Potência com expoente fracionário
Se a é um número real positivo, m é um número inteiro e n é um número natural nao-nulo, temos que:


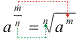
Exemplos




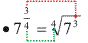
Propriedades dos radicais
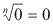Justificativa:
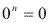 Exemplo

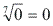
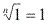
Justificativa: 


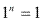
Exemplo: 


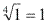
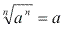
Justificativa: Escrevendo em forma de potência com expoente fracionário:


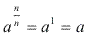
Exemplo: 


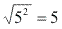
Propriedades operatórias dos radicais
Radical de um produto

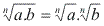
Justificativa:


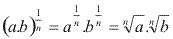
Exemplo


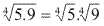
Radical de um quociente

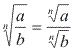
Justificativa:


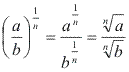
Exemplo


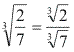
Mudança de índice


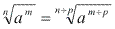
Justificativa:


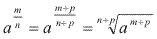
Exemplo


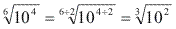
Simplificaçao de radicais
Confira a seguir alguns exemplos de simplificaçao de radicais, com base nas propriedades operatorias do item anterior:

 

 

 

 


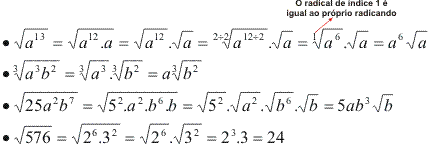
Radicais semelhantes
Radicais semelhantes sao aqueles que têm o mesmo índice e o mesmo radicando.

Exemplos:

 


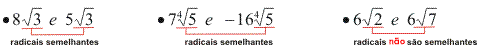
Adiçao e subtraçao de radicais
1º caso: Radicais semelhantes
Fazemos como na redução de termos semelhantes de uma soma algébrica.

Exemplos


 


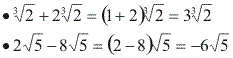
2º caso: Radicais semelhantes após simplificação
Depois de obter radicais semelhantes, procedemos como no 1º caso.


 

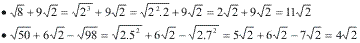
3º caso: Os radicais não são semelhantes
Extraímos as raízes e efetuamos as operações.


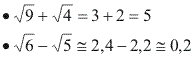
Multiplicação e divisão de radicais
1º caso: Os radicais têm o mesmo índice
Efetuamos a operaçao entre os radicandos.


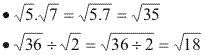
2º caso: Os radicais nao têm o mesmo índice
Primeiramente os reduzimos ao mesmo índice e depois efetuamos as operações.


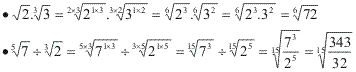
Potência de um radical
Para elevar um radical a uma certa potência, devemos conservar o índice e elevar o radicando à potência indicada.

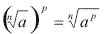
Observe a justificativa dessa propriedade através de um exemplo:


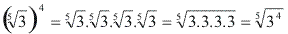
Exemplos


 

 


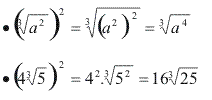
Radical de um radical
Para obter a raiz de uma raiz, devemos conservar o radicando e multiplicar os índices.

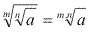
Observe a justificativa dessa propriedade através de um exemplo:


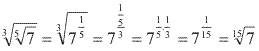
Exemplos


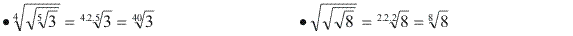
Racionalização de denominadores
Considere a fração abaixo cujo denominador é um número irracional.

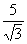
Agora devemos multiplicar o numerador e o denominador desta fração por √3, obtendo uma fração equivalente:

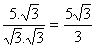
Observe que a fração equivalente possui um denominador racional.

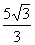
A essa transformação, damos o nome de racionalização de denomindores.
A racionalização de denominadores consiste, portanto, na obtenção de um fração com denominador racional, equivalente a uma anterior, que possuía um ou mais radicais em seu denominador.
Para racionalizar o denominador de uma fração, devemos multiplicar os termos desta fração por uma expressão com radical, denominado fator racionalizante, de modo a obter uma nova fração equivalente com denominador sem radical.

Principais casos de racionalização
1º caso: O denominador é um radical de índice 2. 

Exemplo

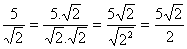
√a e o fator racionalizante √a, pois √a √a √a² = a

2º caso: O denominador é um radical de índice diferente de 2, ou a soma (ou diferença) de dois termos.
Neste caso, é necessário multiplicar o numerador e o denominador da fraçao por um termo conveniente, para que desapareça o radical que se encontra no denominador. 

Exemplo


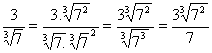
Caso 1
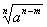E o fator racionalizante de


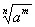
Caso 2

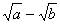
E o fator racionalizante de


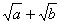
Caso 3

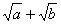
E o fator racionalizante de 


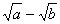
Caso 4

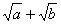
E o fator racionalizante de


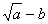
Exemplo


 

 
 

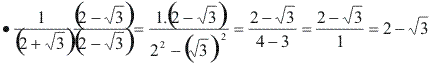
Continua ...