CIRCUNFERENCIA
Professor Diminoi
 Circunferência
Circunferência
E a figura geométrica formada por todos os pontos do plano que distam igualmente de um ponto fixo fixo desse plano. Esse ponto é denominado de Centro da circunferencias.
Elementos do círculo e da circunferência
Os elementos do círculo e da circunferência são raio, diâmetro, corda, arco da circunferência, setor circular e coroa circular, entre outros.
Observação: o compasso é um objeto usado para desenhar círculos e circunferências
Para um dado ponto C, chamado centro, uma cincunferencia é o conjunto de todos os pontos que possuem uma distancia fixa até C. Essa distância geralmente é representada pela letra r. Os circulos, por sua vez, são compostos por todos os pontos de uma circunferência e por seus pontos interiores. A imagem a seguir ilustra uma circunferência e um círculo.
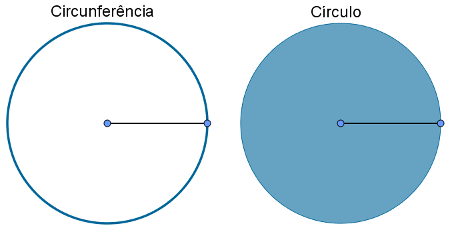 Destacamos a seguir os elementos dessas duas figuras, que possuem grande importância para a Geometria:
Destacamos a seguir os elementos dessas duas figuras, que possuem grande importância para a Geometria:
Raio
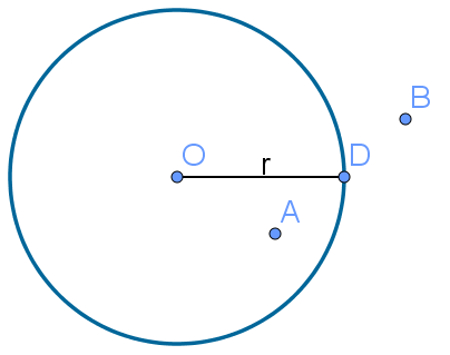
O raio é a distância entre um ponto de uma circunferência e seu centro. O raio do círculo é a distância entre a borda do círculo e seu centro.
Dizemos que um ponto é interior a uma circunferência quando a sua distância até o centro é menor que o raio; o ponto é externo quando a distância entre o centro e ele é maior que o raio; e, por fim, dizemos que um ponto pertence a uma circunferência quando sua distância até o centro é igual ao raio.
O raio da circunferência (e/ou do círculo) é indispensável em cálculos, como comprimento, área etc.
Comprimento da Circunferência
O comprimento de uma circunferência é a medida da união de todos os pontos que a formam, sendo expressa em alguma unidade de comprimento como: metro, centímetro ou milímetros, por exemplo.
Um modo prático para obter este comprimento é utilizar uma fita métrica flexível ou, desfazendo a circunferência, a esticando em linha e, assim, medir seu comprimento.
Como nem sempre é possível desfazer a circunferência ou utilizar uma fita métrica, obtemos esta medida através de um cálculo, utilizando uma medida mais fácil de obter: o raio.
Devido à relação comprimento/diâmetro nas regiões circulares, conseguimos descobrir um valor constante, aproximadamente igual a 3,14. Esse número irracional ficou conhecido por “pi”, o qual é representado pelo símbolo π. Em qualquer região circular basta dividirmos o comprimento da mesma, pela medida do diâmetro, que encontraremos o valor correspondente a 3,14 aproximadamente.
Formula do Comprimento ou Perimetro da circunferencia
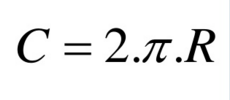 Onde:
Onde:
C = comprimento da circunferência
π ≅ 3,14
r = raio da circunferência
QUESTOES RESOLVIDAS
01) Uma circunferência possui raio medindo 5 cm, calcule o comprimento dela utilizando π = 3,14.
Resolucao
C = 2 . π . r
C = 2 · 3,14 . 5
C = 10 . 3,14
C = 31,4 cm
02) Uma piscina possui formato circular com comprimento igual a 33 metros. Utilizando π = 3, qual é o valor do raio da circunferência?
Resolucao
Sabemos que C = 33 metros, então, temos que:
C = 2 . π . r
33 = 2 . 3 . r
33 = 6r
6r = 33
r = 33/6
r = 5,5 m
03) Calcular o comprimento de uma circunferência de raio igual a 10 cm.
Resolucao
C = 2 . π . r
C = 2 . 3,14 . 10
C = 62,8 cm
04) Calcular o comprimento de uma circunferência de raio igual a 2 metros.
Resolucao
C = 2 . π . r
C = 2 . 3,14 . 2
C = 12,56 m
06) Calcular o comprimento de uma circunferência de raio igual a 50 cm.
Resolucao
C = 2 . π . r
C = 2 . 3,14 . 50
C = 314 cm
06) Em panelas de pressão, é bastante comum que exista um elástico envolvendo a tampa, com o objetivo de vedar e evitar a saída do vapor durante o uso da panela. Se uma determinada tampa possui 12 cm de diâmetro, então, o comprimento desse elástico deve ser igual a:
(Use π = 3,1.)
(A) 34,6 cm
(B) 35,2 cm
(C) 35,8 cm
(D) 37,2 cm
(E) 37,0 cm
Resolução
Se o diâmetro é igual a 12 cm, então o raio é a metade de 12 cm, ou seja, r = 6 cm.
Então, temos que:
r = 6
π = 3,1
C = 2 . π . r
C = 2 . 3,1 . 6
C = 6,2 . 6
C = 37,2 cm
Alternativa D
07) (PM ES – Exatus) Para realizar o teste físico em determinado concurso da PM, os candidatos devem correr ao redor de uma praça circular cujo diâmetro mede 120 m. Uma pessoa que dá 9 voltas ao redor dessa praça percorre: (Dado: π = 3)
(A) 1620 m
(B) 3240 m
(C) 4860 m
(D) 6480 m
(E) 8100 m
Resolução
O raio da circunferência é igual à metade do seu diâmetro, ou seja, d = 120 : 2 = 60 m.
C = 2 . π . r
C = 2 . 3 .60
C = 6 . 60
C = 360 m
Como serão dadas 9 voltas, então, temos que: 360 · 9 = 3240 m.
Alternativa B
Área do Círculo
A área do círculo corresponde ao valor da superfície dessa figura, levando em conta a medida de seu raio (r).
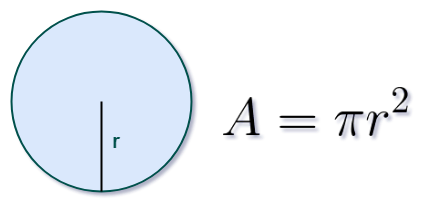 A = area
A = area
π = constante Pi (3,14)
r = raio
QUESTOES RESOLVIDAS
08) Determina a área de uma circunferência de raio = 20 cm. (π = 3,14).
Resolução:
raio = 20 cm
π = 3,14
A = π . r2
A = 3,14 x 202
A = 3,14 x 400
A = 1256 cm2
09) Calcula a área de uma circunferência de 30 cm de diâmetro. (π = 3,14).
Resolução:
d = 30 cm
raio = diâmetro/2
raio = 15.
A = π . r2
A = 3,14 X 152
A = 3,14 x 225
A = 706,5 cm2
10) Determine a área de uma circunferência que possui raio igual 4 cm.
Resolucao
A = π . r2
A = 3,14 . (4)2
A = 3,14 . 16
A = 50,24 cm2
11) Qual a área de uma praça que tem raio medindo 12 metros?
Resolucao
A = π . r2
A = 3,14 . 12²
A = 3,14 . 144
A = 452,16 m²
A área da praça é de 452,16 m²
05) Se a área de uma região circular é de 379,94 m², qual o valor do seu raio?
Resolucao
A = π . r2
379,94 = 3,14 . r²
r² = 379,94 / 3,14
r² = 121 (aplicar raiz quadrada)
r = 11 m
O raio da praça mede 11 metros.
Cordas
Em uma circunferência, a corda é qualquer segmento de reta que liga dois de seus pontos.
Dessa maneira, as cordas, em um círculo, podem ser compreendidas como segmentos de reta que ligam dois pontos distintos de sua borda.
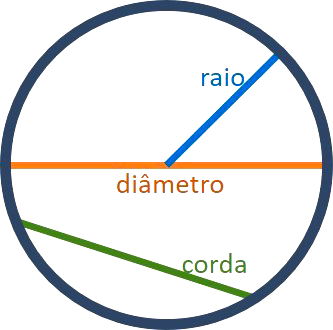 Diâmetro
Diâmetro
O diâmetro é uma corda da circunferência que contém o centro. Dessa maneira, o diâmetro é a maior corda possível em uma circunferência e sua medida é igual a duas vezes o raio.
d = 2r
O resultado da divisao entre o comprimento de uma circunferência e o seu diâmetro sempre será igual a uma constante, representada pela letra grega π, que é aproximadamente 3,14. Isso independe do tamanho da circunferência, pois seu comprimento e seu diâmetro são ptopotcionais e a razão de proporcionalidade é igual a π.
Arco
Considere os pontos A e B sobre uma circunferência. As duas partes formadas que vão de A até B são chamadas de arcos da circunferência, como demonstrado na figura a seguir:
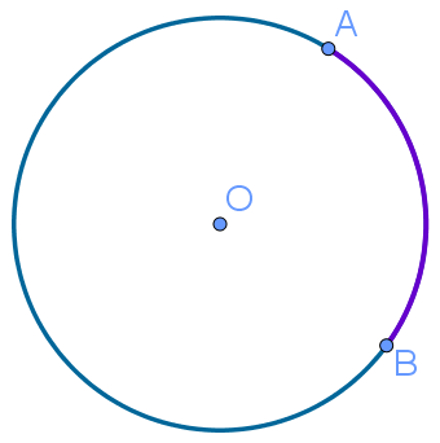 Em outras palavras, o arco é uma parte de uma circunferência limitada por dois pontos.
Em outras palavras, o arco é uma parte de uma circunferência limitada por dois pontos.
Setor circular
É o equivalente ao arco, porém para o círculo. Em dados dois raios distintos de um círculo, o setor circular é a parte limitada por eles.
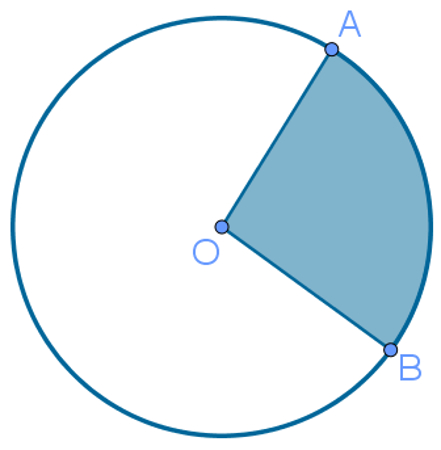 O setor circular é algo que se parece com uma fatia de pizza. A parte restante também é chamada de setor circular.
O setor circular é algo que se parece com uma fatia de pizza. A parte restante também é chamada de setor circular.
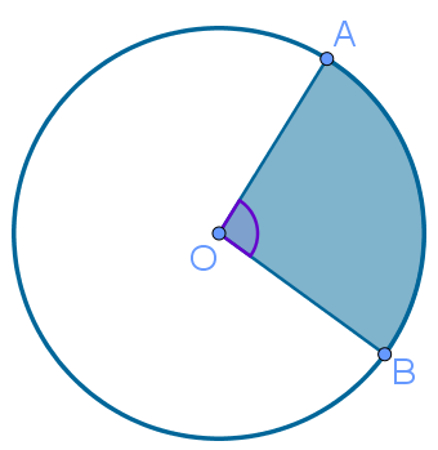
Ângulo central
É um angulo cujo vértice está no centro de um círculo e os lados são seus raios. Um ângulo central está ligado a um arco no círculo onde foi definido. A imagem seguinte mostra um exemplo de ângulo central.
 Coroa circular
Coroa circular
A coroa circular é uma figura geométrica limitada por dois círculos que possuem o mesmo centro (concêntricos) de raios diferentes. Essa figura é a que mais se assemelha a um anel, como mostra a imagem abaixo.
.jpg) QUESTOES SOBRE CIRCUNFERÊNCIA
QUESTOES SOBRE CIRCUNFERÊNCIA
01) Na fazendo do Seu Sebastião, o cultivo de milho é feito em uma área delimitada por uma circunferência. Para evitar invasões de animais na plantação, ele decidiu cercá-la com arame farpado, dando 4 voltas completas. Sabendo que o diâmetro da circunferência é de 1 km, a quantidade mínima de arame necessária para cercar essa área é igual a:
(Use π = 3)
(A) 3 km
(B) 6 km
(C) 12 km
(D) 20 km
(E) 24 km
Resolucao
Queremos calcular o comprimento da circunferencia. Como o diâmetro é de 1 km, o raio será de 0,5 km, que é igual a 500 metros.
C = 2πr
C = 2 . 3 . 0,5
C = 3 km
Como ele deseja 4 voltas, então são necessários 4 · 3 = 12 km de arame, no mínimo.
Alternativa E
02) Sobre a circunferência, julgue as afirmativas a seguir:
I → A circunferência de centro O e raio r é um conjunto de todos os pontos cuja distância até O é igual a r.
II → O comprimento do diâmetro é sempre igual à metade do comprimento do raio.
III → A circunferência é uma área plana limitada por um círculo.
Marque a alternativa correta:
(A) Somente a afirmativa I é verdadeira.
(B) Somente a afirmativa II é verdadeira.
(C) Somente a afirmativa III é verdadeira.
(D) Todas as afirmativas são falsas.
Resolucao
I → Verdadeira: A circunferência de centro O e raio r é o conjunto de todos os pontos cuja distância até O é igual a r. Essa é a definição de circunferência.
II → Falsa: O comprimento do diâmetro é o dobro do comprimento do raio.
III → Falsa: O circulo é a área plana limitada pela circunferência, e não o contrário.
Alternativa A
03) A circunferência c foi representada em uma malha quadriculada, sendo que A é o ponto que representa seu centro.
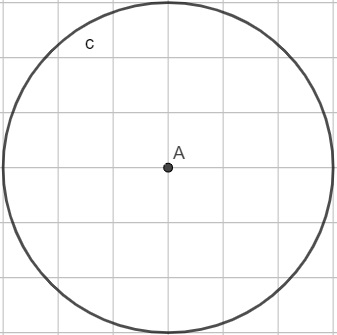 Analisando a figura, podemos afirmar que a área delimitada pela circunferência é igual a:
Analisando a figura, podemos afirmar que a área delimitada pela circunferência é igual a:
(Use π = 3)
(A) 30 u.a.
(B) 27 u.a.
(C) 18 u.a.
(D) 15 u.a.
(E) 12 u.a.
Resolucao
A partir da imagem, percebemos que a circunferência possui raio igual a 3 unidades de medidas (u.m)
Então, a sua área é igual a:
A = πr²
A = 3 . 3²
A = 3 . 9
A = 27 unidades de área (u.a.)
Alternativa B
04) Analise a circunferência a seguir:
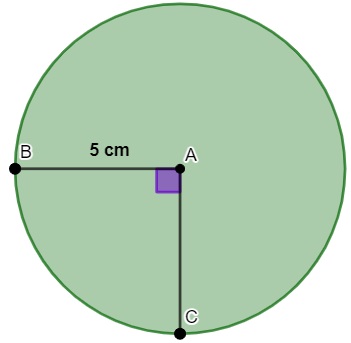 Podemos afirmar que o comprimento do arco BC é igual a:
Podemos afirmar que o comprimento do arco BC é igual a:
(Use π = 3)
(A) 7,5 cm
(B) 15 cm
(C) 20 cm
(D) 22,5 cm
(E) 30 cm
Resolucao
Primeiramente, calcularemos o comprimento dessa circunferencia:
C = 2πr
C = 2 · 3 · 5
C = 30 cm
Note que o ângulo BAC possui 90°. Logo, o arco BC equivale a um quarto do comprimento da circunferência. Assim, o comprimento do arco é de 30 : 4 = 7,5 cm.
Alternativa A
05) Dentro das cozinhas, é bastante comum que seja utilizada a panela de pressão, que possui em sua tampa um elástico, com objetivo de evitar a saída do vapor e acelerar o processo de cozimento. Suponha que uma panela possui uma tampa totalmente circular, com 6 cm de raio. O comprimento do elástico dessa tampa deve ser igual a:
(Use π = 3,1)
(A) 34,9 cm
(B) 35,0 cm
(C) 35,4 cm
(D) 36,6 cm
(E) 37,2 cm
Resolucao
Sabemos que:
r = 6
π = 3,1
Calculando o comprimento, temos:
C = 2πr
C = 2 · 3,1 · 6
C = 6,2 · 6
C = 37,2 cm
Alternativa D
06) (Enem – PPL) Um homem, determinado a melhorar sua saúde, resolveu andar diariamente numa praça circular que há em frente à sua casa. Todos os dias ele dá exatamente 15 voltas em torno da praça, que tem 50 m de raio.
Qual é a distância percorrida por esse homem em sua caminhada diária?
(Use π = 3,0)
(A) 0,30 km
(B) 0,75 km
(C) 1,50 km
(D) 2,25 km
(E) 4,50 km
Resolucao
Inicialmente, calcularemos a distância percorrida pelo homem ao dar uma volta:
C = 2πr
C = 2 . 3 . 50
C = 300 m
Como ele dá 15 voltas, a distância percorrida em metros será de:
300 · 15 = 4500 metros
Convertendo para km, 4500 m = 4,5 km.
Alternativa E
07) (IFG) Se o raio R de uma circunferência for reduzido pela metade, é correto afirmar que:
(A) O valor da área círculo ficará reduzida pela metade do valor da área do círculo inicial de raio R.
(B) O valor da área do círculo ficará a ¾ do valor da área do círculo inicial de raio R.
(C) O comprimento da circunferência se reduzirá a ¼ do valor do comprimento da circunferência inicial de raio R.
(D) O comprimento da circunferência se reduzirá à metade do valor do comprimento da circunferência inicial de raio R.
Resolucao
Se o raio for divido pela metade, obteremos r : 2.
Analisando as alternativas, verificaremos a redução na área e no comprimento.
Sabemos que a área é A = πr². Se o raio for reduzido pela metade, teremos:
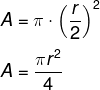
Logo, a área será 1/4 da área anterior, o que faz com que as alternativas A e B sejam falsas.
Calculando o comprimento, temos:
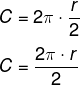
Note que o comprimento foi reduzido pela metade, o que faz com que a alternativa D seja a correta.
Alternativa D
08) (IFG) Dois círculos, C1 e C2, possuem raios com medidas 3x e x+5, em cm, respectivamente. Sabe-se que a razão entre o comprimento de C1 e o comprimento de C2 é igual a 2. Dessa forma, é correto afirmar que as áreas de C1 e C2 valem em cm², respectivamente:
(use π = 3,14)
(A) 900 π e 225 π.
(B) 920 π e 240 π.
(C)905 π e 255 π.
(D) 910 π e 235 π.
Resolucao
Sabemos que a razão entre o comprimento do círculo C1 e do C2 é igual a 2 e que r1 = 3x e r2 = x + 5:
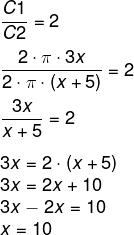
Calculando a área do círculo C1:
A1 = πr²
A1 = π (3x)²
Como x = 10, então:
A1 = π · (3 · 10)²
A1 = π · 30²
A1 = 900π
Agora, calcularemos A2:
A2 = πr²
A2 = π (x + 5)²
Como x = 10, calculamos:
A2 = π · (10 + 5)²
A2 = π · 15²
A2 = 225π
As áreas são, respectivamente, 900π cm² e 225π cm².
Alternativa A
09) (Enem) Em um condomínio, uma área pavimentada, que tem a forma de um círculo com diâmetro medindo 6 m, é cercada por grama. A administração do condomínio deseja ampliar essa área, mantendo seu formato circular e aumentando, em 8 m, o diâmetro dessa região, mantendo o revestimento da parte já existente. O condomínio dispõe, em estoque, de material suficiente para pavimentar mais 100 m² de área. O síndico do condomínio avaliará se esse material disponível será suficiente para pavimentar a região a ser ampliada.
A conclusão correta a que o síndico deverá chegar, considerando a nova área a ser pavimentada, é a de que o material disponível em estoque:
(Use π = 3)
(A) será suficiente, pois a área da nova região a ser pavimentada mede 21 m².
(B) será suficiente, pois a área da nova região a ser pavimentada mede 24 m².
(C) será suficiente, pois a área da nova região a ser pavimentada mede 48 m².
(D) não será suficiente, pois a área da nova região a ser pavimentada mede 108 m².
(E) não será suficiente, pois a área da nova região a ser pavimentada mede 120 m².
Resolucao
A área inicialmente possuía um raio de 3 metros. Como o diâmetro será aumentado em 8m, essa região terá 14 metros de diâmetro, ou seja, 7 metros de raio. Calculando a diferença entre essas áreas:
A1 = πr²
3 . 3² = 27 m²
A2 = πr² = 3 · 7²
147 m²
147 – 27 = 120 m²
Logo, a quantidade de material não será suficiente, pois a área da nova região a ser pavimentada mede 120 m.
Alternativa E
10) Em uma fábrica de embalagens, a tampa de determinado produto possui área igual a 78,5 cm². Sabendo que ele possui formato circular e utilizando 3,14 como aproximação para π, o raio dessa tampa é igual a:
(A) 5 cm
(B) 6 cm
(C) 8 cm
(D) 9 cm
(E) 10 cm
Resolucao
Sabendo que A = πr², calculamos:
78,5 = 3,14 · r²
78,5 : 3,14 = r²
25 = r²
r = √25
r = 5 cm
Alternativa A
11) Sobre a circunferência, julgue as afirmativas a seguir.
I → O diâmetro é um segmento de reta que liga uma extremidade a outra da circunferência, passando pelo centro.
II → A corda é um segmento de reta que liga um ponto da circunferência ao seu centro.
III → A medida do raio da circunferência é sempre igual à metade da medida do seu diâmetro.
Marque a alternativa correta:
(A) Somente a afirmativa I é falsa.
(B) Somente a afirmativa II é falsa.
(C) Somente a afirmativa III é falsa.
(D) Toda as afirmativas são verdadeiras.
Resolucao
I → Verdadeira: A definição de diâmetro está correta.
II → Falsa: O segmento que liga um ponto da circunferência ao centro é o raio, e não a corda.
III → Verdadeira: Para encontrar o comprimento do raio, basta dividir o diâmetro por dois.
Alternativa B
12) Um parque possui formato circular e será cercado para a realização de um evento. Sabendo que para cercar essa região será gasto um total de R$ 9,00 por metro e que o raio desse parque é de 14 metros, o valor gasto para cercá-lo será igual a:
(Use π = 3)
(A) R$ 756,00
(B) R$ 695,00
(C) R$ 640,00
(D) R$ 525,00
(E) R$ 490,00
Resolucao
Primeiramente, calcularemos o comprimento do parque:
C = 2πr
C = 2 ·3 · 14
C = 84 m
Como serão gastos R$ 9,00 por metro, o valor total será de 84 · 9 = R$ 756,00.
Alternativa A
EXERCÍCIOS SOBRE ÁREA DO CÍRCULO
13) Um dos sistemas de irrigação utilizados na Agronomia é o de pivô central. Um braço de metal é preso por uma de suas extremidades ao centro de um círculo e percorre um campo circular durante o dia irrigando os locais por onde passa, de modo que a outra extremidade passa pela borda desse mesmo círculo. O resultado obtido por esse sistema são plantações perfeitamente circulares.
Supondo que o braço utilizado para irrigação de um campo circular tenha o comprimento de 300 metros, qual será a área irrigada por ele em uma volta? (π = 3,14)
(A) 282600 m2
(B) 282000 m2
(C) 300000 m2
(D) 90000 m2
(E) 887364 m2
Resolucao
A fórmula para o cálculo de área de círculos é a seguinte:
A = π . r2
Como o braço está preso à extremidade e ao centro do círculo, então, ele representa seu raio. Desse modo, o raio desse círculo tem 300 metros. Para calcular a área, basta substituir essa informação na fórmula acima.
A = 3,14·3002
A = 3,14·90000
A = 282600 m2
Alternativa A
14) Qual é a metade da área do círculo cujo diâmetro mede 45 metros? (π = 3,14).
(A) 6358,5 m2
(B) 1589,62 m2
(C) 794,81 m2
(D) 1028,25 m2
(E) 93,14 m2
Resolucao
Se o diâmetro de um círculo mede 45 metros, seu raio mede metade disso. Logo, r = 22,5 m. Para calcular a área desse círculo, basta substituir os valores na fórmula. Observe:
A = π . r2
A = 3,14·22,52
A = 3,14·506,25
A = 1589,62 m2
Agora basta calcular a metade dessa área:
A = 1589,62 = 794,81m2
2 2
Alternativa C
15) A área onde será construído um shopping é circular e tem medida igual a 70650 m2. Qual é o raio do círculo descrito por essa área? (π = 3,14).
(A) 22500 m
(B) 120 m
(C) 100 m
(D) 150 m
(E) 200 m
Resolucao
Para calcular o raio desse lote, devemos utilizar a fórmula da área do círculo:
A = π . r2
Substitua os valores conhecidos na fórmula:
70650 = 3,14·r2
70650 = r2
3,14
r2 = 22500
√r2 = √22500
r = 150 m
Alternativa D
16) Planeja-se construir uma piscina circular com uma ilha no meio, também circular. Sabendo que o raio da ilha possui 30 metros e que o raio da piscina possui 50 metros, qual é a área da superfície da piscina? (π = 3,14).
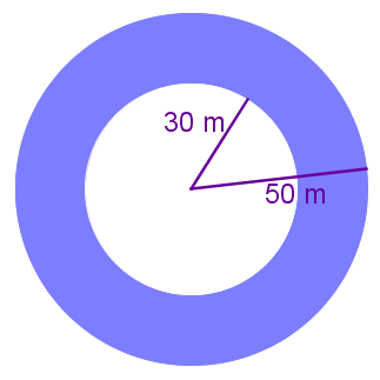 (A) 7850 m2
(A) 7850 m2
(B) 7580 m2
(C) 2826 m2
(D) 2682 m2
(E) 5024 m2
Resolucao
Para encontrar a área da superfície da piscina, basta calcular a área e diminuir pela área da ilha.
Ap = π . r2
Ap = 3,14·502
Ap = 3,14·2500
Ap = 7850 m2
Ai = π·r2
Ai = 3,14·302
Ai = 3,14·900
Ai = 2826 m2
Área da superfície da piscina = 7850 – 2826 = 5024 m2
Alternativa E
17) Calcule a área de um círculo de raio 7 cm.
Resoluco
Basta utilizar a fórmula para área do círculo:
A = π . r2
A = 3,14 · 72
A = 3,14 · 49
A = 153,86 cm2
18) Calcule a área de um círculo cujo diâmetro mede 18 cm.
Resoluco
Utilizando a fórmula da área do círculo, substitua o valor do raio e realize os cálculos:
A = π . r2
A = 3,14 · 92
A = 3,14 · 81
A = 254,34 cm2
Observacao: o valor utilizado para o raio foi 9 cm e não 18 cm. Isso acontece porque 18 cm é o comprimento do diâmetro e não do raio. Uma vez que o raio é metade do diâmetro, basta fazer a substituição correta na fórmula.
19) Qual a área de um círculo no qual foi inscrito um quadrado de lado 4 cm?
Resoluco
Como o quadrado está inscrito no círculo, encontrando sua diagonal encontraremos também o diâmetro do círculo:
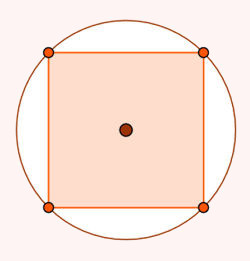 d = l√(2)
d = l√(2)
d = 4√(2)
O raio de um círculo é metade de seu diâmetro, portanto, r = 2√(2)
Agora, basta calcular a área desse círculo.
A = π . r2
A = 3,14 . [2√(2)]2
A = 3,14 . 4 . 2
A = 25,15 cm2
20) (Ufpe) Num círculo, inscreve-se um quadrado de lado 7 cm. Sobre cada lado do quadrado, considera-se a semicircunferência exterior ao quadrado com centro no ponto médio do lado e raio 3,5cm, como na figura a seguir. Calcule a área da região hachurada.
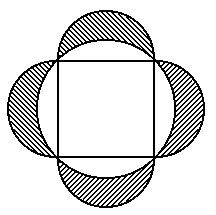 Apesar de parecer difícil, esse exercício exige apenas que você saiba calcular a área do quadrado e do círculo. Todo o trabalho pode ser feito em três passos:
Apesar de parecer difícil, esse exercício exige apenas que você saiba calcular a área do quadrado e do círculo. Todo o trabalho pode ser feito em três passos:
I- calcular a área limitada pelos semicírculos hachurados;
II- calcular a área do círculo e
III- diminuir o resultado da primeira área pelo resultado da segunda.
Resoluco
I- A figura abaixo representa a área limitada pelos semicírculos. Para calculá-la é preciso calcular a área do quadrado e somar com a área dos quatro semicírculos.

O lado do quadrado mede 7 cm. Sua área, portanto, é
Aq = l2 = 72 = 49 cm2
Agora, basta calcular a área de um semicírculo e multiplicar por 4, já que temos 4 deles no exercício.
As = π · r2
2
As = 3,14 · 3,52
2
As = 38,465
2
As = 19,2325 cm2
Para descobrir a área dos quatro semicírculos, basta multiplicar a área do semicírculo por 4
4 . As = 19,2325 · 4
4 . As = 76,93 cm2
Portanto, a área delimitada pelos semicírculos é a área dos semicírculos somada à área do quadrado:
A = 76,93 + 49 = 125,93 cm²
II- Para calcular a área do círculo é necessário saber seu raio, que é metade da diagonal do quadrado.
d = l ·√(2) = 7·√(2) = 9,9 cm
O raio do círculo é metade da diagonal do quadrado:
d = 9,9 = 4,95 cm
2 2
Com o raio do círculo em mãos, calcule sua área:
Ac = π . r2
Ac = 3,14 · 4,952
Ac = 3,14 · 24,5
Ac = 76,93 cm2
III- Basta finalizar o exercício diminuindo a área da região limitada pelos semicírculos pela área do círculo.
A – Ac = 125,93 – 76,96 = 49 cm²
21) (PM ES – Exatus – adaptada) Laura cultiva flores em um canteiro com formato de semicírculo, cujo diâmetro mede 16 m. A área ocupada por esse canteiro é igual a:
(A) 256π m²
(B) 128π m²
(Cc) 64π m²
(D) 32π m²
(E) 16π m²
Resolução
Como o diâmetro do círculo mede 16 m, o raio mede 8 m.
Calculando a área do círculo:
A = π . r²
A = π . 8²
A = 64π m²
A área do semicírculo será a metade da área do círculo: 32π m²
Alternativa D
22) (CFO PM ES – Exatus) Adriana planta flores num canteiro circular de raio 8 m. Ao redor desse canteiro, ela pretende plantar ervas medicinais formando uma coroa circular, de maneira que a parte destinada às flores sofrerá uma redução de 2 m em seu diâmetro. A área ocupada pelas ervas medicinais neste canteiro será igual a:
(A) 13π
(B) 14π
(C) 15π
(D) 16π
(E) 8π
Resolução
Adriana plantava em um circulo cujo raio mede 8 metros. Como ela vai plantar ervas medicinais em volta, reduzindo em 2 metros o diâmetro, o raio passará a medir 7 metros.
A área ocupada pelas ervas medicinais será a diferença entre as áreas dos circulo cujos raios medem 8 e 7 metros.
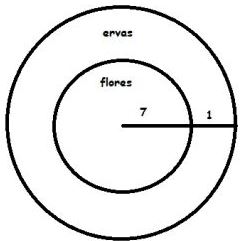
Calculando:
A = π . 8² – π . 7²
A = 64π – 49π
A = 15π
Alternativa C
23) (CEPERJ – SEPLAG) A razão entre a área e o perímetro de uma circunferência de raio R vale:
(A) R/π
(B) π/2
(C) πR/2
(D) 2R
(E) R/2
Resolução
Para resolvermos a questão, basta relembrarmos as fórmulas utilizadas para o cálculo da área do do perímetro de uma circunferência:
A = π.R²
P = 2π.R
Calculando a razão:
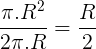
Alternativa E
24) (SESC PA – Coned) Qual o valor da área do círculo inscrito num quadrado, se a área do círculo circunscrito a esse quadrado mede 32π cm² ?
(A) 10 π cm²
(B) 8 π cm²
(C) 16 π cm²
(D) 12 π cm²
(E) 9 π cm²
Resolução
O primeiro passo para resolvermos a questão é calcular o raio do círculo circunscrito, do qual já sabemos a medida da sua área. Vamos utilizar a fórmula que calcula a área em função do raio:
A = π . r²
32π = π.r²
r² = 32
r = 4√2
Podemos observar na figura abaixo que o raio que achamos é a metade da diagonal do quadrado, onde podemos formar o triângulo retângulo ABC, cujo lado BC mede exatamente o raio do círculo inscrito no quadrado.
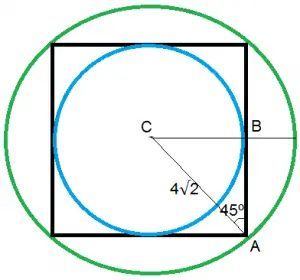
Temos:
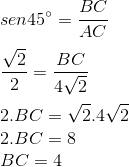
Agora que já sabemos o raio do circulo inscrito, podemos calcular sua área:
A = π.r²
A = π.4²
A = 16π cm²
Alternativa C
25) Uma circunferência possui raio medindo 5 cm, calcule o comprimento dela utilizando π = 3,14.
Resolucao
C = 2 . π . r
C = 2 . 3,14 . 5
C = 10 . 3,14
C = 31,4 cm
26) Uma piscina possui formato circular com comprimento igual a 33 metros. Utilizando π = 3, qual é o valor do raio da circunferência?
Resolucao
Sabemos que C = 33 metros, então, temos que:
C = 2 . π . r
33 = 2 . 3 . r
33 = 6r
6r = 33
r = 33/6
27) Em panelas de pressão, é bastante comum que exista um elástico envolvendo a tampa, com o objetivo de vedar e evitar a saída do vapor durante o uso da panela. Se uma determinada tampa possui 12 cm de diâmetro, então, o comprimento desse elástico deve ser igual a:
(Use π = 3,1.)
(A) 34,6 cm
(B) 35,2 cm
(C) 35,8 cm
(D) 37,2 cm
(E) 37,0 cm
Resolução
Se o diâmetro é igual a 12 cm, então o raio é a metade de 12 cm, ou seja, r = 6 cm.
Então, temos que:
r = 6
π = 3,1
C = 2 . π . r
C = 2 . 3,1 . 6
C = 6,2 . 6
C = 37,2 cm
Alternativa D
28) (PM ES – Exatus) Para realizar o teste físico em determinado concurso da PM, os candidatos devem correr ao redor de uma praça circular cujo diâmetro mede 120 m. Uma pessoa que dá 9 voltas ao redor dessa praça percorre: (Dado: π = 3)
(A) 1620 m
(B) 3240 m
(C) 4860 m
(D) 6480 m
(E) 8100 m
Resolução
O raio da circunferência é igual à metade do seu diâmetro, ou seja, d = 120 : 2 = 60 m.
C = 2 . π . r
C = 2 . 3 . 60
C = 6 . 60
C = 360 m
Como serão dadas 9 voltas, então, temos que: 360 · 9 = 3240 m.
Alternativa B
COMPRIMENTO DA CIRCUNFERENCIA NA AREA DO CIRCULO
Todo polígono regular pode ser inscrito em uma circunferência.
Imagine a seguinte situação, deseja-se projetar um eixo de uma roda cuja circunferência tem 5 cm de diâmetro. Se o eixo for em formato cilíndrico, não há mistério algum, pois terá a mesma medida do diâmetro, mas se o eixo for em formato de um prisma quadrangular, qual será as medidas dos lados?
Há cálculos rápidos para se determinar os lados de um quadrado inscrito e circunscrito em uma circunferência, mas antes vamos ver as relações existentes entre a circunferência e o quadrado através de construções geométricas e cálculos matemáticos.
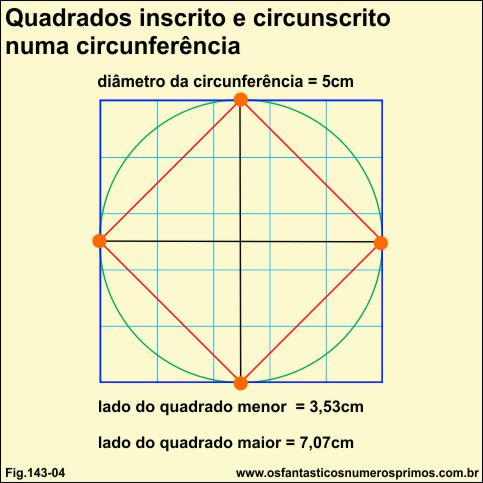
Quadrado inscrito numa circunferência
Desenhando circunferências de dimensões quaisquer e posteriormente traçando-se dois diâmetros perpendiculares em forma de "xis", os pontos em que as linhas dos diâmetros tocam a circunferência determinam as medidas dos lados do quadrado.
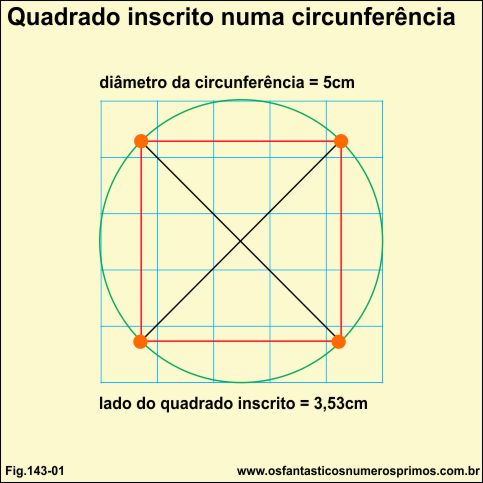 No exemplo acima, a circunferência está desenhada em diagrama quadriculado de 1cm cada.
No exemplo acima, a circunferência está desenhada em diagrama quadriculado de 1cm cada.
A circunferência possui um diâmetro de 5 cm e os lados do quadrado tem 3,53 cm.
Através do Teorema de Pitágoras - método 1
Traçando-se dois diâmetros perpendiculares e posteriormente o quadrado, determinamos também 2 triângulos retângulos isóceles maiores e 4 menores, com os quais podemos utilizar o Teorema de Pitágoras e descobrir as medidas dos lados do quadrado em função do diâmetro.
Observação importante: no quadrado inscrito numa circunferência o diâmetro é também a diagonal do quadrado.
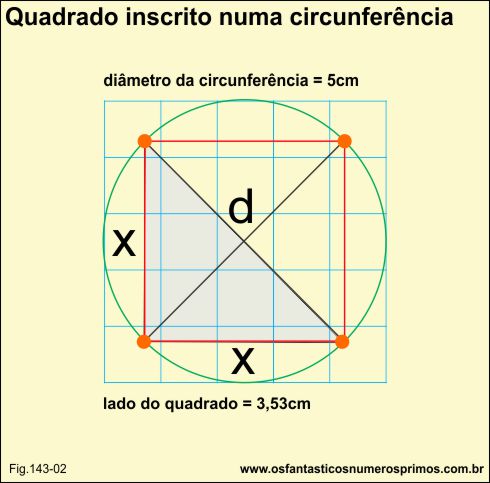 d2 = x2 + x2
d2 = x2 + x2
52 = x2 + x2
25 = 2x2
25/2 = x2
12,5 = x2
√12,5 = x
x = 3,53
Através do Teorema de Pitágoras - método 2
Traçando-se os diâmetros perpenciculares em formato de "xis" e posteriormente o quadrado, determinamos também quatro triângulos retângulos isóceles menores, com os quais podemos utilizar o Teorema de Pitágoras e determinar as medidas dos lados do quadrado em função do raio da circunferência.
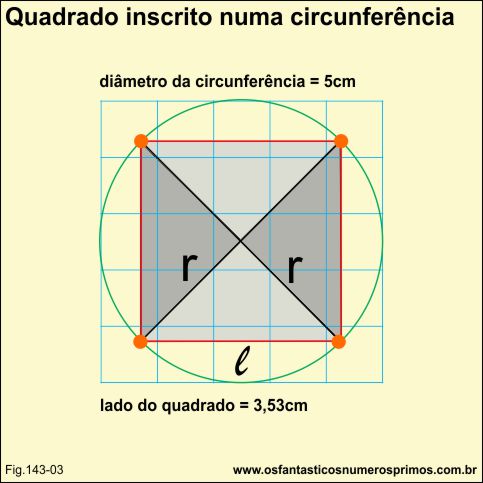
L2 = r2 + r2
L2 = 2,52 +2,52
L2 = 6,25 + 6,25
L2 = 12,5
L = √12,5
L = 3,53
Divisão do diâmetro pela √2 (raiz quadrada de 2)
Outro método de se determinar a medida dos lados do quadrado inscrito num circunferência é dividindo a medida do diâmetro pela raiz quadrada de 2 (√2 ).
5 : √2 = 5 : 1,4142 = 3,5355
Quadrados inscrito e circunscrito numa circunferência
Outra relação interessante existente entre circunferência e quadrado é que a partir do produto do diâmetro pela raiz quadrada de dois (√2 ) determina-se um outro quadrado, só que este circunscrito a circunferência.
Observação importante:
a) no quadrado inscrito numa circunferência o diâmetro é também a diagonal do quadrado.
b) no quadrado circunscrito numa circunferência o diâmetro é também o lado do quadrado.
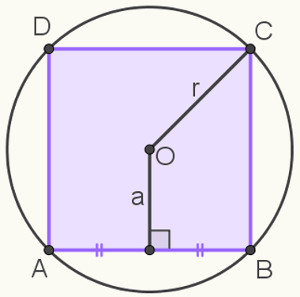
Quadrado inscrito numa circunferência e o apótema
Apótema é o seguimento de reta que parte do ponto médio do lado de um polígono até o centro da circunferência e do polígono.
Tendo-se uma das medidas (raio, lado ou apótema), podemos encontrar as duas outras. Nos cálculos podemos utilizar as relações métricas e trigonométricas nos triângulos retângulos.
Elementos básicos do polígono regular inscrito
1 – Centro: O centro de um polígono regular inscrito tem a mesma localização que o centro da circunferência que o circunscreve.
2 – Raio: O raio de um polígono regular inscrito é a distância entre seu centro e a borda da circunferência. Como se trata de um polígono, essa distância só pode ser obtida entre o centro do polígono e um de seus vértices.
3 – Apótema: É a distância entre o centro de um polígono regular e o ponto médio de um de seus lados. No caso do quadrado inscrito, o apótema também forma um ângulo reto com o lado com o qual faz contato.
A imagem a seguir mostra um exemplo dos elementos citados:
 Exemplo:
Exemplo:
Numa circunferência de 6cm de diâmetro calcular o apótema utilizando o Teorema de Pitágoras.
r2 = L2 + L2
32 = L2 + L2
32 = 2 L2
9 = 2 L2
9/2 = L2
L2 = √4,5
L = 2,12
Verificação:
Diâmento : √2 = lado do quadrado inscrito
6 : √2 = 4,24....
1/2 do lado do quadrado = apótema
1/2 x 4,24 = 2,12
ou
1/2 do diâmetro (raio) : √2 = apótema
3 : √2 = 2,12...
Exemplo:
Calcule a medida do lado e do apótema de um quadrado inscrito em uma circunferência de raio igual a 100 cm.
Resolucao
Para obter essas medidas, basta substituir o valor do raio nas fórmulas do apótema e do lado do quadrado inscrito na circunferência
l = r√2
l = 100√2
a = r√2
2
a = 100√2
2
a = 50√2
Observação
Dependendo da questao podemos aplicar o Teorem de Pitagoras
Teorem de Pitagoras
h2 = a2 + b2
 QUESTOES RESOLVIDAS
QUESTOES RESOLVIDAS
01) Determine a área de um círculo de raio medindo 20 cm. (Use π = 3,14)
Resolucao
r = 20 cm
π = 3,14
A =
A = π r2
A = 3,14 . 202
A = 3,14 .400
A = 1256 cm2
02) Calcule a área de um círculo de 30 cm de diâmetro. (Use π = 3,14)
Resolucao
d = 30 cm
r = d/2
r = 15 cm
A =
A = π r2
A = 3,14?152
A = 3,14?225
A = 706,5 cm2
03) Se um círculo possui a circunferência de 43,96 cm de comprimento, qual será o tamanho de sua área? (Use π = 3,14)
Resolucao
Solução: Note que não temos a medida do raio do círculo. Através do comprimento que foi dado, vamos encontrar a medida do raio. A fórmula do comprimento da circunferência é:
C = 2πr
43,96 = 2?3,14?r
43,96 = 6,28?r
r = 43,96/6,28
r = 7 cm
Conhecendo o valor do raio podemos calcular a área.
A = π r2
A=3,14 . 72
A=3,14 . 49
A=153,86 cm2
04) Um fazendeiro possui 628 m de tela para fazer um galinheiro. Existem dois projetos para a realização desse galinheiro: um galinheiro quadrado e um galinheiro circular. O fazendeiro irá optar pelo projeto que possuir a maior área. Qual dos dois projetos é o que irá satisfazer sua vontade? (Use π = 3,14)
Resolucao
Como o fazendeiro possui 628 m de tela para fazer o galinheiro, o perímetro do quadrado e da circunferência será de 628 m. Vamos então calcular a área de cada uma das figuras, usando a mesma quantidade de tela, e verificar qual dos projetos apresenta a maior área.
Área do quadrado:
Como o perímetro do quadrado é de 628 m, cada lado terá 157 m de comprimento. (628÷4)
Resolucao
A = 1572
A = 24649 m2
Área da circunferência:
Sabemos que o comprimento da circunferência também é 628 m, pois temos a mesma quantidade de tela. Precisamos encontrar a medida do raio dessa circunferência.
Resolucao
C = 2πr
628 = 2?3,14?r
628 = 6,28?r
r = 628/6,28
r = 100 m
Assim,
A = π r2
A = 3,14 . 1002
A = 3,14 . 10000
A = 31400 m2
Portanto, o galinheiro que terá a maior área será o de formato circular.
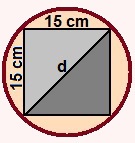
05) Considere um quadrado com lado de 15 cm inscrito em uma circunferência. Considerando π = 3,14 e √2 = 1,41, determine a medida aproximada do comprimento da circunferência com arredondamento de uma casa decimal.
Resolucao
Na figura a seguir há uma interpretação do quadrado inscrito na circunferência como proposto no enunciado:

Por meio do nTeorema de Pitagoras, podemos determinar a medida da diagonal do quadrado, que corresponde exatamente ao diâmetro da circunferência (d):
d² = 15² + 15²
d² = 225 + 225
d² = 450
d = 15√2
d = 15 . 1,41
d = 21,15 cm
Sabendo que o diâmetro mede 21,15 cm, podemos calcular o comprimento da circunferência pela seguinte fórmula:
C = π . d
C = 3,14 .21,15
C = 66,411 cm
Arredondando o resultado para uma casa decimal, podemos concluir que o comprimento da circunferência é de, aproximadamente, 66,4 cm.
06) Considerando que uma pizza tradicional grande possui 35 cm de raio e uma pizza tradicional pequena apresenta 25 cm, determine a diferença entre a área das duas pizzas.
Resolucao
Vamos calcular, separadamente, a área do círculo que corresponde à cada pizza:
Pizza Grande Pizza Pequena
AG = π . r² AP = π . r²
AG = π . (35)² AP = π . (25)²
AG = π . 1225 AP = π . 625
AG = 1225π cm² AP = 625π cm²
Conhecendo as duas áreas, vamos encontrar a diferença entre elas, a qual chamaremos de x:
x = AG – AP
x = 1225π – 625π
x = 600π cm²
Portanto, a diferença entre a área de uma pizza grande tradicional e a área de uma pizza pequena é de 600π cm².
07) Determine a medida do raio de uma praça circular que possui 9420 m de comprimento (Use π = 3,14).
Resolucao
A partir da fórmula do comprimento da circunferência, temos:
C = 2 . π . r
9420 = 2 · 3,14 · r
9420 = 6,28 · r
6,28 · r = 9420
r = 9420
6,28
r = 1500 m
Logo, o raio da praça circular em questão mede 1500 m.
08) (UEM-PR) Uma pista de atletismo tem a forma circular e seu diâmetro mede 80 m. Um atleta treinando nessa pista deseja correr 10 km diariamente. Determine o número mínimo de voltas completas que ele deve dar nessa pista a cada dia.
Resolucao
Se a pista circular possui 80 m de diâmetro, podemos facilmente determinar o comprimento dela por meio da fórmula:
C = π . d
C = π . 80
C = 80π m
Se o atleta corre 10 km (10.000 m) diariamente, podemos determinar o número de voltas (n) percorridas pelo atleta pelo quociente entre 10.000 m e o comprimento da pista:
n = 10000
80π
n = 125 voltas
π
Para um resultado mais preciso, vamos considerar π = 3,14:
n = 125
3,14
n ≈ 39,8 voltas
Podemos afirmar que o atleta dará aproximadamente 40 voltas.
09) (UESPI) Um trabalhador gasta 3 horas para limpar um terreno circular de 6 metros de raio. Se o terreno tivesse 12 metros de raio, quanto tempo o trabalhador gastaria para limpar tal terreno?
(A) 6 h.
(B) 9 h.
(C) 12 h.
(D) 18 h.
(E) 20 h.
Resolucao
Primeiramente, vamos calcular a área dos dois terrenos, A1 e A2:
A1 = π · r² A2 = π · r²
A1 = π · 6² A2 = π · 12²
A1 = 36π m² A2 = 144π m²
Portanto, podemos afirmar que o trabalhador gasta três horas para limpar um terreno de 36π m² e x horas para limpar um terreno de 144π m². Por meio de uma regra de três simples, temos:
3 h –––––– 36π m²
x h –––––– 144π m²
36π · x = 3 · 144π
x = 432 π
36π
x = 12 h
Podemos concluir que o trabalhador gastará 12 h para limpar um terreno de 12 metros de raio.
Alternativa C
10) (Furb - SC) “Lixo é basicamente todo e qualquer resíduo sólido proveniente das atividades humanas ou gerado pela natureza em aglomerados urbanos. O lixo faz parte de nossa vida e tratá-lo bem é uma questão de bom senso, cidadania e bem-estar agora e principalmente no futuro.”(www.loucosporlixo.com.br). Pensando nisso, um grupo teatral quer representar uma peça sobre a importância da reciclagem do lixo. Eles querem montar um cenário no qual 3 paredes de 4 m de altura por 5 m de comprimento deverão ser revestidas de CDs defeituosos. Sabendo-se que cada CD possui 12 cm de diâmetro, quantos Cds, aproximadamente, serão necessários para revestir essas paredes? (Use π = 3,14)
(A) 5200.
(B) 5300.
(C) 5400.
(D) 5500.
(E) 5600.
Resolucao
Sabendo que o raio é a metade do diâmetro, vamos determinar o raio de cada CD em metros:
r = d
2
r = 0,012
2
r = 0,06 m
Conhecido o raio do CD, já podemos identificar a sua área:
Acd = π · r²
Acd = 3,14 · (0,06)²
Acd = 3,14 · 0,0036
Acd = 0,011304 m²
Vamos agora determinar a área do cenário, lembrando que serão três paredes com 4 m de altura por 5 m de comprimento:
Acenário = (base · altura) · 3
Acenário = (5 · 4) · 3
Acenário = 60 m²
Para sabermos a quantidade x de CDs necessária para revestir todo o cenário, basta calcular o quociente entre a área do cenário e a área de cada CD:
x = 60
0,011304
x ≈ 5307,8
Portanto, serão necessários aproximadamente 5308 CDs.
Alternativa B
11) Determine a área destacada da figura, considerando que o raio da circunferência inscrita no quadrado seja igual a 4 metros.
.jpg) Resolução
Resolução
Área do quadrado é dada pela expressão: A = L²
Área da circunferência é dada pela expressão: A = π . r²
O raio da circunferência é igual a 4 metros, dessa forma seu diâmetro vale 8. A medida do lado do quadrado será correspondente ao diâmetro da circunferência, medindo 8 metros.
Área do quadrado
A = l²
A = 8²
A = 64 m²
Área da circunferência
A = π . r²
A = 3,14 . 4²
A = 3,14 . 16
A = 50,24 m²
A área da parte destacada é resultante da subtração entre a área do quadrado e a área da circunferência.
A = 64 – 50,24
A = 13,76 m²
Portanto, a área destacada é igual a 13,76 metros quadrados.
12) (Termomecanica) Um quadrado tem 24√2cm de perímetro. Suas vértices pertencem à circunferência que se vê na figura.
 O comprimento da circunferência será, então, em cm, igual a
O comprimento da circunferência será, então, em cm, igual a
(A) 12 π
(B) 18 π
(C) 24 π
(D) 24 π2
Resolucao
Nesse caso a lada mede 6√2cm
Aplicandso Pitagora
h2 = a2 + b2
h2 = (6√2)2 + (6√2)2
h2 = (36 . 2) + 36 . 2
h2 = 72 + 72
h2 = 144
h = √144
h = 12
Observação 2:
Nesse caso o raio da circunferência equivale a metade da diagonal ou seja o raio = 3
r = 12/2
r = 3
Apliocando a formula d o comprimento da circunferencia
C = 2 π r
C = 2π6
C = 12π
Alternativa A
Continua ...











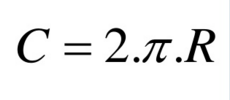
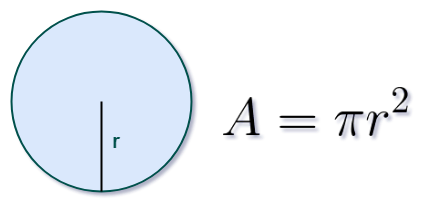


 O setor circular é algo que se parece com uma fatia de pizza. A parte restante também é chamada de setor circular.
O setor circular é algo que se parece com uma fatia de pizza. A parte restante também é chamada de setor circular.
.jpg)


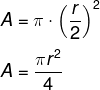
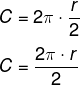
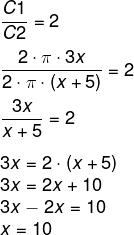












.jpg)

