EF II - DIVISIBILIDADE

Professor Diminoi
DIVISIBILIDADE

Critérios de divisibilidade
Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios de divisibilidade.

Divisibilidade por 2
Um número natural é divisível por 2 quando ele termina em 0, ou 2, ou 4, ou 6, ou 8, ou seja, quando ele é par.

Exemplos:
a) 5040 é divisível por 2, pois termina em 0.
b) 237 não é divisível por 2, pois não é um número par.

Divisibilidade por 3
Um número é divisível por 3 quando a soma dos valores absolutos dos seus algarismos for divisível por 3.

Exemplo:
234 é divisível por 3, pois a soma de seus algarismos é igual a 2 + 3 + 4 = 9, e como 9 é divisível por 3, então 234 é divisível por 3.

Divisibilidade por 4
Um número é divisível por 4 quando termina em 00 ou quando o número formado pelos dois últimos algarismos da direita for divisível por 4.

Exemplo:
1800 é divisível por 4, pois termina em 00.
4116 é divisível por 4, pois 16 é divisível por 4.
1324 é divisível por 4, pois 24 é divisível por 4.
3850 não é divisível por 4, pois não termina em 00 e 50 não é divisível por 4.

Divisibilidade por 5
Um número natural é divisível por 5 quando ele termina em 0 ou 5.

Exemplos:
a) 55 é divisível por 5, pois termina em 5.
b) 90 é divisível por 5, pois termina em 0.
c) 87 não é divisível por 5, pois não termina em 0 nem em 5.

Divisibilidade por 6
Um número é divisível por 6 quando é divisível por 2 e por 3.

Exemplos:
a) 312 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 6).
b) 5214 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 12).
c) 716 não é divisível por 6, (é divisível por 2, mas não é divisível por 3).
d) 3405 não é divisível por 6 (é divisível por 3, mas não é divisível por 2).

Divisibilidade por 8
Um número é divisível por 8 quando termina em 000, ou quando o número formado pelos três últimos algarismos da direita for divisível por 8.

Exemplos:
a) 7000 é divisível por 8, pois termina em 000.
b) 56104 é divisível por 8, pois 104 é divisível por 8.
c) 61112 é divisível por 8, pois 112 é divisível por 8.
d) 78164 não é divisível por 8, pois 164 não é divisível por 8.

Divisibilidade por 9
Um número é divisível por 9 quando a soma dos valores absolutos dos seus algarismos for divisível por 9.

Exemplo:
2871 é divisível por 9, pois a soma de seus algarismos é igual a 2 + 8 + 7 + 1 = 18, e como 18 é divisível por 9, então 2871 é divisível por 9.

Divisibilidade por 10
Um número natural é divisível por 10 quando ele termina em 0.

Exemplos:
a) 4150 é divisível por 10, pois termina em 0.
b) 2106 não é divisível por 10, pois não termina em 0.

Divisibilidade por 11
Um número é divisível por 11 quando a diferença entre as somas dos valores absolutos dos algarismos de ordem ímpar e a dos de ordem par é divisível por 11.
O algarismo das unidades é de 1ª ordem, o das dezenas de 2ª ordem, o das centenas de 3ª ordem, e assim sucessivamente.

Exemplos:
a) 87549
Si (soma das ordens ímpares) = 9 + 5 + 8 = 22
Sp (soma das ordens pares) = 4 + 7 = 11
Si - Sp = 22 - 11 = 11
Como 11 é divisível por 11, então o número 87549 é divisível por 11.

b) 439087
Si (soma das ordens ímpares) = 7 + 0 + 3 = 10
Sp (soma das ordens pares) = 8 + 9 + 4 = 21
Si - Sp = 10- 21
Como a subtração não pode ser realizada, acrescenta-se o menor múltiplo de 11 (diferente de zero) ao minuendo, para que a subtração possa ser realizada: 10 + 11 = 21. Então temos a subtração 21-21 = 0.
Como zero é divisível por 11, o número 439087 é divisível por 11.

Divisibilidade por 12
Um número é divisível por 12 quando é divisível por 3 e por 4.

Exemplos:
a) 720 é divisível por 12, porque é divisível por 3 (soma = 9 ) e por 4 (dois últimos algarismos, 20).
b) 870 não é divisível por 12 (é divisível por 3, mas não é divisível por 4).) 340 não é 3divisível por 12 (é divisível por 4, mas não é divisível por 3).

Divisibilidade por 15
Um número é divisível por 15 quando é divisível por 3 e por 5.

Exemplos:
a) 105 é divisível por 15, porque é divisível por 3 (soma = 6) e por 5 (termina em 5).
b) 324 não é divisível por 15 (é divisível por 3, mas não é divisível por 5).
c) 530 não é divisível por 15 (é divisível por 5, mas não é divisível por 3).

Divisibilidade por 25
Um número é divisível por 25 quando os dois algarismos finais forem 00, 25, 50 ou 75.

Exemplos:
200, 525, 850 e 975 são divisíveis por 25.
 
Números primos
Números primos são os números naturais que têm apenas dois divisores diferentes: o 1 e ele mesmo.

Exemplos:
a)2tem apenas os divisores 1 e 2, portanto 2 é um número primo.
b) 17 tem apenas os divisores 1 e 17, portanto 17 é um número primo.
c) 10 tem os divisores 1, 2, 5 e 10, portanto 10 não é um número primo.

Observações:
1 não é um número primo, porque ele tem apenas um divisor que é ele mesmo.
2 é o único número primo que é par.

Os números que têm mais de dois divisores são chamados números compostos.

Exemplo:
15 tem mais de dois divisores => 15 é um número composto.

Reconhecimento de um número primo
Para saber se um número é primo, dividimos esse número pelos números primos 2, 3, 5, 7, 11, etc, até que tenhamos:
- ou uma divisão com resto zero (e neste caso o número não é primo),
- ou uma divisão com quociente menor que o divisor e o resto diferente de zero. Neste caso o número é primo.

Exemplos:
1) O número 161:
Não é par, portanto não é divisível por 2;
1 + 6 + 1 = 8, portanto não é divisível por 3;
Não termina em 0 nem em 5, portanto não é divisível por 5;
Por 7:  161 / 7 = 23, com resto zero, logo 161 é divisível por 7, e portanto não é um número primo.

2) O número 113:
Não é par, portanto não é divisível por 2;
1 + 1 + 3 = 5, portanto não é divisível por 3;
- não termina em 0 nem em 5, portanto não é divisível por 5;
Por 7:  113 / 7 = 16, com resto 1. O quociente (16) ainda é maior que o divisor (7).
Por 11:  113 / 11 = 10, com resto 3. O quociente (10) é menor que o divisor (11), e além disso o resto é diferente de zero (o resto vale 3), portanto 113 é um número primo

Decomposição em fatores primos
Todo número natural, maior que 1, pode ser decomposto em um produto de dois ou mais fatores.
Decomposição do número 24 em um produto:
24 = 4 x 6
24 = 2 x 2 x 6
24 = 2 x 2 x 2 x 3 = 2³ x 3

No produto 2 x 2 x 2 x 3, todos os fatores são primos.
Chamamos de fatoração de 24 a decomposição de 24 em um produto de fatores primos.
Então a fatoração de 24 é 2³ x 3.
De um modo geral, chamamos de fatoração de um número natural, maior
que 1, a sua decomposição em um produto de fatores primos.

Regra prática para a fatoração
Existe um dispositivo prático para fatorar um número. Acompanhe, no exemplo, os passos para montar esse dispositivo:

1º) Dividimos o número pelo seu menor divisor primo;
2º) a seguir, dividimos o quociente obtido pelo menor divisor primo desse quociente e assim sucessivamente até obter o quociente 1.
A figura mostra a fatoração do número 630.
Então
630 = 2 x 3 x 3 x 5 x 7
630 = 2 x 3² x 5 x 7

Determinação dos divisores de um número
Na prática, determinamos todos os divisores de um número utilizando os seus fatores primos. Vamos determinar, por exemplo, os divisores de 90:
1º) decompomos o número em fatores primos;
2º) traçamos uma linha e escrevemos o 1 no alto, porque ele é divisor de qualquer número;
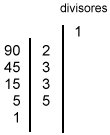3º) multiplicamos sucessivamente cada fator primo pelos divisores já obtidos e escrevemos esses produtos ao lado de cada fator primo;
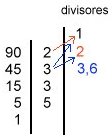4º) os divisores já obtidos não precisam ser repetidos.
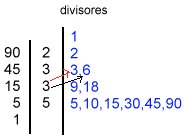Portanto os divisores de 90 são 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90.

Máximo divisor comum (M.D.C.)
Dois números naturais sempre têm divisores comuns. Por exemplo: os divisores comuns de 12 e 18 são 1,2,3 e 6. Dentre eles, 6 é o maior. Então chamamos o 6 de máximo divisor comum de 12 e 18 e indicamos m.d.c.(12,18) = 6.
 
Observação: O maior divisor comum de dois ou mais números é chamado de máximo divisor comum desses números. Usamos a abreviação m.d.c.

Alguns exemplos:
mdc (6,12) = 6
mdc (12,20) = 4
mdc (20,24) = 4
mdc (12,20,24) = 4
mdc (6,12,15) = 3

Cálculo do M.D.C.
Um modo de calcular o m.d.c. de dois ou mais números é utilizar a decomposição desses números em fatores primos.
a) decompomos os números em fatores primos;
b) o d.c. é o produto dos fatores primos comuns.

Acompanhe o cálculo do m.d.c. entre 36 e 90:
36 = 2 x 2 x 3 x 3
90 =     2 x 3 x 3 x 5

O m.d.c. é o produto dos fatores primos comuns => m.d.c.(36,90) = 2 x 3 x 3
Portanto m.d.c.(36,90) = 18.

Escrevendo a fatoração do número na forma de potência temos:
36 = 2² x 3²
90 = 2 x 3² x 5
Portanto m.d.c.(36,90) = 2 x 3² = 18.

Observacao: O m.d.c. de dois ou mais números, quando fatorados, é o produto dos fatores comuns a eles, cada um elevado ao menor expoente.

Cálculo do M.D.C. pelo processo das divisões sucessivas
Nesse processo efetuamos várias divisões até chegar a uma divisão exata. O divisor desta divisão é o m.d.c. Acompanhe o cálculo do m.d.c.(48,30).

Regra prática:
1º) dividimos o número maior pelo número menor;
48 / 30 = 1 (com resto 18)

2º) dividimos o divisor 30, que é divisor da divisão anterior, por 18, que é o resto da divisão anterior, e assim sucessivamente;
30 / 18 = 1 (com resto 12)
18 / 12 = 1 (com resto 6)
12 / 6 = 2 (com resto zero - divisão exata)

3º) O divisor da divisão exata é 6. Então m.d.c.(48,30) = 6.

Números primos entre si
Observação: Dois ou mais números são primos entre si quando o máximo divisor comum desses números é 1.

Exemplos:
Os números 35 e 24 são números primos entre si, pois mdc (35,24) = 1.
Os números 35 e 21 não são números primos entre si, pois mdc (35,21) = 7.

Propriedade do M.D.C.
Dentre os números 6, 18 e 30, o número 6 é divisor dos outros dois. Neste caso, 6 é o m.d.c.(6,18,30). Observe que:
6 = 2 x 3
18 = 2 x 3²
30 = 2 x 3 x 5
Portanto m.d.c.(6,18,30) = 6

Observação: Dados dois ou mais números, se um deles é divisor de todos os outros, então ele é o m.d.c. dos números dados.

Mínimo múltiplo comum (M.M.C.)
Múltiplo de um número natural
Como 24 é divisível por 3, dizemos que 24 é múltiplo de 3.
24 também é múltiplo de 1, 2, 3, 4, 6, 8, 12 e 24.

Observação: Se um número é divisível por outro, diferente de zero, então dizemos que ele é múltiplo desse outro.
Observacaso: Os múltiplos de um número são calculados multiplicando-se esse número pelos números naturais.

Exemplo: os múltiplos de 7 são:
7x0 , 7x1, 7x2 , 7x3 , 7x4 , ...  =  0 , 7 , 14 , 21 , 28 , ...

Observações importantes
a) Um número tem infinitos múltiplos
b) Zero é múltiplo de qualquer número natural

O que é M.M.C.?
Dois ou mais números sempre têm múltiplos comuns a eles. Vamos achar os múltiplos comuns de 4 e 6:
Múltiplos de 6:  0, 6, 12, 18, 24, 30,...
Múltiplos de 4:  0, 4, 8, 12, 16, 20, 24,...
Múltiplos comuns de 4 e 6:  0, 12, 24,...
Dentre estes múltiplos, diferentes de zero, 12 é o menor deles. Chamamos o 12 de mínimo múltiplo comum de 4 e 6.

Observação: O menor múltiplo comum de dois ou mais números, diferente de zero, é chamado de mínimo múltiplo comum desses números. Usamos a abreviação m.m.c.

Cálculo do M.M.C.
Podemos calcular o m.m.c. de dois ou mais números utilizando a fatoração. Acompanhe o cálculo do m.m.c. de 12 e 30:
1º) decompomos os números em fatores primos
2º) o m.m.c. é o produto dos fatores primos comuns e não-comuns:
12   =  2  x  2  x  3
30   =   2  x  3   x  5
m.m.c (12,30)  = 2  x  2  x  3   x  5

Escrevendo a fatoração dos números na forma de potência, temos:
12 = 2²  x  3
30 = 2   x  3  x  5
m.m.c (12,30)  = 2²  x  3  x  5

Observação: O m.m.c. de dois ou mais números, quando fatorados, é o produto dos fatores comuns e não-comuns a eles, cada um elevado ao maior expoente.

Processo da decomposição simultânea
Neste processo, decompomos todos os números ao mesmo tempo, em um dispositivo como mostra a figura ao lado. O produto dos fatores primos que obtemos nessa decomposição é o m.m.c. desses números. A seguir vemos o cálculo do m.m.c.(15,24,60).
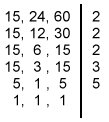Portanto, m.m.c.(15,24,60) = 2 x 2 x 2 x 3 x 5 = 120

Propriedade do M.M.C.
Entre os números 3, 6 e 30, o número 30 é múltiplo dos outros dois. Neste caso, 30 é o m.m.c.(3,6,30).
Veja que:
m.m.c.(3,6,30) = 2 x 3 x 5 = 30
Observação: Dados dois ou mais números, se um deles é múltiplo de todos os outros, então ele é o m.m.c. dos números dados.
Considere os números 4 e 15, que são primos entre si. O m.m.c.(4,15) é igual a 60, que é o produto de 4 por 15.

Veja que:
m.m.c.(4,15) = 2 x 2 x 3 x 5 = 60
Observação: Dados dois números primos entre si, o m.m.c. deles é o produto desses números.


Continua ...