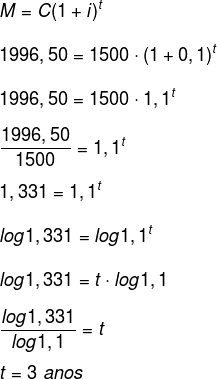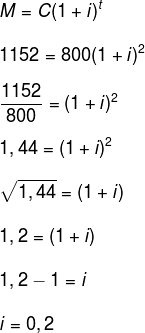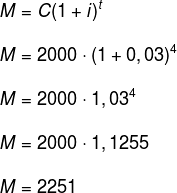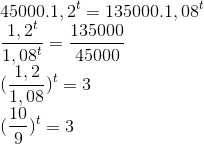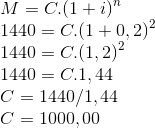MATEMÁTICA FINACEIRA I

Professor Diminoi

O que é e para que serve a matemática financeira?
A matemática financeira ajuda imensamente no planejamento e gestão do dinheiro de uma empresa. Matemática financeira é uma área de aplicação prática da matemática, que consiste em cálculos direcionados à melhor organização e ao maior controle do dinheiro. Para entender melhor, basta lembrar da importância da organização e planejamento ao contratar um empréstimo ou obter um financiamento, seja para aquisição de um veículo ou imóvel.

Qual a importância da matemática financeira no mundo corporativo?
A saúde financeira de uma empresa e o seu fluxo de caixa podem ser calculados com a matemática financeira. Ao observar os exemplos trazidos no tópico anterior, quanto à aplicação da matemática financeira em âmbito pessoal, já dá para ter uma ideia da sua importância para as empresas.

O que são juros
Juros são a contrapartida de emprestar dinheiro (ou outro item) a uma pessoa ou instituição. Eles são representados por um percentual sobre o valor total e podem ser calculados de forma simples ou composta. É uma espécie de cobrança de aluguel.
Ou seja, o tomador do empréstimo recebe uma soma que poderá destinar ao uso que lhe convier.
Enquanto isso, o credor ganha um rendimento por não dispor desse valor para utilização até recebê-lo de volta e pelo risco de calote, que ocorre quando a pessoa ou instituição que contraiu a dívida não a quita.
Em termos práticos, quando você compra um título do Tesouro Direto, por exemplo, você está investindo na dívida do governo. O governo se financia dessa forma: como ele é um bom pagador, ele toma o seu dinheiro e o premia com juros mensais compostos.

Juros simples
No sistema de capitalização simples, os juros são calculados com base no valor da dívida ou da aplicação. Dessa forma, o valor dos juros é igual no período de aplicação ou composição da dívida.

Juros Compostos
Os juros compostos são aqueles nos quais os juros do mês são incorporados ao capital. Com uma taxa assim, o valor cresce muito mais rápido do que com juros simples.

Montante
O Montante, também conhecido como Valor Acumulado, é um dos conceitos básicos da matemática financeira. Dedica-se a estudar e controlar a variação sofrida por uma quantia investida ao longo do tempo.
Em outras palavras, é através deste cálculo que contabilizamos os ganhos (retornos de investimento) de uma pessoa física ou jurídica e os juros (simples ou composto) produzidos sobre essa quantia.
O montante é importante pois permite ter melhor planejamento financeiro (trabalhando com relatórios, históricos e, então, previsões) para evitar o pagamento de juro abusivo. Para isso, precisamos saber como é desenvolvido seu cálculo.

EXERCÍCIOS RESOLVIDOS
01) Qual o valor do montante produzido por um capital de R$ 1.200,00, aplicado no regime de juros simples a uma taxa mensal de 2% durante 10 meses?
Resolução:
C = 1200
i = 2% = 2/100 = 0,02 ao mês (a.m.)
t = 10 meses
J = C . i . t
J = 1200 . 0,02 . 10
J = 240
M = C + j
M = 1200 + 240
M = 1440
Resposta: o montante produzido é de R$ 1.440,00.

02) Determine o valor do capital que, aplicado durante 14 meses a uma taxa de 6%, rendeu juros de R$ 2.688,00.
Resolução:
J = C . i . t
2688 = C . 0,06 . 14
2688 = C . 0,84
C = 2688 / 0,84
C = 3200
Resposta: o valor do capital é de R$ 3.200,00.

03) Qual o capital que, aplicado a juros simples de 1,5% ao mês, rende R$ 3.000,00 de juros em 45 dias?
Resolução:
J = 3000
i = 1,5% = 1,5/100 = 0,015
t = 45 dias = 45/30 = 1,5
J = C . i . t
3000 = C . 0,015 . 1,5
3000 = C . 0,0225
C = 3000 / 0,0225
C = 133.333,33
Resposta: o capital é de R$ 133.333,33.

04) Qual foi o capital que, aplicado à taxa de juros simples de 2% ao mês, rendeu R$ 90,00 em um trimestre?
Resolução:
J = C .  i . t
90 = C . 0,02 . 3
90 = C . 0,06
C = 90 / 0,06
C = 1500
Resposta: o capital corresponde a R$ 1.500,00.

05) Qual o tempo de aplicação para que um capital dobre, considerando uma taxa mensal de juros de 2% ao mês, no regime de capitalização simples?
Resolução:
M = C . [1 + (i . t)]
2C = C . [1 + (0,02 . t)]
2C = C . 1 + 0,02t
2C/C = 1 + 0,02t
2 = 1 + 0,02t
2 – 1 = 0,02t
1 = 0,02t
t = 1 / 0,02
t = 50
Resposta: o tempo para que o capital aplicado a uma taxa mensal de 2% dobre é de 50 meses.

06) Quanto tempo um capital de R$1500 aplicado a juros compostos, com taxa de 10% a.a, leva para gerar um montante de R$1996,50?
Resolução:

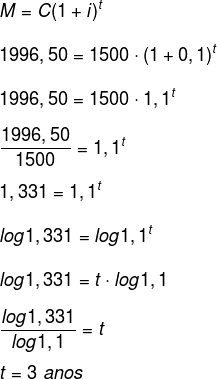
07) Qual é a taxa de juros aplicada ao ano para que um capital de R$800 gere um juros de R$352 em dois anos?
Resolução:

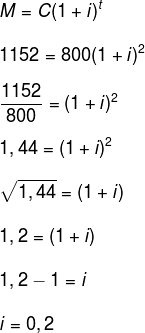
08) Uma pessoa aplicou o capital de R$ 1.200,00 a uma taxa de 2% ao mês durante 14 meses. Determine os juros e o montante dessa aplicação.
Resolução:
C = R$ 1.200,00
t = 14 meses
i = 2% ao mês = 2/100 = 0,02
J = C . i . t
J = 1200 . 0,02 * 14
J = 336
Montante
M = C + J
M = 1200 + 336
M = 1536
Resposta: O valor dos juros da aplicação é de R$ 336,00 e o montante a ser resgatado é de R$ 1.536,00.

09) Um capital aplicado a juros simples durante 2 anos, sob taxa de juros de 5% ao mês, gerou um montante de R$ 26.950,00. Determine o valor do capital aplicado. 
Resolução:
C = R$ 1.200,00
t = 14 meses
i = 2% ao mês = 2/100 = 0,02
Fórmula dos juros simples
J = C . i . t
J = 1200 . 0,02 . 14
J = 336
Montante
M = C + J
M = 1200 + 336
M = 1536
Resposta: o valor dos juros da aplicação é de R$ 336,00 e o montante a ser resgatado é de R$ 1.536,00.

10) Um investidor aplicou a quantia de R$ 500,00 em um fundo de investimento que opera no regime de juros simples. Após 6 meses o investidor verificou que o montante era de R$ 560,00. Qual a taxa de juros desse fundo de investimento?
Resolução:
C = R$ 500,00
M = R$ 560,00
t = 6 meses
Calculando os juros da aplicação
J = M – C
J = 560 – 500
J = 60
Aplicando a fórmula
J = C . i . t
60 = 500 . i . 6
60 = 3000 . i
i = 60/3000
i = 0,02 que corresponde a 2%.
Resposta: A taxa de juros do fundo de investimentos é igual a 2%.

11) (UF–PI) Uma quantia foi aplicada a juros simples de 6% ao mês, durante 5 meses e, em seguida, o montante foi aplicado durante mais 5 meses, a juros simples de 4% ao mês. No final dos 10 meses, o novo montante foi de R$ 234,00. Qual o valor da quantia aplicada inicialmente?
Resolução:
1ª aplicação
i = 6% ao mês = 0,06
t = 5 meses
J = C . i . t
J = C . 0,06 . 5
J = 0,3 . C
M = C + J
M = C + 0,3C
M = 1,3C
2º aplicação
C = 1,3C
i = 4% ao mês = 0,04
t = 5 meses
O capital da 2º aplicação será o montante da 1º
J = C . i . t
J = 1,3C . 0,04 . 5
J = 0,26C
M = C + J
234 = 1,3C + 0,26C
234 = 1,56C
C = 234 / 1,56
C = 150
Resposta: o capital inicial é de R$ 150,00.

12) Quanto conseguirei se investir um capital de R$2000 a juros composto, de 3% a.a., durante um período de 48 meses?
Resolução:
C = 2000,00
i =  % a.a.
t = 48 meses = 4 anos (note que a taxa está em anos)
M =

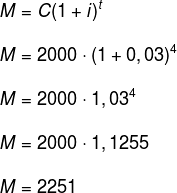
13) Um investidor aplica R$ 1.000,00 a juros simples de 3% ao mês. Determine o valor recebido após um ano:
Resolução:
P = 1.000,00
I = 3% ou 0,03
n = 1 ano = 12 meses
J = P . i . n
J = 1000 . 0,03. 12
J = 360
O juro obtido será de 360, somando-se ao capital, temos:
M = P + j
M  = 1000 + 360
M = 1.360,00
Resolução: após um ano o investidor recebeu R$ 1.360,00.

14) Calcule o juro que renderá um capital de R$ 15.000,00 aplicado a uma taxa de juros simples de 12% ao ano, durante seis meses.
Resolução:
Como a taxa está anual, vamos convertê-la para meses: 12% /12 = 1%
J = P . i . n
J = 15.000 . 0,01. 6
J = 900
Resposta: o juro aplicado será de R$ 900,00.

15) Um capital de 7.500,00 foi aplicado em um investimento que rende juro simples de 5% ao mês. Qual será o saldo dessa aplicação após seis meses?
(A) 2.250,00
(B) 10.000,00
(C) 9.750,00
(D) 8.500,00
Resolução:
p = 7.500,00
i = 5% ou 0,05
n = 6
M = ?
J = P . i . n
J = 7.500 . 0,05 . 6
J = 2.250
M = J + C
M = 2.250 + 7.500
M = 9.750
O saldo dessa aplicação será de R$ 9.750,00.
Alternativa: C

16) Um capital foi aplicado a juro simples com taxa de 10% ao mês, durante cinco meses. Se no fim desse período o juro produzido foi de R$ 305. Qual foi o capital aplicado?
(A) 500,00
(B) 600,00
(C) 390,00
(D) 610,00
Resolução:
J = P . i . n
305 = p . 0,10 . 5
305 = p . 0,50
p = 305/0,5
p = 610
O capital aplicado foi de R$ 610,00.
Alternativa: D

17) Qual o montante produzido por um capital de R$ 2.000,00, aplicado a juros compostos de 2% ao mês, durante um ano?
Resolução:
M = C. (1 + i)t
M = montante
C = capital
i = taxa
t = tempo
Dados
M =
C = 2000
i = 2% = 2/100 = 0,02
t = 1 ano = 12 meses (pois a taxa é ao mês)
M = C . (1 + i)t
M = 2000 . (1+0,02)12
M = 2000 . 1,0212
M = 2000.1,268242
M = 2.536,48
Resposta:  montante produzido ao final de um ano será de R$ 2.536,48.

18) Qual deve ser o capital que, no sistema de juros compostos, à taxa de 4% ao mês, gera um montante de R$ 12.154,90 ao final de 1 ano e 6 meses?
Resolução:
M = 12.154,90
C = ?
i = 4% = 4/100 = 0,04
t = 1 ano e 6 meses = 18 meses
M = C . (1 + i)t
12.154,90 = C . (1 + 0,04)18
12.154,90 = C . 1,0418
12.154,90 = C . 2,0258
C = 12.154,90 / 2,0258
C = 6.000
Resposta: o capital será de R$ 6.000,00.

19) Calcule o montante de um capital de R$ 12.000,00 aplicado durante 3 anos em um banco que paga no regime de juros compostos uma taxa de 1,5% a.m.
Resolução:
M =
C = 12.000
i = 1,5% = 1,5/100 = 0,015
t = 3 anos = 36 meses (pois a taxa de juros é mensal)
M = C. (1 + i)t
M = 12000 . (1 + 0,015)36
M = 12000 . 1,01536
M = 12000 .  1,70914
M = 20.509,68
Resposta: o montante será de R$ 20.509,68.

20) O capital de R$ 1.500,00, aplicado a juros compostos, rendeu, após 2 meses, juros de R$ 153,75. Qual foi a taxa de juros?
Resolução:
M = 1500 + 153,75 = 1653,75
M = C . (1 + i)t
1653,75 = 1500 . (1 + i) 2
1653,75 / 1500 = (1 + i) 2
(1 + i) 2 = 1,1025
√(1 + i) 2 = √1,1025 (use a calculadora para extrair a raiz quadrada de 1,1025)
1 + i = 1,05
i = 1,05 – 1
i = 0,05 ou 5%
Resposta: a taxa de juros empregada foi de 5%.

21) Uma aplicação especial rende 1,5% ao mês em regime de juros compostos. Certa pessoa deseja aplicar a quantia de R$ 620,00 durante 2 anos. Determine o montante gerado por essa aplicação.
Resolução:
C = 620
t = 2 anos = 24 meses
i = 1,5% = 1,5/100 → 0,015
M = C . (1 + i)t
M = 620 . (1 + 0,015)24
M = 620 . 1,01524
M = 620 . 1,429503
M = 886,29
Resposta: o montante gerado será de R$ 886,29. 

22) Um capital de R$ 1 000,00 é aplicado a juros mensais de 4% ao mês, gerando um montante de R$ 1 731,68. Determine o tempo de aplicação desse capital. 
Resolução:
C = 1 000
M = 1 731,68
i = 4% = 4/100 = 0,04
M = C . (1 + i)t
1 731,68 = 1 000 . (1 + 0,04)t
1 731,68 / 1 000 = 1,04t
1,731680 = 1,04t
1,04t = 1,731680  (aplicar propriedade dos logaritmos)
log1,04t = log1,731680
t . log1,04 = log1,731680
t = log1,731680 / log1,04
t = 0,2384 / 0,0170
t = 14
Resposta: o tempo de aplicação o capital foi de 14 meses.

23) Uma aplicação financeira rende 2% a juros compostos. Determine o tempo mínimo necessário para que o capital dobre de valor.
Resolução:
M = 2C
M = C . (1 + i)t
2C = C . (1 + 0,02)t
2C / C = 1,02t
2 = 1,02t
1,02t = 2
log 1,02t = log 2
t . log 1,02 = log 2
t . 0,0086 = 0,30103
t = 0,30103 / 0,0086
t = 35
O tempo que um capital leva para duplicar seu valor, a uma taxa de 2% ao mês, é de 35 meses. Caso queira verificar, basta escolher um capital e aplicá-lo à taxa de 2% ao mês e tempo de 35 meses. Observe:
Capital de R$ 100,00
M = 100 . (1 + 0,02)35
M = 100 . 1,0235
M = 100 . 2
M = 200
Capital de R$ 300,00
M = 300 . 1,0235
M = 300 . 2
M = 600 

24) Aplicando hoje na caderneta de poupança a quantia de R$ 20.000,00, qual será o montante gerado ao final de 4 anos, sabendo que a rentabilidade mensal é de 0,5%?
Resolução:
J = C. (1+i)t
C = 20.000
i = 0,005 a.m
t = 48 meses
Substituindo os valores temos que:
J = 20.000 .(1+0,005)48
J = 20.00 . (1,005)48
J = 25409,78
Resposta: os juros serão de R$25409,78.

25) Quanto receberá de juros, no fim de um semestre, uma pessoa que investiu, a juros compostos, a quantia de R$5.000,00, à taxa de 1% ao mês?
Resolução:
J = C .(1+i)t
C = 5000
i = 0,01 a.m
t = 6 meses
A partir dos dados obtemos que:
J = 5000 . (1+0,01)6         
J = 5000 .(1,01)6
J = 5307,60
Resposta: os juros serão de R$5307,60.

26) (BB – Cesgranrio) João tomou um empréstimo de R$ 900,00 a juros compostos de 10% ao mês. Dois meses depois, João pagou R$ 600,00 e, um mês após esse pagamento, liquidou o empréstimo. O valor desse último pagamento foi, em reais, aproximadamente,
(A) 240,00
(B) 330,00
(C) 429,00
(D) 489,00
(E) 538,00
Resolução:
Valor à vista: 900
t = 10% = 0,1
Observação: quando tratamos de prestações, devemos reduzir todas ao mesmo período através da fórmula:
P/(1 + i)ⁿ
Em nosso caso, vamos reduzir todas ao período de tempo inicial.
A primeira parcela (no ato) já se encontra no período inicial.
A segunda, como é após um mês, basta considerarmos n = 1 na fórmula.
Devemos então resolver a seguinte equação:
900 = 600/1,1² + x/1,1³
900 = 600/1,21 + x/1,331
900 = 495,87 + x/1,331
900 – 495,87 = x/1331
404,13 = x/1,331
x = 404,13.1,331
x = 537,9
Alternativa: E

27) (BB 2011 – FCC) Saulo aplicou R$ 45 000,00 em um fundo de investimento que rende 20% ao ano. Seu objetivo é usar o montante dessa aplicação para comprar uma casa que, na data da aplicação, custava R$ 135 000,00 e se valoriza à taxa anual de 8%. Nessas condições, a partir da data da aplicação, quantos anos serão decorridos até que Saulo consiga comprar tal casa?
(A) 15.
(B) 12.
(C) 10.
(D) 9.
(E) 6.
Resolução:
Sendo t o tempo (em anos) onde o valor aplicado por Saulo é igual ao valor da casa, temos a seguinte equação:
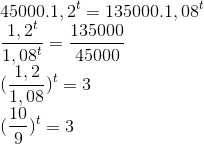Utilizando a definição e as propriedades dos logaritmos:
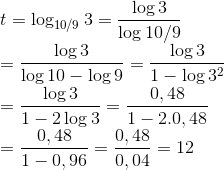Alternativa: B

28) (PM PR – Cops) Qual deve ser o capital inicial que um cidadão deve aplicar em um fundo de renda fixa, que utiliza o sistema de juros compostos e que rende 20% ao ano, de modo que ele tenha R$ 1.440,00 ao final de dois anos?
(A) R$ 960,00
(B) R$ 975,00
(C) R$ 1.000,00
(D) R$ 1.003,00
(E) R$ 1.010,00
Resolução:
Utilizando a fórmula de juros compostos:
Onde:
M = 1440
C =
i = 0,2
n = 2
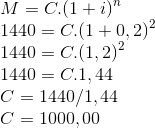Alternativa: C

29) (BASA – Cesgranrio) Um valor inicial C₀ foi capitalizado por meio da incidência de juros compostos mensais constantes iguais a 6,09%. Ao final de 6 meses, isto é, após 6 incidências dos juros, gerou-se o montante M.
A partir do valor inicial C₀, seria alcançado o mesmo montante M ao final de 12 meses (12 incidências), se os juros compostos mensais constantes tivessem sido iguais a
(A) 1,045%
(B) 1,450%
(C) 3,045%
(D) 3,450%
(E) 3,000%
Resolução:
Utilizando a fórmula de juros compostos para n = 6 meses e i = 0,0609 (6,09% ao mês), temos:
M = C . (1 + i)ⁿ
M = C₀ . (1 + 0,0609)⁶
M = C₀ . 1,0609⁶
Utilizando a mesma fórmula, agora para n = 12 meses, e taxa igual a j (ao mês).
M = C₀ . (1 + j)¹²
Igualando as expressões:
C₀ . 1,0609⁶ = C₀ . (1 + j)¹²
1,0609⁶ =(1 + j)¹²
Tirando a raiz sexta em ambos os lados:
1,0609 = (1+j)²
1,03 = 1 + j
j = 1,03 – 1
j = 0,03 = 3% a.m.
Alternativa: E

31) (PM PE – IAUPE) O valor da fatura de um cartão de crédito era de R$ 1.200,00. Tendo sido paga com dois meses de atraso, o cartão de crédito cobrou juros compostos de 17% ao mês. Quanto foi o montante pago?
(A) R$ 1.241,14
(B) R$ 1.505,28
(C) R$ 1.642,68
(D) R$ 1.452,00
(E) R$ 1.228,97
Resolução:
Temos:
C = 1200
i = 0,17
n = 2 meses
Utilizando a fórmula do montante para juros compostos:
M = C.(1 + i)²
M = 1200.(1 + 0,17)²
M = 1200.1,17²
M = 1200.1,3689
M = 1642,68
Alternativa: C

32) (Termomecânica) Uma pessoa aplica R$ 5.400,00 à taxa de 12,5% ao ano, em regime de juros simples. Para que esse capital seja duplicado, o tempo de aplicação deve ser de
(A) 6 meses.
(B) 8 meses.
(C) 7,5 anos.
(D) 8 anos.
(E) 8,5 anos.
Resolução:
J =
c = 5 400,00
i = 12,5
t = 1
j = c . i . t
j = 5 400 . 12,5 . 1/100
j = 675
675 . 8 = 5 400
Alternativa: D

33) (Termomecânica) Para negociar o pagamento de uma dívida de R$ 2,16 milhões com o banco, uma empresa precisará pagar 0,25 do valor da dívida no momento da negociação, como 1.a parcela da quitação. Após trinta dias, pagará uma parcela de R$ 360 mil, sem juros, e o saldo devedor será amortizado em três prestações mensais e iguais, também sem juros. O valor de cada uma dessas prestações será de
(A) R$ 275.000,00.
(B) R$ 302.000,00.
(C) R$ 315.000,00.
(D) R$ 400.000,00.
(E) R$ 420.000,00.
Resolução:
2 160 000,000 milhões
Observação: para facilitar os cálculos vamso trabalhando apenas com numeros diferentes de zero.
216 . 0,25 = 54
Subtraidndo da dívida
216 – 54 = 162
Fazendo 162 – 36 = 126
Dividindo 123/3 = 42
Não esqueça que temso que acresentar  quatro zeros, u seja, o restante fica em três prestações de 420.000,00
Alternativa: E

34) (Termomecânica) Um capital foi colocado em uma aplicação A, a juro simples, com taxa de 0,5% ao mês, durante 7 meses. Se esse mesmo capital tivesse sido colocado em uma aplicação B, durante um ano, teria rendido o triplo do juro obtido na aplicação A. A taxa mensal da aplicação B era
(A) 0,925%.
(B) 0,875%.
(C) 0,785%.
(D) 0,625%.
Resolução:
0,5  . 7 = 10,5
Fazendo 10,5/12 = 0,875
Alternativa: B
 
35) (Termomecânica)  Com de seu salário, Augusto pagou R$ 250,00 de supermercado, R$ 180,00 de condomínio e R$ 70,00 de farmácia. Augusto emprestou, a um colega de serviço, 20% de seu salário a juros simples a uma taxa de 1,5% ao mês. Após 5 meses, o montante de dinheiro devolvido foi de
(A) R$ 268,75.
(B) R$ 278,75.
(C) R$ 287,50.
(D) R$ 292,50.
Resolução:
Primeiro calcular o salário de Augusto
2/5x = 250 + 180 + 7
2/5x = 500
x = 500/(2/5
x = 500 . 5/2
x = 1250/2
x = 1250
Calcular 20% de 1259
1250 --- 100
x      ---  20
100x  = 1259 . 2
100x = 2500
x = 2500/100
x = 250
Calcular o juro
J = c . i .t
J = 250 . 1,5 . 5/100
J = 1875/10
J = 18,75
Montate é Capital (C) + Juroas (J)
M = 250 + 18,75
M = 268,75
Alternativa: A
 
36) (Termomecânica) Joaquim José precisava comprar um automóvel para poder trabalhar. Seu amigo Murilo ofereceu-lhe seu próprio automóvel, pois desejava trocá-lo por um novo. Combinaram que o negócio seria concretizado por R$ 15.000,00. Como Joaquim José não dispunha de todo o dinheiro, ficou acertado que ele daria R$ 5.000,00 no ato da transação e pagaria o restante em 10 prestações mensais, consecutivas e iguais a juros simples de 2,5% ao mês. Ao final do financiamento, esse carro terá custado a Joaquim José a quantia de
(A) R$ 12.500,00.
(B) R$ 17.500,00.
(C) R$ 22.500,00.
(D) R$ 27.500,00.
Resolução:
Valor do carro: R$ 15 000
Entrada: 5 000
Restante: 10 000
Calular o juro de 10 000
J =
c = 10 000
i = 2,5
t = 12
J = c . i . t
J = 10 000 . 2,5 . 12/100
J = 2 500
Valor total: entrada de 5 000 + juros 2 500 + motante 10 000
Tolal: 17 500,00
Alternativa: B

37) (Termomecânica) João dispõe de apenas R$ 3 900,00 para pagar as dívidas A, B, C e D, cujos valores são, respectivamente, R$ 1 200,00, R$ 800,00, R$ 1200,00 e R$ 1 600,00. Decidiu pagar integralmente a dívida A, que era mais antiga, e repartir o restante em partes diretamente proporcionais às quantias devidas para B, C e D. O valor não pago da divida D é
(A) R$ 300,00.
(B) R$ 400,00.
(C) R$ 500,00.
(D) R$ 600,00.
Resolução:
Das alternativas o único valor que dividido por 800, 1200 e 1600 é 400
Alternativa: B

38) (Termomecânica) Camilo recebeu um empréstimo de R$ 8.000,00 de seu irmão e combinou devolver essa quantia, acrescida de juro simples, após 9 meses. Na data programada, Camilo fez um pagamento de R$ 8.576,00 ao irmão e liquidou a dívida. A taxa mensal de juro simples desse empréstimo
foi de:
(A) 0,9%
(B) 0,85%
(C) 0,8%
(D) 0,75%
Resolução:
J = 8 576 – 8 000 = 576
c = 8 000
i =
t = 9
M = 8 576
J = c . i . t
576 = 8000 . i .9
576 = 72 000i
576/7200 = i
0,008 = i
i = 0,008 , 10
i = 0.8
Alternativa: C

39) (Termomecânica) Uma pessoa aplicou, a juros simples, um certo capital durante dez meses a uma taxa mensal fixa. Nesse período, seu dinheiro rendeu 50% de juros. A taxa mensal dessa aplicação foi de
(A) 4,2%.
(B) 4,5%.
(C) 4,8%.
(D) 5,0%.
Resolução:
Montante = Captal + Juros
150 = 100 + (100 . i .9)
150 = 100 + 900i
150 -100 = /900i
50 = 900i
0,05 = i
0,05  .100 = 5
Alternativa: D
 

Continua...