EQUANCÃO DO 2º GRAU - 9º ANO

Professor Diminoi
9ºANO - MATEMATICA

Álgebra
Equações de 2º grau: resolução e problemas
Noções básicas sobre função
A ideia de interdependência

Construção de tabelas e gráficos para representar funções de 1o e 2o graus

EQUAÇÃO DO 2º GRAU
Existem diversos modos de se resolver uma equação do segundo grau, contudo, nem sempre essas formas apresentam o melhor método de resolução. Dessa maneira, para agilizar a solução de exercícios de um modo geral, apresentaremos três passos que facilitarão bastante o processo!
Os três passos seguintes baseiam-se na fórmula de Bhaskara, que é o método resolutivo para equações do segundo grau mais popular entre os estudantes.

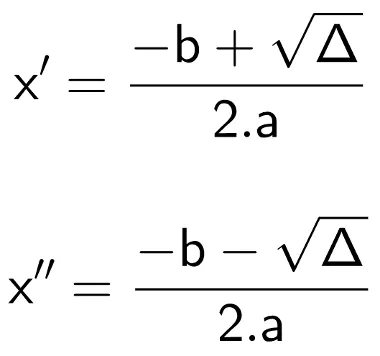
Primeiro passo: 
Escreva os valores numéricos dos coeficientes a, b e c.

Toda equação do segundo grau pode ser escrita na forma ax² + bx + c = 0.
Desse modo:
O coeficiente a é o número que esta companho do x².
O coeficiente b é o número que esta companho do x
O coeficiente c é um número que não esta companho do x.
Portanto, dada uma equação do segundo grau, escreva os valores de a, b e c de forma clara, objetiva e evidente para que eventuais consultas a esses valores sejam feitas rapidamente.
Como exemplo, vamos escrever os coeficientes da equação 2x² + 8x – 24 = 0.
a = 2
b = 8
c = – 24

Segundo passo: 
Calcule o valor de delta.
O valor de delta é dado pela seguinte expressão: Δ = b² – 4ac, em que a, b e c são coeficientes da equação e Δ é delta.

Tomando o exemplo anterior, na equação 2x² + 8x – 24 = 0, delta vale:
Δ = b² – 4ac
Δ = 8² – 4·2·(– 24)
Δ = 64 + 192
Δ = 256

Terceiro passo: 
calcule os valores de x da equação.
Após calcular o valor de delta, os valores de x podem ser obtidos por meio da seguinte expressão:
x = – b ± √Δ
           2·a

Observe que nessa expressão aparece o sinal ±. Isso indica que x possui dois valores: o primeiro para a √Δ (raiz de delta) negativa e o segundo para √Δ positiva.

Tomando o exemplo já citado, observe a conclusão do terceiro passo:
x = – b ± √Δ
           2·a
x = – 8 ± √256
            2·2

Não pare agora... Tem mais depois da publicidade ;)
x = – 8 ± 16
            4

Para √Δ negativa, teremos:
x' = – 8 – 16 = –24 = –6
             4          4         

Para √Δ positiva, teremos:
x'' = – 8 + 16 = 8 = 2
             4         4      

Observações importantes:
Ao calcular o valor de Δ, o aluno depara-se com o jogo de sinais. É preciso ter extrema atenção ao termo “– 4ac”, pois, muitas vezes, c possui um valor negativo, o que torna esse termo positivo em virtude do jogo de sinais.
O mesmo ocorre ao encontrar os valores de x. Repare que existe um “– b” na fórmula. Se b for negativo, por causa do jogo de sinais, – b será positivo (+ b).
O valor de Δ pode ser utilizado como parâmetro para decidir como serão as raízes da equação em que:
Δ > 0 possui duas raízes reais distintas
Δ = 0 possui duas raízes reais iguais ou uma raiz real dupla, isto é, x' = x''
Δ < 0 não possui raízes reais.

Para ajudar a decorar as fórmulas utilizadas, sempre as escreva em seu caderno para cada exercício que for resolvido, recitando-as em voz alta.

Exemplo:
Quais são as raízes da equação x² – x – 30 = 0?

Passo 1:
a = 1
b = – 1
c = – 30.

Passo 2:
cálculo do valor de delta
Δ = b² – 4ac
Δ = (–1)² – 4·1·(–30)
Δ = 1 + 120
Δ = 121

Passo 3:
Calcule os valores de x:
x = – b ± √Δ
     2·a
x = – (–1) ± √121
      2·1
x = 1 ± 11
      2
x' = 1 + 11 = 12 = 6
   2         2
x'' = 1 – 11 = – 10 = – 5
2          2
Logo, as raízes ou valores de x para essa equação são 6 e – 5.

Fórmula de Bhaskara 


Exercícios resolvidos
00) Determinar a solução da seguinte equação do 2º grau: x² + 8x + 16 = 0.
Os coeficientes são:
a = 1
b = 8
c = 16
∆ = b² – 4 . a . c
∆ = 8² – 4 . 1 . 16
∆ = 64 – 64
∆ = 0
x = – b ± √∆
           2a
x = – 8 ± √0
     2 . 1
x' = x'' = –8 = – 4
    2
No exemplo 2, devemos observar que o valor do discriminante é igual a zero. Nesses casos, a equação possuirá somente uma solução ou raiz única.

00) Calcule o conjunto solução da equação 10x² + 6x + 10 = 0, considerada de 2º grau.
∆ = b² – 4 . a . c
∆ = 6² – 4 . 10 . 10
∆ = 36 – 400
∆ = – 364
Nas resoluções em que o valor do discriminante é menor que zero, isto é, o número é negativo, a equação não possui raízes reais.

Questões [a, b, c]
(a) Aplicando a fórmula de Bhaskara, resolva a seguinte equações do 2º grau 3x² – 7x + 4 = 0.
Resolução:


(b) Aplicando a fórmula de Bhaskara, resolva a seguinte equações do 2º grau 9y² – 12y + 4 = 0
Resolução:


(c) Aplicando a fórmula de Bhaskara, resolva a seguinte equações do 2º grauc 5x² + 3x + 5 = 0
Resolução:

00) Determine quais os valores de k para que a equação 2x² + 4x + 5k = 0 tenha raízes reais e distintas. 
Resolução:
Uma equação do 2º grau possui duas raízes reais e distintas quando ∆ > 0, então:


00) Calcule o valor de p na equação x² – (p + 5)x + 36 = 0, de modo que as raízes reais sejam iguais.
Para essa condição, o valor de ∆ precisa ser igual a 0.
Resolução:


00) Resolva a seguinte equação do 2º grau.

Resolução:


00) Resolva a equação do 2° grau 2x² + x – 3 = 0.
Resolução:
Uma das alternativas para solucionar equações do 2° grau é através da fórmula de Bhaskara. Para tanto, precisamos identificar os coeficientes da equação, que são a = 2, b = 1 e c = – 3.

Δ = 1² – 4.2.(– 3)
Δ = 1 + 24
Δ = 25
x = – 1 ± √25
      2.2
x = – 1 ± 5
      4
x' = – 1 + 5 = 4 = 1
     4        4
x'' = – 1 – 5 = – 6 = – 3
         4        4       2
As raízes da equação 2x² + x – 3 = 0 são 1 e ^{– 3}/_2.

00) Determine o conjunto solução da equação – 3x² + 18x – 15 = 0.
Resolução:
Os coeficientes numéricos dessa equação do 2° grau são a = – 3, b = 18 e c = – 15. Observe que todos os coeficientes são múltiplos de 3, por isso podemos dividir todos por 3 para obter valores menores e, consequentemente, mais fáceis de calcular. Os novos coeficientes são: a = – 1, b = 6 e c = – 5. Ao realizar essa simplificação dos coeficientes, o resultado da equação permanece inalterado.
Vamos aplicar esses coeficientes na fórmula de Bhaskara:
Δ = 6² – 4.(– 1).(– 5)
Δ = 36 – 20
Δ = 16
x = – 6 ± √16
      2.(– 1)
x = – 6 ± 4
     – 2
x' = – 6 + 4 = – 2 = 1
    – 2       – 2
x'' = – 6 – 4 = – 10 = 5
      – 2      – 2
O conjunto solução é S = {1; 5}.

00) (Puc – Rio) As duas soluções de uma equação do 2° grau são – 1 e ¹/₃. Então a equação é:
(A) 3x² – x – 1 = 0
(B) 3x² + x – 1 = 0
(C) 3x² + 2x – 1 = 0
(D) 3x² – 2x – 2 = 0
(E) 3x² – x + 1 = 0
Resolução:
Para encontrar a equação do 2° grau a partir de suas raízes, basta fazer:
(x – S₁) · (x – S₂) = 0
S₁ e S₂ são as raízes da equação. Vamos substituí-las na operação acima:
(x – (– 1)) · (x – (¹/₃)) = 0
(x + 1) · (x – (¹/₃)) = 0
x² – (¹/₃)x + x – ¹/₃ = 0
x² + (²/₃)x – ¹/₃ = 0
Podemos multiplicar toda a equação por 3:
3x² + 2x – 1 = 0
Alternativa: C

09) (Cesgranrio) A maior raiz da equação – 2x² + 3x + 5 = 0 vale:
(A) – 1
(B) 1
(C) 2
(D) 2,5
(E) (3 + √19)/4
Resolução:
Para resolver essa equação do 2° grau, vamos utilizar a Fórmula de Bhaskara. Os coeficientes da equação são a = – 2, b = 3 e c = 5. Substituindo-os na fórmula, temos:
Δ = 3² – 4.(– 2).5
Δ = 9 + 40
Δ = 49
x = – 3 ± √49
      2.(– 2)
x = – 3 ± 7
      – 4
x' = – 3 + 7 = 4 = – 1
 – 4     – 4
x'' = – 3 – 7 = – 10 = 2,5
– 4       – 4
Encontramos duas raízes para a equação, x' = – 1 e x'' = 2,5; e a maior delas é x'' = 2,5.
Alternativa: B


00) Resolva a equação: 4x² + 8x + 6 = 0
Resolução:
Os coeficientes da equação são: a = 4, b = 8, c = 6. Substituindo esses valores na fórmula de Bhaskara, temos:
Δ = 8² – 4.4.6
Δ = 64 – 96
Δ = – 32
Como Δ < 0, a equação não possui raiz real.

00) Encontre as raízes da equação: x² – 4x – 5 = 0
Resolução:
Os coeficientes dessa equação são: a = 1, b = – 4, c = – 5. Agora basta aplicar esses valores na fórmula de Bhaskara:
Δ = (– 4)² – 4.1.(– 5)
Δ = 16 + 20
Δ = 36
x = – (– 4) ± √36
             2.1
x = 4 ± 6
         2
x' = 10 = 5
        2
x'' = – 2 = – 1
          2
Nesse caso, a equação tem duas raízes reais: – 1 e 5.

Soma e Produto
A soma e produto é um método prático para encontrar as raízes de equações do 2º grau do tipo x² - Sx + P e é indicado quando as raízes são números inteiros.
Baseia-se nas seguintes relações entre as raízes:
Sendo,
x₁ e x₂: raízes da equação do 2º grau
a, b e c: coeficientes da equação do 2º grau

Desta forma, podemos encontrar as raízes da equação ax² + bx + c = 0, se encontrarmos dois números que satisfaçam simultaneamente as relações indicadas acima.

Se não for possível encontrar números inteiros que satisfaçam as duas relações ao mesmo tempo, devemos utilizar outro método de resolução.

Como encontrar esses números?
Para encontrar a solução devemos começar buscando dois números cujo produto seja igual a  c / a. Depois verificamos se esses números também satisfazem o valor da soma.
Como nem sempre as raízes de uma equação do 2º grau são positivas, devemos aplicar as regras de sinais da soma e da multiplicação para identificarmos quais sinais devemos atribuir as raízes.

Para tal, teremos as seguintes situações:
P > 0 e S > 0 ⇒ As duas raízes são positivas.
P > 0 e S
P 0 ⇒ As raízes possuem sinais diferentes e a de maior valor absoluto é positiva.
P

Exercícios Resolvidos
00) Um retângulo possui a medida de seu lado maior igual ao quádruplo do lado menor, e área medindo 256 m². Determine a medida de seus lados.
Informe que, para calcularmos a área de uma região retangular devemos multiplicar o comprimento pela largura.
Resolução:

O lado de maior comprimento mede 32 metros e o de menor comprimento, 8 metros.
 
00) Um trapézio possui área medindo 384 cm². Temos que a medida da altura é o dobro da medida da base menor, e que a base maior possui a mesma medida da altura. Determine o comprimento da base maior, base menor e altura desta figura.
Resolução:
Área do trapézio

Lado maior: 2 * 8√2 → 16√2 cm
Lado menor: 8√2 cm
Altura: 16√2 cm

00) O dobro de um número subtraído de 20 é igual a 100. Qual é o número?
Resolução:
Um número: x
O dobro do número: 2x
Como estamos subtraindo 2x de 20 a equação será:
20 – 2x = 100
Resolvendo a equação
20 – 2x = 100
– 2x – 20 + 20 = 100 – 20 (adicionamos 20 aos dois lados da equação)
– 2x = 80 (– 1)
2x = – 80
x = – 80
          2
x = – 40
Resposta: o número é igual a – 40.

00) O triplo de um número adicionado ao seu dobro resulta em 600. Qual é o número?
Resolução:
Um número: x
O triplo deste número: 3x
O dobro deste número: 2x
O triplo de um número adicionado ao seu dobro resulta em 600: 3x + 2x = 600
Resolvendo a equação:
3x + 2x = 600
5x = 600
x = 600/5
x = 120
Resposta: temos que o número é igual a 120.

00) Que número eu sou? O dobro de meu antecessor, menos 3, é igual a 25.
Resolução:
Um número: x
Antecessor: x – 1
O dobro de meu antecessor menos 3: 2(x – 1) – 3 = 25
Resolvendo a equação
2(x – 1) – 3 = 25 (aplicar o método da distribuição)
2x – 2 – 3 = 25
2x – 5 = 25
2x = 25 + 5
2x = 30
x = 30/2
x = 15
Resposta: o número é igual a 15.

00) Carlos tinha certa quantia em dinheiro, foi ao shopping e gastou 1/3 da quantia na compra de uma revista, gastou 1/4 da quantia na compra de um CD e ainda ficou com R$ 25,00. Qual era a quantia que Carlos possuía?
Resolução:
Quantia: x
Um terço da quantia: 1/3x
Um quarto da quantia: 1/4x
Equação do problema: (1/3)x + (1/4)x + 25 = x
MMC (3,4) = 12
(4/12)x + (3/12)x + 300 = (12/12)x (simplificando os denominadores)
4x + 3x + 300 = 12x
12x – 4x – 3x = 300
12x – 7x = 300
5x = 300
x = 300/5
x = 60
Resposta: Carlos possuía a quantia de R$ 60,00.

00) Os 44 alunos da 7ª série A de uma escola representam 40% de todos os alunos da 7ª série dessa mesma instituição. Quantos são os alunos da 7ª série dessa escola?
Resolução:
Alunos: x
40% = 40/100 = 2/5 dos alunos
2/5 de x
(2/5)x = 44
2x = 44 * 5
2x = 220
x = 220/2
x = 110
Resposta: a escola possui 110 alunos cursando a 7ª série.

00) Determine três números inteiros positivos e consecutivos tais que o quadrado do menor seja igual a diferença dos outros dois.
Resolução:
Acreditamos que nesse tipo de problema, os alunos têm dificuldade em interpretar corretamente, visto que é muito comum a montagem da equação errada: x² = (x + 1) – (x + 2).
O quadrado de um número não pode ser negativo, portanto, neste caso, devemos fazer (x + 2) – (x + 1) e não o contrário.
Devemos, então, enfatizar, que a leitura atenta do enunciado é fundamental para uma correta interpretação!
Uma proposta de solução:
Interpretando o problema e usando a linguagem algébrica:
x, representa o menor número
x + 1, representa o consecutivo de x
x + 2, representa o consecutivo de x + 1

Observação: Poderíamos também representá-los por x, x – 1 e x – 2. Nesse caso, x representa o maior dos três números.

Como estratégia de resolução, procedemos a montagem da equação de acordo com o enunciado do problema:
x² = (x + 2) – (x + 1)
Desenvolvendo, temos:
x² = x + 2 – x – 1
x² = 1
Lembrando que:
Temos:
Logo, x = 1 ou x = –1
Analisando a condição do problema, “três números inteiros positivos e consecutivos”, a única solução que satisfaz é x = 1.
Resposta: os números são 1, 2 e 3.

00) Pai e filho têm hoje 45 e 15 anos, respectivamente. Há quantos anos a idade do pai era igual ao quadrado da idade do filho?
Resolução:
Em problemas como esse que envolvem tempo decorrido — Há quantos anos... — é importante comentar na turma, que o sinal de menos (–), não significa “retirar” uma quantidade e sim, voltar no tempo! O mesmo vale para situações que se remetem a tempo futuro: “Daqui a quanto tempo...”. O sinal de mais (+) significa avançar no tempo.
Uma proposta de solução:
De acordo com o enunciado, podemos fazer uma representação algébrica das idades do pai e do filho, há x anos.
idade do pai há x anos: 45 – x
idade do filho há x anos: 15 – x
Equalizando as informações: 45 – x = (15 – x)²
Desenvolvendo a equação, obtemos:
45 – x = 225 – 30x + x² Utilizando o princípio de equivalência, temos:
x² – 29x + 180 = 0
Resolvendo a equação utilizando as relações entre coeficientes e raízes:
S = 29
P = 180
Devemos pensar em dois números positivos (soma e produto positivos).
Os números são: 9 e 20.
Analisando os resultados encontrados, o valor 20 não pode ser usado no problema, pois, nesse caso, o filho teria idade negativa!
Portando, para x = 9 temos para idades: 36 e 6 anos.
Resposta: há 9 anos.

Função
Uma função é uma regra que relaciona cada elemento de um conjunto a um único elemento de outro. O primeiro conjunto é chamado de domínio, e o segundo, contradomínio da função.
As funções possuem diversas aplicações no cotidiano, sempre relacionando grandezas, valores, índices, variações entre outras situações. Por exemplo, a inflação é medida através da função que relaciona os preços atuais com os preços anteriores, dentro de um determinado período, caso ocorra variação para mais dizemos que houve inflação, e havendo variação para menos, denominamos deflação. A distância percorrida por um veículo depende da quantidade de combustível presente no tanque. Ciências como a Física, a Química e a Biologia utilizam em seus cálculos as propriedades das funções para demonstrarem a ocorrência de determinados fenômenos. Dessa forma, é muito importante obter o conhecimento adequado sobre as propriedades e definições das funções matemáticas.
A formalização matemática para a definição de função é dada por: Seja X um conjunto com elementos de X e Y um conjunto dos elementos de y, temos que:
f: x → y
Assim sendo, cada elemento do conjunto x é levado a um único elemento do conjunto y. Essa ocorrência é determinada por uma lei de formação.
A partir dessa definição, é possível constatar que x é a variável independente e que y é a variável dependente. Isso porque, em toda função, para encontrar o valor de y, devemos ter inicialmente o valor de x.

Um exemplo prático é a relação existente em um posto de gasolina entre a quantidade de litros de gasolina e o preço a pagar:
Enfatize que existe uma relação lógica entre os dois conjuntos, o valor a ser pago depende da quantidade de litros de gasolina. Podemos perceber que o valor do litro da gasolina é R$2,50. Dizemos que o preço a pagar é dado em função da quantidade de litros. A linguagem matemática utilizada para expressar esse tipo de situação pode ser dada da seguinte maneira:
Cada valor x de A corresponde a um único valor f(x) em B, dado pela função f.

Demonstre a linguagem existente nas funções através de gráficos envolvendo os diagramas de flecha: domínio, contradomínio e imagem.
Ressalte que A é o domínio, B é o contradomínio e C a imagem do conjunto A.
Elemento y de B, associado ao elemento x de A, é denominado imagem de x.

É importante dizer que para ser uma função, todos os elementos do domínio precisam estar associados a um único elemento do contradomínio, formando a imagem.
Observe:
Tipos de funções
As funções podem ser classificadas em três tipos, a saber:

Função injetora ou injetiva
Nessa função, cada elemento do domínio (x) associa-se a um único elemento da imagem f(x). Todavia, podem existir elementos do contradomínio que não são imagem. Quando isso acontece, dizemos que o contradomínio e imagem são diferentes.
Exemplo:
Conjunto dos elementos do domínio da função: D(f) = {-1,5, +2, +8}
Conjunto dos elementos da imagem da função: Im(f) = {A, C, D}
Conjunto dos elementos do contradomínio da função: CD(f) = {A, B, C, D}
Função Sobrejetora ou sobrejetiva
Na função sobrejetiva, todos os elementos do domínio possui um elemento na imagem. Pode acontecer de dois elementos do domínio possuírem a mesma imagem.
Nesse caso, imagem e contradomínio possuem a mesma quantidade de elementos.
Conjunto dos elementos do domínio da função: D(f) = {-10, 2, 8, 25}
Conjunto dos elementos da imagem da função: Im (f) = {A, B, C}
Conjunto dos elementos do contradomínio da função: CD (f) = {A, B, C}
Função bijetora ou bijetiva
Essa função é ao mesmo tempo injetora e sobrejetora, pois, cada elemento de x relaciona-se a um único elemento de f(x). Nessa função, não acontece de dois números distintos possuírem a mesma imagem, e o contradomínio e a imagem possuem a mesma quantidade de elementos.
Conjunto dos elementos do domínio da função: D(f) = {-12, 0, 1, 5}
Conjunto dos elementos da imagem da função: Im (f) = {A, B, C, D}
Conjunto dos elementos do contradomínio da função: CD (f) = {A, B, C, D}
As funções podem ser representadas graficamente. Para que isso seja feito, utilizamos duas coordenadas, que são x e y. O plano desenhado é bidimensional. A coordenada x é chamada de abscissa e a y, de ordenada. Juntas em funções, elas formam leis de formação. Veja a imagem do gráfico do eixo x e y:


Do último ano do Fundamental e ao longo do Ensino Médio, geralmente estudamos doze funções, que são:
1 – Função constante;
2 – Função par;
3 – Função ímpar;
4 – Função afim ou polinomial do primeiro grau;
5 – Função Linear;
6 – Função crescente;
7 – Função decrescente;
8 – Função quadrática ou polinomial do segundo grau;
9 – Função modular;
10 – Função exponencial;
11 – Função logarítmica;
12 – Funções trigonométricas;
13 – Função raiz.

Gráfico e a fórmula geral de cada uma das funções listadas acima:

1 - Função constante
Na função constante, todo valor do domínio (x) tem a mesma imagem (y).

Fórmula geral da função constante:
f(x) = c
x = Domínio
f(x) = Imagem
c = constante, que pode ser qualquer número do conjunto dos reais.

Exemplo de gráfico da função constante: f(x) = 2
2 – Função Par
A função par é simétrica em relação ao eixo vertical, ou seja, à ordenada y. Entenda simetria como sendo uma figura/gráfico que, ao dividi-la em partes iguais e sobrepô-las, as partes coincidem-se perfeitamente.

Fórmula geral da função par:
f(x) = f(- x)
x = domínio
f(x) = imagem
- x = simétrico do domínio

Exemplo de gráfico da função par: f(x) = x²
3 – Função ímpar
A função ímpar é simétrica (figura/gráfico que, ao dividi-la em partes iguais e sobrepô-las, as partes coincidem-se perfeitamente) em relação ao eixo horizontal, ou seja, à abscissa x.
Fórmula geral da função ímpar
f(– x) = – f(x)
– x = domínio
f(– x) = imagem
- f(x) = simétrico da imagem

Exemplo de gráfico da função ímpar: f(x) = 3x
4 – Função afim ou polinomial do primeiro grau
Para saber se uma função é polinomial do primeiro grau, devemos observar o maior grau da variável x (termo desconhecido), que sempre deve ser igual a 1. Nessa função, o gráfico é uma reta. Além disso, ela possui: domínio x, imagem f(x) e coeficientes a e b.

Fórmula geral da função afim ou polinomial do primeiro grau
f(x) = ax + b
x = domínio
f(x) = imagem
a = coeficiente
b = coeficiente

Exemplo de gráfico da função polinomial do primeiro grau: f(x) = 4x + 1
5 – Função Linear
A função linear tem sua origem na função do primeiro grau (f(x) = ax + b). Trata-se de um caso particular, pois b sempre será igual a zero.
Fórmula geral da função linear
f(x) = ax
x = domínio
f(x) = imagem
a = coeficiente

Exemplo de gráfico da função linear: f(x) = -x/3
6 – Função crescente
A função polinomial do primeiro grau será crescente quando o coeficiente a for diferente de zero e maior que um (a > 1).

Fórmula geral da função crescente
f(x) = + ax + b
x = domínio
f(x) = imagem
a = coeficiente sempre positivo
b = coeficiente

Exemplo de gráfico da função crescente: f(x) = 5x

7 – Função decrescente
Na função decrescente, o coeficiente a da função do primeiro grau (f(x) = ax + b) é sempre negativo.

Fórmula geral da função decrescente
f(x) = - ax + b
x= domínio/ incógnita
f(x) = imagem
- a = coeficiente sempre negativo
b = coeficiente

Exemplo de gráfico da função decrescente: f(x) = - 5x

8 – Função quadrática ou polinomial do segundo grau
Identificamos que uma função é do segundo grau quando o maior expoente que acompanha a variável x (termo desconhecido) é 2. O gráfico da função polinomial do segundo grau sempre será uma parábola. A sua concavidade muda de acordo com o valor do coeficiente a. Sendo assim, se a é positivo, a concavidade é para cima e, se for negativo, é para baixo.

Fórmula geral da função quadrática ou polinomial do segundo grau
f(x) = ax² + bx + c
x = domínio
f(x) = imagem
a = coeficiente que determina a concavidade da parábola.
b = coeficiente.
c = coeficiente.

Exemplo de gráfico da função polinomial do segundo grau: f(x) = x² – 6x + 5
9 – Função modular
A função modular apresenta o módulo, que é considerado o valor absoluto de um número e é caracterizado por (| |). Como o módulo sempre é positivo, esse valor pode ser obtido tanto negativo quanto positivo. Exemplo: |x| = + x ou |x| = - x.

Fórmula geral da função modular
f(x) = x, se x≥ 0

ou

f(x) = – x, se x < 0
x = domínio
f(x) = imagem
- x = simétrico do domínio

Exemplo de gráfico da função modular: f(x) =

10 – Função exponencial
Uma função será considerada exponencial quando a variável x estiver no expoente em relação à base de um termo numérico ou algébrico. Caso esse termo seja maior que 1, o gráfico da função exponencial é crescente. Mas se o termo for um número entre 0 e 1, o gráfico da função exponencial é decrescente.

Fórmula geral da função exponencial
f(x) = a^x
a > 1 ou 0 < a < 1
x = domínio
f(x) = imagem
a = Termo numérico ou algébrico

Exemplo de gráfico da função exponencial crescente: f(x) = (2)^x, para a = 2
Exemplo de gráfico da função exponencial decrescente: f(x) = (1/2)^x para a = ½
11 - Função logarítmica
Na função logarítmica, o domínio é o conjunto dos números reais maiores que zero e o contradomínio é o conjunto dos elementos dependentes da função, sendo todos números reais.

Fórmula geral da função logarítmica
f(x) = log_a x
a = base do logaritmo
f(x) = Imagem/ logaritmando
x = Domínio/ logaritmo

Exemplo de gráfico da função logarítmica: f(x) = log₁₀ (5x - 6)

12 – Funções trigonométricas
As funções trigonométricas são consideradas funções angulares e são utilizadas para o estudo dos triângulos e em fenômenos periódicos. Podem ser caracterizadas como razão de coordenadas dos pontos de um círculo unitário. As funções consideradas elementares são:
- Seno: f(x) = sen x
- Cosseno: f(x) = cos x
- Tangente: f(x) = tg x

Exemplo de gráfico da função trigonométrica seno: f(x) = sen (x + 2)

Exemplo de gráfico da função trigonométrica cosseno: f(x) = cos (x + 2)

Exemplo de gráfico da função tangente: f(x) = tg (x + 2)

13 – Função raiz
O que determina o domínio da função raiz é o termo n que faz parte do expoente. Se n for ímpar, o domínio (x) será o conjunto dos números reais; se n for par, o domínio (x) será somente os números reais positivos. Isso porque, quando o índice é par, o radicando (termo que fica dentro da raiz) não pode ser negativo.

Fórmula geral da função raiz
f(x) = x ^1/n 
f(x) = Imagem
x = domínio/ base
1/n = expoente

Exemplo de gráfico da função raiz: f(x) = (x)^1/2

Noção básica de interdependência
Exemplo:
Podemos estabelecer uma relação de dependência entre o preço do litro do combustível e a quantidade de litros usados no abastecimento de um carro. Suponhamos que o preço do litro de gasolina seja R$ 2,50, dessa forma, podemos determinar a seguinte função y = 2,5 . x, que determina o preço a pagar y em decorrência da quantidade de litros abastecidos x.
Exemplo:
Uma viagem, um automóvel mantém uma velocidade constante de 60 km/h. Com o passar do tempo, esse veículo irá percorrer uma determinada distância. De tal modo, podemos determinar a distância percorrida pelo veículo relacionando a velocidade média e o tempo do movimento utilizando a seguinte expressão matemática, D = V . t, onde:

D = distância (m)
V = velocidade média (m/s)
T = tempo (s)

Observe a tabela de valores para essa função:
Exemplo:
Uma indústria de brinquedos possui um custo mensal de produção equivalente a R$ 5.000,00 mais R$ 3,00 reais por brinquedo produzido. Determine a lei de formação dessa função e o valor do custo na produção de 2.000 peças.
A lei de formação será formada por uma parte fixa e outra variável. Observe:
C = 5000 + 3 . p, onde C: custo da produção e p: o número de brinquedos produzidos. Como serão produzidos 2.000 brinquedos temos:
C = 5000 + 3 * 2000
C = 5000 + 6000
C = 11.000
Conclusão: o custo na produção de 2.000 brinquedos será de R$ 11.000,00.

Construção de tabelas e gráficos para representar funções do 1º e do 2º graus

Como construir o gráfico de uma função?
O gráfico de uma função é a imagem que essa função possui. Através do gráfico, podemos identificar qual é o tipo da função.
Quando trabalhamos com funções, a construção de gráficos é de extrema importância. Podemos dizer que assim como vemos nossa imagem refletida no espelho, o gráfico de uma função é o seu reflexo. Através do gráfico, podemos definir de que tipo é a função mesmo sem saber qual é a sua lei de formação. Isso porque cada função tem sua representação gráfica particular.

Plano Cartesiano
É o ambiente onde o gráfico será construído. Ele é estabelecido pelo encontro dos eixos cartesianos x e y, conhecidos como eixo das abcissas e eixo das ordenadas, respectivamente.
Cada ponto do gráfico é conhecido como par ordenado, pois ele é formado pelo encontro de um valor das abcissas com um valor das ordenadas. A linha que une os pares ordenados é conhecida como curva da função.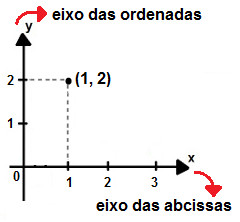
Representação do ponto de coordenadas (1,2) no plano cartesiano

Vamos ver aqui alguns princípios básicos para a construção do gráfico de uma função, seja ela uma função do 1° grau ou uma função do 2° grau.

1°) Escolher valores para x
Para iniciar a construção do gráfico, é necessário escolher valores para a variável x. Esses valores serão substituídos na lei de formação da função para que o valor correspondente de y seja determinado, bem como o par ordenado. Para montar o gráfico de uma função do 1° grau, é necessário encontrar apenas dois pontos que já visualizamos no gráfico.
É também importante escolher valores próximos, como números subsequentes. Além disso, é sempre bom saber os pontos em que x = 0 e y = 0 (zero da função).

Considere a função y = x + 1. Montaremos uma tabela com os valores de x para encontrar os valores de y: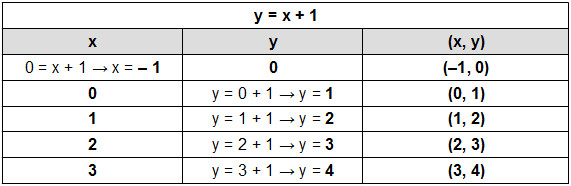

2°) Encontrar os pares ordenados no plano cartesiano
Lançando cada um desses pares ordenados no plano cartesiano, encontramos os seguintes pontos: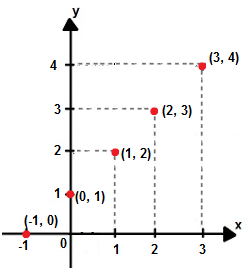
Pares ordenados lançados no plano cartesiano

3°) Traçando o gráfico
Basta ligar os pontos através de uma reta para determinar o gráfico da função y = x + 1.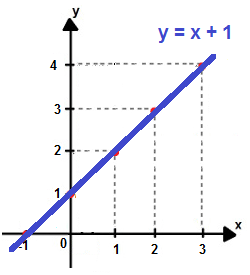
Gráfico da função y = x + 1

Características de um gráfico de uma função do 1º grau
Com a > 0 o gráfico será crescente.
Com a < 0 o gráfico será decrescente.
O ângulo α formado com a reta e com o eixo x será agudo (menor que 90°) quando a > 0.
O ângulo α formado com reta e com o eixo x será obtuso (maior que 90º) quando a < 0.
Na construção de um gráfico de uma função do 1º grau basta indicar apenas dois valores pra x, pois o gráfico é uma reta e uma reta é formada por, no mínimo, 2 pontos.
Apenas um ponto corta o eixo x, e esse ponto é a raiz da função.
Apenas um ponto corta o eixo y, esse ponto é o valor de b.

O gráfico da função é construído no plano de coordenadas cartesianas, onde cada valor de x (eixo das abscissas) possui uma representação em y (eixo das ordenadas).
Função do 1º grau crescente – (a > 0)
A função y = 2x + 5 é representada por uma reta crescente, pois o coeficiente angular é positivo, possuindo valor igual a 2. Veja o gráfico:
Na função crescente, à medida que os valores de x aumentam, os valores de y também aumentam; ou à medida que os valores de x diminuem, os valores de y diminuem.

Função do 1º grau decrescente – (a < 0)
A função y = –2x +3 é representada por uma reta decrescente, pois o coeficiente angular é negativo, possuindo valor igual a –2. Veja o gráfico: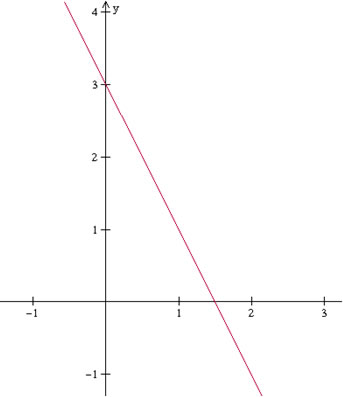
Na função decrescente, à medida que os valores de x aumentam, os valores de y diminuem; ou, à medida que os valores de x diminuem, os valores de y aumentam.

Exercícios resolvidos:

Determine as raízes das funções a seguir:
00) y = 4x + 2
Resolução:
y = 0
4x + 2 = 0
4x = –2
x = –2/4
x = –1/2
Resposta: a reta representada pela função y = 4x + 2 intersecta o eixo x no seguinte valor: –1/2

00) y = – 2x + 10
Resolução:
y = 0
– 2x + 10 = 0
– 2x = – 10 (–1)
2x = 10
x = 10/2
x = 5
Resposta: a reta representada pela função y = – 2x + 10 intersecta o eixo x no seguinte valor: 5 

00) y = – 7x + 7
Resolução:
y = 0
–7x + 7 = 0
–7x = –7
x = 1
Resposta: a reta representada pela função y = –7x + 7 intersecta o eixo x no seguinte valor: 1

00) y = 3x
y = 0
3x = 0
x = 0
Resposta: a reta representada pela função y = 3x intersecta o eixo x no seguinte valor: 0

00) Uma pessoa vai escolher um plano de saúde entre duas opções: A e B.
Condições dos planos:
Plano A: cobra um valor fixo mensal de R$ 140,00 e R$ 20,00 por consulta num certo período.
Plano B: cobra um valor fixo mensal de R$ 110,00 e R$ 25,00 por consulta num certo período.
Temos que o gasto total de cada plano é dado em função do número de consultas x dentro do período pré-estabelecido.
Resolução:
a) A função correspondente a cada plano.
b) Em qual situação o plano A é mais econômico; o plano B é mais econômico; os dois se equivalem.
a) Plano A: f(x) = 20x + 140
Plano B: g(x) = 25x + 110

b) Para que o plano A seja mais econômico:
g(x) > f(x)
25x + 110 > 20x + 140
25x – 20x > 140 – 110
5x > 30
x > 30/5
x > 6
Para que o Plano B seja mais econômico:
g(x) < f(x)
25x + 110 < 20x + 140
25x – 20x < 140 – 110
5x < 30
x < 30/5
x < 6
Para que eles sejam equivalentes:
g(x) = f(x)
25x + 110 = 20x + 140
25x – 20x = 140 – 110
5x = 30
x = 30/5
x = 6
O plano mais econômico será:
Plano A = quando o número de consultas for maior que 6.
Plano B = quando número de consultas for menor que 6.
Reposta: os dois planos serão equivalentes quando o número de consultas for igual a 6.

00) Na produção de peças, uma fábrica tem um custo fixo de R$ 16,00 mais um custo variável de R$ 1,50 por unidade produzida. Sendo x o número de peças unitárias produzidas, determine:
a) A lei da função que fornece o custo da produção de x peças;
b) Calcule o custo de produção de 400 peças.
Resolução:
a) f(x) = 1,5x + 16
b) f(x) = 1,5x + 16
f(400) = 1,5*400 + 16
f(400) = 600 + 16
f(400) = 616
Resposta: o custo para produzir 400 peças será de R$ 616,00.

00) Um motorista de táxi cobra R$ 4,50 de bandeirada mais R$ 0,90 por quilômetro rodado. Sabendo que o preço a pagar é dado em função do número de quilômetros rodados, calcule o preço a ser pago por uma corrida em que se percorreu 22 quilômetros?
Resolução:
f(x) = 0,9x + 4,5
f(22) = 0,9*22 + 4,5
f(22) = 19,8 + 4,5
f(22) = 24,3
Resposta: o preço a pagar por uma corrida que percorreu 22 quilômetros é de R$ 24,30.

00) Determine os zeros das funções a seguir:
a) y = 5x + 2
Resolução:
Primeiramente, façamos y = 0, então:
5x + 2 = 0, o número 2 mudará de lado e o sinal também será mudado.
5x = – 2, o número 5 mudará de lado e realizará uma divisão.
x = – 2
        5
Resposta: o zero da função y = 5x + 2 é o valor: x = – 2
                                                   5
b) y = – 2x
Resolução:
Façamos y = 0, então:
– 2x = 0, o número – 2 mudará de lado e realizará uma divisão. Mas como o número zero dividido por qualquer número resulta em zero, x = 0.
Resposta: o zero da função y = – 2x é x = 0.

c) f(x) = x + 4
            2
Resolução:
Façamos f(x) = 0, então:
x + 4 = 0, o número 4 mudará de lado e o sinal também será mudado.
2
x = - 4, o número 2 mudará de lado e realizará uma multiplicação.
2
x = (– 4) . 2
x = – 8
Resposta: Portanto, o zero da função f(x) = x + 4 é dado por x = – 8.

00) Classifique cada uma das funções seguintes em crescente ou decrescente:
Comentário para resolução: Em uma função do tipo y = ax + b, o coeficiente a de x indica se a função é crescente ou decrescente.
a) y = 4x + 6
Resolução:
Nessa função, a = 4 > 0, portanto, y é uma função crescente.

b) f(x) = – x + 10
Resolução:
Como a = – 1 < 0, f(x) é uma função decrescente.

c) y = (x + 2)²– (x – 1)²
Resolução:
Nesse caso precisamos desenvolver os parênteses através dos produtos notáveis.
x² + 4x + 4 – (x – 1)²
x² + 4x + 4 – (x² – 2x + 1)
x² + 4x + 4 – x² + 2x – 1
6x + 3
y = 6x + 3. Como a = 6 > 0, y é uma função crescente.

00) (UFPI) A função real de variável real, definida por f (x) = (3 – 2a).x + 2, é crescente quando:
(A) a > 0
(B) a < 3/2
(C) a = 3/2
(D) a > 3/2
(E) a < 3
Resolução:
Para que a função seja crescente, é necessário que o coeficiente de x seja positivo, logo:
3 – 2a > 0
– 2a > 0 – 3
(– 1). (– 2a) > (– 3). (– 1)
2a < 3
a < 3
     2
Alternativa: B

00) (FGV) O gráfico da função f (x) = mx + n passa pelos pontos (– 1, 3) e (2, 7). O valor de m é:
(A) 5/3
(B) 4/3
(C) 1
(D) 3/4
(E) 3/5
Resolução:
O primeiro ponto que é dado é o (– 1, 3), em que o valor de x é – 1 e o valor de f(x) é 3. Substituindo esses valores na função, temos:
f (x) = mx + n
3 = m.(– 1) + n
n = 3 + m
Vamos também substituir o segundo ponto (2, 7) na função, sendo que x vale 2 e f(x) vale 7:
f (x) = mx + n
7 = m.2 + n
n = 7 – 2m
Nas duas substituições feitas, encontramos dois valores para n. Se igualarmos essas duas equações, teremos:
3 + m = 7 – 2m
m + 2m = 7 – 3
3m = 4
m = 4
       3
Alternativa: B

Gráfico da função de 2º grau
O gráfico da função de 2º grau é representado pela parábola, que pode ter sua concavidade voltada para cima ou para baixo.
Uma função do 2º grau é definida pela seguinte lei de formação f(x) = ax² + bx + c ou y = ax² + bx + c, em que a, b e c são números reais e a ≠ 0. Sua representação no plano cartesiano é uma parábola que, de acordo com o valor do coeficiente a, possui concavidade voltada para cima ou para baixo. A função do 2º grau assume três possibilidades de resultados ou raízes, que são determinadas quando fazemos f(x) ou y igual a zero, transformando a função em uma equação do 2º grau, que pode vir a ser resolvida por Bháskara.

Gráfico da função do 2º grau
Coeficiente a > 0, parábola com a concavidade voltada para cima
Coeficiente a < 0, parábola com a concavidade voltada para baixo

? > 0 – A equação do 2º grau possui duas soluções distintas, isto é, a função do 2º grau terá duas raízes reais e distintas. A parábola intersecta o eixo das abscissas (x) em dois pontos.
? = 0 – A equação do 2º grau possui uma única solução, isto é, a função do 2º grau terá apenas uma raiz real. A parábola irá intersectar o eixo das abscissas (x) em apenas um ponto.
? < 0 – A equação do 2º grau não possui soluções reais, portanto, a função do 2º grau não intersectará o eixo das abscissas (x).

Pontos notáveis do gráfico de uma função do 2º grau
O vértice da parábola constitui um ponto importante do gráfico, pois indica o ponto de valor máximo e o ponto de valor mínimo. De acordo com o valor do coeficiente a, os pontos serão definidos, observe:

Quando o valor do coeficiente a for menor que zero, a parábola possuirá valor máximo.
Quando o valor do coeficiente a for maior que zero, a parábola possuirá valor mínimo.
Outra relação importante na função do 2º grau é o ponto onde a parábola corta o eixo y. Verifica-se que o valor do coeficiente c na lei de formação da função corresponde ao valor do eixo y onde a parábola o intersecta.

Exercícios resolvidos
00) Encontre o valor de f(x) = x² + 3x – 10 para que f(x) = 0
Resolução:
Os coeficientes dessa função são: a = 1, b = 3 e c = – 10. Para resolver essa equação, vamos utilizar a fórmula de Bhaskara:

Δ = b² – 4.a.c
Δ = 3² – 4.1.(– 10)
Δ = 9 + 40
Δ = 49
x = – b ± √Δ
        2.a
x = – 3 ± √49
           2.1
x = – 3 ± 7
      2
x₁ = – 3 + 7
        2
x₁ = 4
        2
x₁ = 2
x₂ = – 3 – 7
         2
x₂ = – 10
        2
x₂ = – 5
Resposta: os dois valores de x para que f(x) = 0 são x₁ = 2 e x₂ = – 5.

00) Calcule o valor de 5x² + 15x = 0 para que f(x) = 0
Vamos resolver essa função do 2° grau isolando a variável x:
5x² + 15x = 0
5x.(x + 3) = 0
x₁ = 0
x₂ + 3 = 0
x₂ = – 3
Resposta: Portanto, os valores de x para os quais f(x) = 0 são 0 e – 3.

00) (UfSCar–SP) Uma bola, ao ser chutada num tiro de meta por um goleiro, numa partida de futebol, teve sua trajetória descrita pela equação h(t) = – 2t² + 8t (t ≥ 0) , onde t é o tempo medido em segundo e h(t) é a altura em metros da bola no instante t. Determine, apos o chute:
a) o instante em que a bola retornará ao solo.
Resolução:
Houve dois momentos em que a bola tocou o chão: o primeiro foi antes de ela ser chutada e o segundo foi quando ela terminou sua trajetória e retornou para o chão. Em ambos os momentos a altura h(t) era igual a zero, sendo assim:
h(t) = – 2t² + 8t
0 = – 2t² + 8t
2t² – 8t = 0
2t.(t – 4) = 0
t' = 0
t'' – 4 = 0
t'' = 4
Resposta: o segundo momento em que a bola tocou no chão foi no instante de quatro segundos.

b) a altura atingida pela bola.
Resolução:
A altura máxima atingida pela bola é dada pelo vértice da parábola. As coordenadas do seu vértice podem ser encontradas através de:
x_v = – b
          2a
y_v = – Δ
          4a
No caso apresentado, é interessante encontrar apenas y_v:
y_v = – Δ
          4a
y_v = – (b² – 4.a.c)
              4a
y_v = – (8² – 4.(–2).0)
               4.(– 2)
y_v = – (64 – 0)
               – 8
y_v = 8
Resposta: a altura máxima atingida pela bola foi de 8 metros.

00) Determine x pertence aos reais tal que (x² – 100x)².(x² – 101x + 100)² = 0.
Resolução:
Devemos encontrar as raízes de cada equação dentro dos parênteses. Para isso, vamos resolver a primeira equação colocando x em evidência:
x² – 100x = 0
x(x – 100) = 0
x₁ = 0
x₂ – 100 = 0
x₂ = 100
A segunda equação pode ser resolvida pela fórmula de Bhaskara:
x² – 101x + 100 = 0

Δ = b² – 4.a.c
Δ = (– 101)² – 4.1.100
Δ = 10201 – 400
Δ = 9801
x = – b ± √Δ
           2.a
x = – (– 101) ± √9801
              2.1
x = 101 ± 99
           2
x₃ = 101 + 99
             2
x₃ = 200
         2
x₃ = 100
x₄ = 101 – 99
            2
x₄ = 2
       2
x₄ = 1
Resposta: os valores de x que satisfazem a equação são 0, 1 e 100.

00) Calcule o valor de k de modo que a função f(x) = 4x² – 4x – k não tenha raízes, isto é, o gráfico da parábola não possui ponto em comum com o eixo x.
Resolução:
∆ < 0
b² – 4ac < 0
(–4)² – 4 * 4 * (–k) < 0
16 + 16k < 0
16k < – 16
k < –1
Resposta: o valor de k para que a função não tenha raízes reais deve ser menor que – 1.

00) Determine os valores de m, para que a função f(x) = (m – 2)x² – 2x + 6 admita raízes reais.
Resolução:
Para essa situação temos que ∆ ≥ 0.
∆ ≥ 0
b² – 4ac ≥ 0
(–2)² – 4 * (m – 2) * 6 ≥ 0
4 – 4 * (6m – 12) ≥ 0
4 – 24m + 48 ≥ 0
– 24m ≥ – 48 – 4
– 24m ≥ – 52
24m ≤ 52
m ≤ 52/24
m ≤ 13/6
Resposta: o valor de m que satisfaça a condição exigida é m ≤ 13/6.

00) (Vunesp-SP) O gráfico da função quadrática definida por y = x² – mx + (m – 1), em que m Є R, tem um único ponto em comum com o eixo das abscissas. Determine y associado ao valor de x = 2.
Resolução:
Um ponto em comum significa dizer uma única raiz, então ∆ = 0.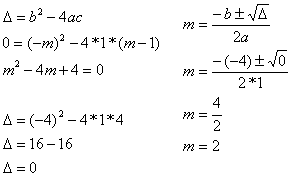

y = x² – mx + (m – 1)
Substituir m = 2, no intuito de obter a lei da função
y = x² – 2x + (2 – 1)
y = x² – 2x +1
Substituindo x = 2, para determinarmos o valor de y
y = 2² – 2 * 2 + 1
y = 4 – 4 + 1
y = 1
Resposta: a equação possui a lei de formação y = x² – 2x +1. E quando x = 2, o valor de y se torna igual a 1.

00) (UCSal-BA) Determine os pontos de intersecção da parábola da função f(x) = 2x² – 3x + 1, com o eixo das abscissas.
Resolução:
No instante em que a parábola cruza o eixo das abscissas o valo de y ou f(x) é igual a zero. Portanto:
f(x) = 0
2x² – 3x + 1 = 0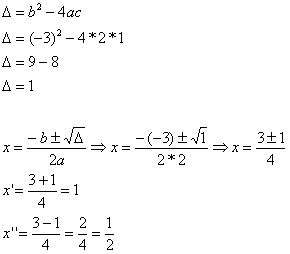

Resposta: os pontos de interseção são:
x = 1 e y = 0
x = 1/2 e y = 0

00) Dada a função y = 2x + 5, construa o gráfico.
Comentário: na função crescente, à medida que os valores de x aumentam, os valores de y também aumentam; ou à medida que os valores de x diminuem, os valores de y diminuem.

00) Dado a função y = –2x +3, construa o gráfico.
Comentário: na função decrescente, à medida que os valores de x aumentam, os valores de y diminuem; ou, à medida que os valores de x diminuem, os valores de y aumentam.

00) Construa o gráfico da função dada pela seguinte lei de formação:  y = f(x) = 2x – 1.
Resolução: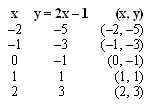

y = 2*(–2) – 1 → y = –4 –1 → y = –5
y = 2*(–1) –1 → y = –2 – 1 → y = –3
y = 2 * 0 – 1 → y = –1
y = 2 * 1 – 1 → y = 2 – 1 → y = 1
y = 2 * 2 – 1 → y = 4 – 1 → y = 3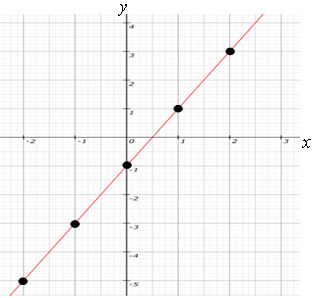

00) Construa o gráfico da função dada por y = f(x) = x².
Resolução: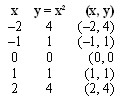

y = (–2)² = 4
y = (–1)² = 1
y = (0)² = 0
y = (1)² = 1
y = (2)² = 4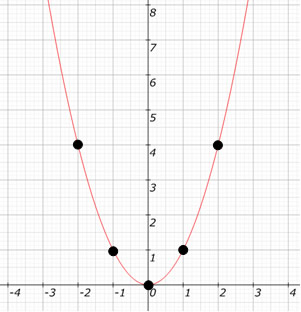

00) Construa o gráfico da função dada por y = f(x) = x³.
Resolução: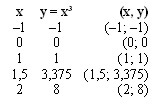

y = (–1)³ = –1
y = 0³ = 0
y = 1³ = 1
y = 1,5³ = 3,375
y = 2³ = 8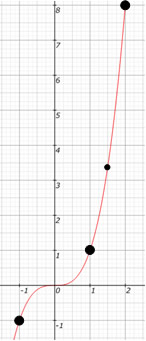


00) Construa o gráfico da função y = f(x) = 4x⁴ – 5x3 – x2 + x – 1.
Resolução: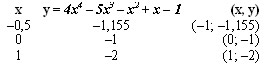

y = 4 * (0,5)4 – 5 * (0,5)3 – 0,52 + 0,5 – 1 = 0,25 – 0,625 – 0,25 + 0,5 – 1 = – 1,155
y = 4 * 04 – 5 * 03 – 02 + 0 – 1 = –1
y = 4 * 14 – 5 * 13 – 12 + 1 – 1 = –2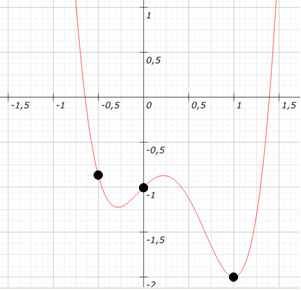
Continua...