EQUACAO DO 2º GRAU

Professor Diminoi

Exemplo de Equação do 2º grau:
x² + 2x – 3 = 0

Passos para resolução da equação do 2º grau.
1º passo: Identificar os valores dos coeficientes.
a = é o valor que está ao lado do x²
b = é o valor que está acompanhado do x sem ser ao quadrado
c = é o valor que não está acompanhado do x

Observação:
2º passo: Para encontrar suas soluções, calcula-se o discriminante Δ e depois utiliza-se a fórmula de Bhaskara.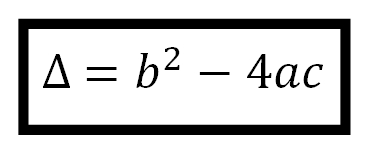

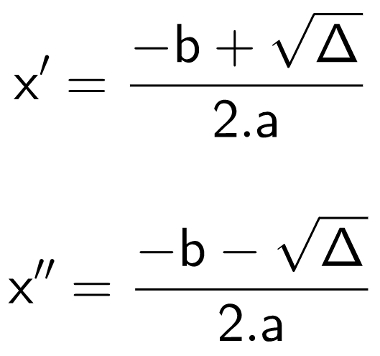
QUESTÕES RESOLVIDAS
Equação completa: quando possui os coeficientes a. b e c.
01) Em cada uma das equações do 2º grau abaixo encontre os valores de a, b e c.
a) 2x² +4x – 6 =
a = 2
b = 4
c = -6

b) x² – 5x + 2 =
a = 1
b = -5
c = 2

c) 0,5x² + x –1 =
a = 0,5
b = 1
c = - 1

Equação incompleta: quando os coeficientes b ou c são iguais a 0.
02) Em cada caso encontre os valores a, b e c.
a) 2x² + 5x = 0 (não tem o termo c)
a = 2
b = 5
c = 0

b) -x² + x = 0 (não tem o termo b)
a = - 1
b = 0
c = 1

c) 2x² + 2x = 0 (não tem o termo c)
a = 2
b = 2
c = 0

03) (Fatec) Se a equação x² - 10x + k = 0 tem uma raiz de multiplicidade 2, então o valor de k é
(A) 100                  
(B) 25 
(C) 5         
(D) 1  
(E) 0
Resolução:
a = 1
b = -10
c = 1

Δ = (-10)² – 4 . 1 . 1
Δ = 100 – 4
Δ = 96
(não é uma raiz exata)

04) Analisando a equação do segundo grau x² – 2x + 1 = 0, podemos afirmar que ela possui:
(A) nenhuma solução real.
(B) uma única solução real.
(C) duas soluções reais.
(D) três soluções reais.
Resolução:
a = 1
b = - 2
c = 1

Δ = (-2)² – 4 . 1 . 1
Δ = 4 – 4
Δ = 0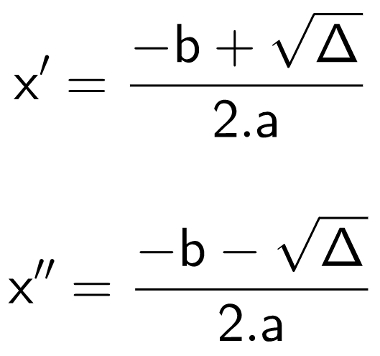

x’ = -(-2) -√0
         2 . -2
x’ = 2/0
x’ = 0
x” = 0
Possui duas raízes reais e iguais
Alternativa: B

05) Uma região retangular teve as suas dimensões descritas em metros, conforme a imagem a seguir:
O valor de x que faz com que a área dessa região seja igual a 21 é:
(A) 1       
(B) 2              
(C) 3         
(D) 4  
(E) -6
Resolução:
A = b . h
A = (x + 3) . (x -1)
A = x² – x +3x -3
A = x² + 2x -3
a = 1
b = 2
c = - 3

Δ = 2² – 4 . 1 . - 3
Δ = 4 + 12
Δ = 16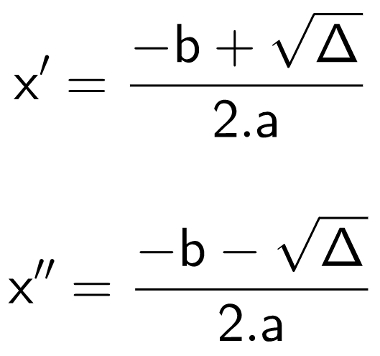

x’ = - 2 + √16
         2 . 1
x’ = - 2 + 4
         2
x’ = 2
        2
x’ = 1
 x” = - 2 - √16
         2 . 1
x” = - 2 - 4
         2
x” = -6
        2
x” = -3
Nesse caso somente o valor positivo é usado, portanto x vale 1.
Alternativa: A

06) Analise as equações do segundo grau a seguir:
I. 2 x²- 8 = 0
II. 3x²+ 2x -3 = 0
III. 5 x² - 2x = 0
Podemos classificar a equação como uma equação completa:
(A) somente na afirmativa I.
(B) somente na afirmativa II.
(C) somente na afirmativa III.
(D) somente nas afirmativas I e III.
Resolução:
Somente a equação II tem os termos: a, b e c.

Soma e produto
07) O produto entre as raízes da equação 2x² + 4x - 6 = 0 é igual a:
(A) - 2      
(B) 2   
(C) 1         
(D) 3  
(E) - 3
Resolução:
a = 2
b = 4
c = -6
Produto:
c / a
- 6 /2 =
- 3

Quadrados  perfeitos
São números que possuem raiz quadrada exata.
Existem dois casos possíveis para a raiz quadrada de um número natural:
O resultado pode ser uma raiz quadrada exata ou não.
Os números que possuem raiz quadrada exata são conhecidos como quadrados perfeitos.
Em cada caso abaixo, encontre os valores de x’ e x” quando possível.
Observação:
x² = √x

08) x² = 169
Resolução:
√169 = 13
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 1 
x” = - 13

09) 2x² – 18 = 0
Resolução:
2x² = 18
x² = 18/2
x² = 9
√9 = 3
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 3 
x” = - 3

10) 289 = x²
Resolução:
√289 = x²
Fazendo 17 . 17 = 289
Portanto √289 = 17
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 17 
x” = - 17

11) x² – 483 = 1
Resolução:
x² = 483 + 1
x² = 484
Fazendo 22 . 22 = 484
Portanto √484 = 22
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 22 
x” = - 22

12) Qual a solução possível da equação 3x² = 0?
Resolução:
3x² = 0
x² = 0 / 0
x² = 0
√0 = 0
Observação: A raiz quadrada de 0 é igual a 0

13) Analise as duas equações: - 3x² = 9 e – 4x² = 2. Para cada equação, encontre o valor x e justifique como resolveu a questão.
a) Primeira equação sendo – 3x² = 9
Resolução:
x² = 9 / -3
x² = - 3
Observação: Tendo em vista as propriedades da potenciação, sabemos que um número ao quadrado é sempre positivo. Isso nos leva a concluir que não é possível extrair raiz quadrada de um número negativo no conjunto dos números reais.

b) Segunda equação sendo – 4x² = 2
Resolução:
x² = 2 / - 4
x² = - 0,5
Observação: Tendo em vista as propriedades da potenciação, sabemos que um número ao quadrado é sempre positivo. Isso nos leva a concluir que não é possível extrair raiz quadrada de um número negativo no conjunto dos números reais.

14) Para a equação 0x² = 16, quais são os possíveis valores de x?
Resolução:
0x² = 16
x² = 16  / 0
0² = 0
√0 = 0
Observação: A raiz quadrada de 0 é igual a 0

15) Seja a equação 4x² = 16, encontre o(s) valor(es) de x que tronem a igualdade verdadeira. Justifique.
Resolução:
4x² = 16
x² = 16 / 4
x² = 4
√4 = 2
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 2 
x” = - 2

16) 2x² = 72
Resolução:
2x² = 72
x² = 72 / 2
x² = 36
√36 = 6
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 6 
x” = - 6

17) - 4x² = 0
Resolução:
4x² = 0
x² = 0 /4
x² = 0
√0 = 0

18) 8x² = 2
Resolução:
8x² = 2
x² = 2 / 8
x² = 0,25
√0,25 = 0,5
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 0,5 
x” = - 0,5

19) - 12x² = 12
Resolução:
- 12x² = 12
x² = 12 - 12
√-1
Observação: Tendo em vista as propriedades da potenciação, sabemos que um número ao quadrado é sempre positivo. Isso nos leva a concluir que não é possível extrair raiz quadrada de um número negativo no conjunto dos números reais.

20) 5x² = 125
Resolução:
5x² = 125
x² = 125 / 2
5x² = 25
√25 = 5
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 5
x” = - 5

21) - 1000x² = - 10
Resolução:
- 1000x² = - 10
x² = - 10 / - 1000
x² = - 1 / 100
x² = - 0,01
√0,01 = 0,1
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 0,1
x” = - 0,1

22) x² = 1 / 25
Resolução:
x² = 1 / 25
x² = 0,04
√0,04 = 0,2
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 0,2
x” = - 0,2

23) x² = 16 / 9
Resolução:
x² = 16 / 9
x² = 1,7
√1,7 = 1,3
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 1,3
x” = - 1,3

24) x² = 1 / 4
Resolução:
x² = 1 / 4
x² = 0,25
√0,25 = 0,5
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 0,5
x” = -  0,5

25) x² = 0,09
Resolução:
x² = 0,09
√0,09 = 0,3
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 0,3
x” = -  0,3

26) A área de um retângulo é igual a 1200m². Sabendo-se que a medida de um lado é o triplo da medida do outro, determine as medidas
Resolução:
Área do retângulo: A = b . h
1200 = x . 3x
1200 = 3x²
1200 / 3 = x²
400 = x²
√400 = 20
Observação: equação do 2º grau tem duas raízes x’ e x”. Portanto:
x’ = 20
x” = - 20
Como se trata de medidas de terrenos, considera-se apenas o valor positivo ou seja 20.
Assim, o lado menor mede 20m e o lado maior por ser o triplo do menor, mede 60 m.

Toda equação do segundo grau pode ser escrita na forma 
ax² + bx + c = 0
a = valor que está ao lado do x²
b = valor que está ao lado do x
c = valor que não está acompanhado de x

27) Observe os valores em cada caso:
(a) 3x² + 4x - 5 = 0 é uma equação de 2º grau completa tem:
a = 3
b = 4
c = -5

(b) x² + 5x = 0 é uma equação de 2º grau imcompleta tem:
a = 1
b = 5
c = 0

(c) 2x² - 9 = 0 é uma equação de 2º grau imcompleta tem:
a = 2
b = 0
c = - 9

(d) 3x² = 0 é uma equação de 2º grau imcompleta tem:
a = 3
b = 0
c = 0

Passos para resolução da equação do 2º grau. 
1º passo: 
Identificar os valores dos coeficientes.
a =
b =
c =

2º passo:
Aplicar a Fórmula de Baskara para calcule o valor do delta.



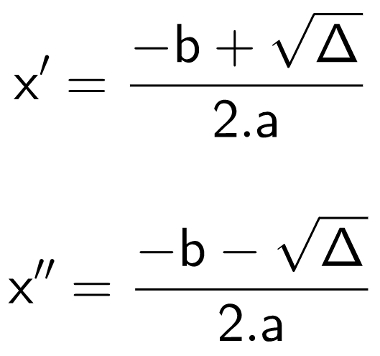
Resumo sobre a equação do 2º grau
ax² + bx + c = 0.
Pode ser completa, se os seus coeficientes forem todos diferentes de zero, e incompleta, caso contrário.
Para encontrar suas soluções, calcula-se o discriminante Δ e depois utiliza-se a fórmula de Bhaskara.
Se Δ > 0, a equação possui duas soluções reais.
Se Δ = 0, a equação possui uma solução real.
Se Δ < 0, a equação não possui solução real.

Exemplo:
28) Encontre as raízes da equação x² + 2x – 3 = 0.
Resolucao
1º passo: encontrar os valores dos coeficientes a, b e c.
a = 1
b= 2
c= –3

2º passo: calcular o delta por meio da substituição do valor dos coeficientes na fórmula.
                                                                               Δ = b² – 4 ac
Δ = 2² – 4· 1 ·(– 3)
Δ = 2² – 4· 1 ·(– 3)
Δ = 4 – 4 ·(– 3)
Δ = 4 + 12
Δ = 16
Como Δ > 0, então essa equação terá duas soluções reais.

3º passo: usar a fórmula de Bhaskara, substituindo as letras pelos valores da equação dos coeficientes e de delta.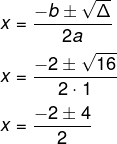

Nesse momento, é necessário dividir as duas soluções: uma será a soma e a outra será a diferença.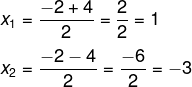

Então as possíveis soluções para essa equação são x = 1 ou x = – 3.

Equações incompletas
Existem três possibilidades de equação incompleta. Para cada uma delas, é possível realizar a resolução por soma e produto ou também pela fórmula de Bhaskara, porém cada uma delas possui uma terceira forma, geralmente com resolução mais rápida.

Equações incompletas do tipo ax² = 0
Nesse caso não há muito o que ser feito, já que b = 0 e c = 0. Aplicar qualquer um dos métodos anteriores seria bastante demorado. Então, basta isolarmos o x.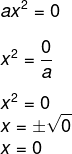

Logo, para qualquer valor de a — lembrando que, por definição, a é diferente de zero —, o valor de x sempre será 0.

Equações incompletas do tipo ax² + bx =0
Nesse caso, quando somente c = 0, é possível colocar o x em evidência na equação, gerando o seguinte produto:
x(ax +b) = 0
Para que uma multiplicação seja igual a zero, um dos seus termos precisa ser zero, logo as possibilidades são:
x= 0 ou ax+b = 0
Uma das soluções é x = 0, e a outra é uma equação do primeiro grau, que podemos resolver isolando o x.

Exemplo:
2x² + 3x = 0
Resolucao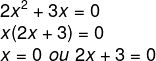
Encontramos uma solução x₁ = 0. Isolando x na segunda equação, temos que: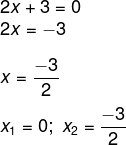


Equações incompletas do tipo ax² + c =0
Nesse caso é possível resolver isolando a incógnita, já que o termo c é independente, ou seja, não acompanha nenhuma incógnita. É necessário o domínio de equação dom 1º grau nesse caso.
Exemplo:
3x² – 12 = 0
Resolucao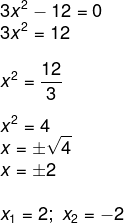


Sistema de equações do segundo grau
Resolver sistemas de equação do segundo grau exige que você tenha domínio da resolução de um sistema de equações do primeiro grau. Nesse caso, é essencial o domínio do método da adição e do método de substituição.

Exemplo:

Resolucao
1º passo: isolar uma das incógnitas na equação do primeiro grau.
Note que a equação II é do primeiro grau, logo reescreveremos isolando o y.
y = 1 – x
2º passo: substituir y na primeira equação.
x² + y² = 5
x² + (1 – x)² = 5
x² + 1 – 2x +x² = 5
2x² – 2x + 1 =5
Note que estamos encontrando uma equação do 2º grau, então vamos igualar a equação a zero.
2x² – 2x + 1 – 5 = 0
2x² – 2x – 4 = 0
Tendo a equação do 2º grau, vamos resolver utilizando soma e produto, mas Bhaskara também seria eficiente nesse caso.
a = 2
b = -2
c = -4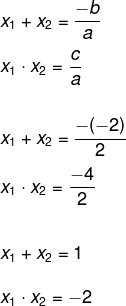

Os possíveis números cujo produto é igual a -2 são:
1 x (-2) = - 2
(-1) x 2 = - 2
Dos resultados possíveis, queremos aquele que a soma seja igual a 1, logo o resultado B é a solução da equação.
x₁ = -1 e x₂ = 2
3º passo: conhecendo o valor de x, vamos encontrar os possíveis valores para y substituindo cada um deles na equação x + y = 1.
x+ y = 1
x = -1
-1 + y = 1
y = 1+1 = 2
O par ( -1, 2) é a solução do sistema de equação.
Agora faremos o seguinte:
x+ y = 1
x = 2
2+y =1
y = 1 – 2
y = -1
O par (2, -1) também é solução do sistema.
As possíveis soluções do sistema são S { (2, -1); (-1, 2)}.

QUESTOES RESOLVIDAS
29) Analisando a equação do segundo grau x² – 2x +1 = 0, podemos afirmar que ela possui:
(A) nenhuma solução real.
(B) uma única solução real.
(C) duas soluções reais.
(D) três soluções reais.
(E) infinitas soluções reais.
Resolução:
Para encontrar o número de soluções reais de uma equação do 2º grau, é necessário encontrar o valor do discriminante (delta). Para isso, encontraremos primeiro o valor dos coeficientes a, b e c na equação:
a = 1
b = -2
c = 1
Agora vamos calcular o valor de delta:
Δ = b² – 4ac
Δ = (-2)² – 4 ·1·1
Δ = 4 – 4
Δ = 0
O valor de delta mostra o número de soluções da equação, sem ter a necessidade de calcular os valores dessas raízes. Como Δ = 0, a equação possui uma única solução real.
Alternativa: B

30) (Fatec) Se a equação x² - 10x + k = 0 tem uma raiz de multiplicidade 2, então o valor de k é
(A) 100
(B) 25
(C) 5
(D) 1
(E) 0
Resolução:
Para que uma raiz tenha multiplicidade 2, a equação precisa ter uma única solução, ou seja, Δ = 0. Vamos calcular o valor de Δ na equação x² - 10x + k = 0, em que
a = 1
b = -10
c = k.
Δ = b² – 4ac
Δ = (-10)² – 4 ·1·k
Δ = 100 – 4k
Mas Δ= 0, então:
100 – 4k = 0
100 = 4k
100 : 4 = k
25 = k
Logo, k = 25 é o valor que faz com que a equação tenha uma solução de multiplicidade 2.
Alternativa B

31) Uma região retangular teve as suas dimensões descritas em metros, conforme a imagem a seguir: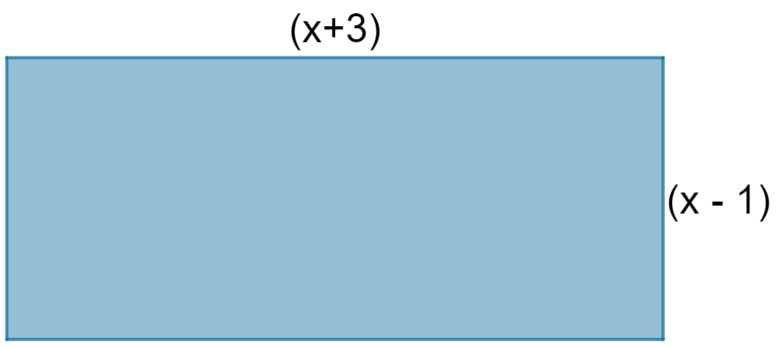
O valor de x que faz com que a área dessa região seja igual a 21 é:
(A) 1
(B) 2
(C) 3
(D) 4
(E) -6
Resolução:
A área de um retângulo é calculada pelo produto entre as medidas de seus lados, então:
(x + 3) ( x – 1) = 21
Aplicando a propriedade distributiva, temos que:
x² – 1x +3x – 3 = 21
x² +2x – 3 = 21
Para que seja possível aplicar a fórmula de Bhaskara, vamos igualar a equação a zero:
x² + 2x – 3 – 21 = 0
x² + 2x – 24 = 0
Os coeficientes da equação são:
a = 1
b= 2
c = - 24
Calculando o valor de delta, temos que:
Δ = b² – 4ac
Δ = (2)² – 4 ·1·(-24)
Δ = 4 + 96
Δ = 100
Aplicando a fórmula de Bhaskara, encontraremos: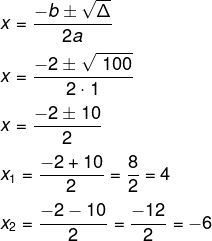

Note que o valor x = -6 faria com que os lados do retângulo fossem valores negativos, logo, entre as soluções da equação, a única que faz sentido é x = 4.
Alternativa: D

32) Uma equação foi descrita da seguinte maneira:
(k² – 4) x³ + ( k – 2 )x² + 7x - 8 = 0
Analisando os coeficientes, o valor de k que faz com que essa equação seja uma equação do 2º grau é:
(A) k = ± 2
(B) k = + 2
(C) k = - 2
(D) k = 0
(E) k = 4
Resolução:
Para que essa equação seja do 2º grau, o coeficiente de x³ tem que ser igual a zero, e o coeficiente de x² tem que ser diferente de zero, ou seja:
Condição I:
k² – 4 = 0
k² = 4
k = ±√4
k = ± 2
Logo, para satisfazer a primeira condição, temos k = 2 ou k = -2.
Agora vamos analisar a segunda condição.
Condição II:
k – 2 ≠ 0
k ≠ 2.
O valor que satisfaz ambas as condições é k = -2.
Alternativa: C

33) Das equações quadráticas abaixo e sabendo que a = 1, qual é a equação que possui as soluções x₁ = 2 e x₂ = - 3?
(A) x² + x – 6 = 0
(B) x² – x – 6 = 0
(C) x² +5x + 6 = 0
(D) x² – 5x +6 = 0
(E) x² + x – 1 = 0
Resolução:
Conhecendo as soluções da equação, temos que:
a(x – x₁) (x – x₂) = 0
Substituindo os valores dados, temos que:
1·( x – 2 ) ( x - (-3)) = 0
(x – 2 ) ( x + 3) = 0
x² +3x – 2x – 6 = 0
x² + x – 6 = 0
Alternativa: A

34) Utilizando seus conhecimentos sobre equação do segundo grau, julgue as afirmativas a seguir como verdadeiras ou falsas.
I – Toda equação do segundo grau possui pelo menos uma solução real.
II – Uma equação do segundo grau é conhecida como incompleta quando o coeficiente b ou c é igual a zero.
III – Quando o valor do discriminante é um número positivo que não possui raiz quadrada exata, dizemos que a equação não possui solução.
Analisando as afirmativas, podemos afirmar que:
(A) todas estão incorretas.
(B) somente a afirmativa I está correta.
(C) somente a afirmativa II está correta.
(D) somente a afirmativa III está correta.
(E) todas estão corretas.
Resolução:
Vamos analisar cada uma das afirmativas.
I – Falsa. Nem sempre a equação do segundo grau possui solução. Uma forma de verificar se a equação possui solução nos números reais é calcular o delta. Caso ele seja negativo, a equação não possui solução real.
II — Verdadeira. Por definição, a equação é incompleta quando b = 0 ou quando c = 0.
III – Falsa. Quando o valor do discriminante é positivo, há duas soluções reais na equação, independentemente de ele possuir raiz quadrada exata ou não.
Alternativa: B

SOMA E MULTIPICAÇÃO
35) (UERGS) Sendo S a soma e P o produto das raízes da equação 2x² − 5x − 7 = 0, pode-se afirmar que:
(A) S − P = 6.
(B) S + P = 2.
(C) S ⋅ P = 4.
(D) S/P= 1
(E) S < P
Resolução:
Dada a equação 2x² − 5x − 7 = 0, sabemos que a soma e o produto das raízes podem ser calculados da seguinte maneira: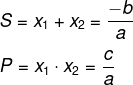
Os coeficientes da equação são:
a = 2
b = -5
c= -7
Então, a soma S e o produto P serão: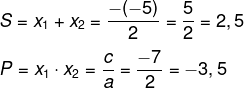
Agora, sabendo que S = 2,5 e P = -3,5 e analisando as afirmativas, é possível verificar que a alternativa A é a correta, pois:
S – P = 6
2,5 - (-3,5) = 6
2,5 + 3,5 = 6
Alternativa: A

36) Como exemplo, vamos escrever os coeficientes da equação 2x² + 8x – 24 = 0.
Resolucao
Primeiro passo
a = 2
b = 8
c = – 24
Segundo passo: 
Calcule o valor de delta.
O valor de delta é dado pela seguinte expressão: Δ = b² – 4ac, em que a, b e c são coeficientes da equação e Δ é delta.
Tomando o exemplo anterior, na equação 2x² + 8x – 24 = 0, delta vale:
Δ = b² – 4ac
Δ = 8² – 4·2·(– 24)
Δ = 64 + 192
Δ = 256

Terceiro passo: 
calcule os valores de x da equação.
Após calcular o valor de delta, os valores de x podem ser obtidos por meio da seguinte expressão:
x = – b ± √Δ
           2·a
Observe que nessa expressão aparece o sinal ±. Isso indica que x possui dois valores: o primeiro para a √Δ (raiz de delta) negativa e o segundo para √Δ positiva.
Tomando o exemplo já citado, observe a conclusão do terceiro passo:
x = – b ± √Δ
           2·a
x = – 8 ± √256
            2·2
Não pare agora... Tem mais depois da publicidade ;)
x = – 8 ± 16
            4
Para √Δ negativa, teremos:
x' = – 8 – 16 = –24 = –6
             4          4         
Para √Δ positiva, teremos:
x'' = – 8 + 16 = 8 = 2
             4         4      

37) Determinar a solução da seguinte equação do 2º grau: x² + 8x + 16 = 0.
Resolução:
Os coeficientes são:
a = 1
b = 8
c = 16
∆ = b² – 4 . a . c
∆ = 8² – 4 . 1 . 16
∆ = 64 – 64
∆ = 0
x = – b ± √∆
           2a
x = – 8 ± √0
     2 . 1
x' = x'' = –8 = – 4
    2
No exemplo 2, devemos observar que o valor do discriminante é igual a zero. Nesses casos, a equação possuirá somente uma solução ou raiz única.

38) Calcule o conjunto solução da equação 10x² + 6x + 10 = 0, considerada de 2º grau.
Resolução:
∆ = b² – 4 . a . c
∆ = 6² – 4 . 10 . 10
∆ = 36 – 400
∆ = – 364
Nas resoluções em que o valor do discriminante é menor que zero, isto é, o número é negativo, a equação não possui raízes reais.

39) Determine quais os valores de k para que a equação 2x² + 4x + 5k = 0 tenha raízes reais e distintas. 
Resolução:
Uma equação do 2º grau possui duas raízes reais e distintas quando ∆ > 0, então:

 

 

 

 

 

 

 

40) Calcule o valor de p na equação x² – (p + 5)x + 36 = 0, de modo que as raízes reais sejam iguais.
Para essa condição, o valor de ∆ precisa ser igual a 0.
Resolução:

41) Resolva a seguinte equação do 2º grau.
Resolução:


42) Resolva a equação do 2° grau 2x² + x – 3 = 0.
Resolução:
Uma das alternativas para solucionar equações do 2° grau é através da fórmula de Bhaskara. Para tanto, precisamos identificar os coeficientes da equação, que são a = 2, b = 1 e c = – 3.
Δ = 1² – 4.2.(– 3)
Δ = 1 + 24
Δ = 25
x = – 1 ± √25
      2.2
x = – 1 ± 5
      4
x' = – 1 + 5 = 4 = 1
     4        4
x'' = – 1 – 5 = – 6 = – 3
           4        4       2
As raízes da equação 2x² + x – 3 = 0 são 1 e ^{– 3}/_2.

43) Determine o conjunto solução da equação – 3x² + 18x – 15 = 0.
Resolução:
Os coeficientes numéricos dessa equação do 2° grau são a = – 3, b = 18 e c = – 15. Observe que todos os coeficientes são múltiplos de 3, por isso podemos dividir todos por 3 para obter valores menores e, consequentemente, mais fáceis de calcular. Os novos coeficientes são: a = – 1, b = 6 e c = – 5. Ao realizar essa simplificação dos coeficientes, o resultado da equação permanece inalterado.
Vamos aplicar esses coeficientes na fórmula de Bhaskara:
Δ = 6² – 4.(– 1).(– 5)
Δ = 36 – 20
Δ = 16
x = – 6 ± √16
      2.(– 1)
x = – 6 ± 4
     – 2
x' = – 6 + 4 = – 2 = 1
    – 2       – 2
x'' = – 6 – 4 = – 10 = 5
      – 2      – 2
O conjunto solução é S = {1; 5}.

44) (Puc – Rio) As duas soluções de uma equação do 2° grau são – 1 e ¹/₃. Então a equação é:
(A) 3x² – x – 1 = 0
(B) 3x² + x – 1 = 0
(C) 3x² + 2x – 1 = 0
(D) 3x² – 2x – 2 = 0
(E) 3x² – x + 1 = 0
Resolução:
Para encontrar a equação do 2° grau a partir de suas raízes, basta fazer:
(x – S₁) · (x – S₂) = 0
S₁ e S₂ são as raízes da equação. Vamos substituí-las na operação acima:
(x – (– 1)) · (x – (¹/₃)) = 0
(x + 1) · (x – (¹/₃)) = 0
x² – (¹/₃)x + x – ¹/₃ = 0
x² + (²/₃)x – ¹/₃ = 0
Podemos multiplicar toda a equação por 3:
3x² + 2x – 1 = 0
Alternativa: C

45) (Cesgranrio) A maior raiz da equação – 2x² + 3x + 5 = 0 vale:
(A) – 1
(B) 1
(C) 2
(D) 2,5
(E) (3 + √19)/4
Resolução:
Para resolver essa equação do 2° grau, vamos utilizar a Fórmula de Bhaskara. Os coeficientes da equação são a = – 2, b = 3 e c = 5. Substituindo-os na fórmula, temos:
Δ = 3² – 4.(– 2).5
Δ = 9 + 40
Δ = 49
x = – 3 ± √49
      2.(– 2)
x = – 3 ± 7
      – 4
x' = – 3 + 7 = 4 = – 1
 – 4     – 4
x'' = – 3 – 7 = – 10 = 2,5
– 4 – 4
Encontramos duas raízes para a equação, x' = – 1 e x'' = 2,5; e a maior delas é x'' = 2,5.
Alternativa: B

46) Resolva a equação: 4x² + 8x + 6 = 0
Resolução:
Os coeficientes da equação são: a = 4, b = 8, c = 6. Substituindo esses valores na fórmula de Bhaskara, temos:
Δ = 8² – 4.4.6
Δ = 64 – 96
Δ = – 32
Como Δ < 0, a equação não possui raiz real.

47) Encontre as raízes da equação: x² – 4x – 5 = 0
Resolução:
Os coeficientes dessa equação são: a = 1, b = – 4, c = – 5. Agora basta aplicar esses valores na fórmula de Bhaskara:

Δ = (– 4)² – 4.1.(– 5)
Δ = 16 + 20
Δ = 36
x = – (– 4) ± √36
             2.1
x = 4 ± 6
         2
x' = 10 = 5
        2
x'' = – 2 = – 1
          2
Nesse caso, a equação tem duas raízes reais: – 1 e 5.

SOMA & PRODUTO
A soma e produto é um método prático para encontrar as raízes de equações do 2º grau do tipo x² - Sx + P e é indicado quando as raízes são números inteiros.
Baseia-se nas seguintes relações entre as raízes:
Sendo,
x₁ e x₂: raízes da equação do 2º grau
a, b e c: coeficientes da equação do 2º grau

Desta forma, podemos encontrar as raízes da equação ax² + bx + c = 0, se encontrarmos dois números que satisfaçam simultaneamente as relações indicadas acima.
Se não for possível encontrar números inteiros que satisfaçam as duas relações ao mesmo tempo, devemos utilizar outro método de resolução.

Como encontrar esses números?
Para encontrar a solução devemos começar buscando dois números cujo produto seja igual a  c / a. Depois verificamos se esses números também satisfazem o valor da soma.
Como nem sempre as raízes de uma equação do 2º grau são positivas, devemos aplicar as regras de sinais da soma e da multiplicação para identificarmos quais sinais devemos atribuir as raízes.
Para tal, teremos as seguintes situações:
P > 0 e S > 0 ⇒ As duas raízes são positivas.
P > 0 e S
P 0 ⇒ As raízes possuem sinais diferentes e a de maior valor absoluto é positiva.

Soma e produto
Nesse método é importante conhecer os divisores de um número. Ele se torna interessante quando as raízes da equação são números inteiros, porém, quando são um número decimal, esse método fica bastante complicado.
A soma e o produto é uma relação entre as raízes x₁ e x₂ da equação do segundo grau, logo devemos buscar quais são os possíveis valores para as raízes que satisfazem a seguinte relação:

Exemplo:
Encontre as soluções para a equação x² – 5x + 6 = 0.
Resolucao
1º passo: encontrar a, b e c.
a = 1
b = -5
c = 6

2º passo: substituir os valores de a, b e c na fórmula.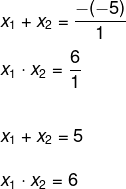

3º passo: encontrar o valor de x₁ e x₂ analisando a equação.
Nesse caso, estamos procurando dois números cujo produto seja igual a 6 e a soma seja igual a 5.
Os números cuja multiplicação é igual a 6 são:
6 x 1 = 6
3 x 2 =6
III. (-6) x (-1) = 6
(-3) x (-2) = 6
Dos possíveis resultados, vamos buscar aquele em que a soma seja igual a 5.
Note que somente a II possui soma igual a 5, logo as raízes da equação são x₁ = 3 e x₂ = 2.

48) Encontre as raízes da equação x² - 7x + 12 = 0
Resolução:
Nesse exemplo temos:

Assim, temos que encontrar dois números cujo produto é igual a 12.
Sabemos que:
1 . 12 = 12
2 . 6 = 12
3 . 4 = 12
Agora, precisamos verificar os dois números cuja soma é igual a 7.
Assim, identificamos que as raízes são 3 e 4, pois 3 + 4 = 7

49) Encontre as raízes da equação x² + 11x + 24
Resolução:

Procurando o produto igual a 24, temos:
1 . 24 = 24
2 . 12 = 24
3 . 8 = 24
4 . 6 = 24
Como o sinal do produto é positivo e o da soma é negativo (- 11), as raízes apresentam sinais iguais e negativos. Sendo assim, as raízes são - 3 e - 8, pois - 3 + (- 8) = - 11.

50) Quais são as raízes da equação 3x² - 21x - 24 = 0?
Resolução:

O produto poderá ser:
1 . 8 = 8
2 . 4 = 8
Sendo o sinal do produto negativo e da soma positivo (+7), concluímos que as raízes possuem sinais diferentes e que o maior valor possui sinal positivo.
Assim, as raízes procuradas são 8 e (- 1), pois 8 - 1 = 7

51) Encontre as raízes da equação x² + 3x + 5
Resolução:

O único produto possível é 5.1, contudo 5 + 1 ≠ - 3. Desta forma, não é possível encontrar as raízes por esse método.
Calculando o discriminante da equação descobrimos que ∆ = - 11, ou seja, essa equação não possui raízes reais (∆)

51) Um retângulo possui a medida de seu lado maior igual ao quádruplo do lado menor, e área medindo 256 m². Determine a medida de seus lados.
Informe que, para calcularmos a área de uma região retangular devemos multiplicar o comprimento pela largura.
Resolução:
O lado de maior comprimento mede 32 metros e o de menor comprimento, 8 metros.
 
53) Um trapézio possui área medindo 384 cm². Temos que a medida da altura é o dobro da medida da base menor, e que a base maior possui a mesma medida da altura. Determine o comprimento da base maior, base menor e altura desta figura.
Resolução:
Área do trapézio
Lado maior: 2 * 8√2 → 16√2 cm
Lado menor: 8√2 cm
Altura: 16√2 cm

54) O dobro de um número subtraído de 20 é igual a 100. Qual é o número?
Resolução:
Um número: x
O dobro do número: 2x
Como estamos subtraindo 2x de 20 a equação será:
20 – 2x = 100
Resolvendo a equação
20 – 2x = 100
– 2x – 20 + 20 = 100 – 20 (adicionamos 20 aos dois lados da equação)
– 2x = 80 (– 1)
2x = – 80
x = – 80
          2
x = – 40
Resposta: o número é igual a – 40.

55) O triplo de um número adicionado ao seu dobro resulta em 600. Qual é o número?
Resolução:
Um número: x
O triplo deste número: 3x
O dobro deste número: 2x
O triplo de um número adicionado ao seu dobro resulta em 600: 3x + 2x = 600

Resolvendo a equação:
3x + 2x = 600
5x = 600
x = 600/5
x = 120
Resposta: temos que o número é igual a 120.

56) Que número eu sou? O dobro de meu antecessor, menos 3, é igual a 25.
Resolução:
Um número: x
Antecessor: x – 1
O dobro de meu antecessor menos 3: 2(x – 1) – 3 = 25
Resolvendo a equação
2(x – 1) – 3 = 25 (aplicar o método da distribuição)
2x – 2 – 3 = 25
2x – 5 = 25
2x = 25 + 5
2x = 30
x = 30/2
x = 15
Resposta: o número é igual a 15.

57) Carlos tinha certa quantia em dinheiro, foi ao shopping e gastou 1/3 da quantia na compra de uma revista, gastou 1/4 da quantia na compra de um CD e ainda ficou com R$ 25,00. Qual era a quantia que Carlos possuía?
Resolução:
Quantia: x
Um terço da quantia: 1/3x
Um quarto da quantia: 1/4x
Equação do problema: (1/3)x + (1/4)x + 25 = x
MMC (3,4) = 12
(4/12)x + (3/12)x + 300 = (12/12)x (simplificando os denominadores)
4x + 3x + 300 = 12x
12x – 4x – 3x = 300
12x – 7x = 300
5x = 300
x = 300/5
x = 60
Resposta: Carlos possuía a quantia de R$ 60,00.

58) Os 44 alunos da 7ª série A de uma escola representam 40% de todos os alunos da 7ª série dessa mesma instituição. Quantos são os alunos da 7ª série dessa escola?
Resolução:
Alunos: x
40% = 40/100 = 2/5 dos alunos
2/5 de x
(2/5)x = 44
2x = 44 * 5
2x = 220
x = 220/2
x = 110
Resposta: a escola possui 110 alunos cursando a 7ª série.

59) Determine três números inteiros positivos e consecutivos tais que o quadrado do menor seja igual a diferença dos outros dois.
Resolução:
Acreditamos que nesse tipo de problema, os alunos têm dificuldade em interpretar corretamente, visto que é muito comum a montagem da equação errada:
x² = (x + 1) – (x + 2).
O quadrado de um número não pode ser negativo, portanto, neste caso, devemos fazer (x + 2) – (x + 1) e não o contrário.
Devemos, então, enfatizar, que a leitura atenta do enunciado é fundamental para uma correta interpretação!
Uma proposta de solução:
Interpretando o problema e usando a linguagem algébrica:
x, representa o menor número
x + 1, representa o consecutivo de x
x + 2, representa o consecutivo de x + 1
Observação: Poderíamos também representá-los por x, x – 1 e x – 2. Nesse caso, x representa o maior dos três números.
Como estratégia de resolução, procedemos a montagem da equação de acordo com o enunciado do problema:
x² = (x + 2) – (x + 1)
Desenvolvendo, temos:
x² = x + 2 – x – 1
x² = 1
Lembrando que:
Temos:
Logo, x = 1 ou x = –1
Analisando a condição do problema, “três números inteiros positivos e consecutivos”, a única solução que satisfaz é x = 1.
Resposta: os números são 1, 2 e 3.

60) Pai e filho têm hoje 45 e 15 anos, respectivamente. Há quantos anos a idade do pai era igual ao quadrado da idade do filho?
Resolução:
Em problemas como esse que envolvem tempo decorrido — Há quantos anos... — é importante comentar na turma, que o sinal de menos (–), não significa “retirar” uma quantidade e sim, voltar no tempo! O mesmo vale para situações que se remetem a tempo futuro: “Daqui a quanto tempo...”. O sinal de mais (+) significa avançar no tempo.

Uma proposta de solução:
De acordo com o enunciado, podemos fazer uma representação algébrica das idades do pai e do filho, há x anos.
idade do pai há x anos: 45 – x
idade do filho há x anos: 15 – x
Equalizando as informações: 45 – x = (15 – x)²
Desenvolvendo a equação, obtemos:
45 – x = 225 – 30x + x² Utilizando o princípio de equivalência, temos:
x² – 29x + 180 = 0
Resolvendo a equação utilizando as relações entre coeficientes e raízes:
S = 29
P = 180
Devemos pensar em dois números positivos (soma e produto positivos).
Os números são: 9 e 20.
Analisando os resultados encontrados, o valor 20 não pode ser usado no problema, pois, nesse caso, o filho teria idade negativa!
Portando, para x = 9 temos para idades: 36 e 6 anos.
Resposta: há 9 anos.
 

Continua...