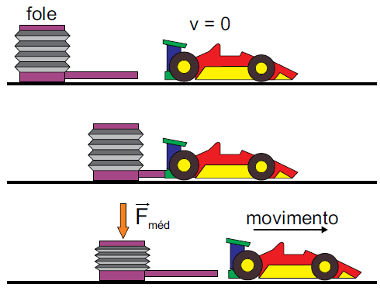
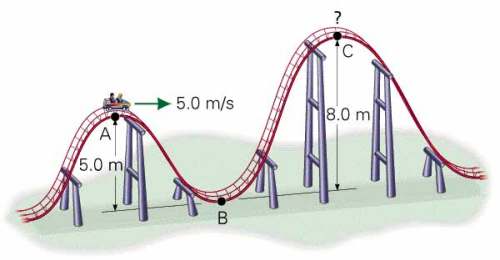
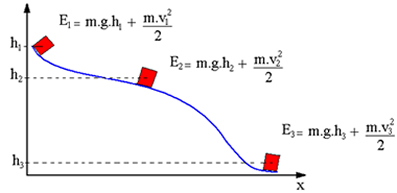
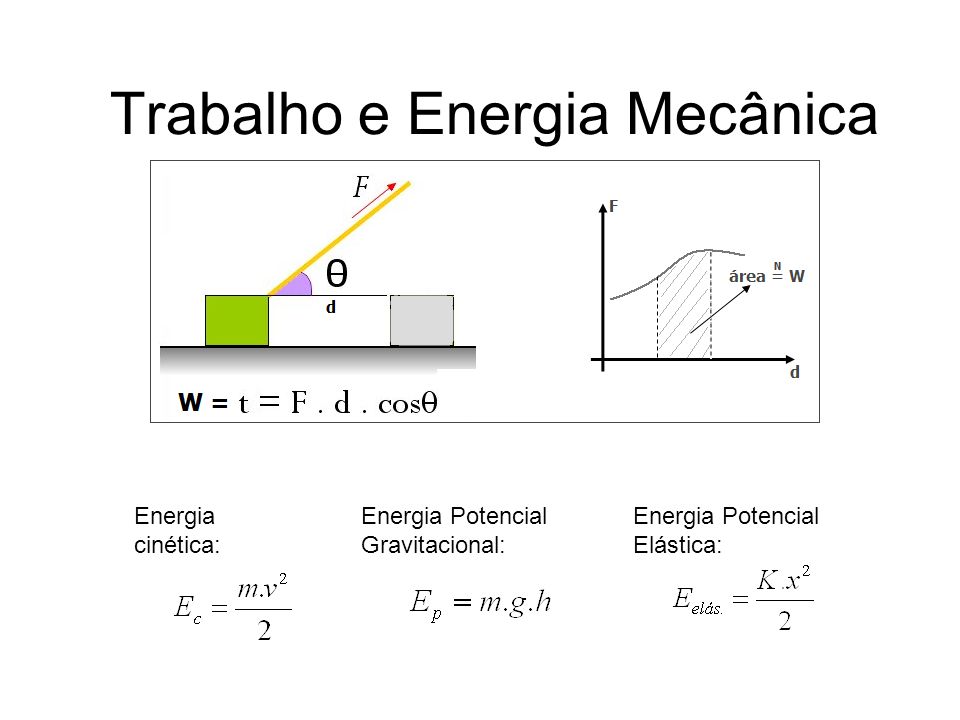
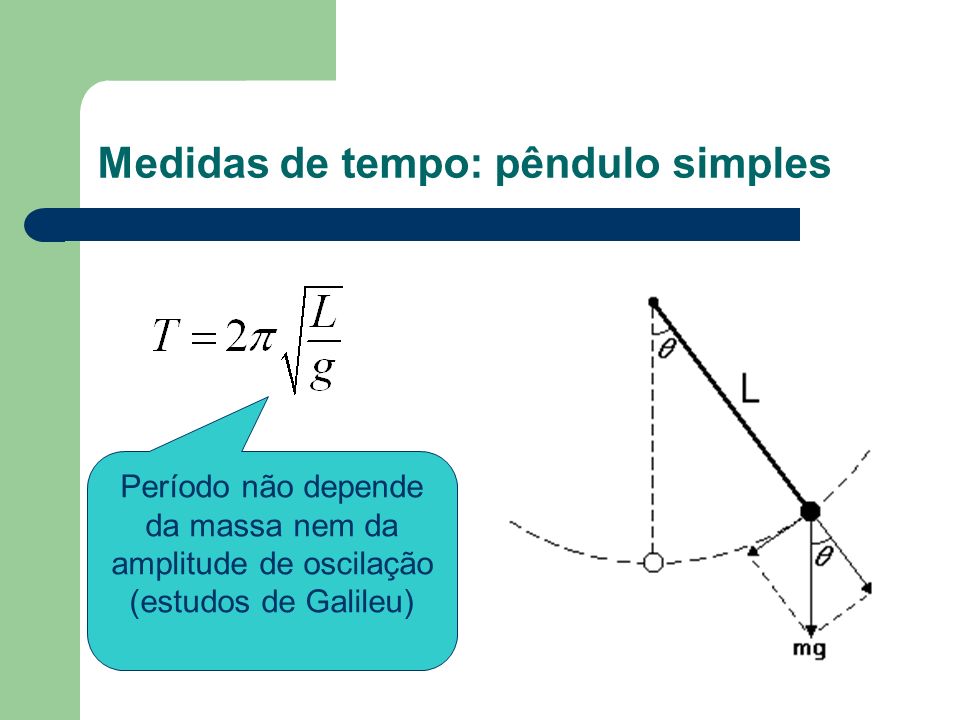
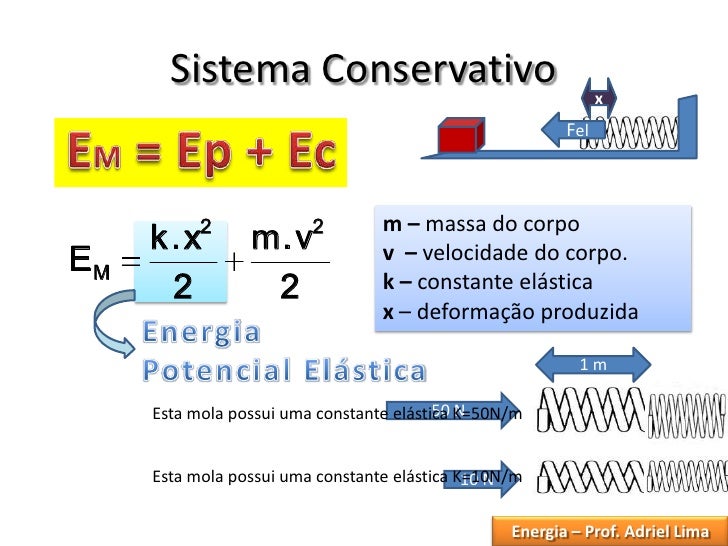
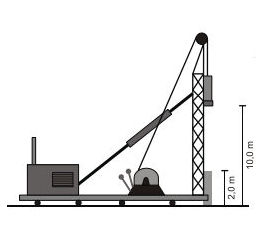
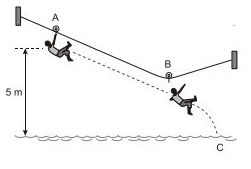
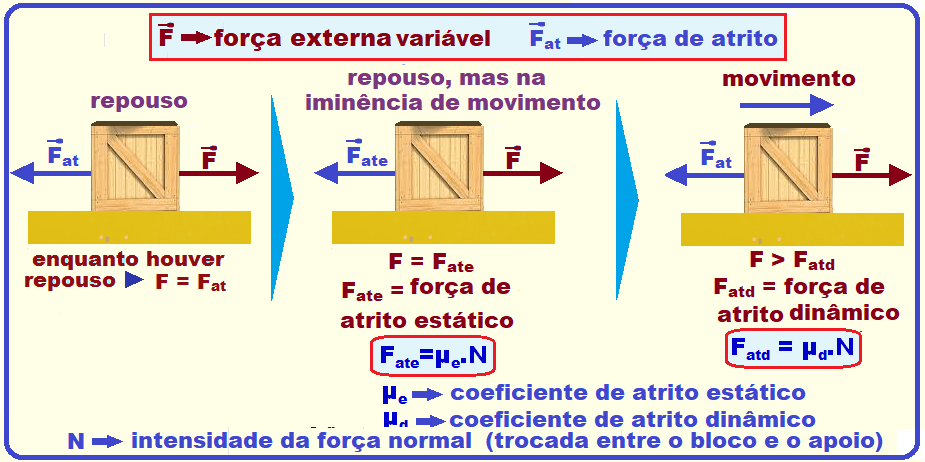
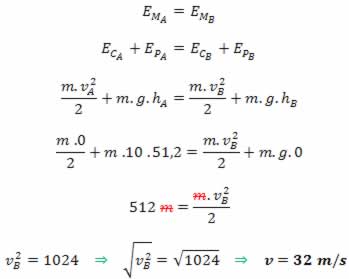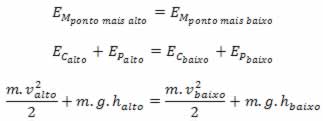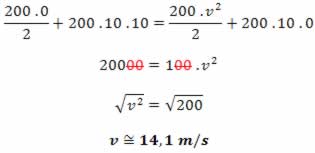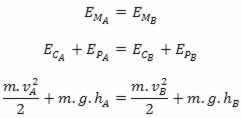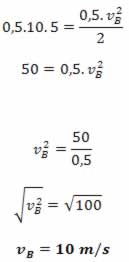Exemplo -1:
Um corpo com massa de 5 kg é submetido a uma força de intensidade 25N. Qual é a aceleração que ele adquire?
Resolução:
F = m . a
a = F
m
a = 25
5
a = 5 m/s2
Exemplo - 2:
(PUC) Quando a resultante das forças que atuam sobre um corpo é 10N, sua aceleração é 4m/s2.
Se a resultante das forças fosse 12,5N, a aceleração seria de:
(A) 2,5 m/s2
(B) 5,0 m/s2
(C) 7,5 m/s2
(D) 2 m/s2
(E) 12,5 m/s2
Resolução:
Inicialmente devemos encontrar a massa desse corpo. Como são dadas a aceleração e a distância, podemos usar a equação:
FR1 = m . a
m = FR1
a
m = 10
4
m = 2,5 kg
Possuindo o valor da massa e a força, utilizaremos novamente a expressão acima para calcular a aceleração:
FR2 = m . a'
a' = FR2
m
a' = 12,5
2,5
a' = 5 m/s2
Alternativa: B
Exemplo - 3:
(PUC-RIO 2008) A primeira Lei de Newton afirma que, se a soma de todas as forças atuando sobre o corpo for zero, o corpo …
(A) terá um movimento uniformemente variado
(B) apresentará velocidade constante
(C) apresentará velocidade constante em módulo, mas sua direção poderá ser alterada.
(D) será desacelerado
(E) apresentará um movimento circular uniforme.
Resolução:
De acordo com a primeira Lei de Newton, se a resultante das forças que atuam sobre um corpo for zero, ele permanecerá em repouso ou em movimento retilíneo uniforme, ou seja, com velocidade constante
Alternativa: D
Exemplo - 4:
Um corpo com massa de 60 kg está na superfície do planeta Marte, onde a aceleração da gravidade é 3,71 m/s2 .
De acordo com esses dados, responda:
a) Qual é o peso desse corpo na superfície de Marte?
b) Suponha que esse mesmo objeto seja trazido para a Terra, onde g = 9,78 m/s2, qual será o seu peso?
Resolução:
a) Na superfície de Marte:
P = m.g
P = 60 . 3,71
P = 222,6 N
b) Na Terra:
P = m.g
P = 60 . 9,78
P = 586,8 N
Exemplo - 5:
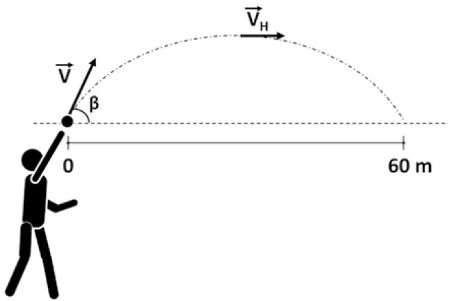
Considere as seguintes forças aplicadas a um corpo:Qual é a força resultante aplicada?
Resolução:
Módulo:
5N - 3N = 2N
Resposta: direção e sentido: O mesmo da força maior em módulo (5N)
Exemplo - 6:
Uma força de 50N é aplicada a um corpo de massa 100kg que se encontra em repouso. Sendo esta a única força que atua no corpo, qual a velocidade alcançada após 10s da aplicação da força?
Resolução:
Exemplo - 7:
Qual a massa de um corpo que, partindo do repouso, atinge uma velocidade de 12m/s em 20s? Sabendo que a força aplicada nele tem módulo igual a 30N.
Resolução:Conhecendo a aceleração do corpo:
Exemplo - 8:
Qual a força mínima que deve ser feita para levantar um automóvel com massa 800kg?
Reolução:
A força deve ser maior ou igual à força peso, então:
Exemplo - 9:
Qual a massa de um corpo com peso 12000kgf?
Resolução:GRAVITAÇÃO UNIVERSAL
Exemplo - 10:
Um satélite de comunicação em órbita circular tem raio R e período T. Um outro satélite de órbita circular tem período T /3 . Qual o raio da órbita do segundo satélite?
Resolução:
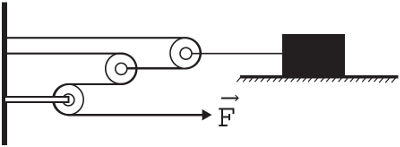
Exemplo - 11:
Qual a intensidade do campo gravitacional da Terra sobre a Lua?
Resolução:Calculo da aceleração gravitacional da Terra sobre a Lua temos:
Exemplo - 12:
(Leis de Kepler) Nicolau Copérnico (1473 – 1543), Tycho Brahe (1546 – 1601) e Johannes Kepler (1571 – 1630) foram grandes estudiosos das órbitas dos planetas. Foi Johannes Kepler, porém, que, após exaustivo trabalho, conseguiu descrever corretamente, pela primeira vez, as órbitas dos planetas do sistema solar, por meio de três leis, denominadas leis de Kepler.
Uma dessas leis é:
(A) as órbitas são elípticas com o Sol ocupando um dos focos.
(B) as órbitas são elípticas com a Terra ocupando um dos focos.
(C) as órbitas são circulares com a Terra ocupando um dos focos.
(E) as órbitas são circulares com o Sol ocupando um dos focos.
(E) as órbitas são elípticas com o Sol ocupando um dos focos e a Terra o outro.
Resolução
De acordo com a 1ª Lei de Kepler, as órbitas são elípticas e o Sol ocupa um dos focos.
Alternativa: A
Exemplo - 13:
(Gravitação Universal) A respeito do planeta júpiter e de um de seus satélites, Io, foram feitas as afirmações:
I. Sobre esses corpos celestes, de grandes, de grandes massas, predominam as forças gravitacionais.
II. É a força de Júpiter em Io que o mantém em órbita em torno do planeta.
III. A força que Júpiter exerce em Io tem maior intensidade que a força exercida por Io em Júpiter.
Deve-se concluir que somente:
(A) I é correta.
(B) II é correta.
(C) III é correta.
(D) I e II são corretas.
(E) II e III são corretas.
Resolução
I. Correta: De acordo com a lei da gravitação, verifica-se que as forças gravitacionais são predominantes em relação a corpos de grande massa.
II. Correta: A força gravitacional faz o papel de resultante centrípeta.
III. Falsa. As forças têm a mesma intensidade.
Alternativa: D
Exemplo - 14:
(FUVEST) A massa da Lua é 81 vezes menor do que a da terra e o seu volume é 49 vezes menor do que o da Terra.
a) Qual a relação entre as densidades da lua a da Terra?
b) Qual a aceleração da gravidade na superfície da Lua?
Resolução:
Determinamos que:
M = massa da Lua
M = 81m: massa da Terra
V = volume da Lua
V= 49v: volume da Terra
A densidade é dada por
d= m/v
logo:
Para a Lua d = m / v e para a Terra D = M / V = 81m / 49v, então:
![]() Sabemos que a intensidade da gravidade na superfície é dada por:
Sabemos que a intensidade da gravidade na superfície é dada por:
g = GM /r2 para a Lua
gT = GM / R2 para a Terra
Agora devemos encontrar uma relação entre os raios da Lua e da Terra, podemos fazer isso utilizando a relação entre os volumes V = 49v: Agora podemos efetuar o quociente g / gT temos:
Agora podemos efetuar o quociente g / gT temos: Resposta: g = 1,7 m/s2
Resposta: g = 1,7 m/s2
Exemplo - 15:
Em um elevador há um homem de massa igual a 95 kg sobre uma balança graduada em newton. Em um instante, o elevador começa a subir com aceleração de 0,5 m/s2. Determine a diferença percentual aproximada entre a marcação do peso do homem no elevador em repouso e em movimento.
Dado: g = 10 m/s2
(A) 7,8 %
(B) 5,8 %
(C) 4,8 %
(D) 2,8 %
(E) 9,8 %
Resolução:
No momento em que o elevador está parado, a marcação da balança, que representa a força normal, é igual à força
P = N
g = N
P = m . g
N = 95 . 10
950 N
No momento em que o elevador inicia a subida, a força resultante será dada pela diferença entre a força normal e o
peso, logo:
FR = m.a
N – P = m.a
N = m.a + mg
N = m.(a + g)
N = 95.(0,5 + 10)
N = 997,5 NA diferença percentual entre as marcações é:
Dp = (997,5 – 950) / 997,5 = 4,76
Alternativa: C
Exemplo - 16:
Determine o peso aparente de uma pessoa de massa igual a 50 kg que está em um elevador que desce com aceleração igual a 1 m/s2.
Dado: g = 10 m/s2
(A) 460 kg
(B) 458 kg
(C) 455 kg
(D) 445 kg
(E) 450 kg
Resolução:
Na descida do elevador, a força resultante é dada pela diferença entre a força peso e a força normal:
FR = m.a
P – N = m.a
N = m.g – m.a
N = m (g – a)
N = 50 (10 – 1)
N = 450 N
A marcação indicada por uma balança corresponde à força normal. Nesse caso, a indicação é menor que o peso real da pessoa, que é de 500N.
Alternativa: E
Exemplo - 17:
(Unifor-CE) Um corpo de massa 2,0 kg está pendurado em um dinamômetro preso ao teto de um elevador. Uma pessoa no interior deste elevador observa que a indicação fornecida pelo dinamômetro é 26N.
Considerando a aceleração local da gravidade de 10 m/s2, o elevador pode estar:
(A) em repouso.
(B) descendo com aceleração de 2,0 m/s
(C) descendo em movimento uniforme
(D) subindo com velocidade constante
(E) subindo com aceleração de 3,0 m/s2
Resolução:
O peso aparente de um corpo que está dentro de um elevador em movimento acelerado será maior que o peso real somente se o elevador estiver subindo. Nesse caso, a força resultante do sistema será a diferença entre a força normal e a força peso.
FR = m.a
N – P = m.a
N = m.a + m.g
N = m. (a + g)
26 = 2 (a + 10)
(a + 10) = 13
a = 3,0 m/s2
Alternativa: E
Exemplo - 18:
(ITA) Uma pilha de seis blocos iguais, de mesma massa m, repousa sobre o piso de um elevador, como mostra a figura. O elevador está subindo em movimento uniformemente retardado com uma aceleração de módulo a. O módulo da força que o bloco 3 exerce sobre o bloco 2 é dado por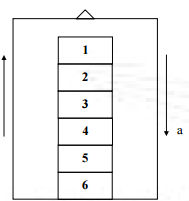 (A) 3m (g + a)
(A) 3m (g + a)
(B) 3m (g – a)
(C) 2m (g + a)
(D) 2m (g – a)
(E) m (2g – a)
Resolução:
A força exercida pelo bloco 3 sobre o bloco 2 é a força normal referente ao peso dos blocos 1 e 2. Nesse caso, a força resultante é dada pela diferença do peso pela força normal, portanto:
FR = 2 m . a
P – N = 2 m . a
N = 2 m . g – 2 m . a
N = 2m (g – a)
Alternativa: B
ENERGIA CINÉTICA
Energia cinética - É um tipo de energia que está relacionada com o movimento dos corpos.
O resultado da energia cinética está intrinsecamente ligado ao valor da massa do objeto e a sua velocidade de movimento.
Exemplo: se dois objetos tiverem a mesma velocidade, mas com massas diferentes, o corpo que tiver a massa mais pesada terá maior energia cinética.
Normalmente, para que um objeto ganhe movimento inicial é preciso a aplicação de uma força que o impulsione (ação esta que na Física é conhecida por “Trabalho”).
Segundo o Teorema da Energia Cinética, “o trabalho da força resultante é medido pela variação da energia cinética”.
Equação da Energia Cinética De acordo com o Sistema Internacional de Unidades, a energia cinética é medida em Joules (J), em referência ao cientista inglês James Prescott Joule.
De acordo com o Sistema Internacional de Unidades, a energia cinética é medida em Joules (J), em referência ao cientista inglês James Prescott Joule.
Para a Física, a energia cinética faz parte do conceito de Energia Mecânica, que também engloba outros modelos de energia, como a Potencial Elástica e a Potencial Gravitacional, por exemplo.
Energia Cinética e Energia Potencial - São inversamente proporcionais. Ao contrário da energia cinética, que gasta energia para executar o movimento, a energia potencial consiste no armazenamento desta energia.
A energia “armazenada” (potencial) pode se manifestar, posteriormente, como energia cinética, a partir do momento em que determinado corpo (“energizado”) começa a se movimentar.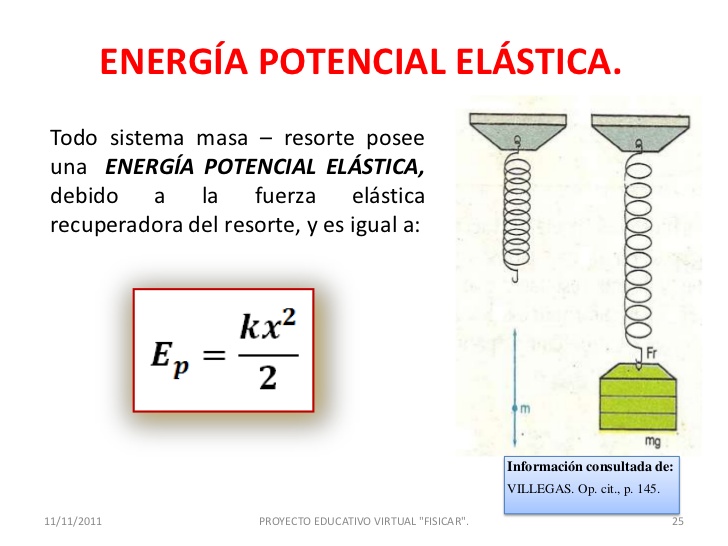
ENERGIA CINÉTICA E ENERGIA POTENCIAL GRAVITACIONAL
01) (PUC-RIO) Sabendo que um corredor cibernético de 80 kg, partindo do repouso, realiza a prova de 200 m em 20 s mantendo uma aceleração constante de a = 1,0 m/s², pode-se afirmar que a energia cinética atingida pelo corredor no final dos 200 m, em joules, é:
(A) 12000
(B) 13000
(C) 14000
(D) 15000
(E) 16000
Resolução:
Não foi informado diretamente o valor da velocidade quando o corredor atinge os 200m, mas foram dadas informações suficientes para calcular a velocidade. Primeiro vamos calcular a velocidade e depois calculamos a energia cinética usando a fórmula.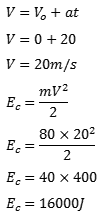
02) Qual a energia cinética de uma partícula de massa 5000g cuja velocidade vale 72km/h?
Resolução:
Observem que a massa foi dada em gramas e a velocidade em km/h. Antes de calcular a energia cinética, temos que passar a massa para quilogramas e a velocidade para m/s. Feito isso, vamos aplicar a fórmula da energia cinética.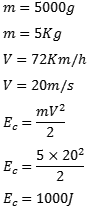
03) Calcule a energia cinética de um corpo de massa de 50Kg que se move a uma velocidade de 10m/s.
Resolução:
Solução do exercício: esse é bem direto. Temos a massa em quilogramas e a velocidade em metros por segundo, então basta aplicar os valores na fórmula da Ec.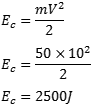
04) Uma moto trafega a uma velocidade constante de 93,6Km/h, quando colide com outro veículo. Qual a energia cinética da moto sabendo que sua massa é de 190000g?
Resolução:
Tanto a velocidade quanto a massa não estão nas unidades de medida adequadas. O primeiro passo é converter a velocidade de km/h para m/s e depois passar a massa de kg para g. Feito isso, utilizamos a fórmula para calcular a Ec da moto.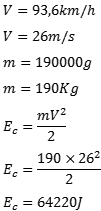
05) Um veículo com 800kg de massa está ocupado por duas pessoas, que juntas possuem 140Kg de massa. A energia cinética do conjunto veículo e passageiros é igual a 423KJ. Calcule a velocidade do veículo.
Resolução:
A pergunta do exercício não é o valor da energia cinética, mas o valor da velocidade do veículo! A massa total é dada pela soma das massas do veículo e dos passageiros. Substituindo os valores e isolando a velocidade encontramos seu valor.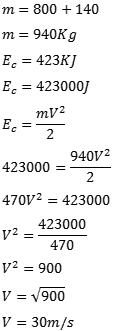 CASOS ESPECIAIS
CASOS ESPECIAIS
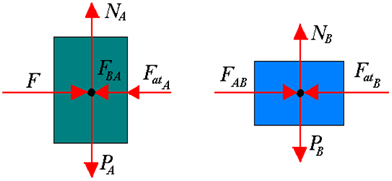
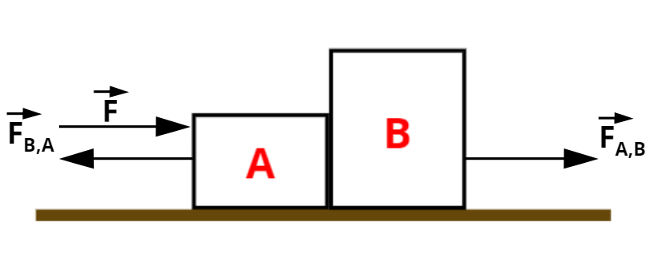
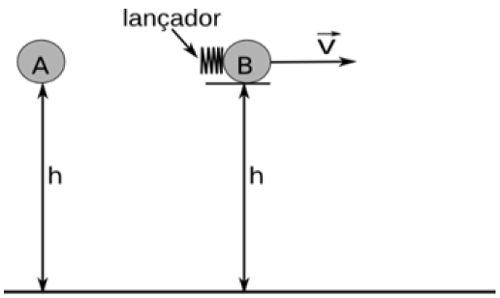
01) Uma força horizontal de intensidade F = 10 N é aplicada no bloco A, de 6 kg, o qual está apoiado em um segundo bloco B, de 4 kg. Os blocos deslizam sobre um plano horizontal sem atrito. Determine:  a) a aceleração do conjunto.
a) a aceleração do conjunto.
Resolução:
A aceleração de conjunto é equivalente a 1m/s².
F - Fab = 6a
10 - Fab = 6a
Fab = - 6a + 10
(que é a força que a exerce em b)
Fab = 4a
-6a + 10 = 4a
10a = 10
a = 10/10
b) a intensidade da força que um bloco exerce no outro.
Resolução:
A intensidade da força que um bloco exerce no outro é equivalente a 4 Newton (quatro Newton).
Fab = 4a
jFab = 4 N ewton, que é o valor exato da força exercida por a sobre o bloco B.
c) a intensidade da força resultante em Ae em B
Resolução:
A intensidade da força resultante em a e em b é equivalente a 6 N (seis Newton).
F - Fab
10 - 4 = 6 Newton.
02) Três blocos A, B e C, de massa mA = 5 kg, mB = 2 kg e mC = 3 kg, estão numa superfície horizontal sem atrito. Aplica-se ao bloco A uma força de 20 N, constante, como indicado na figura. 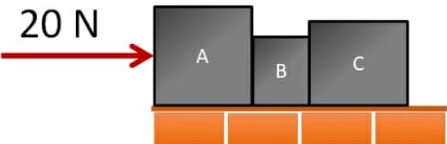 Determine:
Determine:
a) a aceleração do conjunto;
Resolução:
Podemos afirmar que a aceleração do conjunto é equivalente a 2 m/s² (dois metros por segundo ao quadrado).
F = m.a
20 = (5 + 2 + 3) . a
20 = 10a
a = 2 m/s²
b) a intensidade da força que B exerce em C
Resolução:
Podemos afirmar que a intensidade da força que B exerce em C é equivalente a 6 N (seis Newton).
B exerce em c a força necessária pra movimentá-lo a 2m/s²:
F = 3 . 2
F = 6 Newton
c) a intensidade da força que A exerce em B
Resolução:
Podemos afirmar que a intensidade da força que A exerce em B é equivalente a 10 N (dez Newton).
A exerce a força necessária pra mover os corpos B e C:
F = (2 + 3) . 2
F = 5 . 2
F = 10 Newton.
68) Dois blocos de massas mA = 5 kg e mB = 3 kg estão numa superfície horizontal sem atrito e ligados por um fio de massa desprezível. A força horizontal F tem intensidade constante igual a 4 N. Determine a tração no fio que liga os corpos 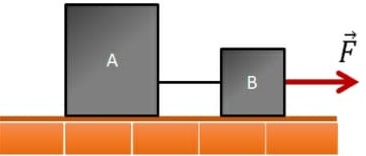 Resolução:
Resolução:
F = (mA + mB) . a
4 = (5 + 3) . a
a = 0,5 m/s²
Corpo B
F - T = mB.a
4 - T = 3.0,5
T = 2,5 N
69) (FEI-SP)Sabendo-se que a tração no fio que une os dois blocos vale 100 N, qual é o valor do módulo da força F? Não há atritos.  Resolução:
Resolução:
bloco maior
F - T = 10.a (I)
bloco menor
T = 5.a (II)
T = 100N
a = 20m/s²
substituindo na equação I os valores.
F - 100 = 200
F = 300
70) (UFRJ) Dois blocos de massa igual a 4 kg e 2 kg, respectivamente, estão presos entre si por um fio inextensível e de massa desprezível. Deseja-se puxar o conjunto por meio de uma força F cujo módulo é igual a 3 N sobre uma mesa horizontal e sem atrito. O fio é fraco e corre o risco de romper-se. Qual é o melhor modo de puxar o conjunto sem que o fio se rompa: pela massa maior ou pela menor? Justifique sua resposta.  Resolução:
Resolução:
Vamos aplicar a segunda lei de newton em ambas as caixas e em ambos os casos. Aplicando 3 N na caixa de 4 Kg e aplicando a segunda lei de newton em ambas as caixas, temos:
F – T = 4 . a
T = 2 . a
F - 2a = 4a
F = 6a
3 = 6a
a =1 /2 m/s ²
T = 1/2.2
T = 1 N
Temos uma tração de 1 N, aplicando a força F de 3 N na caixa de 4.
Fazendo a mesma coisa, só que na de 2 kg.
F - T= 2 .a
T = F - 2a
T = 4a
4a = F- 2a
6a = 3
a = 1/2 m/s²
T = 4 . a
T = 4 . 1/2
T = 2 N
Conclui-se, que ao puxar pela caixa maior, a tração será menor.
71) No arranjo experimental da figura não há atrito algum e o fio tem massa desprezível, os blocos tem massas mA = 2 kg e mB = 3 kg. Adote g = 10 m/s². 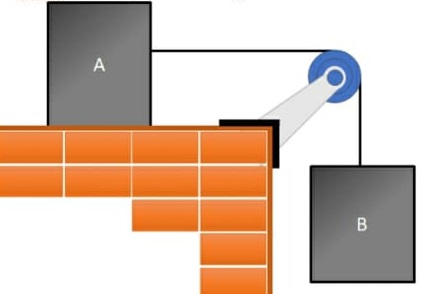 Determine:
Determine:
a) a aceleração do corpo.
Resolução:
mB= 3 kg
mA= 2 kg
peso de B = Pb
Pb= m . g
Pb =3 .10
Pb = 30 N = F
cálculo da aceleração do conjunto = a
F = ( mA + mB)a
30 = (2 + 3)a
30 = 5a
A = 30/5
A = 6m/s²
b) a tração no fio.
Resolução:
Tração no fio = Tf
Tf = mA . a
Tf = 2 . 6
Tf = 12 N
72) Na situação indicada na figura, os fios têm massa desprezível e passam pelas polias sem atrito. Adote g = 10 m/s2. Determine:
Determine:
a) a aceleração do conjunto;
Resolução:
I) PA - T = mA . a
II)T - PB = mB .a
PA - PB = (ma + mb + mc) a
200 - 100 = 40a
100 = 40 a
a = 100 /40
a = 2.5m/s²
b) a tração no fio que liga A B.
Resolução:
Tração do fio A e B de I temos:
I) PA - T = m a
200 - T = 50
-T = -150
T = 150N
c) a tração no fio que liga Ba C.
Resolução:
a tração no fio que liga B e C.
T = PB + mB . a
T = 100 + 10 . 2,5
T = 100 + 25
T = 125N
73) Os corpos A e B têm massas mA = 1 kg e mB = 3 kg. O corpo C, pendurado pelo fio, tem massa mC = 1 kg. O fio é inextensível e tem massa desprezível. Adote g = 10 m/s² e suponha que A e B deslizam sem atrito sobre o plano horizontal.
 Calcule:
Calcule:
a) a aceleração do corpo C
Resolução:
A aceleração de um corpo, primeiro é necessário achar a força resultante do corpo.
Fr = m . a
Considerando que o corpo está em repouso, já que no exercício diz que ele apenas está pendurado, enquanto A e B deslizam, podemos considerar que:
Para corpos em equilíbrio, utilizamos:
Somatório das forças = 0
T- P = 0
T= tração
P= Peso
Logo:
T = P = Força resultante
Portanto, basta aplicar a fórmula da força resultante, igualando-a ao peso
P = Fr
m.g = m.a
g = a = 10m/s²
b) a intensidade da força que o corpo B exerce em A.
Resolução:
A intensidade de uma força é adotada pela relação:
Fr = m.a
m = quilos (Kg)
a = aceleração (m/s²)
logo:
Fr = 3kg . 10m/s²
Fr = 30N
74) No arranjo experimental da figura os fios e a polia têm massas desprezíveis. O fio é inextensível e passa sem atrito pela polia. Adotando g = 10 m/s2, determine:  a) a aceleração dos corpos;
a) a aceleração dos corpos;
Resolução:
Como o bloco A possui 3kg então o seu peso é 30N, pois:
P = m . a
P = 3 . 10
P = 30
E o bloco B possui 1kg, então seu peso é de 10N:
P = 1 . 10
P = 10
Como o peso do bloco A é maior, a tendência é de que o movimento da corda seja puxando o bloco B para cima e o bloco A para baixo.
Para o bloco B temos:
T1 - 10 = 1 . a
Para o bloco A temos:
30 - T1 = 3 . a
b) as trações T1 e T2.
Resolução:
Juntando em um sistema:
T1 - 10 = 1 x a
30 - T1 = 3 x a
20 = 4 . a
a = 20/4
a = 5m/s²
De posse da aceleração, podemos usá-la em alguma das fórmulas obtidas:
T1 - 10 = 1 . a
T1 - 10 = 1 . 5
T1 = 15N
Como o fio que passa pela roldana será puxado por 15N pelos dois lados, T2 terá o valor de 30N, pois a roldana precisa se manter parada, e tudo o que está em cima é igual tudo o que está para baixo.
75) (Olimpíada Paulista de Física) Um homem de 70 kg está em cima de uma balança dentro de um elevador. Determine qual é a indicação da balança, nas seguintes situações:
a) O elevador subindo acelerado com aceleração de 3 m/s².
Resolução:
N - P = m.a
N - mg = m.a
N – 70 . 10 = 70 . 3
N = 210 + 700
N = 910 N
b) O elevador subindo com velocidade constante de 2 m/s.
Resolução:
O elevador sobe com velocidade constante
a = 0m/s²
Fn = m . g
Fn = 70 . 10
Fn = 700 N
c) O elevador descendo acelerado com aceleração de 1 m/s².
Resolução:
O elevador desce com a = 1m/s²
70kg .10m/s² - Fn = 70kg .1m/s²
700N - 70N = Fn
Fn = 630N
d) O elevador caindo em queda livre.
Resolução:
O elevador cai em queda livre
a = g = 10m/s²
Fn = m (a - g)
Fn = m (10 - 10g)
Fn = m . 0
Fn = 0
Considere a balança graduada em newtons e adote: g = 10 m/s².
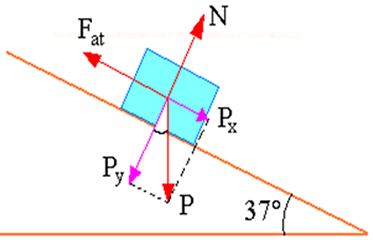
76) (Efoa-MG) No esquema representado na figura abaixo, o bloco C tem massa 0,5 kg e está em repouso sobre o plano inclinado de 37w com a horizontal, preso pelo fio AB. Não há atrito entre o bloco e o plano.  a) Qual é a tração exercida pelo fio?
a) Qual é a tração exercida pelo fio?
Resolução:
A atração exercida pelo fio e a aceleração adquirida pelo bloco é: 3N e 6m/s², respectivamente.
Vamos aos dados/resoluções:
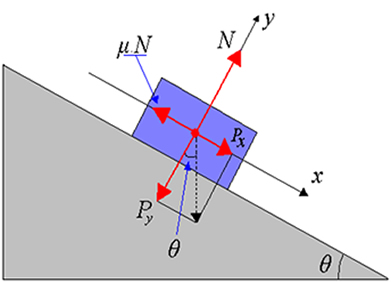
Os corpos que se encontram em cima do plano inclinado acabam apresentando três forças que atuam sobre ele, que são:
- Força Peso (P): É a força associada a gravidade da terra sobre os corpos que apresentam massa;
- Força Normal (N): Essa já é a força de reação contrária a força peso;
- Força de Atrito (Fat): Se encontra como a força de contato entre os materiais sendo esta proporcional à força normal e ao coeficiente de atrito entre os materiais.
T = Pt
T = P.sen37º
T = m . g . sen37º
T = 0,5 . 10 . 0,6
T = 3N
b) Cortando-se o fio, qual é a aceleração adquirida pelo bloco?
(Dados: g = 10 m/s²;
sen 37º = cos 53º = 0,6;
sen 53º = cos 37º = 0,8)
Resolução:
Fr = Pt
M . a = m . g . sen37º
a = 10 . 0,6
a = 6 m/s².
77) Determine a aceleração dos corpos na situação esquematizada abaixo. Adote g = 10 m/s². O fio e a polia têm massa desprezível. Não há atrito (dado: sen 30º = 0,5).  Resolução:
Resolução:
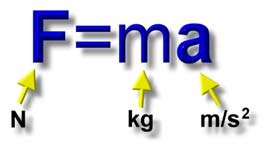
A 2ª lei de Newton é o princípio fundamental da dinâmica (PFD), pois é uma fórmula que explica a causa da movimentação ou não de um corpo. Ela diz que a resultante das forças que atuam sobre um corpo é igual ao produto entre sua massa e sua aceleração:
F = m . a
F = força resultante
m = massa do corpo
a = aceleração do corpo
As unidades de medida no Sistema Internacional (SI) são:
Força = Newton (N)
Massa = quilograma (kg)
Aceleração = metro por segundo ao quadrado (m/s²)
No nosso caso
O bloco sobre o plano inclinado está sob a ação de duas forças:
A tração do fio que o arrasta para cima: T
A componente x de seu peso (ver figura):
Px = P . cos60º
O bloco na vertical também está sujeito a duas forças:
O seu peso que o puxa para baixo = P
A tração que o sustenta = T
Aplicando a 2ª lei de Newton para os dois Somando as expressões membro a membro (cancela T)
Somando as expressões membro a membro (cancela T)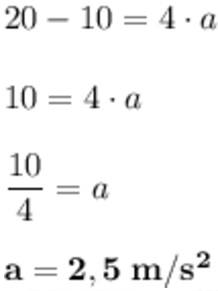
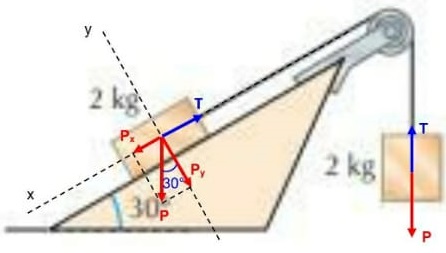
78) (Uerj 2013) Um bloco de madeira encontra-se em equilíbrio sobre um plano inclinado de 45º em relação ao solo. A intensidade da força que o bloco exerce perpendicularmente ao plano inclinado é igual a 2,0 N. Entre o bloco e o plano inclinado, a intensidade da força de atrito, em newtons, é igual a:
(A) 0,7
(B) 1,0
(C) 1,4
(D) 2,0
Resolução:
A intensidade da força de atrito é de 1,4 N.
Sabemos que a força normal que o plano faz sobre o bloco é de 2 N, isso quer dizer que a força peso do bloco também é 2 N. Na direção do plano inclinado, temos que a componente horizontal da força normal e a força de atrito são iguais, já que o bloco está em equilíbrio, ou seja:
P . sen(45°) = Fat
M . g . sen(45°) = u . m . g . cos(45°)
u = m . g . sen(45°)/m . g . cos(45°)
Como sen(45°) = cos(45°), temos:
u = 1
A força de atrito vale:
Fat = m . g . cos(45°)
Fat = 2 . cos(45°)
Fat = 1,4 N Alternativa: C
Alternativa: C
79) (G1 – cftmg) Na figura, estão indicadas as forças atuantes em uma caixa de peso P = 60 N que sobe uma rampa áspera com velocidade constante sob a ação de uma força F = 60 N. 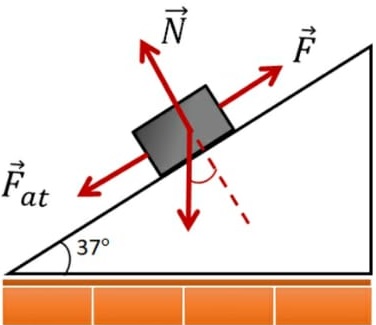 Nessas circunstâncias, o coeficiente de atrito cinético entre a rampa e esse bloco vale
Nessas circunstâncias, o coeficiente de atrito cinético entre a rampa e esse bloco vale
(A) 0,1.
(B) 0,2.
(C) 0,3.
(D) 0,5.
Resolução:
1. Como o movimento é retilíneo e uniforme, as forças (ou componentes) equilibram-se nos dois eixos, x e y.
2. Como os ângulos α e θ têm cada lado de um perpendicular a cada lado do outro, eles são congruentes: α = θ
Eixo y: N = Py ⇒ N = Pcosθ
Eixo y: Fa + Px = F ⇒ μ N + P senθ = F, substituindo N:
μ Pcosθ + P senθ = F, isolando P:
P(μ cosθ + senθ) = F, substituindo os valores de P e F:
60(μ cosθ + senθ) = 60, simplificando os dois valores "60"
jμ cosθ + senθ = 1, isolando μ:
μ = (1 - senθ)/cosθ
μ = (1 - sen37°)/cos37°
μ = (1 - 0,6)/0.8
μ = 0,4/0.8
μ = 0,5 Alternativa: D
Alternativa: D
80) Na figura, os fios e as polias são ideais e não há atrito entre o corpo A e o plano horizontal. Os corpos A e B, de massas mA = 0,5 kg e mB = 2,0 kg, respectivamente, são abandonados do repouso. Determine os módulos das acelerações de A e de B. (Use g = 10 m/s²) 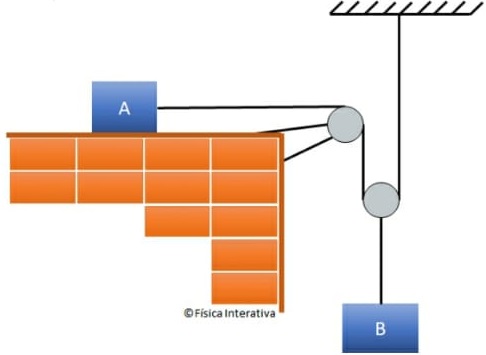 Resolução:
Resolução:
Como a massa do corpo B é maior que a do corpo A, os blocos vão ser puxados para baixo pela força gravitacional. A força resultante no sistema é nula. Ou seja, as força agentes em A são iguais e contrárias e B.
P = m.g
Em A, temos apenas a tensão da corda que liga ao corpo B.
T = mₐ.a (1)
Em B, temos a tensão aplicada no cabo que liga os corpos e a força gravitacional.
P - T = mᵇ . a (2)
Somando as duas equações
mᵇ . g = mₐ . a + mᵇ . a
coloca a em evidência
10 = 2,5 . a
2,5a = 20
a = 8 m/s²
QUESTÕES RESOLVIDAS - SEDUC-SP/2025
TRABALHO REALIZADO POR UMA FORÇA: IDEIAS INICIAIS
Trabalho realizado por uma força – Caso 1
O trabalho realizado por uma força é uma grandeza física que mede a transferência ou transformação de energia quando uma força causa um deslocamento de um objeto. Em termos simples, é o esforço feito por uma força para mover algo de um ponto a outro.
T = F . d
Onde:
F = é a força aplicada (N).
d = é o deslocamento (m).
Trabalho realizado por uma força – Caso 2
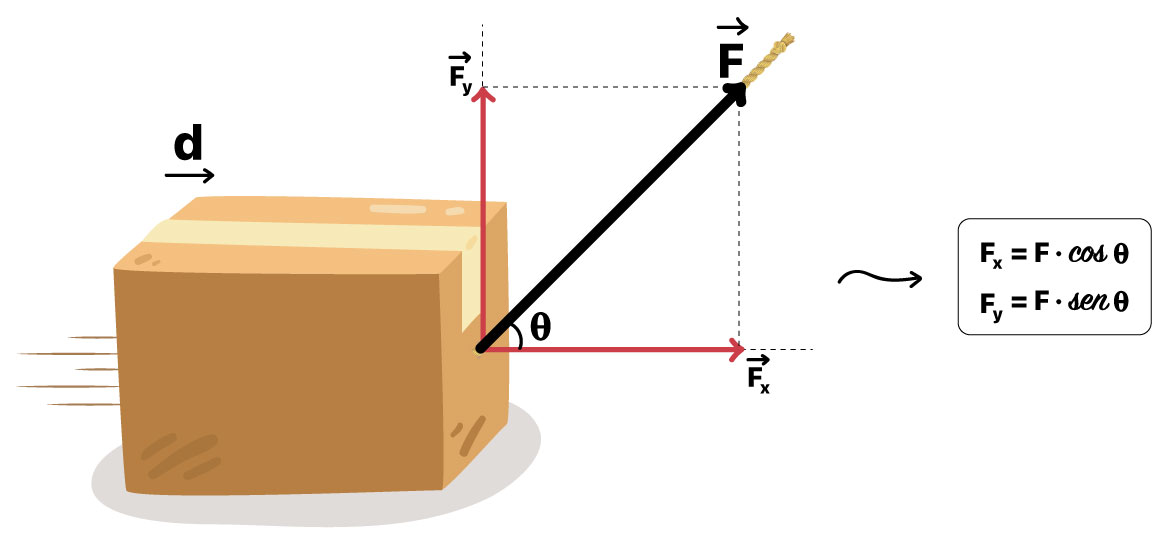
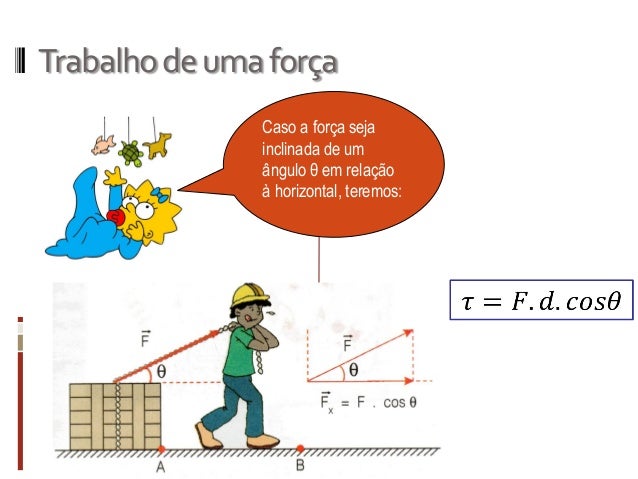
O trabalho é calculado como o produto da força pelo deslocamento, considerando o ângulo entre a direção da força e o deslocamento.
Onde:
F = é a força aplicada (N).
d = é o deslocamento (m).
θ = é o ângulo entre a direção da força e a direção do deslocamento.
Unidade de medida:
A unidade de medida do trabalho no Sistema Internacional (SI) é o Joule (J).
Trabalho de uma força variável:
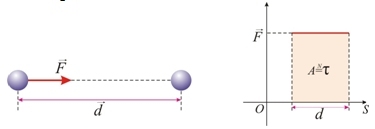
Quando a força varia durante o deslocamento, o trabalho pode ser calculado através da integração ou pela área sob o gráfico da força em função do deslocamento.
Tipos de trabalho:
Trabalho positivo - Ocorre quando a força e o deslocamento têm a mesma direção, resultando em um aumento da energia do sistema.
Trabalho negativo - Ocorre quando a força e o deslocamento têm direções opostas, resultando em uma diminuição da energia do sistema.
Trabalho nulo - Ocorre quando a força é perpendicular ao deslocamento (ângulo de 90°) ou quando não há deslocamento, ou seja, a força não realiza trabalho.
Conceito de trabalho
O conceito de trabalho é fundamental na física, pois está diretamente ligado à transferência de energia e ao estudo dos movimentos.
QUESTÕES RESOLVIDAS – SEDUC-SP/2025
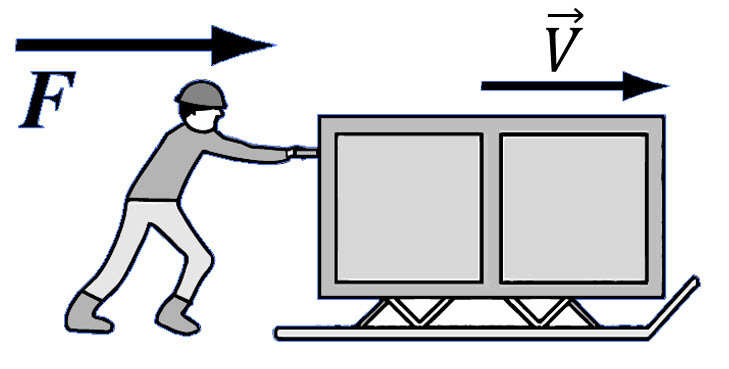
01) (Livro do Aluno/2025-SEDUC-SP) Observe a figura a seguir, que mostra um camponês por uma trilha enquanto carrega um saco de plantas. Considerando que, nesse senário, o camponês manteve uma velocidade constante.

Para que o trabalho seja realizado sobre o saco de plantas, é necessário que pelo menos um componente da força aplicada esteja na mesma direção do deslocamento.
No caso do camponês, a força que ele exerce para sustentar as plantas é vertical (para cima), enquanto o deslocamento ocorre na horizontal. Com base nisso, explique se o camponês está realizando trabalho sobre o saco de plantas.
Resolução:
Com base no que vimos até agora, o camponês não realiza trabalho sobre o feixe de plantas. Para quehaja trabalho, a força aplicada precisa ter um componente na mesma direção do deslocamento. No caso do camponês, a força que ele exerce para segurar o feixe é vertical (para cima), oposta à força peso. Seu deslocamento, no entanto, é horizontal ao longo do percurso. Como a força aplicada é vertical e o deslocamento é horizontal, não há trabalho realizado sobre o feixe de plantas.
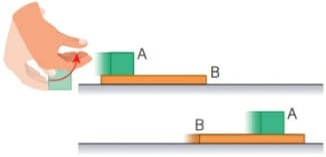
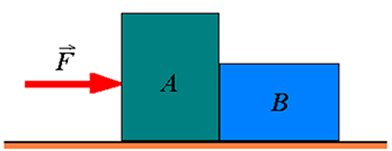
02) (Livro do Aluno/2025-SEDUC-SP) Considere um cenário em que um bloco B está em repouso sobre um plano horizontal liso. De repente, um segundo bloco A é arremessado horizontalmente sobre ele, fazendo que ambos comecem a se mover juntos. Levando em conta a presença de atrito entre os blocos, o trabalho realizado pela força de atrito que o bloco A exerce sobre o bloco B é positivo ou negativo?
Agora, em relação à força resultante que atua sobre os halteres, podemos dizer que a resultante realiza trabalho? Justifique sua resposta com base nas Leis de Newton e nos conceitos sobre trabalho realizado por uma força.
Justifique sua resposta com base na ideia de trabalho como transferência de energia cinética.
Resolução:
O trabalho realizado pela força de atrito que o bloco A exerce sobre o bloco B é considerado positivo.
Quando o bloco A é arremessado sobre o bloco B, que estava em repouso, a força de atrito entre eles possibilita que B comece a se mover. Assim, a energia cinética adquirida pelo bloco B resulta do trabalho dessa força de atrito, que transfere energia de A para B, por isso o trabalho é positivo.
03) (Livro do Aluno/2025-SEDUC-SP) A imagem ao lado mostra um homem realizando exercícios com dois halteres. Suponha que, em um dado momento, ele esteja levantando os halteres verticalmente, mantendo uma velocidade constante.

Nesse cenário, podemos afirmar que a força aplicada pela pessoa nos halteres está realizando trabalho?
Resolução:
Quanto à primeira pergunta, a resposta é afirmativa: a força que a pessoa aplica nos halteres realiza trabalho. Mesmo que esteja levantando-os com velocidade constante, a força que o homem exerce, sobre os halteres, provoca um deslocamento dos halteres.
Agora, em relação à força resultante que atua sobre os halteres, podemos dizer que a resultante realiza trabalho? Justifique sua resposta com base nas Leis de Newton e nos conceitos sobre trabalho realizado por uma força.
04) (Livro do Aluno/2025-SEDUC-SP) Observe o pêndulo simples em oscilação representado na figura. A esfera está presa por um cordão que exerce sobre ela uma força de tração T ao longo de toda a sua trajetória. Durante o movimento, essa tração é sempre perpendicular à trajetória circular descrita pela esfera. Sabendo disso, responda:
A força de tração T realiza trabalho sobre a esfera ao longo da oscilação? Justifique sua resposta com base nos conceitos discutidos nesta aula.
Resolução:
Com relação à segunda pergunta, a força resultante nos halteres não realiza trabalho.
Quando o movimento ocorre com velocidade constante, a força resultante é igual a zero, o que indica que as forças estão em equilíbrio. Isso significa que a força aplicada pelo homem é exatamente igual à soma dos pesos dos halteres. Assim, como a força resultante é zero, o trabalho realizado pela resultante também é zero.
A força de tração T não realiza trabalho sobre a esfera do pêndulo simples. Isso ocorre porque a tração é sempre perpendicular ao deslocamento da esfera ao longo de sua trajetória circular. Como o trabalho depende do componente da força na direção do movimento, e, nesse caso, não há componente da tração ao longo da trajetória, a tração apenas guia o movimento da esfera sem alterar a sua energia cinética.
TRABALHO REALIZADO POR UMA FORÇA INCLINADA E TEOREMA DA ENERGIA CINÉTICA
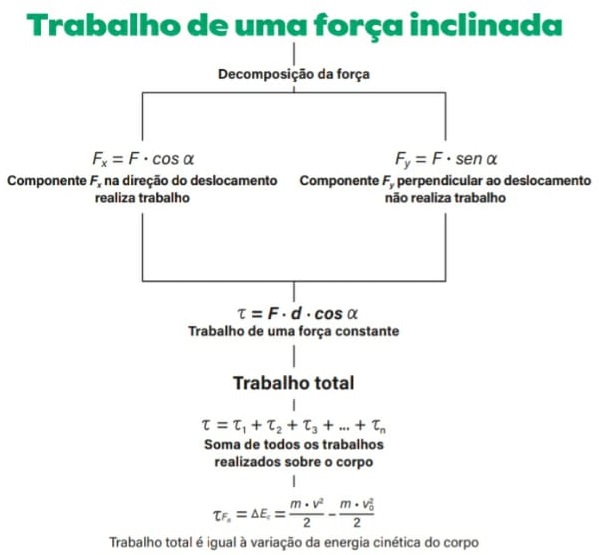
05) (Livro do Aluno/2025-SEDUC-SP) Um bloco de 10 kg é puxado com velocidade constante por uma distância de 8 m em um piso horizontal por uma corda que exerce uma força de 20 N, fazendo um ângulo de 60° acima da horizontal. Sabendo que cos (60°) = 0,5 e sen (60°) = 0,86, o trabalho executado pela corda sobre o bloco é de:
(A) 80 J
(B) 160 J
(C) 240 J
(D) 320 J
Resolução:
τ = F . d . cos 60º
τ = 20 . 8 . 0,5
τ = 80 J
06) (Livro do Aluno/2025-SEDUC-SP) Um corpo de massa 6 kg está inicialmente em repouso. Uma força resultante constante é aplicada a ele, de modo que, após 5 segundos, sua velocidade atinge 20 m/s. Qual é o trabalho realizado pela força resultante durante esse intervalo de tempo?
(A) 200 J
(B) 600 J
(C) 1200 J
(D) 1800 J
(E) 2400 J
Resolução:
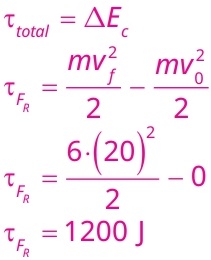
07) (Livro do Aluno/2025-SEDUC-SP - UECE 2021) Um objeto de massa 20 kg desloca-se em linha reta com velocidade de 30 m/s ao longo de uma superfície horizontal sem atrito. A partir de certo momento, esse corpo sofre uma redução de velocidade devido à ação de uma força de atrito com o solo, cujo trabalho resistente foi 5000 J. A seguir, o objeto passa novamente para uma região sem atrito. Após a passagem pela região de atrito, a velocidade, em m/s, com que o objeto passará a se deslocar será igual a:
(A) 10
(B) 20
(C) 15
(D) 25
Resolução:

08) (Livro do Aluno/2025-SEDUC-SP - ENEM 2015) Uma análise criteriosa do desempenho de Usain Bolt na quebra do recorde mundial dos 100 metros rasos mostrou que, apesar de ser o último dos corredores a reagir ao tiro e iniciar a corrida, seus primeiros 30 metros foram os mais velozes já feitos em um recorde mundial, cruzando essa marca em 3,78 segundos. Até se colocar com o corpo reto, foram 13 passadas, mostrando sua potência durante a aceleração, o momento mais importante da corrida. Ao final desse percurso, Bolt havia atingido a velocidade máxima de 12 m/s.
Supondo que a massa desse corredor seja igual a 90 kg, o trabalho total realizado nas 13 primeiras passadas é mais próximo de:
(A) 5,4 × 102 J
(B) 6,5 × 103 J
(C) 8,6 × 103 J
(D) 1,3 × 104 J
(E) 3,2 × 104 J
Resolução:

Alternativa: B
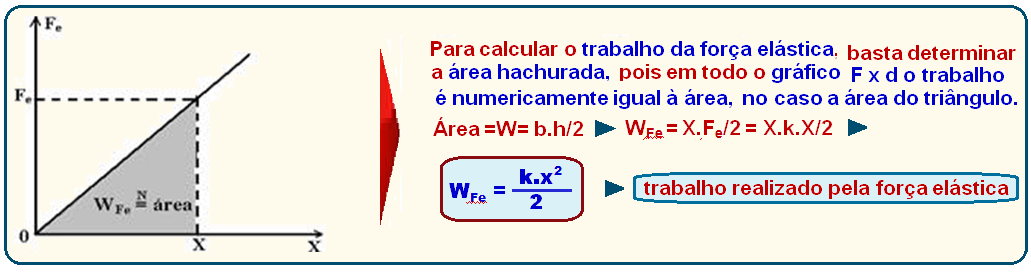
TRABALHO DE FORÇAS VARIÁVEIS E FORÇA ELÁSTICA
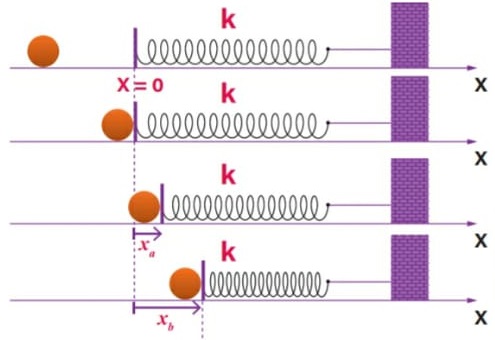
De forma geral, podemos afirmar que, ao comprimir ou estender uma mola entre uma posição inicial (xi) e uma posição final (xf), o trabalho realizado pela força elástica é dado pelas seguintes equações.
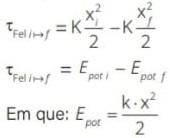
Gráfico de Força versus deslocamento
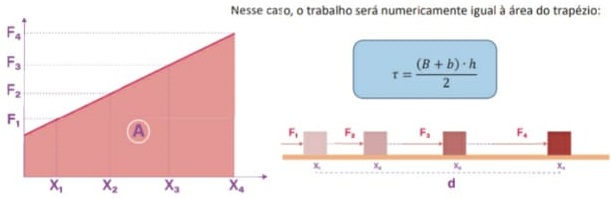
O trabalho realizado por uma força, seja constante ou variável, pode ser calculado a par r de um gráfico que relaciona a força exercida sobre um corpo ao seu deslocamento. Nesse gráfico, o valor do trabalho é numericamente igual à área sob a curva.
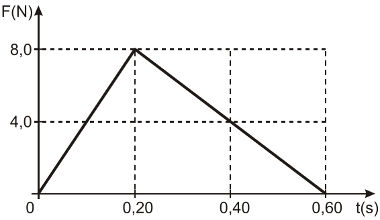
09) (Livro do Aluno/2025-SEDUC-SP) Uma força aplicada sobre uma partícula varia sua intensidade em função do deslocamento, conforme o gráfico a seguir.
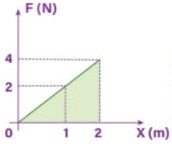
O trabalho da força no deslocamento de 2 m é, em joules, de:
(A) 0
(B) 1
(C) 4
(D) 5
Resolução:
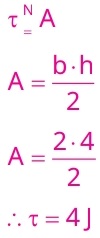
Alternativa: C
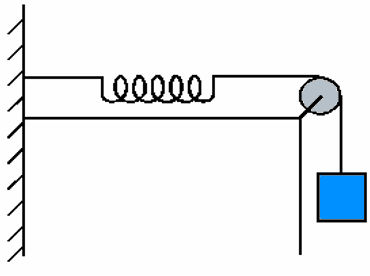
10) (Livro do Aluno/2025-SEDUC-SP) A figura a seguir mostra uma situação inicial em que uma mola, conectada a uma caixa, está relaxada na posição x = 0.
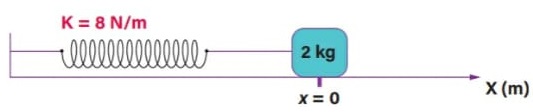
Em seguida, a caixa é deslocada para a posição x = - 2 m e passa a oscilar, a partir do repouso, em uma superfície horizontal sem atrito, entre as posições - 2 m e + 2 m, conforme representado abaixo. Calcule a velocidade da caixa ao passar pela posição x = 0.
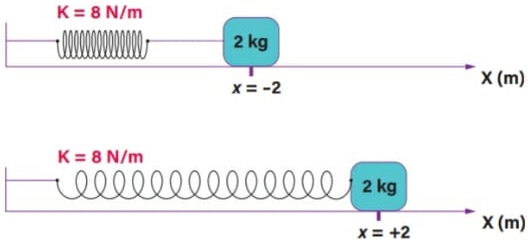
Resolução:
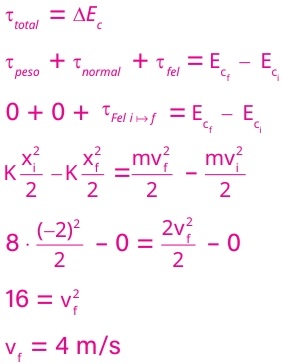
11) (Livro do Aluno/2025-SEDUC-SP - FATEC 2007) Ensaia-se uma mola helicoidal. Desde sua configuração natural, ela sofre distensão x = 10 cm quando se traciona com F = 10 N. A distensão é elástica e produz-se em regime de proporcionalidade.
(A) A constante elástica da mola é k = 100 N/cm.
(B) No processo descrito, a mola adquire energia potencial elástica de 0,50 J.
(C) Se a tração fosse elevada a 5F, a distensão se tornaria 5x, necessariamente.
(D) A energia potencial elástica é diretamente proporcional à força de tração aplicada.
(E) A energia potencial elástica é diretamente proporcional à deformação produzida.
Alternativa: B
12) (Livro do Aluno/2025-SEDUC-SP - (FCC 2003) Uma mola elástica ideal, submetida à ação de uma força de intensidade 10 N, está deformada em 2,0 cm. A energia potencial elástica armazenada na mola é de:
(A) 0,1 J
(B) 0,2 J
(C) 0,5 J
(D) 1,0 J
(E) 2,0 J
Resolução:

Alternativa: A
PRINCÍPIO DA TRAJETÓRIA ALTERNATIVA E TRABALHO DA FORÇA PESO
Considere um objeto em movimento ao longo de uma trajetória genérica, como a representada na figura adiante, indo de uma posição inicial (Si) até uma posição final (Sf).
Durante esse deslocamento, diversas forças atuam sobre o objeto, mudando a direção e o sentido de seu movimento, entretanto iremos analisar apenas a força constante F que age sobre o objeto.
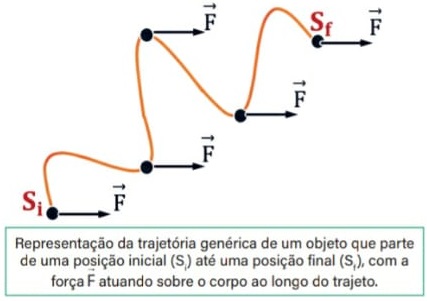
Para realizar essa análise, utilizamos o princípio da trajetória alternativa, que pode ser definido da seguinte maneira:
O trabalho realizado por uma força constante ao longo de um trajeto qualquer, desde uma posição inicial até uma posição final, é independente da trajetória percorrida. Esse trabalho terá o mesmo valor para qualquer trajetória entre os mesmos pontos inicial e final.
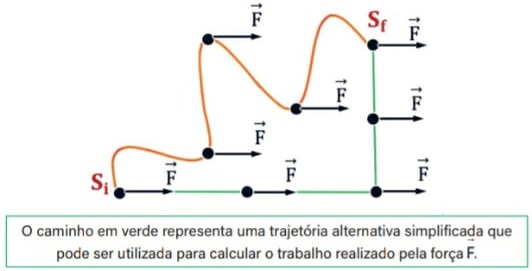
Com base nesse princípio, o trabalho realizado pela força constante F, pode ser calculado utilizando-se uma trajetória alternativa mais simples, como a representada na figura a seguir, desde que ambas as trajetórias tenham os mesmos pontos de partida e chegada. Isso simplifica os cálculos sem comprometer a precisão do resultado.
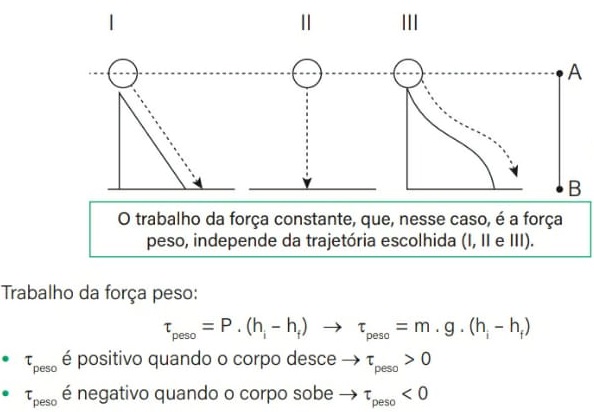
Um exemplo clássico de força constante é a força peso em um campo gravitacional uniforme. Nesse caso, a intensidade da força peso permanece constante, sua direção é sempre vertical e seu sentido aponta para baixo. Isso torna possível calcular o trabalho realizado pela força peso utilizando-se uma trajetória alternativa mais simples.
13) (Livro do Aluno/2025-SEDUC-SP) Um objeto de massa igual a 8 kg é levantado a uma altura de 5 m. Sabendo que g = 10 m/s2, calcule o trabalho da força peso.
Resolução:
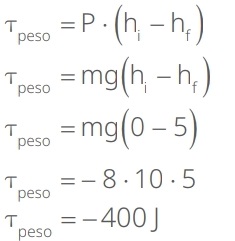
14) (Livro do Aluno/2025-SEDUC-SP) Calcule o trabalho realizado pela força peso no deslocamento de um corpo de massa 10 kg que, após ser abandonado de uma altura inicial 10 metros, atinge uma altura de 5 metros. (Use g = 10 m/s2)
(A) 100 J
(B) 200 J
(C) 500 J
(D) 1000 J
(E) 5000 J
Resolução:

Alternativa: C
15) (Livro do Aluno/2025-SEDUC-SP - CEDERJ – 2020) Uma pessoa segura um pequeno corpo de massa m que está preso a um ponto fixo por um fio flexível de comprimento R. O fio está, inicialmente, estendido horizontalmente. Após ser solto pela pessoa, o corpo faz um movimento
circular de raio R em torno do ponto fixo. Considere o movimento desde a situação inicial descrita até a situação em que o corpo passa pelo ponto mais baixo da trajetória, ou seja, quando o fio está estendido na direção vertical.
Nesse processo, o trabalho realizado pela força peso sobre o corpo vale
(A) -mgR
(B) mgR
(C) (-π/2) mgR
(D) (π2) mgR
Resolução:
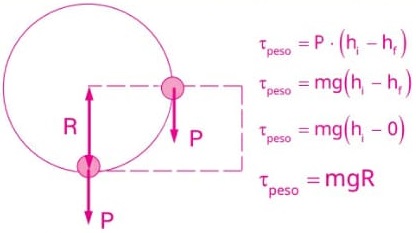
Alternativa: B
16) (Livro do Aluno/2025-SEDUC-SP - PUC-MG 2007) Considere um corpo sendo arrastado, com velocidade constante, sobre uma superfície horizontal onde o atrito não é desprezível. Considere as afirmações I, II e III a respeito da situação descrita.
I O trabalho da força de atrito é nulo.
II O trabalho da força peso é nulo.
III A força que arrasta o corpo é nula.
A afirmação está INCORRETA em:
(A) I apenas.
(B) I e III, apenas.
(C) II apenas.
(D) I, II e III
Resolução:
Algumas observações:
- o trabalho da força peso e o da força normal são nulos, pois essas forças são perpendiculares ao deslocamento;
- o trabalho da força
F é positivo (motor);
- o trabalho da força de atrito é negativo (resistente);
- o módulo do trabalho da força
F é igual ao módulo do trabalho da força de atrito;
- sendo a velocidade constante, teremos ΔEc = 0. Portanto o τtotal = 0.
Resolução:
I – O trabalho da força de atrito não é nulo. (F)
II – O trabalho da força peso é nulo. (V)
III – A força F, que arrasta o corpo, não é nula. (F)
Alternativa: B
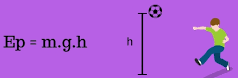
ENERGIA POTENCIAL GRAVITACIONAL E FORÇAS CONSERVATIVAS
Considere um corpo de massa m em queda em um campo gravitacional uniforme, descrevendo uma trajetória parabólica, conforme ilustrado na figura a seguir
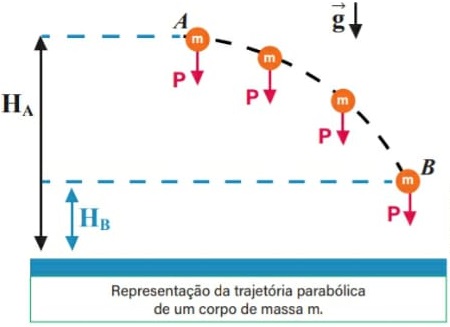
Suponha que apenas a força peso, considerada constante, esteja agindo sobre o corpo ao se deslocar da posição A para a posição B. Para calcular o trabalho realizado pela força peso, utilizaremos uma trajetória alternativa mais simples, que parte do mesmo ponto A e chega ao mesmo ponto B, passando agora pelo ponto C, como mostrado na figura adiante.
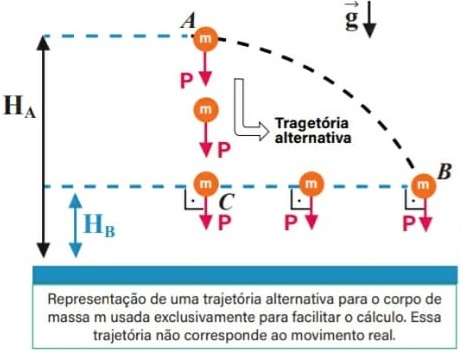
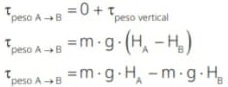
Pelo teorema da energia cinética, temos:
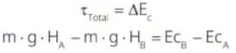
O termo m ⋅ g H pode ser interpretado como energia potencial gravitacional do sistema terra-corpo (EPotG = m g H). Assim, podemos dizer que:
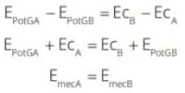
Forças conservativas
São forças para as quais o trabalho realizado ao se deslocar um objeto entre dois pontos depende apenas das posições inicial e final, sendo independente do caminho percorrido entre esses pontos.
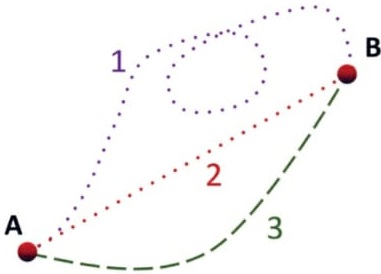
Representação de três trajetórias genéricas que mostram os possíveis caminhos percorridos por um corpo entre os pontos
A e B. Independentemente da trajetória escolhida, o trabalho realizado por uma força conservativa é o mesmo.
17) (Livro do Aluno/2025-SEDUC-SP) Qual é o valor da energia potencial gravitacional armazenada em um livro de massa 2 kg que se encontra a uma altura de 5 m do chão? Considere g = 10 m/s2.
(A) 50 J
(B) 20 J
(C) 100 J
(D) 1000 J
Resolução:
Ep = m . g .h
Ep = 2 . 10 . 5
Ep = 100 J
Alternativa: C
18) Em um laboratório de Física, cientistas realizaram um experimento controlado no qual abandonaram um corpo de massa m a partir de uma altura de 5 metros. O corpo caiu livre da ação de forças dissipativas, ou seja, sem a ação da força de resistência do ar.
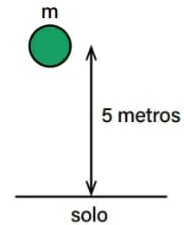
Determine a velocidade com que o corpo chegou ao solo. Considere g = 10 m/s2.
Resolução:
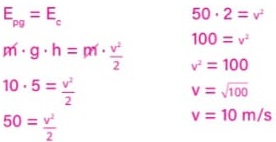
19) (Livro do Aluno/2025-SEDUC-SP) Em um laboratório de Física, cientistas realizaram um experimento controlado no qual abandonaram um corpo de massa m a partir de uma altura de 5 metros. O corpo caiu livre da ação de forças dissipativas, ou seja, sem a ação da força de resistência do ar. Determine a velocidade com que o corpo chegou ao solo. Considere g = 10 m/s2.
(A) 3 m/s
(B) 5 m/s
(C) 7 m/s
(D) 9 m/s
(E) 11 m/s
Resolução:

Alternativa: C
TRABALHO DAS FORÇAS NÃO CONSERVATIVAS

20) (Livro do Aluno/2025-SEDUC-SP - (UNESP 2022) Uma pequena esfera é abandonada do repouso no ponto 1 e, após deslizar sem rolar pela pista mostrada em corte na figura, perde contato com ela no ponto 2, passando a se mover em trajetória parabólica, até atingir o solo horizontal.
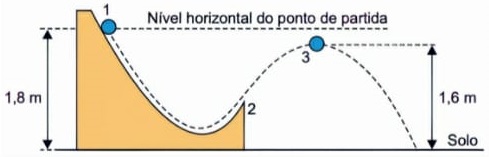
Adotando g = 10 m/s2, desprezando o atrito e a resistência do ar, quando a esfera passar pelo ponto 3, ponto mais alto de sua trajetória fora da pista, a componente horizontal da velocidade vetorial da esfera terá módulo igual a:
(A) 1,0 m/s.
(B) 1,8 m/s.
(C) 2,0 m/s.
(D) 1,5m/s.
(E) 2,5 m/s.
Resolução:
O sistema, neste caso, é conservativo, ou seja, a energia mecânica se conservará, portanto:

Alternativa: C
21) (Livro do Aluno/2025-SEDUC-SP - FUVEST 1989) Um bloco B de 2,0 kg é lançado do topo de um plano inclinado com velocidade de 5,0 m/s, conforme indica a figura. Durante a descida, atua uma força de atrito constante de 7,5 N, que faz o bloco parar após deslocar-se 10 m.
Calcule a altura H.
(A) 1,25 m
(B) 2,00 m
(C) 2,50 m
(D) 3,75 m
(E) 5,00 m
Resolução:
Pelo princípio do trabalho das forças não conservativas, temos:
Alternativa: C
22) (Livro do Aluno/2025-SEDUC-SP - FATEC 2002) Um bloco de massa de 0,60 kg é abandonado a partir do repouso no ponto A de uma pista no plano vertical. O ponto A está a 2,0 m de altura da base da pista, onde está fixa uma mola de constante elástica 150 N/m. São desprezíveis os efeitos do atrito e adota-se g = 10 m/s2.
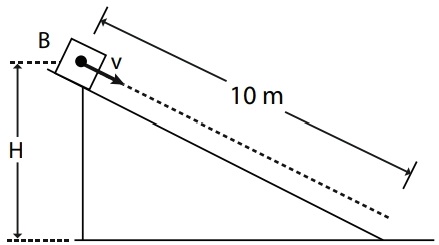
A máxima compressão da mola vale em metros:
(A) 0,80
(B 0,05
(C) 0,20
(D) 0,10
(E) 0,40
Resolução:
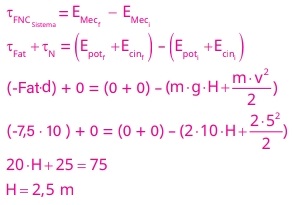
Alternativa: E
23) (Livro do Aluno/2025-SEDUC-SP - PUCRJ 2019) Um corpo de massa igual a 2,0 kg, com velocidade inicial vi = 5,0 m/s, percorre uma rampa curva, como na figura. Ao chegar a um ponto que está 1,0 m acima da posição inicial, sua velocidade final é vf = 1,0 m/s.
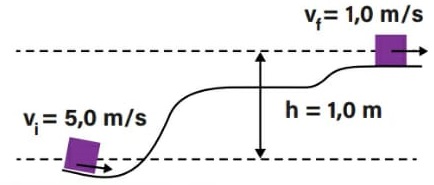
Calcule, em J, a energia dissipada pelo atrito enquanto o corpo se move entre essas duas posições. Dado: g = 10 m/s2
(A) – 25
(B) – 20
(C) – 4
(D) – 1
(E) 0
Resolução:
Pelo princípio do trabalho das forças não conservativas, temos:

Alternativa: C
POTÊNCIAS MÉDIA E INSTANTÂNEA: CONCEITOS E APLICAÇÕES
Potências média e instantânea
Considere um sistema, que chamaremos S1, que transfere uma quantidade de energia ΔE para outro sistema, denominado S2, durante um determinado intervalo de tempo.
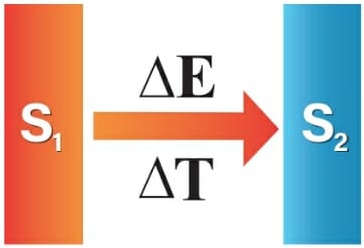
A potência média é definida como o quociente entre a energia transferida (ΔE) e o intervalo de tempo correspondente (Δt). Essa energia transferida corresponde ao trabalho τ. Assim, podemos dizer que:
![]()
Agora, imagine que reduzimos o intervalo de tempo considerado a valores cada vez menores. Quando Δt se torna suficientemente pequeno, a seguinte relação pode ser escrita:
![]()
Quando a potência se mantém constante, o valor instantâneo é igual ao valor médio.
Se a transferência de energia ocorre devido ao trabalho realizado por uma força de intensidade F sobre um objeto em movimento, a potência instantânea pode ser calculada considerando-se a força aplicada e a velocidade do objeto no instante analisado. Nesse caso, a potência instantânea é dada por:
P F ‑ v ⋅ cos θ
Assim:
F = intensidade da força aplicada;
v = velocidade do objeto no instante considerado;
cos = θ é o cosseno do ângulo entre a força e a direção do movimento.
24) (Livro do Aluno/2025-SEDUC-SP) Um motor realiza 1000 J de trabalho em 10 s. Qual é a potência média desse motor?
(A) 20 W
(B) 5 W
(C) 10 W
(D) 100 W
Resolução:
Potm = τ
Δt
Potm = 1000
10
Potm = 100 J
Alternativa: D
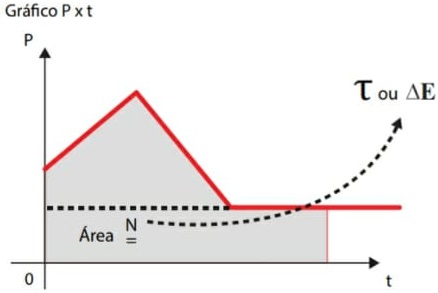
25) (Livro do Aluno/2025-SEDUC-SP - SANTA CASA SP) A potência de uma máquina em função do tempo variou da maneira indicada pelo gráfico.
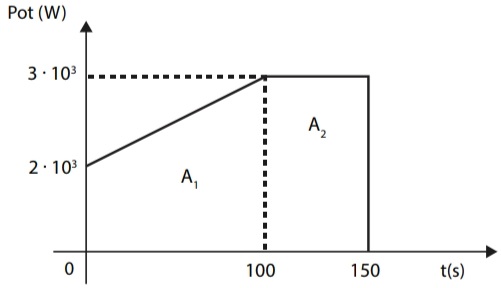
Calcule o trabalho realizado pela máquina desde zero a 150 segundos.
Resolução:
Para determinar o trabalho realizado pela máquina, é necessário calcular a área sob o gráfico.
Assim, temos:
Como o trabalho realizado pela máquina corresponde numericamente à área sob o gráfico, conclui-se que:
τ = 400 . 103 J
τ = 400 kJ
26) (Livro do Aluno/2025-SEDUC-SP - UERJ 2018) Em uma rodovia plana, um veículo apresenta velocidade de 20 m/s no instante em que a potência da força exercida pelo seu motor é igual a 132 kW. Sabendo que o peso do veículo é igual a 2 104 . N, determine a aceleração, em m/s2,do veículo nesse instante.
Resolução:

QUANTIDADE DE MOVIMENTO E IMPULSO: CONCEITOS FUNDAMENTAIS
Quantidade de movimento
A quantidade de movimento é uma grandeza vetorial associada a todo o corpo que tem massa e velocidade:
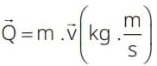
Impulso
Impulso é a grandeza física que mede a atuação de uma força num certo intervalo de tempo:
I = F . Δt (N.s)
27) (Livro do Aluno/2025-SEDUC-SP) Uma bolinha de massa 100 g, com velocidade inicial de 20 m/s, sofre a ação de uma força e, consequentemente, sua velocidade aumenta para 30 m/s. Qual é o valor do módulo do impulso transmitido para a bolinha nesta situação?
(A) 4 N.s
(B) 2 N.s
(C) 1 N.s
(D) 3 N.s
Resolução:

Alternativa: C
28) (Livro do Aluno/2025-SEDUC-SP) Um corpo de massa 5 kg, deslocando-se em linha reta, com velocidade inicial de 10 m/s, sofre ação de uma força resultante de intensidade 100 N aplicada na mesma direção e sentido do movimento. Determine o módulo do impulso fornecido ao corpo durante 2 segundos e o módulo da velocidade da partícula ao fim da aplicação da força.
Resolução:
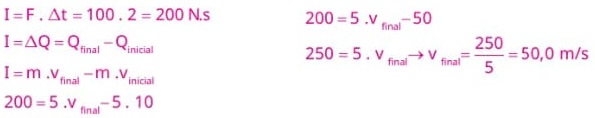
29) (Livro do Aluno/2025-SEDUC-SP - UNICAMP 2013) Muitos carros possuem um sistema de segurança para os passageiros chamado airbag. Este sistema consiste em uma bolsa de plástico que é rapidamente inflada quando o carro sofre uma desaceleração brusca, interpondo-se
entre o passageiro e o painel do veículo. Em uma colisão, a função do airbag é:
(A) aumentar o intervalo de tempo de colisão entre o passageiro e o carro, reduzindo assim a força recebida pelo passageiro.
(B) aumentar a variação de momento linear do passageiro durante a colisão, reduzindo assim a força recebida pelo passageiro.
(C) diminuir o intervalo de tempo de colisão entre o passageiro e o carro, reduzindo assim a força recebida pelo passageiro.
(D) diminuir o impulso recebido pelo passageiro devido ao choque, reduzindo assim a força recebida pelo passageiro.
Resolução:
a) correta, pois o intervalo de tempo e a força são inversamente proporcionais.
b) Incorreta, se a quantidade de movimento aumentar, a força irá aumentar.
c) Incorreta, pois se o intervalo de tempo diminuir, a força irá aumentar.
d) Incorreta, o airbag não irá diminuir o impulso sentido pelo passageiro.
Alternativa: A
30) (Livro do Aluno/2025-SEDUC-SP - UFMS 2023) O airbag e o cinto de segurança são itens de segurança presentes em todos os carros novos fabricados no Brasil. Considere a situação em que um carro, inicialmente a 72 km/h, dirigido por um motorista de massa m = 100 kg, para devido a uma colisão frontal. No momento da colisão, o airbag foi acionado, e o tempo de contato, Δt, entre o corpo do motorista e a bolsa do airbag até que a velocidade fosse reduzida a zero foi de 0,4 s. Nessas condições, determine os módulos do impulso, I, e da força resultante, FR, sobre o motorista.
(A) I = 7200, kg.m/s; FR = 18000 N.
(B) I = 1000, kg.m/s; FR = 2500 N.
(C) I = 2500, kg.m/s; FR = 6250 N.
(D) I = 2000, kg.m/s; FR = 5000 N.
(E) I = 1500, kg.m/s; FR = 3750 N.
Resolução:

Alternativa: D
IMPULSO EM FORÇAS VARIÁVEIS E INTRODUÇÃO AO CONCEITO DE SISTEMA
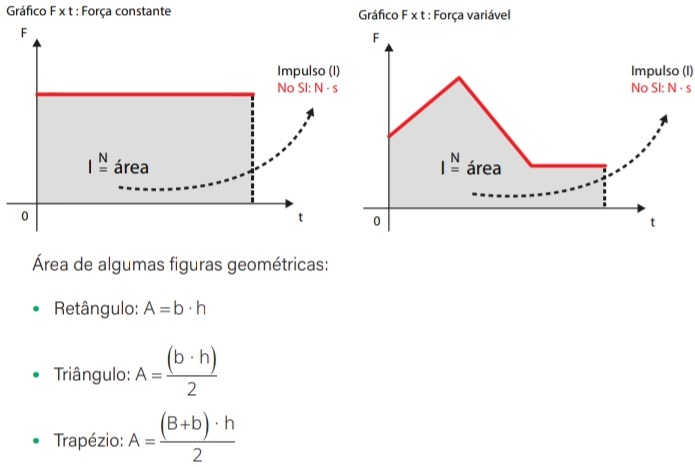
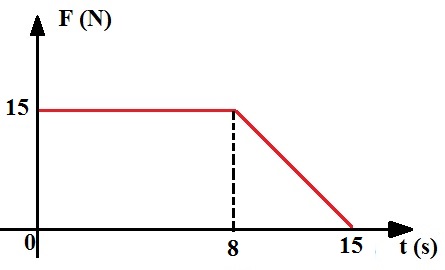
31) (Livro do Aluno/2025-SEDUC-SP) Uma partícula recebe uma força variável durante 10 s, conforme representado no gráfico.
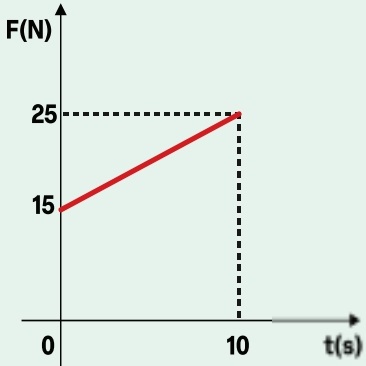
Calcule o impulso sofrido por essa partícula.
Resolução:
Como a força é variável, o impulso é calculado determinando-se a área do gráfico da força x tempo:
![]()
32) (Livro do Aluno/2025-SEDUC-SP - FGV 2010) Um brinquedo muito simples de construir, e que vai ao encontro dos ideais de redução, reutilização e reciclagem de lixo, é retratado na figura.
A brincadeira, em dupla, consiste em mandar o bólido de 100 g, feito de garrafas plásticas, um para o outro. Quem recebe o bólido, mantém suas mãos juntas, tornando os fios paralelos, enquanto que, aquele que o manda, abre com vigor os braços, imprimindo uma força variável, conforme o gráfico.
Considere que:
- a resistência ao movimento causada pelo ar e o atrito entre as garrafas com os fios seja desprezível;
- o tempo que o bólido necessita para deslocar-se de um extremo ao outro do brinquedo seja igual ou superior a 0,60 s.
Dessa forma, iniciando a brincadeira com o bólido em um dos extremos do brinquedo, com velocidade nula, a velocidade de chegada do bólido ao outro extremo, em m/s, é de:
(A) 16
(B) 20
(C) 24
(D) 28
(E) 32
Resolução:
O impulso é numericamente igual à área do gráfico força x tempo:

Pelo teorema do impulso, temos:
Alternativa: C
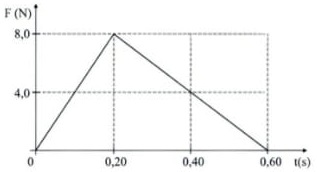
33) (Livro do Aluno/2025-SEDUC-SP - ESPECEX 2001) Um bloco sofre a ação de uma força variável | F | ao longo do tempo t conforme o gráfico abaixo.
O impulso da força F sobre o bloco entre os instantes 0 s e 6 s, em N.s, é de:
(A) 20
(B) 100
(C) 80
(D) 60
(E) 160
Resolução:
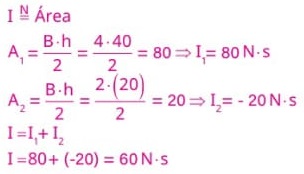
Alternativa: D
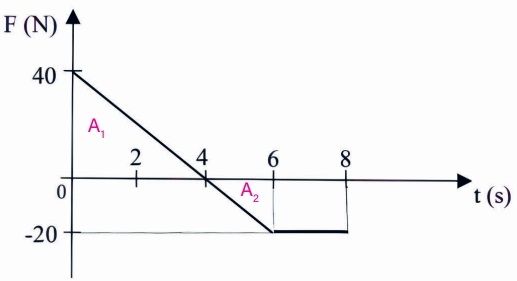
34) (Livro do Aluno/2025-SEDUC-SP - FACERES 2022) O gráfico a seguir mostra a variação de uma força resultante que atua na mesma direção e sentido do movimento de um corpo em função do tempo:
Assinale a alternativa que apresenta a intensidade de uma força constante que produziria o mesmo impulso que a força resultante no intervalo entre 0,1 s e 0,5 s:
(A) 10 N
(B) 15 N
(C) 20 N
(D) 50 N
(E) 75 N
Resolução:

Alternativa: E
35) (Livro do Aluno/2025-SEDUC-SP - FAME 2024) Um engenheiro civil foi contratado para instalar um elevador de carga em uma obra, com o intuito de minimizar as lesões causadas pelo esforço repetitivo ao erguer os materiais de construção, bem como otimizar os processos e reduzir o tempo de execução do projeto.
Dados:
- Potência do elevador: P = 2000 W;
- Aceleração da gravidade: g = 10 m/s2;
- Despreze as perdas de energia por atrito.
Considerando que o elevador consiga erguer uma carga de 500 kg em 22 segundos, qual é a altura, em metros, em que a carga será deslocada?
(A) 6,6
(B) 7,7
(C) 8,8
(D) 9,9
Resolução:
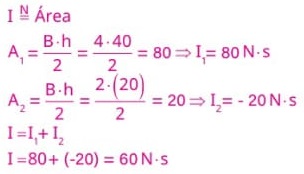
Alternativa: C
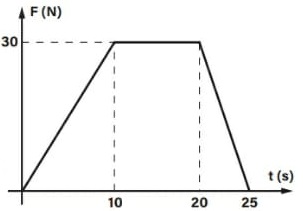
36) (Livro do Aluno/2025-SEDUC-SP - PUC-SP 2005) O gráfico representa a força resultante sobre um carrinho de supermercado de massa total 40 kg, inicialmente em repouso.

A intensidade da força constante que produz o mesmo impulso que a força representada no gráfico durante o intervalo de tempo de 0 a 25 s é, em newtons, igual a:
(A) 1,2
(B) 12
(C) 15
(D)2 0
(E) 21
Resolução:

Alternativa: E
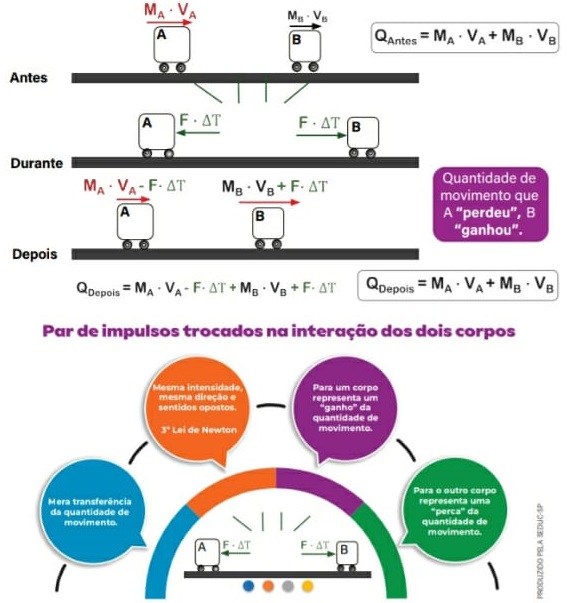
AÇÃO, REAÇÃO E CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
37) (Livro do Aluno/2025-SEDUC-SP - FUVEST 1996 – Adaptada) Uma quantidade de barro de massa 2,0 kg é atirada de uma altura h = 0,45 m, com uma velocidade horizontal ν = 4 m/s, em direção a um carrinho parado, de massa igual a 6,0 kg, como mostra a figura.
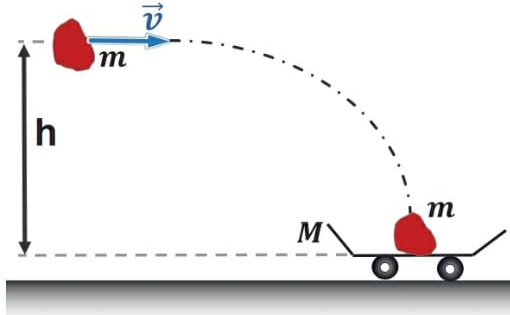
Sabendo que todo o barro ficará grudado ao carrinho no instante em que o atingir, calcule a velocidade inicial do carrinho após o impacto.
Resolução:
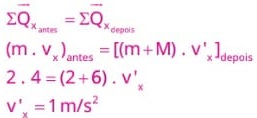
38) (Livro do Aluno/2025-SEDUC-SP) Um corpo A, com massa de 2 kg, desloca-se em linha reta sobre um plano horizontal com velocidade constante de 4 m/s. Durante o movimento, ele colide frontalmente com um corpo B, também com massa de 2 kg, que estava inicialmente em repouso. Após a colisão, o corpo A para completamente. Desprezando-se a ação de forças externas, a nova velocidade do corpo B é:
(A) 2 m/s
(B) 3 m/s
(C) 4 m/s
(D) 16 m/s
(E) 0
Resolução:

Alternativa: C
39) (Livro do Aluno/2025-SEDUC-SP - UNICAMP 2016) Tempestades solares são causadas por um fluxo intenso de partículas de altas energias ejetadas pelo Sol durante erupções solares. Esses jatos de partículas podem transportar bilhões de toneladas de gás eletrizado em altas velocidades, que podem trazer riscos de danos aos satélites em torno da Terra.
Considere que, em uma erupção solar em particular, um conjunto de partículas de massa total m p = 5 kg, deslocando-se com velocidade de módulo vp = 2 . 105 m/s, choca-se com um satélite de massa Ms = 95 kg que se desloca com velocidade de
módulo igual a Vs = 4 . 103 m/s na mesma direção e em sentido contrário ao das partículas. Se a massa de partículas aderir-se ao satélite após a colisão, o módulo da velocidade final do conjunto será de:
(A) 102 000 m/s.
(B) 14 000 m/s.
(C) 6200 m/s.
(D) 3900 m/s.
Resolução:

Alternativa: C
40) (Livro do Aluno/2025-SEDUC-SP - PUC-RIO 2018) Uma arma de tiro esportivo dispara um projétil de massa 2 g contra um bloco de madeira de massa 98 g inicialmente em repouso sobre uma superfície horizontal sem atrito. O projétil fica encrustado no bloco, e o conjunto sai com velocidade de 4 m/s. Qual é a velocidade horizontal do projétil, em m/s, antes de atingir o bloco?
(A) 100
(B) 200
(C) 400
(D) 800
(E) 1600
Resolução:
As forças externas, dissipativas, são desconsideradas. Sendo assim, a quantidade de movimento do sistema, isolado, é conservada. Portanto:

Alternativa: B
SISTEMA MECÂNICO ISOLADO: CONSERVAÇÃO EM AÇÃO
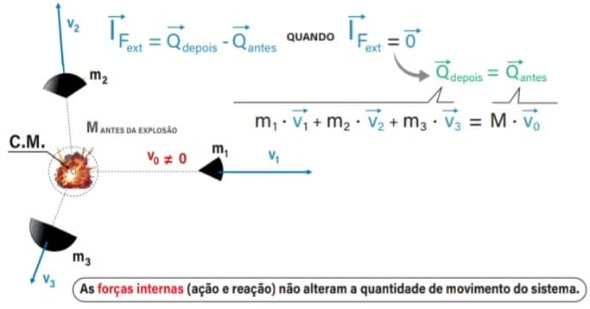
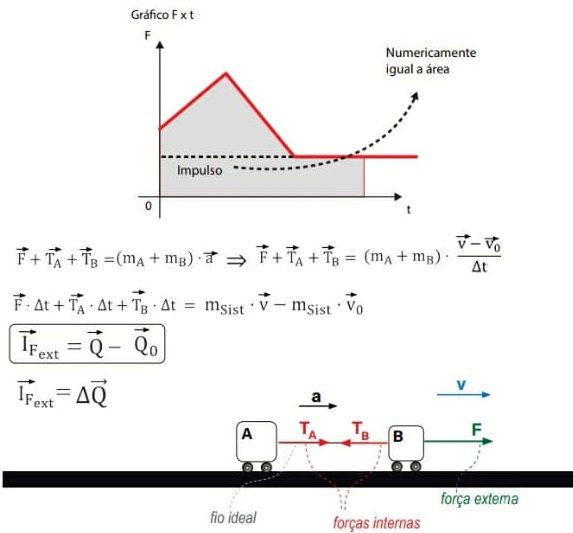
Colisões
A colisão entre dois corpos ocorre em um intervalo de tempo ∆t muito pequeno.
Assim, podemos admitir que as forças externas não atuam na colisão.
Como as forças externas não atuam, trata-se de um sistema mecânico isolado.
Então, a quantidade de movimento antes da colisão é igual à quantidade de movimento logo após a colisão.
Qantas = Qdepos
41) (Livro do Aluno/2025-SEDUC-SP) Após sua explosão, uma bomba, inicialmente em repouso, divide-se em dois fragmentos de massas iguais a 5 kg que se movem em sentidos contrários, na mesma direção. O primeiro fragmento move-se para a direita a uma velocidade de 70 m/s. O módulo da velocidade adquirida pelo segundo fragmento é de:
(A) 40 m/s
(B) 60 m/s
(C) 70 m/s
(D) 100 m/s
Resolução:
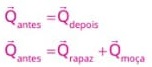
Adotando o referencial no qual o sentido positivo do eixo x é para a direita, de modo que movimentos para a direita têm velocidade positiva, temos:
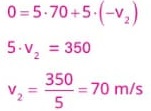
Alternativa: C
42) (Livro do Aluno/2025-SEDUC-SP) Considere um casal que está patinando no gelo. Em determinado momento, a dupla, que inicialmente estava em repouso, empurra-se mutuamente, e, como resultado dessa ação, o rapaz, de massa 70 kg, move-se para a esquerda com velocidade de 0,5 m/s. Com qual velocidade a moça, com massa de 50 kg, move-se para a direita? Desconsidere a ação de forças externas.
Resolução:

Adotando o referencial no qual o sentido positivo do eixo x é para a direita, de modo que movimentos para a direita têm velocidade positiva, temos:

43) (Livro do Aluno/2025-SEDUC-SP - UTFPR 2024 – Adaptada) Popularmente, o estilingue é conhecido como: “Arco atirador com elásticos presos pelas extremidades que, sendo ativado por um gatilho, arremessa pedrinhas, bolas de argila; atiradeira, bado que, bodoque.”
Considere um corpo de argila com massa de 60 g lançado de um estilingue colidindo horizontalmente com um bloco de tijolo liso com massa de 240 g. Sabendo que, no momento da colisão, o corpo de argila apresentava uma velocidade horizontal de 5,0 m/s e o bloco de tijolo estava em repouso sobre uma superfície sem atrito, determine a velocidade do conjunto de corpos argila-tijolo imediatamente após a colisão, sabendo que o bloco de argila se aderiu ao bloco de tijolo.
Despreze a resistência do ar.
(A) 2 m/s
(B) 0,5 m/s
(C) 4 m/s
(D) 1 m/s
(E) 2,5 m/s
Resolução:

Alternativa: D
44) (Livro do Aluno/2025-SEDUC-SP - UPF 2023 – Adaptada) Um carro de massa 2000 kg colidiu com outro de massa 1500 kg que estava parado no semáforo. Considerando que após o choque os dois carros andaram juntos com uma velocidade de 20 km/h, podemos considerar que, entre as velocidades apresentadas a seguir, a mais próxima de ser a do carro que provocou o acidente no exato momento da colisão corresponde, em km/h, a:
(A) 35
(B) 15
(C) 45
(D) 20
(E) 100
Resolução:

Alternativa: A
COLISÕES E A CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
Princípio da Conservação da Quantidade de Movimento
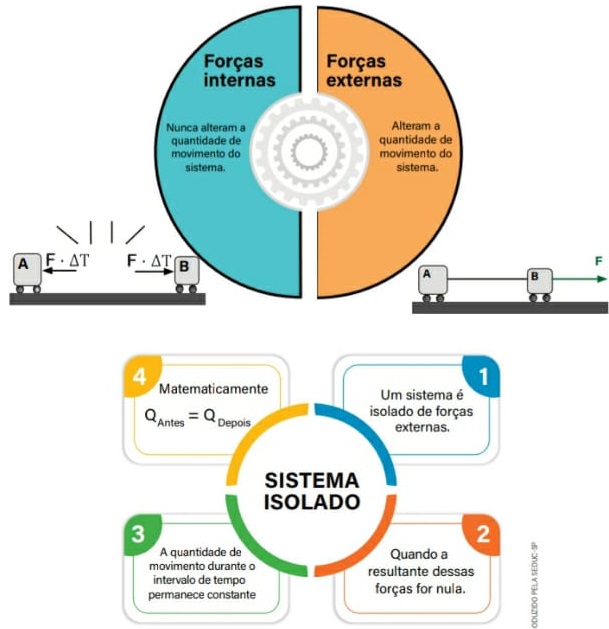
Em um sistema mecânico e isolado de forças externas, a quantidade de movimento total é conservada.
Pelo teorema do impulso, temos:
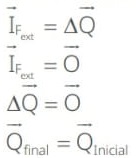
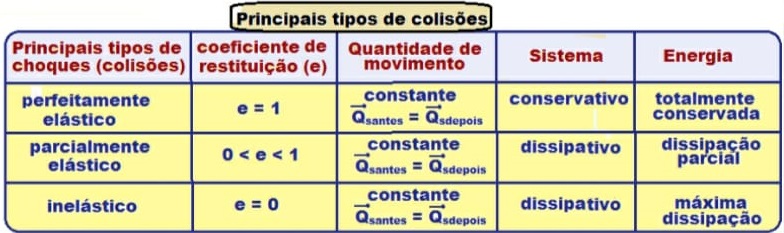
Tipos de Colisões
45) (Livro do Aluno/2025-SEDUC-SP - FUVEST 1990 – ADAPTADA) Dois patinadores de massas iguais deslocam-se numa mesma trajetória retilínea, com velocidades escalares respectivamente iguais a 1,5 m/s e 3,5 m/s. O patinador mais rápido persegue o outro. Ao alcançá-lo, salta verticalmente e agarra-se às suas costas, passando os dois a se deslocarem com velocidade escalar v. Desprezando o atrito, calcule o valor de v.
Resolução:
Como o atrito está sendo desprezado, a quantidade de movimento do sistema irá se conservar, então:

46) (Livro do Aluno/2025-SEDUC-SP) Considere uma partícula movendo-se em linha reta com velocidade de 5 m/s que, de repente, colide com outra partícula idêntica, de mesma massa, inicialmente em repouso. Considerando-se o choque elástico e ignorando-se a ação de forças dissipativas, como será o comportamento de cada partícula após o choque?
Resolução:
Como a colisão será elástica e as partículas são idênticas (massas iguais), após o choque a partícula que inicialmente se desloca com velocidade de 5 m/s irá ficar em repouso, e a partícula que estava em repouso se moverá com velocidade de 5 m/s, ou seja, as partículas trocarão de velocidade.
47) (Livro do Aluno/2025-SEDUC-SP) Em uma rodovia, um automóvel de massa 525 kg, ao trafegar com velocidade de 40 m/s, choca-se com a traseira de outro automóvel, com massa igual a 800 kg, que, no momento da colisão, movia-se com uma velocidade de 30 m/s. Admitindo-se que, a colisão foi inelástica e desprezando-se as forças externas, qual será a velocidade dos automóveis após a colisão?
Resolução:
Como a ação de forças externas está sendo desprezada, a quantidade de movimento do sistema irá se conservar:
Qantes = Q epois
A colisão é inelástica, logo os corpos (carros) ficarão unidos após a colisão:

48) (Livro do Aluno/2025-SEDUC-SP - UNICAMP 2004 – ADAPTADA) O chamado “para-choque alicate” foi projetado e desenvolvido na Unicamp com o
objetivo de minimizar alguns problemas com acidentes. No caso de uma colisão de um carro contra a traseira de um caminhão, a malha de aço de um para--choque alicate instalado no caminhão prende o carro e o ergue do chão pela plataforma. Imagine a seguinte situação: um caminhão de 6.000 kg está a 54 km/h e o automóvel que o segue, de massa igual a 2.000 kg, está a 72 km/h.
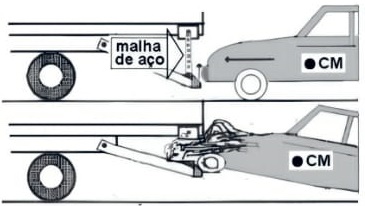
O automóvel colide inelasticamente contra a malha, subindo na rampa. Após o impacto, os veículos permanecem engatados um no outro.
a) Qual a velocidade dos veículos imediatamente após o impacto?
Resolução:

b) Qual a fração da energia cinética inicial do automóvel que foi transformada em energia gravitacional, sabendo-se que o centro de massa do mesmo subiu 50 cm?
Resolução:
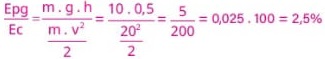
ENERGIA MECÂNICA E COLISÕES UNIDIMENSIONAIS
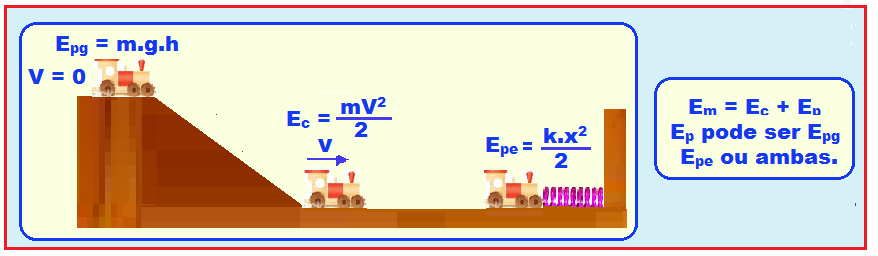
Energia Mecânica do Sistema em Colisões
As colisões entre dois corpos ocorrem em duas fases principais: deformação e restauração. Nelas, há transformações entre energia cinética (Ec) e energia potencial (Ep).
Fases da colisão
1 Período de deformação
- Parte da energia cinética dos corpos é gradualmente convertida em energia potencial.
- Isso ocorre devido ao aumento da área de contato entre os corpos.
- O sistema atinge máxima energia potencial quando a deformação é máxima.
2 Período de restauração
- A energia potencial é convertida de volta em energia cinética.
- A área de contato diminui, podendo retornar ao valor inicial.
- Se os corpos forem suficientemente elásticos, eles retomam sua forma original; caso contrário, ocorre deformação permanente e parte da energia é dissipada (em calor, som etc.).
Classificação das colisões
Para simplificar a análise, consideramos que a energia do sistema é essencialmente cinética antes e depois da colisão, enquanto a energia potencial é considerada apenas durante o breve intervalo de interação entre os corpos. Além disso, nesse momento, estamos considerando que as velocidades e impulsos envolvidos apontam numa mesma direção (colisão unidimensional).
Colisão Elástica
A energia cinética total do sistema é conservada. A energia cinética antes e depois da colisão é a mesma.
![]()
Colisão Parcialmente elástica
Parte da energia cinética do sistema é transformada em calor, energia sonora etc.
![]()
Colisão Inelástica
Toda a energia cinética do sistema é dissipada. Os corpos permanecem juntos após a colisão.
Pontos importantes
A quantidade de movimento do sistema é sempre conservada, independentemente
do tipo de colisão (em um sistema isolado).
A “perda” de energia cinética pode ser calculada pela diferença entre a energia cinética antes e depois da colisão.
49) (Livro do Aluno/2025-SEDUC-SP - URCA 2022.2 – Adaptada) Considere uma partícula “A” se movendo num eixo X com velocidade dada por vx > 0 até colidir frontalmente com outra partícula “B” idêntica a “A”. A velocidade de “B” antes da colisão é dada por 0, 5 · vx. O referencial em consideração é inercial. Suponha que, após a colisão, a partícula “B” tem sua velocidade aumentada para vx. Determine a velocidade final de “A” em relação à sua velocidade inicial Vx.
Resolução:

50) Um projétil atinge um pacote com areia inicialmente em repouso e livre para se mover numa mesa plana e horizontal, sem atrito. Após a colisão, ambos se movem, unidos, na mesma direção do disparo, com velocidade de módulo igual a 2 m/s. Sabendo que a massa do pacote com areia é 10 vezes maior que a massa do projétil, determine o módulo da velocidade do projétil antes da colisão.
Resolução:
Sabemos que m pacote = 10 ⋅ m projétil A quantidade de movimento do sistema irá se conservar:

51) (Livro do Aluno/2025-SEDUC-SP - FUVEST 1995 – Adaptada) Um vagão A, de massa 10 t, move-se com velocidade escalar igual a 0,4 m/s sobre trilhos horizontais sem atrito até colidir com um outro vagão, B, de massa 20 t, inicialmente em repouso. Após a colisão, o vagão A fica parado. Calcule a energia cinética final do vagão B.
Resolução:

52) (Livro do Aluno/2025-SEDUC-SP - FAG 2022 – Adaptada) Dois carros de mesma massa sofrem uma colisão frontal. Imediatamente antes da colisão, o primeiro carro viajava a 72 km/h no sentido norte de uma estrada retilínea, enquanto o segundo carro viajava na contramão da mesma estrada com velocidade igual a 36 km/h, no sentido sul. Considere que a colisão foi perfeitamente inelástica. Qual é a velocidade final dos carros imediatamente após a colisão?
(A) 5 m/s para o norte.
(B) 5 m/s para o sul.
(C) 10 m/s para o norte.
(D) 10 m/s para o sul.
(E) 30 m/s para o norte.
Resolução:

Alternativa: A
COEFICIENTE DE RESTITUIÇÃO: CARACTERIZANDO AS COLISÕES
Velocidade relativa

Classificação das colisões
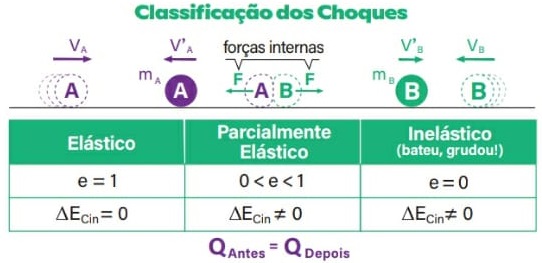
53) (Livro do Aluno/2025-SEDUC-SP) Uma partícula A colide com uma partícula B. Antes da colisão, A tem velocidade escalar de 10 m/s e está indo de encontro à partícula B, que se encontra em repouso. Após a colisão, a partícula A fica parada e a partícula B adquire certa velocidade. Desprezando o atrito e sabendo que o coeficiente de restituição é igual a 1, calcule a velocidade da partícula B após a colisão.
Resolução:
Sabemos que o coeficiente de restituição é calculado da seguinte forma:
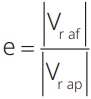
Calculando as velocidades relativas:
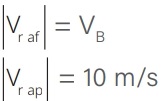
Substituindo os valores:
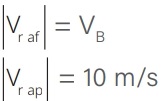
54) (Livro do Aluno/2025-SEDUC-SP) Considere duas partículas, uma verde e outra roxa, prestes a colidir. A figura a seguir mostra as velocidades das partículas antes, durante e depois da colisão.
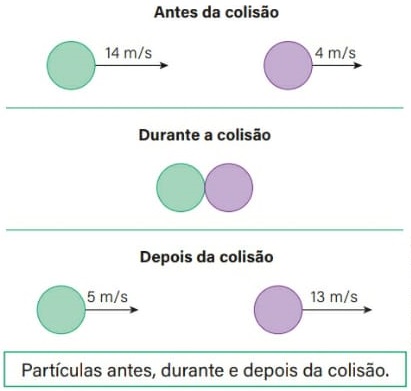
Considerando que o intervalo de tempo da colisão é muito curto, calcule o coeficiente de restituição e classifique a colisão.
Resolução:
Cálculo do coeficiente de restituição:

Antes e depois da colisão, as partículas estão se movimentando no mesmo sentido, então:
O coeficiente de restituição resultou em um valor entre 0 e 1, logo a colisão é parcialmente elástica.

55) (Livro do Aluno/2025-SEDUC-SP) Assinale a alternativa correta:
(A) Na colisão inelástica, o coeficiente de restituição é igual a zero e as partículas separam-se após o choque.
(B) Na colisão elástica, as partículas separam-se após o choque e o coeficiente de restituição é igual a 0.
(C) Na colisão parcialmente elástica, as partículas separam-se após o choque e o valor do coeficiente de restituição fica entre 0 e 1.
(D) Na colisão elástica, o coeficiente de restituição é igual a 1 e a energia mecânica não se conserva.
(E) Na colisão inelástica, o coeficiente de restituição é igual a 0 e a energia mecânica conserva-se.
Resolução:
a) Incorreta, pois, na colisão inelástica, as partículas ficam unidas após a colisão.
b) Incorreta, já que, na colisão elástica, o coeficiente de restituição é igual a 1.
c) Correta.
d) Incorreta, pois na colisão elástica a energia mecânica se conserva.
e) Incorreta, visto que, na colisão inelástica, a energia mecânica não se conserva
Alternativa: C
56) (Livro do Aluno/2025-SEDUC-SP - UFPI 2000) Na figura a seguir, o peixe maior, de massa m = 5,0 kg, nada para a direita a uma velocidade v = 1,0 m/s e o peixe menor, de massa m = 1,0 kg, aproxima--se dele a uma velocidade u = 8,0 m/s para a esquerda. Despreze qualquer efeito de resistência da água.
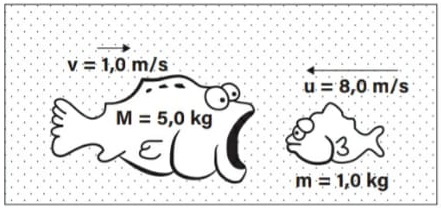
Após engolir o peixe menor, o peixe maior terá uma velocidade de:
(A) 0,50 m/s para a esquerda.
(B) 1,0 m/s para a esquerda.
(C) nula.
(D) 0,50 m/s para a direita.
(E) 1,0 m/s para a direita.
Resolução:
M = 5,0 kg → massa do peixe maior
v = 1,0 m/s → velocidade do peixe maior
m = 1,0 kg → massa do peixe menor
u = 8,0 m/s → velocidade do peixe menor (sentido contrário ao do peixe maior)
Interação inelástica, na qual os corpos permanecem unidos e a quantidade de movimento se conserva:

Alternativa: A
Continua...













.jpg)




.jpg)
.jpg)
.jpg)
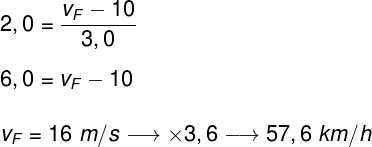
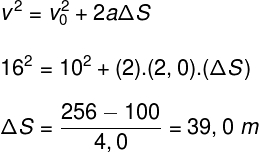




.jpg)






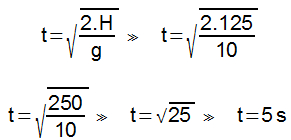
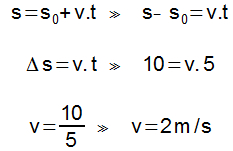
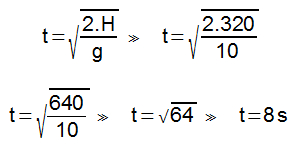






.gif)
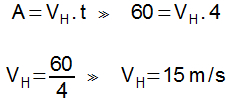
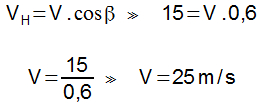
.jpg)



.jpg)












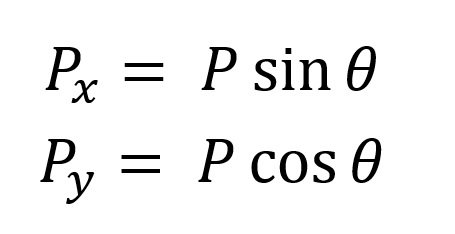
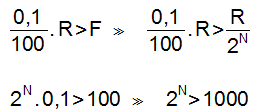
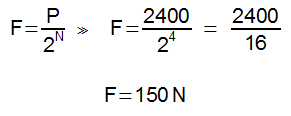
.jpg)
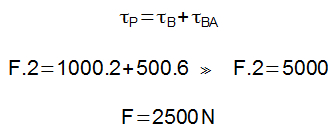
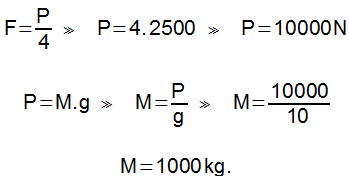
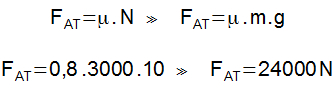
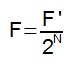
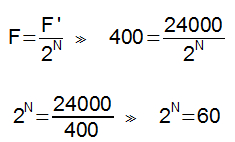
.jpg)



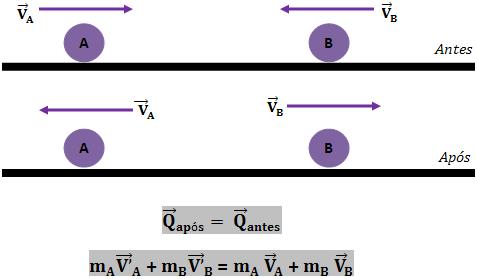



 Como citado anteriormente, nesse caso, ocorre apenas a conservação do momento linear. Podemos obter uma expressão para a velocidade final VF dos objetos. Veja as equações a seguir:
Como citado anteriormente, nesse caso, ocorre apenas a conservação do momento linear. Podemos obter uma expressão para a velocidade final VF dos objetos. Veja as equações a seguir: Após uma colisão parcialmente inelástica, as esferas afastam-se com velocidade relativa diferente da velocidade de aproximação
Após uma colisão parcialmente inelástica, as esferas afastam-se com velocidade relativa diferente da velocidade de aproximação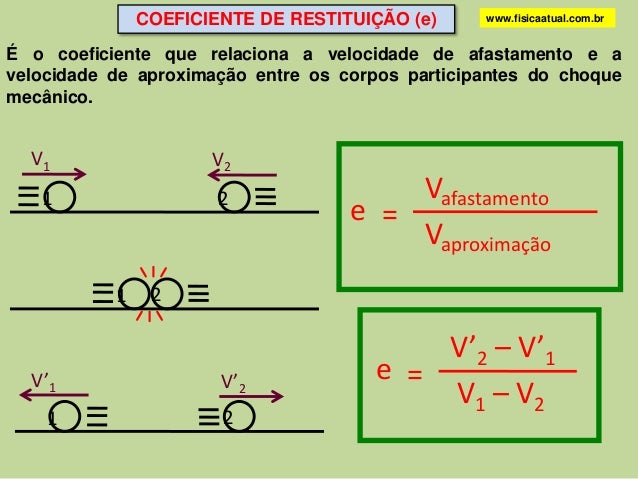

.gif)
.gif)