DIVISAO/MULTIPLICACAO/SOMA/SUBTRACAO

Professor Diminoi
MATEMATICA

DIVISAO/MULTIPLICACAO/SOMA/SUBTRACAO
Nomenclatura de um número decimal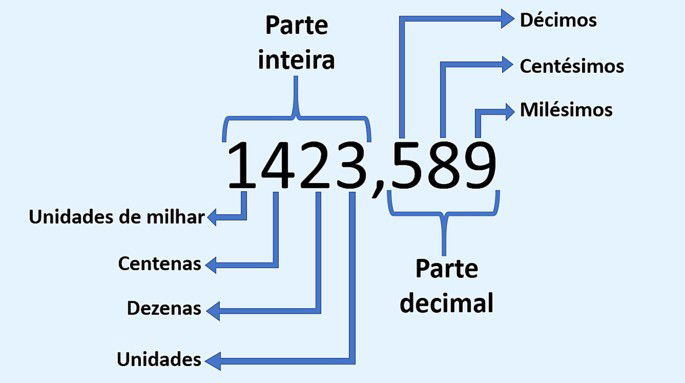

Nomenclatura de números decimais
A fim de facilitar as definições que virão, a seguir estabelecemos algumas nomenclaturas. Um número decimal é formado por sua parte inteira e pela parte decimal. A parte decimal é organizada da seguinte maneira: décimo, centésimo, milésimo, décimo de milésimo, centésimo de milésimo e assim por diante.

Observe o exemplo: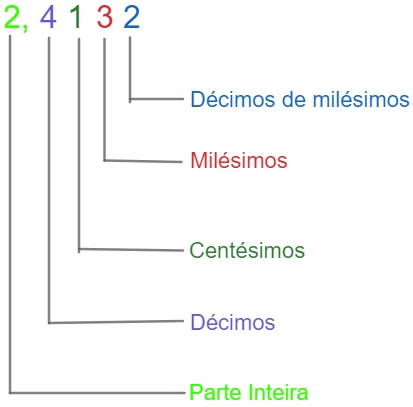
Leitura de números decimais
Para ler números decimais, primeiro devemos observar a posição da vírgula que separa a parte inteira (PI) da parte decimal (PD). Um número decimal pode ser posto na forma genérica:

Centenas, Dezenas, Unidades, Décimos, Centésimos, Milésimos

Por exemplo, o número 130,824, pode ser escrito na forma:
1 Centena, 3 dezenas, 0 unidades, 8 décimos, 2 centésimos e 4 milésimos

Exemplos:
0,6 Seis décimos;
0,37 Trinta e sete centésimos;
0,189 Cento e oitenta e nove milésimos;
3,7 Três inteiros e sete décimos;
13,45 Treze inteiros e quarenta e cinco centésimos;
130,824 Cento e trinta inteiros e oitocentos e vinte e quatro milésimos.

Operações com números decimais
Os números decimais pertencem ao conjunto dos números racionais, nele as quatro operações estão muito bem definidas: adição, subtração, multiplicação e divisão.

Operações com números decimais são muito presentes no dia a dia. Os números decimais, que fazem parte do conjunto dos números racionais, têm como principal característica a representação de seus elementos na forma de fração, ou seja, todo número que pode ser escrito na forma de uma fração é um número decimal. Como bem sabemos, esse conjunto numérico possui as quatro operações básicas bem definidas: adição, subtracao, multiplicação e divisão.

Adição com números decimais
A adição de números decimais é definida de maneira semelhante à adição de números inteiros, nessa operação devemos somar parte inteira com parte inteira, décimos com décimos, centésimos com centésimos, e assim sucessivamente. Em outras palavras, devemos colocar vírgula abaixo de vírgula, veja o exemplo.
Exemplo 1
Vamos determinar a soma dos números 0,65 e 0,792. Lembre-se: o número 0 no final de qualquer número decimal não acresce no valor.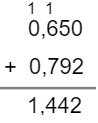


Exemplo 2
Determine o valor da soma 1,442 + 2,4.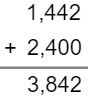


Subtração com números decimais
A subtração entre dois números decimais dá-se do mesmo modo que a sua adição, operamos parte inteira com parte inteira, décimos com décimos, e assim sucessivamente. 
Exemplo 3
Determine a diferença entre os números 3,842 e 1,442.


Uma das quatro operações básicas da matemática e é inversa à multiplicação. A divisão de um número consiste em seu fracionamento, na sua fragmentação, que pode ter como resultado um número inteiro ou um número decimal.
Assim como as outras operações fundamentais da matemática, a divisão também está muito presente em nosso cotidiano, por isso, é essencial conhecer bem esse processo, a fim de adquirir prática e tornar esse cálculo mais ágil.

DIVISÃO COM VÍRGULA
Elementos da divisão
QUESTOES RESOLVIDAS
01) Dividir 24 por 2.
Resolucao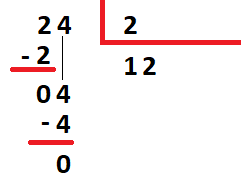


02) Dividir 423 por 3.
Resolucao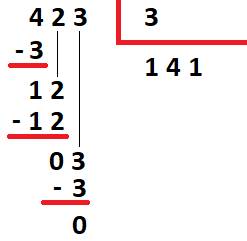


03) Dividir 326 por 3.
Resolucao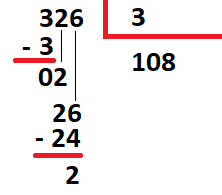


04) Dividir 3456 por 11.
Resolucao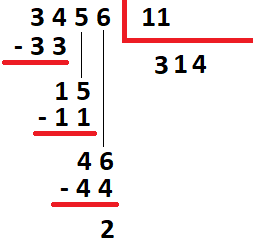


Ao aprender sobre a operação da divisão, sabemos que existem divisões exatas e divisões não exatas (quando há um resto na divisão). Por exemplo, se quisermos dividir 5 por 2, teremos uma divisão não exata, pois haverá um resto.
Mas existe uma possibilidade de terminar essa divisão? Se você tem cinco reais, é possível dividir esse valor para dois amigos? Claro! Cada amigo ganhará dois reais e cinquenta centavos. O “um real” que ficaria no resto foi dividido igualmente e agora não há mais restos nessa divisão.

Vejamos outro cálculo semelhante a esse: a divisão de 225 por 50. Se multiplicarmos 4 por 50, obteremos 200, e assim a divisão terá resto 25. Não existe um número natural que multiplicado por 50 resulte em 25, então, qualquer valor que acrescentarmos ao quociente será menor do que 1. Portanto, para prosseguirmos, teremos uma divisão com vírgula, pois acrescentaremos uma vírgula ao quociente e um zero ao resto. Procuramos agora um número que multiplicado por 50 resulte em 250. Esse número é o 5. Portanto, 225 : 50 = 4,5.
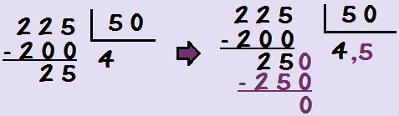
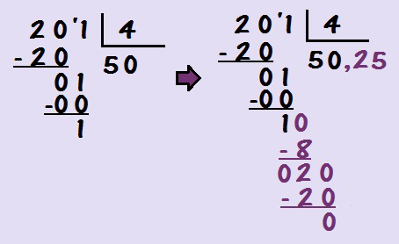
Vamos agora realizar a divisão de 201 por 4. Essa também é uma divisão não exata e deixará resto 1. Quando estivermos próximos de finalizar a divisão e encontrarmos o resto, será necessário acrescentar uma vírgula ao quociente e um zero no fim do resto. A partir daí, basta realizar a divisão normalmente até que não haja resto algum. Nesse caso, há uma divisão com vírgula, pois a divisão de 201 por 4 resulta em 50,25.
Mas e quando o dividendo ou o divisor é um número decimal (com vírgula)? Precisamos lembrar que um número decimal só divide ou é dividido por outro número decimal se houver a mesma quantidade de algarismos depois da vírgula.
Se um dos fatores da divisão é um número decimal, devemos escrever o outro na forma decimal também. Por exemplo, o número 2 pode ser escrito como 2,0; 2,00; 2,000...

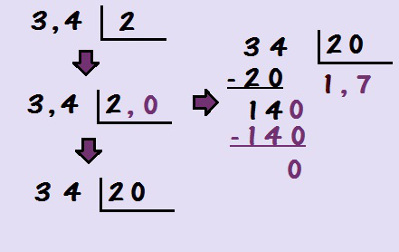
Vejamos como realizar a divisão de 3,4 por 2. O primeiro passo é observar que, como o 3,4 é um número decimal com um algarismo depois da vírgula, o 2 deve ter esse mesmo formato, por isso utilizamos o 2,0 no divisor. Agora que ambos os fatores da divisão possuem a mesma quantidade de algarismos depois da vírgula, nós podemos desconsiderar as vírgulas e realizar a divisão de 34 por 20, obtendo como resultado 1,7. Veja na imagem a seguir todo o processo para realizar essa divisão:
Imagine uma situação nova: no dividendo, há o número natural 30, e no divisor, um número racional 2,5. Lembre-se de que um número decimal só divide ou é dividido por outro número decimal se ambos possuem a mesma quantidade de algarismos após a vírgula.

Para realizar a divisão, vamos escrever o número 30 na forma 30,0. Agora que o dividendo e o divisor têm um número após a vírgula, podemos desconsiderar as vírgulas e realizar a divisão entre 300 e 25, obtendo como resultado o quociente 12, como podemos ver na figura a seguir. Observe que uma divisão com vírgula pode resultar em um quociente sem vírgula!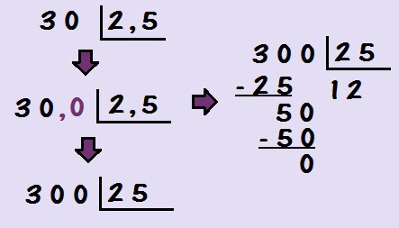

E quando o dividendo e o divisor são decimais? Nesse caso, precisamos apenas igualar a quantidade de algarismos depois da vírgula em ambos os fatores, completando com zeros conforme for necessário. Por exemplo, ao dividir 31,775 por 15,5, precisamos acrescentar dois zeros ao divisor para que ambos tenham três algarismos após a vírgula. Feito isso, nós desconsideramos as vírgulas e realizamos a divisão de 31775 por 15500, obtendo como quociente o número 2,05, como podemos ver na exemplificação a seguir:

QUESTOES RESOLVIDAS
14) (Enem) Um show especial de Natal teve 45 000 ingressos vendidos. Esse evento ocorrerá em um estádio de futebol que disponibilizará 5 portões de entrada, com 4 catracas eletrônicas por portão. Em cada uma dessas catracas, passará uma única pessoa a cada 2 segundos. O público foi igualmente dividido pela quantidade de portões e catracas, indicados no ingresso para o show, para a efetiva entrada no estádio. Suponha que todos aqueles que compraram ingressos irão ao show e que todos passarão pelos portões e catracas eletrônicas indicados.
Qual é o tempo mínimo para que todos passem pelas catracas?
(A) 1 hora
(B) 1 hora e 15 minutos
(C) 5 horas
(D) 6 horas
(E) 6 horas e 15 minutos
Resolucao
Sabemos que há 5 portões e que cada um tem 4 catracas, então, o total de catracas é 5 × 4 = 20. Agora, vamos calcular o número de pessoas que passarão por catraca.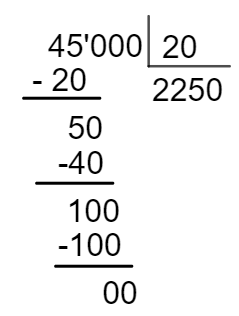

Por catraca, passarão 2250 pessoas, como cada pessoa leva 2 segundos para passar, então, o tempo que elas levarão será de 2250 × 2 = 4500 segundos. Sabemos que 1 hora tem 60 minutos e que 60 minutos têm 60 segundos, logo, 1 hora tem 3600 segundos.
Realizando a divisao: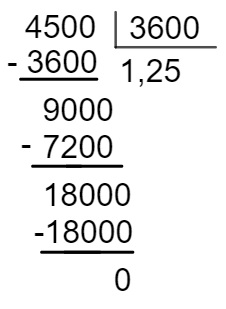

Sabemos que 25 décimos correspondem a 1/4 de hora, ou seja, 15 minutos. Sendo assim, o tempo mínimo para que todas as pessoas passem pelas catracas será de 1 hora e 15 minutos.
Alternativa B

05) (Enem) Cinco empresas de gêneros alimentícios encontram-se à venda. Um empresário, almejando ampliar os seus investimentos, deseja comprar uma dessas empresas. Para escolher qual delas irá comprar, analisa o lucro (em milhões de reais) de cada uma delas, em função de seus tempos (em anos) de existência, decidindo comprar a empresa que apresente o maior lucro médio anual. O quadro apresenta o lucro (em milhões de reais) acumulado ao longo do tempo (em anos) de existência de cada empresa.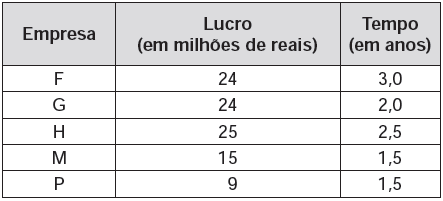
O empresário decidiu comprar a empresa:
(A) F
(B) G
(C) H
(D) M
(E) P
Resolucao
Primeiro vamos calcular o lucro anual de cada uma das empresas:
F = 24 : 3 = 8 milhões p/ano
G = 24 : 2 = 12 milhões p/ano
H = 25 : 2,5 = 10 milhões p/ano
M = 15 : 1,5 = 10 milhões p/ano
P = 9 : 1,5 = 6 milhões p/ano
A empresa que possui maior lucro anual é a G.
Alterntiva B

06) Sara faz a produção de maçãs do amor para vender em eventos como aniversários e festas juninas. Para transportar as maçãs, ela faz uso de uma caixa que cabe até 18 unidades, caso ela coloque mais, correria o risco de estragá-las e danificá-las. Se para um determinado evento foi feito um pedido de 230 unidades de maçã do amor, a quantidade de caixas necessárias para transportar todas essas maçãs é:
(A) 9
(B) 10
(C) 11
(D) 12
(E) 13
Resolucao
Para encontrar a quantidade de caixas necessárias, basta dividir 230 : 18.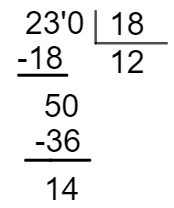

Como restaram 14 maçãs, então, é necessário que sejam adquiridas 12 caixas, que ficarão cheias, e mais 1 caixa, preenchida com as restantes, ou seja, 13 caixas.
Alternativa E

07) Com a meta de arrecadar alimentos para a população mais carente, uma ONG se dividiu em 6 grupos com 8 voluntários cada um deles. O objetivo era atender as 432 famílias carentes da região com a doação de, pelo menos, uma cesta básica para cada família. Suponha que a arrecadação tenha sido feita de forma igualitária por voluntários, então, o número de cestas básicas que cada voluntário conseguiu, no mínimo, foi de:
(A) 12
(B) 11
(C) 10
(D) 9
(E) 8
Resolucao
Primeiro encontraremos a quantidade de voluntários, como eram 6 grupos de 8 pessoas, então eram 6 × 8 = 48 voluntários. Se havia 432 famílias, então, a quantidade que cada voluntário conseguiu pode ser calculada por 432 : 38.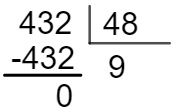

Alternativa D

08) Ingrid e sua irmã, Mariana, decidiram empreender em seu condomínio com a venda de laranjinhas gourmet para os seus vizinhos, com a venda de laranjinhas de 160 ml por R$ 5 cada. Para as suas primeiras vendas, elas produziram 4,8 litros de laranjinha e gastaram R$ 54 na produção. Supondo que não houve desperdício na produção, e que elas dividiram o lucro em partes iguais, então, Ingrid conseguiu um lucro de:
(A) R$ 150
(B) R$ 96
(C) R$ 48
(D) R$ 35
(E) R$ 32
Resolucao
Sabemos que 4,8 litros correspondem a 4800 ml, como cada laranjinha tem 160 ml, então, primeiro, calcularemos quantas laranjinhas foram feitas dividindo 4800 : 160.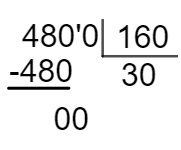

Foram feitas 30 laranjinhas, como cada uma é R$ 5, então, elas receberam 5 × 30 = 150.
Ao subtrair os gastos, vamos encontrar o lucro total com as vendas:
150 – 54 = 96
Por fim, é necessário realizar a divisão de 96 por 2 para encontrarmos quanto cada uma recebeu: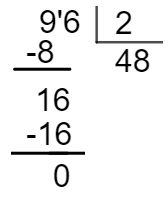

Cada uma teve um lucro de R$ 48.
Alternativa C

09 Uma empresa de transporte divide as viagens de acordo com a carga máxima permitida em seus caminhões. Durante o dia, todas as cargas são pesadas para estimar o total de viagens que devem ser realizadas, já que cada caminhão pode carregar, no máximo, 3 toneladas. Sabendo que há, no início do dia, um total de 50 toneladas em pedidos, a quantidade mínima de viagens necessárias para transportar toda a carga é:
(A) 18 viagens
(B) 17 viagens
(C) 16 viagens
(D) 15 viagens
(E) 14 viagens
Resolucao
Para calcular a quantidade de viagens necessárias, basta dividir 50 : 3.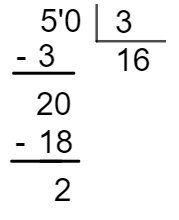

Com 16 viagens, ainda restariam 2 toneladas para serem levadas, então, são necessárias, pelo menos, 17 viagens.
Alternativa B

10) Analisando a sequência {A, B, C, D, A, B, C, D, A, B, C, D,…}, seu 1686º termo será:
(A) A
(B) B
(C) C
(D) D
(E) E
Resolucao
Note que a sequência sempre se repete e que ela possui 4 termos. Então, ao realizar a divisão 1686 : 4, o quociente nos mostrará quantas vezes essa sequência se repetirá, e o resto nos mostrará os termos restantes dela.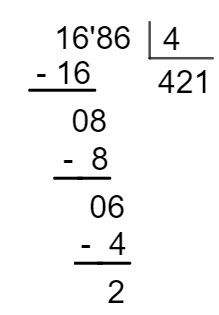

Como o resto é 2, isso significa que a sequência se repetirá 421 vezes e que restarão 2 termos, o segundo termo da sequência é a letra B, então, o 1686º termo será B.
Alternativa B

11) (Enem) Diante da hipótese do comprometimento da qualidade da água retirada do volume morto de alguns sistemas hídricos, os técnicos de um laboratório decidiram testar cinco tipos de filtros de água.
Dentre esses, os quatro com melhor desempenho serão escolhidos para futura comercialização.
Nos testes, foram medidas as massas de agentes contaminantes, em miligrama, que não são capturados por cada filtro em diferentes períodos, em dia, como segue:
Filtro 1 (F1): 18 mg em 6 dias;
Filtro 2 (F2): 15 mg em 3 dias;
Filtro 3 (F3): 18 mg em 4 dias;
Filtro 4 (F4): 6 mg em 3 dias;
Filtro 5 (F5): 3 mg em 2 dias.
Ao final, descarta-se o filtro com a maior razão entre a medida da massa de contaminantes não capturados e o número de dias, o que corresponde ao de pior desempenho.
Disponível em: www.redebrasilatual.com.br. Acesso em: 12 jul. 2015 (adaptado).
O filtro descartado é:
(A) F1
(B) F2
(C) F3
(D) F4
(E) F5
Resolucao
Vamos saber o desempenho de cada um dos filtros e buscar o que possui maior valor calculando as divisões:
F1 = 18 : 6 = 3
F2 = 15 : 3 = 5
F3 = 18 : 4 = 4,5
F4 = 6 : 3 = 2
F5= 3 : 2 = 1,5
O filtro menos eficiente é o F2.
Alternativa B

12) Para ladrilhar um pátio de 24 m², com ladrilhos no formato de um quadrado de 20 cm de lado, são necessários um total de:
(A) 60 ladrilhos
(B) 90 ladrilhos
(C) 600 ladrilhos
(D) 900 ladrilhos
(E) 1000 ladrilhos
Resolucao
Para encontrar a quantidade de pisos, é necessário dividir a área a ser ladrilhada pela área do ladrinho, mas note que as unidades de medidas estão diferentes.
Para transformar 24 m² para cm², é necessário multiplicar por 10.000:
24 × 10.000 = 240.000 cm²
Como o ladrinho é quadrdado, a sua área é calculada por 20² = 400 cm².
Então, para calcular a área do ladrinho, vamos dividir 240.000 : 400 = 600.
Alternativa C

13) (Enem) Para o reflorestamento de uma área, deve-se cercar totalmente, com tela, os lados de um terreno, exceto o lado margeado pelo rio, conforme a figura. Cada rolo de tela que será comprado para confecção da cerca contém 48 metros de comprimento.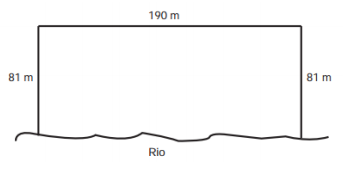
A quantidade mínima de rolos que deve ser comprada para cercar esse terreno é:
(A) 6
(B) 7
(C) 8
(D) 11
(E) 12
Resolucao
Primeiro calcularemos o comprimento que será cercado, que é igual a 81 + 81 + 190 = 352 metros.
Sabemos que cada rolo possui 48 metros, então, realizando a divisão 352 : 48, teremos: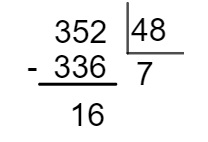

Caso fossem comprados 7 rolos, faltariam 16 metros para cercar, logo, são necessários 8 rolos.
Alternativa C

14) Amanda, Beatriz, Carla e Daniela foram para a lanchonete durante o intervalo do trabalho e gastaram um total de R$ 35. O valor da conta foi dividido igualmente para cada uma delas, e cada uma pagou:
(A) R$ 8
(B) R$ 8,25
(C) R$ 8,50
(D) R$ 8,75
(E) R$ 9,25
Resolucao
Como elas dividiram a conta por 4, basta realizar a divisão 35 : 4.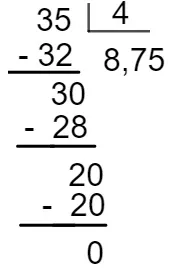

Cada uma pagou R$ 8,75.
Alternativa D

15) (OBMEP) No número 6a78b, o algarismo a é da ordem das unidades de milhar e o algarismo b é da ordem das unidades. Se 6a78b for divisível por 45, então o valor de a + B é:
(A) 5
(B) 6
(C) 7
(D) 8
(E) 9
Resolucao
Sobre a divisibilidade do número 6a78b por 45, podemos fazer a seguinte interpretação:
- Se o número é divisível por 45, então ele também pode ser dividido por 9 e 5, pois 9 x 5 = 45.
- Todo número que é divisível por 5 tem o algarismo da unidade igual a 0 ou 5.
- Todo número que é divisível por 9 possui como resultado da soma dos seus algarismos um múltiplo de 9.
Para o número 6a78b com b igual a 0 ou 5, temos:
I) 6 + 7 + 8 + 0 = 21
II) 6 + 7 + 8 + 0 = 26
Para que o número 6a78b seja múltiplo de 9, temos:
I) 6 + 7 + 8 + 0 = 27
II) 6 + 7 + 8 + 0 = 27
27 é múltiplo de 9, pois 9 x 9 x 9 = 27.
Portanto, a + b é igual a 6, pois
I) a + b = 0 + 6 = 6
II) a + b = 1 + 5 = 6
Podemos fazer a prova que os números são realmente divisíveis por 5, 9 e 45.
Para o número 66780, temos:
Para o número 61785, temos:
Alternativa B

Multiplicação com decimais
As operações com números decimais estão presentes em nossas atividades cotidianas desde a hora que acordamos para ir ao colégio. As horas, o preço do lanche, a quantia em dinheiro que você leva para escola, o valor do combustível no posto de gasolina e até a nota que você tirou na prova são representados por números decimais. Saber realizar as operações com esses números é muito importante para resolver problemas diários que aparecem em nossas vidas.

Multiplicação de um número decimal por um número natural.
01) Sabrina comprou quatro chocolates ao valor de R$ 1, 75 cada. Quanto Sabrina gastou?
Resolucao
Se cada chocolate custou R$ 1,75, vamos utilizar o algoritmo da multiplicação para determinar o valor total da compra de Sabrina.

Resposta: Sabrina gastou R$ 7,00.

02) Para repor seu estoque de extrato de tomate, um atacadista fez um pedido de 2.600 unidades. Sabendo que cada unidade custava de R$ 0,75, o valor gasto nesse pedido foi de:
(A) R$19500,00.
(B) R$ 1950,00.
(C) R$ 950,00.
(D) R$ 9750,00.
(E) R$ 195,00.
Resolução
Como cada unidade custa R$ 0,75 e foram adquiridas 2600, então vamos multiplicar a quantidade pelo valor unitário.
Realizando a MULTIPLICACAO de 2600 × 0,75, temos:
2600 → 0 casa decimal
0,75 → 2 casas decimais
O resultado terá, portanto, duas casas decimais: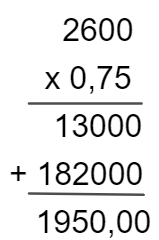

Alternativa B

03) (Enem) Deseja-se postar cartas não comerciais, sendo duas de 100 g, três de 200 g e uma de 350 g. O gráfico mostra o custo para enviar uma carta não comercial pelos Correios: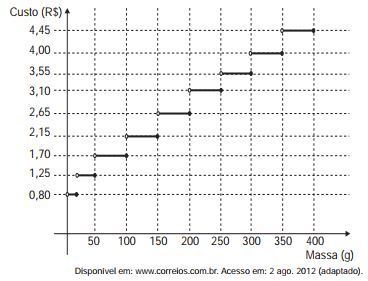
O valor total gasto, em reais, para postar essas cartas é de:
(A) 8,35.
(B) 12,50.
(C) 14,40.
(D) 15,35.
(E) 18,05.
Resolução
Analisando o gráfico, sabemos que há 2 cartas de 100 g e que cada uma custa R$ 1,70; 3 cartas de 200 g e cada uma custa R$ 2,65; e uma carta de 350 g, que custa R$ 4,00.
Então, o valor gasto é de:
2 × 1,70 + 3 × 2,65 + 1 × 4,00
Realizando as multiplicações, temos que:
1,70 → 2 casas decimais
2 → 0 casa decimal
Então, o resultado terá duas casas decimais. Utilizando o mesmo raciocínio para 3× 2,65, temos que: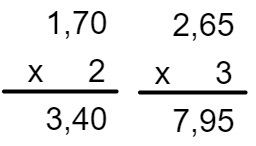

Terminando a SOMA:
3,40 + 7,95 + 4,00 = 15,35
Alternativa D

04) Em uma padaria, são vendidos pedaços de torta no valor de R$ 6,50 cada pedaço. Sabendo que essa torta é composta por 8 pedaços, qual é o valor total da torta?
(A) R$ 35,50
(B) R$ 39,00
(C)R$ 45,50
(D) R$ 50,00
(E) R$ 52,00
Resolução
Para encontrar o valor total da torta, basta multiplicar o preço unitário pelo total de pedaços. Realizando a multiplicação de 6,50 × 8, temos que:
8 → 0 casa decimal
6,50 → duas casas decimais
Então, o produto possuirá duas casas decimais: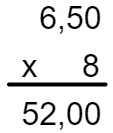

Alternativa E

05) (Enem PPL) Um granjeiro detectou uma infecção bacteriológica em sua criação de 100 coelhos. A massa de cada coelho era de, aproximadamente, 4 kg. Um veterinário prescreveu a aplicação de um antibiótico, vendido em frascos contendo 16 mL, 25 mL, 100 mL, 400 mL ou 1 600 mL. A bula do antibiótico recomenda que, em aves e coelhos, seja administrada uma dose única de 0,25 mL para cada quilograma de massa do animal. Para que todos os coelhos recebessem a dosagem do antibiótico recomendada pela bula, de tal maneira que não sobrasse produto na embalagem, o criador deveria comprar um único frasco com a quantidade, em mililitros, igual a:
(A) 16.
(B) 25.
(C) 100.
(D) 400.
(E) 1 600.
Resolução
Alternativa C.
Como há 100 coelhos e cada um tem massa de aproximadamente 4 kg, deve-se comprar antibiótico para 4 × 100 = 400 kg.
Como para cada quilo é administrado 0,25 ml, faremos a multiplicação de 400 × 0,25. Note que há 2 casas decimais no 0, 25 e nenhuma em 400, então o resultado terá duas casas decimais.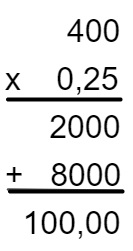

Alternativa C

06) Para realizar um churrasco, Márcia comprou 1,5 kg de alcatra a R$ 32,90 o quilo. O valor pago por Márcia foi de:
(A) R$ 29,90.
(B) R$ 32,90.
(C) R$ 34,40.
(D) R$ 45,75.
(E) R$ 49,35.
Resolução
Realizando a multiplicação do valor pela quantidade, temos que 1,5 × 32,90.
1,5 → 1 casa decimal
32,90 → 2 casas decimais
Note que há 3 casas decimais, então, realizando a multiplicação, o produto terá 3 casas decimais: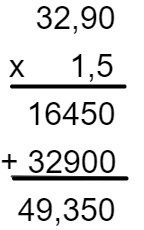

O valor pago pelo cliente foi de R$ 49,35.
Alternativa E

07) Um tecido no formato retangular possui dimensões de 0,8 metro de largura e 1,2 metro de comprimento. A área desse tecido é:
(A) 9,6 m².
(B) 96 m².
(C) 0,90 m².
(D) 0,96 m².
(E) 0,69 m².
Resolução
Como o tecido tem formado retangulo, a área dele é calculada pela multiplicação entre a largura e o comprimento.
A = 1,2 × 0,8
1,2 → 1 casa decimal
0,8 → 1 casa decimal
Então, o produto terá 2 casas decimais: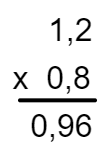

Alternativa D

08) Para repor o estoque de seu escritório e preparar os funcionários para o início do ano, Jean foi até uma papelaria e comprou:
4 agendas, no valor de R$ 9,90 cada;
10 resmas de papel A4, no valor de 27,90 cada;
1 caixa de grampo para grampeador, no valor de 16,50 cada.

Ao final dessa compra, o valor gasto por Jean foi de:
(A) R$ 320,10.
(B) R$ 299,80.
(C) R$ 305,25.
(D) R$ 335,10.
(E) R$ 321,50. 
Resolução
Para calcular o valor total gasto por Jean, temos que:
4 × 9,90 + 10 × 27,90 + 16,50
Vamos realizar cada multiplicação:
4 × 9,90
4 → 0 casa decimal
9,90 → 2 casas demais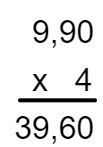

10 × 27,90
10 → 0 casa decimal
27,90 → 2 casas decimais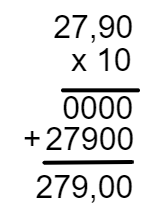

39,60 + 279,00 + 16,50 = 335,10
Alternativa D

09) Ao abastecer o carro, um cliente pediu para completar o tanque. Sabendo que couberam 30,2 litros no tanque e que a gasolina estava a R$ 5,20 o litro, o valor pago por esse cliente foi de:
(A) R$ 125,60.
(B) R$ 142,80.
(C) R$ 175,40.
(D) R$ 157,04.
(E) R$ 151,00.
Resolução
Para encontrar o valor gasto, vamos multiplicar o valor do litro de gasolina pelo total abastecido, então realizaremos a multiplicação 30,2 × 5,20.
30, 2 → 1 casa decimal
5,20 → 2 casas decimais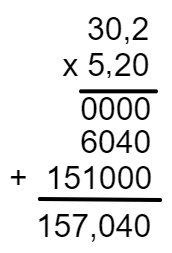

O valor gasto foi de R$ 157,04.
Altenativa D

10) Para ladrilhar uma região do quintal, foram utilizados 42 cerâmicas com 30,5 cm² cada. Então, a área dessa região é igual a:
(A) 1281 cm².
(B) 12,81 cm².
(C) 12810 cm².
(D) 1,281 cm².
(E) 128,1 cm².
Resolução
Para encontrar a área dessa região, basta calcular a multiplicação 42 × 30,5.
42 → 0 casa decimal
30,5 → 1 casa decimal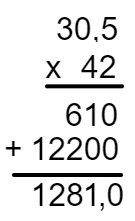

A área é igual a 1281 cm².
Alternativa A

11) Assinale o resultado da expressão a seguir.
5 : 2 × ( 3,5 + 2,7)
(A) R$ 9,75
(B) R$ 10,50
(C) R$ 12,75
(D) R$ 15,50
(E) R$ 18,65
Resolução
Vamos resolver a expressoes começando pelos parênteses:
5 : 2 × (3,5 + 2,7)
5 : 2 × (6,2)
2,5 × 6,2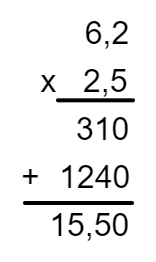

Alternativa D

12) Analise as afirmativas a seguir.
O resultado da multiplicação de 1,1 por 4,7 está entre 5,10 e 5,20.
A multiplicação entre 3,75 e 2,3 é um número entre 8,5 e 8,6

Marque a alternativa CORRETA.
(A) As afirmativas I e II são verdadeiras.
(B) A afirmativa I é verdadeira, e a II é falsa.
(C) A afirmativa I é falsa, e a II é verdadeira.
(D) As afirmativas I e II são falsas.
Resolução
I → 1,1 × 4,7 = 5,17 → verdadeira
II → 3,75 × 2,3 = 8,625 → falsa
Alternativa B

EXERCIOS RESOLVIDOS
01) Analisando o número 293.076, julgue as afirmativas a seguir:
I → o número apresentado é divisível por 2.
II → o número apresentado é divisível por 9.
III → o número apresentado é divisível por 8.
Marque a alternativa correta:
(A) Somente a I é verdadeira.
(B) Somente a II é verdadeira.
(C) Somente a III é verdadeira.
(D) Somente a I e a II são verdadeiras.
(E) Somente a I e a III são verdadeiras.
Resolução
I → o número apresentado é divisível por 2. (verdadeira)
O número 293.076 termina em 6, que é par, logo, ele é divisível por 2.
II → o número apresentado é divisível por 9. (verdadeira)
Para verificar se 293.076 é divisível por 9, somaremos os algarismos: 2 + 9 + 3 + 0 + 7 + 6 = 27. Como 27 é múltiplo de 9, então, ele é divisível por 9.
III → o número apresentado é divisível por 8. (falsa)
Para que 293.076 seja divisível por 8, os números 076 precisam ser divisíveis por 8, o que é falso, pois 76 : 8 deixa resto 4.
Alternativa D

02) Após a aula de matemática sobre os critérios de divisibilidade, Samanta escreveu três sentenças:
I → Todo número divisível por 10 é também divisível por 5.
II → Todo número par é divisível por 6.
III → Todo número divisível por 6 é par.
Marque a alternativa correta:
(A) Somente a afirmativa I está incorreta.
(B) Somente a afirmativa II está incorreta.
(C) Somente a afirmativa III está incorreta.
(D) Todas as afirmativas estão corretas.
Resolução
I → Todo número divisível por 10 é também divisível por 5. (verdadeira)
Para que o número seja divisível por 10, ele precisa terminar em 0, critério esse que também serve para verificar se o número é divisível por 5, logo, todo número divisível por 10 é divisível por 5 também.
II → Todo número par é divisível por 6. (falsa)
Existem números que são pares e não são divisíveis por 6.
III → Todo número divisível por 6 é par. (verdadeira)
Um dos critérios para que o número seja divisível por 6 é que ele seja divisível por 2 também, sendo assim, esse número é obrigatoriamente par.
Alternativa B

03) (PM SE – IBFC) Um número é composto por 3 algarismos. O algarismo da centena é o 7 e o da unidade é o 4. A soma dos possíveis algarismos da dezena desse número de modo que ele seja divisível por 3 é:
(A) 15
(B) 18
(C) 12
(D) 9
Resolução:
A regra para que o número seja divisível por 3 é que a soma dos algarismos seja divisível por 3. Nesse caso, chamaremos o número de x, então, temos a seguinte situação:
7x4
Nesse caso, as possibilidades para que essa soma seja divisível por 3 seriam:
7 + 1 + 4 = 12
7 + 4 + 4 = 15
7 + 7 + 4 = 18
Como o exercício pede a soma dos possíveis algarismos, temos: 1 + 4 + 7 = 12.
Alternateniva C

04) (Prova Resolvida PM Acre Músico-Funcab) 00) Sendo D o número de divisores naturais de 252, e N o número de divisores  naturais de 1296, então o valor de 2.D + 3.N será:
(A) 18
(B) 25
(C) 43
(D) 75
(E) 111
Resolucao
Fatorando os números temos:
252 = 2.2.3.3.7
1296 = 2.2.2.2.3.3.3.3
Para saber o número de divisores, basta somar 1 a cada quantidade de primos e multiplicá-los:
252 tem 3.3.2 = 18 divisores
1296 tem 5.5 = 25 divisores
2.18 + 3.25 = 36 + 75 = 111

05) (PM SE-IBFC) Um número é composto por 3 algarismos sendo que o algarismo da centena é o 7 e o da unidade é o 4. A soma dos possíveis algarismos da dezena desse número de modo que ele seja divisível por 3 é:
(A) 15
(B) 18
(C) 12
(D) 9
Resolução
Um número é divisível por 3 quando a soma dos seus algarismos é igual a um número divisível por 3.
Por exemplo, 222 é divisível por 3 porque 2+2+2 = 6, que é divisível por 3.
Nas condições propostas, os números divisíveis por 3 são 714, 744 e 774.
7 + 1 + 4 = 12
7 + 4 + 4 = 15
7 + 7 + 4 = 18
Somando os algarismos das dezenas:
1 + 4 + 7 = 12
Alternativa C

06) (Algás-UFAL) Critério de divisibilidade por 11: Esse critério é semelhante ao critério de divisibilidade por 9. Um número é divisível por 11 quando a soma alternada dos seus algarismos é divisível por 11. Por soma alternada queremos dizer que somamos e subtraímos algarismos alternadamente (539 ⇒5 – 3 + 9 = 11).
Se A e B são algarismos do sistema decimal de numeração e o número 109AB é múltiplo de 11, então
(A) B = A.
(B) A + B = 1.
(C) B – A = 1.
(D) A – B = 10.
(E) A + B = -10.
Resolução
Efetuando a soma alternada:
1 – 0 + 9 – A + B = 10 – A + B = 10 + (B – A)
A e B são algarismos do sistema decimal, ou seja, pertencem ao conjunto {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Se 10 + (B – A) é um número múltiplo de 11, e A e B estão entre 0 e 9, podemos concluir que:
10 + (B – A) = 11
B – A = 11 – 10
B – A = 1
Alternativa C
 

Continua ....