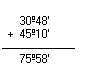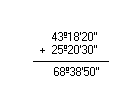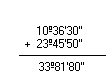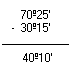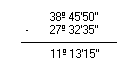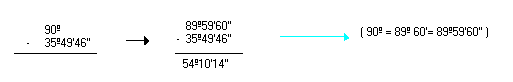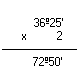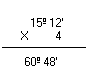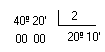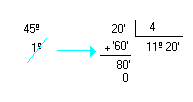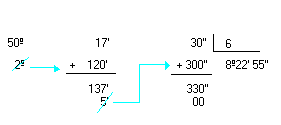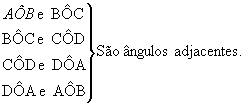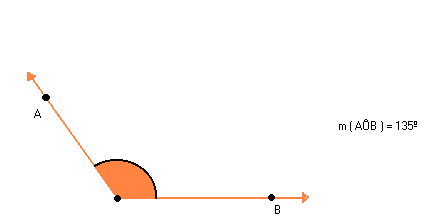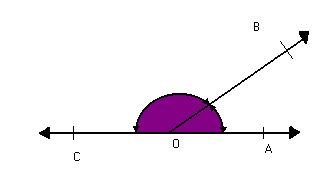EF II - ANGULOS

Professor Diminoi
ANGULOS

O ângulo e seus elementos
Duas semirretas que não estejam contidas na mesma reta, e que tenham a mesma origem, dividem o plano em duas regiões: uma convexa e outra não-convexa.
Cada uma dessas regiões, junto com as semirretas, forma um ângulo. Assim, as duas semirretas determinam dois ângulos:
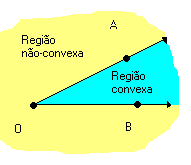
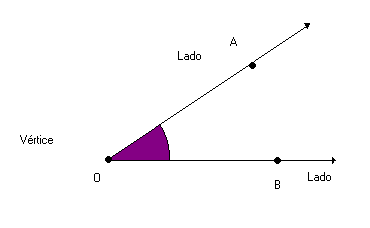
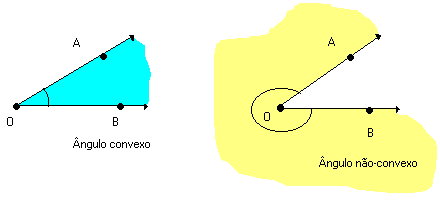Todo ângulo possui dois lados e um vértice. Os lados são as semirretas que o determinam. O vértice é a origem comum dessas semirretas.

O ângulo convexo de vértice O e lados

é indicado por: AÔB, BÔA ou Ô.


Ângulo nulo e ângulo raso
Observe agora dois casos em que as semirretas de mesma origem estão contidas na mesma reta. Nesses casos, formam-se também ângulos.

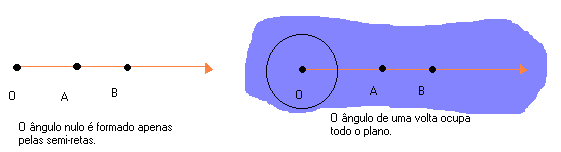
Ângulo nulo e ângulo de uma volta
As semirretas
Coincidem. Temos aí o ângulo nulo e o ângulo de uma volta.

Ângulo raso ou ângulo de meia-volta
As semirretas não coincidem.
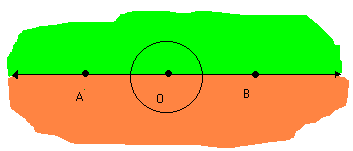
Temos aí dois ângulos rasos ou de meia-volta.
Podemos, então, estabelecer que:
Ângulo é a região do plano limitada por duas semirretas que têm a mesma origem.

Medida de um ângulo
A medida de um ângulo é dada pela medida de sua abertura. A unidade padrão de medida de um ângulo é o grau, cujo símbolo é º.
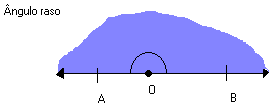
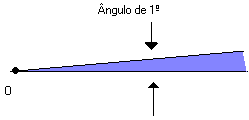
Tomando um ângulo raso ou de meia-volta e dividindo-o em 180 partes iguais, determinamos 180 ângulos de mesma medida. Cada um desses ângulos representa um ângulo de 1º grau (1º).
Para medir ângulos, utilizamos um instrumento denominado transferidor. O transferidor já vem graduado com divisões de 1º em 1º.

Existem dois tipos de transferidor: de 180º e de 360º.
O grau compreende os seguintes submúltiplos:
O minuto corresponde do grau
1/60
Indica-se um minuto por 1'.
O segundo corresponde a
1/60
do minuto. Indica-se um segundo por 1''.
1` = 60”
Logo, podemos concluir que:
1º = 60`. 60 = 3600

Quando um ângulo é medido em graus, minutos e segundos, estamos utilizando o sistema sexagesimal.

Usando o transferidor
Como medir um ângulo, utilizando o transferidor
Observe a sequência:
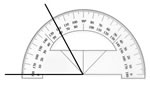
O centro O do transferidor deve ser colocado sobre o vértice do ângulo.

A linha horizontal que passa pelo centro deve coincidir com uma das semirretas do ângulo OA.
Verificamos a medida da escala em que passa a outra semirreta OB
Como construir um ângulo utilizando o transferidor
Observe a sequência utilizada na construção de um ângulo de 50º:
Traçamos uma semirreta AB.
Colocamos o centro do transferidor sobre a origem da semirreta (A).
Identificamos no transferidor o ponto (C) correspondente à medida de 50º.
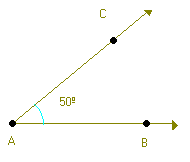Traçamos a semirreta AC, obtendo o ângulo BÂC que mede 50º.
Os ângulos de 30º, 45º, 60º e 90º  são ângulos especiais. Eles podem ser desenhados com esquadro.

Leitura de um ângulo
Observe as seguintes indicações de ângulos e suas respectivas leituras:
15º   (lê-se "15 graus'')
45º50'   (lê-se ''45 graus e 50 minutos'')
30º48'36''   (lê-se ''30 graus, 48 minutos e 36 segundos'')

Observações:
Além do transferidor, existem outros instrumentos que medem ângulos com maior precisão. Como exemplos temos o teodolito, utilizado na agrimensura, e o sextante, utilizado em navegação.
A representação da medida de um ângulo pode ser feita também através de uma letra minúscula ou de um número.
Um ângulo raso ou de meia-volta mede 180º.
O ângulo de uma volta mede 360º.

Questões envolvendo medidas de ângulos
Observe a resolução das questões abaixo:

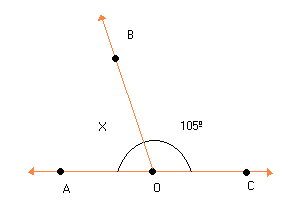
a) Determine a medida do ângulo AÔBna figura:
Resolucao
Medida de AÔB = x
Medida de BÔC = 105º
Como m (AÔC) é 180º, pois é um ângulo raso, temos:
m (AÔB) + m (BÔC) = m (AÔC)
x + 105º = 180º
x   = 180º - 105º
x   = 75º
Logo, a medida de AÔB é 75º.

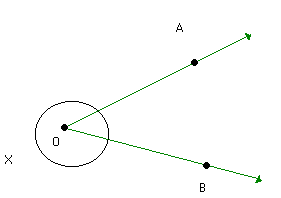
b) Determine a medida do ângulo não convexo na figura:
Resolucao
Verificamos que o ângulo não convexo na figura (x) e o ângulo convexo (50º) formam juntos um ângulo de uma volta, que mede 360º. Assim:
x + 50º = 360º
x = 360º - 50º
x = 310º
Logo, o valor do ângulo não convexo é 310º.

Transformação de unidades
Como vimos, quando trabalhamos com medidas de ângulos, utilizamos o sistema sexagesimal. Observe nos exemplos como efetuar transformações nesse sistema:

a) Transforme 30º em minutos.
Resolucao
Sendo 1º = 60', temos:
30º = 30 . 60'= 1.800'
Logo, 30º = 1.800 minutos

b) Transforme 5º35' em minutos.
Resolucao
5º = 5 . 60' = 300'
300' +  35'= 335'
Logo, 5º35'= 335'.

c) Transforme 8º em segundos.
Resolucao
Sendo 1º = 60', temos:
8º = 8 . 60'= 480'
Sendo 1'= 60'', temos:
480'= 480 . 60'' = 28.800''
Logo, 8º = 28.800''.

d) Transforme 3º35' em segundos.
Resolucao
3º = 3 . 60'= 180'
180' +  35' = 215'
215' .  60''  = 12.900''
Logo, 3º35'= 12.900''

e) Transforme 2º20'40'' em segundos.
Resolucao
2º = 2 . 60' = 120'
120' + 20'  = 140'
140'. 60''= 8.400''
8.400'' + 40'' = 8.440''
Logo, 2º20'40'' = 8.440''

Transformando uma medida de ângulo em número misto
a) Transforme 130' em graus e minutos.
Resolucao


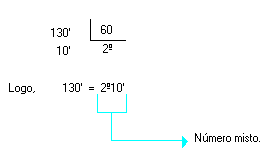
b) Transforme 150'' em minutos e segundos.
Resolucao


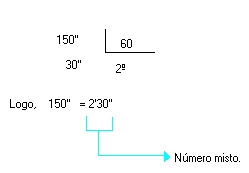
c) Transforme 138'' em graus, minutos e segundos.
Resolucao

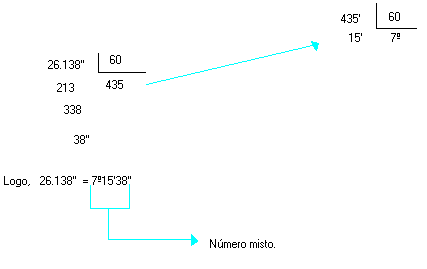
Medidas fracionárias de um ângulo
a) Transforme 24,5º em graus e minutos.
Resolucao
0,5º  = 0,5 . 60' = 30'
24,5º= 24º + 0,5º = 24º30'
Logo, 24,5º = 24º30'.

b) Transforme 45º36' em graus.
Resolucao
60'    1º
      36'    x       

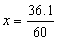
x = 0,6º  (lê-se ''seis décimos de grau'')
Logo, 45º36'= 45º + 0,6º = 45,6º.   

c) Transforme 5'54''  em minutos.
Resolucao
                                                                60''   1'
                                                                54''    x         

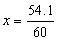
x = 0,9'  ( lê-se ''nove décimos de minuto'')
Logo, 5'54'' = 5'+ 0,9'= 5,9'

Operações com medidas de ângulos
Observe alguns exemplos de operações envolvendo medidas de ângulos.
Adição
a) 30º48'  +  45º10'


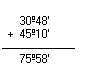
b) 43º18'20''  +  25º20'30''


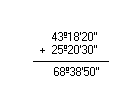
c) 10º36'30''  +  23º45'50''

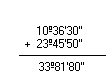
Simplificando 33º81'80'', obtemos:

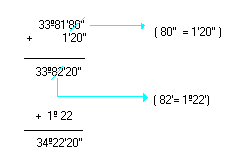
Logo, a soma é 34º22'20''.

Subtração
Observe os exemplos
a) 70º25' -  30º15


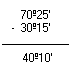
b) 38º45'50''  - 27º32'35''


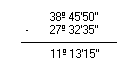
c) 90º  -  35º49'46''


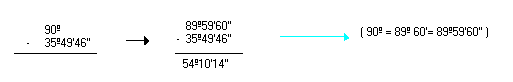
d) 80º48'30''  -  70º58'55''
Observe que:

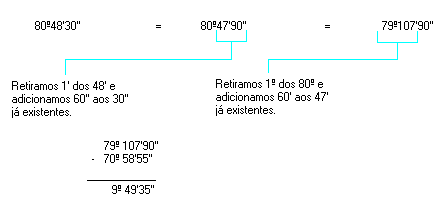
Logo, a diferença é 9º 49'35''.

Multiplicação e divisão de um ângulo por um número natural
Multiplicação por um número natural
Observe os exemplos:
a) ( 36º 25')


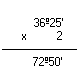
b) ( 15º 12')


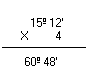
c) ( 12º36'40'')

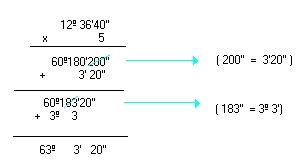
Logo, o produto é 63º3'20''.

Divisão por um número natural
Observe os exemplos
a) ( 40º 20') : 2


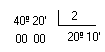
b) ( 45º20' ) : 4


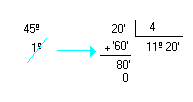
c) ( 50º17'30'' ) : 6


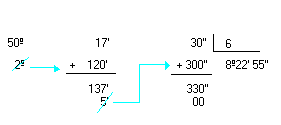
Ângulos congruentes
Observe os ângulos abaixo:
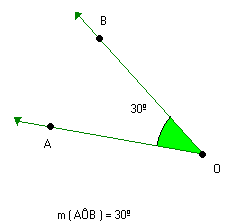
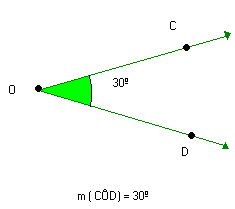Verifique que AÔB e CÔD têm a mesma medida. Eles são ângulos congruentes e podemos fazer a seguinte indicação:

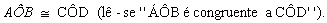
Assim: Dois ângulos são congruentes quando têm a mesma medida.
 
Propriedades da Congruência

Reflexiva:

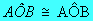
Simétrica: 

Transitiva:


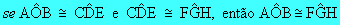
Ângulos consecutivos
Observe a figura:
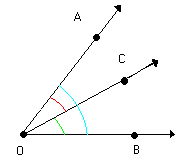Nela identificamos os ângulos AÔC, CÔB e AÔB. Verifique em cada uma das figuras abaixo que:
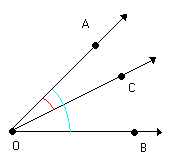
Os ângulos AÔC  e CÔB possuem:
Vértice comum: O
Lado comum: OC
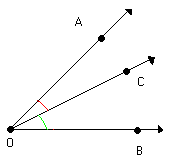
Os ângulos AÔC e AÔB possuem:
Vértice comum: O
Lado comum: OA
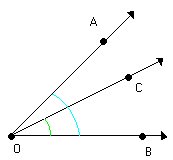Os ângulos CÔB  e AÔB possuem:
Vértice comum: O
Lado comum: OB

Os pares de ângulos AÔC  e CÔB, AÔC  e AÔB, CÔB  e AÔB são denominados ângulos consecutivos.
Assim: Dois ângulos são consecutivos quando possuem o mesmo vértice e um lado comum.

Ângulos adjacentes
Observe os exemplos de ângulos consecutivos vistos anteriormente e verifique que:
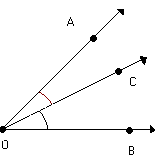Os ângulos AÔC e CÔB não possuem pontos internos comuns.
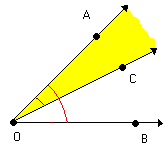Os ângulos AÔC  e  AÔB possuem pontos internos comuns.
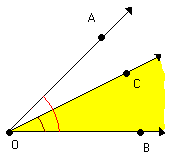Os ângulos CÔB  e AÔB possuem pontos internos comuns
   
Verifique que os ângulos AÔC  e CÔB são consecutivos e não possuem pontos internos comuns. Por isso eles são denominados ângulos adjacentes.       
Assim: Dois ângulos são adjacentes quando são consecutivos e não possuem pontos internos comuns.

Observação
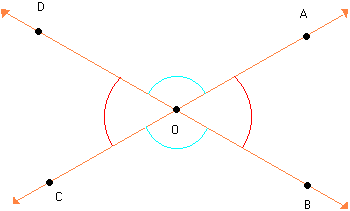
Duas retas concorrentes determinam vários ângulos adjacentes.

Exemplos:

 

 

 

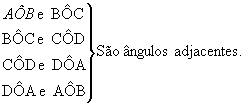
Bissetriz de um ângulo
Observe a figura abaixo

m (AÔC)  = m (CÔB) = 20º

Verifique que a semirreta OC divide o ângulo AÔB em dois ângulos (AÔC e CÔB) congruentes. Nesse caso, a semirreta OC é denominada bissetriz do ângulo AÔB.
Assim Bissetriz de um ângulo é a semirreta com origem no vértice desse ângulo e que o divide em dois outros ângulos congruentes.:

Utilizando o compasso na construção da bissetriz de um ângulo
Determinação da bissetriz do ângulo AÔB
Centramos o compasso em O e com uma abertura determinamos os pontos C e D sobre as semirretas AO e OB, respectivamente.
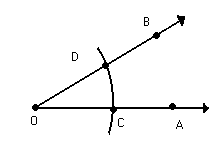Centramos o compasso em C e D e com uma abertura superior à metade da distância de C  a D traçamos arcos que se cruzam em E.
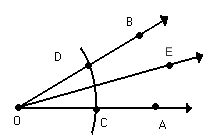
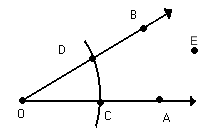Traçamos OE, determinando assim a bissetriz de AÔB.
Ângulo agudo, obtuso e reto
Podemos classificar um ângulo em agudo, obtuso ou reto.

Ângulo agudo é o ângulo cuja medida é menor que 90º.

Exemplo
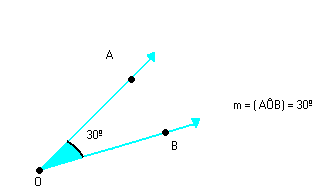Ângulo obtuso é o ângulo cuja medida é maior que 90º.

Exemplo
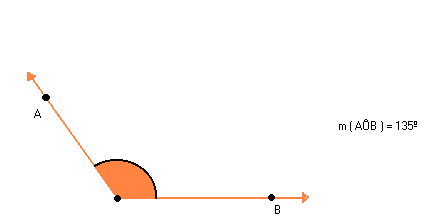Ângulo reto é o ângulo cuja medida é 90º.
Exemplo

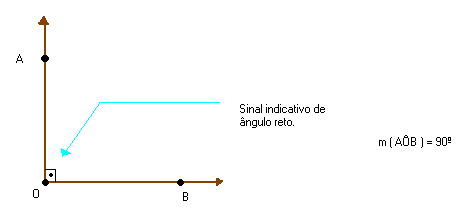
Retas perpendiculares
As retas r e s da figura abaixo são concorrentes e formam entre si quatro ângulos retos.
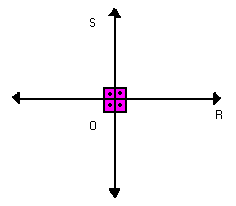Dizemos que as retas r e s são perpendiculares e indicamos:


 

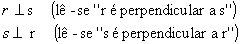
Observação
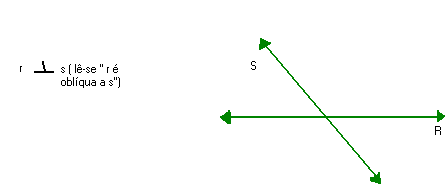
Duas retas concorrentes que não formam ângulos retos entre si são chamadas de oblíquas.

Exemplo

Ângulos complementares
Observe os ângulos AÔB  e BÔC na figura abaixo:
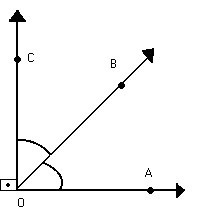Verifique que:
m (AÔB) + m (BÔC) = 90º
Nesse caso, dizemos que os ângulos AÔB  e BÔC são complementares. 

Dois ângulos são complementares quando a soma de suas medidas é 90º

Exemplo
Os ângulos que medem 42º e 48º são complementares, pois 42º + 48º = 90º.
Dizemos que o ângulo de 42º é o complemento do ângulo de 48º, e vice-versa.
Para calcular a medida do complemento de um ângulo, devemos determinar a diferença entre 90º e a medida do ângulo agudo dado.
Fazendo a regra de tres
Medida do ângulo                Complemento
x                                             90º  - x

Exemplo
Qual a medida do complemento de um ângulo de 75º?
Resolucao
Medida do complemento = 90º - medida do ângulo
Medida do complemento = 90º - 75º
Medida do complemento = 15º
Logo, a medida do complemento do ângulo de 75º é 15º.

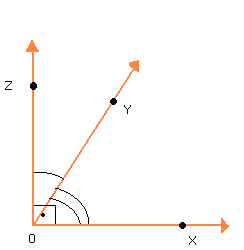
Observação
Os ângulos XÔY  e YÔZ  da figura ao lado, além de complementares, são também adjacentes. Dizemos que esses ângulos são adjacentes complementares.
Ângulos suplementares
Observe os ângulos AÔB e BÔC na figura abaixo:
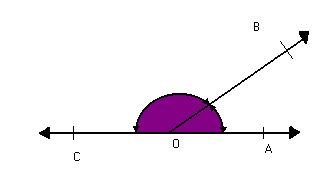As semirretas AO e OC formam um ângulo raso.
Observe que:
m (AÔB)  + m (BÔC) = 180º
Nesse caso, dizemos que os ângulos AÔB e BÔC são suplementares. Assim:

a) Dois ângulos são suplementares quando a soma de suas medidas é 180º.
Exemplo
Os ângulos que medem 82º e 98º são suplementares, pois 82º + 98º = 180º.
Dizemos que o ângulo de 82º é o suplemento do ângulo de 98º, e vice-versa.
Para calcular a medida do suplemento de um ângulo, devemos determinar a diferença entre 180º e a medida do ângulo agudo dado.
Fzendo a regra de tres
Medida do ângulo                Suplemento
x                                             180º  - x
 
Exemplo
b) Qual a medida do suplemento de um ângulo de 55º?
Resolucao
Medida do suplemento = 180º - medida do ângulo
Medida do suplemento = 180º - 55º
Medida do suplemento = 125º
Logo, a medida do suplemento do ângulo de 55º é 125º.

Observação:
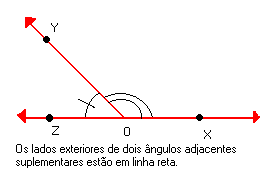
Os ângulos XÔY e YÔZ da figura abaixo, além de suplementares, são também adjacentes. Dizemos que esses ângulos são adjacentes suplementares.

Ângulos opostos pelo vértice
Observe os ângulos AÔB e CÔD na figura abaixo:
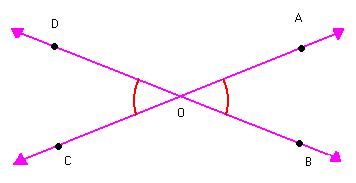Observe que:

Nesse caso, dizemos que os ângulos AÔB  e CÔD são opostos pelo vértice (o.p.v).
Assim:
Dois ângulos são opostos pelo vértice quando os lados de um deles são semirretas opostas aos lados do outro.
Na figura abaixo, vamos indicar:
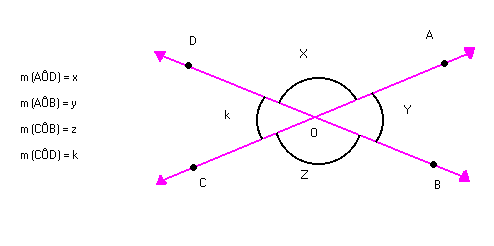Sabemos que:
X + Y = 180º  (ângulos adjacentes suplementares)
X  + K = 180º (ângulos adjacentes suplementares)
Então:
Logo: y = k
Assim:
m (AÔB) = m (CÔD)  AÔB    CÔD
m (AÔD) = m (CÔB)  AÔD    CÔB
Daí a propriedade:
Dois ângulos opostos pelo vértice são congruentes.
Observe uma aplicação dessa propriedade na resolução de um problema:

Dois ângulos opostos pelo vértice têm medidas, em graus, expressas por x + 60º  e 3x - 40º. Qual é o valor de x?
Resolucao
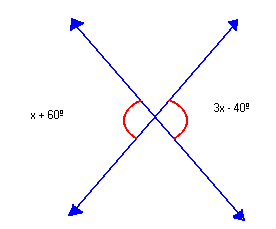x + 60º  = 3x-40º
Angulos o.p.v
x - 3x  = - 40º-60º
-2x = -100º
x = 50º
Logo, o valor de x é 50º.

 

Continua...