GEOMETRIA PLANA III
Professor Diminoi
GEOMETRIA PLANA
A geometria plana estuda o comportamento de estruturas no plano, a partir de conceitos básicos primitivos como ponto, reta e plano. Estuda o conceito e a construção de figuras planas como quadriláteros, triângulos, círculos, suas propriedades, formas, tamanhos e o estudo de suas áreas e perímetro.
Conceitos básico
Os conceitos básicos, ou primitivos, da geometria plana, são chamados de axiomas, ou seja, são aceitos sem demonstrações. São apenas noções que auxiliam no entendimento de conceitos mais completos.
Ponto
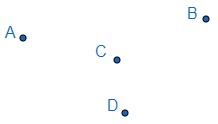
Segundo “Os Elementos”, de Euclides, um ponto é definido como "o que não tem partes". É apenas uma posição no espaço. É representado por letras maiúsculas.
Reta
Uma reta é a reunião de infinitos pontos. É uma “linha” com comprimento, mas sem largura. É sempre representada por uma letra minúscula. Se tivermos dois pontos, eles determinam uma reta. Há apenas uma reta que passa por esses dois pontos. Por um ponto passam infinitas retas.

Plano
Um plano é uma região onde há infinitos pontos e infinitas retas. É um elemento com comprimento e largura. Geralmente é representado por letras gregas. Um plano é determinado por três pontos não colineares (pontos não alinhados). Se uma reta tem dois pontos distintos em um plano, então esta reta está contida nesse plano.

O plano apresenta duas dimensões e é representado por uma letra grega (α, β, γ, … ).
Segmento de Reta
Dados dois pontos distintos A e B, a união desses pontos com o conjunto de pontos compreendidos entre A e B é chamado de segmento de reta.
 Representamos esse segmento de reta AB por overline AB.
Representamos esse segmento de reta AB por overline AB.
Semirreta
Dados dois pontos distintos A e B, a reunião do segmento de reta overline AB com o conjunto dos pontos X tais que B está entre A e X é a semirreta AB, indicada por overrightarrowAB.
 Ângulos
Ângulos
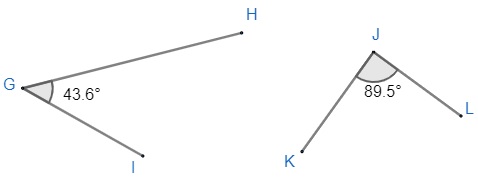
Chama-se ângulo a região entre duas semirretas que partem de uma mesma origem. Podemos dizer, ainda que um ângulo é a medida da abertura de duas semirretas que partem da mesma origem.
 Tipos de triângulos
Tipos de triângulos

Triângulo
Para calcular a área de um triângulo, basta multiplicar a medida da base (b) com a medida da altura (h) e dividir o resultado por dois.

Quadrado
Sabemos que os lados do quadrado são todos iguais. Para calcular sua área, multiplicamos a medida da base com a medida altura. Como as medidas são as mesmas, multiplicá-las é o mesmo que elevar o lado ao quadrado.


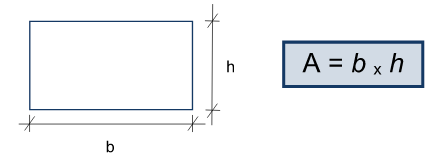
Retângulo
A área do retângulo é dada pela multiplicação da base pela altura.
Losango
A área do losango é dada pelo produto da diagonal maior (D) com a diagonal menor (d) dividido por dois.

Trapézio
A área do trapézio é dada pelo produto da altura com a soma da base maior (B) e a base menor (b) dividido por dois.

Círculo
A área do círculo de raio r é dada pelo produto do raio ao quadrado com o número irracional ℼ (em geral utilizamos o valor ℼ = 3,14).

Teorema de Pitágoras
O Teorema de Pitágoras é um dos assuntos mais aplicados na matemática, principalmente em problemas da Geometria e Trigonometria.
O teorema serve, sobretudo, para relacionar os lados de um triângulo retângulo – figura geométrica plana composta por um ângulo reto (90°) e outros dois ângulos agudos (menores que 90°).
Expressão que relaciona as medidas do triângulo retângulo
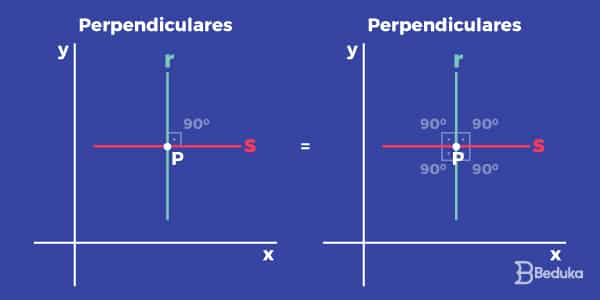
Reta - É representada por letra minúscula, é uma linha ilimitada unidimensional (possui o comprimento como dimensão) e pode se apresentar em três posições:

Observação: retas perpendiculares são retas que formam um ângulo de 90º entre si.
 QUESTÕES RESOLVIDAS
QUESTÕES RESOLVIDAS
01) Calcule a área de uma quadra de basquete com 40 m de largura e 70 m de comprimento.
(A) 800 m²
(B) 2800 m²
(C) 3800 m²
(D) 110 m²
Resolução:
A área é calculada em figuras retangulares multiplicando o comprimento pela largura. Então:
A = b . h
A = 70 . 40
A = 2800 m²
Alternativa: B
02) Retângulo de base 15 cm e altura de 10 cm.
(A) 150 cm2
(B) 50 cm2
(C) 120 cm2
(D) 1510 cm2
Resolução:
A = b . h
A = 15 . 10
A = 150 cm2
Alternativa: A
03) Quadrado com lado de 19 cm.
(A) 61 cm2
(B) 361 cm2
(C) 36 cm2
(D) 1919 cm2
Resolução:
A = L2
A = 192
A = 361 cm2
Alternativa: B
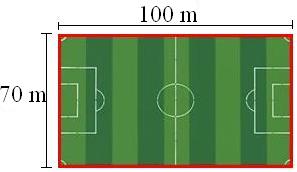
04) Observe um campo de futebol e calcule o seu perímetro.
 A alternativa correta é a a alternativa:
A alternativa correta é a a alternativa:
(A) 170 m
(B) 280 m
(C) 140 m
(D) 340 m
Resolução:
Pra fazermos o cálculo do perímetro devemos somar todos os seus lados:
P = 100 + 70 + 100 + 70
P = 340 m
Alternativa: D
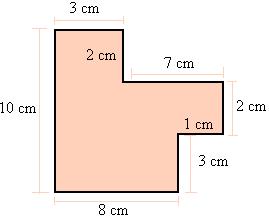
05) Qual o perímetro da figura abaixo.
 A alternativa correta é a a alternativa:
A alternativa correta é a a alternativa:
(A) 220
(B) 321
(C) 14
(D) 36
Resolução:
O perímetro da figura é a soma de todos os seus lados:
P = 10 + 8 + 3 + 1 + 2 + 7 + 2 +3
P = 18 + 4 + 9 + 5
P = 22 + 14
P = 36
Alternativa: D
06) Qual o perímetro de um quadrado com lado de 20 cm.
(A) 20
(B) 40
(C) 60
(D) 80
Resolução:
P = L + L + L + L
P = 20 + 20 + 20 + 20
P = 80 cm
Alternativa: D
07) O triângulo com dois lados de 6 cm e um lado com 12 cm. Qual o seu perímetro?
(A) 24
(B) 12
(C) 36
(D) 30
Resolução:
P = L + L + L
P = 6 + 6 + 12
P = 24
Alternativa: A
Teorema de Pitágoras
O teorema de Pitágoras relaciona as medidas dos lados de um triângulo retângulo da seguinte maneira:
“Em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.”
Fórmula de Pitágoras
O teorema de Pitágoras é muito importante para a Matemática, tendo influenciado outros grandes resultados matemáticos.

Fórmula do teorema de Pitágoras
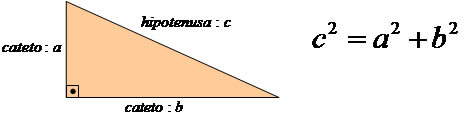
Para aplicação do teorema de Pitágoras, é necessário compreender as nomenclaturas dos lados de um triângulo retângulo. O maior lado do triângulo fica sempre oposto ao maior ângulo, que é o ângulo de 90°. Esse lado recebe o nome de hipotenusa e será representado aqui pela letra a.
Os demais lados do triângulo são chamados de catetos e serão aqui representados pelas letras b e c.
01) (ETEC) O Teorema de Pitágoras, provavelmente a relação mais conhecida da Matemática, afirma que em todo triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Atribui-se a Pitágoras, matemático grego do século VI a.C., a primeira demonstração desse teorema, embora essa relação já fosse aplicada pelo menos mil anos antes. Pensando nisso, analise a seguinte situação: um helicóptero, para sobrevoar uma região, parte do ponto A do solo e sobe verticalmente 250 m; em seguida, voa horizontalmente 160 m para o leste; finalmente, desce verticalmente 130 m até o ponto B.
Nessas condições, a distância entre os pontos A e B é, em metros,
(A) 120.
(B) 180.
(C) 200.
(D) 260.
(E) 280.
Resolução:
Fórmula de Pitágoras:
Substituindo os valores no segundo triângulo retângulo cujas medidas são: a = 120, b =160 e a hipotenusa valendo x
Pitágoras
h2 = a2 + b2
h2 = 1202 + 1602
h2 = 14400 + 25600
h2 = 40000
h = √40000
h = 200
Alternativa: C
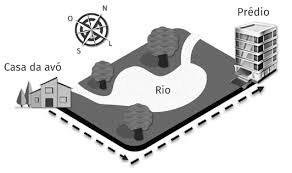
02) (ETEC) Admita que a menina dos quadrinhos esteja visitando a avó que mora em outra cidade. A fim de voltar da casa de sua avó para o prédio onde mora, usando a bota de 7 léguas da história, a menina dá 3 passos para leste e 4 passos para o norte. A figura representa de modo esquemático esse trajeto realizado pela garota.
 A distância entre a casa da avó e o prédio no qual a menina mora é, em quilômetros, igual a
A distância entre a casa da avó e o prédio no qual a menina mora é, em quilômetros, igual a
(A) 323,4
(B) 231,0
(C) 142,6
(D) 46,2
(E) 35,0
Resolução:
A menina estava calçada com uma bota 7 léguas. Isso quer dizer que a cada passo ela caminhava 7 léguas.
Para o leste ela caminhou 3 . 7 = 21 léguas
Para o norte ela caminhou 4 . 7 = 28 léguas
Olhando o desenho podemos aplicar Pitágoras:
h2 = a2 + b3
h2 = 212 + 493
h2 = 441 + 784
h2 = 1225
h = √1225
h = 35 légua
Uma légua tem 6600m = 6,6km
Para transforma léguas 35 em km basta multiplicar 35 . 6,6 = 231
Alternativa: B
03) Determine o raio de uma circunferência que possui diâmetro medindo 40 cm.
(A) 80
(B) 60
(C) 40
(D) 20
Resolução:
Sabemos que o diâmetro é o dobro do raio, assim:
d = 2 .r
d = 2r
r = 40/2
r = 20
Alternativa; D
03) Determine o comprimento da circunferência de raio 5 cm. O raio da circunferência é igual 5 cm, logo, para determinar o comprimento da circunferência, devemos substituir esse valor na fórmula.
(A) 131,2
(B) 321,2
(C) 41,2
(D) 31,2
Resolução:
C = 2πr
C = 2(3,14)(5)
C = 6,24 · 5
C = 31,2 cm
Alternativa: D
04) Determine a área de uma circunferência que possui raio igual 4 cm. Temos que o raio da circunferência é igual a 4 cm, logo, podemos substituir essa medida na fórmula da área.
(A) 50,24 cm2
(B) 40,24 cm2
(C) 30,24 cm2
(D) 30,24 cm2
Resolução:
A = π · r2
A = 3,14 · (4)2
A = 3,14 · 16
A = 50,24 cm2
Alternativa: A
05) Determine a medida do raio de uma praça circular que possui 9420 m de comprimento (Use π = 3,14.).
(A) 1500 cm
(B) 1500 m
(C) 2000 m
(D) 2500m
Resolução:
A partir da fórmula do comprimento da circunferência, temos:
C = 2 . π . r
9420 = 2 . 3,14 . r
9420 = 6,28 . r
6,28 . r = 9420
r = 9420
6,28
r = 1500 m
Alternativa: B
06) Determine a medida do raio de uma praça circular que possui 9420 m de comprimento (Use π = 3,14.).
(A) 1500 cm
(B) 1500 m
(C) 2000 m
(D) 2500m
Resolução:
A partir da fórmula do comprimento da circunferência, temos:
C = 2 . π . r
9420 = 2 . 3,14 . r
9420 = 6,28 . r
6,28 . r = 9420
r = 9420
6,28
r = 1500 m
Alternativa: B
07) Uma pista de atletismo tem a forma circular e seu diâmetro mede 80 m. Um atleta treinando nessa pista deseja correr 10 km diariamente. Determine o número mínimo de voltas completas que ele deve dar nessa pista a cada dia.
Resolução:
Primeiro vamos descobrir o valor do perímetro da pista que o atleta treinará. Se o diâmetro da pista é 80m, logo seu raio será 40m, sendo assim:
C = 2πr
C = 2 . 3,14 . 40
C = 251,2 metros
Antes de prosseguir, é necessário converter a distância que o atleta deseja correr para metros. Se temos 10km, logo são 10.000 metros. O número de voltas será o resultado da divisão da distância desejada pelo comprimento da pista.
Voltas = 10000 / 251,2
Voltas = 39,8
O valor encontrado é 39,8, desse modo teremos aproximadamente 40 voltas.
08) Donato, patrulheiro militar, utiliza uma bicicleta no exercício da sua função, que é patrulhar uma região turística de Vitória-ES. Sabe-se que o pneu dessa bicicleta possui formato circular de diâmetro medindo 70 cm. Considerando que na última quinta-feira Donato percorreu 21,4 km com essa bicicleta em serviço de patrulhamento, é correto afirmar que o pneu dessa bicicleta deu: (Dado π= 3)
(A) 20.190,4
(B) 30.190,4
(C) 70.190,4
(D) 10.190,4
(E) 9.190,4
Resolução:
O primeiro passo é calcular o comprimento da roda da bicicleta.
C = 2πr
Se o diâmetro da roda é 70cm, temos que o raio equivale a 35cm.
C = 2π35
C = 70 . 3
C = 210 cm = 2,1 metros
Em seguida devemos converter o valor percorrido de metros para centímetros e assim dividi-los para obter o valor das voltas dadas pela roda da bicicleta.
21,4 km = 21400 metros
Voltas 21 400 / 2,1
O número de voltas foi 10.190,4
Alternativa: D
09) Para realizar o teste físico em determinado concurso da PM, os candidatos devem correr ao redor de uma praça circular cujo diâmetro mede 120 m. Uma pessoa que dá 9 voltas ao redor dessa praça percorre: (Dado: π = 3).
(A) 1620 m
(B) 3240 m
(C) 4860 m
(D) 6480 m
(E) 8100 m
Resolução:
Se o diâmetro equivale a 120 metros, temos que o raio é 60 metros.
Para resolver a questão precisamos apenas calcular o valor do comprimento da circunferência, que equivale a uma volta ao redor da praça, e multiplica-lo por 9.
C = 2πr
C = 2 . 3 . 60
C = 360 m
360 . 9 = 3240 metros
Alternativa: B
10) Se o raio de uma circunferência tiver um acréscimo de 50% então o acréscimo percentual em seu comprimento será igual a:
(A) 25%
(B) 50%
(C) 100%
(D) 150%
Resolução:
Para facilitar a resolução de tal questão podemos supor um valor. Digamos que o raio inicial seja 10, logo um acréscimo de 50% significa que o segundo raio vale 15.
Agora precisamos calcular o comprimento da circunferência dos dois raios.
C1 = 2πr
C1 = 2π10
C1 = 20π
C2 = 2π15
C2 = 30π
Dividindo o segundo comprimento pelo primeiro encontraremos o valor acrescido nas circunferências.
Acréscimo = 30π / 20π
O acréscimo é de 50%.
Alternativa: B
11) Uma circunferência possui perímetro igual a 628 cm. Determine o diâmetro dessa circunferência (adote π = 3,14).
Resolução
Como o perímetro é igual a 628 cm, podemos substituir esse valor na expressão de comprimento da circunferência.
C = 2π . r
628 = π . r
628 = 9 .3,14 . r
638 = 6,28r
r = 628/6,28
r = 100m
12) (Exatus) Donato, patrulheiro militar, utiliza uma bicicleta no exercício da sua função, que é patrulhar uma região turística de Vitória-ES. Sabe-se que o pneu dessa bicicleta possui formato circular de diâmetro medindo 70 cm. Considerando que na última quinta-feira Donato percorreu 21,4 km com essa bicicleta em serviço de patrulhamento, é correto afirmar que o pneu dessa bicicleta deu:
(Dado π = 3)
(A) 10000 voltas
(B) 10190 voltas
(C) 10199 voltas
(D) 10210 voltas
(E) 10220 voltas
Resolução:
Vamos primeiro calcular quanto o patrulheiro anda após uma volta do pneu.
Pela fórmula do comprimento de uma circunferência:
C = 2.π.r = 2.3.35 = 210 cm = 2,1 metros
Repare que usamos r = 35 cm pois o diâmetro da roda é 70 cm.
Temos que 21,4 km equivalem a 21400 metros.
Como em uma volta ele anda 2,1 metros, e no total ele andou 21400 metros, basta efetuar a divisão:
21400/2,1 = 10190,4 voltas
Alternativa: B
13) (Exatus) Para realizar o teste físico em determinado concurso da PM, os candidatos devem correr ao redor de uma praça circular cujo diâmetro mede 120 m. Uma pessoa que dá 9 voltas ao redor dessa praça percorre: (Dado: π = 3).
(A) 1620 m
(B) 3240 m
(C) 4860 m
(D) 6480 m
(E) 8100 m
Resolução:
Comprimento de uma circunferência = 2π.r = 2.3.60 = 360m
Como a pessoa dá 9 voltas: 9×360 = 3240m
Alternativa: B
14) (Cesiep) Se o raio de uma circunferência tiver um acréscimo de 50% então o acréscimo percentual em seu comprimento será igual a:
(A) 25%
(B) 50%
(C) 100%
(D) 150%
Resolução:
Relembrando a fórmula do comprimento de uma circunferência:
C = 2.π.r
Temos uma função afim.
Claramente se o raio dobra, o comprimento também dobra, se cresce 50%, o comprimento também cresce 50%…
Alternativa: B
15) (Prefeitura de Bombinhas – SC) Quantas voltas dá uma roda de 20 cm de raio para percorrer 7536 metros?
(A) 1000 voltas
(B) 2000 voltas
(C) 3000 voltas
(D) 6000 voltas
Resolução:
Calculando o comprimento da circunferência da roda, onde consideramos que o raio de 20 cm equivale a 0,2 metros.
C = 2.π.r
C = 2 . 3,14 . 0,2
C = 1,256 metros
Como o objetivo é percorrer 7536 metros, basta dividirmos este valor pelo comprimento da circunferência:
7536 / 1,256 = 6000 voltas
Alternativa: D
16) (FGV) Em uma praça há uma pista de corrida circular com 50m de raio. Um corredor deu 7 voltas completas nessa pista.
Esse corredor percorreu, aproximadamente:
(A) 2000m;
(B) 2200m;
(C) 2400m;
(D) 2800m;
(E) 3000m.
Resolução:
Como a pista tem formato circular, podemos calcular o comprimento da pista através da seguinte fórmula:
C = 2.π.r
C = 2 . 3,14 . 50
C = 314 metros
Como o corredor deu 7 voltas:
314 . 7 = 2198 metros
Alternativa: B
17) (Consulplan) Maria faz, diariamente, caminhadas em volta da lagoa de sua cidade. Considerando que a lagoa tem formato circular de raio igual a 20 metros e que π = 3,14, ela se propôs a dar 3 voltas ao redor da lagoa por dia. De acordo com as informações apresentadas, quantos metros Maria caminha por semana?
(A) 376,8 m.
(B) 1888,4 m.
(C) 2337,2 m.
(D) 2637,6 m.
Resolução:
Calculando o comprimento da circunferência que representa o formato circular da pista de caminhada:
C = 2.π.r
C = 2 . 3,14 . 20
C = 125,60
Considerando que uma semana possui 7 dias, e que Maria dá 3 voltas por dia, temos:
125,60 . 7 . 3 = 2637,60 metros
Alternativa: D
18) Questão 1. Deseja-se pregar uma fita decorativa ao redor da tampa de um pote redondo. Se o diâmetro da tampa mede 12 cm, qual o comprimento mínimo que a fita deve ter para dar a volta completa na tampa?
Resolução:
A medida do contorno do pote corresponde ao comprimento de uma circunferência com diâmetro igual a 12 cm.
Para calcular o comprimento, precisamos do raio.
O raio de uma circunferência é igual à metade da medida do diâmetro, então, o raio é igual a 6 cm.
Substituindo r por 6 e por 3,14, na fórmula do comprimento da circunferência, temos que:
C = 75,37
Como a medida do raio está em centímetros, o resultado do comprimento também será em centímetros.
Logo, a fita deve ter no mínimo 75,36 centímetros de comprimento para dar a volta completa na tampa do pote.
19) O contorno de uma peça circular tem 190 cm de comprimento. Qual a medida do diâmetro dessa peça?
Resolução:
Sabendo a medida do comprimento de uma circunferência, podemos determinar o valor do raio.
Veja que substituindo C por 190 e π por 3,14 na fórmula, temos que:
190 = 6,28 . r
r = 30,24
Com a medida do raio, podemos determinar o diâmetro.
r =2r
d = 60,48
Como a medida do comprimento foi dada em centímetros, então, o raio e o diâmetro calculados também estão em centímetros.
Assim, o diâmetro da peça mede 60,48 cm.
20) A roda de um ônibus tem 90 cm de raio. Que distância o ônibus terá percorrido quando a roda der 120 voltas?
Resolução:
Em cada volta que a roda dá, a distância percorrida é igual à medida do comprimento do contorno da roda.
Assim, o que temos que fazer é calcular tal comprimento e depois multiplicar o valor obtido por 120, que é o número total de voltas.
Substituindo r por 90 e por 3,14 na fórmula do comprimento, obtemos:
C = 2 . 3,14 . 90
C = 565,2
Então, o comprimento do contorno da roda é igual a 565,2 cm.
Vamos multiplicar por 120 para obter a distância percorrida:
565,2 . 120 = 67824
Até agora, utilizamos as medidas em centímetros, então, o resultado também está em centímetros.
Para indicar a distância percorrida pelo ônibus, vamos fazer a transformação para metros:
67824 : 100 = 678,24
Portanto, a distância percorrida pelo ônibus foi de 678,24 metros.
21) Qual é a área de um círculo cuja circunferência tem 40 metros de comprimento?
Resolução:
A área do círculo depende da medida do raio.
Para saber a medida do raio, vamos utilizar a informação do comprimento da circunferência:
40 -2 . 3,14 . r
40 = 6,28 . r
r = 40/6,28
r = 6,37
Agora, já podemos calcular a área do círculo:
A = π . r2
A = 3,14 . (6,37)2
A = 127,4
As medidas utilizadas estavam em metros, então, a área será em metros ao quadrado. Portanto, a área do círculo é igual a 127,4 m².
O perímetro de um círculo corresponde a medida do seu contorno, que é o comprimento da circunferência.
O comprimento da circunferência depende do valor do raio. Para determinar esse valor, vamos utilizar a informação da área do círculo:
A = π . r2
18 = 3,14 . r2
r2 = 18 /3,14
r = 2,393
Agora que já sabemos a medida do raio, podemos calcular o comprimento da circunferência:
C =2 .3,14 . 2,393
C = 15,01
Portanto, o comprimento da circunferência (perímetro do círculo) é igual a 15,01 cm.
22) Um círculo tem 18 cm² de área. Qual é o seu perímetro?
Resolução:
O perímetro de um círculo corresponde a medida do seu contorno, que é o comprimento da circunferência.
O comprimento da circunferência depende do valor do raio. Para determinar esse valor, vamos utilizar a informação da área do círculo:
A = π . r2
A = π . r2
18 = 3,14 . r2
r2 = 18 /3,14
r = 2,393
Agora que já sabemos a medida do raio, podemos calcular o comprimento da circunferência:
C =2 .3,14 . 2,393
C = 15,01
Portanto, o comprimento da circunferência (perímetro do círculo) é igual a 15,01 cm.
23) A superfície de uma mesa é formada por um quadrado de lado igual a 2 m e dois semicírculos, um em cada lateral, conforme mostra a figura.
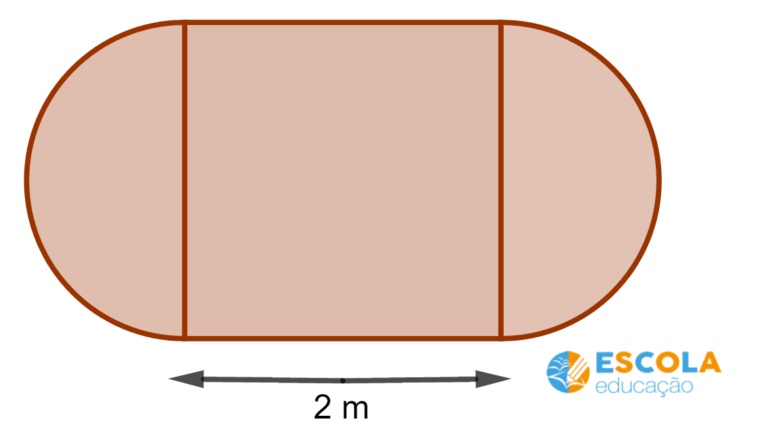 Calcule o perímetro e a área da superfície da mesa.
Calcule o perímetro e a área da superfície da mesa.
Resolução:
O perímetro corresponde a medida do contorno da figura. Assim, basta calcular o perímetro do círculo e somar com os dois lados do quadrado.
Perímetro do círculo:
O círculo tem diâmetro igual a 2 (é o lado do quadrado), logo, o raio é igual a 1.
Pela fórmula do comprimento da circunferência, temos que:
P = 2 . 3,14 . 1
O que significa que o círculo tem 6,28 metros de perímetro.
Perímetro da superfície da mesa:
P = 6,28 + 2 + 2
P = 10,28
Logo, o perímetro da superfície da mesa mede 10,28 metros.
Para o cálculo da área da superfície, o procedimento é semelhante. Calculamos a área do círculo e somamos com a área do quadrado.
A área do quadrado de lado 2 m é igual a 4 m².
Área do círculo de raio 1:
A = 3,14 . 12
A = 3,14
Área da superfície da mesa:
A = 4 + 3,14 = 7,14
Portanto, a área da superfície da mesa é igual a 7,14 m².
Figuras da Geometrias Planas
Calculando Área e Perímetro

Área do setor circular
O setor de um círculo é uma região delimitada por dois segmentos de retas que partem do centro para a circunferência. Esses segmentos de reta são os raios do círculo, veja a figura:
.jpg)
O ângulo α é chamado de ângulo central.
Dessa forma, percebemos que o setor circular é uma parte da região circular, ou seja, ele é uma fração da área do círculo. Assim podemos afirmar que a área do setor circular é diretamente proporcional ao valor de α, pois a área de todo o círculo é diretamente proporcional a 360º.
Assim podemos montar a seguinte relação (regra de três):
360º ------------- π . r²
θº ---------------- x
Onde:
π = 3,14
r = raio do círculo
θº = medida do ângulo central
x = área do arco
Exemplo -1: Determine a área de um segmento circular com ângulo central de 32º e raio medindo 2 m.
Resolução:
360º ------------- π . r²
32º -------------- x
360x = 32 . π . r²
x = 32 . π . r² / 360
x = 32 . 3,14 . 2² / 360
x = 32 . 3,14 . 4 / 360
x = 401,92 / 360
x = 1,12
A área do segmento circular possui aproximadamente 1,12 m².
Exemplo - 2: Qual a área de um setor circular com ângulo central medindo 120º e comprimento do raio igual a 12 metros.
Resolução:
360º ------------- π . r²
120º ------------------ x
360x = 120 . π . r²
x = 120 . π .. r² / 360
x = 120 . 3,14 . 12² / 360
x = 120 . 3,14 . 144 / 360
x = 54259,2 / 360
x = 150,7
A área do setor circular citado corresponde, aproximadamente, a 150,7 m².
Exemplo - 3: Qual a área de um segmento circular cujo ângulo central é 32º e o raio mede 2 m?
Resolução:
360º _________ π . r²
32º ____________ x
360x = 32 . π . r²
x = 32 . π . r² / 360
x = 32 . 3,14 . 2² / 360
x = 32 . 3,14 . 4 / 360
x = 401,92 / 360
x = 1,12
Assim, conclui que a área do segmento circular possui cerca de 1,12m².
Exemplo - 4: Um setor circular cujo ângulo central mede 120º e raio com comprimento equivalente a 12 metros terá sua área igual a?
Resolução:
360º __________ π . r²
120º __________ x
360x = 120 . π . r²
x = 120 . π . r² / 360
x = 120 . 3,14 . 12² / 360
x = 120 . 3,14 . 144 / 360
x = 54259,2 / 360
x = 150,7
Assim, conclui-se que a área do setor circular desta situação compreende cerca de 150,7 m².
Exemplo - 5: Determine a área do setor circular abaixo. (Use π = 3,14)
 ResoluçãO:
ResoluçãO:
Como conhecemos o raio e a medida do ângulo central, basta substituir esses valores na fórmula da área do setor circular.
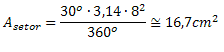
Exemplo - 6: Numa circunferência de área igual a 121π cm2, calcule a área do setor circular delimitado por um ângulo central de 120o.
Resolução:
Para solução desse problema devemos verificar que no numerador da fórmula da área do setor circular, a medida do ângulo central α está multiplicando a área da circunferência, dessa forma teremos:
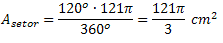
QUESTÕES RESOLVIDAS
01) Seja um triângulo isósceles com dois lados medindo 5 cm e a base medindo 6 cm. Qual a área desse triângulo?
Resolução:
Como podemos ver nessa questão, não temos a altura do triângulo, e não podemos aplicar a fórmula diretamente.
Para encontrar a altura, vamos aplicar o teorema de Pitágoras.
a² = h² + b²
5² = h² + 3²
25 = h² + 9
h² = 25 – 9
h = √16
h = 4
Como queremos calcular a altura no triângulo isósceles, e sabendo que a altura divide o triângulo em dois triângulos retângulos simétricos, então a base será a metade no triângulo retângulo. Entenda no artigo sobre triângulo isósceles.
Agora que temos a altura do triângulo, podemos aplicar a fórmula:
A = (b . h) / 2
A = (6 . 4) / 2
A = 24/2
A = 12 cm²
02) Considere um quadrado com aresta de 5 cm, qual a área deste quadrado?
Resolução:
A fórmula para calcular a área de um quadrado é:
A = L²
A = 5²
A = 25 cm²
03) Um campo de futebol possui 75 metros de largura e 105 metros de comprimento. Qual a área deste campo de futebol?
Resolução:
Sabendo que um campo de futebol possui uma forma retangular e a fórmula do retângulo é:
A = b . h.
A = 75 . 105
A = 7875 m²
04) Considere um trapézio onde a base menor mede 5 cm, a maior 8 cm e altura de 3 cm. Calcule a área desse trapézio.
Resolução:
Fórmula da área do trapézio:
A = ((B + b) . h) / 2
A = ((8 + 5) . 3) / 2
A = 39/2
A =19,5 cm²
05) Seja um losango com diagonal maior de 10 cm e a menor medindo 5 cm. Qual a área deste losango?
Resolução:
A = (D1 . D2) / 2
A = (10 . 5) / 2
A = 50/2
A = 25 cm²
06) Uma moeda possui diâmetro de 20 mm, qual a área dessa moeda?
Resolução:
O diâmetro é o dobro do raio.
d = 2r
d = d/2
20 = 2r
r = 20/2
r = 10 mm
A área de uma forma circular é calculada pela fórmula:
A = πr²
A = π . 10²
A = 3,14159 . 100
A = 314,159 mm²
07) Calcule a área de um quadrado que possui perímetro igual a 24 cm.
Resolução:
O perímetro de um quadrado corresponde a soma das medidas dos lados do quadrado. Como todos os lados tem o mesmo tamanho, basta dividir o perímetro por 4 para saber a medida do lado.
Lado do quadrado
24/4
L = 6
Assim, o lado desse quadrado mede 6 cm. Utilizando a fórmula da área de um quadrado, temos que:
A = L2
A = 62
A = 36 cm2
08) Calcule a área de um retângulo cuja base mede 1800 centímetros e a altura, 9 metros.
Resolução:
No cálculo de áreas, precisamos das medidas na mesma unidade. Nesse retângulo, a medida da base é dada em centímetros e a altura, em metros.
Antes de calcular a área vamos transformar a medida da base para metros, dividindo por 100:
1800cm/100 = 18m
Ab = 18m2
h = 9m
Utilizando a fórmula da á área de um retângulo, temos que:
A = b . h
A = 18 . 9
A = 162m2
09) Calcule a área de um canteiro de flores em formato de losango, que possui diagonal maior medindo 10 metros e diagonal menor medindo 5 metros.
Resolução:
A área deum losango é dada pelo produto das medidas das diagonais dividido por 2. Assim, nesse canteiro, a área é dada por:
A = (D . d) / 2
A = (10 . 5) / 2
A = 50/2
A = 25m2
10) Qual é a área de um triângulo com base medindo 30 cm e altura igual a 2/5 da medida da base?
Resolução:
Para calcular a área de um retângulo, precisamos da medida da base ( ) e da medida da altura ( ).
Nesse exercício, temos
b = 30cm
h = 2/5 da medida da base
Para saber o valor da altura, basta multiplicar a fração 2/5 pelo valor da base:
h = 2 / 5 . 5
h = 2 . 30 / 5h = 60/5
h = 12cm
Assim, a área do triângulo é:
A = (b . h) / 2
A = (30 . 60) / 2
A = 180cm2
11) Com uma lata de tinta dá para pintar 10 m² de um muro. É necessário comprar quantas latas de tinta para pintar o muro todo sabendo que ele tem 20 metros de comprimento e 2,8 metros de altura?
Resolução:
Para resolver esse exercício, precisamos calcular a área total do muro. Para isso, vamos utilizar a fórmula da área de um retângulo.
Temos base igual a 20 metros e altura igual a 2,8 metros, então:
A = b . h
A = 20 . 2,8
A = 56m2
A área total do muro é igual a 56 m² e a cada 10 m² de muro será necessária uma nova lata de tinta.
Para saber o número de latas de tinta para pintar todo o muro, basta dividir a área do muro pela área que podemos pintar com uma lata, ou seja:
56m2 / 10m2
5,6
Esse número significa que serão necessárias cinco latas completas e um pouco mais da metade de uma lata para pintar o muro. Assim, é necessário comprar 6 latas de tinta para pintar o muro todo.
12) Em uma praça com formato circular, a distância do centro da praça até a extremidade da praça é de 15,7 metros. Qual a área total dessa praça?
Resolução:
A praça tem o formato de um círculo, então, para saber a área da praça, basta calcular a a área de um círculo. O raio ( ) é dado pela distância do centro do círculo até a extremidade, então temos
r = 15,7m
π = 3,14
Assim,
A = π . r2
A = 3,14 . 15,72
A = 774,9786m2
13) (FUVEST) Na figura ABC é retângulo com catetos BC = 3 e AB = 4. Além disso, o ponto D pertence ao cateto AB, o ponto E pertence ao cateto BC e o ponto F pertence a hipotenusa AC, de tal forma que DECF...
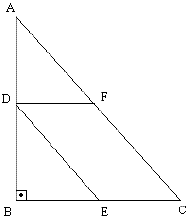 Resolução:
Resolução:
14) (ENEM) Em 20 de fevereiro de 2011, ocorreu a grande erupção do vulcão Bulusan nas Filipinas. A sua localização geográfica no globo terrestre é dada pelo GPS com longitude de 124° 3’ 0’’ a leste do Meridiano de Greenwich. (Dado: 1° equivale a 60’ e 1 equivale a 60″.)
A representação angular da localização do vulcão com relação a sua longitude de forma decimal é:
(A) 124,02°
(B) 124,05°
(C) 124,20°
(D)124,30°
(E)124,50°
Resolução:
Para resolver o exercício, devemos transformar 124° 3’ e 0″ (lê-se: cento e vinte e quatro graus, três minutos e zero segundos) para graus. Para isso, basta escrevermos os 3 minutos em graus e, já que a localização possui 0″, não há nada a fazer.
Foi fornecido pelo exercício que 1° equivale a 60’. Vamos utilizar uma regra de três para determinar quantos graus temos em 3 minutos.
1° – – – 60’
x° – – – 3’
60x = 3
x = 3 ÷ 60
x = 0,05°
Assim, 124° 3’ e 0″ é equivalente a escrever:
124° + 0,05° + 0°
124,05°
Alternativa: B
15) (ENEM) Uma escola tem um terreno vazio no formato retangular cujo perímetro é de 40 m, onde se pretende realizar uma única construção que aproveite o máximo de área possível. Após a análise realizada por um engenheiro, este concluiu que, para atingir o máximo de área do terreno com uma única construção, a obra ideal seria:
(A) um banheiro com 8 m2.
(B) uma sala de aula com 16 m2.
(C) um auditório com 36 m2.
(D) um pátio com 100 m2.
(E) uma quadra com 160 m2.
Resolução:
Como desconhecemos as dimensões do terreno retangular, vamos nomeá-las por x e y.
 De acordo com o enunciado, o perímetro é igual a 40 m, ou seja, a soma de todos os lados é igual a 40 m, logo:
De acordo com o enunciado, o perímetro é igual a 40 m, ou seja, a soma de todos os lados é igual a 40 m, logo:
x + x + y + y = 40
2x + 2y = 40
2(x +y) = 40
x + y = 20
y = 20 – x
Sabemos também que a área de um retângulo é dada pelo produto da base com a altura, assim:
A = x . y
Substituindo o valor de y, isolado anteriormente, temos:
A = x · (20 – x)
A = – x2 + 20x
Agora, para sabermos qual é a área máxima, basta determinar o valor máximo da função A, ou seja, determinar o vértice da parábola. O valor de xv é dado por:
Para determinar o valor do yv, vamos substituir o valor de xv na função A.
A = – x2 + 20x
A = – (10)2 + 20(10)
A = – 100 + 200
A = 100 m2
16) (ENEM) O Esquema I mostra a configuração de uma quadra de basquete. Os trapézios em cinza, chamados de garrafões, correspondem a áreas restritivas.
 Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diversas ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.
Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diversas ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.
 Após executdas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a)
Após executdas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a)
(A) aumento de 5 800 cm².
(B) aumento de 75 400 cm².
(C) aumento de 214 600 cm².
(D) diminuição de 63 800 cm².
(E) diminuição de 272 600 cm².
Resolução:
Comecemos pela área do trapézio da figura I, que é dada por (600 + 360).580 / 2 = 278 400. Calculando a área da figura II temos 580 . 490 = 284 200 cm².
Assim, o aumento da área foi de 5 800 cm².
Alternativa: A
17) (ENEM) Um senhor, pai de dois filhos, deseja comprar dois terrenos, com áreas de mesma medida, um para cada filho. Um dos terrenos visitados já está demarcado e, embora não tenha um formato convencional (como se observa na Figura B), agradou ao filho mais velho e, por isso, foi comprado. O filho mais novo possui um projeto arquitetônico de uma casa que quer construir, mas, para isso, precisa de um terreno na forma retangular (como mostrado na Figura A) cujo comprimento seja 7 m maior do que a largura.
 Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a
Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a
(A) 7,5 e 14,5.
(B) 9,0 e 16,0.
(C) 9,3 e 16,3.
(D) 10,0 e 17,0.
(E) 13,5 e 20,5.
Resolução:
Primeiramente, dividimos a figura B em dois triângulos B1 e B2, um com altura de 21 m e base de 3 m e outro com altura e base medindo 15 m.
Assim, temos que área da figura A = área da figura
B = B1 + B2
x(x + 7) = 15.15 / 2 + 21.3/2 = 144
Fatorando 144, temos que:
x(x + 7) = 9.16
x(x + 7) = 9(9 + 7)
Assim, as medidas do retângulo são 9 m e 16 m
Alternativa: B
24) Calcule a medida da hipotenusa do triângulo retângulo presente na figura a seguir.
Resolução:
Observe que 3 cm e 5 cm são as medidas dos catetos do triângulo acima. A outra medida refere-se ao lado oposto ao ângulo reto, portanto, a hipotenusa. Usando o teorema de Pitágoras, teremos:
a2 = b2 + c2
a2 = 42 + 32
a2 = 16 + 9
a2 = 25
a = √25
a = 5
A hipotenusa desse triângulo mede 5 centímetros.
18) O lado oposto ao ângulo reto de um triângulo retângulo mede 15 centímetros e um dos outros dois lados mede 12 centímetros. Calcule a medida do terceiro lado.
Resolução:
O lado oposto ao ângulo reto é a hipotenusa. Os outros dois são catetos. Representando o cateto que falta pela letra b, podemos usar o teorema de Pitágoras para descobrir a terceira medida. Basta lembrar que ela também é um cateto. Sendo assim, teremos:
a2 = b2 + c2
152 = b2 + 122
Observe que a medida da hipotenusa foi colocada no lugar da letra a, pois essa letra representa essa medida. Resolvendo a equação, encontraremos o valor de b:
225 = b2 + 144
225 – 144 = b2
81 = b2
b2 = 81
b = √81
b = 9
19) (ENEM) Na figura abaixo, que representa o projeto de uma escada com 5 degraus de mesma altura, o comprimento total do corrimão é igual a:
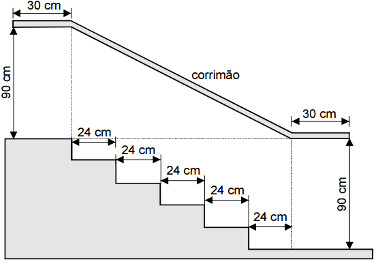 (A) 1,8 m.
(A) 1,8 m.
(B 1,9 m.
(C) 2,0 m.
(D) 2,1 m.
(E) 2,2 m.
Resolução:
Observe o seguinte triângulo retângulo sobre o corrimão da imagem do exercício.
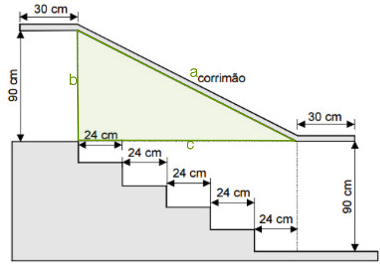
Perceba que o comprimento do corrimão é igual à soma 30 + a + 30 e que “a” é a medida da hipotenusa do triângulo colocado sobre a imagem. Além disso, note que b = 90 e que c = 24 + 24 + 24 + 24 + 24 = 120. Assim, para descobrir a medida de a, faremos:
a2 = b2 + c2
a2 = 902 + 1202
a2 = 8100 + 14400
a2 = 22500
a = √22500
a = 150
A medida do corrimão é 30 + 150 + 30 = 210 cm ou 2,1 m.
Resolução: D
20) Determine a medida c dos catetos de um triângulo retângulo isósceles em que a hipotenusa mede 30 cm.
Resolução:
Sabemos que o triângulo isósceles possui dois lados iguais. Então:
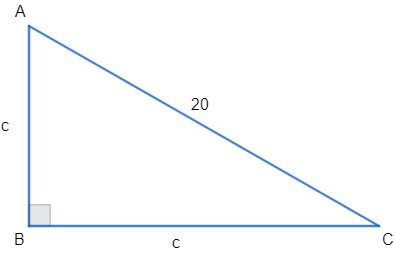
Aplicando o Teorema de Pitágoras, vamos ter que:
202 = c2 + c2
2c2 = 400
c2 = 200
Assim, as medidas dos catetos do triângulo medem, respectivamente:
21) Qual a área e o perímetro de um campo de futebol, de base 25 m e altura 5 m?
(A) A= 100m², P= 50m
(B) A= 150 m², P= 60m
(C) A= 125 m², P= 60 m
(D) A= 120 m², P= 50 m
Resolução:
Esse campo tem a forma de um retângulo, então para calcularmos a área basta multiplicar a base pela altura:
A= 25 . 5= 125 m²
O perímetro é a soma de todos os lados:
P = 25 + 5 + 25 + 5
P = 60 m.
Alternativa: C
22) Um campo de futebol de formato retangular tem 100 metros de largura por 70 metros de comprimento. Antes de cada treino, os jogadores de um time dão cinco voltas e meia correndo ao redor do campo. Sendo assim, determine:
a) Quantos metros os jogadores correm ao dar uma volta completa no campo?
b) Quantos metros eles percorrem ao dar as cinco voltas e meia ao redor do campo?
c) Se eles repetem essa corrida cinco vezes por semana, quantos metros os jogadores correm em uma semana?
Resolução:
a) Vamos calcular o perímetro do campo:
2p = 100 + 100 + 70 + 70
2p = 200 + 140
2p = 340 m
Ao dar uma volta completa, os jogadores percorrem 340 metros.
b) Se ao dar uma volta, os jogadores percorrem 340 metros, ao dar cinco voltas, eles percorrem 340 * 5 = 1700 metros. Para cinco voltas e meia, ele vai andar os 1700metros e metade de uma volta (340 : 2 = 170).Basta somar 1700 +170: 1870 metros.
c) Considerando que os jogadores correm 5 vezes por semana, se todos os dias eles correm 1870 metros, façamos 1870 * 5 = 9.350. Em uma semana, os jogadores correm 350 metros.
23) Sabendo que o perímetro de um hexágono regular é 48,6 cm. Qual é a medida de cada lado do hexágono?
Resolução:
Um hexágono regular possui seis lados de mesma medida, e o perímetro é a soma desses lados. Portanto, para saber a medida de cada lado, basta fazer:
48,6 : 6 = 8,1 cm
Cada lado do hexágono mede 8,1 cm.
24) Sabe-se que o perímetro de um retângulo é 60 cm e o comprimento desse retângulo é de 22 cm. Defina a largura do retângulo.
Resolução:
Um retângulo possui lados paralelos de medidas iguais. Então, se um lado do retângulo mede 22 cm, o lado paralelo a esse deve medir 22 cm também. Considere que a largura da figura é x. Visualizemos a figura:
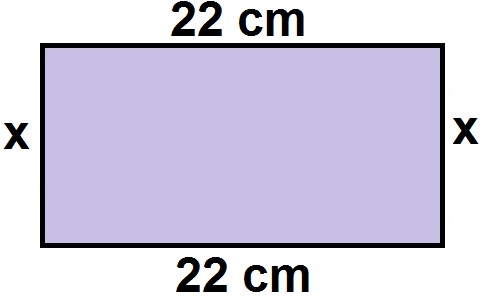 Se o perímetro, que é a soma de todos os lados do retângulo, é 60 cm, então temos:
Se o perímetro, que é a soma de todos os lados do retângulo, é 60 cm, então temos:
2p = 22 + x + 22 + x
60 = 44 + 2x
2x = 60 – 44
2x = 16
x = 16
2
x = 8,0 cm.
Portanto, a largura do retângulo é de 8,0 cm.
25) Calcule a área e o perímetro do losango de diagonal maior 8 cm e diagonal menor 4 cm.
Resolução:
Vamos esboçar esse losango:
8 cm
.jpg)
Para calcular a área de um losango, multiplica-se a diagonal maior pela menor e divide por dois:
A= D . d
2
A= 8 . 4
2
A = 32/2
A= 16 cm ²
Para calcular o perímetro precisaremos descobrir a medida de um lado. Podemos usar o teorema de Pitágoras para calcular essa medida. Basta tomar como catetos metade das medidas das diagonais, pois, além de se encontrarem em seus pontos médios, ainda são perpendiculares, o que garante a existência de um triângulo retângulo que possui essas medidas e o lado do losango como hipotenusa. Observe:
l2 = 42 + 22
l2 = 16 + 4
l2 = 20
√l2 = √20
l = 4,47
Agora basta multiplicar o lado por 4 para obter o perímetro.
P = 4·4,47
P = 17,88 cm
26) (ENEM) Em canteiros de obras de construção civil, é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo conforme pode ser visto na figura, em que as estacas foram indicadas por letras.
.JPG) A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto. Nessas condições, a área a ser calçada corresponde
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto. Nessas condições, a área a ser calçada corresponde
(A) à mesma área do triângulo AMC.
(B) à mesma área do triângulo BNC.
(C) à metade da área formada pelo triângulo ABC.
(D) ao dobro da área do triângulo MNC.
(E) ao triplo da área do triângulo MNC.
Resolução:
Para solucionar essa questão, devemos determinar a medida dos segmentos BP, PA, BM, MC, AN e NC. Essas medidas são estabelecidas por meio do ponto médio, que é o ponto que divide o segmento em duas partes iguais. Observe no desenho as medidas dos segmentos de acordo com os seus três pontos médios: M, N e P.
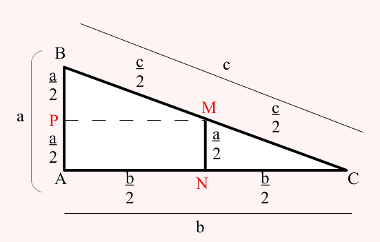
Agora que sabemos as medidas dos segmentos descritos anteriormente, podemos calcular a área.
Dados para o cálculo da área do triângulo MCN:
a = base
2
b = altura
2
Fórmula para calcular a área do triângulo: A = base . altura
2
Cálculo da área do triângulo MCN:
AMCN = a . b
2 2
2
AMCN = ab . 1
4 2
AMCN = ab
8
8 . AMCN = ab
Dados para o cálculo da área do triângulo BAC:
a = base
b = altura
Fórmula para calcular a área do triângulo: A = base . altura
2
Cálculo da área do triângulo MCN:
ABAC = a . b
2
ABAC = 8 . AMCN
2
ABAC = 4 AMCN
ABAC = 3 AMCN + AMCN
Logo, AABMN = 3 AMCN
A área a ser calçada corresponde a 3 AMCN .
Alternativa: E
27) (UFMT) Assinale a medida do lado de um quadrado, sabendo-se que o número que representa o seu perímetro é o mesmo que representa sua área.
(A) 5
(B) 4
(C) 6
(D) 8
Resolução:
Essa questão será resolvida pelo método de tentativas. Sendo assim, consideremos que o quadrado possui como medida de lado: 4, 5, 6 ou 8.
O cálculo da área de um quadrado é dado pela seguinte fórmula:
A = l2
Já a fórmula do perímetro é a soma dos quatro lados do quadrado:
P = l1+ l2 + l3 + l4
→ Considerando o lado do quadrado como 4, temos:
A = l2
A = 42
A = 16
P = l1 + l2 + l3 + l4
P = 4 + 4 + 4 + 4
P = 16
Quando o lado do quadrado é 4, a área é igual ao perímetro.
Considerando o lado do quadrado como 5:
A = l2
A = 52
A = 25
P = l1 + l2 + l3 + l4
P = 5 + 5 + 5 + 5
P = 20
Quando o lado do quadrado é 5, a área é diferente do perímetro.
Considerando o lado do quadrado como 6:
A = l2
A = 62
A = 36
P = l1 + l2 + l3 + l4
P = 6 + 6 + 6 + 6
P = 24
Quando o lado do quadrado é 6, a área é diferente do perímetro.
Considerando o lado do quadrado como 8:
A = l2 → A = 82 → A = 64
P = l + l + l + l
P = 8 + 8 + 8 + 8
P = 32
Quando o lado do quadrado é 8, a área é diferente do perímetro.
Alternativa: D
28) Uma escola pretende ladrilhar o seu pátio retangular, que possui as seguintes dimensões: 4 m e 5,5 m. Os ladrilhos utilizados são quadrados com 16 cm de lado. Calcule o número de ladrilhos necessários.
Resolução:
Dados da questão:
Dimensão do pátio: 4 m e 5,5 m
Dimensão do lado do ladrilho: 16 cm → 0,16 m
Cálculos:
Área total do pátio = 4 m x 5,5 m = 22 m2
Área do ladrilho = (0,16 m)2 = 0,0256 m2
Quantidade de ladrilhos necessários: 22 m2 : 0,0256 m2 = 859, 375 ladrilhos.
São necessários aproximadamente 859 ladrilhos para cobrir toda a área do pátio da escola.
29) Uma cadeira tem o seu assento na forma de um quadrado. Suponhamos que uma formiga, partindo de um dos cantos da cadeira, andou três metros para contornar todo o assento. Qual é a área do assento da cadeira?
Resolução:
Para solucionar essa questão, devemos realizar o cálculo do perímetro (que é a soma dos lados de um polígono) com a finalidade de descobrir a medida do lado do assento da cadeira. Como o assento é quadrado, todos os seus lados possuem a mesma medida.
P = l + l + l + l
3 = 4l
3/4 = l
0,75 = l
Cada lado do assento da cadeira mede 0,75 metros. Para saber a sua área, vamos utilizar a fórmula para o cálculo de área de um quadrado.
A = l2
A = (0,75 m)2
A = 0,5625 m2
A área do assento da cadeira é de: 0,5625 m2.
30) (PM Pará 2012) A figura abaixo mostra um telhado de uma casa, onde AB = AC, BC = 4 m, AM = 1,5 m, CD = BF = 15 m e M é o ponto médio de BC. Considerando que para cobrir um metro quadrado de telhado são utilizadas 16 telhas, a quantidade de telhas para cobrir esse telhado será de:
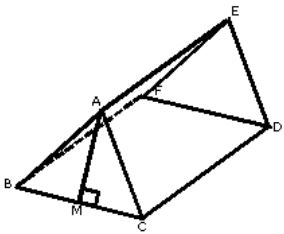 (A) 800
(A) 800
(B) 900
(C) 1000
(D) 1200
(E) 1500
Resolução:
Primeiramente vamos calcular a medida de AC:
Como AB = AC e M é ponto médio de BC, temos que AMC é um triângulo retângulo, onde AC é a hipotenusa, MC = 2 pois BC = 4 e AM = 1,5.
Utilizando o Teorema de Pitágoras:
AC² = MC² + AM²
AC² = 2² + 1,5²
AC² = 4 + 2,25
AC² = 6,25
AC = 2,5m
Agora vamos calcular a área de um dos lados do telhado, depois multiplicar por 2:
Área = AC.CD = 2,5.15 = 37,5m²
2.37,5 = 75m²
Como cada m² equivale a 16 telhas:
16 . 75 = 1200
Alternativa: D
31) (PM-Pará) Um empresário possui um espaço retangular de 110 m por 90 m para eventos. Considerando que cada metro quadrado é ocupado por 4 pessoas, a capacidade máxima de pessoas que esse espaço pode ter é:
(A) 32.400
(B) 34.500
(C) 39.600
(D) 42.500
(E) 45.400
Resolução:
Vamos calcular a área do espaço:
A = 90 x 110 = 9900 m²
Como cabem 4 pessoas por m²:
Capacidade = 4.9900 = 39600
Alternativa: C
32) (PM Pará 2012) Os pontos (2,3), (5,3) e (2,7) são vértices de um triângulo retângulo. A área desse triângulo é:
(A) 5 u.a
(B) 6 u.a
(C) 7 u.a
(D) 8 u.a
(E) 9 u.a
Resolução:
Veja no desenho como fica o triângulo:
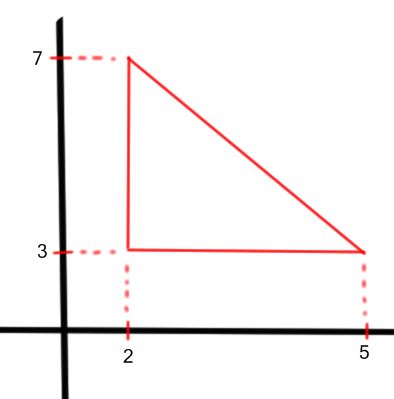
Fórmula para cálculo de área de um triângulo:
base = 5 – 2 = 3
altura = 7 – 3 = 4
A = (b . h) / 2
A = 3 . 4 / 2
A = 6
Alternativa: B
33) (CFO-PM ES–Exatus) Adriana planta flores num canteiro circular de raio 8 m. Ao redor desse canteiro, ela pretende plantar ervas medicinais formando uma coroa circular, de maneira que a parte destinada às flores sofrerá uma redução de 2 m em seu diâmetro. A área ocupada pelas ervas medicinais neste canteiro será igual a:
(A) 14π
(B) 12π
(C) 5π
(D) 15π
Resolução:
Adriana planta em um circulo de raio 8, de onde podemos concluir que o diâmetro mede 16 metros.
Se reduzirmos o diâmetro em 2 metros, passando a medir 14 metros, o raio passará a medir 7 metros.
Assim, a área da coroa circular será a diferença entre a área do circulo de raio 8 e do circulo de raio 7 (Área circunferência = π.r²):
π.8² – π.7² = 64π – 49π = 15π
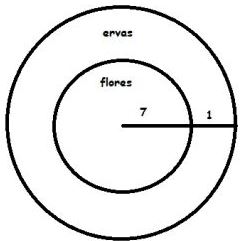
Alternativa: D
34) (PM-ES–Funcab) Um para-raios instalado em um determinado prédio protege uma área circular de raio R = 20 m no solo. O valor total da área do solo, em metros quadrados, protegida por esse para-raios, é de:
(Adote o valor aproximado de π= 3,14)
(A) 1.256 m²
(B) 1.294 m²
(C) 1.306 m²
(D) 1.382 m²
(E) 1.416 m²
Resolução:
Calculando a área do círculo:
Área = π . r²
Área = 3,14 . 20²
Área = 3,14 . 400
Área = 1256
Alternativa: A
35) (PM Acre Músico - Funcab). A área de um triângulo isósceles cujos lados iguais medem 4, e dois de seus ângulos medem 45º, corresponde a:
(A) 4 u.a.
(B) 8 u.a.
(C) 12 u.a.
(D) 16 u.a.
(E) 20 u.a.
Resolução:
Temos um triângulo retângulo (o valor da altura e da base é 4).
A = (b . h) / 2
A = (4 . 4) /2
A = 8
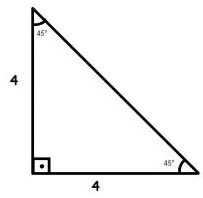
Alternativa: B
36) (Correio–Cespe) Em 2008, nos 200 anos do Banco do Brasil, os Correios lançaram um selo comemorativo com uma tiragem de 1.020.000 unidades. No selo, cujo formato é de um retângulo medindo 40 mm × 30 mm, a estampa ocupa um retângulo que mede 35 mm × 25 mm. Dadas essas condições, é correto afirmar que a área do retângulo da estampa é
(A) superior a 90% da área do retângulo do selo.
(B) inferior a 75% da área do retângulo do selo.
(C) superior a 75% e inferior a 80% da área do retângulo do selo.
(D) superior a 80% e inferior a 85% da área do retângulo do selo.
(E) superior a 85% e inferior a 90% da área do retângulo do selo.
Resolução:
Como estamos trabalhando com porcentagem, não há necessidade de utilizar a medida mm.
Basta dividirmos a área da estampa pela área do selo. Veja:
Alternativa: B
37) (PM-Paraná–Cops) Considere uma placa de trânsito na forma de um hexágono regular com lados de L centímetros. Sabe-se que um hexágono regular de lados L é formado por seis triângulos equiláteros de lados L. Como a leitura desta sinalização (placa) depende da área A da placa, temos que A, em função do comprimento L, é dada por:
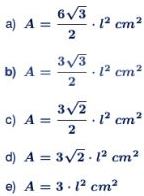
Resolução
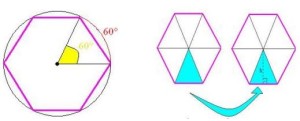
Primeiramente, a área do hexágono é 6x a área do triângulo.
Aplicando o Teorema de Pitágoras, vamos descobrir a altura h do triângulo para descobrirmos sua área:
l² = h² + (l/2)²
l² – l²/4 = h²
(4l² – l²)/4 = h²
3l²/4 = h²
h = l√3/2
Calculando a área:
A∆ = l . l√3/2/2
A∆ = l² √3 /4
A área do hexágono regular será igual a 6 vezes a área do triângulo equilátero.
A = 6 . l² √3/4
A = 3 l² √3 / 2
Alternativa: B
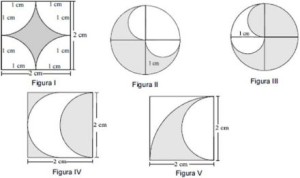
38) (PRF–Cespe) Considerando, em relação às figuras abaixo, que, na figura I, as 4 curvas são quartos de circulo; nas figuras II, III e IV, as curvas são 2 semicírculos; na figura V, aparece 1 quarto de círculo e, interno a ele, um semicírculo, nessa situação, as figuras em que as partes sombreadas têm áreas iguais são:
 (A) I e IV.
(A) I e IV.
(B) I e V.
(C) II e III.
(D) II e V.
(E) III e IV
Resolução
Figura I:
Temos um quadrado com 4 semicírculos inscritos, que resultam em um círculo completo. Então a área sombreada será a área do quadrado menos a área do círculo com raio de 1 cm. Calculando as áreas:
Área do quadrado: 2 x 2 = 4 cm²;
Área do círculo: ∙π 1² = π cm²;
Área sombreada: 4 – π.
Figura II:
A área sombreada é formada por 3/4 da área de um círculo com raio de 1 centímetro, menos a área de 2 semicírculos de raio igual a 1/2 centímetro. Lembre que dois semicírculos formam um círculo. Então:
Área do círculo com raio de 1 cm: π 1² = π cm²;
3/4 da área do círculo anterior: 3π/4
Área do círculo com raio igual de 1/2 cm: π.(1/2)² = π/4
Área sombreada: 3π/4 – π/4 = 2π/4 = π/2cm².
Figura III:
Se o semicírculo sombreado trocar de lugar com o semicírculo brando, a área sombreada será igual a 3/4 da área do círculo de raio de 1 cm. Veja:
Área do círculo de raio de 1 cm: π1² = π cm²;
Área sombreada: 3π/4 cm².
Figura IV
Se encaixarmos o semicírculo sombreado no semicírculo branco, têm-se um retângulo com a metade sombreada e a outra branca. Dessa forma, a área sombreada seria igual a metade da área de um retângulo de 2 x 2. Veja:
Área sombreada: 2.2/2 = 2 cm².
Figura V:
A área sombreada será obtida com a subtração da área de um quarto de círculo de raio igual a 2 centímetro pela metade de um semicírculo de raio igual a 1 centímetro. Calculando as áreas:
Área de 1/4 de círculo de 2 cm de raio: π2²/4 = πcm².
Área de um semicírculo de 1 cm de raio: π1²/2 = π/2cm².
Área sombreada: π – π/2 = π/2 cm².
Alternativa: D
39) (SAP-SP) Ricardo esteve em um lançamento imobiliário onde a maquete, referente aos terrenos, obedecia a uma escala de 1:500. Ricardo se interessou por um terreno de esquina, conforme mostra a figura da maquete.
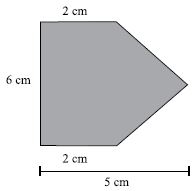 A área, em metros quadrados, desse terreno é de
A área, em metros quadrados, desse terreno é de
(A) 300.
(B) 755.
(C) 120.
(D) 525.
(E) 600.
Resolução
Primeiramente, vamos utilizar a escala 1:500 para sabermos as dimensões reais do terreno:
2cm equivale a 2.500 = 1000cm = 10m
6cm equivale a 6.500 = 3000cm = 30m
5cm equivale a 5.500 = 2500cm = 25m
Sabendo disto, para calcularmos a área é muito simples, basta dividirmos a figura em duas, um retângulo e um triângulo:
O retângulo terá base 30m (6cm) e altura 10m (2cm):
Área = 30 . 10 = 300m²
O triângulo terá base 30m (6cm) e altura 15m (3cm):
Área = 30 . 15/2 = 225m²
Área total = 300 + 225 = 525m²
Alternativa: D
40) O professor Diminoi informou aos seus alunos que usariam um dos 4 símbolos nacionais para reforçarem o cálculo de área e perímetro. Para isto, pediu-lhes que eles analisassem a figura abaixo. Em seguida ela apresentou uma bandeira do Brasil aos alunos, conforme o desenho a seguir, e pediu-lhes que calculassem o quanto foi gasto de tecido para confeccionar as partes verde e amarela presentes nesta bandeira.
 Resolução:
Resolução:
A parte verde tem a forma de um retângulo de medidas 14 cm de altura e 20 cm de base. Sabe-se Área do retângulo = base x altura.
Área do retângulo = 20 ∙ 14 = 280 cm2
A parte amarela tem a forma de um losango.
Área do Losango = diagonal maior ∙ diagonal menor / 2
Diagonal maior do losango = 20 1,7 1,7 = 16,6 cm.
Diagonal menor do losango = 14 1,7 1,7 = 10,6 cm.
Área do losango = 16,6 ∙ 10,6 / 2 = 87,98 cm2
Logo, foi gasto 280 cm2 de tecido verde e 87,98 cm2 de tecido amarelo, na condição de que o losango que representa a parte amarela da bandeira foi costurado sobre a parte verde.
Continua...
































.jpg)
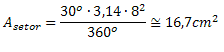

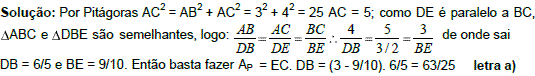

 Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diversas ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.
Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diversas ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.
 Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a
Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a



.jpg)





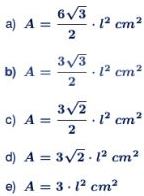

 (A) I e IV.
(A) I e IV.

