MATRIZES
Professor Diminoi

MATRIZES
O crescente uso dos computadores tem feito com que a teoria das matrizes seja cada vez mais aplicada em áreas como Economia, Engenharia, Matemática, Física, dentre outras. Vejamos um exemplo. A tabela a seguir representa as notas de três alunos em uma etapa:
Se quisermos saber a nota do aluno B em Literatura, basta procurar o número que fica na segunda linha e na terceira coluna da tabela.
Considere uma tabela de números dispostos em linhas e colunas, como no exemplo acima, mas colocados entre parênteses ou colchetes:
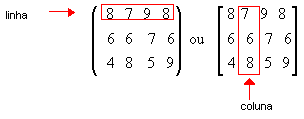 Em tabelas assim dispostas, os números são os elementos. As linhas são enumeradas de cima para baixo e as colunas, da esquerda para direita:
Em tabelas assim dispostas, os números são os elementos. As linhas são enumeradas de cima para baixo e as colunas, da esquerda para direita:
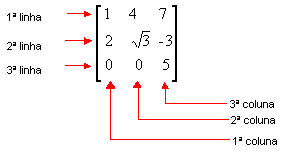
Tabelas com m linhas e n colunas (m e n números naturais diferentes de 0) são denominadas matrizes m x n. Na tabela anterior temos, portanto, uma matriz 3 x 3. Veja mais alguns exemplos:
é uma matriz do tipo 2 x 3
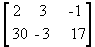
é uma matriz do tipo 2 x 2
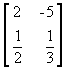
Trata-se de uma representação matemática que inclui em linhas (horizontais) e colunas (verticais) alguns números naturais não-nulos.
Os números, chamados de elementos, são representados entre parênteses, colchetes ou barras horizontais.
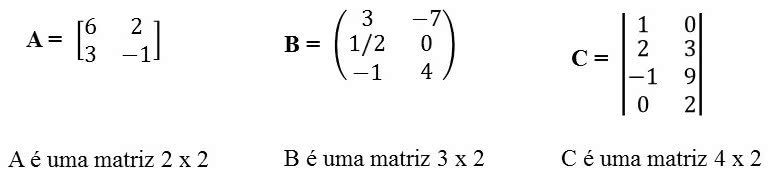
TIPOIS DE MATRIZES
Matrizes Especiais
Há quatro tipos de matrizes especiais:
Matriz Linha
Formada por uma única linha, por exemplo:
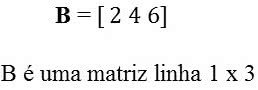
Matriz Coluna
Formada por uma única coluna, por exemplo:

Matriz Nula
Formada por elementos iguais a zero, por exemplo:
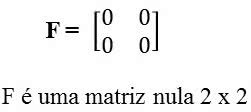
Matriz Quadrada
Formada pelo mesmo número de linhas e colunas, por exemplo:
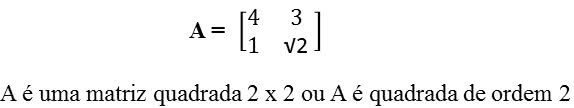
Matriz Transposta
A matriz transposta (indicada pela letra t) é aquela que apresenta os mesmos elementos de uma linha ou coluna comparada com outra matriz.
No entanto, os elementos iguais entre as duas são invertidos, ou seja, a linha de uma apresenta os mesmos elementos que a coluna de outra. Ou ainda, a coluna de uma possui os mesmos elementos da linha de outra.
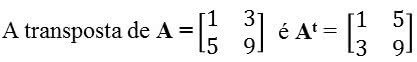
Matriz Oposta
Na matriz oposta, os elementos entre duas matrizes apresentam sinais diferentes, por exemplo:
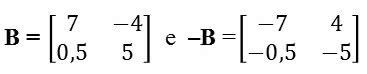
Matriz Identidade
A matriz identidade ocorre quando os elementos da diagonal principal são todos iguais a 1 e os outros elementos são iguais a 0 (zero):

Matriz Inversa
A matriz inversa é uma matriz quadrada. Ela ocorre quando o produto de duas matrizes for igual a uma matriz identidade quadrada de mesma ordem.
A . B = B . A = In (quando a matriz B é inversa da matriz A)
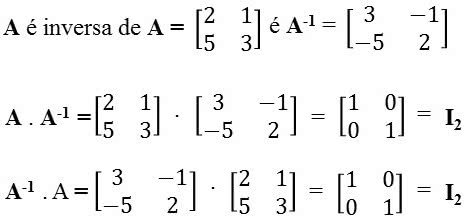
Observação: Para encontrar a matriz inversa utiliza-se a multiplicação de matrizes.
Igualdade de Matrizes
Quando temos matrizes iguais, os elementos das linhas e das colunas são correspondentes:

Determinante de uma matriz
Matriz de ordem 2
O determinante de ordem dois possui uma diagonal principal e uma diagonal secundária.
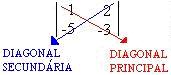 Exemplo:
Exemplo:
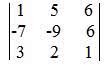 Assim, para calcular o Determinante da Matriz Quadrada:
Assim, para calcular o Determinante da Matriz Quadrada:
Deve se repetir as 2 primeiras colunas
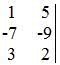
Encontrar as diagonais e multiplicar os elementos, não esquecendo de trocar o sinal no resultado da diagonal secundária:
Diagonal principal (da esquerda para a direita): (1,-9,1) (5,6,3) (6,-7,2)
Diagonal secundária (da direita para a esquerda): (5,-7,1) (1,6,2) (6,-9,3)
Portanto, o Determinante da matriz 3 x 3 = 182.
Propriedades das matrizes e dos determinantes
- O determinante de uma matriz quadrada A é igual ao determinante da sua transposta: det (A) = det (At);
- Caso exista uma linha ou coluna na matriz igual a zero, o determinante é zero;
- Caso exista duas filas paralelas, iguais ou proporcional, o determinante é zero;
- O determinante do produto de um número real k por uma matriz A é igual ao produto de k elevado a n, onde n é o número de linhas de A, pelo determinante de A: det (k . A) = kn . det (A);
- Caso os elementos abaixo ou acima da diagonal principal forem nulos, o determinante será o produto dos elementos da diagonal principal;
Teorema de Binet: Seja A e B matrizes quadradas de ordem n, o determinante do produto de A por B é igual ao produto dos determinantes de A e B.
Exercícios resolvidos
01) O cálculo do seu valor numérico é feito pela diferença do produto da diagonal principal com o produto da diagonal secundária.
Resolução:
det A =
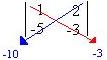
= - 3 – (- 10) = - 3 + 10 = 7
02) Dada a matriz baixo encontre o valor do seu determinante
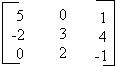 Resolução:
Resolução:
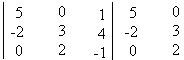
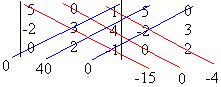 Deve-se pegar o oposto dos produtos das diagonais secundárias e somar com os produtos das diagonais principais.
Deve-se pegar o oposto dos produtos das diagonais secundárias e somar com os produtos das diagonais principais.
Det B = – (0 + 40 + 0) –15 + 0 – 4 = – 40 – 19 = – 59
Essa regra utilizada no cálculo do determinante de matriz de ordem 3 é chamada de Regra de Sarrus.
03) Determinante de uma matriz A de ordem 2 x 2.
.jpg) Resolução:
Resolução:
Diagonal principal: 2 . 6 = 12
Diagonal secundária: 9 . (–1) = – 9
DetA = 12 – (–9)
DetA = 12 + 9
DetA = 21
04 Determinante de uma matriz B de ordem 3 x 3.
Resolução:
Regra de Sarrus
.jpg) Diagonal principal
Diagonal principal
2 . 6 . 3 = 36
5 . 7 . (–1) = – 35
6 . 1 . 2 = 12
Soma
36 + (–35) + 12
36 – 35 + 12
48 – 35
13
Diagonal secundária
6 . 6 . (–1) = –36
2 . 7 . 2 = 28
5 . 1 . 3 = 15
Soma
–36 + 28 + 15
–36 + 43
7
DetB = 13 – 7
DetB = 6
05) Calcule o determinante da matriz abaixo:
 Resolução:
Resolução:
A matriz M é quadrada de ordem 2 x 2. Assim, seu determinante será dado por:
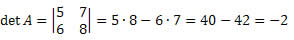
06) Calcule o determinante da matriz
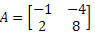 Resolução:
Resolução:
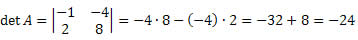
07) Dada a matriz M3 x 3 abaixo, calcule seu determinante.
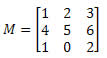 Resolução:
Resolução:
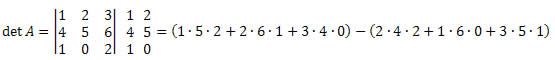 det A = (10+12+0) - (16+0+15)=22-31 = -9
det A = (10+12+0) - (16+0+15)=22-31 = -9
08) Calcule o determinante da matriz 3 x 3 abaixo:
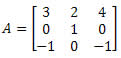 Resolução:
Resolução:
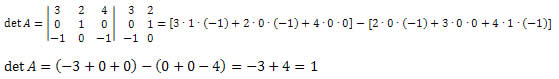
09) (Unicap – PE) Calcule o valor de x, a fim de que o determinante da matriz A seja nulo.
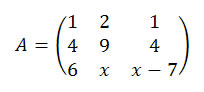 Resolução:
Resolução:
Aplicando a regra de Sarrus, temos que o determinante será da seguinte forma.
.jpg)
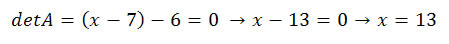
10) (U.F. Ouro Preto – MG) Considere a matriz:
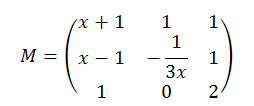 Resolução:
Resolução:
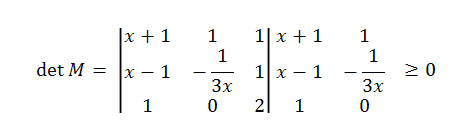
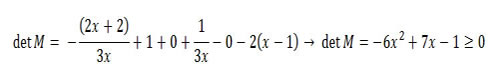 Conclusão: ao resolver esta desigualdade obteremos o seguinte conjunto solução:
Conclusão: ao resolver esta desigualdade obteremos o seguinte conjunto solução:
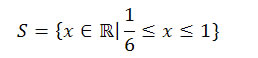
11) Determine o valor de x para que o determinante da matriz A seja igual a 8.
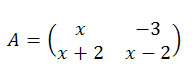 Resolução:
Resolução:
.jpg) Ou seja, temos dois valores para x que fazem com que o determinante da matriz A seja igual a 8.
Ou seja, temos dois valores para x que fazem com que o determinante da matriz A seja igual a 8.
.jpg)
12) O determinante da matriz A é igual a -2. Se B e C são as matrizes obtidas, respectivamente, pela substituição em A do menor e do maior valor de y encontrados, calcule a matriz transposta do produto de B por C.
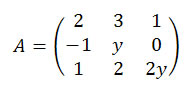 Resolução:
Resolução:
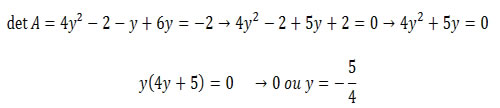 Façamos as matrizes B e C.
Façamos as matrizes B e C.
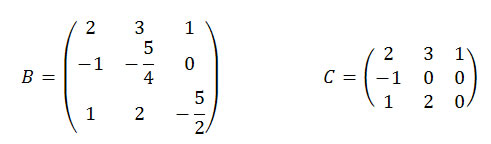
.jpg)
15) (Unicamp - SP) Seja a um número real e seja:
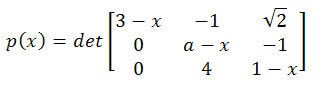 a) Para a = 1, encontre todas as raízes da equação p(x) = 0
a) Para a = 1, encontre todas as raízes da equação p(x) = 0
b) Encontre os valores de a para os quais a equação p(x) = 0 tem uma única raiz real.
Resolução:
a) Façamos o determinante com o valor de a = 1:
.jpg) Temos o produto de duas parcelas igual a zero, então teremos duas situações:
Temos o produto de duas parcelas igual a zero, então teremos duas situações:
3 - x = 0 ou (1 - x) 2 + 4 = 0
Na primeira temos que x = 3; na segunda não é possível determinar uma solução.
Logo, temos apenas uma raiz possível quando a for igual a 1.
b)
.jpg)
Novamente teremos duas situações: uma onde x=3 e a outra temos que determinar para quais valores de a teremos apenas a solução x = 3:
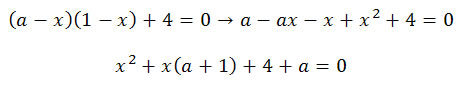 Para que só exista uma única raiz, essa equação do segundo grau não deve ter raiz, ou seja, seu discriminante deve ser menor que zero.
Para que só exista uma única raiz, essa equação do segundo grau não deve ter raiz, ou seja, seu discriminante deve ser menor que zero.


Determinante para matrizes de ordem 4 ou superior
Para calcularmos o determinante de matrizes de ordem igual ou superior a 4×4, devemos utilizar o teorema de Laplace para o cálculo do determinante dessas matrizes.
É importante lembrar que o teorema de Laplace pode ser aplicado em matriz de ordem nxn, com n > 1, porém, matriz de ordem 2×2 e 3×3, as regras anteriores ensinadas são mais eficientes, isto é, dão menos trabalho para calcular.
Antes de mostrarmos o teorema de Laplace precisamos entender alguns conceitos que precisamos saber para entender o teorema.
Menor complementar (Dij)
O menor complementar de um elemento aij, em uma matriz A, é obtido eliminando a linha i e coluna j de aij. Dessa forma, teremos uma matriz de ordem n – 1, e o determinante Dij dessa matriz é o menor complementar do elemento aij.
Cofator ou complemento algébrico (Aij)
Chamamos de cofator ou complemento algébrico de um elemento aij, para matrizes de ordem n, isto é, matrizes quadradas, um número Aij, de forma que:
Aij = (-1)i + j . Dij
Teorema de Laplace
Nos cálculos dos determinantes, as regras práticas se estendem, em sua maioria, apenas para as matrizes quadradas de ordem igual ou menor que três. Para calcular o determinante das demais, é necessário usar o teorema de Laplace.
Para o cálculo de determinantes de matrizes quadradas de ordem menor ou igual a 3 (n≤3), temos algumas regras práticas para realizar estes cálculos. Entretanto, quando a ordem é superior a 3 (n>3), muitas destas regras não são aplicáveis.
Por isso veremos o teorema de Laplace, que, utilizando o conceito do cofator, conduz o cálculo dos determinantes para regras que se aplicam a quaisquer matrizes quadradas.
O teorema de Laplace consiste em escolher uma das filas (linha ou coluna) da matriz e somar os produtos dos elementos dessa fila pelos seus respectivos cofatores.
Ilustração algébrica:
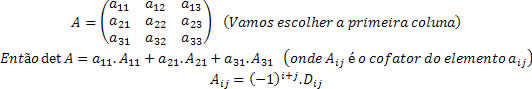 Calcule o determinante da matriz C, utilizando o teorema de Laplace:
Calcule o determinante da matriz C, utilizando o teorema de Laplace:
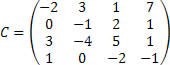 De acordo com o teorema de Laplace, devemos escolher uma fila (linha ou coluna) para calcular o determinante. Vamos utilizar a primeira coluna:
De acordo com o teorema de Laplace, devemos escolher uma fila (linha ou coluna) para calcular o determinante. Vamos utilizar a primeira coluna:
Precisamos encontrar os valores dos cofatores:
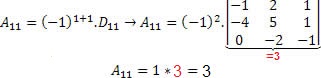
.jpg)
.jpg)
Sendo assim, pelo teorema de Laplace, o determinante da matriz C é dado pela seguinte expressão:
.jpg)
Note que não foi preciso calcular o cofator do elemento da matriz que era igual a zero, afinal, ao multiplicarmos o cofator, o resultado seria zero de qualquer forma. Diante disso, quando nos depararmos com matrizes que possuem muitos zeros em alguma de suas filas, a utilização do teorema de Laplace se torna interessante, pois não será necessário calcular diversos cofatores.
Vejamos um exemplo deste fato:
Calcule o determinante da matriz B, utilizando o teorema de Laplace:
.jpg)
Veja que a segunda coluna é a fila que possui maior quantidade de zeros, portanto utilizaremos esta fila para calcular o determinante da matriz através do teorema de Laplace.
Portanto, para determinar o determinante da matriz B, basta encontrar o cofator A22.
.jpg)
Sendo assim, podemos finalizar os cálculos do determinante:
det B = (- 1) . (- 65) = 65
Regra de Chió nos cálculos dos determinante
Os conceitos aprendidos sobre o cálculo do determinante se aplicam com facilidade em matrizes com ordem menor ou igual a três (Exemplo: A3x3). Contudo, nem todas as matrizes serão com esta ordem. Para isso, necessitamos de um dispositivo para nos auxiliar quanto aos determinantes de matrizes com ordem maior que três.
A regra de Chió nos ajuda a construir uma matriz com determinante igual a uma matriz dada, entretanto com a ordem menor. Em uma linguagem matemática, a regra de Chió nos permite calcular o determinante de uma matriz de ordem n através de uma matriz de ordem n-1 (uma ordem abaixo).
Existe uma condição importante para a aplicação do processo da regra de Chió, sendo que o primeiro elemento da matriz, o elemento a11 deve ser igual a 1. Tendo isso, é possível aplicar o processo da regra de Chió de modo a obter uma matriz com ordem menor.
A regra de Chió é dada da seguinte forma:
Suprima a primeira linha e a primeira coluna da matriz.
Dos elementos que restaram na matriz, subtraia o produto dos dois elementos suprimidos (um da linha e o outro da coluna) correspondente a este elemento restante. Por exemplo, no elemento a23 você realizará o produto do elemento da segunda linha da coluna que foi suprimida pelo elemento da terceira coluna da linha que foi suprimida.
Com os resultados das subtrações realizadas no passo anterior, será obtida uma nova matriz, com ordem menor, entretanto com determinante igual à matriz original.
Vale ressaltar novamente que para que o determinante continue o mesmo, o a11 tem que ser igual a 1.
Para uma melhor compreensão destes passos, vejamos um exemplo utilizando o processo da regra de Chió.
.png)
Temos uma matriz quadrada de ordem 5. Sabemos que não é possível aplicar a regra de Sarrus para calcular este determinante, com isso buscaremos baixar a ordem desta matriz. Desse modo, a fim de encontrar seu valor, utilizaremos alguma propriedade de determinantes.
Veja que o primeiro elemento da matriz equivale a 1 (a11=1), logo, é possível aplicar a regra de Chió. Façamos o procedimento:
.png)
Destacamos os elementos que serão suprimidos; agora iremos montar a nossa matriz de menor ordem seguindo o segundo passo da regra:
.png)
.png)
.png)
.jpg)
De tal modo, obtemos o determinante da matriz inicial A5x5. Note que nenhuma das matrizes é igual, mas, pela regra de Chió, podemos afirmar que o determinante de todas elas é o mesmo.
.png)
Veja que aplicamos duas vezes a regra de Chió, mas isso foi porque o primeiro elemento era igual a 1. Em casos em que o elemento não seja igual a 1, podemos aplicar algumas propriedades de determinantes de forma a encontrar uma matriz em que o primeiro elemento seja igual a 1.
Continua....









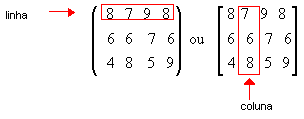 Em tabelas assim dispostas, os números são os elementos. As linhas são enumeradas de cima para baixo e as colunas, da esquerda para direita:
Em tabelas assim dispostas, os números são os elementos. As linhas são enumeradas de cima para baixo e as colunas, da esquerda para direita:
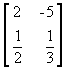
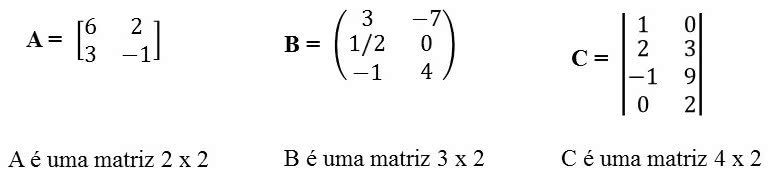
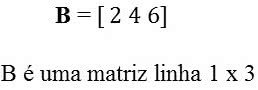

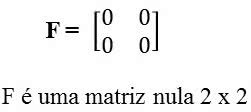
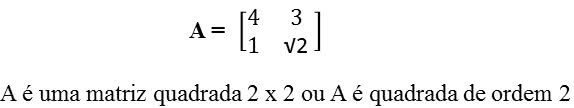
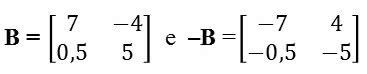

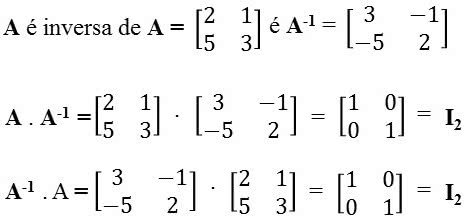

 Exemplo:
Exemplo: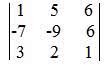 Assim, para calcular o Determinante da Matriz Quadrada:
Assim, para calcular o Determinante da Matriz Quadrada: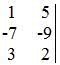

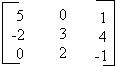
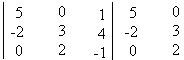

.jpg)
.jpg)
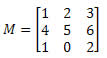
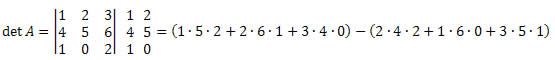
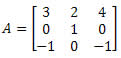
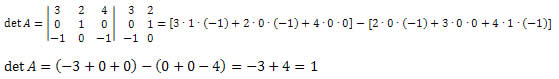
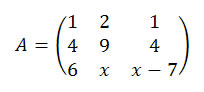
.jpg)
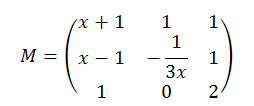
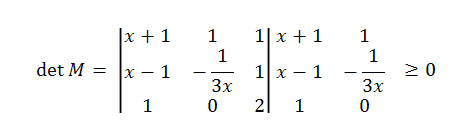
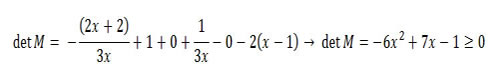
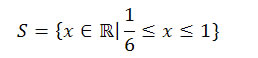
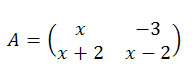
.jpg)
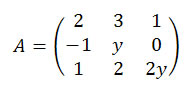
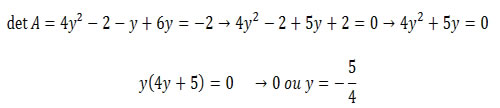
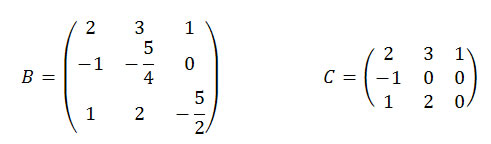
.jpg)
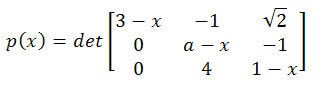 a) Para a = 1, encontre todas as raízes da equação p(x) = 0
a) Para a = 1, encontre todas as raízes da equação p(x) = 0.jpg)
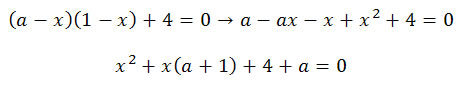


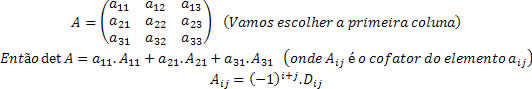 Calcule o determinante da matriz C, utilizando o teorema de Laplace:
Calcule o determinante da matriz C, utilizando o teorema de Laplace: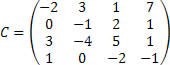 De acordo com o teorema de Laplace, devemos escolher uma fila (linha ou coluna) para calcular o determinante. Vamos utilizar a primeira coluna:
De acordo com o teorema de Laplace, devemos escolher uma fila (linha ou coluna) para calcular o determinante. Vamos utilizar a primeira coluna: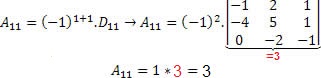
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.png)
.png)
.png)
.png)
.png)
.jpg)
.png)
