Professor Diminoi
TERMOLOGIA Termologia (termo = calor, logia = estudo)
Termologia (termo = calor, logia = estudo)
É a parte da Física encarregada de estudar o calor e seus efeitos sobre a matéria. A termologia está intimamente ligada à energia térmica, estudando a transmissão dessa energia e os efeitos produzidos por ela quando é fornecida ou retirada de um corpo. Temperatura
Temperatura
É a grandeza que mede o estado de agitação das moléculas. Quanto mais quente estiver uma matéria, mais agitadas estarão suas moléculas. Assim, a temperatura é o fator que mede a agitação dessas moléculas, determinando se uma matéria está quente, fria, etc. Calor
Calor
É a energia que flui de um corpo com maior temperatura para outro de menor temperatura. (energia térmica em transito) Como sabemos, a unidade de representação de qualquer forma de energia é o joule (J), porém, para designar o calor, é adotada uma unidade prática denominada caloria, em que 1 cal = 4,186 J. Equilíbrio térmico
Equilíbrio térmico
Ocorre quando dois corpos com temperaturas diferentes são colocados em contato, estes trocam calor até que estejam na mesma temperatura. Nesse momento, dizemos que os corpos atingiram o equilíbrio térmico. Lembrando que o calor é a energia em transito e passa do corpo mais quente para o mais frio.
Energia interna de um sistema (U)
As partículas de um sistema têm vários tipos de energia, e a soma de todas elas é o que chamamos Energia interna de um sistema. Para que este somatório seja calculado, são consideradas as energias cinéticas de agitação, potencial de agregação, de ligação e nuclear entre as partículas. Nem todas estas energias consideradas são térmicas. Ao ser fornecida a um corpo energia térmica, provoca-se uma variação na energia interna deste corpo. Esta variação é no que se baseiam os princípios da termodinâmica. Ou seja, a energia interna é a energia que um sistema de partículas possui em virtude tanto do seu grau de agitação, quanto da sua interação.
Nem todas estas energias consideradas são térmicas. Ao ser fornecida a um corpo energia térmica, provoca-se uma variação na energia interna deste corpo. Esta variação é no que se baseiam os princípios da termodinâmica. Ou seja, a energia interna é a energia que um sistema de partículas possui em virtude tanto do seu grau de agitação, quanto da sua interação. 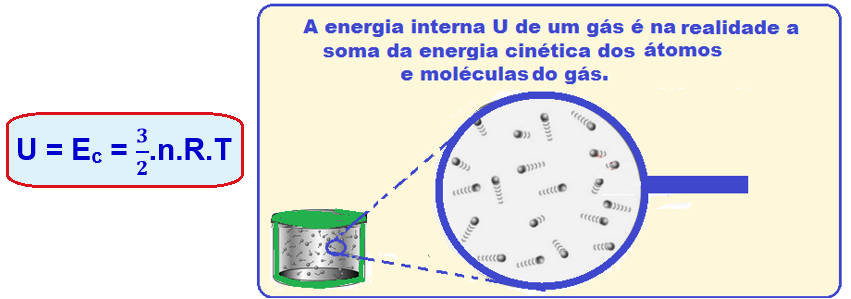
Energia interna de um sistema (U) é a soma das energias cinética e potencial das partículas que constituem um gás. Esta energia é uma característica do estado termodinâmico e deve ser considerada como mais uma variável que pode ser expressa em termos de pressão, volume, temperatura e número de mols.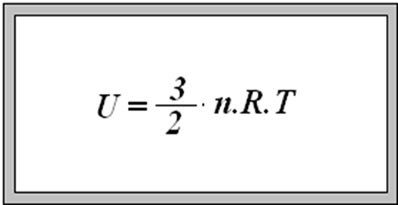 Onde:
Onde:
U = energia interna do gás;
n = número de mol do gás;
R = constante universal dos gases perfeitos;
T = temperatura absoluta (kelvin).
Equilíbrio térmico
É o estado em que a temperatura de dois ou mais corpos são iguais. Assim, quando um corpo está em equilíbrio térmico em relação a outro, cessam os fluxos de troca de calor entre eles.
 TERMOMETRIA
TERMOMETRIA
É a parte de termologia que se preocupa com a medida da temperatura e o instrumento utilizado para medir a temperatura é o termômetro.
ESCALAS TERMOMÉTRICAS
Escala Celsius
É a escala usada no Brasil e na maior parte dos países, oficializada em 1742 pelo astrônomo e físico sueco Anders Celsius (1701-1744). Esta escala tem como pontos de referência a temperatura de congelamento da água sob pressão normal (0°C) e a temperatura de ebulição da água sob pressão normal (100°C). Curiosidade: quando Anders Celsius (1701 – 1744) criou a escala de Celsius, inventou de forma contrária que, o 0°C seria o ponto de ebulição da água e 100°C seria o ponto de congelamento. Isso foi revertido no ano de sua morte por Carolus Linnaeus.
Curiosidade: quando Anders Celsius (1701 – 1744) criou a escala de Celsius, inventou de forma contrária que, o 0°C seria o ponto de ebulição da água e 100°C seria o ponto de congelamento. Isso foi revertido no ano de sua morte por Carolus Linnaeus.
Escala Fahrenheit
Outra escala bastante utilizada, principalmente nos países de língua inglesa, principalmente Estados Unidos e Inglaterra criada em 1708 pelo físico alemão Daniel Gabriel Fahrenheit (1686-1736). Esta escala tem como pontos de referência a temperatura de congelamento da água sob pressão normal (32°F) e a temperatura de ebulição da água sob pressão normal (212°F). Escala Kelvin
Escala Kelvin
Também conhecida como escala absoluta, foi verificada pelo físico inglês William Thompson (1824-1907), também conhecido como Lorde Kelvin. Esta escala tem como pontos de referência a temperatura de congelamento da água sob pressão normal (273K) e a temperatura de ebulição da água sob pressão normal (373K). Esta escala só os cientistas que usam em laboratórios, para seus cálculos em fins científicos. Obervação: por convenção, não se usa "grau" para esta escala, ou seja 0 K, lê-se zero kelvin e não zero grau kelvin. Em comparação com a escala Celsius:
Obervação: por convenção, não se usa "grau" para esta escala, ou seja 0 K, lê-se zero kelvin e não zero grau kelvin. Em comparação com a escala Celsius: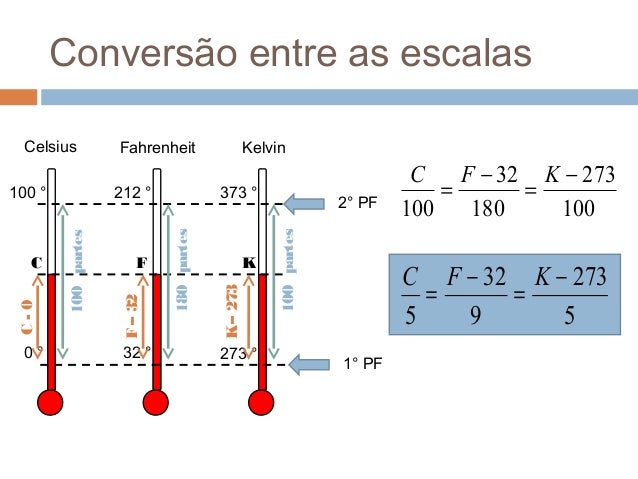 O que são graus Rankine?
O que são graus Rankine?
Os graus Rankine (com o símbolo ºR ou ºRa) foram propostos no séc. XIX. Foi William John Macquorn Rankine, físico escocês, que deu nome a esta escala de temperatura. Assim, 0ºR é o zero absoluto da escala. A variação de um grau Rankine é equiparável à variação de um grau Fahrenheit, por exemplo. Não é uma medida muito utilizada, mas ainda se pode ver em alguns campos na área da engenharia, nomeadamente nos Estados Unidos da América.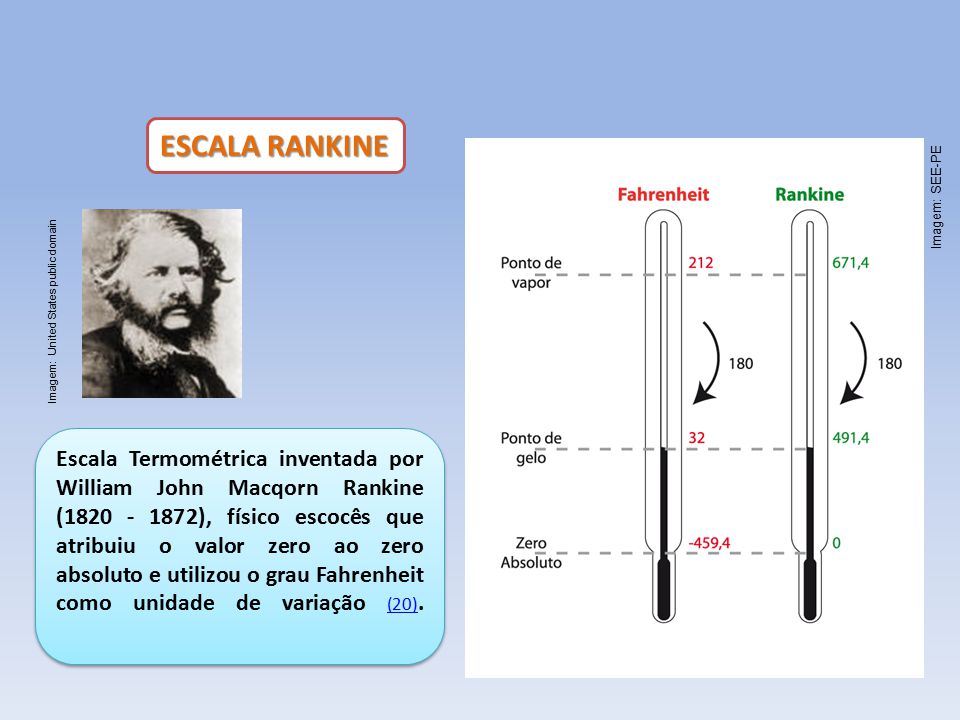 O que são graus Réaumur?Os pontos fixos da escala Réaumur (ºRe ou ºRé) são o ponto de congelamento da água (que corresponde a 0°Ré) e o seu ponto de ebulição (a 80°Ré). O termómetro deverá conter álcool diluído e foi construído sob o princípio de tomar o ponto de congelamento da água como zero. A escala Réaumur é uma escala de temperatura proposta pelo físico francês René-Antoine Ferchault de Réaumur.
O que são graus Réaumur?Os pontos fixos da escala Réaumur (ºRe ou ºRé) são o ponto de congelamento da água (que corresponde a 0°Ré) e o seu ponto de ebulição (a 80°Ré). O termómetro deverá conter álcool diluído e foi construído sob o princípio de tomar o ponto de congelamento da água como zero. A escala Réaumur é uma escala de temperatura proposta pelo físico francês René-Antoine Ferchault de Réaumur. RESOLVIDOS – ESCALAS TERMOMÉTRICAS
RESOLVIDOS – ESCALAS TERMOMÉTRICAS
01) (ITA) O verão de 1994 foi particularmente quente nos Estados Unidos da América. A diferença entre a máxima temperatura do verão e a mínima do inverno anterior foi de 60ºC.
Qual o valor dessa diferença na escala Fahrenheit?
(A) 33ºF
(B) 60ºF
(C) 92ºF
(D) 108ºF
(E) 140ºF
Resolução:
Para fazer a conversão da escala Celsius para a escala Fahrenheit, usa-se a seguinte fórmula:
ΔTC/5 = ΔTF/9
Substituindo 60°C da equação acima, temos
60/5 = ΔTF/9
12 = ΔTF/9
ΔTF = 12.9
ΔTF = 108 °F
Alternativa: D
02) (Unesp 2003) Uma panela com água é aquecida de 25°C para 80°C. A variação de temperatura sofrida pela panela com água, nas escalas Kelvin e Fahrenheit, foi de:
(A) 32 K e 105°F.
(B) 55 K e 99°F.
(C) 57 K e 105°F.
(D) 99 K e 105°F.
(E) 105 K e 32°F.
Resolução:
Primeiro precisamos saber qual foi a variação na escala Celsius. Esse valor é obtido através da diferença entre o valor final e o valor inicial:
ΔC = C2 - C1
ΔC = 80-25
ΔC = 55 °C
Quando a temperatura varia 1° na escala Celsius, ela sofre a mesma variação na escala Kelvin. Portanto, se a variação foi de 55° na escala Celsius, também foi de 55 em na escala Kelvin.
Na escala Fahrenheit, essa mesma variação é dada por:
C/5 = F/9
Substituindo C por 55, temos:
55/5 = F/9
11 = F/9
F = 9.11
F = 99 °F
Alternativa: B
03) Julgue as afirmações abaixo:
I – A escala Celsius atribui 0° para o ponto de fusão do gelo e 100º para o ponto de ebulição da água;
II – O limite inferior para a escala Kelvin corresponde aproximadamente - 273°C;
III – 1°C equivale a 1°F.
Estão corretas:
(A) I e II apenas
(B) I e III apenas
(C) I, II e III
(D) II e III apenas
(E) I apenas
Resolução:
A afirmação I porque a escala Celsius atribui 0° para o ponto de fusão do gelo e 100º
A afirmativa II está correta porque o limite inferior da escala Kelvin é o zero absoluto, que corresponde a - 273°C.
A Afirmação III está errada
Alternativa: A
04) Existe uma temperatura que tem o mesmo valor na escala Celsius e na escala Fahrenheit. Qual é essa temperatura?
Resolução:
C/5 = F – 32/9
Se F = C, podemos reescrever a equação
C/5 = C – 32/9
9C = 5(C-32)
9C = 5C - 160
9C - 5C = -160
4C = -160
C = -160/4
C = - 40º
A temperatura que coincide nas escalas Celsius e Fahrenheit é - 40°.
05) (Mackenzie SP/2006) Um viajante, ao desembarcar no aeroporto de Londres, observou que o valor da temperatura do ambiente na escala Fahrenheit é o quíntuplo do valor da temperatura na escala Celsius.
Essa temperatura é de:
(A) 5°C
(B) 10 °C
(C) 15 °C
(D) 20 °C
(E) 25 °C
Resolução:
Chamando essa temperatura na escala Celsius de x, temos:
C = x
F = 5x
A fórmula de conversão entre as duas escalas é:
C/5 = (F – 32)/9
Substituindo, temos:
x/5 = (5x – 32)/9
Multiplicando cruzado, temos:
9x = 25x – 160. Isolando x, temos:
-16x = -160
x = -160/-16
x = 10
Logo C = 10°C e F = 50 °F
Alternativa: B
06) (UFAC/AC/2004) Uma variação de temperatura de 300K equivale na escala Fahrenheit à uma variação de:
(A) 540 ºF
(B) 54 ºF
(C) 300 ºF
(D) 2700 ºF
(E) n.d.a
Resolução:
ΔK/100 = ΔF/180
300/100 = ΔF/180
3 = ΔF/180
ΔF = 540 °F
Alternativa: A
07) A temperatura é uma grandeza física que mede:
(A) grau de agitação das moléculas
(B) calor
(C) pressão
(D) volume
(E) densidade
Resolução:
A temperatura é a medida do grau de agitação das moléculas de um corpo.
Alternativa: A
08) O calor é definido como uma energia térmica que flui entre os corpos. O fluxo de calor entre dois corpos em contato se deve inicialmente a:
(A) temperaturas dos corpos serem iguais
(B) temperatura dos corpos serem diferentes
(C) os corpos estarem muito quentes
(D) os corpos estarem muito frios
(E) nda
Resolução:
O calor será trocado entre os corpos até que ocorra o equilíbrio térmico entre eles.
Alternativa: B
09) Maria usou um livro de receitas para fazer um bolo de fubá. Mas, ao fazer a tradução do livro do inglês para o português, a temperatura permaneceu em Fahrenheit (ºF). A receita disse que o bolo deve ser levado ao forno a 392 ºF e permanecer nessa temperatura por 30 minutos. Qual é a temperatura em graus Celsius que Maria deve deixar o forno para não errar a receita?
Resolução:
Para resolver essa questão, podemos usar a seguinte expressão:
ºC = (ºF – 32)
1,8
Assim, temos:
ºC = (392– 32) = 200 ºC
1,8
10) (ENEM) Em um experimento foram utilizadas duas garrafas PET, uma pintada de branco e a outra de preto, acopladas cada uma a um termômetro. No ponto médio da distância entre as garrafas, foi mantida acesa, durante alguns minutos, uma lâmpada incandescente. Em seguida a lâmpada foi desligada. Durante o experimento, foram monitoradas as temperaturas das garrafas: a) enquanto a lâmpada permaneceu acesa e b) após a lâmpada ser desligada e atingirem equilíbrio térmico com o ambiente.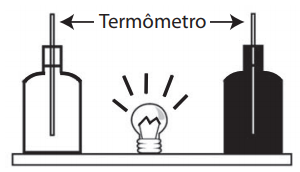 Esquema que representa duas garrafas sendo aquecidas por uma lâmpada incandescente
Esquema que representa duas garrafas sendo aquecidas por uma lâmpada incandescente
A taxa de variação da temperatura da garrafa preta, em comparação à da branca, durante todo experimento, foi
(A) igual no aquecimento e igual no resfriamento.
(B) maior no aquecimento e igual no resfriamento.
(C) menor no aquecimento e igual no resfriamento.
(D) maior no aquecimento e menor no resfriamento.
(E) maior no aquecimento e maior no resfriamento.
Resolução
As cores das garrafas determinam a sua capacidade de absorver energia, que, nesse caso, é o calor. A cor branca reflete praticamente todo o calor que recebe, absorvendo pouco calor. Já a cor preta absorve a maior parte da energia que recebe.
Sendo assim, enquanto a luz permanecer acesa, a garrafa preta absorverá mais calor e aumentará mais a sua temperatura em comparação à garrafa branca.
Quando a lâmpada é desligada, a garrafa preta, que estava mais aquecida, emite mais calor do que a garrafa branca. Portanto, também varia mais a sua temperatura.
Observação: a variação da temperatura da garrafa preta, em comparação à da branca, será maior no aquecimento e maior no resfriamento.
Alternativa: E
12) (ENEM) Uma garrafa térmica tem como função evitar a troca de calor entre o líquido nela contido e o ambiente, mantendo a temperatura de seu conteúdo constante. Uma forma de orientar os consumidores na compra de uma garrafa térmica seria criar um selo de qualidade, como se faz atualmente para informar o consumo de energia de eletrodomésticos. O selo identificaria cinco categorias e informaria a variação de temperatura do conteúdo da garrafa, depois de decorridas seis horas de seu fechamento, por meio de uma porcentagem do valor inicial da temperatura de equilíbrio do líquido na garrafa.
O quadro apresenta as categorias e os intervalos de variação percentual da temperatura. Para atribuir uma categoria a um modelo de garrafa térmica, são preparadas e misturadas, em uma garrafa, duas amostras de água, uma a 10°C e outra a 40°C, na proporção de um terço de água fria para dois terços de água quente. A garrafa é fechada. Seis horas depois, abre-se a garrafa e mede-se a temperatura da água, obtendo-se 16°C.
Para atribuir uma categoria a um modelo de garrafa térmica, são preparadas e misturadas, em uma garrafa, duas amostras de água, uma a 10°C e outra a 40°C, na proporção de um terço de água fria para dois terços de água quente. A garrafa é fechada. Seis horas depois, abre-se a garrafa e mede-se a temperatura da água, obtendo-se 16°C.
Qual selo deveria ser posto na garrafa térmica testada?
(A) A
(B) B
(C) C
(D) D
(E) E
Resolução:
Cálculo da temperatura final de equilíbrio, considerando que não há perda de calor com o meio exterior:
Qfria + Qquente = 0
(m/3) . cágua.(θf - 10) + (2m/3).cágua.(θf - 40) = 0
θf = 30 °C
Variação porcentual de temperatura em 6h:
(θf - θ) / θf
(30°C - 16°C) / 30°C
≅ 0,47 = 47%
Resposta: D
13) (ENEM) Um motor só poderá realizar trabalho se receber uma quantidade de energia de outro sistema. No caso, a energia armazenada no combustível é, em parte, liberada durante a combustão para que o aparelho possa funcionar. Quando o motor funciona, parte da energia convertida ou transformada na combustão não pode ser utilizada para a realização de trabalho. Isso significa dizer que há vazamento da energia em outra forma.
De acordo com o texto, as transformações de energia que ocorrem durante o funcionamento do motor são decorrentes de a:
(A) liberação de calor dentro do motor ser impossível.
(B) realização de trabalho pelo motor ser incontrolável.
(C) conversão integral de calor em trabalho ser impossível.
(D) transformação de energia térmica em cinética ser impossível.
(E) utilização de energia potencial do combustível ser incontrolável.
Resolução:
O calor cedido para a fonte quente em uma máquina térmica é transferido em parte para a realização de trabalho, sendo o restante fornecido para a fonte fria. Pelo Teorema da Conservação da Energia, em um modelo real e não ideal, é impossível a conversão total do calor da fonte quente em trabalho, parcela da energia é dissipada em forma sonora, atrito, etc.
Alternativa: C
15) Qual é a temperatura na escala Fahrenheit que corresponde a 40ºC?
(A) 313.
(B) 4,444.
(C) 39,2.
(D) 2,25.
(E) 104.
Resolução:
ºC = (ºF – 32)
1,8
40 = (ºF – 32)
1,8
40 . 1,8 = ºF – 32
72 = ºF – 32
ºF = 72 + 32
ºF = 104
Alternativa: E
16) (ITA-SP) O verão de 1994 foi particularmente quente nos Estados Unidos da América. A diferença entre a máxima temperatura do verão e a mínima do inverno anterior foi de 60ºC.
Qual o valor desta diferença na escala Fahrenheit?
(A) 108ºF
(B) 60ºF
(C) 140ºF
(D) 33ºF
(E) 92ºF
Resolução:
ºC = (ºF – 32)
1,8
60 = (ºF – 32)
1,8
60 . 1,8 = ºF – 32
108 = ºF – 32
ºF = 108 + 32
ºF = 140
Alternativa: C
17) UNESP-SP) Um estudante desenvolve um termômetro para ser utilizado especificamente em seus trabalhos de laboratório.
Sua idéia é medir a temperatura de um meio fazendo a leitura da resistência elétrica de um resistor, um fio de cobre, por exemplo, quando em equilíbrio térmico com esse meio. Assim, para calibrar esse termômetro na escala Celsius, ele toma como referências as temperaturas de fusão do gelo e de ebulição da água.
Depois de várias medidas, ele obtém a curva apresentada na figura. A correspondência entre a temperatura T, em °C, e a resistência elétrica R, em Ω, é dada pela equação
A correspondência entre a temperatura T, em °C, e a resistência elétrica R, em Ω, é dada pela equação
(A) T = 100.(R - 16) / 6,6.
(B) T = 100.6,6 / (R - 16).
(C) T = (R - 6,6) / (6,6.100).
(D) T = 100.(R - 16) / 16.
(E) T = 100.(R - 6,6) / 16.
Resolução:
Primeiro deve-se comparar as duas grandezas: Resposta: A
Resposta: A
18) Um turista brasileiro sente-se mal durante uma viagem à Nova Iorque. Ao ser examinado em um hospital local a enfermeira lhe diz que sua temperatura no momento era 105°, mas que ele deveria ficar tranquilo, pois já havia baixado 4°. Após o susto, o turista percebeu que sua temperatura havia sido medida em uma escala Fahrenheit. Qual era a sua temperatura anteriormente e qual sua temperatura atual?
Anterior: 105° + 4° = 109°F Resolução:
Atual: 105°F
19) Um astrônomo analisa um buraco negro no espaço. Após muitos estudos ele chegou a conclusão que este corpo celeste tinha temperatura de 10K.
Qual a temperatura do buraco negro em escala Celsius? Resolução:
20) Um estudante de física criou uma escala (°X) , comparada com a escala Celsius ele obteve o seguinte gráfico:
Qual a equação de conversão entre as duas escalas?
Resolução:
21) Um termômetro de mercúrio é calibrado de modo que, na temperatura de 0°C, a altura da coluna é de 4 cm e, na temperatura de 100°C, a altura é de 8 cm.
Determine:
a) A função termométrica que relaciona a temperatura (Tc) com a altura (h) da coluna de mercúrio.
b) A altura da coluna quando a temperatura é de 40°C
Resolução
a) É importante fazer um esboço das escalas para visualizar melhor o problema. Utilizando a proporcionalidade entre os segmentos correspondentes escrevemos:
Utilizando a proporcionalidade entre os segmentos correspondentes escrevemos: 4Tc= 100h-400
4Tc= 100h-400
Tc = 25h – 100
Resposta: tc = 25h – 100
b) Usando a função obtida no item a, temos:
Tc = 25h - 100
40 = 25h - 100
h = 5,6 cm
Resposta: h = 5,6 cm
22) Ao nível do mar, a água ferve a 100 °C e congela a 0°C. Assinale a alternativa que indica o ponto de congelamento e o ponto de fervura da água, em Guaramiranga, cidade localizada a cerca de 1.000 m de altitude.
(A) A água congela abaixo de 0 °C e ferve acima de 100 °C.
(B) A água congela acima de 0 °C e ferve acima de 100 °C.
(C) A água congela abaixo de 0 °C e ferve abaixo de 100 °C.
(D) A água congela acima de 0 °C e ferve abaixo de 100 °C.
(E) A água congela a 0 °C e ferve a 100 °C.
Resolução
Quanto maior a altitude, menor a pressão e, acontece uma baixa do ponto de ebulição e elevação do ponto de fusão.
Alternativa: D
23) Em um dia calmo de verão, Paula está em uma praia sob forte incidência de raios solares. Lembrando-se de que o calor específico da água é bem maior do que o da terra, ela observou atentamente alguns fenômenos, buscando relacioná-los com as explicações e comentários apresentados nas aulas de física para os mesmos.
Considerando a situação descrita, assinale com V (verdadeiro) ou F (falso) as seguintes proposições.
( ) Durante o dia, a temperatura da terra é maior que a da água porque o calor específico da terra é menor que o da água.
( ) Durante a noite, percebia-se na praia uma brisa soprando do mar para a terra. Uma possível justificativa é porque a massa de ar junto ao mar estava mais aquecida que a massa de ar junto à terra.
( ) Após o pôr-do-sol, a água se resfriou mais rapidamente do que a terra,
porque o calor específico da água é maior do que o da terra.
( ) Após o pôr-do-sol, a terra se resfriou mais rapidamente que a água do mar, porque o calor específico da água é bem maior que o da terra.
( ) foi possível observar que a água e a terra apresentaram a mesma temperatura, sempre.
Resolução
( V ) A terra absorve e perde energia mais rapidamente que a água, já que seu calor específico é menor.
( F ) a brisa sopra da terra para o mar.
( F ) A água se resfria mais lentamente que a terra, pois o calor específico da água é maior que o da terra.
( V ) Calor específico da água é maior que o calor específico da terra.
( F ) Como existe uma diferença no calor específico, suas temperaturas serão diferentes, já que cada uma absorve energia de uma maneira diferente da outra.
24) O congelador é colocado na parte superior dos refrigeradores, pois o ar se resfria nas proximidades dele, _________ a densidade e desce. O ar quente que está na parte de baixo, por ser ________, sobe e resfria-se nas proximidades do congelador. Nesse caso, o processo de transferência de energia na forma de calor recebe o nome de _________.
Assinale a alternativa que preenche corretamente as lacunas.
(A) aumenta – mais denso – convecção.
(B) diminui – mais denso – condução.
(C) aumenta – menos denso – condução.
(D) diminui – menos denso – irradiação.
(E) aumenta – menos denso – convecção.
Resolução:
O ar frio é mais denso e desce, o ar quente é menos denso e sobe. Este processo é conhecido como convecção.
Alternativa: E
TRANSMISSÃO DE CALOR
É a propagação do calor entre dois sistemas pode ocorrer através de três processos diferentes: a condução, a convecção e a irradiação. 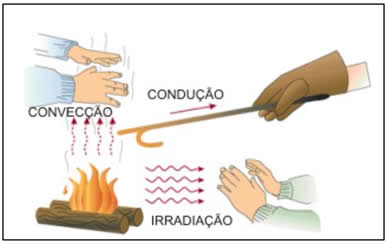 Condução
Condução
Como detalharemos adiante, é um processo lento de transmissão de energia, de molécula para molécula, sempre no sentido das temperaturas mais altas para as mais baixas. 
 Convecção
Convecção
As partes diferentemente aquecidas de um fluido movimentam-se no seu interior devido às diferenças de densidades das porções quente e fria do fluido. Tanto a convecção como a condução não podem ocorrer no vácuo, pois necessitam de um meio material para que possam ocorrer. 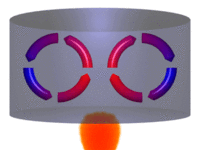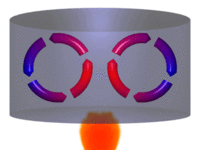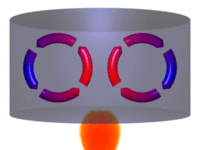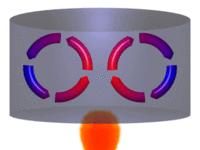
Irradiação
É a propagação de energia através de ondas eletromagnéticas. Quando a energia dessas ondas é absorvida por um corpo, intensifica-se a agitação de suas moléculas, acarretando aumento de temperatura. Esse tipo de propagação energética pode ocorrer no vácuo. 
Isolante Térmico
É todo equipamento ou recipiente que evita/dificulta a troca de calor da parta interna com o maio. 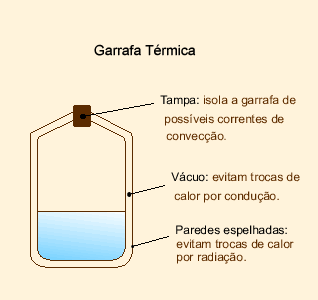 EXERCÍCIOS RESOLVIDOS - TRANSMISSÃO DE CALOR
EXERCÍCIOS RESOLVIDOS - TRANSMISSÃO DE CALOR
25) (UNISA-SP) Uma panela com água está sendo aquecida num fogão. O calor das chamas se transmite através da parede do fundo da panela para a água que está em contato com essa parede e daí para o restante da água.
Na ordem desta descrição, o calor se transmitiu predominantemente por:
(A) radiação e convecçãoB) radiação e condução
(C) convecção e radiação
(D) condução e convecção
(E) condução e radiação
Resolução:
Primeiramente o calor da chama propaga-se através da parede do fundo da panela por condução. O calor é transferido para a parte inferior da água e é transmitido para o restante por meio do processo de convecção térmica.
Portanto, os dois processos que ocorrem durante a transmissão de calor são condução e
Alternativa: D
26) (UNIFENAS) A transmissão de calor por convecção só é possível:
(A) no vácuo
(B) nos sólidos
(C) nos líquidos
(D) nos gases
(E) nos fluidos em geral.
Resolução:
A transmissão de calor por convecção ocorre nos líquidos e nos gases em razão da diferença de densidade entre as partes internas desses fluidos.
Alternativa: E
27) Sobre a transmissão de calor por condução, é correto afirmar que:
(A) ocorre somente nos sólidos;
(B) pode ocorrer no vácuo;
(C) caracteriza-se pela transmissão de calor entre partículas em razão da diferença de temperatura;
(D) caracteriza-se pelo transporte de matéria entre regiões de um fluído em razão da diferença de densidade.
Resolução:
No processo de transmissão de calor por condução, ocorre uma transferência da agitação térmica de partículas de uma região de maior temperatura para outra de menor temperatura. Isso só é possível em meios materiais.
Alternativa: C
28) Observe as afirmações a seguir:
O Sol aquece a Terra por meio do processo de _____________ térmica;
As panelas são feitas de metal porque esses materiais têm maior capacidade de transmissão de calor por _______________;
Os aparelhos de ar-condicionado devem ficar na parte superior de uma sala para facilitar o processo de __________________.
As palavras que completam as frases acima corretamente de acordo com os princípios físicos dos processos de transmissão de calor são, respectivamente:
(A) condução, convecção, irradiação;
(B) convecção, irradiação, condução;
(C) irradiação, convecção, condução;
(D) irradiação, condução, convecção;
(E) condução, irradiação, convecção.
Resolução:
1-O Sol aquece a Terra por meio do processo de irradiação térmica, o que ocorre por meio de ondas eletromagnéticas que podem propagar-se no vácuo;
2-As panelas são feitas de metal porque esses materiais têm maior capacidade de transmissão de calor por condução, uma vez que eles possuem maior quantidade de cargas livres que podem fazer o transporte de calor entre as partículas que os constituem.
3-Os aparelhos de ar-condicionado devem ficar na parte superior de uma sala para facilitar o processo de convecção.
Portanto, as palavras que completam as afirmações são:
Alternativa: D
29) (UNISA-SP) Uma panela com água está sendo aquecida num fogão. O calor das chamas se transmite através da parede do fundo da panela para a água que está em contato com essa parede e daí para o restante da água. Na ordem desta descrição, o calor se transmitiu predominantemente por:
(A) radiação e convecção
(B) radiação e condução
(C) convecção e radiação
(D) condução e convecção
(E) condução e radiação
Resolução:
Primeiramente o calor da chama propaga-se através da parede do fundo da panela por condução. O calor é transferido para a parte inferior da água e é transmitido para o restante por meio do processo de convecção térmica. Portanto, os dois processos que ocorrem durante a transmissão de calor são condução e convecção.
Alternativa D
30) (UNIFENAS) A transmissão de calor por convecção só é possível:
(A) no vácuo
(B) nos sólidos
(C) nos líquidos
(D) nos gases
(E) nos fluidos em geral.
Resolução:
A transmissão de calor por convecção ocorre nos líquidos e nos gases em razão da diferença de densidade entre as partes internas desses fluidos.
Alternativa: E
31) Sobre a transmissão de calor por condução, é correto afirmar que:
(A) ocorre somente nos sólidos;
(B) pode ocorrer no vácuo;
(C) caracteriza-se pela transmissão de calor entre partículas em razão da diferença de temperatura;
(D) caracteriza-se pelo transporte de matéria entre regiões de um fluído em razão da diferença de densidade.
Resolução:
No processo de transmissão de calor por condução, ocorre uma transferência da agitação térmica de partículas de uma região de maior temperatura para outra de menor temperatura. Isso só é possível em meios materiais.
Alternativa: C
32) Observe as afirmações a seguir:
I - O Sol aquece a Terra por meio do processo de _____________ térmica;
II - As panelas são feitas de metal porque esses materiais têm maior capacidade de transmissão de calor por _______________;
III - Os aparelhos de ar-condicionado devem ficar na parte superior de uma sala para facilitar o processo de __________________.
As palavras que completam as frases acima corretamente de acordo com os princípios físicos dos processos de transmissão de calor são, respectivamente:
(A) condução, convecção, irradiação;
(B) convecção, irradiação, condução;
(C) irradiação, convecção, condução;
(D) irradiação, condução, convecção;
(E) condução, irradiação, convecção.
Resolução:
I) O Sol aquece a Terra por meio do processo de irradiação térmica, o que ocorre por meio de ondas eletromagnéticas que podem propagar-se no vácuo;
II) As panelas são feitas de metal porque esses materiais têm maior capacidade de transmissão de calor por condução, uma vez que eles possuem maior quantidade de cargas livres que podem fazer o transporte de calor entre as partículas que os constituem.
III) Os aparelhos de ar-condicionado devem ficar na parte superior de uma sala para facilitar o processo de convecção.
Portanto, as palavras que completam as afirmações são: irradiação, condução e convecção.
Alternativa: D
33) (UFSCar) Um recipiente cilíndrico de vidro tem área da base relativamente pequena se comparada com sua altura. Ele contém água em temperatura ambiente até quase a sua borda e é colocado sobre a chama de um fogão, como ilustra a figura. A transmissão do calor por meio das moléculas da água durante seu aquecimento ocorre apenas por
A transmissão do calor por meio das moléculas da água durante seu aquecimento ocorre apenas por
(A) condução.
(B) convecção.
(C) irradiação.
(D) condução e convecção.
(E) convecção e irradiação.
Resolução:
O calor flui através de um líquido por meio da convecção, processo de transferência de calor que ocorre entre fluidos a partir do deslocamento de massa.
Alternativa: B
34) (Acafe-SC) Preparar um bom churrasco é uma arte e, em todas as famílias, sempre existe um que se diz bom no preparo. Em algumas casas, a quantidade de carne assada é grande e se come no almoço e no jantar. Para manter as carnes aquecidas o dia todo, alguns utilizam uma caixa de isopor revestida de papel alumínio. A figura a seguir mostra, em corte lateral, uma caixa de isopor revestida de alumínio com carnes no seu interior.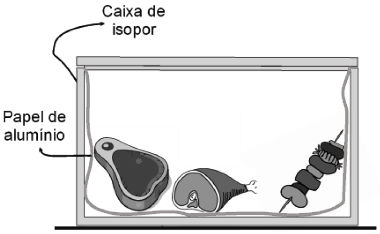 Considerando o exposto, assinale a alternativa correta que completa as lacunas das frases a seguir.
Considerando o exposto, assinale a alternativa correta que completa as lacunas das frases a seguir.
A caixa de isopor funciona como recipiente adiabático. O isopor tenta ______ a troca de calor com o meio por ________ e o alumínio tenta impedir _________.
(Aa) impedir - convecção - irradiação do calor
(B) facilitar - condução - convecção
(C) impedir - condução - irradiação do calor
(D) facilitar - convecção - condução
Resolução:
O contato entre as carnes e o meio ambiente origina um fluxo de calor. O isopor, como isolante térmico, impede essa transferência, que ocorreria por condução. Todo corpo aquecido produz ondas de calor. A função do alumínio é refletir essas ondas e impedir a perda de energia.
A caixa de isopor funciona como recipiente adiabático. O isopor tenta impedir a troca de calor com o meio por condução e o alumínio tenta impedir a irradiação de calor.
Alternativa: C
35) Marque a alternativa correta a respeito dos processos de propagação de calor.
(A) Os processos de propagação de calor por condução e convecção ocorrem em todos os tipos de meios.
(B) O processo de irradiação de calor ocorre somente no vácuo.
(C) A convecção é o processo de propagação de calor que proporciona o efeito das brisas marítimas.
(D) A condução térmica ocorre somente em líquidos.
(E) A irradiação é um processo de transferência de calor que ocorre por meio de ondas eletromagnéticas pertencentes ao espectro visível.
Resolução:
a) Errada. Condução e convecção só ocorrem em meios materiais.
b) Errada. A irradiação de calor ocorre em qualquer meio material.
c) Correta.
d) Errada. A troca de calor nos líquidos ocorre por meio da convecção.
e) Errada. A irradiação é um processo de transferência de calor que ocorre por meio de ondas eletromagnéticas.
Alternativa: C
36) Menino do Rio
Menino do Rio, calor que provoca arrepio
Dragão tatuado no braço, calção corpo aberto no espaço
Coração de eterno flerte, adoro ver-te
Menino vadio, tensão flutuante do rio
Eu canto para Deus proteger-te
O Havaí, seja aqui, tudo o que tu sonhares
Todos os lugares, as ondas dos mares
Pois quando eu te vejo eu desejo o teu desejo
Menino do Rio, calor que provoca arrepio toma esta canção
como um beijo.
A música acima, de autoria de Caetano Veloso e interpretada por Baby Consuelo, foi composta em 1979. Logo na primeira frase, existe um contraste entre as palavras calor e arrepio, que é o efeito de eriçamento dos pelos do corpo por causa da sensação de frio. Marque a alternativa correta a respeito das trocas de calor entre os corpos.
(A) O calor é uma energia térmica em trânsito e é apenas transmitido por meios materiais.
(B) A sensação de frio é provocada pela perda de calor do corpo para o meio ambiente por meio do processo de convecção térmica.
(C) O calor é uma energia térmica em trânsito motivada pela igualdade de temperatura, que se transfere por meio de três processos: condução, convecção e irradiação térmica.
(D) O único processo de transferência de calor que ocorre no vácuo é a convecção.
(E) O calor que provoca arrepio pode ser entendido como o calor perdido pelo corpo de uma pessoa por meio do processo de condução térmica.
Resolução:
As trocas de calor entre o corpo humano e o ambiente são um dos motivos que geram eriçamento dos pelos. Esse efeito é provocado quando o corpo perde calor para o ambiente, ou seja, quando a diferença de temperatura entre os elementos provoca um fluxo de energia térmica. A forma de propagação de calor, nesse caso, é a condução térmica.
Alternativa: E
37) (UFAL) Selecione a alternativa que supre as omissões das afirmações seguintes:
I - O calor do Sol chega até nós por _________________________.
II - Uma moeda bem polida fica __________ quente do que uma moeda revestida de tinta preta, quando ambas são expostas ao sol.
III - Numa barra metálica aquecida numa extremidade, a propagação do calor se dá para a outra extremidade por ________________________.
(A) radiação - menos - convecção.
(B) convecção - mais - radiação.
(C) radiação - menos - condução.
(D) convecção - mais - condução.
(E) condução - mais - radiação.
Resolução
I – O calor do Sol chega até nós por radiação, pois entre o Sol e a Terra não existe meio material. Assim, não é possível que o calor se propague de outra forma;
II – Uma moeda bem polida fica menos quente do que uma moeda revestida de tinta preta, quando ambas são expostas ao sol. Isso porque uma moeda polida refletirá a energia que recebe, enquanto a moeda revestida de tinta preta absorverá o calor que recebe;
III – Em uma barra metálica aquecida em uma extremidade, a propagação do calor ocorre para a outra extremidade por condução, uma vez que, em meios sólidos, o calor somente se propaga por meio da condução.
39) (PUC-RS) No inverno, usamos roupas de lã baseados no fato de a lã:
(A) ser uma fonte de calor.
(B) ser um bom absorvente de calor.
(C) ser um bom condutor de calor.
(D) impedir que o calor do corpo se propague para o meio exterior.
(E) n.d.a
Resolução:
As roupas de lã são utilizadas porque evitam a perda de calor do corpo para o meio externo. Isso ocorre porque a lã possui “espaços vazios”, que são os furinhos que podemos observar nas roupas feitas por esse material. Esses espaços são ocupados por ar, que funciona como um excelente isolante térmico.
39) Julgue as afirmações a seguir:
I – A transferência de calor de um corpo para outro ocorre em virtude da diferença de temperatura entre eles;
II – A convecção térmica é um processo de propagação de calor que ocorre apenas nos sólidos;
III – O processo de propagação de calor por irradiação não precisa de um meio material para ocorrer.
Estão corretas:
(A) Apenas I
(B) Apenas I e II
(C) I, II e III
(D) I e III apenas;
(E) Apenas II e III.
Resolução:
As afirmações I e III são corretas;
A afirmativa II está incorreta porque a convecção térmica ocorre apenas em líquidos e gases, que são fluidos. Nos sólidos, a propagação de calor ocorre por condução.
Alternativa: D
ESTADO FÍSICO DA MATÉRIA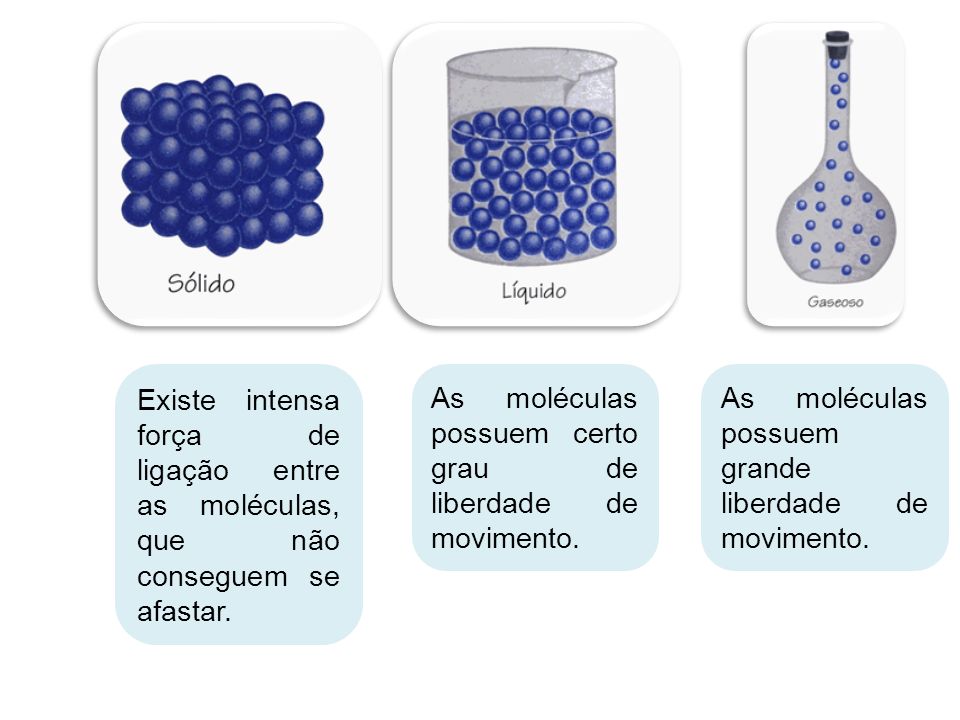 MUDANÇA DE FASE
MUDANÇA DE FASE
Solidificação – Passagem de um corpo do estado líquido para o sólido
Fusão - Passagem do estado sólido para o líquido, sem aumentar a temperatura do corpo.
Vaporização - Passagem de um corpo do estado líquido para o gasoso.
Sublimação - Passagem do estado sólido direto para o estado gasoso,
Estados Físicos da Matéria
Os três estados físicos da matéria são:
Sólido
Liquido
Gasoso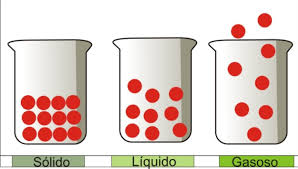 As substâncias que estão à nossa volta apresentam diferentes estados físicos. Veja o caso da água: na nossa cozinha podemos achá-la na forma sólida (gelo), na forma líquida (saindo da torneira) e na forma de vapor (como a “fumacinha” que sai da chaleira).
As substâncias que estão à nossa volta apresentam diferentes estados físicos. Veja o caso da água: na nossa cozinha podemos achá-la na forma sólida (gelo), na forma líquida (saindo da torneira) e na forma de vapor (como a “fumacinha” que sai da chaleira).
Mas, o que faz com que as substâncias tenham diferentes estados físicos? E o que faz com elas mudem este estado físico? Saiba disso e muito mais nesta aula completa e no resumo do professor Felipe Sobis! 😀 Os três estados físicos da matéria
Os três estados físicos da matéria
O que determina o estado em que a matéria se encontra é a proximidade das partículas que a constitui. Essa característica obedece a fatores como:
Força de Coesão: faz com que as moléculas se aproximem umas das outras;
Força de Repulsão: faz com que as moléculas se afastem umas das outras.
O volume, a densidade e a forma de um composto podem variar com a temperatura, sendo assim, os compostos apresentam características de acordo com o estado físico em que se encontram.
Sólido - No estado conhecido como sólido, as moléculas da matéria se encontram muito próxima. Sendo assim, possuem forma fixa, volume fixo e não sofrem compressão.
Líquido - Ao contrário do estado sólido, nesse estado as moléculas estão mais afastadas. Assim, os elementos que se encontram nesse estado possuem forma variada, mas volume constante. Além disso, possuem facilidade de escoamento e adquirem a forma do recipiente que os contém.
Gasoso - A movimentação das moléculas nesse estado é bem maior do que no estado líquido ou sólido. Assim, se variarmos a pressão exercida sobre um gás, podemos aumentar o diminuir o seu volume. Ou seja, pode-se dizer que sofre compressão e expansão facilmente.
Dessa maneira, os elementos gasosos tornam a forma do recipiente que os contém. Além disso, muito se fala sobre o estado de plasma.
Exemplo: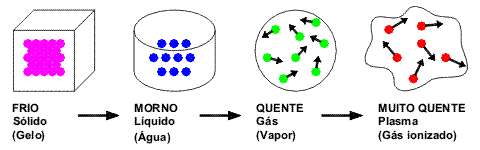
Mudanças de estado físico da matéria
As passagens entre os três estados físicos (sólido, líquido e gasoso) têm o nome de mudanças de estado físico e você pode conferir o nome de cada um na figura abaixo: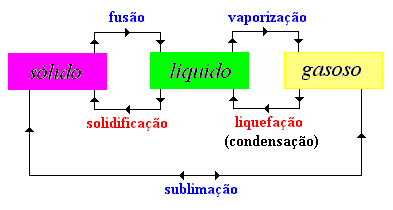
Fusão - Passagem, provocada por um aquecimento, do estado sólido para o estado líquido.
A temperatura não aumenta enquanto está acontecendo a fusão, isto é, somente depois que toda a substância passar para o estado líquido é que a temperatura volta a aumentar.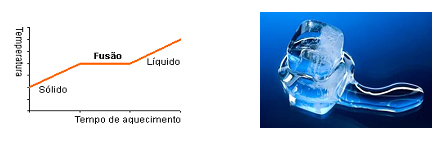 Solidificação - Passagem do estado líquido para o estado sólido, através de arrefecimento (resfriamento).
Solidificação - Passagem do estado líquido para o estado sólido, através de arrefecimento (resfriamento).
Quando a substância líquida inicia a solidificação, a temperatura fica inalterada até que a totalidade esteja no estado sólido, e só depois a temperatura continua a baixar. Vaporização - Passagem do estado líquido para o estado gasoso, por aquecimento.
Vaporização - Passagem do estado líquido para o estado gasoso, por aquecimento.
Durante a ebulição a temperatura da substância que está a passar do estado líquido para o estado gasoso permanece inalterada, só voltando a aumentar quando toda a substância estiver no estado gasoso.
Condensação -Passagem do estado gasoso para o estado líquido, devido ao um arrefecimento (resfriamento).
Quando a substância gasosa inicia a condensação, a temperatura fica inalterada até que a totalidade esteja no estado líquido, e só depois a temperatura continua a baixar. Sublimação - Passagem direta de uma substância do estado sólido para o estado gasoso. A Sublimação acontece por aquecimento quando do estado sólido para o gasoso, ou do estado gasoso para o estado sólido por arrefecimento. Ex. Gelo seco, naftalina.
Sublimação - Passagem direta de uma substância do estado sólido para o estado gasoso. A Sublimação acontece por aquecimento quando do estado sólido para o gasoso, ou do estado gasoso para o estado sólido por arrefecimento. Ex. Gelo seco, naftalina.
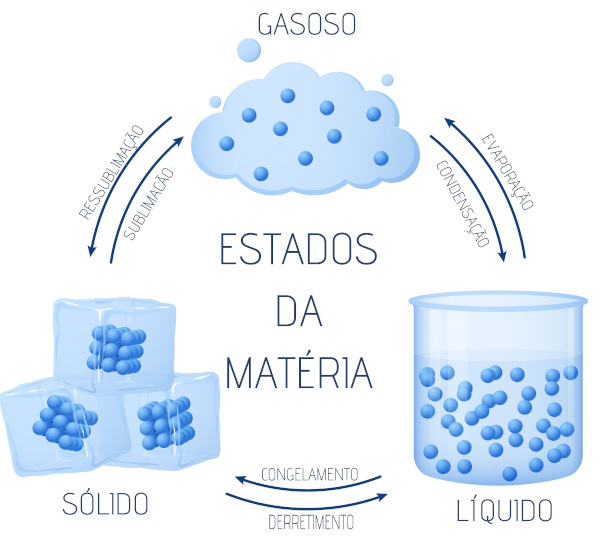

01) A tabela a seguir traz os pontos de fusão e ebulição, em ºC, sob pressão de 1 atm, de alguns materiais. Com base nas informações da tabela, assinale a alternativa que indica quais materiais estão no estado de agregação líquido à temperatura ambiente (cerca de 25ºC):
Tabela com pontos de fusão e ebulição de várias substâncias (A) Oxigênio e Metanol
(A) Oxigênio e Metanol
(B) Metanol, acetona e mercúrio
(C) Metanol e mercúrio
(D) Amônia, acetona, mercúrio e alumínio
(E) Nenhuma das alternativas.
Resolução:
Vamos transportar os dados da tabela para um esquema representando a temperatura dada (25ºC) e os pontos de fusão e ebulição das substâncias:
Esquema para responder a exercício sobre estados físicos da matéria
Veja que, na temperatura de 25ºC, somente o metanol, a acetona e o mercúrio estão no estado líquido, enquanto o oxigênio e a amônia estão no estado gasoso, e o alumínio está no estado sólido.
Alternativa: B
02) (Vunesp) O naftaleno, comercialmente conhecido como naftalina, empregado para evitar baratas em roupas, funde em temperaturas superiores a 80°C. Sabe-se que bolinhas de naftalina, à temperatura ambiente, têm suas massas constantemente diminuídas, terminando por desaparecer sem deixar resíduo. Essa observação pode ser explicada pelo fenômeno da:
(A) fusão.
(B) sublimação.
(C) solidificação.
(D) liquefação.
(E) ebulição.
Resolução:
A sublimação é a passagem direta do estado sólido para o gasoso.
Alternativa: B
03) (Mackenzie-SP) As fases de agregação para as substâncias abaixo, quando expostas a uma temperatura de 30 ºC , são, respectivamente:
Tabela com pontos de fusão e ebulição de alguns materiais (A) sólido, líquido, gasoso e líquido.
(A) sólido, líquido, gasoso e líquido.
(B) líquido, sólido, líquido e gasoso.
(C) líquido, gasoso, líquido e sólido.
(D) gasoso, líquido, gasoso e sólido.
(E) sólido, gasoso, líquido e gasoso.
Resolução:
A 30 ºC, temos:
Mercúrio – líquido
Amônia – gasoso
Benzeno – líquido
Naftaleno – sólido
Para confirmar, veja o esquema abaixo: Alternativa: C
Alternativa: C
04) O ponto de fusão do cobre é igual a 1083 ºC e o ponto de ebulição é de 2 310 ºC. Assinale a alternativa que indica corretamente o estado físico do cobre em 20ºC, 100ºC, 1000ºC e 2500ºC, respectivamente:
(A) sólido, sólido, líquido, gasoso.
(C) Sólido, sólido, sólido, sólido.
(C) Sólido, sólido, sólido, gasoso.
(D) Sólido, sólido, sólido, líquido.
(E) Sólido, líquido, líquido, gasoso.
Resolução:
Se o ponto de fusão do cobre é igual a 1083 ºC, nas temperaturas abaixo dessa, que são 20ºC, 100ºC e 1000ºC, ele estará no estado sólido. Tendo em vista que seu ponto de ebulição é de 2 310 ºC, na temperatura de 2500ºC, ele já terá passado para o estado gasoso.
Alternativa: C
01) Solidificação é
(A) Passagem do estado sólido direto para o estado gasoso
(B) Passagem do estado sólido para o líquido, sem aumentar a temperatura do corpo.
(C) Passagem de um corpo do estado líquido para o gasoso.
(D) Passagem de um corpo do estado líquido para o sólido
Alternativa: D
05) Fusão é:
(A) Passagem do estado sólido direto para o estado gasoso,
(B) Passagem de um corpo do estado líquido para o sólido
(C) Passagem do estado sólido para o líquido, sem aumentar a temperatura do corpo.
(D) Passagem de um corpo do estado líquido para o gasoso
Alternativa: C
06) Vaporização é:
(A) Passagem do estado sólido direto para o estado gasoso,
(B) Passagem de um corpo do estado líquido para o gasoso.
(C) Passagem do estado sólido para o líquido, sem aumentar a temperatura do corpo.
(D) Passagem de um corpo do estado líquido para o sólido
Alternativa: B
07) Sublimação é:
(A) Passagem do estado sólido direto para o estado gasoso
(B) Passagem de um corpo do estado líquido para o gasoso.
(C) Passagem do estado sólido para o líquido, sem aumentar a temperatura do corpo
(D) Passagem de um corpo do estado líquido para o sólido
Alternativa: A
08) (Facimpa) Observe:
I – Uma pedra de naftalina deixada no armário.
II – Uma vasilha de água deixada no freezer.
III- Uma vasilha de água deixada no fogo.
IV – O derretimento de um pedaço de chumbo quando aquecido.
Nesses fatos estão relacionados corretamente os seguintes fenômenos:
(A) I. Sublimação; II. Solidificação; III. Evaporação; IV. Fusão.
(B) I. Sublimação; II. Sublimação; III. Evaporação; IV. Solidificação.
(C) I. Fusão; II. Sublimação; III. Evaporação; IV. Solidificação.
(D) I. Evaporação; II. Solidificação; III. Fusão; IV. Sublimação.
(E) I. Evaporação; II. Sublimação; III. Fusão; IV. Solidificação.
Resolução
I – Sublimação: A naftalina é um composto apolar e de ponto de ebulição muito alto. Esse composto vai do estado sólido ao gasoso sem passar pelo estado líquido.
II – Solidificação: A água submetida à baixa temperatura do freezer congela, o que quimicamente chamamos de solidificação, que é a passagem do estado líquido para o estado sólido.
III – Evaporação: A água deixada num vasilhame ao fogo sofre um aumento de temperatura. O ponto de ebulição da água é 100°C, sendo assim, quando o sistema atingir essa temperatura, ela começará a evaporar, passando do estado líquido para o estado sólido.
IV – Fusão: O chumbo tem ponto de fusão de 327,5°C, que é uma temperatura relativamente alta; no entanto, o derretimento do chumbo é um processo comum nas indústrias, que nada mais é do que a passagem do estado sólido para o estado líquido.
Alternativa: A
09) (Unicamp) Icebergs flutuam na água do mar, assim como o gelo em um copo com água potável. Imagine a situação inicial de um copo com água e gelo, em equilíbrio térmico à temperatura de 0°C. Com o passar do tempo, o gelo vai derretendo. Enquanto houver gelo, a temperatura do sistema
(A) permanece constante, mas o volume do sistema aumenta.
(B) permanece constante, mas o volume do sistema diminui.
(C) diminui e o volume do sistema aumenta.
(D) diminui, assim como o volume do sistema.
Resolução
A temperatura mantém-se constante até que o iceberg derreta-se por inteiro, pois acontece uma troca de calor em busca de equilíbrio térmico entre as duas fases da matéria. A água é um dos poucos elementos que admitem densidade diferente para diferentes estados físicos do mesmo composto.
Visualmente podemos verificar que a densidade do gelo é menor. No caso do iceberg e em um copo com água e gelo, o gelo fica na superfície. Isso acontece porque, ao se congelar a água, no processo de formação do gelo, ela ganha volume, mas a massa mantém-se a mesma de quando era água no estado líquido. Portanto, quando o iceberg derrete, ocorre uma diminuição do volume do sistema.
Alternativa: B
10) Toda substância apresenta uma propriedade física que determina qual é a quantidade de calor necessária por unidade de massa desse corpo para que a sua temperatura varie em 1ºC ou 1K. Essa propriedade e sua unidade física, no Sistema Internacional de Unidades, são, respectivamente, iguais a:
(A) calor específico e J/kg.K.
(B) calor específico e cal/gº.C.
(C) capacidade térmica e J/K.
(D) calor latente e J/kg.
(E) coeficiente de dilatação volumétrica e ºC-1.
Resolução:
O calor específico de uma substância mede a quantidade de calor em Joules necessária para variar 1 g de sua massa em até 1ºC ou em 1 K, portanto, sua unidade, segundo o SI, é o J/kg.K.
Alternativa: B
11) Um corpo de 10 kg precisa receber 2500 J de calor sensível para ter sua temperatura variada em 10 K. Determine sua capacidade térmica.
(A) 250 J/K
(B) 25 J/K
(C) 2500 J/K
(D) 150 J/K
(E) 50 J/K
Resolução:
A capacidade térmica de um corpo pode ser determinada por meio da seguinte equação:![]()
C = capacidade térmica
Q = quantidade de calor
m = massa do corpo
c = calor específico
Analisando os dados fornecidos pelo enunciado do exercício, percebe-se que só é possível utilizar a primeira equação, que relaciona a quantidade de calor recebido com a variação de temperatura do corpo.![]()
O resultado encontrado indica que o corpo precisa absorver 2500 J para variar sua temperatura em 10 K. Portanto, a alternativa correta é a letra A.
Alternativa: A
12) Um corpo com 10,0 kg de massa tem capacidade térmica igual a 20,0 J/K. Determine o seu calor específico.
(A) 200,0 J/kg.K
(B) 0,2 J/kg.K
(C) 10,0 J/kg.K
(C) 2,0 J/kg.K
(E) 20,0 J/kg.K
Resolução:
A capacidade térmica de um corpo pode ser calculada por meio do produto entre sua massa e seu calor específico.
Alternativa; C
13) Um corpo de 500 g que se encontra a uma temperatura inicial de 25 ºC recebe de um aquecedor uma quantidade de calor sensível igual a 5000 cal, atingindo uma temperatura de 30 ºC ao final do processo de aquecimento. Determine o calor específico desse corpo.
(A) 0,005 cal/gºC
(B) 0,2 cal/gºC
(C) 1,0 cal/gºC
(D) 2,0 cal/gºC
(E) 2,5 cal/gºC
Resolução:
Para calcularmos o calor específico do corpo que foi descrito no enunciado do exercício, é necessário utilizar a equação fundamental da calorimetria, que calcula o módulo do calor sensível.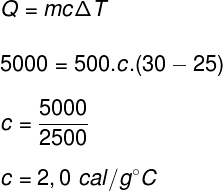
De acordo com os resultados obtidos, o corpo em questão necessita receber 2,0 cal a cada grama de massa para ter sua temperatura variada em 1 ºC.
Alternativa: D
QUESTÕES RESOLVIDAS – MUDANÇA DE FASE
45) (UFSM-RS) Assinale falso (F) ou verdadeiro (V) em cada afirmativa.
( ) A água pode evaporar a uma temperatura menor do que 100°C.
( ) A sensação de frio ocasionada pela evaporação da água sobre a pele deve-se à absorção de energia da pele pelo líquido.
( ) A velocidade de evaporação da água não depende da pressão externa.
A sequência correta é
(A) V - V – F.
(B) F - F – V.
(C) F - F – F.
(D) V - F – F.(E) V - V – V.
Resolução:
A primeira afirmativa é verdadeira, pois a temperatura de evaporação de uma substância depende da pressão à qual essa substância é submetida. A água somente evapora a 100ºC se a pressão for 1 atm, se a pressão for reduzida, a temperatura de evaporação será menor;
A segunda afirmação também é verdadeira. Quando colocamos um líquido sobre a nossa pele, ele absorve energia e evapora;
A terceira afirmativa é falsa. Como já citado, a velocidade da água depende de vários fatores, entre eles, a pressão externa;
A sequência correta então é V – V – F.
Alternativa: A
46) (PUC-MG) Na questão a seguir assinale a afirmativa INCORRETA.
(A) Todos os materiais expandem-se quando aquecidos.
(B) A temperatura de fusão de uma substância depende da pressão.
(C) Durante uma mudança de fase, a temperatura permanece constante.
(D) A temperatura em que a água ferve depende da pressão.
Resolução:
Alguns materiais contraem-se quando aquecidos. Esses materiais são chamados de NTE, que significa materiais com expansão térmica negativa.
Alternativa: A
47) Sobre as mudanças de fase da matéria, assinale a alternativa incorreta:
(A) A pressão externa à qual uma substância é submetida interfere em sua mudança de fase;
(B) O aumento da superfície livre ocupada por um líquido favorece a sua evaporação;
(C) A velocidade em que uma substância evapora depende de sua temperatura;(D) O fato de uma substância em estado líquido estar em ambiente fechado ou aberto não interfere em sua evaporação.
Resolução:
Se uma substância evapora em ambiente fechado, sua concentração no ambiente aumenta, o que dificulta a evaporação.
Alternativa: D
48) (UFSM) Quando se está ao nível do mar, observa-se que a água ferve a uma temperatura de 100 °C. Subindo uma montanha de 1 000 m de altitude, observa-se que:
(A) a água ferve numa temperatura maior, pois seu calor específico aumenta.
(B) a água ferve numa temperatura maior, pois a pressão atmosférica é maior.
(C) a água ferve numa temperatura menor, pois a pressão atmosférica é menor.
(D) a água ferve na mesma temperatura de 100 °C, independente da pressão atmosférica.
(E) a água não consegue ferver nessa altitude.
Resolução:
Quando estamos acima do nível do mar, a pressão é reduzida, por isso as partículas ficam mais afastadas umas das outras e evaporam-se mais rápido.
Alternativa: C
49) (MED. POUSO ALEGRE - MG) Observe os seguintes fatos:
I - Uma pedra de naftalina deixada no armário.
II - Uma vasilha com água deixada no freezer.
III - Uma vasilha com água deixada no fogo.
IV - O derretimento de um pedaço de chumbo quando aquecido.
Nesses fatos, estão relacionados corretamente os seguintes fenômenos:
(A) I. sublimação, II. solidificação, III. evaporação, IV. fusão;
(B) I. sublimação, II. solidificação, III. fusão, IV. evaporação;
(C) I. fusão, II. sublimação, III. evaporação, IV. solidificação;
(D) I. evaporação, II. solidificação, III. fusão, IV. sublimação;
(E) I. evaporação, II. sublimação, III. fusão, IV. solidificação.
Resolução:
I – Passagem do sólido diretamente para o gasoso: sublimação
II – Passagem do líquido para o sólido: solidificação
III – Passagem do líquido para o gasoso: evaporação
IV – Passagem do sólido para o líquido: fusão
Alternativa: A
50) Observe na tabela a seguir o ponto de ebulição e de fusão de algumas substâncias: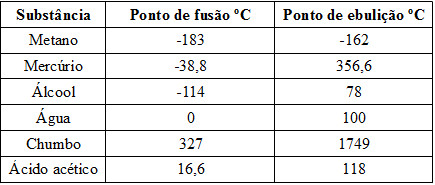 Identifique quais dessas substâncias são encontradas no estado líquido em temperatura ambiente (aproximadamente 25 ºC).
Identifique quais dessas substâncias são encontradas no estado líquido em temperatura ambiente (aproximadamente 25 ºC).
(A) Chumbo, metano, água e mercúrio;
(B) Ácido acético, álcool, mercúrio e água;
(C) Metano, álcool, água e mercúrio;
(D) Álcool, água, metano e chumbo;
(E) Ácido acético, metano, chumbo e água.
Resolução:
Encontram-se no estado líquido as substâncias que apresentam ponto de fusão inferior a 25ºC e ponto de ebulição superior a 25ºC. Analisando a tabela, vemos que essas substâncias são a água, o álcool, o mercúrio e o ácido acético.
Alternativa: B
51) O ponto de fusão do bromo é -7,2 ºC, já o seu ponto de ebulição é 58,8 ºC. Identifique o estado físico dessa substância nas seguintes temperaturas:
(A) - 30ºC
(B) 0 ºC
(C) 35 ºC
(D) 80 ºC
(E) 110ºC
Resolução:
A) -30 ºC – Sólido
B) 0ºC – Líquido
C) 35ºc – Líquido
D) 80ºC – gasoso
E) 110ºC - gasoso
52) O ponto de fusão do ferro é igual a 1530 ºC e o ponto de ebulição é de 2 450ºC. Baseado nisso, qual será o estado físico do ferro nas seguintes temperaturas:
(A) 25 ºC:
(B) 130 ºC:
(C) 1 459 ºC:
(D) 2 235 ºC:
(E) 3 002 ºC:
Resolução:
A) 25 ºC: sólido;
B) 130 ºC: sólido;
C) 1 459 ºC: sólido;
D) 2 235 ºC: líquido;
E)3 002 ºC: gasoso.
53) Observe a tabela abaixo e identifique quais estão sólidos em temperatura ambiente (considere 20 ºC como a temperatura ambiente) e pressão de 1 atm: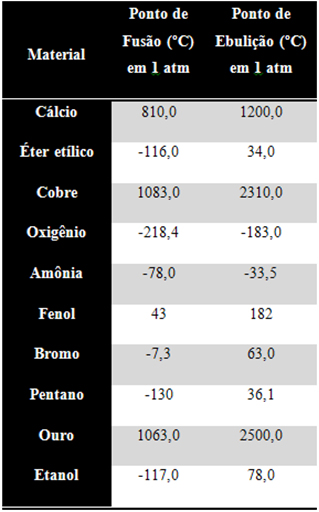 (A) Oxigênio, amônia, fenol e etanol.
(A) Oxigênio, amônia, fenol e etanol.
(B) Éter, bromo, pentano e etanol.
(C) Fenol, bromo e ouro.
(D) Oxigênio, amônia e fenol.
(E) Cálcio, cobre, fenol e ouro
Resolução:
Estados físicos à temperatura ambiente e pressão de 1 atm de cada um:
-
Sólidos: Cálcio, cobre, fenol e ouro.
-
Líquidos: Éter etílico, bromo, pentano e etanol.
-
Gasosos: – Oxigênio, amônia.
Alternativa: E
54) Para combater traças e baratas, era comum colocar algumas bolinhas de naftalina no guarda-roupa. Com o passar do tempo, essas bolinhas diminuíam de tamanho. Esse fenômeno é uma mudança de estado físico chamada de:
(A) Solidificação.
(B) Condensação.
(C) Fusão.
(D) Sublimação.
(E)Evaporação.
Resolução:
Sublimação é a passagem direta do estado sólido para o estado gasoso.
Alternativa: D
55) (Unifor-CE) Considere a tabela de pontos de fusão e de ebulição das substâncias a seguir, a 1 atm de pressão. A 50ºC, encontram-se no estado líquido: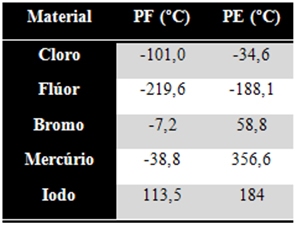 (A) cloro e flúor.
(A) cloro e flúor.
(B) cloro e iodo.
(C) mercúrio e iodo.
(D) flúor e bromo.
(E) bromo e mercúrio.
Resolução:
Estados físicos à temperatura de 50ºC de cada um:
Sólidos: Iodo;
Líquidos: Bromo e mercúrio;
Gasosos: – Cloro e flúor.
Alternativa: E
56) (Facimpa – MG ) Observe:
I – Uma pedra de naftalina deixada no armário;
II – Uma vasilha de água deixada no freezer;
III- Uma vasilha de água deixada no fogo;
IV – O derretimento de um pedaço de chumbo quando aquecido;
Nesses fatos estão relacionados corretamente os seguintes fenômenos:
(A) I. Sublimação; II. Solidificação; III. Evaporação; IV. Fusão.
(B) I. Sublimação; II. Sublimação; III. Evaporação; IV. Solidificação.
(C) I. Fusão; II. Sublimação; III. Evaporação; IV. Solidificação.
(D) I. Evaporação; II. Solidificação; III. Fusão; IV. Sublimação.
(E) I. Evaporação; II. Sublimação; III. Fusão; IV. Solidificação.
Resolução:
I – Uma pedra de naftalina deixada no armário. – passagem direta do estado sólido para o gasoso – sublimação;
II – Uma vasilha de água deixada no freezer. – passagem do estado líquido para o sólido – solidificação;
III- Uma vasilha de água deixada no fogo. – passagem do estado líquido para o de vapor – evaporação;
IV – O derretimento de um pedaço de chumbo quando aquecido. – passagem do estado sólido para o líquido – fusão.
Alternativa: A
57) (Mackenzie-SP) Pela análise dos dados da tabela, medidos a 1 atm, podemos afirmar que à temperatura de 40 ºC e 1 atm:
Pela análise dos dados da tabela, medidos a 1 atm, podemos afirmar que à temperatura de 40 ºC e 1 atm:
(A) O éter e o etanol encontram-se na fase gasosa.
(B) O éter se encontra na fase gasosa e o etanol na fase líquida.
(C) Ambos encontram-se na fase líquida.
(D) O éter encontra-se na fase líquida e o etanol na fase gasosa.
(E) Ambos se encontram na fase sólida.
Resolução:
Pegando os dados do problema e colocando em um esquema que representa a temperatura de 40 ºC e os pontos de fusão e ebulição do etanol e do éter etílico, temos: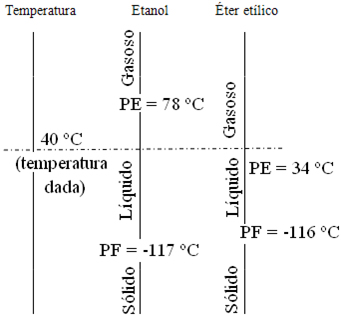 Observe que a linha tracejada horizontal correspondente a 40ºC corta a linha do etanol na região do líquido e a linha do éter etílico na região do gasoso.
Observe que a linha tracejada horizontal correspondente a 40ºC corta a linha do etanol na região do líquido e a linha do éter etílico na região do gasoso.
Alternativa: B
TROCA DE CALOR
Troca de calor – Isso acontece quando dois ou mais corpos com temperaturas diferentes são colocados em contato em um mesmo ambiente (sistema isolado) e, depois de certo tempo, alcançam o equilíbrio térmico.
As trocas de calor acontecem porque o calor é um tipo de energia que transita entre os corpos, ocasionando esse movimento, fato que acontece até que haja o equilíbrio térmico entre ambos. Esse processo acontece porque os corpos sentem a necessidade de ceder e receber calor.
Calor Específico - É a quantidade de calor que deve ser fornecida para que 1 g de substância tenha a sua temperatura elevada em 1°C. Cada substância possui um determinado valor de calor específico, que é geralmente expresso em cal/g.°C.
Quanto maior for o calor específico de uma substância, maior será a quantidade de calor que deverá ser fornecida ou retirada dela para que ocorram variações de temperatura. A água, quando comparada com várias outras substâncias, possui o maior calor específico, que corresponde a 1 cal/g.ºC Calor Sensível - É energia térmica em trânsito que flui entre os corpos em razão da diferença de temperatura entre eles. Dessa forma, imagine uma barra de ferro que receba ou perca certa quantidade de calor (Q). Esse calor que a barra ganhou ou perdeu é denominado de calor sensível, pois ele provoca apenas variação na temperatura do corpo sem que aconteça mudança em seu estado de agregação, ou seja, se o corpo é sólido, continua sólido.
Calor Sensível - É energia térmica em trânsito que flui entre os corpos em razão da diferença de temperatura entre eles. Dessa forma, imagine uma barra de ferro que receba ou perca certa quantidade de calor (Q). Esse calor que a barra ganhou ou perdeu é denominado de calor sensível, pois ele provoca apenas variação na temperatura do corpo sem que aconteça mudança em seu estado de agregação, ou seja, se o corpo é sólido, continua sólido.
Calor Latente - É a grandeza física que está relacionada à quantidade de calor que um corpo precisa receber ou ceder para mudar de estado físico.
Onde L é o calor latente da substância e tem como unidade a cal/g. O calor latente pode assumir tanto valores positivos quanto negativos. Se for positivo, quer dizer que o corpo está recebendo calor; se negativo, ele está cedendo calor.
Capacidade Térmica - Determina a quantidade calor que um corpo precisa receber para alterar sua temperatura em uma unidade. Cada corpo comporta-se de forma diferente ao receber uma determinada quantidade de calor, e um exemplo em que podemos perceber isso facilmente ocorre na praia. A areia e a água do mar estão submetidas à mesma fonte de calor, o sol, mas a areia fica muito mais quente do que a água. Isso acontece porque a areia e a água possuem capacidades térmicas diferentes.
Sendo assim, a capacidade térmica é uma grandeza que depende da quantidade de calor recebida e da variação de temperatura sofrida por um corpo. Ela pode ser definida da seguinte forma:
“A capacidade térmica (C) é a razão entre a quantidade de calor (Q) recebida por um corpo e a variação de temperatura (ΔT) sofrida por ele.”
Matematicamente, essa relação é dada pela expressão:
C = Q
ΔT
Observação: A unidade de medida da capacidade térmica no Sistema Internacional é calorias por grau Celsius (cal/ºC). Um exemplo para compreender melhor a interpretação dessa grandeza é a seguinte situação:
Se um corpo recebe 1000 cal e aumenta sua temperatura em 20ºC, sua capacidade térmica é?
C = Q = 1.000 = 50 cal/ºC
ΔT 20
Ou seja, a cada 50 calorias que o corpo recebe, sua temperatura varia em 1ºC.
A capacidade térmica é uma propriedade dos corpos que depende apenas de sua massa, sendo assim, dois corpos feitos do mesmo material podem sofrer variações de temperatura diferentes ao receberem a mesma quantidade de calor se suas massas são diferentes. Por exemplo: se quisermos aquecer duas chapas de metal, uma com 5 kg e outra com 10 kg, será necessário fornecer maior quantidade de calor à chapa de 10 kg, já que sua massa é maior.
Observação: a capacidade térmica é a grandeza que caracteriza a variação de temperatura sofrida por corpos. É uma característica do corpo, e não da substância.
EXERCÍCIOS RESOLVIDOS
58) (Fuvest) Em um laboratório de Física, uma amostra de 20 g de cobre recebeu 186 cal de calor de uma determinada fonte térmica. Sabendo que o calor específico do cobre é 0,093 cal/g°C, determine a variação de temperatura sofrida pela amostra.
Q = m.c.Δt
186 = 20 . 0,093 . Δt
186 = 1,86. Δt
Δt = 186 ÷ 1,86
Δt = 100 °C
59) (PUC) Determine a capacidade térmica de um corpo que recebeu 2000 calorias de calor de uma fonte térmica e sofreu uma variação de temperatura de 40°C.
C = Q ÷ Δt
C = 2000 ÷ 40
C = 50 cal/°C
60) (Fuvest) Determine o calor específico em cal/g°C de uma substância com massa de 1 kg que, ao receber 5000 cal de calor de uma fonte térmica, teve a sua temperatura elevada em 20 °C.
Q = m . c . ΔT
5000 = 1000 . c . 20
5000 = 20.000 c
c = 5000
20.000
c = 5
20
c = 1
4
c = 0,25 cal/g°C
61) (UF - Paraná) Para aquecer 500 g de certa substância de 20 ºC para 70 ºC, foram necessárias 4 000 calorias. A capacidade térmica e o calor específico valem respectivamente:.gif)
63) (Makenzie - SP) Em uma manhã de céu azul, um banhista na praia observa que a areia está muito quente e a água do mar está muito fria. À noite, esse mesmo banhista observa que a areia da praia está fira e a água do mar está morna.
O fenômeno observado deve-se ao fato de que:
(A) a densidade da água do mar é menor que a da areia.
(B) o calor específico da areia é menor que o calor específico da água.
(C) o coeficiente de dilatação térmica da água é maior que o coeficiente de dilatação térmica da areia.
(D) o calor contido na areia, à noite, propaga-se para a água do mar.
(E) a agitação da água do mar retarda seu resfriamento.
Alternativa: B
64) (FUVEST – SP) Um amolador de facas, ao operar um esmeril, é atingido por fagulhas incandescentes, mas não se queima.
Isso acontece porque as fagulhas:
(A) tem calor específico muito grande.
(B) tem temperatura muito baixa.
(C) tem capacidade térmica muito pequena.
(D) estão em mudança de estado.
(E) não transportam energia.
Alternativa: C
65) (UFU) 240 g de água (calor específico igual a 1 cal/g°C) são aquecidos pela absorção de 200 W de potência na forma de calor. Considerando 1 cal = 4 J, o intervalo de tempo necessário para essa quantidade de água variar sua temperatura em 50 °C será de?
(A) 1 min
(B) 3 min
(C) 2 min
(D) 4min
Resolução:
Massa: 240 g
Potência fornecida: 200 W
Variação de temperatura: Δθ = 50 °C
A potência é definida como a razão entre a quantidade de energia e o tempo:
P = E/Δt
O calor é a energia fornecida à água, sendo assim, podemos escrever:
P = m.c.Δθ / Δt
Δθ é a variação de temperatura e Δt é a variação do tempo.
Unidade W corresponde a J/s.
Calor específico (c) da água é 1.
1joule = 4 J/g.ºC.
Substituindo os valores, teremos:
200 = (240.4.50) / Δt
Δt = (240.4.50) / 200
Δt = 48000 / 200
Δt = 240s
Δt = 4 min
Alternativa: D
66) (UFV-MG) Uma potência de 2000 watts é usada durante 1,0 min para elevar a temperatura, de 10°C para 60°C, de um sólido de massa 0,5kg. Considerando que não há mudança de fase durante a elevação da temperatura, o calor específico desse sólido, em unidade de J/(Kg°C), é:
(A) 4,8 . 103
(B) 3,4 . 103
(C) 5,6 . 103
(D) 1,2 . 103
(E) 0,8 . 103
Resolução:
Variação de tempo:
Δt = 1,0 = 60s
Variação de temperatura:
Δθ = 60 – 10
Δθ = 50°C
A potência é definida como a razão entre a quantidade de energia e o tempo, sendo assim, temos:
P = E/Δt
O calor foi a energia fornecida à água, sendo assim, podemos escrever:
P = m.c.Δθ / Δt
Isolando o calor específico, teremos:
c = P. Δt / m. Δθ
Substituindo os valores, teremos:
c = 2000 W.60 s / 0,5 Kg. 50°C
c = 120000 / 25
c = 4800 = 4,8 . 103 J/(Kg°C)
Alternativa: A
67) (IFPE) No preparo de uma xícara de café com leite, são utilizados 150ml (150g) de café, a 80ºC, e 50ml (50g) de leite, a 20ºC. Qual será a temperatura do café com leite?
(Utilize o calor específico do café = calor específico do leite = 1,0cal/gºC)
(A) 65 ºC
(B) 50 ºC
(C) 75 ºC
(D) 80 ºC
(E) 90 ºC
Resolução:
Como foi dito, a soma das quantidades de calor deve ser nula. Assim, temos:.jpg)
Alternativa: A
68) (Enem) Aquecedores solares usados em residências têm o objetivo de elevar a temperatura da água até 70°C. No entanto, a temperatura ideal da água para um banho é de 30°C. Por isso, deve-se misturar a água aquecida com a água à temperatura ambiente de um outro reservatório, que se encontra a 25°C.
Qual a razão entre a massa de água quente e a massa de água fria na mistura para um banho à temperatura ideal?
(A) 0,111.
(B) 0,125.
(C) 0,357.
(D) 0,428.
(E) 0,833.
Resolução
O equilíbrio térmico é atingido quando as temperaturas dos dois corpos ficam iguais. Quando isso ocorre, a quantidade de calor cedida pela água quente é igual ao calor recebido pela água fria.
Assim, podemos utilizar a equação:
Q1= - Q2
m1 . c . ΔT1= - m2 . c . ΔT2
O índice 2 é atribuído à água quente, e o índice 1, à água fria. O sinal negativo é dado a Q2 porque a água quente cede calor para a água fria, ou seja, perde parte de sua energia.
Como c é um valor constante, já que se trata da mesma substância, ele pode ser simplificado na equação, e o ΔT deve ser substituído pela diferença entre as temperaturas final e inicial da água:
m1 . (Tf - Ti) 1 = - m2 . (Tf - Ti)2
Substituindo os dados do problema, temos:
m1.(30 - 70) = - m2.(30 – 25)
m1 . (- 40) = - m2 . (5)
m1 = 5 / m2 = 40
m1= 0,125
Alternativa: B
69) Para derreter uma barra de um material w de 1kg é necessário aquecê-lo até a temperatura de 1000°C. Sendo a temperatura do ambiente no momento analisado 20°C e o calor específico de w=4,3J/kg.°C, qual a quantidade de calor necessária para derreter a barra?
70) Um bloco de ferro de 10cm³ é resfriado de 300°C para 0°C. Quantas calorias o bloco perde para o ambiente?
Dados: densidade do ferro = 7,85g/cm³ e calor específico do ferro = 0,11cal/g.°C
Resolução:
O primeiro passo é descobrir a massa do bloco, sabendo sua densidade e seu volume (é importante prestar bastante atenção nas unidades de cada grandeza).
Conhecendo a massa, podemos calcular a quantidade de calor do corpo:
Como Q < 0, a transferência de calor acontece no sentido do bloco para o meio ambiente (libera calor).
71) Qual a quantidade de calor absorvida para que 1L d'água congelado e à -20°C vaporize e chegue a temperatura de 130°C.
Dados:
Calor latente de fusão da água: L = 80cal/g
Calor latente de vaporização da água: L = 540cal/g
Calor específico do gelo: c = 0,5cal/g.°C
Calor específico da água: c =1cal/g.°C
Calor específico da água: c = 0,48cal/g.°C
Densidade da água: d:1g/cm³
1L = 1dm³ = 1000cm³
M = d . V
M = 1000g
72) Um bloco de uma material desconhecido e de massa 1kg encontra-se à temperatura de 80°C, ao ser encostado em outro bloco do mesmo material, de massa 500g e que está em temperatura ambiente (20°C). Qual a temperatura que os dois alcançam em contato? Considere que os blocos estejam em um calorímetro.
73) Em uma cozinha, uma chaleira com 1L de água ferve. Para que ela pare, são adicionados 500mL de água à 10°C. Qual a temperatura do equilíbrio do sistema?
Qualquer quantidade de água que esteja fervendo encontra-se à temperatura de 100°C, se a temperatura for superior a esta, não haverá água líquida, apenas vapor.
74) (UEA-AM) Dois blocos, A e B, feitos do mesmo material, apresentam os seguintes dados iniciais: Após troca de calor somente entre eles, e uma vez estabelecido o equilíbrio térmico, a temperatura final dos blocos será igual a:
Após troca de calor somente entre eles, e uma vez estabelecido o equilíbrio térmico, a temperatura final dos blocos será igual a:
(A) 10 ºC.
(B) 15 ºC.
(C) 20 ºC.
(D) 25 ºC.
(E) 30 ºC.
Resolução
A soma das quantidades de calor deve ser nula, sendo assim, temos:
.jpg)
Alternativa: D
75) (IFPE) No preparo de uma xícara de café com leite, são utilizados 150 ml (150 g) de café, a 80 ºC, e 50 ml (50 g) de leite, a 20 ºC. Qual será a temperatura do café com leite? (Utilize o calor específico do café = calor específico do leite = 1,0 cal/gºC)
(A) 65 ºC
(B) 50 ºC
(C) 75 ºC
(D) 80 ºC
(E) 90 ºC
Resolução:
A soma das quantidades de calor deve ser nula. Assim, temos:.jpg)
Alternativa: A
76) Determine a variação de temperatura sofrida por 3 kg de uma substância, de calor específico igual a 0,5 cal/g°C, que fica exposta durante 30 s a uma fonte térmica que fornece 1000 cal/s.
(A) 10 °C
(B) 15 °C
(C) 20 °C
(D) 30 °C
(E) 40 °C
Resolução:
Durante 30 segundos de exposição à fonte, a substância recebeu 30.000 cal de calor. Sabendo que 3 kg equivalem a 3.000 g, temos:.jpg)
Alternativa: C
77) Uma massa de 2 kg de água está a 100 °C. Determine a quantidade de calor necessária para que 20 % da substância sofra mudança para o estado gasoso.
Dado: LVAPORIZAÇÃO = 540 cal/g
(A) 200.000 cal
(B) 166.000 cal
(C) 216.500 cal
(D) 216.000 cal
(E) 116.000 cal
Resolução:
A massa total da substância corresponde a 2000 g, e a massa transformada corresponde a 400 g. Aplicando a equação para a quantidade de calor latente, temos:![]()
Alternativa: D
78) Em um laboratório de Física, uma amostra de 20 g de cobre recebeu 186 cal de calor de uma determinada fonte térmica. Sabendo que o calor específico do cobre é 0,093 cal/g°C, determine a variação de temperatura sofrida pela amostra.
(A) 50 °C
(B) 100°C
(C) 105°C
(D) 200°C
(E) 250°C
Resolução:
A partir da equação que determina a quantidade de calor sensível fornecida ou retirada de um corpo, temos:
Q = m.c.Δt
186 = 20 . 0,093 . Δt
186 = 1,86. Δt
Δt = 186 ÷ 1,86 = 100 °C
Alternativa: B
79) Determine a capacidade térmica de um corpo que recebeu 2000 calorias de calor de uma fonte térmica e sofreu uma variação de temperatura de 40 °C.
(A) 10 cal/°C
(B) 20 cal/°C
(C) 30 cal/°C
(D) 40 cal/°C
(E) 50 cal/°C
Resolução:
A capacidade térmica é o produto da massa do corpo pelo calor específico, portanto:
C = m.c
A partir da equação que determina a quantidade de calor sensível fornecida ou retirada de um corpo, temos:
Q = m.c.Δt
Q = C.Δt
Logo:
C = Q ÷ Δt
C = 2000 ÷ 40
C = 50 cal/°C
Alternativa: D
80) (UFU) 240 g de água (calor específico igual a 1 cal/g°C) são aquecidos pela absorção de 200 W de potência na forma de calor. Considerando 1 cal = 4 J, o intervalo de tempo necessário para essa quantidade de água variar sua temperatura em 50 °C será de?
(A) 1 min
(B) 3 min
(C) 2 min
(D) 4min
Resolução:
Dados da questão
Massa: m = 240 g
Potência fornecida: 200 W
Variação de temperatura: Δθ = 50 °C
A potência é definida como a razão entre a quantidade de energia e o tempo:
P = E/Δt
O calor é a energia fornecida à água, sendo assim, podemos escrever:
P = m.c.Δθ
Δt
Δθ é a variação de temperatura e Δt é a variação do tempo.
A unidade W corresponde a J/s. Portanto o calor específico deverá estar definido em joule, sendo assim o valor utilizado para o calor específico da água será 4 J/g.ºC
Substituindo os valores, teremos:
200 = 240.4.50
Δt
Δt = 240.4.50
200
Δt = 48000
200
Δt = 240 s = 4 min
Alternativa: D
81) (UFV-MG) Uma potência de 2000 watts é usada durante 1,0 min para elevar a temperatura, de 10 °C para 60°C, de um sólido de massa 0,5 Kg. Considerando que não há mudança de fase durante a elevação da temperatura, o calor específico desse sólido, em unidade de J/(Kg°C), é:
(A) 4,8 x 10 3
(B) 3,4 x 10 3
(C) 5,6 x 10 3
(D) 1,2 x 10 3
(E) 0,8 x 10 3
Resolução:
Dados da questão:
Variação de tempo:
Δt = 1,0 = 60s
Variação de temperatura:
Δθ = 60 – 10 = 50 °C
A potência é definida como a razão entre a quantidade de energia e o tempo, sendo assim, temos:
P = E/Δt
O calor foi a energia fornecida à água, sendo assim, podemos escrever:
P = m.c.Δθ
Δt
Isolando o calor específico, teremos:
c = P. Δt
m. Δθ
Substituindo os valores, teremos:
c = 2000 W.60 s
0,5 Kg. 50°C
c = 120000
25
c = 4800 = 4,8 x 103 J/(Kg°C)
Alternativa: A
82) Adriana colocou 70 ml de café em uma xícara. Após tomar 20 ml do líquido, decidiu parar, pois o gosto não havia lhe agradado. O restante do café permaneceu na xícara exposto ao ambiente. Sabendo que o café sobressalente estava inicialmente a 75 °C, determine o módulo da quantidade de calor perdida pelo líquido para que a sua temperatura atingisse um valor correspondente a 25 °C.
Dados: Calor específico do café = 1 cal/g.°C; densidade do café = 1 g/cm3. (A) 2 Kcal
(A) 2 Kcal
(B 2,5 Kcal
(C) 3 Kcal
(D) 1,5 Kcal
(E) 1 Kcal
Resolução:
A quantidade de café a ser considerada é de 50 ml. Sendo assim, sabendo que a densidade considerada para o café foi de 1 g/cm3, podemos definir a massa do líquido a partir da equação da densidade.
d = m ÷ V
1 g/ cm3 = m ÷ 50 ml
Sabendo que a unidade ml corresponde à unidade cm3, temos:
1 g/ cm3 = m ÷ 50 cm3
m = 1 g/cm3 . 50 cm3
m = 50 g
Utilizando a equação para a quantidade de calor sensível, temos:
Q = m . c . ΔT
Q = 50 . 1 . ( 25 – 75 )
Q = 50 . 1 . (-50)
Q = - 2500 cal = - 2,5 Kcal
| Q | = 2,5 Kcal.
Alternativa: B
83) (Fatec) Um chuveiro elétrico de potência 4200 W é usado para aquecer 100 g de água por segundo em regime permanente. O calor específico da água é c = 4,2 J/g.°C. Despreze a possível perda de calor para o ambiente. Se a temperatura de entrada da água no chuveiro é de 23°C, sua temperatura de saída é de:
(A) 28 °C
(B) 33 °C
(C) 38 °C
(D) 41 °C
(E) 45 °C
Resolução:
Considerando uma quantidade de 100 g de água e sabendo que a unidade watt (W) é dada em J/s (joules por segundo), podemos dizer que, em 1s, a energia fornecida para a massa de água foi de 4200 J. Sendo assim, temos:
Q = m . c . ΔT
4200 = 100 . 4,2 ( TFINAL – 23)
4200 = 420 ( TFINAL – 23)
TFINAL – 23 = 4200 ÷ 420
TFINAL – 23 = 10
TFINAL = 10 + 23
TFINAL = 33 °C
Alternativa: B
84) (UFG) O cérebro de um homem típico, saudável e em repouso consome uma potência de aproximadamente 16 W. Supondo que a energia gasta pelo cérebro em 1 min fosse completamente usada para aquecer 10 ml de água, a variação de temperatura seria de, aproximadamente:
DADOS: densidade da água: 1,0 x 103 kg/m3; calor específico da água: 4,2 x 103 J/kg °C)
(A) 0,5 °C
(B) 2 °C
(C) 11 °C
(D) 23 °C
(E) 48 °C
Resolução:
Sabendo que a potência é fruto da razão entre a energia (E) consumida e o intervalo de tempo (Δt) e que 1 min corresponde a 60 s, temos:
P = E ÷ Δt
16 = E ÷ 60
E = 16 . 60
E = 960 J
A energia consumida pelo cérebro em repouso é de 960 J.
Determinando a massa de água:
10 ml correspondem a 10 cm3 de água; 10 cm3 = 10 x 10 – 6 m3 = 1 x10– 5 m3.
Por meio da equação de densidade, temos:
d = m ÷ V
1,0 x 103 = m ÷ 1 x10 – 5
m = 1,0 x 103 . 1 x10 – 5
m = 1,0 x 10 -2 kg
Aplicando a equação da quantidade de calor sensível, temos:
Q = m . c . ΔT
960 = 1,0 x 10 -2 . 4,2 x 103 . ΔT
960 = 4,2 x 10 . ΔT
960 = 42 . ΔT
ΔT = 22,8 °C ≈ 23°C
Alternativa: D
85) A embalagem de um produto alimentício traz a informação de que a quantidade de calorias existentes em uma porção de 240 ml de seu conteúdo é 150 Kcal. Qual seria a variação de temperatura de 30 kg de água se toda a energia disponível em 1200 ml desse determinado alimento fosse completamente utilizada para aquecê-la?
DADOS: 1 Kcal = 4,0 KJ; calor específico da água: 4 KJ/kg °C
(A) 25 °C
(B) 30 °C
(C) 15 °C
(D) 10 °C
(E) 5 °C
Resolução:
A energia disponível em 1200 ml do alimento é 5 vezes maior que aquela disponível em 240 ml (240 x 5 = 1200). Sendo assim, a energia será:
150 Kcal . 5 = 750 Kcal
Sabendo que cada Kcal corresponde a 4 KJ, temos: 750 Kcal . 4 = 3000 KJ
Aplicando a equação da quantidade de calor sensível, temos:
Q = m . c . ΔT
3000 = 30. 4 . ΔT
ΔT = 3000 ÷ 120
ΔT = 25°C
Alternativa: A
Lei de Fourier
A lei da condução térmica, também conhecida como lei de Fourier, estabelece que o fluxo de calor através de um material é proporcional à temperatura.
Ao estudarmos a transmissão de calor por condução vimos que esse processo de transferência de calor ocorre através de todo o material através da troca de energia entre partículas próximas, ou seja, entre partículas adjacentes. O mecanismo de condução ocorre quando moléculas ou átomos que estão a uma temperatura mais elevada transferem parte da energia para as moléculas ou átomos próximos que estão com baixa energia. Assim, dizemos que a energia se transfere da região de alta temperatura para a região de baixa temperatura. A condução térmica visa o equilíbrio térmico do material.
Vamos agora apresentar a lei que rege a condução térmica, também conhecida como lei de Fourier. Ela recebeu esse nome em homenagem ao cientista que primeiro estudou detalhadamente a transmissão de calor por condução.
Na figura acima temos uma barra metálica ligada a dois recipientes, um contendo água em ebulição e outro contendo uma mistura de água e gelo. Pela figura vemos que a barra está isolada lateralmente.
Joseph Fourier, através de experimentos, conseguiu observar que a temperatura varia linearmente por toda a barra, ou seja, de uma extremidade a outra. Sendo assim, o fluxo de calor Φ através da barra é proporcional à área de seção A da barra e à diferença de temperatura, ΔT = Tf - Ti, entre as duas extremidades; e inversamente proporcional ao comprimento, L, da barra. Veja a figura abaixo: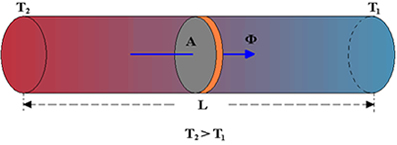 Podemos definir matematicamente que o fluxo de calor nada mais é do que o quociente do calor Q transmitido de uma face para outra, num intervalo de temperatura. Então, o fluxo de calor é definido por:
Podemos definir matematicamente que o fluxo de calor nada mais é do que o quociente do calor Q transmitido de uma face para outra, num intervalo de temperatura. Então, o fluxo de calor é definido por:![]() Analiticamente, a lei de Fourier, ou lei da condução térmica, pode ser expressa por:
Analiticamente, a lei de Fourier, ou lei da condução térmica, pode ser expressa por:![]() Na equação acima, k é uma constante que depende do material e é denominada condutividade térmica do material. O valor desse coeficiente é elevado para os bons condutores de calor; e baixo para os maus condutores, conhecidos como isolantes térmicos.
Na equação acima, k é uma constante que depende do material e é denominada condutividade térmica do material. O valor desse coeficiente é elevado para os bons condutores de calor; e baixo para os maus condutores, conhecidos como isolantes térmicos.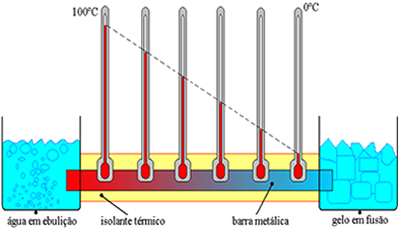
FLUXO DE CALOR
Fluxo de calor - Seja Q a quantidade de calor que passa por uma superfície S num intervalo de tempo Δt. Definimos fluxo de calor (ɸ) como sendo o quociente entre Q e Δt:
Observação: a unidade de fluxo de calor no SI é o watt (W) , isto é, joule por segundo. No entanto, são muito usadas as unidades caloria por segundo (cal/s) e caloria por minuto (cal/min). A definição de fluxo de calor é válida qualquer que seja o processo de propagação de calor através da superfície.
QUESTÕES RESOLVIDAS
01) Sabendo que o calor transmitido, durante 100s, é 200.000J, determine o fluxo de calor.
Resolução:
Calcularemos o fluxo de calor por meio da fórmula que o relaciona à quantidade de calor e à variação de tempo:
Φ =
Q = 200 000
Δt = 100
Φ = Q/Δt
Φ = 200 . 000/100
Φ = 2000 W
02) 30 000J de calor foi transmitida, durante dois minutos, determine o fluxo de calor.
Resolução:
Calcularemos o fluxo de calor por meio da fórmula que o relaciona à quantidade de calor e à variação de tempo:
Φ =
Q = 30 000
Δt = 120
Φ = Q/Δt
Φ = 300 000/120
Φ = 250 W
03) Dois cômodos vizinhos, separados por uma parede de 2 m de espessura e área de 10 m2, estão em temperaturas de T1 = 300 K e T2 = 500 K. Considerando que a condutividade térmica dessa parede é de 2 W/m.K, calcule o fluxo de calor entre eles.
Resolução:
Calcularemos o fluxo de calor por meio da fórmula que o relaciona à condutividade térmica, à área da secção transversal, à variação da temperatura e à espessura da parede:
Φ =
k = 2
A = 10
ΔT = 200
Tf = 500
Ti = 300
l = 4
Φ = k . A . ΔT
l
Φ = k . A - (Tf−Ti)
l
Φ = 2 . 10 . (500 −300)
4
Φ = 2 . 10 . 200
4
Φ = 100 W
04) Dois cômodos vizinhos, separados por uma parede de 0,5 m de espessura e área de 100 m2, estão em temperaturas de T1 = 288 K e T2 = 353 K. Considerando que a condutividade térmica dessa parede é de 2,5 W/m.K, calcule o fluxo de calor entre eles.
Resolução:
Calcularemos o fluxo de calor por meio da fórmula que o relaciona à condutividade térmica, à área da secção transversal, à variação da temperatura e à espessura da parede:
Φ =
k = 2,5
A = 100
ΔT = 65
Tf = 335
Ti = 288
l = 0,5
Φ = k . A . ΔT
l
Φ = k . A - (Tf−Ti)
l
Φ = 2,5 . 100⋅(353−288)
0,5
Φ = 2,5 . 100 . 65
0,5
Φ = 32 500 W
05) Qual será o fluxo de calor em uma barra de alumínio de espessura 30 cm e área de 600 cm2. O coeficiente de condutividade térmica do alumínio é: K = 0,5 cal/s.cm.°C. A barra sofreu uma variação de 30°C em sua temperatura. Use a equação:
(A) 300 cal/s
(B) 600 cal/s
(C) 60 cal/s
(D) 3.000 cal/s
Alternativa: A
02) Durante um dia ensolarado, uma grande quantidade de calor – cerca de 180 cal – passa através das janelas de um veículo que ficou estacionado em um local aberto, durante um tempo de 15 minutos. Determine o fluxo de calor através das janelas desse veículo nessa situação.
(A) 10.000 cal/s
(D) 2000 cal/s
(C) 50 cal/s
(D) 300 cal/s
(E) 500 cal/s
Resolução:
Para resolver o exercício, basta calcular a quantidade de calor que passa através das janelas do veículo a cada segundo. Observe: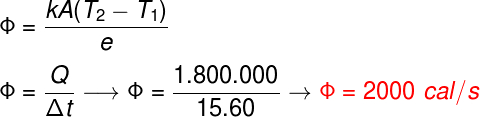
De acordo com o cálculo feito, cerca de 2000 calorias passam pelas janelas do veículo a cada segundo.
Alternativa: B
03) Assinale a alternativa em que ocorre exclusivamente condução de calor:
(A) Água quente sendo misturada com água fria.
(B) Papel sendo queimado pela luz solar, concentrada por uma lupa.
(C) Ferro de passar roupa queimando uma camisa.
(D) Vapor de água cozinhando um vegetal.
Resolução:
Entre os processos listados, o primeiro é uma transmissão de calor por convecção; em seguida, temos radiação, na letra B; condução, na letra C; por fim, na última alternativa, convecção novamente.
Alternativa: C
04) (UNIFENAS) A transmissão de calor por convecção só é possível:
(A) no vácuo
(B) nos sólidos
(C) nos líquidos
(D) nos gases
(E) nos fluidos em geral.
Resolução:
A transmissão de calor por convecção ocorre nos líquidos e nos gases em razão da diferença de densidade entre as partes internas desses fluidos.
Alternativa: E
05) (UNIFENAS) A transmissão de calor por convecção só é possível:
(A) no vácuo
(B) nos sólidos
(C) nos líquidos
(D) nos gases
(E) nos fluidos em geral.
Resolução:
A transmissão de calor por convecção ocorre nos líquidos e nos gases em razão da diferença de densidade entre as partes internas desses fluidos.
Alternativa: E
06) Marque a alternativa correta a respeito da Lei de Fourrier.
(A) A Lei de Fourier determina a quantidade de calor trocada entre duas regiões de uma superfície em função de suas dimensões.
(B) A Lei de Fourier determina o fluxo de calor entre duas regiões de uma superfície em função de suas dimensões.
(C) A Lei de Fourier mostra que o fluxo de calor entre duas regiões de uma superfície independe de suas dimensões.
(D) Na lei de Fourier, o fluxo de calor e a condutividade térmica do material que compõe a superfície são inversamente proporcionais.
(E) Todas as alternativas anteriores estão incorretas.
Resolução:
A Lei de Fourier determina o fluxo de calor entre duas regiões de uma superfície em função de suas dimensões.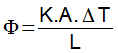
Alternativa: B
07) A condutividade térmica é a constante de proporcionalidade presente na Lei de Fourier. Sobre essa constante, marque a alternativa correta.
(A) É uma característica própria de cada material.
(B) Depende do estado de agregação das moléculas do material.
(C) Possui um valor fixo preestabelecido.
(D) É determinada na unidade Joule por segundo (J/s).
(E) Todas as alternativas estão incorretas.
Resolução:
A constante de proporcionalidade presente na Lei de Fourier caracteriza o material pelo qual flui o calor.
Alternativa: A
08) (IME-RJ) Um objeto de 160 g de massa repousa, durante um minuto, sobre a superfície de uma placa de 30 cm de espessura (L) e, ao final desse experimento, percebe-se que o volume do objeto é 1% superior ao inicial. A base da placa é mantida em 195 ºC, e nota-se que a sua superfície permanece em 175 ºC. A fração de energia, em percentagem, efetivamente utilizada para deformar a peça é:
Dados:
Condutividade térmica da placa (K): 50 w/m°C
Calor específico do objeto (c): 432 J/kg°C
Coeficiente de dilatação linear(α): 1,6.10–5 ºC–1
Área da placa (A): 0,6 m2
(A) 4
(B) 12
(C) 18
(D) 36
(E) 60
Resolução:
Inicialmente, utilizando a Lei de Fourier, deve-se determinar o fluxo de calor (Φ):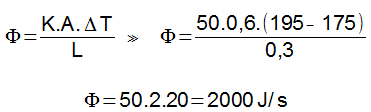
Sabendo que o fluxo de calor é definido pela razão entre o calor transmitido e o tempo, podemos determinar a quantidade de calor total transmitida entre as duas regiões da placa.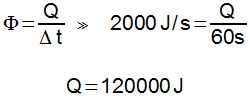
A partir da equação da dilatação volumétrica, podemos determinar a variação de temperatura sofrida pelo objeto. Devemos lembrar que o coeficiente de dilatação volumétrica (γ) corresponde ao triplo do coeficiente de dilatação linear (α).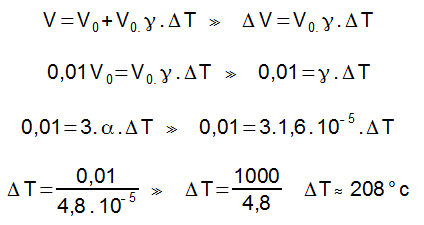
De posse da variação de temperatura sofrida pelo objeto, podemos agora determinar a quantidade de calor efetivamente recebido por ele.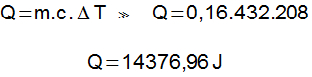
O calor efetivamente recebido pelo objeto (14376,96 J) corresponde a aproximadamente 12% do calor total (120000J) trocado entre as superfícies da placa.
Alternativa: B
09) (UFT-TO) Uma sala de estúdio é mantida à temperatura de 20 ºC e encontra-se separada de uma sala vizinha, à temperatura ambiente de 30 ºC, por uma janela retangular de vidro, de 8,0 mm de espessura, 1,0 m de altura por 1,5 m de largura. Sabendo que a condutividade térmica do vidro é 0,80 W/m.K, o total de calorias transmitidas pela janela, após 4,2 minutos é de, aproximadamente:
(A) 1,50 kcal.
(B) 37,8 kcal.
(C) 60,0 kcal.
(D) 90,0 kcal.
(E) 126 kcal.
Resolução:
Inicialmente, deve-se determinar o fluxo de calor (Φ) entre as duas salas: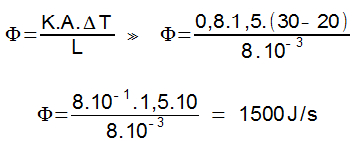
Sabendo que o fluxo de calor é definido pela razão entre o calor transmitido e o tempo, podemos determinar a quantidade de calor total transmitida.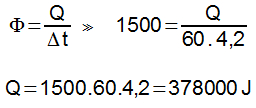
Adotando que 1 cal = 4,2 J, temos:![]()
Alternativa: D
FLUXO DE CALOR – RESOLVIDAS
86) (IME-RJ) Um objeto de 160 g de massa repousa, durante um minuto, sobre a superfície de uma placa de 30 cm de espessura (L) e, ao final desse experimento, percebe-se que o volume do objeto é 1% superior ao inicial. A base da placa é mantida em 195 ºC, e nota-se que a sua superfície permanece em 175 ºC. A fração de energia, em percentagem, efetivamente utilizada para deformar a peça é:
Dados:
-
Condutividade térmica da placa (K): 50 w/m°C
-
Calor específico do objeto (c): 432 J/kg°C
-
Coeficiente de dilatação linear( α): 1,6.10–5ºC–1
-
Área da placa (A): 0,6 m2
(A) 4
(B) 12
(C) 18
(D) 36
(E) 60
Resolução:
Inicialmente, utilizando a Lei de Fourier, deve-se determinar o fluxo de calor (Φ):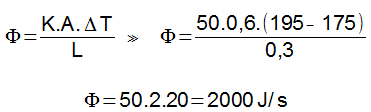
Sabendo que o fluxo de calor é definido pela razão entre o calor transmitido e o tempo, podemos determinar a quantidade de calor total transmitida entre as duas regiões da placa.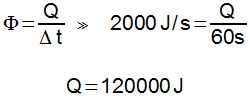
A partir da equação da dilatação volumétrica, podemos determinar a variação de temperatura sofrida pelo objeto. Devemos lembrar que o coeficiente de dilatação volumétrica (γ) corresponde ao triplo do coeficiente de dilatação linear (α).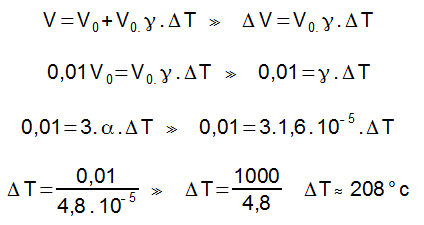
De posse da variação de temperatura sofrida pelo objeto, podemos agora determinar a quantidade de calor efetivamente recebido por ele.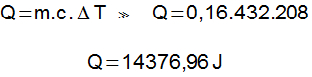
O calor efetivamente recebido pelo objeto (14376,96 J) corresponde a aproximadamente 12% do calor total (120000J) trocado entre as superfícies da placa.
Alternativa: B
87) (UFT-TO) Uma sala de estúdio é mantida à temperatura de 20 ºC e encontra-se separada de uma sala vizinha, à temperatura ambiente de 30 ºC, por uma janela retangular de vidro, de 8,0 mm de espessura, 1,0 m de altura por 1,5 m de largura. Sabendo que a condutividade térmica do vidro é 0,80 W/m.K, o total de calorias transmitidas pela janela, após 4,2 minutos é de, aproximadamente:
(A) 1,50 kcal.
(B) 37,8 kcal.
(C) 60,0 kcal.
(D) 90,0 kcal.
(E) 126 kcal.
Resolução:
Inicialmente, deve-se determinar o fluxo de calor (Φ) entre as duas salas: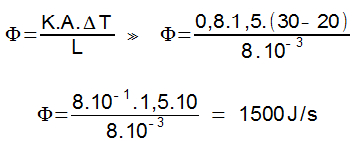
Sabendo que o fluxo de calor é definido pela razão entre o calor transmitido e o tempo, podemos determinar a quantidade de calor total transmitida.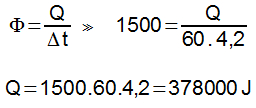
Adotando que 1 cal = 4,2 J, temos:![]()
Alternativa: D
88) Marque a alternativa correta a respeito da Lei de Fourrier.
(A) A Lei de Fourier determina a quantidade de calor trocada entre duas regiões de uma superfície em função de suas dimensões.
(B) A Lei de Fourier determina o fluxo de calor entre duas regiões de uma superfície em função de suas dimensões.
(C) A Lei de Fourier mostra que o fluxo de calor entre duas regiões de uma superfície independe de suas dimensões.
(D) Na lei de Fourier, o fluxo de calor e a condutividade térmica do material que compõe a superfície são inversamente proporcionais.
(E) Todas as alternativas anteriores estão incorretas.
Resolução:
A Lei de Fourier determina o fluxo de calor entre duas regiões de uma superfície em função de suas dimensões.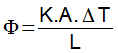
Alternativa: B
89) A condutividade térmica é a constante de proporcionalidade presente na Lei de Fourier. Sobre essa constante, marque a alternativa correta.
(A) É uma característica própria de cada material.
(B Depende do estado de agregação das moléculas do material.
(C) Possui um valor fixo preestabelecido.
(D) É determinada na unidade Joule por segundo (J/s).
(E) Todas as alternativas estão incorretas.
Resolução:
A constante de proporcionalidade presente na Lei de Fourier caracteriza o material pelo qual flui o calor.
Alternativa: A
DILATAÇÃO TÉRMICA Dilatação Térmica - Quando a temperatura de um corpo aumenta, a velocidade cinética das moléculas do corpo também aumenta, os espaço entre as moléculas e consequentemente o seu volume também aumenta. Do mesmo modo quando a temperatura de um corpo diminui a velocidade cinética das moléculas diminuem, os espaços entre as moléculas diminuem e consequentemente seu tamanho diminui.
Dilatação Térmica - Quando a temperatura de um corpo aumenta, a velocidade cinética das moléculas do corpo também aumenta, os espaço entre as moléculas e consequentemente o seu volume também aumenta. Do mesmo modo quando a temperatura de um corpo diminui a velocidade cinética das moléculas diminuem, os espaços entre as moléculas diminuem e consequentemente seu tamanho diminui.
Os prefixos nano, micro e pico são símbolos que indicam a potência de uma unidade de medida.
Micro (µ) = 10-6
Nano (n) = 10-9
Pico (p) = 10-12
Coeficiente de dilatação linear = α
Coeficiente de dilatação superficial = 2α
Coeficiente de dilatação volumétrica = 3α
DILATAÇÃO LINEAR
Dilatação Linear – Considera-se apenas a alteração do comprimento do corpo.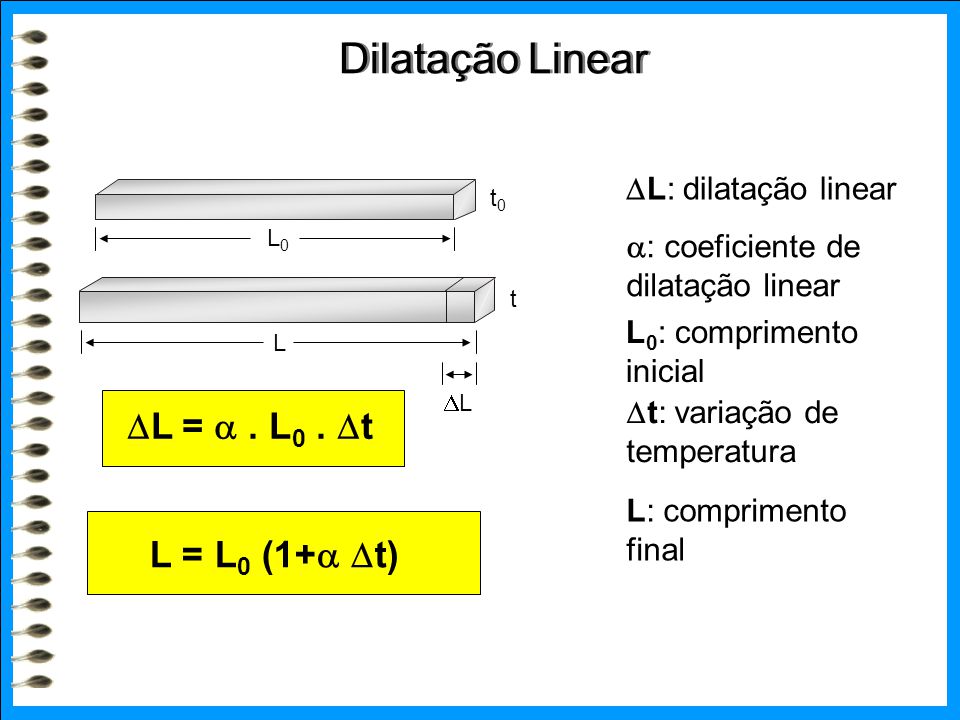

QUESTÕES RESOLVIDAS – DILATAÇÃO LINEAR
90) (UDESC/2012) Em um dia típico de verão utiliza-se uma régua metálica para medir o comprimento de um lápis. Após medir esse comprimento, coloca-se a régua metálica no congelador a uma temperatura de -10ºC e esperam-se cerca de 15 min para, novamente, medir o comprimento do mesmo lápis.
O comprimento medido nesta situação, com relação ao medido anteriormente, será:
(A) maior, porque a régua sofreu uma contração.
(B) menor, porque a régua sofreu uma dilatação.
(C) maior, porque a régua se expandiu.
(D) menor, porque a régua se contraiu.
(E) o mesmo, porque o comprimento do lápis não se alterou.
Resolução:
Ao colocar a régua dentro do congelador, ela sofre uma contração em seu comprimento. Ao medir o lápis com essa régua, o comprimento será maior do que o medido anteriormente.
Alternativa: A
91) Uma barra de 10 metros de alumínio a uma temperatura inicial de 20ºC fica exposta ao sol, sendo sua temperatura elevada para 40ºC. Sabendo que o coeficiente de dilatação do alumínio é αAl = 22.10 -6 ºC-1, calcule a dilatação sofrida pela barra.
Resolução:
A dilatação linear é dada pela equação:
ΔL = L0 . α . Δθ
Dados do problema:
L0 = 10 m
α = 22 . 10-6 ºC-1
Δθ = θf – θi = 40 – 20 = 20ºC
Substituindo os dados na equação, temos que:
ΔL = 10 . 22 . 10-6 . 20
ΔL = 44 . 10-4 m = 4,4 . 10-3 m
92) (UFLA-95) Uma barra de ferro homogênea é aquecida de 10ºC até 60ºC. Sabendo-se que a barra a 10ºC tem um comprimento igual a 5 m e que o coeficiente da dilatação linear do ferro é igual 1,2 x 10-6 ºC-1, podemos afirmar que a variação de dilatação ocorrida e o comprimento final da barra foram de:
(A) 5×10-4m; 5,0005m
(B) 2×10-4m; 5,0002m
(C) 4×10-4m; 5,0004m
(D) 3×10-4m; 5,0003m
(E) 6×10-4m; 5,0006m
Resolução:
L0 = 5m
Δθ = θf – θi = 60 – 10 = 50ºC
α = 1,2 x 10-6 ºC-1
Utilizamos a fórmula ΔL = L0 . α . Δθ para encontrar a dilatação.
Substituindo os dados, temos que:
ΔL = 5 . 1,2 x 10-6 . 50
ΔL = 300 . 10-6 m
ΔL = 3 . 10-4 m
O comprimento final é a soma do comprimento inicial mais a dilatação:
Lf = L0 + ΔL
Lf = 5 + 0,0003
Lf = 5,0003 m
93) Marque nas opções abaixo qual grandeza não interfere na dilatação dos sólidos:
(A) Natureza do material
(B) Comprimento inicial do sólido
(C) Variação de temperatura sofrida pelo sólido
(D) Tempo em que o sólido fica exposto à fonte de calor.
Resolução:
A equação utilizada para calcular a dilatação tem as seguintes grandezas:
L0 – é o comprimento inicial;
Δθ – é a variação de temperatura;
α - é o coeficiente de dilatação. Essa grandeza assume um valor para cada material utilizado.
O tempo não interfere na dilatação de um sólido.
Alternativa: D
95) A figura a seguir mostra uma esfera de aço de 50,1mm de diâmetro apoiada num anel de alumínio, cujo diâmetro interno é de 50,0 mm, ambos à mesma temperatura. Qual o acréscimo de temperatura que esse conjunto deve sofrer para que a esfera passe pelo anel?
Qual o acréscimo de temperatura que esse conjunto deve sofrer para que a esfera passe pelo anel?
Dados:
α aço = 1,08. 10-5 °C-1
e α al = 2,38 . 10-5 °C-1
Resolução:
Temos que admitir que quando a esfera passa pelo anel, o diâmetro da esfera de aço (L aço ) é igual ao diâmetro interno do anel de alumínio (L al ).
Portanto, basta determinar o valor de ∆T para que essa igualdade ocorra.
Assim, da expressão L = Lo + ∆L, podemos fazer:
L aço = L al → Lo aço + ∆L aço = Lo al + ∆L al → ∆L al - ∆L aço = Lo aço- Lo al (1)
Substituindo a expressão ∆L = α Lo ∆T em 1, obtemos:
α al Lo al ∆T - α aço Lo aço ∆T = Lo aço - Lo al
2,38.10-5.50,0.∆T - 1,08.10-5.50,1.∆T = 50,1 – 50,0
119.10-5 ∆T – 54,1. 10-5∆T = 0,1
64,9.10-5 ∆T = 0,1
∆T = 154 °C
97) A extensão de trilhos de ferro sofre dilatação linear, calcule o aumento de comprimento que 1000 m dessa ferrovia sofre ao passar de 0°C para 20°C, sabendo que o coeficiente de dilatação linear do ferro é 12.10-6 °C-1.
Resolução:
Obs: Aumento de comprimento sempre indica variação, ou seja, ∆L.
∆L = Lo α ∆T (o primeiro passo é substituir os valores dados na equação)
∆L = 1000. 12.10-6 .20
∆L = 20 000. 12.10-6 (nesse momento foi multiplicado os termos inteiros para depois trabalharmos com o expoente de base 10).
∆L = 24.10-2 (transformação de notação científica para forma decimal).
∆L = 0,24 m
DILATAÇÃO SUPERFICIAL
Dilatação Superficial – Considera-se apenas a alteração da superfície do corpo.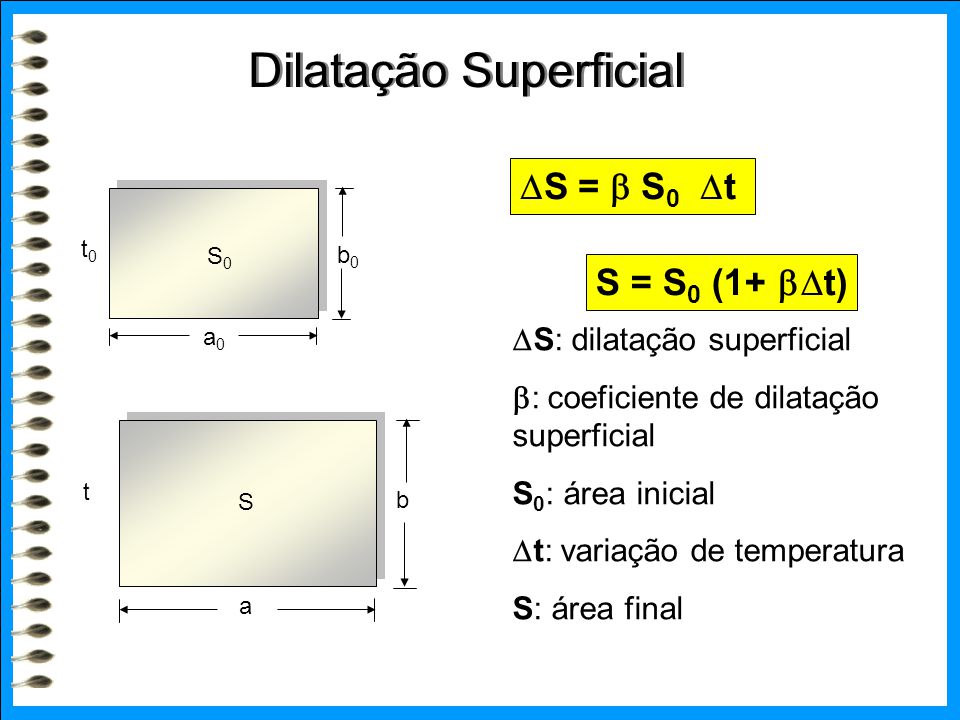 Observação: se soubermos o valor do coeficiente de dilatação linear (α) de uma determinada substância, poderemos também saber o valor do coeficiente de dilatação superficial (β) e o coeficiente de dilatação volumétrica (γ) da mesma.
Observação: se soubermos o valor do coeficiente de dilatação linear (α) de uma determinada substância, poderemos também saber o valor do coeficiente de dilatação superficial (β) e o coeficiente de dilatação volumétrica (γ) da mesma.
Observe a relação entre: α, β e γ
α
β = 2α
γ = 3α
RESOLVIDAS – DILATAÇÃO SUPERFICIAL
101) Um quadrado de lado 2m é feito de um material cujo coeficiente de dilatação superficial é igual a 1,6.10-4. Determine a variação de área deste quadrado quando aquecido em 80°C.
Resolução:
ΔA = Ao.β.ΔӨ
ΔA = 4.1,6 .10-4 .80
ΔA = 0,0512 m²
102) Uma placa retangular de alumínio tem 10cm de largura e 40cm de comprimento, à temperatura de 20ºC. Essa placa é colocada num ambiente cuja temperatura é de 50ºC. Sabendo que al = 46.10-6 °C-1, calcule:
a) A dilatação superficial da placa.
b) A área da placa nesse ambiente.
Resolução:
a) Cálculo da área inicial:
Si = 10 . 40 = 400cm2
Calculo da dilatação superficial:
S = Sit
S = 400.46.10-6.(50 - 20)
S = 0,522cm2
b) Sf = Si + S
Sf = 400 + 0,552
Sf = 400,552cm2
103) A área de uma chapa quadrada varia de 0,14 cm2 quando submetida a uma variação de 1000C na sua temperatura. Sendo a aresta do quadrado inicial de 10cm determine o coeficiente de dilatação linear (α) do material que constitui a chapa.
Resolução:
Dados:
∆S = 0,14 cm2
∆t = 100 0C
S0 = a
a = 10 cm x 10 cm =100 cm2.
∆S = S0 . β . ∆t
0,14 = 100.β . 100
β = 14. 10-6 0C-1
O coeficiente de dilação superficial é igual ao coeficiente de dilatação linear dividido por dois.
Dados:
β = 2.α
α = β / 2
α = 7 . 10-6 0C-1
Resposta: α = 7.10-6 0C-1
105) A superfície de um corpo é dilatada ao ser aquecido. Calcule a dilatação desse corpo sabendo que o coeficiente de dilatação superficial é de 20µ °C-1, a superfície inicial é de 100 cm² e que a variação da temperatura foi de 130°C. µ = 10-6
Resolução:
Dados:
ΔS = ?
ΔΘ = 130 °C
β = 20µ °C-1
Si = 100 cm²
Agora é só substituir na fórmula da dilatação superficial.
ΔS = Si x β x ΔΘ
ΔS = 100 x 20µ x 130
ΔS = 260000 µ
ΔS = 0,26 cm²
A superfície do corpo dilatou 0,26 cm²
106) Um corpo sofre dilatação ao ser aquecido e contrai ao ser resfriado. Um corpo foi resfriado, passando de 800 °C para 50 °C. A superfície inicial do corpo media 40 m² e o coeficiente de dilatação superficial do corpo é de 90µ °C-1. Calcule a variação da superfície do corpo. µ = 10-6
Resolução:
ΔΘ = 50 – 800 = -750 °C
β = 90µ °C-1
Si = 40 m²
Agora é só substituir na fórmula da dilatação superficial.
ΔS = Si x β x ΔΘ
ΔS = 40 x 90µ x (-750)
ΔS = -2700000 µ
ΔS = -2,7 m²
A superfície contraiu 2,7 m²
DILATAÇÃO VOLUMÉTRICA
Dilatação Volumétrica – Considera-se a alteração do volume do corpo.
RESOLVIDAS – DILATAÇÃO VOLUMÉTRICA
107) (MACK-SP) No estudo dos materiais utilizados para a restauração de dentes, os cientistas pesquisam entre outras características o coeficiente de dilatação térmica. Se utilizarmos um material de dilatação térmica inadequado, poderemos provocar sérias lesões ao dente, como uma trinca ou até mesmo sua quebra.
Nesse caso, para que a restauração seja considerada ideal, o coeficiente de dilatação volumétrica do material de restauração deverá ser:
(A) igual ao coeficiente de dilatação volumétrica do dente.
(B) maior que o coeficiente de dilatação volumétrica do dente, se o paciente se alimenta predominantemente com alimentos muito frios.
(C) menor que o coeficiente de dilatação volumétrica do dente, se o paciente se alimenta predominantemente com alimentos muito frios.
(D) maior que o coeficiente de dilatação volumétrica do dente, se o paciente se alimenta predominantemente com alimentos muito quentes.
(E) menor que o coeficiente de dilatação volumétrica do dente, se o paciente se alimenta predominantemente com alimentos muito quentes.
Resolução:
Para que não ocorram danos aos dentes, é necessário utilizar um material que sofra a mesma variação de volume que o dente com uma determinada variação de temperatura. Portanto, o material deve ter o mesmo coeficiente de dilatação volumétrica do dente.
Alternativa: A
108) (Cesesp-PE) O tanque de gasolina de um carro, com capacidade para 60 litros, é completamente cheio a 10°C, e o carro é deixado num estacionamento onde a temperatura é de 30°C.
Sendo o coeficiente de dilatação volumétrica da gasolina iguala 1,1 10-3 °C-1 e considerando desprezível a variação de volume do tanque, a quantidade de gasolina derramada é, em litros:
(A) 1,32
(B) 1,64
(C) 0,65
(D) 3,45
(E) 0,58
Resolução:
Vi = 60 L
ti = 10 °C
tF 30 °C
γgasol. = 1,1 10-3 °C-1
Usamos a fórmula:
ΔV = Vi . γ (tf – ti)
ΔV = 60. 1,1 10-3 (30 – 10)
ΔV = 66 . 10-3 . 20
ΔV = 1,320 L
Alternativa: A
109) Três litros de água, a 30ºC, foram colocados em uma panela de ferro e aquecidos até atingir a temperatura final de 90ºC. Desconsiderando a dilatação sofrida pela panela, calcule o volume da água, após o aquecimento, sabendo que seu coeficiente de dilatação volumétrica é γ = 1,3 . 10-4 ºC-1.
Resolução:
Vi = 3L
ti = 30ºC
tf = 90ºC
γ =1,3 . 10-4 ºC-1.
Usamos a fórmula:
ΔV = Vi . γ (tf – ti)
ΔV = 3. 1,3 . 10-4 . (90 – 30)
ΔV = 3,9 . 10-4 . 60
ΔV = 234 . 10-4
ΔV = 0,0234 L
O volume final é dado pela soma do volume inicial com a dilatação sofrida pela água:
Vf = Vi + ΔV
Vf = 3 + 0,0234
Vf = 3,0234 L
110) Uma substância, ao ser submetida a uma variação de temperatura de 80ºC, sofreu dilatação, aumentado seu volume em 10L.
Calcule o coeficiente de dilatação volumétrica dessa substância. Considere o volume inicial Vi = 500L.
Resolução:
ΔV = 10L
Δt = 80ºC
Vi = 500 L
ΔV = Vi . γ Δt
γ = ΔV
Vi . Δt
γ = 10
500 . 80
γ = 10
40000
γ = = 2,5 . 10-4 ºC-1
111) A respeito da dilatação dos líquidos e da dilatação irregular da água, marque o que for falso.
(A) No aquecimento da água entre 0°C e 4°C, ocorre aumento de volume.
(B) A 4 °C, a água assume a sua maior densidade dentro do intervalo de 0°C a 4°C.
(C) A dilatação irregular da água ocorre somente em recipientes com coeficiente de dilatação que corresponda ao dobro do valor do coeficiente de dilatação da água.
(D) Pode-se considerar que, entre 0°C e 4°C, o coeficiente de dilatação da água é negativo.
Resolução:
A dilatação irregular da água ocorre independentemente do valor do coeficiente de dilatação do recipiente.
Alternativa: C
112) Um recipiente de vidro comum, de coeficiente de dilatação linear igual a 9,0 x 10– 6 °C – 1, está completamente cheio de álcool etílico, de coeficiente de dilatação volumétrica igual a 0,75 x 10– 3°C – 1. Após o conjunto sofrer uma variação de temperatura (ΔT), ocorre vazamento de líquido.
Determine o valor aproximado do coeficiente de dilatação volumétrica aparente para o álcool etílico.
(A) 1,23 x 10- 4°C- 1
(B) 6,00 x 10- 4°C- 1
(C) 6,23 x 10- 4°C- 1
(D) 7,23 x 10- 4°C- 1
(E) 2,23 x 10- 4 °C- 1
Resolução:
Da dilatação volumétrica dos líquidos, sabemos que:
ΔVREAL = ΔVAP + ΔVREC
ΔVAP corresponde à variação de volume aparente do líquido e ΔVREC refere-se à variação de volume do recipiente.
Substituindo na equação de dilatação volumétrica, teremos:
ΔVREAL = ΔVAP + ΔVREC
V0 . γ REAL. ΔT = V0 . γ AP. ΔT + V0 . γ REC. ΔT
γ REAL= γ AP + γ REC
0,75 x 10 – 3 = γ AP + 27 x 10 – 6
γ AP = 0,75 x 10 – 3 - 0,027 x 10 – 3
γ AP = 7,23 x 10 - 4 °C - 1
Alternativa: D
113) (AFA) Um recipiente de vidro de 200ml de volume está completamente cheio de mercúrio, e ambos se encontram a 30°C. Se a temperatura do sistema líquido-recipiente sobe para 90°C, qual é o volume de mercúrio, em ml, que transborda do recipiente?
Dados
γHg = 1,8 x 10– 4 °C–1
γvidro = 3,0 x 10–5 °C–1
(A) 1,8
(B) 2,6
(C) 5,0
(D) 9,0
Resolução:
Da dilatação volumétrica dos líquidos, sabemos que:
ΔVREAL = ΔVAP + ΔVREC
Substituindo na equação de dilatação volumétrica, teremos:
V0 . γHg. ΔT = V0 . γVIDRO. ΔT + ΔVAP
200 . 1,8 x 10 – 4 . (90 – 30) = 200 . 3,0 x 10 –5 . (90 – 30) + ΔVAP
2,16 = 0,36 + ΔVAP
ΔVAP = 1,8 ml
Alternativa: A
114) (AFA) Um recipiente tem capacidade de 3000cm3 a 20°C e está completamente cheio de um determinado líquido. Ao aquecer o conjunto até 120°C, transbordam 27cm3. O coeficiente de dilatação aparente desse líquido, em relação ao material de que é feito o recipiente, é, em °C– 1, igual a:
(A) 3,0 x 10– 5
(B) 9,0 x 10– 5
(C) 2,7 x 10– 4
(D) 8,1 x 10– 4
Resolução:
O volume extravasado corresponde à variação de volume aparente do líquido ΔVAP. Portanto:
ΔVAP = V0 . γAP ΔT
27 = 3000 . γAP . (120 – 20)
27 = 300.000 . γAP
γAP = 27
300.000
γAP = 9,0 x 10 – 5 °C - 1
Alternativa: B
115) (ENEM) Durante uma ação de fiscalização em postos de combustíveis, foi encontrado um mecanismo inusitado para enganar o consumidor. Durante o inverno, o responsável por um posto de combustível compra álcool por R$ 0,50/litro, a uma temperatura de 5°C. Para revender o liquido aos motoristas, instalou um mecanismo na bomba de combustível para aquecê-lo, para que atinja a temperatura de 35 °C, sendo o litro de álcool revendido a R$ 1,60. Diariamente o posto compra 20 mil litros de álcool a 5°C e os revende.
Com relação à situação hipotética descrita no texto e dado que o coeficiente de dilatação volumétrica do álcool é de 1×10−3 °C−1, desprezando-se o custo da energia gasta no aquecimento do combustível, o ganho financeiro que o dono do posto teria obtido devido ao aquecimento do álcool após uma semana de vendas estaria entre
(A) R$ 500,00 e R$ 1.000,00.
(B) R$ 1.050,00 e R$ 1.250,00.
(C) R$ 4.000,00 e R$ 5.000,00.
(D) R$ 6.000,00 e R$ 6.900,00.
(E) R$ 7.000,00 e R$ 7.950,00.
Resolução
∆V = V0⋅y⋅∆T
∆V = 20000⋅1 . 10−3 ⋅ 30
∆V = 600 litros = variação volumétrica do álcool.
Para saber o lucro de uma semana, basta multiplicar por 7 dias, a R$ 1,60 por dia.
1,60 x 7 x 600 = 6720 reais.
Alternativa: D
116) (Unitau-SP) Um cubo metálico é constituído de um material cujo coeficiente de dilatação linear é α. Os lados desse cubo são iguais a x quando o objeto está em uma temperatura de vinte e cinco graus centígrados. Quando a temperatura do cubo é aumentada em 40%, a variação do volume do cubo será de?
(A) ΔV = 30 α . x3
(B) ΔV = 40 α . x3
(C) ΔV = 65 α . x3
(D) ΔV = 10 α . x3
(E) ΔV = 25 α . x3
Resolução:
A temperatura inicial é de 25°C. Se o aumento foi de 40% (0,4), a temperatura final é:
25 + 25.0,4 = 25 + 10 = 35°C
Aplicando a equação da dilatação linear, teremos:
ΔV = V0 . γ . ΔT
ΔV = (x.x.x) . γ .(35 – 25)
ΔV = x3 . γ .10
Como γ = 3.α, teremos:
ΔV = x3 . 3. α .10
ΔV = 30 α . x3
Alternativa: A
RESOLVIDAS – DILATAÇÃO TÉRMICA
117) (ITA) O vidro pirex apresenta maior resistência ao choque térmico do que o vidro comum porque:
(A) possui alto coeficiente de rigidez.
(B) tem baixo coeficiente de dilatação térmica.
(C) tem alto coeficiente de dilatação térmica.
(D) tem alto calor específico.
(E) é mais maleável que o vidro comum.
Resolução:
No momento do choque térmico, o material que possuir o menor coeficiente de dilatação será o mais resistente, uma vez que sofrerá uma menor dilatação e, assim, não comprometerá a sua estrutura.
Alternativa: B
118) Dois fios metálicos A e B, feitos de materiais diferentes, possuem mesmo comprimento e temperatura iniciais. Quando a temperatura aumenta para um valor T, os comprimentos de A e B aumentam 2% e 6% , respectivamente.
Determine a razão aproximada entre o coeficiente de dilatação do fio A pelo coeficiente do fio B.
(A) 0,18
(B) 0,22
(C) 0,33
(D) 0,25
(E) 0,58
Resolução:
A dilatação dos fios corresponde à porcentagem de aumento referente ao tamanho inicial deles. A variação de temperatura sofrida por eles é igual, portanto:
Para o fio A, temos:
0,02 L0 = L0 . αA . ΔT
αA = 0,02
ΔT
Para o fio B, temos:
0,06 L0 = L0 . αB . ΔT
αB= 0,06
ΔT
A razão entre αA e αB será:
αA = 0,33
αB
Alternativa: C
119) (UPE) Uma barra de coeficiente de dilatação α = 5π x 10-4ºC-1, comprimento 2,0m e temperatura inicial de 25ºC está presa a uma parede por meio de um suporte de fixação S. A outra extremidade da barra B está posicionada no topo de um disco de raio R = 30cm. Quando aumentamos lentamente a temperatura da barra até um valor final T, verificamos que o disco sofre um deslocamento angular Δθ = 30º no processo.
Observe a figura a seguir:.jpg) Supondo que o disco rola sem deslizar e desprezando os efeitos da temperatura sobre o suporte S e também sobre o disco, calcule o valor de T.
Supondo que o disco rola sem deslizar e desprezando os efeitos da temperatura sobre o suporte S e também sobre o disco, calcule o valor de T.
(A) 50 °C
(B) 75 °C
(C) 125 °C
(D) 300 °C
(E) 325 °C
Resolução:
O deslocamento linear Y correspondente ao giro de 30° do disco pode ser determinado pelo produto entre o ângulo em radianos e o raio do disco.
Sabendo que 30° = π temos:
6
Y = Δθ . R = π . 30 = 5 π cm
6
Sabendo que o deslocamento linear Y corresponde à dilatação da barra, temos:
Y = l0 .α . ΔT
5 π = 200 . 5π x 10-4 . ΔT
1 = 200 x 10-4 ΔT
ΔT . 2 x 10 – 2 = 1
ΔT = 1 = 50 °C
2 x 10 – 2
Como ΔT = T – T0 , temos:
50 = T – 25
T = 75 °C
Alternativa: B
120) Qual deve ser a variação de temperatura aproximada sofrida por uma barra de alumínio para que ela atinja uma dilatação correspondente a 0,2% de seu tamanho inicial?
Dados:
Coeficiente de dilatação do alumínio como 23 x 10 – 6 °C – 1.
(A) 97 °C
(B) 7 °C
(C) 70 °C
(D) 58 °C
(R) 87 °C
Resolução:
A dilatação sofrida pela barra corresponde à porcentagem de aumento, portanto:
0,002 L0 = L0 . αBARRA . ΔT
0,002 = 23x10 – 6 ΔT
ΔT = 86,9°C
Alternativa: E
121) (Fuvest) Para ilustrar a dilatação dos corpos, um grupo de estudantes apresenta, em uma feira de ciências, o instrumento esquematizado na figura abaixo. Nessa montagem, uma barra de alumínio com 30cm de comprimento está apoiada sobre dois suportes, tendo uma extremidade presa ao ponto inferior do ponteiro indicador e a outra encostada num anteparo fixo.
O ponteiro pode girar livremente em torno do ponto O, sendo que o comprimento de sua parte superior é 10cm e, o da inferior, 2cm. Se a barra de alumínio, inicialmente à temperatura de 25ºC, for aquecida a 225ºC, o deslocamento da extremidade superior do ponteiro será, aproximadamente, de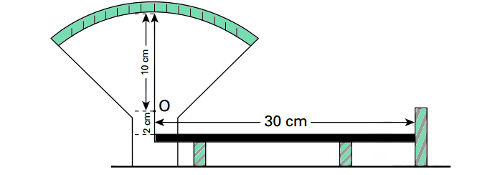 Dados
Dados
Coeficiente de dilatação linear da barra é de 2x10 – 5 °C - 1
(A) 1 mm
(B) 3 mm
(C) 6mm
(D) 12mm
(E) 30mm
Resolução:
O deslocamento do ponteiro inferior será igual à dilatação sofrida pela barra, portanto:
Δlinf = l0 .α . ΔT
Δlinf = 30x10 – 2 . 2x10 – 5 . ( 225 – 25)
Δlinf = 60x10 – 7 . 200
Δlinf = 120x10 – 5
Δlinf = 1,2x10 – 3 = 1,2 mm
A figura abaixo mostra o deslocamento dos ponteiros. Como o deslocamento angular α é pequeno, podemos considerar que os deslocamentos das partes superior e inferior são praticamente retilíneos.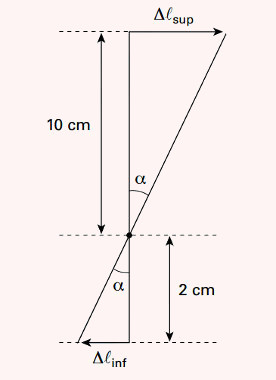 Aplicando a semelhança de triângulos, temos:
Aplicando a semelhança de triângulos, temos:
Δlsup = 10 portanto, Δlsup = 5 . Δlinf → Δlinf = 5 . 1,2mm = 6 mm
Δlinf 2
Alternativa: C
122) Uma barra de cobre com coeficiente de dilatação linear de 17x10–6 °C-1 está inicialmente a 30°C e é aquecida até que a sua dilatação corresponda a 0,17% de seu tamanho inicial.
Determine a temperatura final dessa barra.
(A) 85 °C
(B) 65 °C
(C) 105 °C
(D) 70 °C
(E) 80 °C
Resolução:
O aumento da barra deve corresponder a 0,17% do valor de seu comprimento inicial, portanto:
Δl = 0,17% l0
Δl = 0,0017 . l0
Δl = 1,7 x 10 – 3 . l0
Substituindo esse valor na equação da dilatação linear, temos:
Δl = l0 .α . ΔT
1,7 x 10 – 3 . l0 = l0 .α . ΔT
1,7 x 10 – 3 = α . ΔT
1,7 x 10 – 3 = ΔT. 17x10 – 6
ΔT = 1,7 x 10 – 3
17x10 – 6
ΔT = 100 °C
Como ΔT = T – T0 , temos:
100 = T – 30
T = 70 °C
Alternativa: D
123) Uma lâmina bimetálica composta por zinco e aço está fixada em uma parede de forma que a barra de aço permanece virada para cima. O que ocorre quando a lâmina é resfriada?
O que ocorre quando a lâmina é resfriada?
Dado:
αzinco = 25x10 – 6 °C – 1
αaço = 11x10 – 6 °C – 1
(A) As duas barras sofrem a mesma dilatação.
(B) A lâmina bimetálica curva-se para cima.
(C) A lâmina bimetálica curva-se para baixo.
(D) A lâmina quebra-se, uma vez que é feita de materiais diferentes.
(E) Lâminas bimetálicas não podem ser resfriadas.
Resolução:
Como o zinco possui maior coeficiente de dilatação, ele sofrerá maior contração no resfriamento, puxando a barra de aço. Logo, o sistema curva-se para baixo.
Alternativa: C
124) (ITA) O vidro pirex apresenta maior resistência ao choque térmico do que o vidro comum porque:
(A) possui alto coeficiente de rigidez.
(B) tem baixo coeficiente de dilatação térmica.
(C) tem alto coeficiente de dilatação térmica.
(D) tem alto calor específico.
(E) é mais maleável que o vidro comum.
Resolução:
No momento do choque térmico, o material que possuir o menor coeficiente de dilatação será o mais resistente, uma vez que sofrerá uma menor dilatação e, assim, não comprometerá a sua estrutura.
Alternativa: B
125) (UDESC-SC) A tabela abaixo apresenta uma relação de substâncias e os seus respectivos valores de coeficiente de dilatação linear e condutividade térmica, ambos medidos à temperatura de 20°C.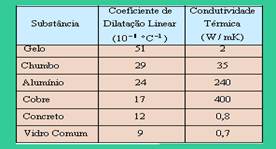 Assinale a alternativa correta, tomando como base as informações acima.
Assinale a alternativa correta, tomando como base as informações acima.
(A) Barras do mesmo comprimento dos metais listados na tabela sofrerão dilatações iguais, quando submetidas a uma variação de temperatura de 20 °C.
(B) A condutividade térmica das substâncias permanece constante, independentemente da temperatura em que estas se encontram.
(C) Substâncias que possuem maior condutividade térmica também apresentam maiores coeficientes de dilatação.
(D) Dentre as substâncias listadas na tabela, o cobre é a melhor opção para fazer isolamentos térmicos.
(E) Duas chapas de dimensões iguais, uma de alumínio e outra de concreto, são submetidas à mesma variação de temperatura. Constata-se então que a variação de dilatação superficial da chapa de alumínio é duas vezes maior que a da chapa de concreto.
Resolução:
Observe que o valor do coeficiente de dilatação do alumínio é o dobro do coeficiente de dilatação do concreto e, como elas tem as mesmas dimensões iniciais e sofrem a mesma variação de temperatura, a chapa de alumínio se dilata duas vezes mais do que a de concreto.
Alternativa: E
126) Uma lâmina de ferro tem dimensões 10m x 15m em temperatura normal. Ao ser aquecida 500ºC, qual será a área desta superfície?
Resolução:
DILATAÇÃO DOS LÍQUIDOS
Os líquidos se dilatam obedecendo as mesmas leis de dilatação dos sólidos. Primeiramente devemos nos lembrar que os líquidos não têm forma própria, e sim a forma do recipiente aonde eles se encontram. Portanto precisamos do estudo da dilatação volumétrica, pois quando aquecemos um liquido, aquecemos também o recipiente no qual ele esta contido.
Vamos entender melhor este processo. Imagine um liquido com coeficiente de dilatação volumétrica γL, que esteja contido em um recipiente de dilatação volumétrica γR, e inicialmente o volume ocupado pelo liquido seja de V0. Aquecendo o conjunto de forma que a temperatura varie Δθ, o liquido sofre uma dilatação volumétrica real igual a ΔVL, e o recipiente sofre uma dilatação volumétrica ΔVR. Essas variações podem ser escritas conforme:
ΔVL = γL . V0 . Δθ *
ΔVR = γR . V0 . Δθ **
Para relacionar essas duas relações, vamos admitir que elas ocorram em processos separados, ou seja, primeiro o líquido se dilata e posteriormente o recipiente. Com o líquido se dilatando primeiro temos um aumento do volume do mesmo no recipiente, que vamos chamar de ΔVL. Na fase em que o recipiente se dilata, o nível do líquido deve baixar, assim o aumento observado será chamado de dilatação volumétrica aparente (ΔVAp) e será dada como:
ΔVAp = ΔVL - ΔVR ***
Substituindo * e ** em ***:
ΔVAp = γL . V0 . Δθ - γR . V0 . Δθ
ΔVAp = (γL - γR) . V0 . Δθ
DILATAÇÃO APARENTE
Dilatação aparente - Como já mencionamos anteriormente, para aquecer um liquido, aquecemos também o recipiente onde o liquido esta contido. Assim ambos se dilatarão, e a capacidade do frasco também aumentará, portanto a dilatação que observaremos será a dilatação aparente. Deste modo, o coeficiente da dilatação aparente será a diferença entre o coeficiente de dilatação do liquido e o coeficiente de dilatação do recipiente:
γAp = γL - γR
Assim podemos concluir que a dilatação volumétrica aparente do líquido será dada por:
ΔVAp = γAp . V0 . Δθ
DILATAÇÃO ANÔMALA DA ÁGUA
A água possui um comportamento anômalo em sua dilatação.
Observe o diagrama volume x temperatura a seguir, no qual e mostrado esse comportamento incomum da água.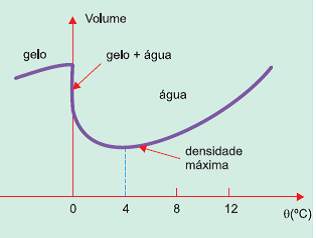 Assim como os corpos sólidos, os líquidos também têm seu volume aumentando ao ser aquecido (dilatação). Com isso, sua densidade diminui. No entanto, a água possui uma dilatação irregular. Por que isso ocorre? Existem outras substâncias que apresentam o mesmo comportamento?
Assim como os corpos sólidos, os líquidos também têm seu volume aumentando ao ser aquecido (dilatação). Com isso, sua densidade diminui. No entanto, a água possui uma dilatação irregular. Por que isso ocorre? Existem outras substâncias que apresentam o mesmo comportamento?
Existem outras substâncias que apresentam em determinadas faixas de temperatura um comportamento irregular em relação com a variação térmica; como por exemplo, o ferro.
O que realmente ocorre com a água?
Note que a 4°C o volume da água e mínimo e a sua densidade e máxima. Isto ocorre em virtude da formação das pontes de hidrogênio, abaixo de 4°C, quando as moléculas de H2O ficam maiores.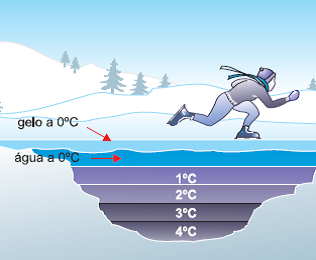 Na faixa de 0°C a 4°C o volume da água (H2O) diminui porque pontes de hidrogênio são quebradas. Acima de 4°C, predomina o aumento das distâncias médias entre as moléculas, ou seja, dilatação térmica.
Na faixa de 0°C a 4°C o volume da água (H2O) diminui porque pontes de hidrogênio são quebradas. Acima de 4°C, predomina o aumento das distâncias médias entre as moléculas, ou seja, dilatação térmica.
O que esse comportamento irregular da água pode causar no nosso cotidiano?
Com esse comportamento irregular da água, além de manter o clima mantém a vida nas regiões frias. Já pensou se a água não tivesse esse tipo de comportamento, a vida na terra já teria se extinguindo, se lembramos de que a terra já passou por vários períodos glaciais.
Nos países frios essa característica é fundamental, pois a uma gama de animais que vivem nessas regiões e que sem essa característica da água, não teriam da onde tirar o seu alimento.
Os diagramas abaixo ilustram o comportamento do volume e da densidade em função da temperatura.
Então, a 4°C, tem-se o menor volume para a água e, consequentemente, a maior densidade da água no estado líquido.
Observação: a densidade da água no estado sólido (gelo) é menor que a densidade da água no estado líquido.
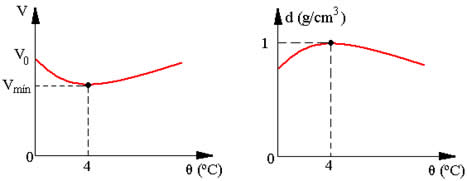
RESOLVIDOS - DILATAÇÃO DOS LÍQUIDOS
127) (ENEM) A gasolina é vendida por litro, mas em sua utilização como combustível, a massa é o que importa. Um aumento da temperatura do ambiente leva a um aumento no volume da gasolina. Para diminuir os efeitos práticos dessa variação, os tanques dos postos de gasolina são subterrâneos.
Se os tanques NÃO fossem subterrâneos:
I. Você levaria vantagem ao abastecer o carro na hora mais quente do dia pois estaria comprando mais massa por litro de combustível.
II. Abastecendo com a temperatura mais baixa, você estaria comprando mais massa de combustível para cada litro.
III. Se a gasolina fosse vendida por kg em vez de por litro, o problema comercial decorrente da dilatação da gasolina estaria resolvido.
Destas considerações, somente
(A) I é correta.
(B) II é correta
(C) III é correta
(D) I e II são corretas.
(E) II e III são corretas.
Resolução:
A densidade é a razão entre a massa e o volume. Um aumento de temperatura provoca um aumento de volume e consequentemente uma diminuição na densidade. Assim, a gasolina aquecida é menos densa que a gasolina fria. Ao comprar gasolina à uma temperatura mais baixa, teria mais massa por unidade de volume do que com temperatura mais alta.
Alternativa: E
128) Um recipiente tem capacidade de 5000cm3 a 40°C e está completamente cheio de um determinado líquido. Ao aquecer o conjunto até 140°C, transbordam 70cm3.
O coeficiente de dilatação aparente desse líquido, em relação ao material que constitui o recipiente, é, em °C – 1 , igual a
(A) 3,0 x 10– 5
(B) 9,0 x 10– 5
(C) 2,7 x 10– 4
(D) 1,4 x 10– 4
Resolução:
O volume extravasado corresponde à variação de volume aparente do líquido ΔVAP. Portanto, da dilatação volumétrica dos líquidos, temos:
ΔVAP = V0 . γAP ΔT
70 = 5000 . γAP . (140 – 40)
70 = 500.000 . γAP
γAP = 70
500.000
γAP = 1,4 x 10 – 4 °C - 1
Alternativa: E
129) O coeficiente de dilatação volumétrica do petróleo é de 0,9 x 10–3 °C-1 . Um recipiente, completamente cheio, contém três litros de petróleo e sofre uma variação de temperatura de 50°C.
Sabendo que o volume extravasado de petróleo corresponde a 115 ml, determine a variação de volume do recipiente.
(A) 20 ml
(B) 40 ml
(C) 50 ml
(D) 60 ml
(E) 70 ml
Resolução:
O volume extravasado corresponde à variação de volume aparente do líquido ΔVAP. Portanto, da dilatação volumétrica dos líquidos e sabendo que 3 l = 3000 ml, temos:
ΔVREAL = ΔVAP + ΔVREC
V0 . γ. ΔT = ΔVAP + ΔVREC
3000 . 0,9 x 10 – 3 . 50 = 115 + ΔVREC
135 = 115 + ΔVREC
ΔVREC = 135 – 115
ΔVREC = 20 ml
Alternativa: A
130) (MACKENZIE-SP) Quando um recipiente totalmente preenchido com um líquido é aquecido, a parte que transborda representa sua dilatação ________. A dilatação ________ do líquido é dada pela ______ da dilatação do frasco e da dilatação ________.
Com relação à dilatação dos líquidos, assinale a alternativa que, ordenadamente, preenche de modo correto as lacunas do texto acima.
(A) aparente ___________ real ___________ soma ___________ aparente
(B) real ___________ aparente ___________ soma ___________ real
(C) aparente ___________ real ___________ diferença ___________ aparente
(D) real ___________ aparente ___________ diferença ___________ aparente
(E) aparente ___________ real ___________ diferença ___________ real
Resolução:
O volume extravasado corresponde à variação de volume aparente do líquido ΔVAP. Da dilatação dos líquidos, sabemos que:
ΔVREAL = ΔVAP + ΔVREC
Alternativa: A
131) A respeito da dilatação irregular da água, marque o que for verdadeiro.
(A) Todos os líquidos, ao sofrerem variação de temperatura de 0 °C até 4 °C, diminuem seu volume. Somente a água faz o contrário.
(B) Quando a temperatura da água aumenta, entre 0 °C e 4 °C, seu volume diminui.
(C) Quando a água está a 4 °C, a sua densidade é a mínima possível.
(D) A dilatação irregular da água é percebida entre os intervalos de 0 °C a 4 °C e de 40 °C a 60 °C.
Resolução:
Quando a temperatura de um fluido aumenta, ele sofre aumento de volume. Todavia, a água, entre o intervalo de 0 °C e 4 °C, sofre diminuição de volume, sendo esse um comportamento anômalo.
Alternativa: B
132) A respeito da dilatação dos líquidos e da dilatação irregular da água, marque o que for falso.
(A) No aquecimento da água entre 0°C e 4°C, ocorre aumento de volume.
(B) A 4°C, a água assume a sua maior densidade dentro do intervalo de 0°C a 4°C.
(C) A dilatação irregular da água ocorre somente em recipientes com coeficiente de dilatação que corresponda ao dobro do valor do coeficiente de dilatação da água.
(D) Pode-se considerar que, entre 0°C e 4°C, o coeficiente de dilatação da água é negativo.
Resolução:
A dilatação irregular da água ocorre independentemente do valor do coeficiente de dilatação do recipiente.
Alternativa: C
133) Um recipiente de vidro comum, de coeficiente de dilatação linear igual a 9,0 x 10–6 °C–1, está completamente cheio de álcool etílico, de coeficiente de dilatação volumétrica igual a 0,75x10–3°C– . Após o conjunto sofrer uma variação de temperatura (ΔT), ocorre vazamento de líquido.
Determine o valor aproximado do coeficiente de dilatação volumétrica aparente para o álcool etílico.
(A) 1,23 x 10-4°C- 1
(B) 6,00 x 10-4°C-1
(C) 6,23 x 10-4°C-1
(D) 7,23 x 10-4°C-1
(E) 2,23 x 10-4°C-1
Resolução:
Da dilatação volumétrica dos líquidos, sabemos que:
ΔVREAL = ΔVAP + ΔVREC
ΔVAP corresponde à variação de volume aparente do líquido e ΔVREC refere-se à variação de volume do recipiente. Substituindo na equação de dilatação volumétrica, teremos:
ΔVREAL = ΔVAP + ΔVREC
V0 . γ REAL. ΔT = V0 . γ AP. ΔT + V0 . γ REC. ΔT
γ REAL= γ AP + γ REC
0,75 x 10 – 3 = γ AP + 27 x 10 – 6
γ AP = 0,75 x 10 – 3 - 0,027 x 10 – 3
γ AP = 7,23 x 10 - 4 °C - 1
Alternativa: D
134) (AFA) Um recipiente de vidro de 200ml de volume está completamente cheio de mercúrio, e ambos se encontram a 30°C. Se a temperatura do sistema líquido-recipiente sobe para 90°C, qual é o volume de mercúrio, em ml, que transborda do recipiente?
Dados:
γHg = 1,8 x 10–4 °C–1
γvidro = 3,0 x 10–5 °C–1
(A) 1,8
(B) 2,6
(C) 5,0
(D) 9,0
Resolução:
Da dilatação volumétrica dos líquidos, sabemos que: ΔVREAL = ΔVAP + ΔVREC. Substituindo na equação de dilatação volumétrica, teremos:
V0 . γHg. ΔT = V0 . γVIDRO. ΔT + ΔVAP
200 . 1,8 x 10 – 4 . (90 – 30) = 200 . 3,0 x 10 –5 . (90 – 30) + ΔVAP
2,16 = 0,36 + ΔVAP
ΔVAP = 1,8 ml
Alternativa: A
135) (AFA) Um recipiente tem capacidade de 3000cm3 a 20°C e está completamente cheio de um determinado líquido. Ao aquecer o conjunto até 120°C, transbordam 27cm3.
O coeficiente de dilatação aparente desse líquido, em relação ao material de que é feito o recipiente, é, em °C–1, igual a:
(A) 3,0 x 10–5
(B) 9,0 x 10–5
(C) 2,7 x 10–4
(D) 8,1 x 10–4
Resolução:
O volume extravasado corresponde à variação de volume aparente do líquido ΔVAP. Portanto:
ΔVAP = V0 . γAP ΔT
27 = 3000 . γAP . (120 – 20)
27 = 300.000 . γAP
γAP = 27
300.000
γAP = 9,0 x 10 – 5 °C - 1
Alternativa: B
136) O cilindro circular de aço do desenho abaixo se encontra em um laboratório a uma temperatura de -100ºC. Quando este chegar à temperatura ambiente (20ºC), quanto ele terá dilatado?
Resolução:
DadoSabendo que a área do cilindro é dada por:

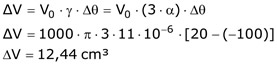
137) Um copo graduado de capacidade 10dm³ é preenchido com álcool etílico, ambos inicialmente à mesma temperatura, e são aquecidos em 100ºC. Qual foi a dilatação real do álcool?
Resolução:
Dado
A dilatação térmicas nas ferrovias
A dilatação térmica também pode causar problemas. Ferrovias podem ser fortemente danificadas se não forem planejadas adequadamente.
Os trilhos são feitos de metais que normalmente têm coeficiente de dilatação bem elevado, ou seja, com uma pequena variação de temperatura podem variar bastante seu volume. Neste caso, a oscilação da temperatura durante o dia podem entortá-los. Por isso as ferrovias são construídas com juntas de dilatação que, nesse caso, podem ser folgas planejadas para essas variações.
 Conclusão
Conclusão
O estudo sobre a dilatação térmica trouxe varias possibilidades para a Ciência. A própria invenção do termômetro foi muito importante para a comprovação de diversas teorias. Esse conhecimento também nos acarretou melhorias nas grandes construções que encontramos nas cidades, aumentando a confiabilidade das estruturas e a prevenção de acidentes. Vale lembrar que quando um corpo cede (perde) calor ele sofre contração térmica.
EXEMPLOS DE DILAÇÃO TÉRMICA DO DIA A DIA
Existem inúmeras situações nas quais os fenômenos de dilatação térmica são influentes em nossas vidas. Na grande maioria delas, sequer percebemos essa importância, seja pelo desconhecimento, seja pelos pequenos valores em que essas dilatações acontecem. Vamos enumerar algumas delas:
Exemplo 1: Ao colocarmos líquidos muito quentes em um copo de vidro, este pode rachar. Isso acontece porque o vidro, mal condutor de calor, se aquece mais rapidamente do lado de dentro do que do lado de fora. Desta forma, a parte interna do copo tende a dilatar mais rápido que a parte externa, causando uma tensão no vidro. Exemplo 2: Em pontes, viadutos e entre trilhos de trem e metrô, existem pequenos espaços deixados entre as placas de concreto ou entre os trilhos de ferro. Isso é feito de forma intencional. Esses espaços são chamados de juntas de dilatação. Servem para permitir que esses materiais, aquecidos pela passagem dos automóveis, possam dilatar sem deformar ou ruir as estruturas.
Exemplo 2: Em pontes, viadutos e entre trilhos de trem e metrô, existem pequenos espaços deixados entre as placas de concreto ou entre os trilhos de ferro. Isso é feito de forma intencional. Esses espaços são chamados de juntas de dilatação. Servem para permitir que esses materiais, aquecidos pela passagem dos automóveis, possam dilatar sem deformar ou ruir as estruturas. Exemplo 3: Em odontologia, os materiais utilizados para a realização de restaurações dentárias devem possuir coeficiente de dilatação muito próximo ao do esmalte dos dentes. Do contrário, ao serem aquecidas ou resfriadas durante a ingestão de algum alimento, as restaurações poderiam dilatar mais ou menos do que os dentes, danificando sua estrutura.
Exemplo 3: Em odontologia, os materiais utilizados para a realização de restaurações dentárias devem possuir coeficiente de dilatação muito próximo ao do esmalte dos dentes. Do contrário, ao serem aquecidas ou resfriadas durante a ingestão de algum alimento, as restaurações poderiam dilatar mais ou menos do que os dentes, danificando sua estrutura. Exemplo 4: A água, graças às suas características moleculares, possui uma característica incomum. Ao resfriarmos uma porção de água, por exemplo, a partir de 10 °C, a água tem seu volume diminuído. Mas isso deixa de acontecer a partir de 4 °C, quando seu volume passa a aumentar. Esse fato é conhecido como dilatação anômala da água e tem uma consequência interessante: o fato de que lagos localizados em regiões muito frias congelam apenas em sua superfície. Isso acontece porque, quando resfriada abaixo até 4°C, o volume da água diminui, aumentando sua densidade e fazendo com que as porções de água fria desçam, dando espaço para as camadas de água mais quentes do fundo, que serão resfriadas também. Isso ocorre até que toda a água do lago atinja 4°C, pois, a partir dessa temperatura, quando resfriada, o volume da água aumenta, diminuindo sua densidade e encerrando o movimento das camadas superiores, que serão resfriadas até 0 °C, quando a superfície congela.
Exemplo 4: A água, graças às suas características moleculares, possui uma característica incomum. Ao resfriarmos uma porção de água, por exemplo, a partir de 10 °C, a água tem seu volume diminuído. Mas isso deixa de acontecer a partir de 4 °C, quando seu volume passa a aumentar. Esse fato é conhecido como dilatação anômala da água e tem uma consequência interessante: o fato de que lagos localizados em regiões muito frias congelam apenas em sua superfície. Isso acontece porque, quando resfriada abaixo até 4°C, o volume da água diminui, aumentando sua densidade e fazendo com que as porções de água fria desçam, dando espaço para as camadas de água mais quentes do fundo, que serão resfriadas também. Isso ocorre até que toda a água do lago atinja 4°C, pois, a partir dessa temperatura, quando resfriada, o volume da água aumenta, diminuindo sua densidade e encerrando o movimento das camadas superiores, que serão resfriadas até 0 °C, quando a superfície congela.
TRANSFORMAÇÃO GASOSA
 Transformação Gasosa - No século XVII, vários cientistas realizaram experiências com o intuito de descobrir as particularidades das transformações gasosas. Dentre eles, podemos citar: Torriceli, Robert Boyle, Mariotte, Guericke, entre outros.
Transformação Gasosa - No século XVII, vários cientistas realizaram experiências com o intuito de descobrir as particularidades das transformações gasosas. Dentre eles, podemos citar: Torriceli, Robert Boyle, Mariotte, Guericke, entre outros.  Transformação Isotérmica ou Lei de Boyle-Mariotte - É a transformação na qual a temperatura T do gás se mantém constante, variando sua pressão p e seu volume V. Vale a seguinte relação:
Transformação Isotérmica ou Lei de Boyle-Mariotte - É a transformação na qual a temperatura T do gás se mantém constante, variando sua pressão p e seu volume V. Vale a seguinte relação:



Transformação Isobárica ou Lei de Gay-Lussac - A transformação isobárica, como o nome diz, é uma transformação em que variam somente o volume e a temperatura de um gás, sendo a pressão mantida constante. Nesse caso o trabalho realizado pode ser expresso por:
Nesse caso o trabalho realizado pode ser expresso por: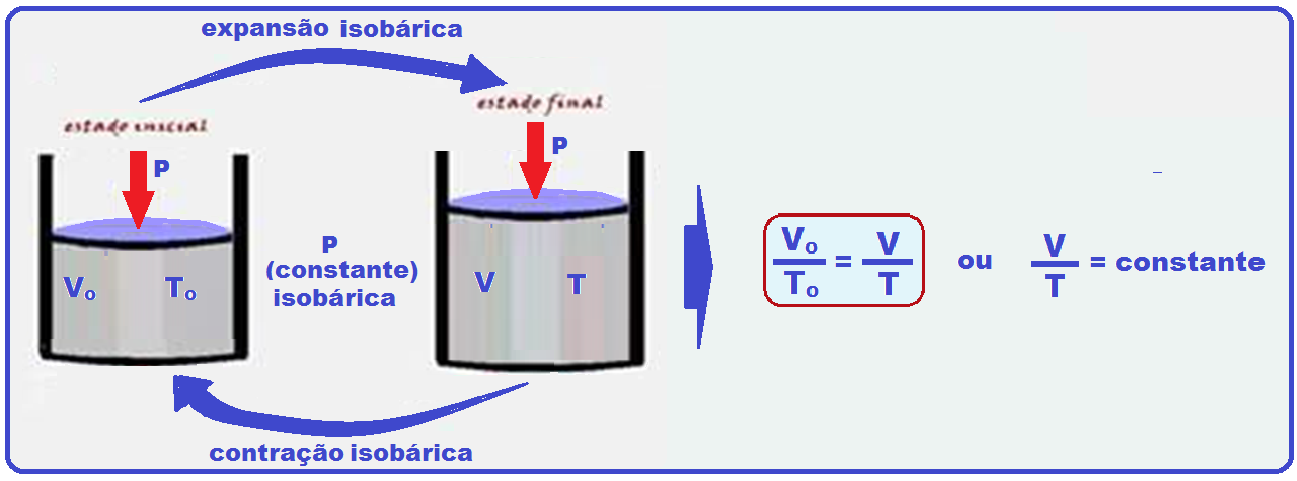


Observação: caso haja uma expansão (aumento de volume) o trabalho será positivo; em caso contrário, numa contração do gás, o trabalho será negativo.
Transformação isocórica ou Isovolumétrica ou Lei de Charles – Ocorre a volume constante.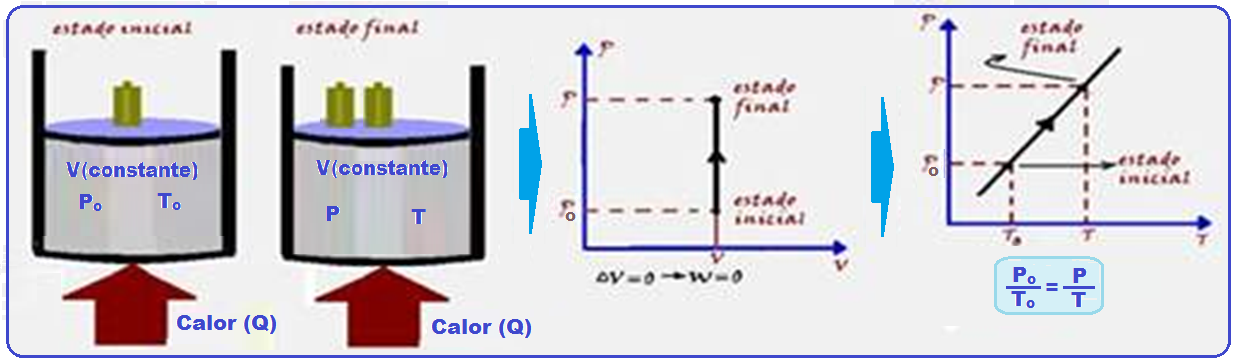
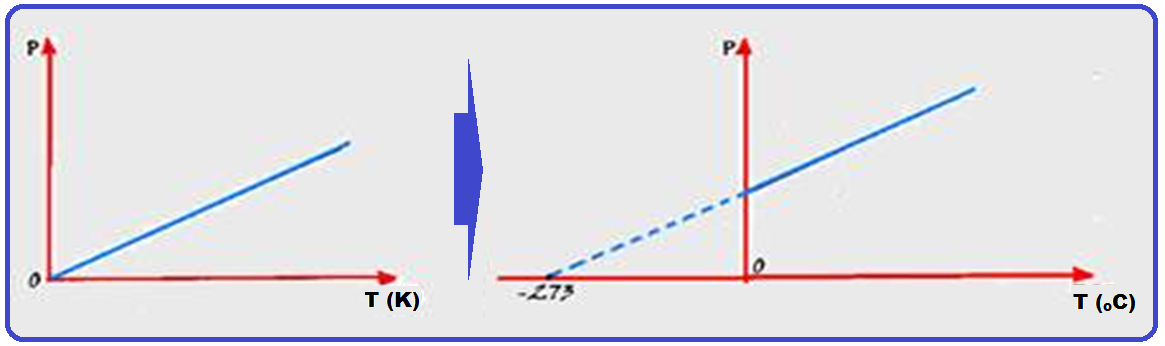
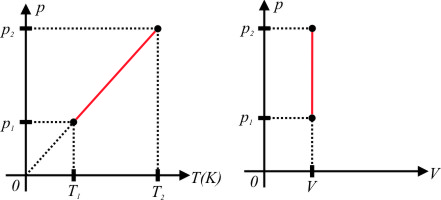 Observação:
Observação:
GASES PERFEITOS
Gases Perfeitos - Segundo essa lei, uma massa de gás inicialmente definida pelas variáveis de estado (p1,V1 e T1), ao sofrer uma transformação gasosa, passa a ter as variáveis de estado (p2,V2 e T2) que caracterizam o estado final do gás. Essas variáveis obedecem à seguinte relação: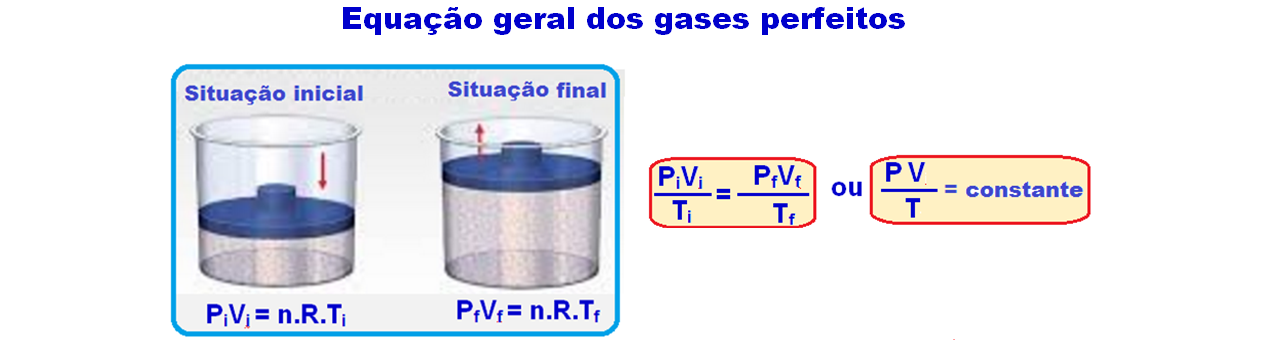
----------------------------------- Em resumo ----------------------------------------


RESOLVIDAS - TRANSFORMAÇÃO GASOSA
142)
145) (OSEC-SP) Um carro-tanque transportou gás cloro para uma estação de tratamento de água. Sabe-se que o volume do tanque que continha gás cloro era de 30 m3, que a temperatura era mantida a 20oC para a pressão ser de 2 atm e que, na estação de tratamento de água, esse cloro foi transferido para um reservatório de 50 m3 mantido a 293 K. Ao passar do carro-tanque para o reservatório, o gás sofreu uma transformação........e a pressão do reservatório era.............. As lacunas são completamente preenchidas, respectivamente, com os dados:
(A) isotérmica, 1,2 atm.
(B) isométrica, 117 atm.
(C) isobárica, 2 atm.
(D) isocórica, 2 atm.
(E) isovolumétrica, 1,2 atm.
Resolução:
Os dados fornecidos pelo exercício são:
→ Temperatura inicial (T1) = 20oC
OBS.: Em exercícios de transformações gasosas, a temperatura deve ser sempre trabalhada na unidade Kelvin. Para tal, basta somar a temperatura em graus Celsius com 273. No caso dessa questão, a temperatura T1 é de 293 K.
Pressão inicial (P1) = 2 atm
Volume inicial (V1) = 30 m3
Volume final (V2) = 50 m3
Pressão final (P2) = ?
Temperatura final (T2) = 293 K
Como a temperatura não sofreu alteração, temos uma transformação isotérmica (aquela que ocorre quando a temperatura é constante). A fórmula que deve ser utilizada é:
P1.V1 = P2.V2
2.30 = P2.50
50P2 = 60
P2 = 60
50
P2 = 1,2 atm
Alternativa: A
146) (INTEGRADO-RJ) O gráfico abaixo representa um processo cíclico (ciclo) a que é submetido um gás ideal: Analise-o. A opção em que aparece a correspondência das etapas numeradas (1 → 2 → 3 e 3 → 1), com suas respectivas denominações, é:
Analise-o. A opção em que aparece a correspondência das etapas numeradas (1 → 2 → 3 e 3 → 1), com suas respectivas denominações, é:
(A) Isobárica, Adiabática e Isotérmica;
(B) Isovolumétrica, Isobárica e Isotérmica;
(C) Isovolumétrica, Isotérmica e Isobárica;
(D) Isotérmica, Isobárica e Isovolumétrica;
(E) Isovolumétrica, Isobárica e Adiabática.
Resolução:
A seta 2 para 3: Indica a parte da abscissa onde está a temperatura. Por essa razão, temos a representação de uma transformação isotérmica;
A seta 1 para 2: Indica a parte da ordenada onde está o volume. Por essa razão, temos a representação de uma transformação isocórica ou isovolumétrica;
A seta 3 para 1: Indica a variação da temperatura e do volume (são diretamente proporcionais), fato esse que está relacionado com uma situação em que a pressão é constante. Por essa razão, temos uma transformação isobárica.
Alternativa: C
147) (PUC) Antes de realizar uma viagem de carro, em um dia cuja temperatura era de 30oC, um senhor calibrou os pneus utilizando 3 atm de pressão. Quando chegou ao destino, depois de 5 horas de viagem, mediu novamente a pressão dos pneus e constatou 3,4 atm de pressão. Sabendo que a variação de volume dos pneus é desprezível, marque a alternativa que indica a temperatura em que se encontravam os pneus:
(A) 70,4 oC
(B) 115,2 oC
(C) 125,1 oC
(D) 121,5 oC
(E) 152,1oC
Resolução:
O enunciado diz que o volume dos pneus é desprezível, por isso, temos uma transformação isovolumétrica (aquela em que não temos modificação do volume). Além disso, o enunciado fornece os seguintes dados:
→ Temperatura inicial (T1) = 30oC
OBS.: Em exercícios de transformações gasosas, a temperatura deve ser sempre trabalhada na unidade Kelvin. Para tal, basta somar a temperatura em graus Celsius com 273. No caso desse exercício, a temperatura T1 é de 303 K.
Pressão inicial (P1) = 3 atm;
Pressão final (P2) = 3,4 atm;
Temperatura final (T2) = ?
Como temos uma transformação isovolumétrica, a fórmula que será utilizada para determinar o valor da temperatura final é:
P1 = P2
T1 T2
3 = 3,4
303 T2
3.T2 = 303.3,4
T2 = 1030,2
3
T2 = 343,4 K
Como as respostas estão em graus Celsius, devemos subtrair o valor encontrado por 273 para encontrar o valor de T2.
T2 = 343,4 – 273
T2 = 70,4 oC.
Alternativa: A
148) (FEI) Uma empresa pretende utilizar balões para realizar uma operação de publicidade em uma praia. Os balões foram preenchidos com uma pressão de 760 mmHg, a uma temperatura de 32 oC. Ao chegar à praia, a temperatura estava em 42oC, mas a pressão ainda era de 760 mmHg. Quantas vezes o volume dos balões foi alterado ao chegar à praia?
(A) 1,3
(B) m3
(C) 3,01
(D) 1,03
(E) 0,331
Resolução:
Os dados fornecidos pelo exercício são:
→ Temperatura inicial (T1) = 32oC
OBS.: Em exercícios de transformações gasosas, a temperatura deve ser sempre trabalhada na unidade Kelvin. Para tal, basta somar a temperatura em graus Celsius com 273. No caso desse exercício, a temperatura T1 é de 305 K.
Pressão inicial (P1) = 760 mmHg
Volume inicial (V1) = x?
Volume final (V2) = y?
Pressão final (P2) = 760 mmHg
Temperatura final (T2) = 42 oC
OBS.: Somando a temperatura em graus Celsius com 273, a temperatura T2é de 315 K.
Como a pressão não não sofreu alteração, temos uma transformação isobárica (aquela que ocorre quando a pressão é constante). A fórmula que deve ser utilizada é:
V1 = V2
T1 T2
x = y
305 315
305.y = 315.x
Obs.: Como o exercício questiona quantas vezes o volume dos balões foi alterado (final), devemos isolar o valor de y na fórmula:
y = 315x
305
y = 1,03 x
Alternativa: D
149) Qual a velocidade média das moléculas de um gás que ocupa um recipiente de capacidade igual a 2 litros, tem massa igual a 20 gramas e pressão equivalente a 2 atmosféras?
Resolução:
Lembrando que existe uma relação entre estas grandezas expressa por:![]()
Podemos isolar a grandeza que desejamos calcular, ou seja, a velocidade:![]()
Convertendo os dados do problema para grandezas do SI: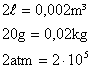
Utilzando os dados na equação: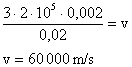
150) Em um tubo com pressão constante de 1atm ocorre uma transformação. Sendo a temperatura inicial igual a 20°C e a final igual a 0°C, de quantas vezes o volume foi modificado?
Resolução:
Como pressão não pode ser diferente da pressão atmosférica, então a transformação é Isobárica, sendo regida por:![]()
Neste caso, não é necessário converter as unidades para o SI, pois ambas têm mesma característica:![]()
Lembrando que é necessário que as temperaturas estejam em escala absoluta: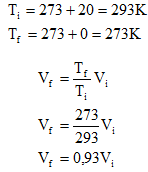
Então o volume final é menor que o inicial, com a razão de 0,93.
151) Qual a energia cinética média das moléculas de 10 mols de um gás perfeito, na temperatura de 100°C? E na temperatura de 100K? Considere R=8,31 J/mol.K
Resolução:
Sabemos que a energia cinética média das moléculas de um gás é dado por:![]()
No entanto a temperatura utilizada é a absoluta, por isso deve ser convertida, para o primeiro caso:![]()
Aplicando estes valores na equação: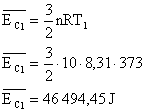
Para o segundo caso (T=100K):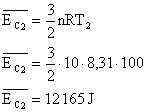
152) Um gás sofre uma expansão sob temperatura constante, o volume ocupado inicialmente pelo gás era 0,5 litros, e no final do processo passou a ser 1,5 litros. Sabendo que a pressão inicial sob o gás era o normal no ambiente, ou seja, 1 atm, qual a pressão final sob o gás?
Resolução:
Como a temperatura não é modificada durante a transformação, esta é Isotérmica, sendo regida pela equação:![]()
Neste caso não é necessário converter as unidades para o SI pois ambas têm mesma característica, ou seja volume é expresso em litros e pressão em atm, portanto, a pressão final será dada em atm: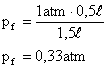
153) Em um tubo aberto ocorre uma grande compressão em um gás que torno o volume ocupado por ele 10 vezes menor. Sendo a temperatura inicial igual a 20°C, qual será a temperatura final?
Resolução:
Como o tubo é aberto, a pressão não pode ser diferente da pressão atmosférica, então a transformação é Isobérica, sendo regida por:![]()
Neste caso não é necessário converter as unidades para o SI pois ambas têm mesma característica:![]()
Mas o volume inicial é igual a 10 vezes o volume final:![]()
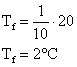
154) Um botijão de gás não pode variar o volume do gás que se encontra em seu interior. Se este for tirado de um ambiente arejado, onde a pressão interna é 3 atm e a temperatura 15°C, e é posto sob o Sol, onde a temperatura é 35°C. Supondo que o gás seja ideal, qual será a pressão após a transformação?
Resolução:
Como o volume não varia durante a transformação, esta é Isométrica, sendo regida por:![]()
Mas as temperaturas devem ser medidas em escala absoluta, ou seja:![]()
Isolando-se a pressão final: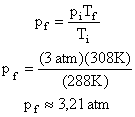
155) Um gás perfeito à temperatura de 0°C e sob pressão de uma atmosfera ocupa um volume igual a 22,4 litros. Qual seria o volume ocupado por 5 mols deste gás a 100°C, sob a pressão de 1 atm?
Resolução:
Utilizando a Equação de Clapeyron para ambas situações podemos chegar a um sistema de equações: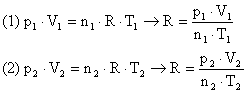
Igualando as equações:![]()
A temperatura deve ser passada para escala absoltura para que não haja indeterminações nos cálculos: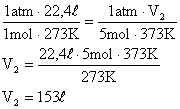
DILATAÇÃO TÉRMICA (anômala) DA ÁGUA
Certamente você já deve ter visto, em desenhos animados ou documentários, pessoas pescando em buracos feitos no gelo. Mas como vimos, os líquidos sofrem dilatação da mesma forma que os sólidos, ou seja, de maneira uniforme, então como é possível que haja água em estado líquido sob as camadas de gelo com temperatura igual ou inferior a 0°C?
Este fenômeno ocorre devido ao que chamamos de dilatação anômala da água, pois em uma temperatura entre 0°C e 4°C há um fenômeno inverso ao natural e esperado. Neste intervalo de temperatura a água, ao ser resfriada, sofre uma expansão no seu volume, e ao ser aquecida, uma redução. É isto que permite a existência de vida dentro da água em lugares extremamente gelados, como o Pólo Norte.
A camada mais acima da água dos lagos, mares e rios se resfria devido ao ar gelado, aumentando sua massa específica e tornando-o mais pesado, então ocorre um processo de convecção até que toda a água atinja uma temperatura igual a 4°C, após isso o congelamento ocorre no sentido da superfície para o fundo.
Podemos representar o comportamento do volume da água em função da temperatura:Como é possível perceber, o menor volume para a água acontece em 4°C.
TERMODINÂMICA
É a parte da Física que estuda a transformação de energia térmica em trabalho. A utilização direta desses princípios em motores de combustão interna ou externa, faz dela uma importante teoria para os motores de carros, caminhões e tratores, nas turbinas com aplicação em aviões, etc.


A lei de Joule (também conhecida como efeito Joule ou efeito térmico) - É uma lei física que expressa a relação entre o calor gerado e a corrente elétrica que percorre um condutor em determinado tempo. Um resistor é um dispositivo que transforma a energia elétrica integralmente em calor. Ou seja, efeito Joule é a transformação de energia térmica em trabalho. Máquinas Térmicas
Máquinas Térmicas
Máquina Térmica - São dispositivos que transforma calor em trabalho.
 Primeira lei da termodinâmica ou Princípio da conservação de energia - aplicado a sistemas termodinâmicos. O princípio da conservação da energia baseia-se no fato de que a energia não é criada e nem destruída, mas sim transformada de uma forma para outra.
Primeira lei da termodinâmica ou Princípio da conservação de energia - aplicado a sistemas termodinâmicos. O princípio da conservação da energia baseia-se no fato de que a energia não é criada e nem destruída, mas sim transformada de uma forma para outra.
Segunda Lei da Termodinâmica – Existem várias fontes de energia na natureza tais com: energia nuclear, elétrica, mecânica, solar dentre outras, mas é possível transformá-las integralmente em calor.

SISTEMAS DISSIPATIVOS
Forças dissipativas - Na física, definimos forças dissipativas, que também podem ser denominadas de forças não conservativas, como sendo as forças que transformam a energia mecânica em outras formas de energia, como por exemplo, o som, calor e deformação.
A força de atrito faz um objeto parar, transformando sua energia cinética inicial em calor e som. Sempre que houver força de atrito, parte da energia mecânica do sistema vai ser transformada em calor e som. É possível verificar isso quando um carro freia bruscamente: escutamos o som característico da freada e vemos a fumaça dos pneus queimando em virtude do aumento da temperatura devido à força de atrito com o asfalto.
Maquinas térmicas
São dispositivos que transformam energia em trabalho.

Potência de uma máquina – É definida pelo quociente entre o trabalho realizado por ela e o tempo gasto nessa tarefa.![]() Rendimento de uma máquina térmica – É a energia útil menos a energia dissipada (energia perdida).
Rendimento de uma máquina térmica – É a energia útil menos a energia dissipada (energia perdida).![]() Unidades especiais de potência que são importantes:
Unidades especiais de potência que são importantes:
1cv (cavalo-vapor) = 735 W
1HP (horse power) = 746 watts.
Teorema de Carnot
O físico e engenheiro militar Nicolas Léonard Sadi Carnot no ano de 1824. Ele pode ser representado por uma seqüência de transformações gasosas onde uma máquina térmica tem o seu rendimento máximo operando em ciclos, diante de duas fontes térmicas. Carnot mostrou que quanto maior a temperatura da fonte quente, maior seria seu rendimento para uma substância que se comportasse como um gás ideal.
O ciclo de Carnot é constituído de duas transformações isotérmicas: uma para a temperatura T1 da fonte quente onde ocorre o processo de expansão e a outra temperatura T2 referente a fonte fria onde ocorre o processo de compressão. Cada uma dessas transformações é intercalada com duas transformações adiabáticas.
Na máquina térmica frigorífica, a intenção é utilizar uma fonte de energia mecânica externa, por exemplo, um motor elétrico, para transferir calor de uma fonte de menor temperatura para uma de maior temperatura.
Ciclo de Carnot
Até meados do século XIX, acreditava-se ser possível a construção de uma máquina térmica ideal, que seria capaz de transformar toda a energia fornecida em trabalho, obtendo um rendimento total (100%).
Para demonstrar que não seria possível, o engenheiro francês Nicolas Carnot (1796-1832) propôs uma máquina térmica teórica que se comportava como uma máquina de rendimento total, estabelecendo um ciclo de rendimento máximo, que mais tarde passou a ser chamado Ciclo de Carnot.
Este ciclo seria composto de quatro processos, independente da substância:Uma expansão isotérmica reversível. O sistema recebe uma quantidade de calor da fonte de aquecimento (L-M)
Uma expansão adiabática reversível. O sistema não troca calor com as fontes térmicas (M-N)
Uma compressão isotérmica reversível. O sistema cede calor para a fonte de resfriamento (N-O)
Uma compressão adiabática reversível. O sistema não troca calor com as fontes térmicas (O-L)
Numa máquina de Carnot, a quantidade de calor que é fornecida pela fonte de aquecimento e a quantidade cedida à fonte de resfriamento são proporcionais às suas temperaturas absolutas, assim:
Assim, o rendimento de uma máquina de Carnot é: e
Logo:
Sendo:
T2 = temperatura absoluta da fonte de resfriamento
T1 = temperatura absoluta da fonte de aquecimento
Com isto se conclui que para que haja 100% de rendimento, todo o calor vindo da fonte de aquecimento deverá ser transformado em trabalho, pois a temperatura absoluta da fonte de resfriamento deverá ser 0K.
Partindo daí conclui-se que o zero absoluto não é possível para um sistema físico.
RESUMO - 2ª LEI DA TERMODINÂMICA
Podemos chamar de rendimento de uma máquina a relação entre a energia utilizada como forma de trabalho e a energia fornecida:
Mas como constatado:
logo, podemos expressar o rendimento como: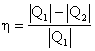
n = rendimento;
T= trabalho convertido através da energia térmica fornecida;
Q1 = quantidade de calor fornecida pela fonte de aquecimento;
Q2 = quantidade de calor não transformada em trabalho.
O valor mínimo para o rendimento é 0 se a máquina não realizar nenhum trabalho, e o máximo 1, se fosse possível que a máquina transformasse todo o calor recebido em trabalho, mas como visto, isto não é possível. Para sabermos este rendimento em percentual, multiplica-se o resultado obtido por 100%.
RESOLVIDOS - MÁQUINAS TÉRMICAS
156) (CEFET - PR) O 2° princípio da Termodinâmica pode ser enunciado da seguinte forma:
"É impossível construir uma máquina térmica operando em ciclos, cujo único efeito seja retirar calor de uma fonte e convertê-lo integralmente em trabalho."
Por extensão, esse princípio nos leva a concluir que:
(A) sempre se pode construir máquinas térmicas cujo rendimento seja 100%;
(B) qualquer máquina térmica necessita apenas de uma fonte quente;
(C) calor e trabalho não são grandezas homogêneas;
(D) qualquer máquina térmica retira calor de uma fonte quente e rejeita parte desse calor para uma fonte fria;
(E) somente com uma fonte fria, mantida sempre a 0°C, seria possível a uma certa máquina térmica converter integralmente calor em trabalho.
Resolução:
Uma máquina térmica recebe calor de uma fonte quente, converte uma parte desse calor em trabalho e rejeita outra parte para uma fonte fria. O calor nunca é convertido completamente em trabalho.
Alternativa: D
157) (UNIVALI - SC) Uma máquina térmica opera segundo o ciclo de Carnot entre as temperaturas de 500K e 300K, recebendo 2 000J de calor da fonte quente.
O calor rejeitado para a fonte fria e o trabalho realizado pela máquina, em joules, são, respectivamente:
(A) 500 e 1 500
(B) 700 e 1 300
(C) 1 000 e 1 000
(D) 1 200 e 800
(E) 1 400 e 600
Resolução:
Calculando o calor da fonte quente:
Por aproximação, podemos considerar a resposta como 1200 J.
Calculando o trabalho:
Alternativa: D
158) Uma máquina térmica cíclica recebe 5000 J de calor de uma fonte quente e realiza trabalho de 3500 J. Calcule o rendimento dessa máquina térmica.
Resolução:
O rendimento é dado pela razão entre o trabalho realizado e o calor recebido:
N = T
Q1
N = 3.500
5000
N= 0,7 ou 70%
159) Uma máquina térmica recebe 800 J de calor de uma fonte quente, em uma temperatura de 400 K, e rejeita 300 J para uma fonte fria. Calcule a temperatura da fonte fria e o trabalho realizado pela máquina.
Resolução:
A temperatura da fonte fria:
Q2 = T2
Q1 T1
300 = T2
800 400
0,375 . 400 = T2
T2 = 150 K
O trabalho realizado:
T = Q2 - Q1
T = 800 – 300
T = 500 J
160) (ENEM-MEC) Um motor só poderá realizar trabalho se receber uma quantidade de energia de outro sistema. No caso, a energia armazenada no combustível é, em parte, liberada durante a combustão para que o aparelho possa funcionar. Quando o motor funciona, parte da energia convertida ou transformada na combustão não pode ser utilizada para a realização de trabalho. Isso significa dizer que há vazamento da energia em outra forma.
Quando o motor funciona, parte da energia convertida ou transformada na combustão não pode ser utilizada para a realização de trabalho. Isso significa dizer que há vazamento da energia em outra forma.
CARVALHO, A. X. Z. Física Térmica. Belo Horizonte: Pax, 2009 (adaptado).
De acordo com o texto, as transformações de energia que ocorrem durante o funcionamento do motor são decorrentes de a:
(A) liberação de calor dentro do motor ser impossível.
(B) realização de trabalho pelo motor ser incontrolável.
(C) conversão integral de calor em trabalho ser impossível.
(D) transformação de energia térmica em cinética ser impossível.
(E) utilização de energia potencial do combustível ser incontrolável.
Resolução:
A) Incorreto. É exatamente a liberação de calor, decorrente da queima do combustível dentro do motor, que faz o carro andar.
B) Incorreto. É controlável sim. Quem controla é o próprio motorista, quando acelera ou freia o carro, por exemplo.
C) Correto. A 2° lei da termodinâmica fala exatamente sobre isso. Sempre haverá uma perda de energia nessa conversão.
D) Incorreto. É possível sim.
E) Incorreto. É controlável. Algo no motor está incontrolável, alguma coisa está errada.
Alternativa: C
161) (AFA) Com relação às máquinas térmicas e a Segunda Lei da Termodinâmica, analise as proposições a seguir.
I. Máquinas térmicas são dispositivos usados para converter energia mecânica em energia térmica com consequente realização de trabalho.
II. O enunciado da Segunda Lei da Termodinâmica, proposto por Clausius, afirma que o calor não passa espontaneamente de um corpo frio para um corpo mais quente, a não ser forçado por um agente externo como é o caso do refrigerador.
III. É possível construir uma máquina térmica que, operando em transformações cíclicas, tenha como único efeito transformar completamente em trabalho a energia térmica de uma fonte quente.
IV. Nenhuma máquina térmica operando entre duas temperaturas fixadas pode ter rendimento maior que a máquina ideal de Carnot, operando entre essas mesmas temperaturas.
São corretas apenas
(A) I e II
(B) II e III
(C) I, III e IV
(D) II e IV
Resolução:
I– Incorreto. Máquinas térmicas são dispositivos usados para converter energia térmica em realização de trabalho.
II- Correto. Espontâneo na natureza, sempre será de quem tem mais para quem tem menos. No caso da energia, o mais quente possui mais energia, logo o processo natural seria o calor passar para o corpo mais frio, caso contrário é preciso a realização de trabalho.
III– Incorreto. Isso vai contra a 2° lei da termodinâmica.
IV- Correto. A máquina ideal de Carnot é uma máquina que tem um funcionamento apenas teórico. Nenhuma máquina possui um rendimento maior que ela.
Alternativa: D
162) (PUC-RS-010) Para responder a questão, considere o texto e o gráfico, o qual relaciona o rendimento de uma máquina de Carnot e a razão T2/T1 das temperaturas em que opera a máquina.
O ciclo de Carnot é um ciclo termodinâmico especial, pois uma máquina térmica que opera de acordo com este ciclo entre duas temperaturas T1 e T2, com T1 maior do que T2 obtém o máximo rendimento possível. O rendimento r de uma máquina térmica é definido como a razão entre o trabalho líquido que o fluido da máquina executa e o calor que absorve do reservatório à temperatura T1. Pode-se concluir, pelo gráfico e pelas leis da termodinâmica, que o rendimento da máquina de Carnot aumenta quando a razão T2/T1 diminui,
Pode-se concluir, pelo gráfico e pelas leis da termodinâmica, que o rendimento da máquina de Carnot aumenta quando a razão T2/T1 diminui,
(A) alcançando 100% quando T2vale 0ºC.
(B) alcançando 100% quando T1é muito maior do que T2.
(C) alcançando 100% quando a diferença entre T1e T2é muito pequena.
(D) mas só alcança 100% porque representa o ciclo ideal.
(E) mas nunca alcança 100%.
Resolução:
A segunda lei da Termodinâmica diz que nenhuma máquina térmica, consegue transformar integralmente calor em trabalho, logo o rendimento nunca pode chegar a 100%. O maior rendimento possível é igual ao da máquina de Carnot. Quando analisamos o gráfico, vemos que, para o rendimento ser de 100%, a razão T2/T1 teria que ser nula. P para isso T2=0 K, o que é impossível.
Alternativa: E
163) Tem-se uma máquina térmica frigorífica que realiza, durante um ciclo completo, um trabalho de 4 . 104 J e cede, à fonte fria, 12 . 104 J. Com essas informações, calcule a eficiência da máquina térmica e marque a opção correta.
(A) 1
(B) 3
(C) 3,5
(D) 2,4
(E) 4
Resolução:
A eficiência de uma máquina térmica é dada pela seguinte equação:![]()
Onde Q2 é o calor retirado da fonte fria e τ é o trabalho externo. Sendo assim, temos:![]()
Alternativa: B
164) Certa máquina térmica realiza por ciclo um trabalho de 3000 J e cede à uma fonte fria 3200 calorias. Com esses dados, determine, aproximadamente, o rendimento percentual e a eficiência dessa máquina térmica. (Adote 1 cal = 4,2 J).
(A) 45 % e 18
(B) 16 % e 3
(C) 18 % e 5,4
(D) 18 % e 4,5
(E) 12 % e 3
Resolução:
O rendimento de uma máquina térmica é dado pela seguinte função:![]()
E a eficiência da máquina térmica é dada por:![]()
Com os dados do exercício podemos calcular o que se pede:
Q2 = 3200 cal = (3200 x 4,2) = 13440 J
τ = 3000 J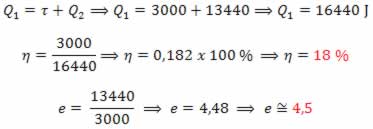
Alternativa: D
165) Tem-se uma máquina térmica cujo rendimento é igual a 0,2. Supondo que essa mesma máquina absorva da fonte quente 104 J de calor, determine o trabalho realizado e o calor perdido para a fonte fria dessa máquina térmica.
(A) τ = 8000 J e Q1= 2000 J
(B) τ = 3000 J e Q1= 8000 J
(C) τ = 2000 J e Q1 = 6000 J
(D) τ = 5000 J e Q1 = 5000 J
(E) τ = 2000 J e Q1 = 8000 J
Resolução:
Primeiramente devemos retirar as informações dadas pelo exercício:
η = 0,2 e Q1 = 104 J
Agora podemos determinar o trabalho através da equação do rendimento da máquina térmica. Portanto, temos: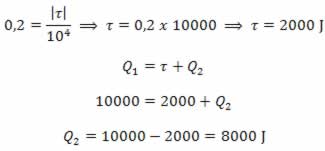
Alternativa: E
166) Calcule o rendimento de uma máquina térmica que segue um ciclo descrito no diagrama, sabendo que ela absorve 4 . 104 J de calor por ciclo.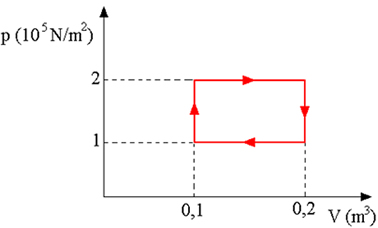 (A) 15 %
(A) 15 %
(B) 20 %
(C) 25 %
(D) 30 %
(E) 35 %
Resolução:
Q1 = 40000 J
τ = área interna = 0,1 x 1 x 105 = 104 J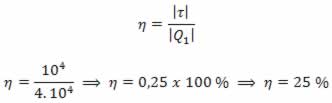
168) (ENEM) Um motor só poderá realizar trabalho se receber uma quantidade de energia de outro sistema. No caso, a energia armazenada no combustível é, em parte, liberada durante a combustão para que o aparelho possa funcionar. Quando o motor funciona, parte da energia convertida ou transformada na combustão não pode ser utilizada para a realização de trabalho. Isso quer dizer que há vazamento da energia em outra forma.
CARVALHO, A. X. Z. Física Térmica. Belo Horizonte: Pax, 2009 (adaptado).
De acordo com o texto, as transformações de energia que ocorrem durante o funcionamento do motor são decorrentes da
(A) liberação de calor dentro do motor ser impossível.
(B) realização de trabalho pelo motor ser incontrolável.
(C) conversão integral de calor em trabalho ser impossível.
(D) transformação de energia térmica em cinética ser impossível.
(E) utilização de energia potencial do combustível ser incontrolável.
Resolução
Em uma máquina térmica, como o motor de combustão interna, é impossível a conversão integral de calor em trabalho, pois, no processo de conversão de energia, ocorrem perdas, que podem ser oriundas, por exemplo, do atrito entre as peças do motor por falta de lubrificação ou de perdas de calor por radiação e convecção para o meio externo.
Alternativa: C
169) (CEFET - PR) O 2° princípio da Termodinâmica pode ser enunciado da seguinte forma:"É impossível construir uma máquina térmica operando em ciclos, cujo único efeito seja retirar calor de uma fonte e convertê-lo integralmente em trabalho."Por extensão, esse princípio nos leva a concluir que:
(A) sempre se pode construir máquinas térmicas cujo rendimento seja 100%;
(B) qualquer máquina térmica necessita apenas de uma fonte quente;
(C) calor e trabalho não são grandezas homogêneas;
(D) qualquer máquina térmica retira calor de uma fonte quente e rejeita parte desse calor para uma fonte fria;
(E) somente com uma fonte fria, mantida sempre a 0°C, seria possível a uma certa máquina térmica converter integralmente calor em trabalho.
Resolução:
Uma máquina térmica cíclica recebe 5000 J de calor de uma fonte quente e realiza trabalho de 3500 J. Calcule o rendimento dessa máquina térmica.
Alternativa: D
170) (UNIVALI - SC) Uma máquina térmica opera segundo o ciclo de Carnot entre as temperaturas de 500K e 300K, recebendo 2 000J de calor da fonte quente. O calor rejeitado para a fonte fria e o trabalho realizado pela máquina, em joules, são, respectivamente:
(A) 500 e 1 500
(B) 700 e 1 300
(C) 1 000 e 1 000
(D) 1 200 e 800
(E) 1 400 e 600
Resolução:
Calculando o calor da fonte quente:
Por aproximação, podemos considerar a resposta como 1200 J. Calculando o trabalho:
Alternativa D
171) Uma máquina térmica cíclica recebe 5000 J de calor de uma fonte quente e realiza trabalho de 3500 J. Calcule o rendimento dessa máquina térmica.
Resolução:
O rendimento é dado pela razão entre o trabalho realizado e o calor recebido:
N = T
Q1
N = 3.500
5000
N= 0,7 ou 70%
172) Uma máquina térmica recebe 800 J de calor de uma fonte quente, em uma temperatura de 400 K, e rejeita 300 J para uma fonte fria. Calcule a temperatura da fonte fria e o trabalho realizado pela máquina.
Resolução:
A temperatura da fonte fria:
Q2 = T2
Q1 T1
300 = T2
800 400
0,375 . 400 = T2
T2 = 150 K
O trabalho realizado:
T = Q2 - Q1
T = 800 – 300
T = 500 J
173) (CEFET - PR) O 2° princípio da Termodinâmica pode ser enunciado da seguinte forma:"É impossível construir uma máquina térmica operando em ciclos, cujo único efeito seja retirar calor de uma fonte e convertê-lo integralmente em trabalho."Por extensão, esse princípio nos leva a concluir que:
(A) sempre se pode construir máquinas térmicas cujo rendimento seja 100%;
(B) qualquer máquina térmica necessita apenas de uma fonte quente;
(C) calor e trabalho não são grandezas homogêneas;
(D) qualquer máquina térmica retira calor de uma fonte quente e rejeita parte desse calor para uma fonte fria;
(E) somente com uma fonte fria, mantida sempre a 0°C, seria possível a uma certa máquina térmica converter integralmente calor em trabalho.
Resolução:
Uma máquina térmica recebe calor de uma fonte quente, converte uma parte desse calor em trabalho e rejeita outra parte para uma fonte fria. O calor nunca é convertido completamente em trabalho.
Alternativa: D
174) (UNIVALI - SC) Uma máquina térmica opera segundo o ciclo de Carnot entre as temperaturas de 500K e 300K, recebendo 2 000J de calor da fonte quente. O calor rejeitado para a fonte fria e o trabalho realizado pela máquina, em joules, são, respectivamente:
(A) 500 e 1 500
(B) 700 e 1 300
(C) 1 000 e 1 000
(D) 1 200 e 800
(E) 1 400 e 600
Resolução:
Calculando o calor da fonte quente:
Por aproximação, podemos considerar a resposta como 1200 J.
Calculando o trabalho:
Alternativa D
175) Uma máquina térmica cíclica recebe 5000 J de calor de uma fonte quente e realiza trabalho de 3500 J. Calcule o rendimento dessa máquina térmica.
Resolução:
O rendimento é dado pela razão entre o trabalho realizado e o calor recebido:
N = T
Q1
N = 3.500
5000
N= 0,7 ou 70%
176) Uma máquina térmica recebe 800 J de calor de uma fonte quente, em uma temperatura de 400 K, e rejeita 300 J para uma fonte fria. Calcule a temperatura da fonte fria e o trabalho realizado pela máquina.
Resolução:
A temperatura da fonte fria:
Q2 = T2
Q1 T1
300 = T2
800 400
0,375 . 400 = T2
T2 = 150 K
O trabalho realizado:
T = Q2 - Q1
T = 800 – 300
T = 500 J
177) (ITA) Uma máquina térmica opera segundo o ciclo JKLMJ mostrado no diagrama T-S da figura.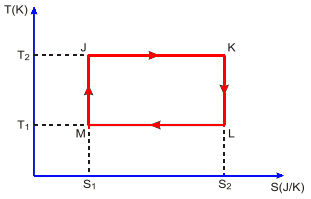 Pode-se afirmar que
Pode-se afirmar que
(A) processo JK corresponde a uma compressão isotérmica.
(B) o trabalho realizado pela máquina em um ciclo é W = (T2 – T1)(S2 – S1).
(C) o rendimento da máquina é dado por η = 1 – T2/T1
(D) durante o processo LM, uma quantidade de calor QLM = T1(S2 – S1) é absorvida pelo sistema.
(E) outra máquina térmica que opere entre T2 e T1 poderia eventualmente possuir um rendimento maior que a desta.
Resolução:
O gráfico dado na questão é de temperatura versus entropia e mostra um ciclo no sentido horário operado por uma máquina térmica.
a) ERRADO: No processo JK, há aumento de entropia (S2> S1), o que indica que o sistema recebeu calor, logo, realizou trabalho.
b) CORRETO: O trabalho de um sistema cíclico é dado pela área da figura geométrica que forma o ciclo. Nesse caso, a área de um retângulo (base x altura).
c) ERRADO: A razão das temperaturas para o cálculo do rendimento é entre a menor e maior temperatura. Nesse caso, teríamos η = 1 – T1/T2já que T1< T
d) ERRADO: Durante o processo LM, há diminuição de entropia, o que indica perda de calor.
e) ERRADO: Outra máquina operando sob o mesmo ciclo realizaria o mesmo trabalho.
Alternativa: B
178) Uma máquina térmica que trabalha entre as temperaturas 27°C e 327°C possui 80% do rendimento ideal para uma máquina térmica. Se essa máquina recebe 1000 J da fonte quente, qual é o trabalho realizado por ela?
(A) 400 J
(B) 500 J
(C) 350 J
(D) 600 J
(E) 250 J
Resolução:
Transformação de temperaturas: As temperaturas devem sempre estar expressas em K. Como TK = TC + 273, sendo TK a temperatura em Kelvin e TC a temperatura em °C, temos:
27 + 273 = 300 K
327 + 273 = 600 K
O rendimento ideal citado na questão refere-se ao ciclo de Carnot, logo, temos:
η I = 1 – T2/T1
Para essa equação, podemos escrever que:
η I = Rendimento ideal
T2 = Temperatura da fonte fria
T1 = Temperatura da fonte quente
η I = 1 – 300/600
η I = 1 – 0,5
η I = 0,5
O rendimento real da máquina η R corresponde a 80% do rendimento ideal η I , logo:
η R = 80% η I
η R = 0,8. 0,5
η I =0,8 x 0,5
η I = 0,4 ou 40 %
Sendo o rendimento a razão entre o trabalho e o calor fornecido (Q1), temos:
η I = τ ÷ Q1
0,4 = τ ÷ 1000
τ = 400 J
Alternativa: A
179) Determine o trabalho realizado por uma máquina de Carnot que recebe 2000 J de calor de uma fonte quente e trabalha sob as temperaturas de 400 K e 700 K.
(A) 1000 J
(B) 780 J
(C) 800 J
(D) 860 J
(E) 560 J
Resolução:
A partir do rendimento para uma máquina de Carnot, temos:
η = 1 – T2/T1
η = 1 – 400/700
η = 1 – 0,57
η = 0,43 ou 43 %
Sendo o rendimento a razão entre o trabalho e o calor fornecido (Q1), temos:
η = τ ÷ Q1
0,43 = τ ÷ 2000
τ = 2000. 0,43 = 860 J
Alternativa: D
180) (CEFET-PR) O 2° princípio da Termodinâmica pode ser enunciado da seguinte forma: "É impossível construir uma máquina térmica operando em ciclos, cujo único efeito seja retirar calor de uma fonte e convertê-lo integralmente em trabalho." Por extensão, esse princípio nos leva a concluir que:
(A) sempre se pode construir máquinas térmicas cujo rendimento seja 100%;
(B) qualquer máquina térmica necessita apenas de uma fonte quente;
(C) calor e trabalho não são grandezas homogêneas;
(D) qualquer máquina térmica retira calor de uma fonte quente e rejeita parte desse calor para uma fonte fria;
(E) somente com uma fonte fria, mantida sempre a 0°C, seria possível a uma certa máquina térmica converter integralmente calor em trabalho.
Resolução:
Qualquer máquina térmica, ao receber calor, executa a sua função (trabalho) e perde calor para uma fonte fria.
Alternativa: D
25) Um motor à vapor realiza um trabalho de 12kJ quando lhe é fornecido uma quantidade de calor igual a 23kJ. Qual a capacidade percentual que o motor tem de transformar energia térmica em trabalho?
Resolução:
181) Qual o rendimento máximo teórico de uma máquina à vapor, cujo fluido entra a 560ºC e abandona o ciclo a 200ºC?
Resolução:
ENTALPIA
Em termodinâmica, entropia é a medida de desordem das partículas em um sistema físico. Utiliza-se a letra S para representar esta grandeza.
Comparando este conceito ao cotidiano, podemos pensar que, uma pessoa ao iniciar uma atividade tem seus objetos organizados, e a medida que ela vai os utilizando e desenvolvendo suas atividades, seus objetos tendem a ficar cada vez mais desorganizados.
Voltando ao contexto das partículas, como sabemos, ao sofrem mudança de temperatura, os corpos alteram o estado de agitação de suas moléculas. Então ao considerarmos esta agitação como a desordem do sistema, podemos concluir que:
Quando um sistema recebe calor Q > 0, sua entropia aumenta;
Quando um sistema cede calor Q < 0, sua entropia diminui;
Se o sistema não troca calor Q = 0, sua entropia permanece constante.
Segundo Rudolf Clausius, que utilizou a idéia de entropia pela primeira vez em 1865, para o estudo da entropia como grandeza física é mais útil conhecer sua variação do que seu valor absoluto. Assim, Clausis definiu que a variação de entropia (ΔS) em um sistema como:Para processos onde as temperaturas absolutas (T) são constantes.
Para o caso onde a temperatura absoluta se altera durante este processo, o cálculo da variação de entropia envolve cálculo integral, sendo que sua resolução é dada por:Observando a natureza como um sistema, podemos dizer que o Universo está constantemente recebendo energia, mas não tem capacidade de cedê-la, concluindo então que a entropia do Universo está aumentando com o passar do tempo.
GASES NOBRES ou "GASES RAROS"
Os gases nobres, também chamados de "gases raros", compõem os elementos do grupo 18 (família 8A) da tabela periódica.
A principal característica dos gases nobres é a dificuldade que eles possuem de se combinar com outros átomos.
Quais são os Gases Nobres?
São 7 os gases nobres:
Hélio (He)
Neônio (Ne)
Argônio (Ar)
Criptônio (Kr)
Xenônio (Xe)
Radônio (Rn)
Ununóctio (Uuo)
CARACTERÍSTICAS DOS GASES NOBRES
Possuem baixa reatividade (consiste na tendência que uma reação química tem em acontecer).
Apresentam fraca atração interatômica (força entre dois átomos ou moléculas em função da distância entre eles.).
Possuem baixo ponto de fusão e ebulição (Entende-se por ponto de fusão a temperatura em que uma substância passa do estado sólido passa o estado líquido, e por ponto de ebulição a temperatura em que uma substância líquida passa para o estado gasoso, à determinada pressão.)
Estabilidade atômica, isto é, não precisam associar-se a outro elemento para ficar estável. (é um fenômeno que ocorre quando um átomo livre na natureza consegue ter a estabilidade eletrônica de um gás nobre. Isso se dá quando o átomo em questão completa a sua última camada (camada de valência) com 8 elétrons (ou 2 elétrons, como é o caso do hidrogênio, que se iguala ao hélio).
Elevada energia de ionização (Energia de Ionização, também denominada de Potencial de ionização, corresponde à energia mínima necessária para retirar um elétron de um átomo ou íon no estado gasoso. O átomo ou íon só perderá elétrons se ele receber energia suficiente, que é a energia de ionização.)
Difundem-se facilmente por meio do vidro e da borracha.
Estabilidade atômica (inércia química) isto é os átomos de gases nobres são denominados estáveis por não apresentarem a necessidade de associar-se a outro átomo de um elemento diferente, ou seja, os gases nobres dificilmente formam substâncias químicas compostas. Isso acontece apenas em condições laboratoriais específicas.
Ocorrência na natureza e utilização:
Estado físico - Em condições naturais de temperatura e pressão, ou seja, a 25 oC e 1 atm, os elementos da família VIII A somente são encontrados no estado físico gasoso, pois apresentam um baixo ponto de ebulição.
Os gases nobres são encontrados na natureza na forma de gases monoatômicos. O gás nobre Hélio é formado na crosta terrestre a partir de Urânio e Tório, e o gás nobre Radônio é originado na crosta terrestre a partir de Rádio e Tório, sempre por meio do processo de decaimento radioativo.
Os gases nobres, de uma forma geral, estão presentes na atmosfera terrestre. A quantidade de cada um deles na atmosfera não é grande, pois, de todos os gases que compõem a atmosfera terrestre, eles constituem apenas 0,91%. O mais comum é o gás argônio.
A utilização desses gases monoatômicos pelo ser humano engloba diversos ramos de atividades, a saber:
Hélio - cilindro utilizado por mergulhadores e em balões e dirigíveis.
Neônio - Utilizado em válvulas estabilizadoras de tensão e anúncios luminosos.
Argônio - Utilizado em atmosferas inertes para realização de fusão de materiais; utilizado também na solda de metais.
Criptônio - Ainda não é utilizado em nenhuma atividade humana importante;
Xenônio - Utilizado em iluminação pública e na produção de flashes eletrônicos.
Radônio - É utilizado para a determinação da idade geológica de algumas rochas.
GASES NOBRES, INERTES ou RAROS
(família, grupo ou coluna 18 da T.P. ou T.Q.): HÉLIO:
HÉLIO:
Gás nobre presente na constituição das estrelas. Do grego “Hélios”= "Sol".
O Hélio (He), tem massa atômica (A) = 4 u, número atômico (Z) = 2 (2 prótons).
À temperatura ambiente, o Hélio encontra-se no estado gasoso, situado na Tabela Periódica na família (coluna ou grupo 18) dos Gases Nobres, Raros ou Inertes. Descoberto em 1868 por Júlio Janssen e Norman Lockyer.
É considerado um gás nobre por não se misturar com outros elementos, ou seja, é apático a se envolver em reações químicas. Podemos apelidar este gás de "esnobe", pois, mesmo na presença de outros átomos, age com indiferença e não reage para originar novos compostos.
Esta é uma propriedade de todos os outros gases do grupo 18 da Tabela Periódica (Ne, Ar, Kr, Xe, Rn e Uuo) que possuem nível de energia completo, apresentando as características de um gás nobre, ou seja, é inerte (não reage) como os demais elementos como dissemos em aula recentemente.
Propriedades físicas do Hélio: é um gás monoatômico, incolor e inodoro. O Hélioequivale ao 2° elemento químico mais abundante no universo e só perde para oHidrogênio, é encontrado em 20% da matéria das estrelas, mas na atmosfera terrestre a quantidade é mínima. Existe Hélio na Lua (observado em 2012 pela sonda Lunar Reconnaissance Orbiter [LRO]).
Existem depósitos naturais de Hélio nos EUA, Rússia e Argélia, onde é possível obter quantidades significativas deste gás. Encontra-se amostras do gás Hélio em águas minerais e erupções vulcânicas.
A densidade do Hélio é menor que a densidade do ar, tornando-o mais leve.
Aplicações do Hélio: é usado para encher bolas de aniversário, balões e dirigíveis (por ser um o gás menos inflamável). É aplicado como líquido refrigerante de materiais supercondutores, é um meio que se tem para refrigerar reatores atômicos e como gás de equipamentos para mergulhos de grande profundidade.
NEÔNIO:
Gás raro presente na luz roxa("luz negra") das lâmpadas fluorescentes (foto ao lado). Do grego “Néons”= "novo".
Os Gases Nobres receberam esta denominação, por uma questão de afinidade, neste aspecto, o comportamento pode ser comparado ao do ser humano: quando você não se simpatiza com uma pessoa, fica indiferente a ela, não quer se juntar e procura esquivar-se. É exatamente assim que o gás Neônio (Ne) se comporta em relação aos outros elementos da T.P. ou T.Q., não interage com nenhum outro, como eu já havia dito em aula para você, isto acontece com todos os integrantes da família dos Gases Nobres, Raros ou Inertes, ou seja, não reagem quimicamente com os demais membros da tabela periódica. Descoberto em 1898 por Willian Ramsay e Morris W. Travers.
Observação: o Neônio ao ser atravessado por uma corrente elétrica sob baixa pressão, emite uma luz brilhante com tom de roxo, que dá luz as conhecidas lâmpadas fluorescentes. Os letreiros luminosos (luzes de Néon) usados para anúncios e propagandas, existem graças ao Neônio. O número atômico (Z) do Neônio é 10 (10 prótons), seu peso atômico é: 20,183 uma (u), sendo considerado o 2° gás nobre mais leve. Obtem-se Neônio, separado-o durante a destilação fracionada do ar líquido.
Aplicações do Neônio:
Misturado ao seu vizinho de baixo, o Argônio, dá origem a válvulas para raios-X.
Muito útil em laboratórios na forma de detector de íons (cátions e ânios).
Pequenas lâmpadas de sinalização usadas em aparelhos eletrônicos contêm Neônioem sua composição.
Nos sensores ultra-sensíveis de infravermelho, o Neônio é usado na forma líquida.
Em lâmpadas para neblina.
Usados em tubos (de imagem) de TVs anteriores aos televisores de plasma.
Misturado com um pouco de vapor de Mercúrio (dentro da lâmpada) e revestido porFósforo (internamente ao redor da lâmpada = no vidro ou tubo) gera a "Luz Negra" (foto abaixo): Como funciona a "Luz Negra"?
Como funciona a "Luz Negra"?  Os marca textos comuns (foto acima) funcionam bem como "canetas de luz negra". Sob a luz negra, a tinta fluorescente brilha.
Os marca textos comuns (foto acima) funcionam bem como "canetas de luz negra". Sob a luz negra, a tinta fluorescente brilha.
Uma das primeiras coisas que as pessoas observam quando se acende uma luz negra é que algumas peças de suas roupas brilham, isso por que a maioria dos sabões em pó contém Fósforo para "fazer o branco parecer mais branco" à luz do Sol. A luz solar contém luz UV que faz o branco brilhar "mais claro do que o branco". As roupas escuras não brilham porque os pigmentos escuros absorvem a luz UV.
Além de fazer as pessoas e os cartazes fluorescentes parecerem mais interessantes, aluz negra tem aplicações práticas.
Por exemplo:
Avaliadores a utilizam para detectar falsificações de antiguidades e artes. As tintas atuais contém fosforosos (materiais com Fósforo) que brilham sob a luz negra, enquanto que a maioria das tintas antigas não;
Técnicos em reparos a utilizam para encontrar vazamentos invisíveis em maquinários, injetando um pouco de corante fluorescente no combustível que supre a máquina, iluminando-o com luz negra. Detectar, por exemplo, um vazamento invisível no ar condicionado acrescentando corante fluorescente ao líquido refrigerante;
Policiais podem usá-la para identificar dinheiro, passaporte ou documentos falsificados. Nos EUA e muitos outros países incluem uma tira fluorescente invisível dentro das notas de maior valor, que aparece somente sob luz negra; Parques de diversão e clubes a utilizam para identificar carimbos fluorescentes invisíveis nas mãos, que permitem o reingresso;
Parques de diversão e clubes a utilizam para identificar carimbos fluorescentes invisíveis nas mãos, que permitem o reingresso;
Os cientistas forenses a usam para analisar cenas de crimes. Para colher impressões digitais, por exemplo, eles geralmente espalham corante fluorescente sob a luz negra. Isso facilita separar as impressões digitais da sujeira ao redor. A luz negra também identifica o sêmen e outros
Fluidos corporais que fluorescem naturalmente. ARGÔNIO:
ARGÔNIO:
Gás inerte que protege os filamentos de lâmpadas. Do grego “Árgon”= "preguiçoso" // "inativo".
Argônio é o gás nobre mais abundante em nosso planeta. A maior quantidade de gás Argônio que se encontra na mistura gasosa do ar atmosférico, constitui 0,93% do volume do ar que respiramos.
Existe Argônio na Lua (observado em 1972 pelos astronautas da Apollo 17).
Propriedades periódicas do Argônio: símbolo Ar, número atômico (Z) = 18 (18 prótons), massa atômica (A) = 40 u, se encontra na forma gasosa em temperatura ambiente. Descoberto em 1884 por William Ramsay e Walter Rayleigh.
Aplicações do Argônio: tem vasta utilização na conservação de materiais oxidáveis, isto se explica pela propriedade inerte deste gás. Veja onde pode ser empregado:
Devido a sua pouca reatividade, o Argônio é aplicado em peças de museus para uma melhor conservação das relíquias.
Aplicado em lâmpadas incandescentes para evitar a corrosão do filamento deTungstênio (W) presente neste tipo de lâmpada (veja foto acima).
Nas soldas, evita oxidação, protegendo-as das substâncias ativas do ar. Esta é a chamada soldagem especial com atmosfera protetora.
Ainda usado para inflar airbags de automóveis.
Usados em Contador Geiger (G-M. ou Contador Geiger-Müller = contadores de radiação - desenvolvido pelo cientista Johannes (Hans) Wilhelm Geiger juntamente com Walther Müller).
Lasers a base de Argônio são aplicados na medicina em cirurgias dos olhos. CRIPTÔNIO:
CRIPTÔNIO:
Um dos gases eliminados por vulcões, como por exemplo, o complexo vulcânico Puyehue-Cordón Caulle entrou em erupção no Chile em 04/6/2011.
Seu nome vem do grego "Kryptos" = "oculto" ou "escondido", não é difícil saber o porquê desta nomenclatura para o
Criptônio, já que é um gás raro na atmosfera terrestre, da ordem de 1 ppm(partes por milhão). As regiões onde pode se encontrar Criptônio são as que contem vulcões, lá o elemento pode ser extraído dos gases vulcânicos e das águas termais. O método usado para esta extração é a destilação fracionada. Estudos recentes revelaram a presença de 0,3 ppm de Criptônio na atmosfera do planeta Marte ("deus da guerra"). Descoberto em 1898 por Willian Ramsay e Morris W. Travers.
Seu símbolo é o Kr e possui número atômico (Z) = 36 (36 prótons) e massa atômica (A) = 83,8 u, e se encontra inserido na T.P. na família 18 (Gases Nobres). Junto com os gases Neônio e Argônio, constituem componentes na fabricação de lâmpadas incandescentes e fluorescentes. Em lâmpadas fluorescentes tubulares (como as de sua salade aula).
A potencialidade de iluminação dada por estes gases nobres vai mais além, os sistemas de iluminação de aeroportos utilizam a mistura destes gases para obter uma luz vermelha, cujo alcance é bem maior que das lâmpadas comuns. Este tipo de iluminação é usada também no cinema, presente nos projetores cinematográficos e, ainda, na forma de flash fotográfico para fotografar em altíssima velocidade.
Para exemplificar a eficiência da energia oferecida por este gás nobre, o laser deCriptônio é usado na medicina para cirurgia da retina dos olhos. XENÔNIO:
XENÔNIO:
Gás nobre presente em TV’s de plasma. Do grego “Xénos”= "estrangeiro".
O elemento químico Xenônio de símbolo Xe e de número atômico (Z) = 54 (54 prótons) possui massa atômica (A) = a 131,3 u e consiste num gás à temperatura ambiente, pertencente à família dos G.N. da T.P. ou T.Q. (coluna 18). O Xenônio é um gás inodoro, de peso elevado e incolor. Descoberto em 1898 por William Ramsay e Morris W. Travers.
Aplicações do Xenônio: O gás nobre Xenônio possui diversas utilizações que vão da medicina até a propulsão de foguetes. Mas as aplicações são limitadas devido ao seu elevado custo e reduzida abundância (gás raro), confira:
O gás nobre Xenônio possui diversas utilizações que vão da medicina até a propulsão de foguetes. Mas as aplicações são limitadas devido ao seu elevado custo e reduzida abundância (gás raro), confira:
Xenônio pode ser usado como anestésico em anestesia geral.
Submetido a acelerador de partículas, o elemento dá origem a íons de Xenônio usados na projeção de foguetes espaciais.
Usado em dispositivos emissores de luz, como tubos eletrônicos e em lâmpadas ultravioletas (aquelas de bronzeamento artificial = foto ao lado).
Uma aplicação recente de Xenônio é na obtenção dos displays de plasma para os televisores anteriores a geração "LED".
Em locais que se deseja uma visão noturna satisfatória é aconselhável o uso de lâmpadas de alta energia à base da luz ultravioleta, esta é obtida a partir do Xenônio presente também em lâmpadas especiais para aviação e projeções cinematográficas (lâmpadas de cinema).
Lâmpadas especiais para flashes fotográficos e até mesmo para destruição de bactérias (lâmpadas bactericidas) contam com a presença deste gás nobre em sua composição.
Outra recente aplicação do Xenônio, está nos faróis de veículos, com a vantagem de iluminar 3 vezes mais e ainda consomem 40% menos de bateria elétrica do que os faróis comuns.
Do Hélio até o Xenônio temos a seguinte foto que ilustra a intensidade de brilho/luz:
RADÔNIO:
Gás raro usado no tratamento contra o câncer.
O Radônio é um elemento químico de símbolo Rn, de número atômico (Z) = 86 (86 prótons), com massa atômica (A) de aproximadamente 222 u, pertencente à família dos G.N. no grupo 18 da T.P. (ou T. Q.). Descoberto em 1899 por E. Dorn e N. E. Rutherford.
Características físicas do Radônio: em temperatura ambiente é um gás incolor, mas quando submetido ao resfriamento abaixo do ponto de solidificação, passa a exibir uma fosforescência brilhante de tom amarelado quando está com a temperatura reduzida e vermelha alaranjada quando começa a atingir o estado de ar liquefeito. Pode acumular-se em porões, adegas e lugares com pouca ventilação, assumindo propriedades radioativas e até causar algumas formas de câncer.
Aplicações do Radônio: é usado na radioterapia e na composição de cápsulas para aplicação em pacientes com câncer. Para esta última finalidade o gás é obtido a partir do elemento químico radioativo: Rádio (Ra).
Usado em Sismógrafos (verificador de terremotos) [clique em "Cientistas" no índice desta página em Charles Francis Richter - veja a escala de terremotos e ossismógrafos].
UNUNÓCTIO:
Gás inerte sintético (artificial) com propriedades similares aos outros gases de sua família (nobre) principalmente com o Radônio, por isso foi "apelidado" de "eka-radônio" no mundo científico, está sendo estudado e em análise pelos cientistas desde 1999 até 2007, ainda esperando conclusões. Tem Massa Atômica aproximada a 293 u, Número atômico (Z) = 118 (118 prótons), exatamente o que determina seu nome Un = 1; un = 1 e óctio = 8. Sabe-se que é radioativo.
Uma curiosidade de ficção: no universo ficcional de Star Trek: The Next Generation, o episódio Rascals descreveu uma “tabela trans-periódica” contendo o elemento de número 118, denominado "Accurentum".
QUESTÕES RESOLVIDAS
182) “Os gases nobres possuem na última camada .......... elétrons, exceto o Hélio, que só possui .......... elétrons.”
Os espaços acima são corretamente preenchidos pela alternativa:
(A) sete / dois.
(B dois / oito.
(C) seis / um.
(D) oito / dois.
(E) oito / um.
Resolução:
“Os gases nobres possuem na última camada oito elétrons, exceto o Hélio, que só possui dois elétrons.”
Alternativa: D
183) Os gases nobres são os únicos elementos químicos encontrados na natureza na forma de átomos isolados. Isso ocorre porque:
(A) eles são muito estáveis na forma isolada e não possuem a tendência de doar ou receber elétrons.
(B) por serem gasosos, a interação com outros elementos é dificultada.
(C) eles possuem a camada de valência totalmente preenchida com 18 elétrons.
(D)d) por serem extremamente raros, não há ocorrência de outros elementos próximos a eles.
(E) eles não possuem elétrons que possam ser compartilhados ou transferidos, por isso, sua família na Tabela Periódica também é chamada de grupo zero.
Resolução:
Por possuírem a camada de valência totalmente preenchida com oito elétrons (e 2 no caso do hélio que possui apenas a camada K), os gases nobres são muito estáveis e não possuem a tendência de doar ou receber elétrons. Os demais elementos formam compostos químicos, compartilhando, doando ou recebendo elétrons com outros elementos a fim de ficarem com a configuração eletrônica dos gases nobres e assim se tornarem estáveis, em conformidade com o que é dito pela Teoria do Octeto.
Alternativa: A
184) (UFPA) Um átomo, cujo número atômico é 18, está classificado na Tabela Periódica como:
(A) metal alcalino.
(B) metal alcalinoterroso.
(C) metal terroso.
(D) ametal.
(E) gás nobre.
Resolução:
O átomo que possui número atômico 18 possui a seguinte configuração eletrônica em ordem de camadas eletrônicas: 2 – 8 – 8. Se possui oito elétrons na camada de valência, ele é então um gás nobre; no caso, o argônio (Ar).
Alternativa: E
185) (Unisinos-RS) Temos, abaixo, as configurações eletrônicas de alguns elementos no estado fundamental. A configuração eletrônica que corresponde a um gás nobre é:
(A) 1s2 2s2 2p6 3s2 3p6
(B) 1s2 2s2 2p6 3s2 3p6 4s2
(C) 1s2 2s2 2p6 3s2 3p2
(D) 1s2 2s2 2p6 3s2 3p6 4s2 3d10
(E) 1s2 2s2 2p6 3s2 3p3
Resolução:
Basta somar a quantidade de elétrons na última camada, se der 2 ou 8, trata-se de um gás nobre:
a) 1s22s22p6 3s2 3p6 = 2 + 6 = 8 → gás nobre
b) 1s2 2s2 2p6 3s2 3p6 4s2 = 2 → família 2 ou IIA (metais alcalinoterrosos)
c) 1s2 2s2 2p6 3s2 3p2 = 2 + 2 = 4 → família 14 ou IV A (grupo do carbono)
d) 1s2 2s2 2p6 3s2 3p6 4s2 3d10 = 2 → família 12 ou 2B (elemento de transição, pois termina com subnível “d”)
e) 1s2 2s2 2p6 3s2 3p3 = 2 + 3 = 5 → família 15 ou V A (família do nitrogênio)
Outra forma de resolver esse problema é somar todos os elétrons, descobrindo assim o número atômico do elemento e a família a que ele pertence:
a) 1s22s22p6 3s2 3p6 = total de 18 elétrons = argônio (gás nobre)
b) 1s2 2s2 2p6 3s2 3p6 4s2 = total de 20 elétrons = Cálcio (metal alcalinoterroso)
c) 1s2 2s2 2p6 3s2 3p2 = total de 14 elétrons = silício (família 14)
d) 1s2 2s2 2p6 3s2 3p6 4s2 3d10 = total de 30 elétrons = zinco (família 12)
e) 1s2 2s2 2p6 3s2 3p3 = total de 15 elétrons = fósforo (família 15)
Alternativa: A
QUESTÕES RESOLVIDAS SEDUC-SP/2025
01) (Livro do aluno/2025-SEDUC-SP) Um médico verifica a temperatura de um paciente colocando o termômetro na axila. De acordo com seus conhecimentos, responda: por que o médico deve esperar um tempo para retirar o termômetro de seu paciente?
Resolução:
É necessário aguardar para que o termômetro e o corpo do paciente atinjam o equilíbrio térmico.
02) (Livro do aluno/2025-SEDUC-SP) O corpo A apresenta partículas com estado de agitação maior do que as partículas do corpo B. Dessa maneira, podemos afirmar que:
(A) a temperatura dos dois corpos é a mesma.
(B) a temperatura do corpo B é maior que a temperatura do corpo A.
(C) a temperatura do corpo A é maior que a temperatura do corpo B.
(D) as partículas do corpo B apresentam maior energia cinética do que as partículas do corpo A.
(E) o estado de agitação não tem relação alguma com a temperatura.
Alternativa: C
03) (Livro do aluno/2025-SEDUC-SP - ENEM 2012) Em um centro de pesquisa de alimentos, um técnico efetuou a determinação do valor calórico de determinados alimentos da seguinte forma: colocou uma massa conhecida de água em um recipiente termicamente isolado. Em seguida, dentro desse recipiente, foi queimada uma determinada massa do alimento. Como o calor liberado por essa queima é fornecido para a água, o técnico calculou a quantidade de calor que cada grama do alimento libera. Para a realização desse teste, qual aparelho de medida é essencial?
(A) Cronômetro.
(B) Dinamômetro.
(C) Termômetro.
(D) Radiômetro.
(E) Potenciômetro
Alternativa: C
04) (Livro do aluno/2025-SEDUC-SP) Em um dia de verão, o termômetro digital de uma piscina marca a temperatura de 32,2 °C. Qual seria o valor da temperatura na escala Kelvin?
Resolução:
Vamos aplicar a equação de transformação entre as escalas Celsius e Kelvin.
Tc = TK – 273
Devemos substituir o termo referente à escala Celsius por 32,2. Obtém-se, então:
32,2 = TK - 273
Isolando o termo da temperatura em Kelvin:
TK = 32,2 + 273
TK = 305,2 K
05) (Livro do aluno/2025-SEDUC-SP) O zero absoluto (0 K) é a temperatura em que se tem o menor estado de agitação das partículas de um sistema.
Qual é o valor do zero absoluto na escala Celsius?
Resolução:
Vamos aplicar a equação de transformação entre as escalas Celsius e Kelvin.
Tc = TK – 273
Devemos substituir o termo referente à escala Kelvin por 0. Obtém-se, então:
Tc = 0 – 273 °C
Portanto:
Tc = - 273 oC
06) Livro do aluno/2025-SEDUC-SP A temperatura média da superfície do sol é de, aproximadamente, 5772 K.
Qual é o valor dessa temperatura em Celsius?
Resolução:
Vamos aplicar a relação de transformação entre as escalas Celsius e Kelvin: Tc = TK - 273
Devemos substituir o termo referente à escala Kelvin por 5772.
Obtém-se, então:
Tc = 5772 - 273
Tc = 5499 °C
07) (Livro do aluno/2025-SEDUC-SP – ENEM 2021 — Adaptada) A temperatura do argônio nos tanques é TAr = – 184 oC. Usualmente, a grandeza “temperatura”, em física, é expressa na escala Kelvin (K). Sabendo-se que as temperaturas aproximadas do ponto de ebulição (TE) e do ponto de solidificação (TS) da água à pressão atmosférica são, respectivamente, TE ≈ 373 K e TS ≈ 273 K, a temperatura do argônio nos tanques será igual a:
(A) 20 K
(B) 89 K
(C) 189 K
(D) 57 K
Resolução:
TK = Tc + 273
TK = -184 + 273
TK = 89 K
Alternativa: B
08) (Livro do aluno/2025-SEDUC-SP) Numa padaria, o café foi preparado a uma temperatura de, aproximadamente, 95 °C. Porém, ao receber a xícara de café, o cliente esperou um certo tempo para tomá-lo; assim, na escala Fahrenheit, o café atingiu a temperatura de 122 °F.
Assinale a alternativa que corresponda à temperatura, na escala Kelvin, da xícara de café quando o cliente o ingeriu.
(A) 323 K
(B) 359 K
(C) 363 K
(D) 383 K
Resolução:
Primeiramente, vamos fazer a conversão de graus Fahrenheit para graus Celsius. Para isso, iremos utilizar a relação entre essas duas escalas. Assim, temos:
Tc = Tf – 32
5 9
Tc = 122 – 32
5 9
Tc = 50
Agora, aplicaremos a relação de transformação entre as escalas Celsius e Kelvin:
Tc = TK - 273
Tc = TK – 273
TK = 273 + 50
TK = 323 K
09) (Livro do aluno/2025-SEDUC-SP - ENEM 2022 - ) Um menino está ajudando sua mãe na cozinha. Ela lhe pede que tire do fogo uma panela que já estava lá há bastante tempo, em fogo baixo, orientando-lhe que tome cuidado para não se queimar, buscando tocar apenas no cabo de madeira, e não na base de metal da panela. A mãe lhe fez essa recomendação porque o metal, em relação à madeira, apresenta maior:
(A) calor específico.
(B) energia térmica.
(C) temperatura.
(D) condutividade térmica.
(E) coeficiente de dilatação linear
Alternativa: D
10) (Livro do aluno/2025-SEDUC-SP) Uma panela contendo água é levada ao fogão para ser aquecida. Que tipo de processo de transferência de calor está ocorrendo na água da panela e por que isso acontece?
Resolução:
O processo de transferência de calor observado é a convecção térmica. Isso acontece porque a água mais quente, que é menos densa, sobe para a superfície, enquanto a água mais fria, que é mais densa, desce para o fundo da panela, criando correntes de convecção.
11) (Livro do aluno/2025-SEDUC-SP) Por que nos sentimos aquecidos quando ficamos próximos a uma fogueira, mesmo sem tocá-la, e qual processo de transferência de calor está ocorrendo?
Resolução:
Sentimo-nos aquecidos, próximos a uma fogueira, devido ao processo de radiação térmica. A fogueira emite energia por meio de ondas eletromagnéticas (principalmente infravermelho), que se propagam pelo ar e aquecem nosso corpo.
12) (Livro do aluno/2025-SEDUC-SP) Por que a água com tinta azul parece ir para o fundo do recipiente, enquanto a água com tinta vermelha parece se mover para superfície?
Resolução:
Quando aquecemos a água, alteramos sua densidade. Por isso, a água com a tinta vermelha vai subir à superfície, espalhando-se pelo recipiente. Dessa maneira, com a porção de água quente na superfície, a água com corante azul (que está mais fria) tende a descer para o fundo do recipiente, pois sua densidade é maior. Esse é o processo da convecção térmica.
13) (Livro do aluno/2025-SEDUC-SP - ENEM 2021) Na cidade de São Paulo, as ilhas de calor são responsáveis pela alteração da direção do fluxo da brisa marítima que deveria atingir a região de mananciais. Mas, ao cruzar a ilha de calor, a brisa marítima agora encontra um fluxo de ar vertical, que transfere para ela energia térmica absorvida das superfícies quentes da cidade, deslocando-a para altas altitudes.
Dessa maneira, há condensação e chuvas fortes no centro da cidade, em vez de na região de mananciais. A imagem apresenta os três subsistemas que trocam energia nesse fenômeno. No processo de fortes chuvas no centro da cidade de São Paulo, há dois mecanismos dominantes de transferência de calor: entre o Sol e a ilha de calor, e entre a ilha de calor e a brisa marítima.
Esses mecanismos são, respectivamente:
(A) irradiação e convecção.
(B) irradiação e irradiação.
(C) condução e irradiação.
(D) convecção e irradiação.
(E) convecção e convecção.
Alternativa: A
14) (Livro do aluno/2025-SEDUC-SP - UECE 2024) O copo Stanley (copo térmico) consiste em um dispositivo muito comum que pode ilustrar princípios fundamentais da Física relacionados à transferência de calor e ao isolamento térmico. Ele é famoso pelo fato de funcionar como um bom isolante térmico, mantendo as bebidas quentes ou frias por longos períodos de tempo. Sobre as propriedades térmicas do copo Stanley, são feitas as seguintes afirmações:
I - Suas paredes duplas separadas por vácuo ajudam a evitar trocas de calor entre o líquido contido no copo e o meio externo.
II - A corrente de convecção tende a se estabelecer mais facilmente quando o copo contém líquido gelado, sendo necessário o uso de tampa para evitá-la.
III - A superfície interna do copo Stanley é construída com um material que tende a evitar trocas de calor ou irradiação térmica.
É correto o que se afirma somente em:
(A) I e II.
(B) I e III.
(C) II.
(D) III.
Alternativa: B
15) (Livro do aluno/2025-SEDUC-SP - FUVEST 2019) O aquecimento global resulta do seguinte fenômeno: parte daenergia solar incidente sobre a Terra é irradiada de volta ao espaço, sendo bloqueada, em grande parte, por gases de efeito estufa, o que aumenta a temperatura do planeta. As alternativas apresentam:
I - o motivo pelo qual os raios solares conseguem penetrar a atmosfera terrestre, mas, ao serem refletidos, são barrados, em grande parte, pelos gases de efeito estufa;
II - uma das causas diretas do aumento da concentração de gases de efeito estufa na atmosfera.
Os itens I e II estão corretamente indicados em:
(A) I. A energia solar incide na atmosfera em comprimentos de onda menores, e é refletida em comprimentos de onda maiores. Destruição de florestas nativas.
(B) I. A energia solar incide na atmosfera em comprimentos de onda maiores, e é refletida e comprimentos de onda menores. Represamento dos rios para o abastecimento de hidrelétricas.
(C) I. A energia solar incide na atmosfera, e é refletida em ondas de mesmo comprimento. II. Plantio de árvores exóticas no lugar de árvores nativas.
(D) I. A energia solar incide na atmosfera em comprimentos de onda maiores, e é refletida em comprimentos de onda menores. Uso de combustível fóssil.
(E) I. A energia solar incide na atmosfera em comprimentos de onda menores, e é refletida em comprimentos de onda maiores. II. Uso da água dos rios para o abastecimento domiciliar.
Resolução:
Os raios solares conseguem atravessar a atmosfera da Terra, pois ela é relativamente transparente à luz. Quando a luz atinge a superfície terrestre, ocorre a reflexão, gerando ondas eletromagnéticas na faixa do infravermelho, que têm comprimentos de onda maiores do que os da luz visível.
A destruição de florestas nativas provoca a queima ou decomposição da matéria orgânica, resultando na liberação de dióxido de carbono, que é um gás do efeito estufa.
Alternativa: A
16) (Livro do aluno/2025-SEDUC-SP - UDESC 2012) Em um dia típico de verão, utiliza-se uma régua metálica para medir o comprimento de um lápis. Após medir esse comprimento, coloca-se a régua no congelador a uma temperatura de -10 °C e, após 15 minutos, mede-se novamente o lápis. O comprimento medido nesta nova situação será:
(A) maior, porque a régua sofreu uma contração.
(B) menor, porque a régua sofreu uma dilatação.
(C) maior, porque a régua se expandiu.
(D) menor, porque a régua se contraiu.
(E) o mesmo, porque o comprimento do lápis não se alterou.
Alternativa: A
17) (Livro do aluno/2025-SEDUC-SP) Determine o coeficiente de dilatação linear de uma barra metálica de 100 cm de comprimento inicial, que se expandiu 0,016 cm quando foi submetida a uma variação de temperatura de 10 °C.
Resolução:
Vamos aplicar a equação da dilatação linear:
ΔL = L0 ⋅ α ⋅ Δθ
Devemos substituir os termos correspondentes, obtendo:
0,016 = 100 ⋅ α ⋅ 10
Isolando o termo do coeficiente de dilatação linear:
α = 0,016
1000
α = 1,6 . 10-5 ºC-1
18) (Livro do aluno/2025-SEDUC-SP) Uma placa de ferro tem dimensões de 10 cm x 15 cm, em temperatura ambiente de 25 °C. Determine a nova área dessa lâmina, quando colocada em uma temperatura de 225 °C.
Adote β = 2,4 . 10-5 °C-1
Resolução:
Precisamos determinar a área inicial da lâmina, seguindo as dimensões dadas a 25 °C.
A0 = 10 ⋅ 15 = 150 cm2
Vamos calcular agora a variação da área, usando a expressão de dilatação superficial:
ΔA = A0 ⋅ β ⋅ Δθ = 150 ⋅ 2,4 ⋅ 10-5 ⋅ 200 = 0,72 cm2
Para obter a área da placa expandida, fazemos:
ΔA = Af - A0
Af = ΔA + A0
Substituindo pelos valores:
Af = 0,72 + 150 = 150,72 cm2
19) (Livro do aluno/2025-SEDUC-SP) Um bloco cúbico de vidro comum, de 5 cm de aresta, tem sua temperatura elevada de 27 °C para 57 °C. Calcule o volume final do cubo. Adote γ = 2,4 . 10-5 °C-1.
Resolução:
Calculando o V0 = 53 = 125 cm3.
Então,
Vf = V0 + ΔV = V0 + V0 ⋅ γ ⋅ Δθ = V0 ⋅ (1 + γ ⋅ Δθ)
Portanto:
Vf = 125 ⋅ (1 + 2,4 ⋅ 10-5 ⋅ 30)
Vf = 125,09 cm3
20) (Livro do aluno/2025-SEDUC-SP - ENEM 2014) Para a proteção contra curtos-circuitos em residências, são utilizados disjuntores, compostos por duas lâminas de metais diferentes, com suas superfícies soldadas uma à outra, ou seja, uma lâmina bimetálica. Essa lâmina toca o contato elétrico, fechando o circuito e deixando a corrente elétrica passar. Durante a passagem de uma corrente superior à estipulada (limite), a lâmina se curva para um dos lados, afastando-se do contato elétrico e, assim, interrompendo o circuito. Isso ocorre porque os metais da lâmina têm uma característica física cuja resposta é diferente para a mesma corrente elétrica que passa no circuito. A característica física que deve ser observada para a escolha dos dois metais dessa lâmina bimetálica é o coeficiente de:
(A) Dureza.
(B) Elasticidade.
(C) Dilatação térmica.
(D) Compressibilidade.
(E) Condutividade elétrica.
Alternativa: C
21) (Livro do aluno/2025-SEDUC-SP - UFPR 2023) Uma barra metálica retilínea tem um comprimento inicial L0, a uma temperatura T0. O material do qual a barra é feita tem um coeficiente de dilatação linear térmico de valor α = 5 ⋅ 10-6 °C-1. Considerando as informações apresentadas, assinale a alternativa que exiba corretamente o valor da variação de temperatura DT necessária para que essa barra apresente uma variação DL em seu comprimento, igual a 0,2% de seu comprimento inicial.
(A) ΔT = 500 °C
(B) ΔT = 400 °C
(C) ΔT = 300 °C
(D) ΔT = 200 °C
(E) ΔT = 100 °C
Resolução:
Como ∆L = L0 ⋅ α ⋅ ∆θ, e, segundo o enunciado,
∆L = 0,2 . L0
100
podemos escrever:
0,2 . L0 = L0 . 5 . 10-6 ∆θ
00
Portanto,
∆θ = 2 . 10-3
5 . 10-6
∆θ = 400ºC
Alternativa: B
22) (Livro do aluno/2025-SEDUC-SP) Determine a quantidade de calor cedida por um corpo feito de ferro com massa de 1 kg, que é resfriado de 100 °C para 50 °C. Adote o calor específico do ferro igual a 0,11 cal/g °C.
Resolução:
Como o corpo feito de ferro diminui de temperatura, conforme indicado no enunciado, calcularemos a quantidade de calor cedida por ele através da seguinte expressão:
Q = m ⋅ c ⋅ Δθ
É necessário converter a massa de 1 kg para gramas. Assim, temos: 1 kg = 1000 g.
Substituindo os valores na equação, temos:
Q = 1000 ⋅ 0,11 ⋅ (50 - 100)
Q = 110 ⋅ (-50)
Q = -5500 cal
23) (Livro do aluno/2025-SEDUC-SP) Durante uma atividade de campo na praia, estudantes coletaram 10 g de areia em um recipiente e 10 g de água em outro frasco, ambos a 25 °C. As amostras foram aquecidas até atingirem 40 °C. Calcule, para cada uma das amostras, a quantidade de calor necessária para esse aquecimento. Dados: careia = 0,2 cal/g o C; cágua = 1,0 cal/g oC.
Resolução:
Qareia = m ⋅ c ⋅ ∆θ
Qareia = 10 ⋅ 0,2 ⋅ 15 = 30 cal.
Qareia = 30 cal
Qágua = m ⋅ c ⋅ ∆θ
Qágua = 10 ⋅ 1 ⋅ 15
Qágua = 150 cal.
24) (Livro do aluno/2025-SEDUC-SP - ENEM 2013) Aquecedores solares usados em residências têm o objetivo de elevar a temperatura da água até 70 °C. No entanto, a temperatura ideal da água para um banho é de 30 °C. Por isso, deve-se misturar a água aquecida com a água à temperatura ambiente de um outro reservatório, que se encontra a 25 °C.
Qual é a razão entre a massa de água quente e a massa de água fria na mistura para um banho à temperatura ideal?
(A) 0,111
(B) 0,125
(C) 0,357
(D) 0,428
(E) 0,833
Resolução:
Q1 + Q2 = 0
Q1 = - Q2
m1 . cágua . ∆θ1 = - m2 . cágua ∙ ∆θ2
Considerando-se cágua um valor constante, ele pode ser simplificado na equação.
Assim, teremos:
m1 ∙ (θf - θi)1 = - m2 ∙ (θf - θi)2
Substituindo os dados do enunciado, obteremos:
m1 . (30 - 70) = - m2 . (30 - 25)
m1 . (- 40) = - m2 . (5)
m1 = 5
m2 10
m1/m2 = 0,125
Alternativa: B
25) (Livro do aluno/2025-SEDUC-SP - ENEM 2020) Mesmo para peixes de aquário, como o peixe arco-íris, a temperatura da água fora da faixa ideal (26 °C a 28 °C), bem como sua variação brusca, pode afetar a saúde do animal. Para manter a temperatura da água dentro do aquário na média desejada, utilizam-se dispositivos de aquecimento com termostato.
Por exemplo, para um aquário de 50 L, pode-se utilizar um sistema de aquecimento de 50 W otimizado para suprir sua taxa de resfriamento. Essa taxa pode ser considerada praticamente constante, já que a temperatura externa ao aquário é mantida pelas estufas. Utilize para a água o calor específico 4,0 kJ kg-1 K-1 e a densidade 1 kg L-1.
Se o sistema de aquecimento for desligado por 1 h, qual o valor mais próximo para a redução da temperatura da água do aquário?
(A) 4,0 °C
(B) 3,6 °C
(C) 0,9 °C
(D) 0,6 °C
(E) 0,3 °C
Resolução:
- Considerando o exemplo do enunciado, no qual 50 litros de água precisam de um aquecedor de 50 W para manter a temperatura da água no valor desejado, observamos uma relação constante de 1:1 entre a potência e o volume de água.
- Aplicando o mesmo raciocínio à densidade da água, que é, de 1 kg/L, também obtemos uma proporção de 1:1 entre a massa e o volume. Dessa forma, podemos concluir que 1 W de potência é capaz de aquecer 1 kg de água.
- Lembrando que c = 4000J/kg ⋅ K, temos:
P = Q
ΔT
P = m . c. Δθ
ΔT
50 = 50 . 4000 . Δθ
3600
Δθ = 3600
4000
Δθ = 0,9ºC
Alternativa: C
26) (Livro do aluno/2025-SEDUC-SP) Dentro de uma panela, que está sendo aquecida no fogão, há 500 mL de água em ebulição. Calcule a quantidade de calor necessária para vaporizar toda a água, dado que o calor latente de vaporização da água é de 540 cal/g.
Resolução:
QL = m ∙ L
QL = 500 ∙ 540
QL = 270 000 cal
26a) (Livro do aluno/2025-SEDUC-SP)Observe o texto e o gráfico abaixo para responder as questões 27, 28 e 29
Foi feito um estudo da temperatura de um material de 10 g, que estava, inicialmente, no estado sólido, à medida que recebia calor. O resultado do estudo é mostrado no gráfico abaixo.
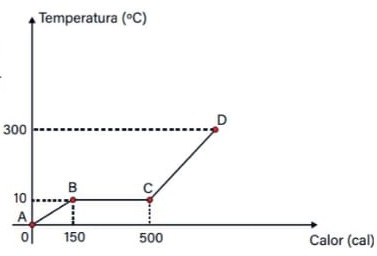
Com base em seus conhecimentos, responda:
27) Qual é o estado físico do material nos segmentos: AB, BC e CD?
Resposta:
AB – Estado sólido
BC – Sólido + líquido
CD – Estado líquido
28) Calcule o calor específico do material em seu estado sólido.
Resposta:
Q= m ∙ c ∙ ∆θ
150 = 100 ∙ c
c = 1,5 cal/g °C
29) Calcule o calor latente de fusão desse material.
Resposta:
QL= m ∙ L
350 = 10 ∙ L
L = 35 cal/g
30) (Livro do aluno/2025-SEDUC-SP - ENEM 2023) Em uma indústria alimentícia, para a produção de doce de leite, utiliza-se um tacho de parede oca, com uma entrada para vapor de água a 120 °C, e uma saída para água líquida, em equilíbrio com o vapor a 100 °C.
Ao passar pela parte oca do tacho, o vapor de água se transforma em líquido, liberando energia.
A parede transfere essa energia para o interior do tacho, resultando na evaporação de água e na consequente concentração do produto.
No processo de concentração do produto, é utilizada energia proveniente:
(A) somente do calor latente de vaporização.
(B) somente do calor latente de condensação.
(C) do calor sensível e do calor latente de vaporização.
(D) do calor sensível e do calor latente de condensação.
(E) do calor latente de condensação e do calor latente de vaporização.
Resolução:
Durante a produção do doce de leite, mencionada no enunciado, a energia utilizada está relacionada a dois processos:
Primeiramente, ocorre o resfriamento do vapor d'água, que passa de 120 °C para 100 °C. Nesse caso, a energia transferida está associada ao calor sensível, pois houve variação de temperatura.
Em seguida, ocorre a condensação do vapor d'água.
Nesse processo, como há uma mudança de estado
físico, a energia transferida está associada ao calor latente.
Alternativa: D
31) (Livro do aluno/2025-SEDUC-SP - ENEM 2012) Para possibilitar a ocorrência do fato observado na tirinha, a partir do menor aquecimento do conjunto, o parafuso e a porca deverão ser feitos, respectivamente, de:

(A) aço e níquel.
(B) alumínio e chumbo.
(C) platina e chumbo.
(D) ouro e latão.
(E) cobre e bronze.
Resolução:
Quanto mais a porca se dilatar em comparação ao parafuso, menor será o aquecimento necessário para soltá-la. Assim, entre os materiais listados, o parafuso deverá ser feito do material com o menor coeficiente de dilatação (platina), enquanto a porca deverá ser feita do material com o maior coeficiente (chumbo).
Alternativa: C
32) (Livro do aluno/2025-SEDUC-SP - ENEM 2016) O quadro apresenta alguns exemplos de combustíveis empregados em residências, indústrias e em meios de transporte.
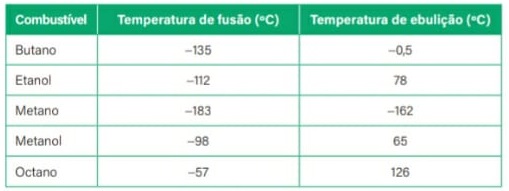
São combustíveis líquidos, à temperatura ambiente de 25 °C:
(A) butano, etanol e metano.
(B) etanol, metanol e octano.
(C) metano, metanol e octano.
(D) metanol e metano.
(E) octano e butano.
Resolução:
Para que o combustível esteja no estado líquido, a temperatura deverá estar entre o ponto de fusão e o ponto de ebulição, ou seja, entre o estado sólido e o gasoso. Analisando a tabela, verificamos que, à temperatura ambiente de 25 °C, apenas o etanol, o metanol e o octano permanecem líquidos.
Alternativa: B
33) (Livro do aluno/2025-SEDUC-SP - ENEM 2023) De acordo com a Constituição Federal, é competência dos municípios o gerenciamento dos serviços de limpeza e de coleta dos resíduos urbanos (lixo). No entanto, há relatos de que parte desse lixo acaba sendo incinerada, liberando substâncias tóxicas no meio ambiente e causando acidentes por explosões – principalmente quando ocorre a incineração de frascos de aerossóis (por exemplo: desodorantes, inseticidas e repelentes). A temperatura elevada provoca a vaporização de todo o conteúdo dentro desse tipo de frasco, aumentando a pressão em seu interior até culminar na explosão da embalagem.
Suponha que um frasco metálico de um aerossol tivesse capacidade igual a 100 mL, contendo 0,1 mol de produtos gasosos à temperatura de 650 °C, no momento da explosão. Considere: R = 0,082 L atm / mol . K.
A pressão, em atm, dentro do frasco, no momento da explosão, é mais próxima de:
(A) 756
(B) 533
(C) 76
(D) 53
(E) 13
Resolução:
Aplicando a equação de Clapeyron, com a temperatura em Kelvin e o volume em litros (L), obtemos:
P = n . R . T
V
P = 0,1 . 0,082 . 923
0,1
P = 76 atm
Alternativa: C
34) (Livro do aluno/2025-SEDUC-SP) No livro Cinco semanas num balão, de Júlio Verne, de 1863, o explorador Samuel Fergusson atravessa o continente africano em um balão de hidrogênio chamado Victoria, que tem um volume de 2500 m3. Considere que o balão, antes da viagem, estivesse completamente vazio, ocupando, portanto, um volume inicial igual a zero. Agora, imagine, como muito fazia o visionário escritor Júlio Verne, que Samuel Fergusson possuía um aparelho semelhante a um compressor de gás hidrogênio, que enchia o balão a uma taxa constante, contra uma pressão atmosférica de 1,0 . 105 Pa.
Calcule o trabalho realizado pelo gás nesse processo.
Resolução:
Basta aplicar a a seguinte expressão.
τ = P ⋅ ∆V = 1 ⋅ 105 ⋅ (2500 - 0)
τ = 2,5 ⋅ 108J
35) (Livro do aluno/2025-SEDUC-SP - FUVEST 2023) Diversos processos na indústria de óleo e gás podem envolver misturas de gases a diferentes temperaturas. Um sistema isolado é composto por dois compartimentos de mesmo volume: o primeiro é ocupado por n1 = 1 mol e o segundo é ocupado por n2 = 2 mols de um gás ideal monoatômico. Inicialmente, cada compartimento encontra-se em equilíbrio térmico, com temperatura T1 = 4T e T2 = T, respectivamente, conforme mostra a figura:
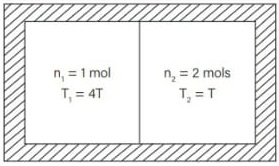
Note e adote: A energia interna de um gás ideal monoatômico é dada por U = 3nRT/2, sendo n o número de mols, R a constante universal dos gases ideais e T a temperatura absoluta.
A partir de certo instante, a parede que separa os compartimentos é removida e, após algum tempo, o sistema atinge uma nova temperatura de equilíbrio Tm. Supondo que não há trabalho realizado após a remoção da parede, nem troca de calor entre o sistema e o ambiente externo, a temperatura de equilíbrio Tm é dada por:
(A) T
(B) 3T/2
(C) 2T
(D) 5T/2
(E) 4T
Resolução:
Aplicando a equação da energia interna para cada um dos gases, temos:
U = 3n . R T
2
U1 = 3 . 1 . R . 4T = 6RT
2
U2 = 3 .2 . R . T = 3RT
2
Agora, igualamos a energia total (soma das energias individuais) à relação envolvendo a temperatura de equilíbrio com o número total de mol (3).
U1 + U2 = 3n . R .Tm
2
9RT = 3 . 3 . R . Tm
2
9T = 9Tm = Tm = 2T
2
Alternativa: C
36) (Livro do aluno/2025-SEDUC-SP - FUVEST 2016) Uma garrafa tem um cilindro afixado em sua boca, no qual um êmbolo pode se movimentar sem atrito, mantendo constante a massa de ar dentro da garrafa, como ilustra a figura.

Inicialmente, o sistema está em equilíbrio à temperatura de 27 °C.
O volume de ar na garrafa é igual a 600 cm3 e o êmbolo tem uma área transversal igual a 3 cm2.
Na condição de equilíbrio, com a pressão atmosférica constante, para cada 1 °C de aumento da temperatura do sistema, o êmbolo subirá aproximadamente:
(A) 0,7 cm
(B) 1,4 cm
(C) 2,1 cm
(D) 3,0 cm
(E) 6,0 cm
Resolução:
V1 = T1
V2 T2
V2 = V1(T1 + 1)
T1
V1 + V1
T1
ΔV = V1
T1
ΔV = 600
300
ΔV = 2 cm3
Sabendo que ΔV = Sêmbolo . Δh 0 7, temos
2 = 3Δh
Δh = 0 7, cm
Alternativa: A
37) (Livro do aluno/2025-SEDUC-SP) Um bloco de gelo, de massa 10 g, inicialmente a -20 ºC, é aquecido até se transformar completamente em água, a 40 ºC. Vamos calcular a quantidade total de calor necessária para essa transformação.
Dados: cgelo = 0,5 cal/g ºC; cágua = 1,0 cal/g ºC; Lfusão = 80 cal/g.
Resolução:
Para calcular a quantidade de calor necessária para transformar 10 g de gelo, inicialmente a -20 °C, em água líquida, a 40 °C, usaremos as fórmulas de calor sensível e latente. Assim, teremos:
QTotal = Q1 + Q2 + Q3
Observe que o gelo deverá receber uma quantidade de calor sensível, variando suatemperatura de -20 °C até 0 °C. Quando atinge essa temperatura, receberá calor latente para mudar de fase. Então, já no estado líquido, subirá até 40 °C. Assim, fazemos:
QTotal = (m ∙ c ∙ ∆θ)gelo + m ∙ LFusão + (m ∙ c ∙ ∆θ) água
QTotal = (10g . 0,5cal/gºC . 20ºC)gelo + 10g . 80cal/g + (1,0g . 10cal/gºC) . 40ºC
QTotal = 100 cal + 800 cal + 400 cal
QTotal = 1300 cal
38) (Livro do aluno/2025-SEDUC-SP) Um gás perfeito sofre uma expansão isobárica sob pressão de 5,0 Pa. Durante essa transformação, seu volume aumenta de 0,20 m³ para 0,60 m³. Calcule a variação de energia interna do gás, sabendo que ele recebeu 5,0 J de calor do ambiente.
Resolução:
Primeiro, calcularemos o trabalho realizado pelo gás durante a expansão isobárica.
Para isso, temos:
τ = P · ΔV
τ = 5 · (0,6 – 0,2)
τ = 5 · (0,4) = 2 J
Agora, vamos calcular a variação da energia interna, considerando que o gás recebeu 5 J de energia na forma de calor. Dessa forma, obtemos:
∆U = Q – τ
∆U = 5 – 2
∆U = 3 J
39) (Livro do aluno/2025-SEDUC-SP) Analise a situação ilustrada na imagem e responda:
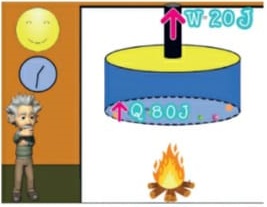
a) A temperatura do sistema aumentou ou diminuiu? Justifique sua resposta, levando em conta a energia recebida ou cedida pelo sistema por meio da realização de trabalho e das trocas de calor com o meio externo.
Resposta:
A temperatura aumentou, porque o sistema recebeu mais energia na forma de calor do que cedeu na forma de trabalho.
b) Qual foi a variação da energia interna?
Resposta:
60 J
40) (Livro do aluno/2025-SEDUC-SP) Analise a situação ilustrada na imagem e responda:
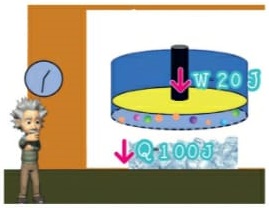
a) A temperatura do sistema aumentou ou diminuiu? Justifique sua resposta, levando em conta a energia recebida ou cedida pelo sistema por meio da realização de trabalho e das trocas de calor com o meio externo.
Resposta:
A temperatura diminuiu porque o sistema cedeu mais energia na forma de calor do que recebeu na forma de trabalho.
b) Qual foi a variação da energia interna?
Resposta:
− 80 J
41) (Livro do aluno/2025-SEDUC-SP) Analise a situação ilustrada na imagem e responda:
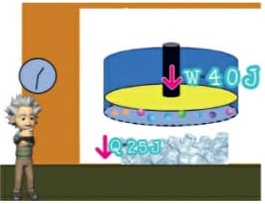
a) A temperatura do sistema aumentou ou diminuiu? Justifique sua resposta, levando em conta a energia recebida ou cedida pelo sistema por meio da realização de trabalho e das trocas de calor com o meio externo.
Resposta:
A temperatura aumentou, pois o sistema recebeu mais energia por meio do trabalho realizado sobre o gás do que cedeu, ao meio externo, pela transferência de energia térmica.
b) Qual foi a variação da energia interna?
Resposta:
15 J
42) (Livro do aluno/2025-SEDUC-SP) Analise a situação ilustrada na imagem e responda:
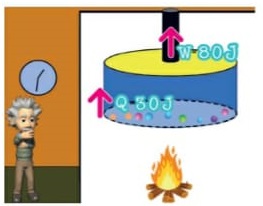
a) A temperatura do sistema aumentou ou diminuiu? Justifique sua resposta, levando em conta a energia recebida ou cedida pelo sistema por meio da realização de trabalho e das trocas de calor com o meio externo.
Resposta:
A temperatura diminuiu, porque o sistema cedeu mais energia na forma de trabalho do que recebeu na forma de calor
b) Qual foi a variação da energia interna?
Resposta:
− 50 J
43) (Livro do aluno/2025-SEDUC-SP) Analise a situação ilustrada na imagem e responda:
a) A temperatura do sistema aumentou ou diminuiu? Justifique sua resposta, levando em conta a energia recebida ou cedida pelo sistema por meio da realização de trabalho e das trocas de calor com o meio externo.
Respostas:
A temperatura diminuiu. Observe que, nesse caso, o sistema não está recebendo energia, mas apenas cedendo ao meio externo, tanto na forma de calor quanto na de trabalho, o que faz que a temperatura diminua.
b) Qual foi a variação da energia interna?
- 120J
44) (Livro do aluno/2025-SEDUC-SP - UNESP 2008) Um recipiente contendo um certo gás tem seu volume aumentado graças ao trabalho de 1664 J realizado pelo gás. Neste processo, não houve troca de calor entre o gás, as paredes e o meio exterior. Considerando que o gás seja ideal, a energia de 1 mol desse gás e a sua temperatura obedecem à relação U = 20,8T, onde a temperatura T é medida em kelvins e a energia U em joules.
Pode-se afirmar que, nessa transformação, a variação de temperatura de um mol desse gás, em kelvins, foi de:
(A) 50
(B) – 60
(C) – 80
(D) 100
(E) 90
Resolução:
Como nenhum calor foi trocado entre o gás e as paredes do recipiente,
podemos dizer que, Q = 0. Dessa forma:
ΔU = − τgás
Vamos escrever a variação da energia interna em
função da variação de temperatura:
ΔU = 20,8 · ΔT
Igualando as equações, temos:
20,8 · ΔT= − τgás
Sabendo que o trabalho realizado pelo gás é de 1664 J, obtemos:
20,8 · ΔT= − 1664 ∴ ΔT= − 80 K
Alternativa: C
45) (Livro do aluno/2025-SEDUC-SP) Um sistema termodinâmico de um gás ideal realiza o ciclo ABCDA, representado adiante. Na imagem, estão indicados os valores dos calores trocados entre o gás e o meio externo. Com base nessas informações, calcule o trabalho realizado pelo gás ou sobre ele no ciclo indicado.
Sabendo que:
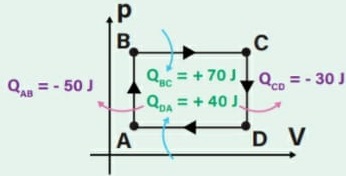
QCiclo = τCiclo ⇒ τCiclo = + 30 J
Resolução:
Para calcular a quantidade total de calor trocada no ciclo, basta realizar a soma algébrica da quantidade referente a cada etapa. Dessa forma, teremos:
Qciclo = QAB + QBC+ QCD + QDA
Qciclo = – 50 J + 70 J – 30 J + 40 J
Qciclo = + 30 J
46) (Livro do aluno/2025-SEDUC-SP - FUVEST 2019) No diagrama P x V da figura, A, B e C representam transformações possíveis de um gás entre os estados I e II.
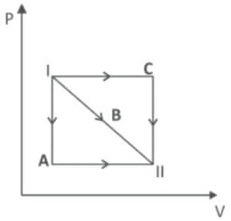
Em relação à variação ΔU da energia interna do gás e ao trabalho W por ele realizado, entre esses estados, é correto afirmar que:
(A) ΔUA = ΔUB = ΔUC e WC > WB > WA
(B) ΔUA > ΔUC > ΔUB e WC = WA < WB
(C) ΔUA < ΔUB < ΔUC e WC > WB > WA
(D) ΔUA = ΔUB = ΔUB e WC = WA > WB
(E) ΔUA > ΔUB > ΔUC e WC = WB = WA
Resolução:
O diagrama P-V nos mostra que os estados iniciais (I) e final (II) do gás são os mesmos para as três transformações. Dessa maneira, podemos concluir que: ∆UA = ∆UB = ∆UC
Para comparar os trabalhos realizados pelo gás nos três caminhos, analisaremos as áreas sob as curvas.
Como: AC > AB > AA → WC > WB > WA.
Alternativa: A
47) (Livro do aluno/2025-SEDUC-SP - UNIFESP/EPM 2004) O diagrama PV da figura mostra a transição de um sistema termodinâmico de um estado inicial A para o estado final B, segundo três caminhos possíveis.
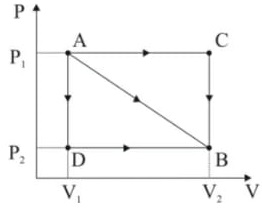
O caminho pelo qual o gás realiza o menor trabalho e a expressão correspondente são, respectivamente:
(A) A → C → B e P1 (V2 − V1).
(B) A → D → B e P2 (V2 − V1).
(C) A → B e (P1 + P2) (V2 − V1)/2.
(D) A → B e (P1 − P2) (V2 − V1)/2.
(E) A → D → B e (P1 + P2) (V2 − V1)/2.
Resolução:
O menor trabalho realizado pelo gás corresponde ao caminho no qual a área sob o gráfico P x V é menor.
Assim, A → D → B é o caminho de menor trabalho.
τADB = τAD + τDB
τADB = 0 + P2(V2 − V1)
τADB = P2 (V2 − V1)
Alternativa: B
48) (Livro do aluno/2025-SEDUC-SP) Uma amostra de 50 g de um gás ideal recebe calor de modo que sua temperatura varia de 300 K para 380 K. Sabendo que este gás está em um recipiente que não permite a variação de seu volume e que os calores específicos sob pressão e volume constantes são, respectivamente, 0, 32cal / (g.K) e 0, 25cal /g.K , calcule a variação de energia interna desse gás.
Resolução:
Para calcular a variação da energia interna, vamos recorrer à 1ª lei da termodinâmica:
∆U = Q ‑ τ
O enunciado nos indica que o aquecimento é isovolumétrico, ou seja, não há variação de volume e, consequentemente,
t = 0
O calor total trocado nesse aquecimento será dado por:
Q = m . c . ΔT
Q = 50 . 025 (380 – 300) 1000 cal
Logo,
∆U = Q ‑ τ = Q = 1000 al
49) (Livro do aluno/2025-SEDUC-SP) Um gás ideal monoatômico passa por dois processos distintos para elevar sua temperatura em 10 °C. No primeiro processo, ele é aquecido sob volume constante e, no segundo, sob pressão constante. Sabe-se que o calor específico molar sob volume constante para um gás ideal monoatômico é cv = 12,5J/mol.K . Qual é a quantidade de calor necessária para o aquecimento sob pressão constante, sabendo-se que R = 8,31 J/mol.K e que a amostra tem 1 mol?
(A) 83,1 J
(B) 125 J
(C) 166 J
(D) 208 J
(E) 303 J
Resolução:
Aplicamos a relação a seguir para calcular o calor específico sob pressão constante:
cp = cv + R
cp = 12,5 + 8,31
cp = 20,81 J/mol.K
Agora, calculamos a quantidade de calor utilizando a relação:
Q = n . cp . ∆θ
Q = 1 . 20, 81 . 10
Q = 208,1 J
Alternativa: D
50) (Livro do aluno/2025-SEDUC-SP - UECE 2022) Um estudante de Física observou, em laboratório, que, ao fornecer 100 cal a uma amostra contendo 2 moles de um gás ideal, sua temperatura variava em 5 °C, desde que a pressão durante o processo fosse mantida constante. Em um segundo momento, o estudante optou por manter o volume da amostra constante durante o referido processo, ao invés da pressão. Neste caso, para a mesma variação de temperatura, a quantidade de calor necessária seria:
Considere a constante universal dos gases R = 2 cal/(mol · K).
(A) 100 cal
(B) 80 cal
(C) 50 cal
(D) 200 cal
Resolução:
Com as informações fornecidas, podemos determinar o calor específico molar sob pressão constante desse gás:
Qp = n · Cp · ΔT
100 = 2 · Cp · 5
Cp = 10 cal/(mol · K)
Precisamos agora calcular o calor trocado sob volume constante (Qv). Para isso vamos recorrer, primeiro, à relação de Mayer:
Cp – Cv = R
10 – Cv = 2
Cv = 8 cal/(mol · K)
Sabendo-se o valor do calor específico molar sob volume constante (Cv), o calor trocado sob volume constante (Qv) será:
Q = n · Cv · ΔT
Q = = 2 · 8 · 5
Q = 80 cal
Alternativa: B
51) (Livro do aluno/2025-SEDUC-SP - ENEM 2011) Um motor só poderá realizar trabalho se receber uma quantidade de energia de outro sistema. No caso, a energia armazenada no combustível é, em parte, liberada durante a combustão para que o aparelho possa funcionar. Quando o motor funciona, parte da energia convertida ou transformada na combustão não pode ser utilizada para a realização de trabalho. Isso significa dizer que há vazamento da energia em outra forma.
De acordo com o texto, as transformações de energia que ocorrem durante o funcionamento do motor são decorrentes de a:
(A) liberação de calor dentro do motor ser impossível.
(B) realização de trabalho pelo motor ser incontrolável.
(C) conversão integral de calor em trabalho ser impossível.
(D) transformação de energia térmica em cinética ser impossível.
(E) utilização de energia potencial do combustível ser incontrolável.
Resolução:
A segunda lei da termodinâmica estabelece que nenhuma máquina térmica pode chegar a um rendimento de 100%, portanto a transformação integral de calor em trabalho é impossível.
Alternativa: C
52) (Livro do aluno/2025 - ENEM 2016) Até 1824 acreditava-se que as máquinas térmicas, cujos exemplos são as máquinas a vapor e os atuais motores a combustão, poderiam ter um funcionamento ideal. Sadi Carnot demonstrou a impossibilidade de uma máquina térmica, funcionando em ciclos entre duas fontes térmicas (uma quente e outra fria), obter 100% de rendimento. Tal limitação ocorre porque essas máquinas:
(A) realizam trabalho mecânico.
(B) produzem aumento da entropia.
(C) utilizam transformações adiabáticas.
(D) contrariam a lei da conservação de energia.
(E) funcionam com temperatura igual à da fonte quente.
Resolução:
De acordo com o ciclo de Carnot, na segunda lei da termodinâmica, uma máquina térmica não consegue obter 100% de rendimento porque produz aumento da entropia em razão da perda de energia para o aquecimento do motor, ruídos, vibrações etc.
Alternativa: B
53) (Livro do aluno/2025-SEDUC-SP - UPE 2016) Com base nas Leis da Termodinâmica, analise as afirmativas a seguir:
I Existem algumas máquinas térmicas que, operando em ciclos, retiram energia, na forma de calor, de uma fonte, transformando-a integralmente em trabalho.
II Não existe transferência de calor de forma espontânea de um corpo de temperatura
menor para outro de temperatura maior.
III Refrigeradores são dispositivos, que transferem energia na forma de calor de um sistema de menor temperatura para outro de maior temperatura.
Está(ão) CORRETA(S):
(A) apenas I.
(B) apenas II.
(C) apenas I e III.
(D) apenas II e III.
(E) I, II e III.
Alternativa: D
54) (Livro do aluno/2025-SEDUC-SP - ENEM 2009) A invenção da geladeira proporcionou uma revolução no aproveitamento dos alimentos ao permitir que fossem armazenados e transportados por longos períodos.
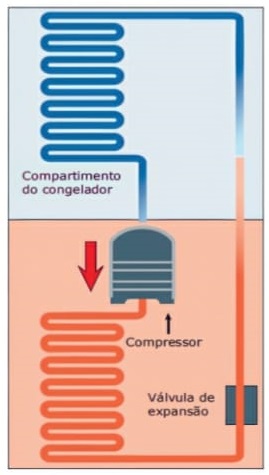
A figura apresentada ilustra o processo cíclico de funcionamento de uma geladeira, em que um gás no interior de uma tubulação é forçado a circular entre o congelador e a parte externa da geladeira. É por meio dos processos de compressão, que ocorre na parte externa, e de expansão, que ocorre na parte interna, que o gás proporciona a troca de calor entre o interior e o exterior da geladeira.
Nos processos de transformação de energia envolvidos no funcionamento da geladeira:
(A) a expansão do gás é um processo que cede a energia necessária ao resfriamento da parte interna da geladeira.
(B) o calor flui de forma não espontânea da parte mais fria, no interior, para a mais quente, no exterior da geladeira.
(C) a quantidade de calor cedida ao meio externo é igual ao calor retirado da geladeira.
(D) a eficiência é tanto maior quanto menos isolado termicamente do ambiente externo for o seu compartimento interno.
(E) a energia retirada do interior pode ser devolvida à geladeira abrindo-se a sua porta, o que reduz seu consumo de energia.
Resolução:
Vamos analisar as alternativas individualmente:
a) Está incorreta. Para ser resfriado, a expansão deve retirar calor do gás.
b) Está correta.
c) Está incorreta. A quantidade de calor cedida ao meio externo está relacionada ao calor retirado da fonte fria e ao trabalho realizado.
d) Está incorreta. A eficiência está relacionada apenas ao calor retirado da fonte fria e ao trabalho, não havendo relação com o isolamento.
e) Está incorreta. O calor enviado ao meio externo se dissipa, não podendo ser aproveitado novamente.
Alternativa: B
55) (Livro do aluno/2025-SEDUC-SP - UFF 2002) O esquema a seguir representa o ciclo de operação de determinada máquina térmica cujo combustível é um gás. Quando em funcionamento, a cada ciclo, o gás absorve calor (Q1) de uma fonte quente, realiza trabalho mecânico (W) e libera calor (Q2) para uma fonte fria, sendo a eficiência da máquina medida pelo quociente entre W e Q1.
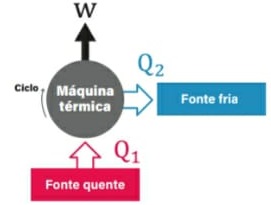
Uma dessas máquinas, que, a cada ciclo, realiza um trabalho de 3,0 × 104 J com uma eficiência de 60%, foi adquirida por certa indústria. Em relação a essa máquina, conclui-se que os valores de Q1, de Q2 e da variação da energia interna do gás são, respectivamente:
(A)1,8 × 104 J; 5,0 × 104 J; 3,2 × 104 J
(B) 3,0 × 104 J; zero; zero
(C) 3,0 × 104 J; zero; 3,0 × 104 J
(D)5,0 × 104 J; 2,0 × 104 J; zero
(E) 5,0 × 104 J; 2,0 × 104 J; 3,0 × 104 J
Resolução:
Para calcular o valor de Q1, utilizaremos a expressão do rendimento de uma máquina térmica. Assim, temos:
η = W = 0,6
Q1
0,6 = 3 . 104
Q1
Q1 = 3 . 104
0,6
Q1 = 2,0 . 104 J
Para calcular o valor de Q2, faremos:
W = Q1 – Q2 ⇒ 3 ⋅104 J = 5 0 104 , ⋅ J – Q2
Q2 = 2,0 ⋅ 104 J
Conforme visto na teoria, em todo ciclo termodinâmico, a variação da energia interna é nula, ou seja, ∆U.
Alternativa: D
56) (Livro do aluno/2025-SEDUC-SP - MACKENZIE 2019 – Adaptada) A segunda lei da termodinâmica afirma, em sucintas palavras, que não há a possibilidade de converter integralmente calor em trabalho. Esquematicamente, a figura abaixo revela como funciona uma máquina térmica.
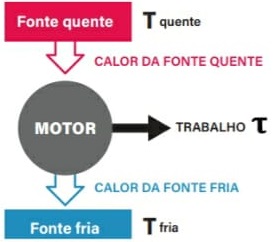
Considerando-se que o trabalho realizado nessa máquina valha 1,2 kJ e que a parte energética rejeitada para a fonte fria valha dois quintos da recebida da fonte quente, é correto afirmar que o rendimento da máquina retratada na figura e a parte energética rejeitada (em kJ) valem, respectivamente:
(A) 40% e 1,2
(B) 60% e 0,80
(C) 40% e 1,0
(D) 60% e 1,2
(E) 40% e 0,60
Resolução:
Podemos escrever que: Qf = 2. Então, o trabalho será dado por: τ = Qq - 2 . Qq.
5 5
Substituindo: 1,2 = 3 . Qq
5
Qq = 2KJ
Qf = 2 . 2 = 0,8KJ
5
O rendimento será: η = τ
η = 1,2
2
η = 0,6 ou 60%.
Alternativa: B
57) (Livro do aluno/2025-SEDUC-SP - AFA 2024) A figura a seguir representa trocas de calor e realização de trabalho em uma máquina térmica. Nela, estão indicados os valores da temperatura T1 e da quantidade de calor cedido Q1 , relativos à fonte quente, e do trabalho τ realizado por essa máquina. Além disso, tem-se que T2 e Q2 correspondem, respectivamente, à temperatura e à quantidade de calor rejeitada para a fonte fria.
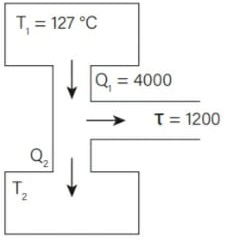
Seu rendimento corresponde a 75% do rendimento da máquina de Carnot em regime de funcionamento entre as temperaturas T1 e T2. Nessas condições, a temperatura T2, da fonte fria é, em Kelvin:
(A) 100
(B) 240
(C) 613
(D) 513
Resolução:
Podemos escrever:
ηM = 3 . ηcarnot
4
O cálculo do rendimento da máquina é feito por meio da fórmula:
ηM = τ = 1200 = 3
Q1 4000 10
Obtendo o rendimento da máquina de Carnot:
ηcarnot = 4 . 3 = 2
3 10 5
Agora, obtemos a temperatura:
2 = 1 – T2
5 400
T2 = 3
400 5
T2 = 240K
Alternativa: B
58) (Livro do aluno/2025-SEDUC-SP - UNCISAL 2019) Na geladeira doméstica, o fluido de trabalho (fréon) opera em ciclos, transportando energia térmica. A figura a seguir ilustra de forma simplificada as trocas de calor envolvidas no funcionamento de uma geladeira. Na saída para a parte externa, o fréon é comprimido, recebe energia na forma de trabalho (W) e atinge uma temperatura elevada. Na serpentina, o fréon libera calor para o ambiente (Qamb) e, ao retornar para o interior, sofre uma expansão rápida, com grande queda de temperatura. Dessa maneira, o fréon torna-se capaz de retirar calor do interior da geladeira (Qint) antes de retornar ao compressor, realizando, assim, um ciclo completo.
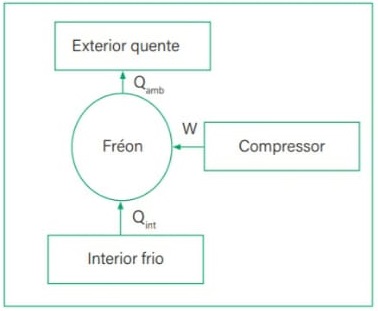
No processo de funcionamento de uma geladeira:
(A) a temperatura média do ambiente externo à geladeira diminuirá se sua porta permanecer aberta.
(B) a variação da energia em seu interior é diferente de zero em um ciclo completo.
(C) a quantidade de calor Qamb é superior à quantidade de calor Qint.
(D) a quantidade de calor Qamb é igual à quantidade de trabalho W.
(E) o calor flui espontaneamente de seu interior para o exterior.
Resolução:
A quantidade de calor liberada ao ambiente é maior do que a quantidade interna da geladeira.
Alternativa: C
59) (Livro do aluno/2025-SEDUC-SP - PUCRS 2023) A figura abaixo representa o diagrama pV de um 1 mol de um gás ideal, retratando diferentes processos termodinâmicos. Com base no diagrama, é correto afirmar que:
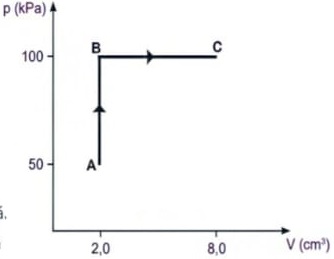
(A) em A → B a temperatura dogás aumentará.
(B) em B → C a temperatura do gás diminuirá.
(C) a temperatura em C é igual à temperatura em A.
(D) a temperatura se mantém constante durante A → B → C.
Resolução:
Vamos analisar as alternativas individualmente:
a) Está correta, pois, como a transformação é isovolumétrica, ao aumentarmos a pressão exercida sobre o gás, a temperatura do gás aumentará.
b) Está incorreta, uma vez que se trata de uma transformação isobárica com aumento de volume, o que resulta em elevação de temperatura.
c) Está incorreta, pois a temperatura em A é menor do que a temperatura em C.
d) Está incorreta, já que a temperatura se altera no decorrer do ciclo.
Alternativa: A
60) (Livro do aluno/2025-SEDUC-SP - CEDERJ 2022) Em uma etapa do ciclo executado por um gás ideal em um aparelho de ar-condicionado, a pressão do gás é aumentada, mantendo o seu volume constante. Nessa etapa do ciclo, o trabalho W realizado pelo gás, a quantidade de calor Q absorvida por ele e a variação ΔT da sua temperatura são, respectivamente:
(A) W < 0, Q < 0 e ΔT < 0
(B) W = 0, Q > 0 e ΔT > 0
(C) W = 0, Q = 0 e ΔT = 0
(D) W > 0, Q > 0 e ΔT > 0
Resolução:
Como o volume é mantido constante, trata-se de uma transformação isovolumétrica; assim, o trabalho realizado (W) é igual a zero.
O fato de o trabalho ser zero implica que a variação da energia interna é igual ao calor trocado com o ambiente.
Como a variação da energia interna se relaciona com a variação da temperatura, percebemos que tanto ela quanto a quantidade de calor devem ser maiores que zero.
Alternativa: B
61) Uma máquina frigorífica retira da fonte fria 35 J de calor e transfere para o exterior 40 J de calor, a cada ciclo. Calcule:
a) o trabalho realizado pelo compressor a cada ciclo é:
Resolução:
O trabalho da máquina frigorífica é a diferença entre o calor direcionado à fontequente (Qq) e o calor retirado da fonte fria (Qf).
τ = Qq − Qf
τ = 40 − 35
τ = 5 J
b) a eficiência da máquina frigorífica.
Resolução:
A eficiência é dada pela razão entre a quantidade retirada da fonte fria e o trabalhorealizado no ciclo.
e = Qf /τcilco
e = 35
5
e = 7
62) (Livro do aluno/2025-SEDUC-SP - UPE 2016) Um refrigerador foi construído, utilizando-se uma máquina de Carnot cuja eficiência, na forma de máquina de calor, é igual a 0,1. Se esse refrigerador realiza um trabalho de 10 J, é CORRETO afirmar que a quantidade de calor removida do reservatório de menor temperatura foi, em joules, de:
(A) 100
(B) 99
(C) 90
(D) 10
(E) 1
Resolução:
Da equação do rendimento de uma máquina térmica, temos que
η = τ
Assim, temos que
τ = Qq – Qf
Logo, o calor retirado da fonte fria é de
10 = 100 - Qf
Qf = 90 J
Alternativa: C
63) (Livro do aluno/2025-SEDUC-SP - UFRGS 2020) Uma máquina de Carnot apresenta um rendimento de 40%, e a temperatura de sua fonte quente é 500 K. A máquina opera a uma potência de 4,2 kW e efetua 10 ciclos por segundo. Qual é a temperatura de sua fonte fria e o trabalho que a máquina realiza em cada ciclo?
(A) 200 K – 42 J
(B) 200 K – 420 J
(C) 200 K – 42 000 J
(D) 300 K – 42 J
(E) 300 K – 420 J
Resolução:
Primeiramente, vamos obter a temperatura da fonte fria a partir da equação do rendimento:
η = 1 – TF
Tq
0,4 = 1 – Tf
Tq
Tf = 300k
A temperatura da fonte fria é de 300 K. A partir da potência (4,2 kW) e do tempo de duração do ciclo (10 ciclos por segundo) podemos obter o trabalho.
10 ciclos = 1s
1 ciclo = x
x = 0,1s.
Utilizando a fórmula da potência.
P = τ
Δt
4200 = τ
0,1
τ = 420 J
Alternativa:
64) (Livro do aluno/2025-SEDUC-SP - UEMG 2017) Uma máquina térmica que opera segundo o ciclo de Carnot executa 10 ciclos por segundo. Sabe-se que, em cada ciclo, ela retira 800 J da fonte quente e cede 400 J para a fonte fria. Se a temperatura da fonte fria é igual a 27 °C, o rendimento dessa máquina e a temperatura da fonte quente valem, respectivamente:
(A) 20%; 327 K
(B) 30%; 327 K
(C) 40%; 700 K
(D) 50%; 600 K
Resolução:
Vamos transformar o valor da temperatura da fonte fria para a temperatura Kelvin:
Tq = 27 + 273 = 300 K
Agora, substituímos os valores do enunciado na seguinte relação:
Qq = Tq
Qf Tf
800 = Tf
400 300
Tq = 600 K
Agora calculamos o rendimento:
η = 1 – Tf
Tq
η = 1 – 300
600
η = 0,6 0u 50%
Alternativa: D
65) (Livro do aluno/2025-SEDUC-SP - (UECE 2015) O biodiesel é um combustível biodegradável que pode ser produzido a partir de gorduras animais ou óleos vegetais. Esse combustível substitui total ou parcialmente o óleo diesel de petróleo em motores de ciclo diesel automotivos.
Considere que a queima de 1,0 g de biodiesel libera x Joules de energia e o rendimento do motor é de 15%. Qual o trabalho mecânico realizado pelo motor, em Joules, resultante da queima de 10 g desse combustível?
(A) 1,5x/100
(B) 150x/10
(C) 15x/100
(D) 15x/10
Resolução:
O rendimento de uma máquina térmica é calculado por: η = τ
Qtotal
Substituindo o valor do rendimento dado na fórmula para a queima de 1 g teremos,
15% = τ1g
x
τ1g = 0,15x
Para queimar 10 g de combustível, teremos que o trabalho total é
τ10g = 10 . t1g
Logo,
τ10g = 10 . (0,15x) = 1,5x
Multiplicando-se divisor e numerador por 10,
τ10g = 1,5x = 15x
1 10
Alternativa: D
Continua...










